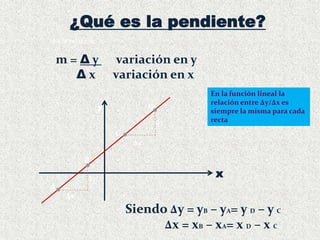
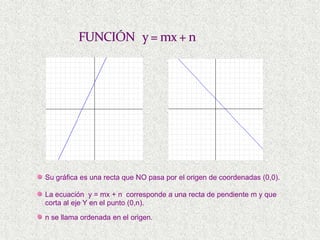
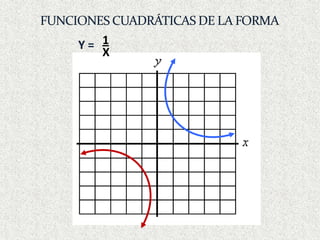
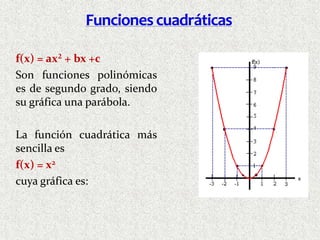
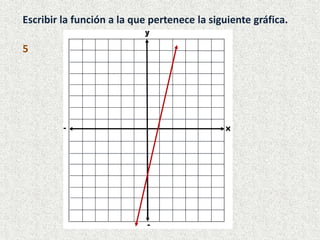
1) El documento habla sobre funciones lineales y cuadráticas, explicando conceptos como pendiente, ordenada al origen, y cómo graficar estas funciones. 2) Se incluyen ejemplos de funciones lineales de la forma y=mx+b y funciones cuadráticas de la forma y=ax2+bx+c. 3) También se presentan actividades para que el estudiante grafique diferentes funciones lineales y cuadráticas.

1. FUNCIONES LINEALESESC. SEC. ING. JORGE L. TAMAYOPROFESOR: C. JOEL VIVEROS JUAREZMATEMATICAS SEGUNDO GRADO

2. Cuando recibes la factura de tu celular, podéis ver que el abono que pagarás a fin de mes está formado por un valor fijo y otro variable que depende de la cantidad de minutos que hablaste.Cantidad fija = $18Cantidad variable = $0,20 cada minuto Con esta información podemos encontrar la relación entre los minutos que hablamos y el costo a pagar.

3. En primer lugar debemos ponernos de acuerdo sobre cuáles son las variables.t: es la letra con la que identificaremos el tiempo que vamos a hablar, es decir, la cantidad de minutos que usaremos el teléfono.El costo, por supuesto, depende del tiempo que hablamos.EL COSTO DEPENDEDEL TIEMPO

4. Es por esto que el costo es la variable dependiente Y el tiempo es la variable independiente.(t) Veamos algunos casos en particular:Si t = 42 minutosC = $0,20•42 +$18 C = $8,4 + $18 C = $26,40Si t = 50 minutos C = $0,20•50+$18 C = $28C = $10 + $18 Si t = 120 minutos C = $0,20•120+$18 C =$24 + $18 C = $42

5. Generalizando:Costo C= 0,20.t + 18(donde t son los minutos hablados)Esto que acabamos de encontrares la fórmula matemáticapara relacionar tiempo con costoen nuestra factura telefónica.

6. La característica particular que tienen las funciones linealeses que a variaciones iguales de x, corresponde siemprela misma variación en y.y8642x-2012-1Cada vez que x aumenta 1y aumenta 2

7. Veamos otros ejemplos:yEs función lineal432x123Si x aumenta 1, ydisminuye 1 y disminuye de 4 a 3x aumenta de 1 a 2y disminuye de 3 a 2x aumenta de 2 a 3

8. Se llama función lineal a la relación entre variablestal que su expresión sea:y = m x + bDónde m: pendienteb: ordenada al origen

9. ¿Qué es la pendiente?Es la relación:m = Δ y variación en yΔ x variación en x En la función lineal la relación entre ∆y/∆x es siempre la misma para cada rectaDy∆yC∆xBx∆yA∆xSiendo Δy = yB – yA= y D – y CΔx = xB – xA= x D – x C

10. En las funciones linealesexiste una relación entre lavariación de la variable independiente xy la variable dependiente y,que se mantiene constante.A esa relación se la llama pendiente

11. ¿Qué es la ordenada al origen?En la forma explícita de la recta, el término independiente, indica el lugar donde la gráfica de la recta corta al eje Y,yEje de ordenadasy=mx+bbEje de abscisasx

12. yy = m x + b(Forma explícita)bxraízm: pendienteb: ordenada al origen

13. La pendiente m se asocia a la inclinaciónde la rectayym -m +xx

14. "Un padre que estuvo observando desde el balcón a su hijo Alberto como iba al colegio:- De casa salió a las 8.30 y fue seguidito hasta casa de su amigo Tomás. Lo esperó un rato sentado en el banco y luego se fueron juntos, muy despacio, hacia el colegio. Cuando ya estaban llegando, mi hijo se dio cuenta de que había dejado la cartera en el banco; volvió corriendo, la recogió y llegó a la escuela a las 9 en punto."

15. 7.- Un ciclista decide salir de ruta y durante un tiempo pedalea por un camino hasta que llega a una zona de descanso en donde se para para comer. A continuación, sigue avanzando durante otro rato más, momento en que decide volver a casa por el mismo camino que había elegido para la ida.

17. ACTIVIDADES: Observando la gráfica anterior, responde: ¿A cuántos kilómetros de su casa decide parar a comer? ¿Qué tiempo había transcurrido cuando decide esa parada? ¿Cuánto tiempo ha estado comiendo? ¿Cuánto tarda en volver a casa desde que decide regresar? ¿En qué momento de la ida tenía el camino una pendiente más pronunciada? ¿Durante qué franja de tiempo pedaleó a más velocidad el ciclista? ¿Cuántos kilómetros ha recorrido entre la ida y la vuelta?

18. CÓMO GRAFICAR UNA RECTASupongamos que queremos graficar la recta: Existen varias formas de hacerlo:Utilizando una tabla de valoresB)Ubicando la ordenada al origen y usando el concepto la pendiente

19. A - Utilización de la tabla de valores En este caso vamos a asignarle valores a la variable x, reemplazamos en la función, y obtenemos el valor de la variable y. Con estos valores formamos puntos (x;y) que luego ubicamos sobre el sistema de ejes cartesianos. Veamos como hacerlo: Vamos a graficar la recta tomo valores de x (los que quiera), y los reemplazo en la función:x-3-10 13

20. Los valores obtenidos, los ubico en un sistema de ejes cartesianos:yx

21. ACTIVIDAD 1EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Una gráfica por ejercicioY = 2X – 3 X = {1, 2, 3, 4, 5}1Y = 3X + 2 X = {1, 2, 3, 4, 5}23Y = 4X – 1 X = {1, 2, 3, 4, 5}4Y = X + 2 X = {1, 2, 3, 4, 5}Y = X – 5 X = {1, 2, 3, 4, 5}5

22. ACTIVIDAD 2EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un mismo plano cartesiano para las 3 gráficasy = 2X – 5Y = 2X – 1Y = 2X + 3X = { – 3, – 2, – 1, 0, 1, 2, 3, 4, 5}12y = – 2X – 3Y = – 2X + 2Y = – 2X + 5X = { – 3, – 2, – 1, 0, 1, 2, 3, 4, 5}

23. ACTIVIDAD 3EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un mismo plano cartesiano para las 3 gráficasy = – 2X – 2y = X – 2Y = 4X – 2 X = { – 3, – 2, – 1, 0, 1, 2, 3, 4, 5}12y = – 3X + 3Y = – X + 3Y = 3X + 3X = { – 3, – 2, – 1, 0, 1, 2, 3, 4, 5}

24. ACTIVIDAD 4EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un mismo plano cartesiano para las 3 funcionesFUNCIONES DE LA FORMA y = mx + bY = 3x -4 Y = 3x Y = 3x + 3y = - 3x – 2y = x - 2 y = 2x - 2y = -2x + 5y = -2x +1y = -2x – 3x={ -3, -2, -1, 0, 1, 2, 3}

25. Cómo hallar la ecuación de una rectaSupongamos que conozco dos de lospuntos por donde pasa una recta:P1 (2; 4) P2 (-1; -3)yY quiero conocer la ecuación de lafunción lineal4y = m x + b-1Voy a mostrar dos formas para encontrarla:xMétodo A2Método B-3

26. Método A:Sé que la recta debe incluir a los puntosP1 (2;4)P2 (-1;-3)reemplazo entonces por ambos puntos en la fórmula de la recta , y = m x + b, ubicando el primer valor del par en x y el segundo en y(2;4) 4 = m . 2 + b 4 = 2 m + b Ecuación I(-1;-3) -3 = m. (-1) + b - 3 = -m + b Ecuación II despejo b de ecuaciónIIb = -3 +m Ecuación III Reemplazo en ecuaciónI

27. Continuación:4 = 2 m + (- 3 + m)4 = 2 m - 3 + m4 + 3 = 2 m + m7 = 3 m7 : 3 = mreemplazo en ecuaciónIIISiCon lo que queda:

28. Método B:P1 (2; 4)P2 (-1;-3)Sé que la recta debe incluir a los puntos:También sabemos que la pendiente “m” es la variación en y sobre la variación en xóReemplazo con los valores de los puntos:Con lo que la ecuación quedaría:ITodavía falta conocer el valor de b, para hacerlo puedo usar alguno de los puntos que tenia como dato, reemplazando en el x e y de la expresión I, usaré el (2;4):Con lo que resulta:

29. FUNCIÓN y = mx + nSu gráfica es una recta que NO pasa por el origen de coordenadas (0,0).La ecuación y = mx + n corresponde a una recta de pendiente m y que corta al eje Y en el punto (0,n).n se llama ordenada en el origen.

30. Escribir la función a la que pertenece la siguiente gráfica.

31. Escribir la función a la que pertenece la siguiente gráfica.1

32. Escribir la función a la que pertenece la siguiente gráfica.2

33. Escribir la función a la que pertenece la siguiente gráfica.3

34. Escribir la función a la que pertenece la siguiente gráfica.4

35. Escribir la función a la que pertenece la siguiente gráfica.5

36. Funciones cuadráticas

37. FUNCIONES CUADRÁTICASLa grafica es una parábola

38. Funciones cuadráticasf(x) = ax² + bx +c Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.La función cuadrática más sencilla esf(x) = x2cuya gráfica es:

39. ACTIVIDAD 5EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un mismo plano cartesiano para las 3 funcionesFUNCIONES DE LA FORMA y = ax2 + bY = x2 + 4 Y = x2 + 1 Y = x2 – 2 y = x2y = 2x2y = 3x2y = – x2 + 3y = – x2 + 1y = – x2 – 3x={ -3, -2, -1, 0, 1, 2, 3}

40. FUNCIONES CUADRÁTICAS DE LA FORMA

41. ACTIVIDAD 6EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un mismo plano cartesiano para las 3 funcionesFUNCIONES DE LA FORMA y = (x2 + b)Y = (x + 4)2 Y =(x + 1)2 Y =(x – 2)2y = (x + 5)2y = (x + 3)2y = (x – 4)2y = (x + 2)2y = (x – 1)2y = (x2 – 3)

42. ACTIVIDAD 7EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un mismo plano cartesiano para las 3 funcionesFUNCIONES DE LA FORMA y = (x2 + b)Y = (x + 2)2 + 1 Y =(x + 4)2 – 2 Y =(x – 2)2 – 3y = (x – 5)2 – 4 y = (x + 1)2 + 2y = (x – 1)2 + 5

43. Funciones de 2º grado La función cúbicaEs la de forma a: y = ax3 + bx2 + cx + dEjemplo: y = 2x3 + 3x2 – 12x.Generamos una tabla de valores, graficamos y verificamos el dominio y el recorrido.X –4 –3 –2 –1 0 1 2 3Y –32 9 20 13 0 –7 4 45

44. ACTIVIDAD 8EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un plano cartesiano para cada funciónY = x3Y = x3+ 1 Y = x3– 1y = x3 – 4 y = x3 + 2

45. ACTIVIDAD 9EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un plano cartesiano para cada funciónY = x3 + 2x Y = x3 + x2y = x3 – x2 – x y = x3 + 2x + 1y = x3 + x2+ x

46. Funciones racionalesEl criterio viene dado por un cociente entre polinomios:Por ejemplo: Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:

47. FUNCIONES CUADRÁTICAS DE LA FORMA1Y = X

48. FUNCIONES CUADRÁTICAS DE LA FORMA1Y = XX ={ – 4, – 2, – 1, – ½, – ¼, ¼, ½, 1, 2, 4}

49. ACTIVIDAD 10EN HOJAS MILIMETRICAS TRAZA LAS GRAFICAS DE LOS SIGUIENTES EJERCICIOS.NOTA: Un plano cartesiano para cada función2111Y = + 1Y = – 2XXX ={ – 4, – 2, – 1, – ½, – ¼, ¼, ½, 1, 2, 4}

50. Una función racional está definida en todo IR excepto en los puntos donde el denominador se anula. En su dominio de definición, las funciones racionales son continuas e indefinidamente derivables.

51. F I N.