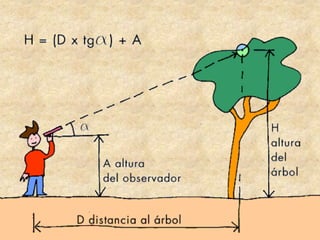
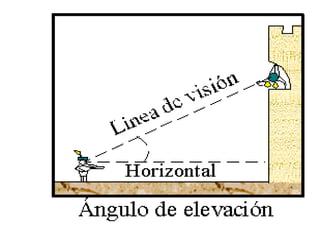
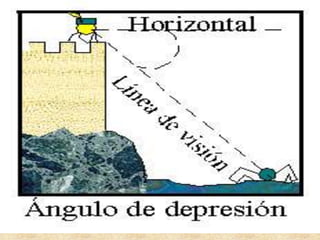
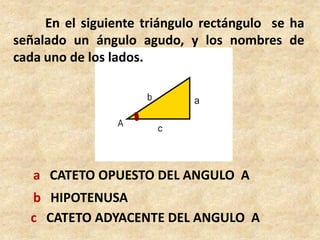
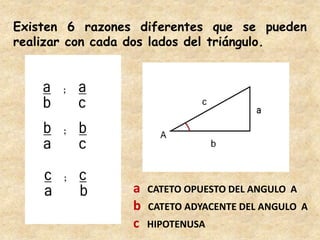
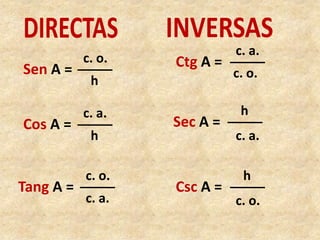
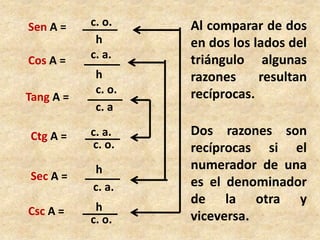
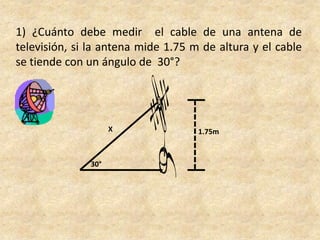
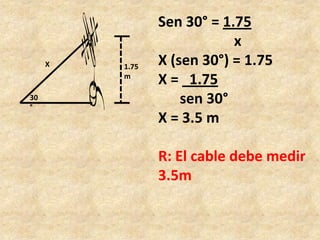
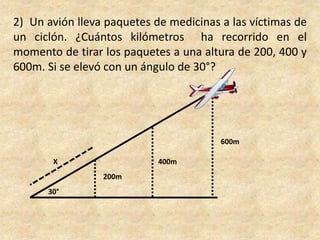
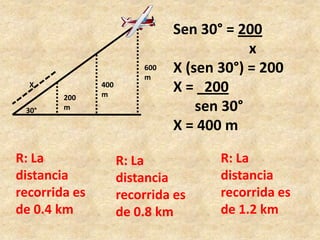
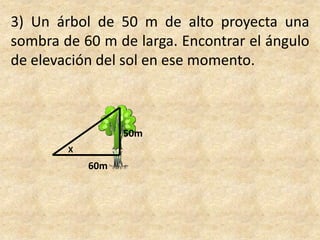
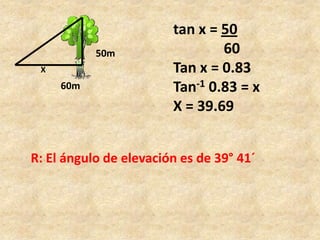
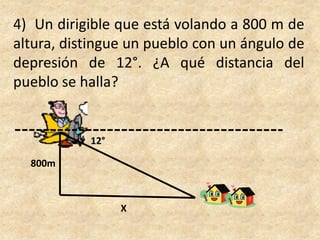
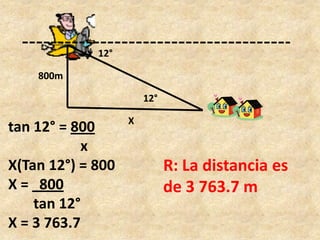
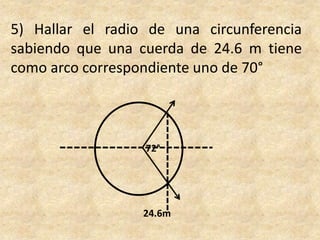
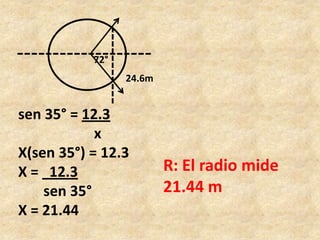
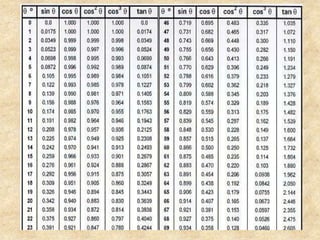
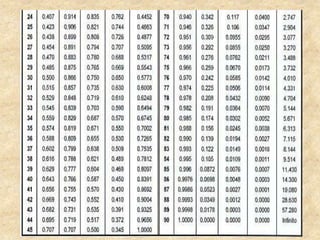
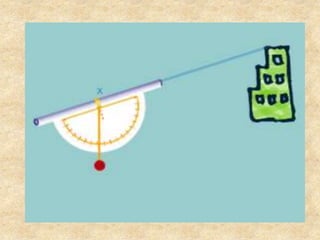
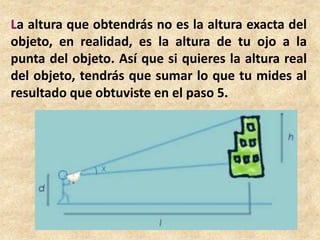
Este documento presenta información sobre trigonometría en triángulos rectángulos. Explica las seis razones trigonométricas y cómo se calculan a partir de las medidas de los lados del triángulo. Luego, resuelve cinco problemas de aplicación usando las razones trigonométricas para calcular distancias y ángulos desconocidos. Finalmente, ofrece instrucciones para construir un astrolabio primitivo y usarlo para medir alturas.

1. ESC. SEC. “ING. JORGE L. TAMAYO”MATEMATICAS IIIBLOQUE 4PROFR. C. JOEL VIVEROS JUÁREZTEHUACAN, PUE.

2. ENFOQUEMediante el estudio de las matemáticas se busca que los niños y jóvenes desarrollen una forma de pensamiento que les permita expresar matemáticamente situaciones que se presentan en diversos entornos socioculturales, así como utilizar técnicas adecuadas para reconocer, plantear y resolver problemas; al mismo tiempo, se busca que asuman una actitud positiva hacia el estudio de esta disciplina y de colaboración y crítica, tanto en el ámbito social y cultural en que se desempeñen como en otros diferentes.

3. Conocimientos y habilidades Orientaciones didácticas4.3. Reconocer y determinar las razones trigonométricas en familias de triángulos rectángulos semejantes, como cocientes entre las medidas de los lados. Calcular medidas de lados y de ángulos de triángulos rectángulos a partir de los valores de razones trigonométricas.Resolver problemas sencillos, en diversos ámbitos, utilizando las razones trigonométricas.

4. TRIGONOMETRÍA

8. En el siguiente triángulo rectángulo se ha señalado un ángulo agudo, y los nombres de cada uno de los lados.a CATETO OPUESTO DEL ANGULO Ab HIPOTENUSAc CATETO ADYACENTE DEL ANGULO A

9. Existen 6 razones diferentes que se pueden realizar con cada dos lados del triángulo.a CATETO OPUESTO DEL ANGULO AbCATETO ADYACENTE DEL ANGULO AcHIPOTENUSA

10. A partir del ángulo agudo y con el propósito de identificar a la razón que se está considerando, se les asignó un nombre particular.seno A = cateto opuesto hipotenusacoseno A = cateto adyacente hipotenusatangente A = cateto opuesto cateto adyacente

11. cotangente A = cateto adyacente cateto opuestosecante A = hipotenusa cateto adyacentecosecante A = hipotenusa cateto opuesto

12. c. o.c. a.c. o.c. a.hhDIRECTASINVERSASSen A = Cos A = Tang A = Ctg A = SecA = Csc A = hhc. a.c. o.c. a.c. o.

13. Al comparar de dos en dos los lados del triángulo algunas razones resultan recíprocas.c. o.hc. a.c. o.c. a.hSen A = Cos A = Tang A = Ctg A = SecA = Csc A = c. o.c. o.c. ac. a.hhDos razones son recíprocas si el numerador de una es el denominador de la otra y viceversa.

14. PROBLEMAS

15. 1) ¿Cuánto debe medir el cable de una antena de televisión, si la antena mide 1.75 m de altura y el cable se tiende con un ángulo de 30°?X1.75m30°

16. Sen 30° = 1.75 xX (sen 30°) = 1.75X = 1.75sen 30°X = 3.5 mR: El cable debe medir 3.5mX1.75m30°

17. 2) Un avión lleva paquetes de medicinas a las víctimas de un ciclón. ¿Cuántos kilómetros ha recorrido en el momento de tirar los paquetes a una altura de 200, 400 y 600m. Si se elevó con un ángulo de 30°?600mX400m200m30°

18. Sen 30° = 200 xX (sen 30°) = 200X = 200sen 30°X = 400 m600mR: La distancia recorrida es de 0.4 kmR: La distancia recorrida es de 1.2 kmR: La distancia recorrida es de 0.8 kmX400m200m30°

19. 3) Un árbol de 50 m de alto proyecta una sombra de 60 m de larga. Encontrar el ángulo de elevación del sol en ese momento.50mX60m

20. tan x = 50 60Tan x = 0.83Tan-1 0.83 = xX = 39.6950mXR: El ángulo de elevación es de 39° 41´60m

21. 4) Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?12°800mX

22. tan 12° = 800 xX(Tan 12°) = 800X = 800 tan 12°X = 3 763.712°R: La distancia es de 3 763.7 m800m12°X

23. 5) Hallar el radio de una circunferencia sabiendo que una cuerda de 24.6 m tiene como arco correspondiente uno de 70° 72°24.6m

24. sen 35° = 12.3 xX(sen 35°) = 12.3X = 12.3sen 35°X = 21.4472°R: El radio mide 21.44 m24.6m

25. TABLAS TRIGONOMÉTRICAS

28. Construyendo un astrolabioMATERIALun popote cordón delgado

29. pegamento

30. un poquito de plastilina

31. un transportador de 180º Pega el popote al transportador, de manera que el centro del transportador coincida con la mitad del popote, justo en el lugar en donde está amarrado el cordón.En el extremo del cordón amarra una bola de plastilina.Tu astrolabio primitivo ya está listo.

33. Con el astrolabio primitivo podrás calcular la altura de árboles, edificios…..1. Escoge el objeto que quieres medir2. Párate a cierta distancia del objeto y mirando a través del popote, enfoca el astrolabio a la punta del objeto.Es muy importante que cuando enfoques el objeto, el ángulo 0º quede del lado de tu ojo.

34. 3. Al tu enfocar la punta del objeto que quieres medir, el cordón con la bolita de plastilina se moverá y marcará un ángulo en el transportador. Pídele a un compañero que te diga cuál es el ángulo marcado o, si estás solo, agarra con cuidado el cordón y pégalo al transportador para que no se mueva de la posición en la que está. Llamaremos a este ángulo x.

35. 4. Mide la distancia a la que tú estás del objeto. Llamaremos a esta distancia l.5. Si llamamos h a la altura del objeto, usando trigonometría, podemos saber que: tan x = cateto opuestocateto adyacente tan x = h l entonces la Altura será: h = l (tan x)