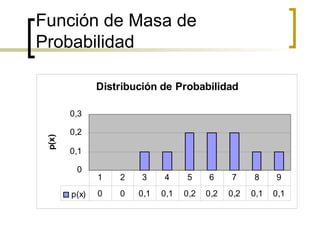
El documento describe cómo calcular la función de masa de probabilidad para una variable aleatoria X que representa la suma de los números en dos cubos extraídos sin reposición de una urna que contiene cubos numerados del 1 al 5. Explica que la función de masa de probabilidad incluye los valores discretos posibles de X de 3 a 9, y calcula las probabilidades de cada valor usando combinatorias para contar los casos posibles considerando el muestreo sin reposición.

1. Función de Masa de Probabilidad Ejemplo: Una urna contiene cinco cubos numerados del uno al cinco. Se extraen, sin reposición, muestras aleatorias de dos cubos. Se define una variable aleatoria de modo que sus valores sean iguales a la suma de los números correspondientes a los dos cubos que conforman cada muestra. Hallar la distribución de probabilidad para la variable aleatoria

2. Función de Masa de Probabilidad Solución: “ Una distribución de probabilidades que incluyen solamente valores discretos de x suele llamarse función de masa probabilidad”. Sea X la variable aleatoria que representa la suma de los números en los dos cubos extraídos. Tenemos: X= Suma de los números x= 3,4,5,6,7,8,9

3. Función de Masa de Probabilidad Como la extracción es sin reposición, para hallar el total de casos, tenemos: C= Combinatoria

4. Función de Masa de Probabilidad Y así sucesivamente hasta obtener la siguiente tabla de distribución de probabilidades y el gráfico correspondiente: esto es considerando que la única forma de que la suma sea 3, al extraer dos cubos es sacando el par (1,2)

5. Función de Masa de Probabilidad Luego para hallar la función de masa de probabilidad, como el muestreo es sin reposición, usamos la siguiente relación:

6. Función de Masa de Probabilidad