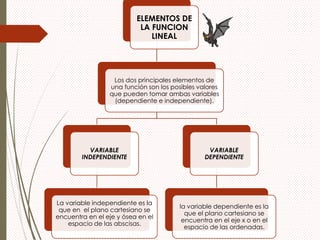
Una función lineal es una función cuyo dominio y codominio son los números reales y cuya expresión analítica es un polinomio de primer grado de la forma f(x) = ax + b, donde a y b son números reales. Las funciones lineales se representan por la ecuación y = mx + b, donde m es la pendiente y b es el punto donde la función corta el eje y. Las funciones lineales pueden crecer o decrecer dependiendo del signo de m.