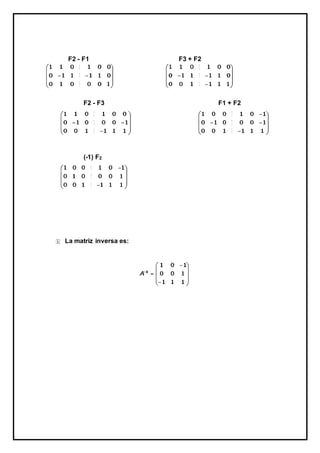
El documento describe el método de Gauss-Jordan para calcular la inversa de una matriz cuadrada. El método involucra colocar la matriz junto a una matriz identidad del mismo tamaño y aplicar operaciones de fila para transformar la matriz en una identidad, dejando la inversa en la parte derecha. Se explican los pasos de construir la matriz combinada, aplicar el método de Gauss para transformar la mitad izquierda en una identidad, dejando la inversa en la derecha.

1. MATRIZ INVERSA POR EL MÉTODO DE GAUSS JORDAN
MATERIA: MATEMÁTICAS
PROFESOR: LIC. EDGAR GERARDO MATA ORTIZ
NOMBRE: SANJUANA BARRIENTOS CHAGOYA
GRUPO Y SECCIÓN: 1º “C”

2. MATRIZ INVERSA
MÉTODO POR GAUSS JORDAN
Introducción Matriz Inversa:
Si es una matriz cuadrada, se llama matriz inversa de A y se denota A-1 a una
matriz del mismo orden que A, que verifica la siguiente igualdad: 1 1 (A A). Si
una matriz es inversa se dice que es invertible en caso contrario se llama
singular, debido a que no todas las matrices cuadradas pueden tener inversa.
Este método consiste en colocar junto a la matriz de partida (A) la matriz
identidad (I) y hacer operaciones por filas, afectando esas operaciones tanto a
A como a I, con el objeto de transformar la matriz A en la matriz identidad, la
matriz resultante de las operaciones sobre I es la inversa de A (A-1).
Para calcular la matriz inversa de A, que denotaremos como A-1 seguiremos los
siguientes pasos:
 Construir una matriz de tipo M = (A | I), es decir, A está en la mitad
izquierda de M y la matriz Identidad I en la derecha. Consideremos una
matriz 3x3 arbitraria.
La ampliamos con una matriz identidad de orden 3.
 Utilizando el método de Gauss vamos a transformar la mitad izquierda,
A, en la matriz identidad, que ahora está a la derecha, y la matriz que
resulte en el lado derecho será la matriz inversa: A-1

3. F2 - F1 F3 + F2
F2 - F3 F1 + F2
(-1) F2
 La matriz inversa es: