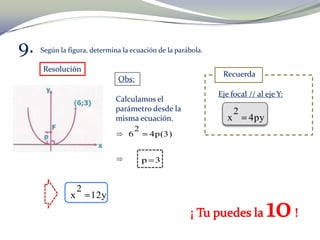
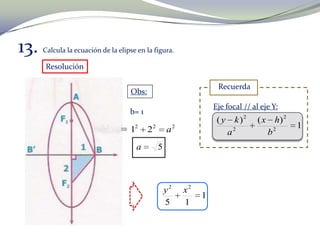
El documento habla sobre Michael Jordan, un jugador de baloncesto conocido por sus espectaculares saltos. Explica que cuando salta, su cuerpo describe una parábola. Luego, presenta varios ejercicios relacionados con parábolas y elipses, incluyendo calcular ecuaciones y determinar elementos como el área.

1. Prof. Jesús Pizarro Rosales 5to Sandra - 2012

2. 5to Sandra - 2012

3. MOTIVACIÓN
El jugador de baloncesto profesional
Michael Jordan es conocido por su
espectacular salto cuando intenta encestar
en la red del equipo contrario. Los
periodistas deportivos se refieren al
momento que permanece suspendido en el
aire el jugador , como el tiempo en el que
parece que está en la altura máxima de su
salto a la vez que flota hacia la canasta.
Durante el salto. el centro de gravedad de
Jorda (ubicado aproximadamente
a la altura del ombligo).
La figura descrita por el balón es una PARÁBOLA.
La abertura de esta parábola depende de la
velocidad con la que Jordan corra horizontalmente
en el momento de dar el salto. Este es uno de los
tantos ejemplos en donde aparece esta curva
,descrita anteriormente como una de las secciones
cónicas

4. EJERCICIOS
RELACIONADOS SOBRE
PARÁBOLA

5. Nota: Los ejercicios son de la página 123 y 126
2. Determina la ecuación de la párabola cuyo vértice y foco tienen por coordenadas
(-8 ; 6) y (-2 ; 6) respectivamente.
Resolución
6(-8)-2-VFp
Recuerda
Eje focal // al eje X:
h)-4p(x
2
K)-(y
C 0p;6p
Obs:
Necesitamos solo
el parámetro (p)
para determinar la
ecuación.
6)-4(6)(x
2
(-8))-(y
8)24(x
2
6)-(y

6. C
4. Según el gráfico, calcula la ecuación de la parábola si se sabe que el área de la región
cuadrada VMPQ =9 u2.
Resolución Recuerda
Eje focal // al eje X:
4px
2
y
(3; 3)
3
3
Obs:
Calculamos el
parámetro desde la
misma ecuación.
4px
2
y
4p(3)
2
3
4
3
p
3x
2
y

7. 5. Según el gráfico, Calcula la ecuación de la parábola PQ : Lado recto. (PQ = |4p|).
Resolución
Obs:
Del gráfico
aplicamos
PITÁGORAS.
2
(2P)
2
P
2
)5(
C 1P
Recuerda
Eje focal // al eje X:
4px
2
y
4x
2
y

8. 6. En una parábola P de foco F, se traza la cuerda focal BC y se ubica el punto A en la
región interior, de manera que ABC es un triángulo equilátero. Si AB es paralelo al
eje focal y BF=3u, calcula AC.
OBS:Resolución
12uAC
B
C
A
F
60°
3u
3u
3u a
3u+a
60°
BC = 2a
3 + 3 + a = 2a
a = 6u

9. 8. El eje de una parábola es paralelo al eje X, su foco es (4;3) y la longitud de su lado
recto es 10u. Determina la ecuación de la parábola si se sabes, además, que el vértice
está a la derecha del foco.
Resolución
Lado recto: |4p|
4p = 10
p = 5/2
Calculamos “ h ”:
P = VF = F - V
-5/2 = 4 – h
h = 13/2
Recuerda
Eje focal // al eje X:
h)-4p(x
2
k)-(y
13/2)-10(x
2
3)-(y

10. 9. Según la figura, determina la ecuación de la parábola.
Resolución
Recuerda
Eje focal // al eje Y:
4py
2
x
C
Obs:
Calculamos el
parámetro desde la
misma ecuación.
4p(3)
2
6
3p
12y
2
x

11. 14. Determina la ecuación de la parábola. (F: foco) S=64u2.
Resolución
Recuerda
Eje focal // al eje X:
h)-4p(x
2
k)-(y
8
8
p = 4
8
(4;16)
4)-16(x
2
16)-(y

12. 17. Según la figura, calcula la ecuación de la parábola mostrada en el gráfico si A=(6;10)
y B=(6;2), AB = lado recto.
Resolución Recuerda
Eje focal // al eje X:
h)-4p(x
2
k)-(y(6;10)
(6;2)
V(4;6)
4
p=2
C
Obs:
10 – 2 = 4p.
2p
4)-8(x
2
6)-(y

13. 18. En la figura , G es baricentro del triángulo ABC , AB=16 y m<ACB106°. Determina la
ecuación de la parábola cuyo eje focal está contenido en el eje “ y ”, además C es foco.
Resolución Recuerda
Eje focal // al eje Y:
Obs:
p = -4
88
37°
4
2
G(0;-2)
k)-4p(y
2
h)-(x
)216(y-
2
x

14. EJERCICIOS
RELACIONADOS SOBRE
ELIPSE

15. 3. Calcula el área de la elipse.
Resolución
Recuerda
El área de la Elipse
abAelipse
8u
Obs:
a = 10u y b= 8u
2
80 uAelipse

16. 12. Determina la ecuación de una elipse cuyo centro es (3;4), la longitud de su eje mayor
es 18, la longitud de su eje menor es 10 y sus eje focal es paralelo al eje de abscisas.
Resolución
Recuerda
Eje focal // al eje X:
1
)()(
2
2
2
2
b
ky
a
hx
Obs:
C=(3;4)
2a = 18 a = 9
2b = 10 b = 5
1
25
)4(
81
)3( 22
yx

17. 13. Calcula la ecuación de la elipse en la figura.
Resolución
Obs:
b= 1
222
21 a
5a
Recuerda
Eje focal // al eje Y:
1
)()(
2
2
2
2
b
hx
a
ky
1
15
22
xy

18. 16. Determinar la ecuación de una elipse cuyos vértices son: (0;-9) y (0;9) y sus
focos: (0;-6) y (0; 6)
Resolución
Recuerda
Eje focal // al eje Y:
1
)()(
2
2
2
2
b
hx
a
ky
Obs:
F1F2= 12 2c= 12 c= 6
V1V2= 18 2a= 18 a= 9
222
bca
452
b
1
4581
22
xy
C= (0;0)