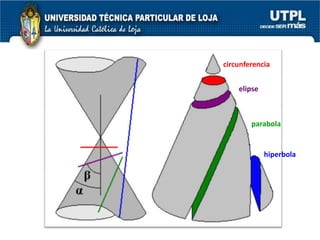
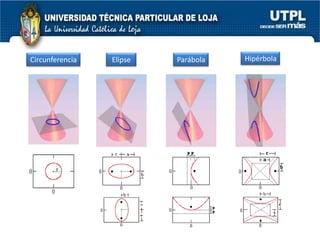
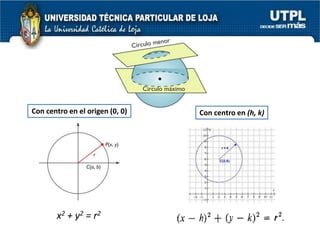
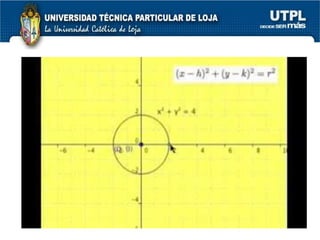
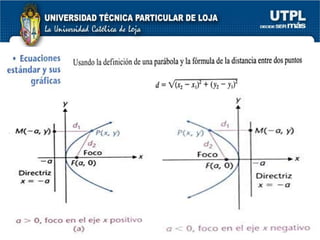
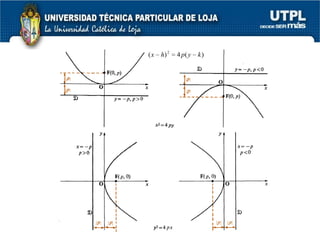
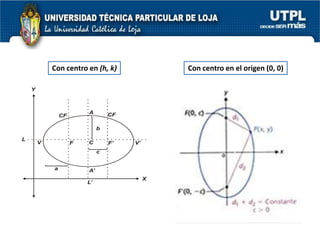
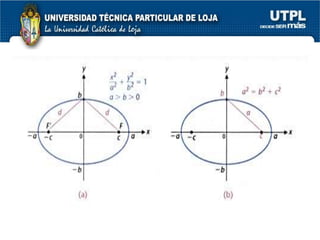
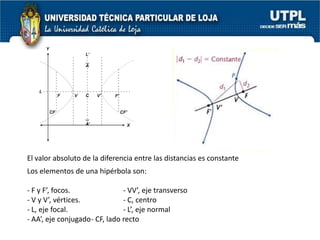
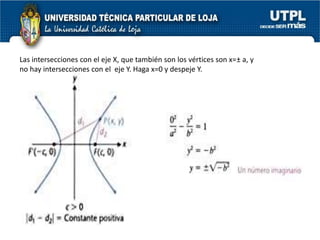
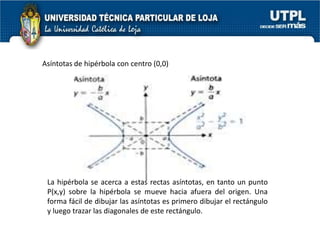
El documento aborda las secciones cónicas en matemáticas, incluyendo definiciones y características de la circunferencia, parábola, elipse e hipérbola. Se presentan sus ecuaciones canónicas y la relación entre sus elementos, como focos, vértices y ejes. También se incluye la metodología para resolver problemas y ejercicios aplicados a cada tipo de sección cónica.

1. MATEMÁTICAESCUELA DE ARQUITECTURACapituloNro. 01SECIONES CÓNICASLA CIRCUNFERENCIA, LA PARÁBOLA, LA ELIPSE Y LA HIPÉRBOLA. Autores: ING. SONIA LORENA GONZAGA V. (slgonzaga@utpl.edu.ec)ING. LAPO PAUTA CARMEN MIREYA. (cmlapo@utpl.edu.ec)ING. PINEDA PUGLLA EDGAR IVAN. (eipineda@utpl.edu.ec)ING. IRENE ROBALINO PEDRO DANIEL. (pdriene@utpl.edu.ec)

2. Definiciones:Se denomina sección cónica a la curva intersección de un conocon un plano que no pasa por su vértice.Intersección de un plano y un cono de dos hojas.Cambiando el ángulo y el lugar de la intersección, podemos crear un círculo, un elipse, una parábola o una hipérbola; o en el caso especial cuando el plano se pone en contacto con el vértice: un punto, una línea o 2 líneas intersectadas.

3. circunferenciaelipseparabolahiperbola

5. HipérbolaCircunferenciaElipseParábola

6. LA CIRCUNFERENCIAAlgebraicamente las secciones cónicas se pueden definir en términos de la ecuación general de segundo grado.

7. La circunferencia se define como el lugar geométrico de todos los puntos que satisfacen cierta propiedad geométrica.

8. Conjunto de todos los puntos (x,y) que son equidistantes de un punto fijo (h,k).

9. Forma canónica o estándar de la circunferencia.Con centro en el origen (0, 0)Con centro en (h, k)x2+ y2 = r2

11. LA PARÁBOLA

14. La forma estándar o canónica de la ecuación de la parábola con vértice (h,k) y directriz y= k- p es:Y sus elementos son:Foco (h, k + p)Directriz y = k – pEje focal x = hSi p > 0 la parábola se abre hacia arriba.Si p < 0 la parábola se abre hacia abajo.Eje vertical

15. La ecuación de una parábola de vértice (h, k) y eje focal paralelo al eje X es de la forma:(y - k)² = 4p(x - h) eje horizontal Y sus elementos son los siguientes:Foco (h + p, k)

16. Directriz x = h – p

17. Eje focal y = k

18. Donde 4| p | es la magnitud del lado recto y siendo | p | la longitud entre el foco y el vértice.

19. Si p > 0 la parábola se abre hacia la derecha.

20. Si p < 0 la parábola se abre hacia la izquierda.Cuerda focal es el segmento de recta que pasa por el foco de una parábola y tiene sus extremos en la misma.

21. La cuerda focal perpendicular al eje de la parábola es el lado recto.PROBLEMAS Y EJERCICIOS DE APLICACION

22. LA ELIPSELa forma canónica estándar de la ecuación de una elipse con centro (h,k) y longitudes de los ejes mayor y menor 2a y 2b, respectivamente, donde a>b, es

23. Los focos se encuentran en el eje mayor, a c unidades del centro.La ecuación de una elipse con C(h, k) y eje focal paralelo al eje Y esta dada por

24. También para cada elipse, la longitud de cada uno de sus lados rectos es: 2b² / a y la excentricidad e = c / a.Con centro en (h, k)Con centro en el origen (0, 0)

26. LA HIPERBOLAEs el conjunto de todos los puntos (x,y) para los que el valor absoluto de la diferencia entre las distancias a dos puntos fijos llamados focos es constante. La recta que pasa por los dos focos corta a la hipérbola en dos puntos llamados vértices. El segmento de recta que une a los vértices es el eje transversal, y el punto medio del eje transversal es el centro de la hipérbola . Tiene dos ramas separadas.

27. El valor absoluto de la diferencia entre las distancias es constante Los elementos de una hipérbola son:- F y F’, focos. - VV’, eje transverso - V y V’, vértices. - C, centro- L, eje focal. - L’, eje normal- AA’, eje conjugado - CF, lado recto

28. La ecuación de una hipérbola con centro en el punto C(h, k), y eje focal paralelo al eje X es de la forma: