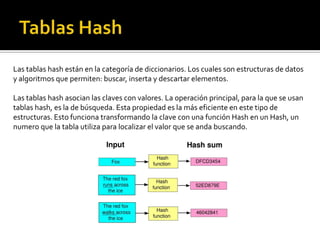
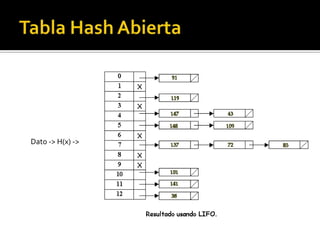
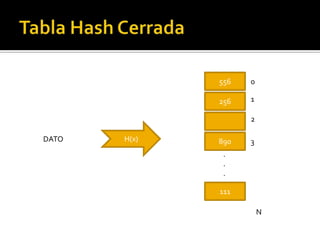
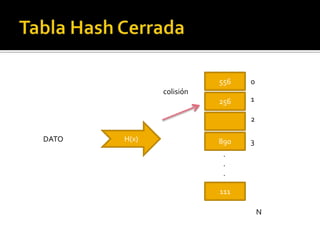
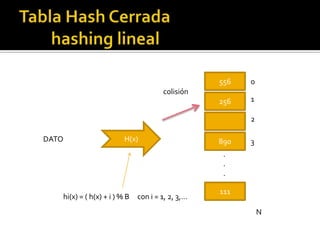
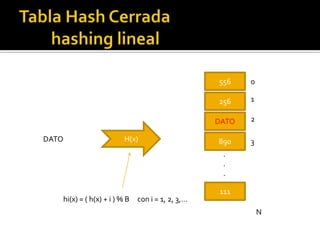
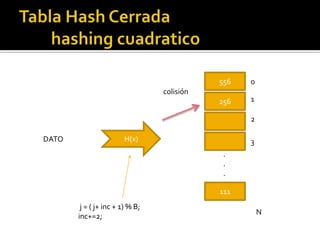
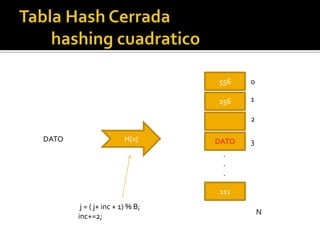
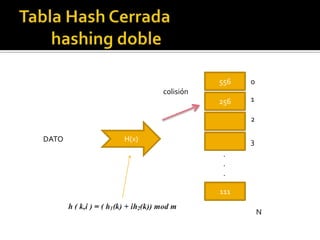
Las tablas hash son estructuras de datos que permiten la búsqueda, inserción y eliminación de elementos mediante el uso de una función hash para transformar claves en índices. Pueden presentar colisiones al insertar datos, para lo cual se utilizan técnicas como el hashing abierto y cerrado, así como diversas estrategias para resolver colisiones, como el hashing lineal y cuadrático. Ejemplos ilustran cómo insertar elementos en tablas de hash y resolver colisiones utilizando diferentes métodos.

1. Piero Divasto
Estudiante Ing. Civil Informatica
Universidad de Valparaiso

2. Las tablas hash están en la categoría de diccionarios. Los cuales son estructuras de datos
y algoritmos que permiten: buscar, inserta y descartar elementos.
Las tablas hash asocian las claves con valores. La operación principal, para la que se usan
tablas hash, es la de búsqueda. Esta propiedad es la más eficiente en este tipo de
estructuras. Esto funciona transformando la clave con una función Hash en un Hash, un
numero que la tabla utiliza para localizar el valor que se anda buscando.

3.  Al ingresas elementos, el problema que
puede surgir es que pueden existir colisiones
al ingresar dos datos.
 Para la resolución de estas colisiones hay dos
formas.
 Hashing Abierto
 Hashing Cerrado

4. Dato -> H(x) ->

5. 556 0
256 1
2
DATO H(x) 890 3
.
.
.
111
N

6. 556 0
colisión
256 1
2
DATO H(x) 890 3
.
.
.
111
N

7.  Hay varias formas para resolver las colisiones
en este tipo de tablas.
 Hashing lineal
 Hashing cuadratico
 Hashing doble

8. 556 0
colisión
256 1
2
DATO H(x) 890 3
.
.
.
111
hi(x) = ( h(x) + i ) % B con i = 1, 2, 3,…
N

9. 556 0
256 1
DATO 2
DATO H(x) 890 3
.
.
.
111
hi(x) = ( h(x) + i ) % B con i = 1, 2, 3,…
N

10. 556 0
colisión
256 1
2
DATO H(x) 3
.
.
.
111
j = ( j+ inc + 1) % B;
N
inc+=2;

11. 556 0
256 1
2
DATO H(x) DATO 3
.
.
.
111
j = ( j+ inc + 1) % B;
N
inc+=2;

12. 556 0
colisión
256 1
2
DATO H(x) 3
.
.
.
111
N

13. Sea T una tabla de hash de tamaño 10 y h la siguiente función de hash.
h(k) = 4 + 3k mod10
Se quieren insertar en T elementos con claves 1, 11, 5, 15, 55, 6, 26, 90, 50, 20 en ese
mismo orden usando h(k).
(a) Determine el resultado de insertar las claves en T si las colisiones se resuelven por
encadenamiento (suponga que un nuevo elemento se agrega al final de una lista).
(b) Determine el resultado de insertar las claves en T si las colisiones se resuelven por
examinación lineal.

14. Teniendo las siguiente funciones hash:
h1(x) = x mod 13 y h2(x)= 1+(x mod 1 1)
i = 1,2,3….
Insertar los siguiente numero en una tabla de hashing cerrado de tamaño 13:
79-69-98-72-50-14