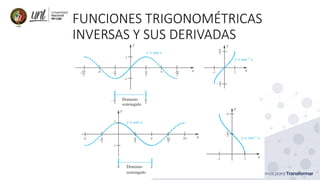
Este documento presenta una introducción a las funciones trascendentales como el logaritmo natural, funciones exponenciales, funciones trigonométricas inversas y funciones hiperbólicas. Incluye definiciones de estas funciones, sus derivadas, y ejemplos sobre cómo calcular derivadas de funciones compuestas y funciones inversas.

2. CÁLCULO DIFERENCIAL E
INTEGRAL
UNIDAD 3: APLICACIONES EN INGENIERÍA
Marcelo Fernando Valdiviezo Condolo
Primero ‘B’
Carrera de Telecomunicaciones

3. FUNCIONES TRASCENDENTALES

4. LA FUNCIÓN LOGARITMO NATURAL
( ) ( )
x
a
F x f t dt= 
( ) ( )
2 2
1 0 1 2 31
, , ?? , ,
2 2
x x x x x
x x
D x D x x D x D x D x
x
−
− − −    
= = = − = − =    
    

5. LA FUNCIÓN LOGATIRMO NATURAL
DEFINICIÓN: Función Logaritmo Natural

6. LA FUNCIÓN LOGARITMO NATURAL
Derivada de la Función logaritmo natural
Aplicando la regla de la cadena

7. EJEMPLO
Encuentre ( )lnxD x
1
2
u x x= =
( ) ( )1 1
2 2
1 1
2 2
1 1 1 1
ln
2 2
x xD x D x x
xx x
−
=  =  =

8. EJEMPLO
Encuentre ( )2
ln 2xD x x− −
( )( )2
2 2 1 0 1 2x x x x x x− − = − +   − 
( ) ( )2 2
2 2
1 2 1
ln 2 2
2 2
x x
x
D x x D x x
x x x x
−
− − =  − − =
− − − −
( ) ( ): , 1 2,D − −  

9. EJEMPLO
Encuentre
5
2 7
dx
x +
2 7
2
u x
du dx
= +
=
5 5 1 5 1
2
2 7 2 2 7 2
dx dx du
x x u
= =
+ +  
5 5
ln ln 2 7
2 2
u C x C= + = + +

10. EJEMPLO
Encuentre
3
2
1
10
x
dx
x−
−
2
10
2
u x
du xdx
= −
= −
21 1
ln ln 10
2 2
u C x C= − + = − − +
2 2
1 2 1 1
10 2 10 2
x x
dx dx du
x x u
−
= − = −
− −  
33
2
2
11
1 1 1 1
ln 10 ln1 ln9 ln9
10 2 2 2 2
x
dx x
x −−
 
= − − = − + = −  


11. EJEMPLO
Encuentre
2
1
x x
dx
x
−
+
( )
2
1
2 2
1 1
x x
dx x dx dx
x x
−
= − +
+ +  
2
1
2 2
2 1
x
x dx
x
= − +
+
2
2 2ln 1
2
x
x x C= − + + +

12. LA FUNCIÓN LOGARITMO NATURAL
TEOREMA: Propiedades del Logaritmo Natural

13. EJEMPLO
Encuentre si
dy
dx
3
2
1
ln , 1
x
y x
x
 −
=   
 
( ) ( )
1
3
2
2 2
1 1 1 1
ln ln ln 1 ln
3 3
x x
y x x
x x
− −     = = = − −        
( ) ( )
1
ln 1 2ln
3
x x= − −  
( )
1 1 2 2
3 1 3 1
dy x
dx x x x x
− 
= − = − − 

14. EJEMPLO
Derive
( )
2
2
3
1
1
x
y
x
−
=
+

15. FUNCIONES INVERSAS Y SUS
DERIVADAS
TEOREMA: Existencia de la función inversa

16. EJEMPLO
Demuestre que tiene una inversa y encuentre su fórmula( ) 2 6f x x= +
2 6y x= +
( )' 2 0f x =  Creciente en toda la recta real, por lo tanto tiene inversa
Igualamos a y
6
2
y
x
−
= Despejamos x
( )16
2
y
x f y−−
= =
( )( ) ( )
( )1 1 2 6 6
2 6
2
x
f f x f x x− − + −
= + = =
( )( )1 6 6
2 6
2 2
y y
f f y f y− − −   
= = + =   
   

17. FUNCIONES INVERSAS Y SUS
DERIVADAS
TEOREMA: Derivada de la función inversa

18. EJEMPLO
Sea Encuentre( ) 5
2 1,y f x x x= = + +
( ) 4
' 5 2f x x= +
( ) ( )1
' 4f −
( ) ( )
( )
1 1 1 1
' 4
' 1 5 2 7
f
f
−
= = =
+
( ) ( ) ( )
5
1 1 2 1 1 4y f= = + + =

19. LA FUNCIÓN EXPONENCIAL NATURAL
DEFINICIÓN

20. EJEMPLO
Encuentre
2
lnx x
xD e
( )
2 2
ln ln 2
lnx x x x
x xD e e D x x=
2
ln 2 1
2 lnx x
xe x x x
x
 
=  + 
 
( )
2
ln 2
1 lnx x
xe x= +

21. EJEMPLO
Evalúe
3
2 x
x e dx−

3
2
3
u x
du x dx
= −
= −
( )
3 3
2 21
3
3
x x
x e dx e x dx− −
= − − 
1 1
3 3
u u
e du e C= − = − +
31
3
x
e C−
= − +

22. FUNCIONES EXPONENCIALES Y
LOGARÍTMICAS GENERALES
DEFINICIÓN
TEOREMA: Propiedades

23. FUNCIONES EXPONENCIALES Y
LOGARÍTMICAS GENERALES
DEFINICIÓN
TEOREMA: Reglas de la función exponencial

24. EJEMPLO
Encuentre ( )3 x
xD u x=
( ) 3 ln3
3 3 ln3
2
x
x x
x xD D x
x
=  =

25. EJEMPLO
Encuentre
3
2
2x
x dx
3
2
3
u x
du x dx
=
=
( )
3 3
2 21 1
2 2 3 2
3 3
x x u
x dx x dx du= =  
3
1 2 2
3 ln 2 3ln 2
u x
C C= + = +

26. FUNCIÓN Loga
DEFINICIÓN
logay x= y
x a=

27. EJEMPLO (Método I)
Si , 0, Encuentre Dx
xy x x y= 
lnx x x
y x e= =
( ) ( )ln 1
ln ln 1 lnx x x x
x xD y e D x x x x x x x
x
 
= =  + = + 
 

28. EJEMPLO (Método II)
Si , 0, Encuentre Dx
xy x x y= 
x
y x=
ln ln x
y x=
ln lny x x=
1 1
lnxD y x x
y x
=  +
( ) ( )1 ln 1 lnx
xD y y x x x= + = +

29. FUNCIONES TRIGONOMÉTRICAS
INVERSAS Y SUS DERIVADAS
DEFINICIÓN

30. FUNCIONES TRIGONOMÉTRICAS
INVERSAS Y SUS DERIVADAS

31. FUNCIONES TRIGONOMÉTRICAS
INVERSAS Y SUS DERIVADAS
DEFINICIÓN

32. FUNCIONES TRIGONOMÉTRICAS
INVERSAS Y SUS DERIVADAS

33. FUNCIONES TRIGONOMÉTRICAS
INVERSAS Y SUS DERIVADAS
TEOREMA: Identidades

34. FUNCIONES TRIGONOMÉTRICAS
INVERSAS Y SUS DERIVADAS
TEOREMA: Derivadas Funciones Trigonométricas Inversas

35. FUNCIONES HIPERBÓLICAS Y SUS
INVERSAS
Funciones Hiperbólicas

36. FUNCIONES HIPERBÓLICAS Y SUS
INVERSAS
TEOREMA: Derivadas de Funciones Hiperbólicas

37. PREGUNTAS