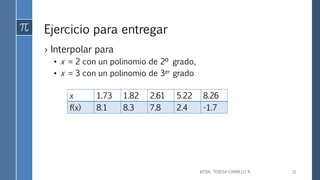
Este documento introduce el concepto de interpolación polinomial y el polinomio de Lagrange. Explica que la interpolación polinomial permite encontrar un polinomio único que pasa por una serie de puntos de datos (x, y). También describe cómo el polinomio de Lagrange permite determinar el polinomio de grado más bajo que interpola exactamente los datos, mediante la suma de términos que dependen de los puntos de datos. Finalmente, presenta un ejemplo numérico de interpolación polinomial.

1. Interpolación polinomial.
Polinomio de Lagrange
Mtra. Teresa Carrillo

2. Introducción
Es común encontrar datos tabulados de la forma (xi, yi), para i = 0, 1,
…, n, (la presión de una sustancia vs temperaturas, la población vs
tiempos, distancias vs velocidades, …)
Donde y = f(x) y f(x) es una función desconocida pero se requiere
conocer algún valor de y para alguna x que no se encuentra en la
tabla. Este procedimiento es lo que se conoce como Interpolación.
TERESA CARRILLO RAMÍREZ

3. Interpolación
Es el cálculo de valores para una función tabulada en puntos que no
se encuentran en la tabla de valores.
Obtiene una representación explícita de una aproximación a f(x),
Se emplea para construir fórmulas de diferenciación e integración
numérica y obtener formas simplificadas de funciones complejas
La interpolación de polinomios sirve como introducción de algunas
técnicas para suavizar curvas.
TERESA CARRILLO RAMÍREZ

4. Interpolación polinomial
› Si se tiene un conjunto de n + 1 puntos (xi , yi) para i = 0, 1, ... , n
para representar a y como una función de valuación única de x, es
posible encontrar un polinomio único de grado n que pasa por los
puntos.
› Por ejemplo, se desea determinar un polinomio de grado uno que
pase por los puntos distintos (x0, y0) y (x1, y1). Este problema es el
mismo que el de aproximar una función f, para la cual f(x0) = y0 y
f(x1) = y1, por medio de un polinomio de primer grado.
TERESA CARRILLO RAMÍREZ

5. Para dos puntos
𝑃 𝑥 =
(𝑥 − 𝑥1)
(𝑥0 − 𝑥1)
𝑦0 +
(𝑥 − 𝑥0)
(𝑥1 − 𝑥0)
𝑦1
Generalización del cociente de Lagrange
TERESA CARRILLO RAMÍREZ






nkkkkkkk
nkk
kn
xxxxxxxxxx
xxxxxxxxxx
xL
1110
1110
,
)())(())((
)())(())((
)(



6. Polinomio de Lagrange
TERESA CARRILLO RAMÍREZ
Si x0, x1, ... , xn son (n + 1) números diferentes y f es una función
cuyos valores están dados en estos puntos, entonces existe un único
polinomio P de grado a los más n con la propiedad de que f(xk) =
P(xk) para cada k = 0, 1, ... , n.
Este polinomio está dado por
𝑃 𝑥 = 𝑓 𝑥0 𝐿 𝑛,0 𝑥 + 𝑓 𝑥1 𝐿 𝑛,1 𝑥 + ⋯ + 𝑓 𝑥 𝑛 𝐿 𝑛,𝑛 𝑥
=
𝑘=0
𝑛
𝑓 𝑥 𝑘 𝐿 𝑛,𝑘 𝑥

7. Ejemplo
› La siguiente tabla presenta las temperaturas de
ebullición de la acetona a diferentes presiones. Obtener
una aproximación para t(7) mediante un polinomio de
Lagrange cuadrático y uno cúbico
TERESA CARRILLO RAMÍREZ
k P (atm) t (°C)
0 1 56.5
1 2 78.6
2 5 113.0
3 10 144.5

8. TERESA CARRILLO RAMÍREZ
4 6 8 10
80
100
120
140
2 4 6 8 10
80
100
120
140
2 4 6 8 10
80
100
120
140
2 4 6 8 10
80
100
120
140

9. Consideraciones
Los datos no requieren
estar igualmente
espaciados.
No se requiere que los
datos estén ordenados,
aunque es
recomendable.
El grado del polinomio
no suele ser muy
grande.
Es ideal si se conoce de
antemano el grado del
polinomio.
Cambiar el grado del
polinomio implica
realizar todos los
cálculos desde un
inicio.
TERESA CARRILLO RAMÍREZ

10. Generalidades
› Los polinomios de grados elevados producen oscilaciones.
› La implementación del método de Lagrange en un programa de
computadora es bastante sencillo.
› Un polinomio de interpolación, aunque pase por los puntos que se
utilizaron en su construcción, en general no proporciona valores
exactamente correctos, ya que f(x) normalmente no es un
polinomio del mismo grado o no es un polinomio.
› Es común su uso como parte de otros métodos, como por
ejemplo, métodos para la solución de ecuaciones diferenciales.
TERESA CARRILLO RAMÍREZ

11. Ejercicio para entregar
› Interpolar para
• x = 2 con un polinomio de 2º grado,
• x = 3 con un polinomio de 3er grado
MTRA. TERESA CARRILLO R. 11
x 1.73 1.82 2.61 5.22 8.26
f(x) 8.1 8.3 7.8 2.4 -1.7