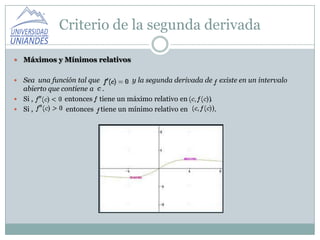
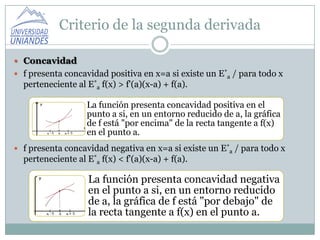
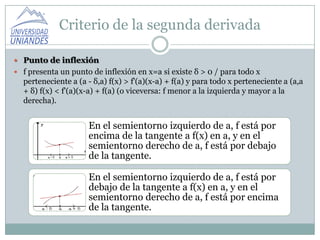
Este documento presenta un resumen del criterio de la segunda derivada para determinar máximos, mínimos, concavidad y puntos de inflexión de una función. Explica que si la segunda derivada es positiva en un punto, la función tiene un mínimo en ese punto, y si es negativa tiene un máximo. También define la concavidad positiva y negativa y los puntos de inflexión de una función basados en si está por encima o debajo de la tangente.

1. UNIVERSIDAD REGIONAL
AUTONOMA DE LOS ANDES
FACULTA DE INGENIERIA EN
SISTEMAS E INFORMATICA
MATEMATICAS II
Nombre: Alexis Balseca
Nivel: 2 Nivel

2. Criterio de la segunda derivada
CRITERIO DE LA II DERIVADA
Teorema o método de el cálculo matemático que se utiliza para efectuar una
prueba simple correspondiente a los máximos y mínimos relativos.
Se llama derivada segunda de una función f(x) a la derivada de la derivada de
dicha función.
Notación: f''(x).
Este concepto se puede extender a la derivada n-ésima de una función.

3. Criterio de la segunda derivada
 Máximos y Mínimos relativos
 Sea una función tal que y la segunda derivada de existe en un intervalo
abierto que contiene a .
 Si , entonces tiene un máximo relativo en .
 Si , entonces tiene un mínimo relativo en .

4. Criterio de la segunda derivada
 Concavidad
 f presenta concavidad positiva en x=a si existe un E*a / para todo x
perteneciente al E*a f(x) > f'(a)(x-a) + f(a).
La función presenta concavidad positiva en el
punto a si, en un entorno reducido de a, la gráfica
de f está "por encima" de la recta tangente a f(x)
en el punto a.
 f presenta concavidad negativa en x=a si existe un E*a / para todo x
perteneciente al E*a f(x) < f'(a)(x-a) + f(a).
La función presenta concavidad negativa
en el punto a si, en un entorno reducido
de a, la gráfica de f está "por debajo" de
la recta tangente a f(x) en el punto a.

5. Criterio de la segunda derivada
 Punto de inflexión
 f presenta un punto de inflexión en x=a si existe δ > 0 / para todo x
perteneciente a (a - δ,a) f(x) > f'(a)(x-a) + f(a) y para todo x perteneciente a (a,a
+ δ) f(x) < f'(a)(x-a) + f(a) (o viceversa: f menor a la izquierda y mayor a la
derecha).
En el semientorno izquierdo de a, f está por
encima de la tangente a f(x) en a, y en el
semientorno derecho de a, f está por debajo
de la tangente.
En el semientorno izquierdo de a, f está por
debajo de la tangente a f(x) en a, y en el
semientorno derecho de a, f está por encima
de la tangente.

6. GRACIAS