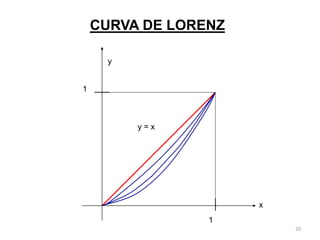
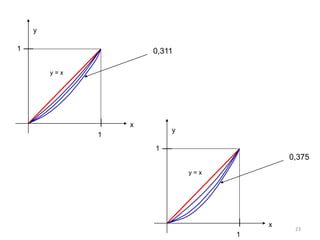
El documento trata sobre conceptos matemáticos avanzados como las integrales y la integración. Explica que la integración es igual al área delimitada entre la gráfica de una función y los límites de integración. Presenta casos prácticos sobre el cálculo de participación de mercado y costos, ingresos y ganancias usando integrales definidas e indefinidas.

1. 1
INTEGRALES
• La integración es un concepto fundamental de las
matemáticas avanzadas, especialmente en los campos del
cálculo y los sumandos, infinitamente pequeños.
• Dada una función f(x) de una variable real x y un intervalo
[a,b] de la recta real, la integral
• Es igual al área de la región del plano xy limitada entre la
gráfica de f, el eje x, y las líneas verticales x = a y x = b, donde
son negativas las áreas por debajo del eje x.

2. 2
LA INTEGRACIÓN
Integración indefinida
Integración definida
ANTIDERIVADA
Una función F es una antiderivada de f en un intervalo I si
F’(x) = f(x) para toda x en I.
Teorema:
Sea G una antiderivada de una función f. Entonces cada
antiderivada F de f debe ser de la forma F(x) = G(x) + C,
donde C es una constante.

3. 3
CASO PRÁCTICO 1
Si la proporción de autos nuevos producidos por Landa y
vendidos en cierto país está cambiando a razón de:
f(t) = - 0.01875t2 + 0.15t – 1.2; 0 ≤ t ≤ 12
Por ciento al año t (t = 0 corresponde al inicio de 1996). La
participación de la empresa en el mercado al inicio de 1996
era de 48.4%. ¿Cuál era la participación de Landa en el
mercado al inicio del 2008?

4. 4
Solución:
Sea M (t) la participación de Landa en el mercado en el año
t. Entonces:
M (t) =  f(t) dt
=  (-0.01875t2 + 0.15t – 1.2) dt
= - 0.00625t3 + 0.075 t2 – 1.2t + C
Para determinar el valor de C, se utiliza la condición M(0) =
48.4, con lo que se obtiene C = 48.4. Por lo tanto;
M(t) = -0.00625t3 + 0.075t2 – 1.2t + 48.4
En particular, la participación de Landa en el mercado de
autos nuevos al inicio del 2008 está dada por:
M(12) = -0.00625 (12)3 + 0.075 (12)2 - 1.2 (12) + 48.4
= 34 ó 34%

5. 5
CASO PRÁCTICO 2
La demanda semanal de las videocaseteras Pulsar está dada por
la ecuación de demanda:
p = - 0.02 x + 300; 0 ≤ x ≤ 15 000
Donde p denota el precio unitario al mayoreo en dólares, y x la
cantidad demandada. La función de costo total semanal
relacionada con la fabricación de estas videocaseteras es:
C(x) = 0.000003x3 – 0.04x2 + 200x + 70 000
Dólares:
a.Halle la función de ingreso R y la función de ganancia P.
b.Halle la función de costo marginal C’, la función de ingreso
marginal R’ y la función de ganancia marginal P’.
c.Encuentre la función de costo promedio marginal C’.
d.Calcule C’ (3000), R’ (3000) y P’ (3000) e interprete los
resultados.

6. 6
Solución:
a)
R(x) = px
= x (- 0.02x + 300)
= - 0.02x2 + 300x
P(x) = R(x) – C(x)
= - 0.02x2 + 300x – (0.000003x3- 0.04x2 + 200x +
70,000)
= - 0.000003x3 + 0.02x2 + 100x – 70,000

7. 7
b)
C’(x) = 0.000009x2 – 0.08x + 200
R’(x) = - 0.04x + 300
Y
P’(x) = -0.000009x2 + 0.04x + 100
c)
La función de costo promedio es:
x
x
C
x
C
)
(
)
( 
x
x
x
x 70000
200
04
.
0
000003
.
0 2
3




x
x
x
70000
200
04
.
0
000003
.
0 2





8. 8
Por lo tanto, la función de costo promedio marginal es:
d) Con los resultados de (b) se tiene:
C’(3000) = 0.000009 (3000)2 – 0.08(3000) + 200
= 41
Es decir, cuando el nivel de producción es de 3000
viodecaseteras el costo real de producción de una
videocasetera más es aproximadamente $41.
2
70000
04
.
0
000006
.
0
)
(
x
x
x
C 



9. 9
Luego:
R’(3000) = -04 (3000) + 300 = 180
Es decir, el ingreso real obtenido por la venta de la
videocasetera 3001 es de unos $180. Por último:
P’(3000) = -0.000009 (3000)2 + 0.04 (3000) + 100
= 139
Esto es, la ganancia real obtenida por la venta de la
videocasetera 3001 es aproximadamente $ 139.

10. 10
INTEGRAL DEFINIDA
Sea f definida en [a, b]. Si
[f(x1) x + f(x2) x + … + f(xn) x]
Existe para todas las elecciones de los puntos
representativos x1, x2, …, xn en los n subintervalos de [a, b]
con igual longitud x = (b – a)/n, entonces este límite es la
integral definida de f de a a b y se denota . Así,
El número a es el límite inferior de integración y el número b
es el límite superior de integración.


n
lim

b
a
dx
x
f )
(
 
x
x
f
x
x
f
x
x
f
dx
x
f n
n
b
a









 )
(
.....
)
(
)
(
lim
)
( 2
1

11. 11
Teorema fundamental del cálculo:
Sea f continua en [a, b]. Entonces:
= F (b) – F (a)
Donde F es cualquier antiderivada de f, es decir F’ (x) = f(x).
Al aplicar el teorema fundamental del cálculo, se tiene:
Luego, la ecuación se escribe:

b
a
dx
x
f )
(
)
(
)
(
)
( a
F
b
F
x
F
b
a


)
(
)
(
)
(
)
( a
F
b
F
x
F
dx
x
f
b
a
b
a





12. 12
Valor promedio de una función:
Supóngase que f es integrable en [a, b] Entonces tenemos que
el valor promedio de f en [a, b] es:
CASO PRÁCTICO
El precio medio de un departamento en Miraflores entre el 1 de
enero del 2004 y el 1 de enero del 2009 se aproxima mediante
la función:
f(t) = t3 – 7t2 + 17t + 130; 0 ≤ t ≤ 5
Donde f(t) se mide en miles de dólares y t se expresa en años
(t = 0 corresponde al inicio del año 2004). ¿Cuál es el precio
medio promedio de un departamento en Miraflores en ese
intervalo?


b
a
dx
x
f
a
b
)
(
1

13. 13
El precio medio de un departamento en Miraflores en el
periodo indicado está dado por:
ò
5
0
5
0
2
3
4
2
3
130
2
17
3
7
4
1
5
1
)
130
17
7
(
0
5
1
 













t
t
t
t
dt
t
t
t









 )
5
(
130
)
5
(
2
17
)
5
(
3
7
)
5
(
4
1
5
1 2
3
4
417
.
145

417
.
145
$


14. 14
 

x
x
p
dx
x
D
CS
0
)
(
Excedente de los consumidores:
El excedente de los consumidores está dado por:
Donde D es la función de demanda, p es el precio unitario de
mercado y x es la cantidad vendida.
El excedente de los productores:
El excedente de los productores está dado por:
Donde S(x) es la función de oferta, p es el precio unitario en el
mercado y x es la cantidad ofrecida.



x
dx
x
S
x
p
PS
0
)
(

15. 15
Valor futuro total o acumulado de un flujo de ingresos:
El valor futuro total, o acumulado, después de T años, de
un flujo de ingresos de R(t) dólares por año, que ganan
intereses a razón de r por año compuesta en forma
continua, está dado por.
dt
e
t
R
e
A rt
T
rT 


0
)
(

16. 16
CASO PRÁCTICO
En fecha reciente el Grifo Capsol compró una máquina
automática para el lavado de autos que se espera que
genere $40 000 de ingresos por año, dentro de t años,
durante los próximos cinco años. Si los ingresos se
reinvierten en una empresa que genera intereses a razón
de 12% por año compuestos en forma continua, determinar
el valor total acumulado de este flujo de ingresos al cabo de
cinco años.

17. 17
Solución:
Se pide hallar el valor total futuro del flujo de ingresos dado
después de cinco años. Se utiliza (15) con R(t) = 40 000, r =
0.12 y T = 5, se ve que el valor pedido está dado por:
dt
e
e 12
.
0
5
0
)
5
(
12
.
0
40000 

5
0
12
.
0
6
.
0
12
.
0
40000







  t
e
e
60
.
039
274
)
1
(
12
.
0
40000 6
.
0
6
.
0



 
e
e
Se integra con la sustitución
u = -0.12t
O alrededor de $ 274 040.

18. 18
Valor presente de un flujo de ingresos:
El valor presente de un flujo de ingresos de R(t) dólares
por año, que genera intereses a razón de r por año
compuestos en forma continua, está dado por:
dt
e
t
R
PV rt
T



0
)
(

19. 19
CASO PRÁCTICO:
El dueño de un cine local está considerando dos planes
alternativos para renovar y mejorar el local. El plan A requiere
un desembolso inmediato de $250 000, mientras que el plan B
precisa un desembolso de $180 000. Ha estimado que la
adopción del plan A significaría un flujo neto de ingresos
generados a razón de
f(t) = 630 000
dólares por año, mientras que la adopción del plan B
representaría un flujo neto de ingresos generados a razón de
g (t) = 580 000
dólares por año durante los próximos tres años. Si la tasa de
interés prevaleciente durante los próximos cinco años fuese de
10% por año, ¿Cuál plan generaría el mayor ingreso neto al
cabo de tres años?
Rpta:
Plan A $ 1’382 845.00
Plan B $ 1’323 254.00

20. 20
CURVA DE LORENZ
y = x
y
x
1
1

21. 21
Coeficiente de desigualdad de una curva de Lorentz
El coeficiente de desigualdad de una curva de Lorentz es:
CASO PRÁCTICO
En un estudio realizado por el Comité de Desarrollo
Económico de un país en relación con la distribución del
ingreso de ciertos segmentos de la fuerza de trabajo del
país, se vio que las curvas de Lorentz para la distribución
del ingreso de los médicos y de los actores (y actrices) de
cine se describen mediante las funciones.
 dx
x
f
x
L  

1
0
)
(
2

22. 22
respectivamente. Calcular el coeficiente de desigualdad
para cada curva de Lorentz. ¿Cuál profesión tiene una
distribución del ingreso más equitativa?
Solución:
x
x
x
g
y
x
x
x
f
8
3
8
5
)
(
15
1
15
14
)
( 4
2




dx
x
x
x
L  














1
0
2
1
15
1
15
14
2
1
0
3
2
3
1
2
1
15
28







 x
x
311
,
0

375
,
0
2 
L

23. 23
y = x
y
x
1
1
0,311
y = x
y
x
1
1
0,375