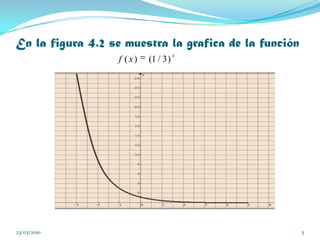
Este documento proporciona información sobre funciones exponenciales y logarítmicas. Explica que una función exponencial tiene la forma f(x)=bx donde b es la base mayor que cero. También describe las propiedades de estas funciones, como que si b es mayor que uno, f(x) aumenta a medida que x aumenta. Además, presenta ejemplos de crecimiento exponencial como poblaciones bacterianas y costos con tasas anuales.

1. 04/03/20101 FUNCIONES EXPONENCIALESUNIDAD 4 Y LOGARITMICAS

2. Una función exponencial es una función de la forma f (x)=bx donde la base es b> 0, el dominio son todos los números reales y el ámbito son todos los números reales positivos.☺EJEMPLO. Trazar las graficas de las funciones 3x y (1/3)x☺SOLUCIONSe elaborara la tabla de valores para la primera función con ayuda de la calculadora04/03/20102FUNCION EXPONENCIAL

3. 04/03/20103Figura 4.1 grafica de la función

4. 04/03/20104Se elabora la tabla de valores para la segunda función, con ayuda de la calculadora.

5. En la figura 4.2 se muestra la grafica de la función 04/03/20105

6. PROPIEDADES DE LA FUNCION EXPONENCIALPara toda b>0, la función f(x)=bx se llama función exponencial con base b. la función tiene las siguientes propiedades :El dominio son todos los números realesEl ámbito o rango son todos los números reales positivosSi b>1, cuando aumenta x aumenta, f(x) aumentaSi 0<b<1, cuando x aumenta, f(x) disminuyeSi b=1, f(x) es la función constante f(x)=104/03/20106

7. Para comprender esto podríamos responder la pregunta ¿Cuál es la potencia x de b?. Así evaluar y=37 equivale a determinar que y= 2187; lo cual se puede hacer mediante la calculador04/03/20107

8. El uso mas común de la función exponencial es el estudio del crecimiento y decaimiento exponenciales. Por ejemplo, la expresión “la población crece exponencialmente” puede ser expresada en forma matemática por medio de la función:F=F(t)=FobKDonde:b> 1☺Fo= Cantidad presente en el tiempo t=0 K es una cantidad positiva que depende de la tasa de crecimiento04/03/20108

9. Ejemplos de poblaciones que crecen de manera exponencial son las siguientes:El crecimiento de una población de bacterias esta dado por: B(t) = 2tEl crecimiento de la población del mundo (en billones) se puede expresar como:P(t)= 4(2)t/35El crecimiento de los costos de los artículos, si se tiene una tasa anual del 12%, se expresa como, al considerar un costo inicial de algún articulo de 100 pesos; C(t)= 100 (1.2)t04/03/20109

10. EJEMPLO Algunas cuentas de ahorros pagan 5.5% de interés capitalizable trimestralmente, ¿Cuál será la tasa de porcentaje anual efectiva en tal cuenta?SOLUCIÓNSi se depositan 100 pesos en una cuenta de ahorros de este tipo y calculamos el monto al final del año, se puede determinar la tasa de porcentaje anual.P=100(1+0.055/4)4=105.61Por lo tanto, la tasa de porcentaje anual es 5.61%04/03/201010

11. LA BASE NATURALLa base natural de la función que mas frecuentemente se encuentra en las aplicaciones es un numero irracional. Para ver como ocurre esto, consideremos la formula para determinar el monto acumulado en una cuenta con interés compuesto, la cual esta dada por. At= P (1+I/n)ntDONDE I= tasa de interés. t= numero de años, n= numero de veces al año en que se compone el interés, P= capital y A= monto acumulado después de t años.Para simplificar el problema considere que se invirtió $1 por un año a una tasa de interés del 100%; es decir, P= I t= 1. Por lo que, la expresión anterior se reduce:A=(1+1/n)n04/03/201011

12. ¿Qué ocurre cuando n aumenta?Esto es, si invertimos $1 durante un año al 100% ¿Cuánta diferencia hay en que tan a menudo se capitaliza el interés? Se encontrara la cantidad redituada si el interés se compone anualmente, semestralmente, semanalmente, etc., hasta llegar a horas; esto se logra haciendo n=1,2,4,12,52,380,8640. En la siguiente tabla se encontrara la información .04/03/201012

13. 04/03/201013

14. Observe que se reciben aumentos sustanciales hasta los cálculos semanales (52) o diarios (360) y después los aumentos son insignificantes. De hecho no importa que tan a menudo se capitalice el interés, el monto acumulado no excede un numero que es aproximadamente 2.7182818 y se denota por el símbolo e04/03/201014

15. La base natural tiene muchas aplicaciones ya que describe el crecimiento continuo. Si el interés se capitalizara continuamente, se podría escribir la formula de interés compuesto como la función:At=PeltEjemplo:El municipio de Llera de Juárez en Tamaulipas tenia una población de 15000 habitantes en 1980 y crece de acuerdo a la función y=y0e0.04t donde t esta dado en años ¿cuál será su población en el año 2000? SoluciónUtilizando la función se tiene;Y=15000 e0.04(20)= 33383 habitantes, t=2004/03/201015

16. 4.5 FUNCIONES LOGARITMICASPara cada b> 1 existe una función llamada la función logaritmo en la base b.La aseveración , es equivalente a la aseveración . Note que en el exponente es y, donde .El echo de que el logaritmo, es un exponente. Es la potencia a la cual la base b debe ser elevada para obtener x . Analice los datos de la sig. Tabla: 04/03/201016

17. 04/03/201017Ejemplo: despejar x de (a), (b) y (c) solución: (a) (b) (c)

18. 04/03/201018Ejemplo: trazar la grafica de la función solución: para obtener los valores de esta grafica se elaborara la tabla siguiente:

19. En la figura 4.3 se presenta la grafica de la función04/03/201019

20. PROPIEDADES DE LA FUNCIÓN LOGARITMO.1 L(1)=0, para cualquier b>1.2 El dominio de L(x) son todos los números reales positivos3 El ámbito o rango de L(x)son todos los números reales4 A medida que x aumenta, L(x) aumentaLa relación entre la función exponencial y la función logaritmo es la misma que la que hay entre la función de elevar al cuadrado y la raíz cuadrada aplicada a números positivos.04/03/201020

21. Cuando elevamos al cuadrado un numero positivo c, se obtiene . Si luego se extrae la raíz cuadrada de se regresa a c. Por ejemplo: si se considera b=3 y x=9, entonces se eleva el 3 a la novena potencia y se obtiene 19638. después, obteniéndose el logaritmo de 19638 en base 3, se regresa al 9. alternativamente si tomamos el logaritmo de 9 en la base 3 se tiene 2; si después se eleva 3 a la segunda potencia se regresa al 9.04/03/201021

22. PRINCIPIOS DE LOS LOGARITMOSPara localizar los logaritmos de números pequeños y grandes que se pueden expresar en notación científica, se usan los principios algebraicos de los logaritmos que se derivan de las exponenciales y que a continuación se presentan . Para cualquier base b>1 y cualesquiera números reales positivos r y s;12 3 04/03/201022

23. Ejemplo: utilizando los principios anteriores despejar la variable x de:Log (x+3) + log(x)=1Solución: log (x+3) + log (x) = 1 por el principio 1 se puede expresar como:Log(x(x+3))=1 por la definición de logaritmo se tiene factorizando se obtendrá: toma solo el valor positivo ya que no se puede obtener el log de un valor negativo X=204/03/201023

24. Ejemplo: calcular el valor deSolución: se toma entoncesLogLogLogLog log10=1LogLogEn general, si el numero real x se expresa en notación científica:Entonces:el entero c se llama la característica de x y log m se llama la mantisa de c 04/03/201024

25. Crecimiento logarítmico.Algunas cantidades carecen en forma logarítmica. El ejemplo típico que presenta en este caso es el del sonido en el cual se señala que la intensidad del sonido es directamente proporcional al logaritmo de la potencia del sonido. Es decir:N=N(I)=10log(I/Io)Donde:N=numero de decubeles (intensidad del sonido)I=potencia del sonido en watts por cm cuadradoIo=constante que presenta la potencia del sonido justo por debajo del umbral de audición ( aproximadamente watts por centímetro cuadrado).La grafica de N=10log(I/Io)se presenta en la figura 4.4 04/03/201025

26. Figura 4.4 grafica de la función N=10log(I/Io)04/03/201026

27. ECUACIONES EXPONENCIALE S Y LOGARITMICASexisten algunas aplicaciones que requieren la solución de una ecuación que incluye una función logarítmica o exponencial, como se muestra en el siguiente ejemplo.Ejemplo: La población mundial en 1975 fue de cerca de 4 billones y se ha duplicado cada 35 años. Suponiendo que esta tasa de crecimiento continua, estimas el año en el cual la población mundial alcanzara: (a)32 billones, (b)37 billones.04/03/201027

28. Solución: Si P(y) representa la población del año, entonces:P(y)= Por lo que:32=3=(y-1975)/352080=y04/03/201028

29. Por lo tanto, la población alcanzara los 32 billones en el año 2080 y los 37 billones en el año de 2087.33, si continua la tasa de crecimiento señalada.Ejemplo:Los materiales traslucidos tienen la propiedad de reducir la intensidad de la luz que pasa atraves de ellos, 1 hoja de un mm de espesor de un cierto plástico translucido reduce la intensidad de la luz en 8%. ¿Cuántas hojas de este tipo se necesitan para reducir la intensidad de un haz de luz a un 25% de su valor original?Solución: cada hoja de plástico reduce la intensidad de luz al 92% de su valor original. Por lo que:Por lo tanto con 17 hojas seria suficiente04/03/201029

30. ejercicios1.- Resuelva mediante la calculadora: A) 54.37 B)(-3.25)101 C) (2)102 x (5)3.15 2.- trazar las siguientes graficas de las funciones exponenciales: A) Y=4 B) Y=2-3 C) Y=1+33.- Una hoja de papel tiene 0.076 mm de espesor. Doblándola una vez da un espesor de dos hojas ¿Qué espesor tendrá la hoja si se doblo 20 veces?4.- Si se depositan 1500 en una cuenta de ahorros ¿Cuánto tendrá al final de 5 años si el interés es: A) 5.25% capitalizable trimestralmente B)5% capitalizable semestralmente04/03/201030

31. 5.- Usted compro un anillo por $200, ¡Cuánto valdrá este anillo en 10 años si: a)El valor aumenta 12% cada año?b)Su valor después de t años esta dado por ?6.- despeje x sin calculadora:(a) (b) (c)7.-despeja x usando la calculadora:(a) (b) (c)8.-trace las graficas de las siguientes funciones:(a)y=log x (b)y=Ln x (c)y=4+log x (d) 04/03/201031

32. 9.- un temblor de tierra registro 8.7 en la escala de Richter, ¿Cuántas veces es mas fuerte este que uno de 5.5 en la misma escala?10.-¿en que año la población mundial llegara a los 25 billones y en cual a los 50 billones de habitantes, de acuerdo con el ejemplo mostrado en paginas anteriores?04/03/201032