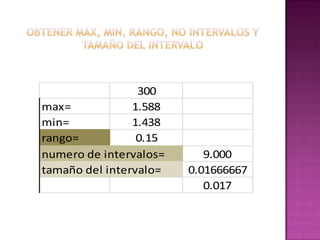
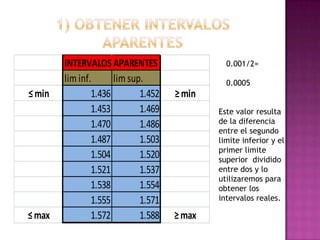
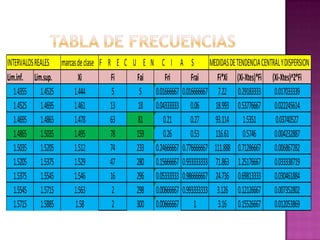
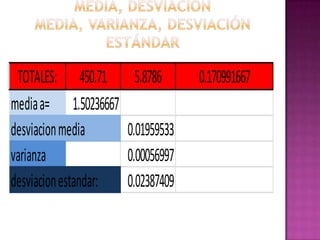
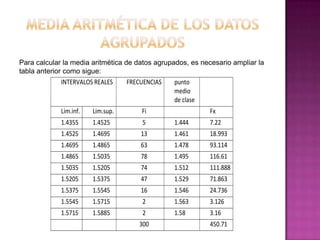
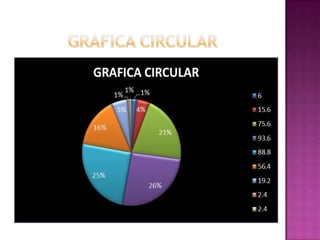
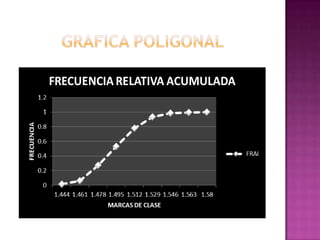
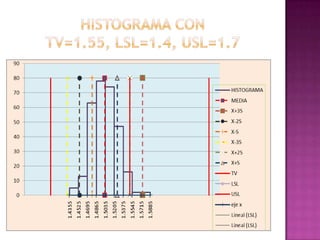
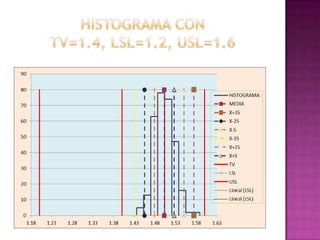
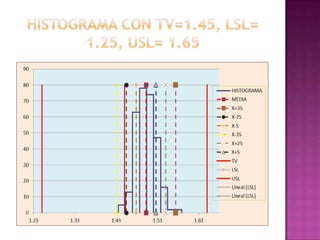
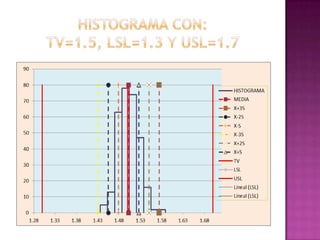
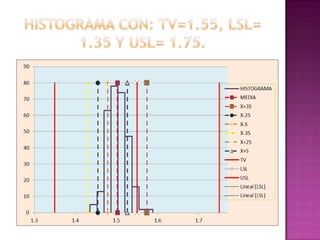
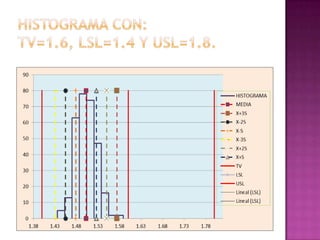
Este documento presenta los resultados de un estudio estadístico descriptivo realizado sobre una muestra de 300 pernos para determinar si cumplen con las especificaciones del cliente en términos de su diámetro. Se agruparon los datos en intervalos y se calcularon medidas como la media, mediana y moda. Los resultados muestran que la media es 1.50236667 cm, la mediana es 1.47883333 cm y la moda es 1.495 cm, indicando que el lote de pernos cumple con los estándares requeridos. Sin embargo, los resultados deben reinterpre

1. PRESENTADO POR:
MARIA GUADALUPE RODRIGUEZ
MARTHELL
2 CUATRIMESTRE SECCION D
UNIVERSIDAD TECNOLOGICA DE
TORREON

2. PROCESOS DE PRODUCCION AREA MANUFACTURA
PROBABILIDAD Y ESTADISTICA
“ESTADISTICA DESCRIPTIVA Y SU RELACION CON LA PROBABILIDAD”
PRESENTADO POR:
MARIA GUADALUPE RODRIGUEZ MARTHELL
2° CUATRIMESTRE SECCION D
PROFESOR:
LIC. G. EDGAR MATA ORTIZ
16 DE FEBRERO DEL 2012

3. La estadística es la ciencia que da sentido a los datos
numéricos. Cuando un grupo de gerentes de una empresa
tiene que decidir cómo cumplir las nuevas especificaciones
del cliente, pueden guiarse por sus propios conocimientos e
intuición o mas acertadamente, realizar herramientas con las
cuales pueden apoyarse para saber si la empresa puede o
esta cumpliendo con dichas especificaciones.
Además, gracias a ella, podemos hacer un pronóstico de lo
que venderemos en un futuro, si obtendremos ganancias, si la
empresa necesita mejorar o si nuestros proyectos
implementados están funcionando. Mediante
diagramas, datos reales, tablas estadísticas (grafico de
cajas, grafica circular, graficas de barras, pero muy
especialmente el histograma), demostramos a las altas
gerencias que hace falta una mejoría o que el sistema o
método que estamos implementando nos está ayudando a
aumentar nuestro servicio o producto terminado.

4. En la fabricación de pernos, el diámetro es
una característica importante para su uso. Con
el objeto de determinar si un lote cumple con
las especificaciones del cliente, se extrae una
muestra de 300 piezas y se inspecciona. Se
realiza un estudio estadístico agrupando los
datos en 9 intervalos, se calcula media
aritmética, mediana, moda, desviación
media, varianza y desviación estándar.

6. 300
max= 1.588
min= 1.438
rango= 0.15
numero de intervalos= 9.000
tamaño del intervalo= 0.01666667
0.017

7. INTERVALOS APARENTES 0.001/2=
lim inf. lim sup. 0.0005
≤ min 1.436 1.452 ≥ min
1.453 1.469 Este valor resulta
1.470 1.486 de la diferencia
entre el segundo
1.487 1.503 limite inferior y el
primer limite
1.504 1.520 superior dividido
1.521 1.537 entre dos y lo
utilizaremos para
1.538 1.554 obtener los
1.555 1.571 intervalos reales.
≤ max 1.572 1.588 ≥ max

8. Estos intervalos reales se obtienen
de la suma entre los limites
inferiores en los intervalos
aparentes y 0.005; y los limites
superiores es la resta entre los
superiores aparentes y 0.005.

9. INTERVALOS REALES marcas de clase F R E C U E N C I A S MEDIDAS DE TENDENCIA CENTRAL Y DISPERSION
Lim.inf. Lim.sup. Xi Fi Fai Fri Frai Fi*Xi (Xi-Xtes)*Fi (Xi-Xtes)^2*Fi
1.4355 1.4525 1.444 5 5 0.01666667 0.016666667 7.22 0.29183333 0.017033339
1.4525 1.4695 1.461 13 18 0.04333333 0.06 18.993 0.53776667 0.022245614
1.4695 1.4865 1.478 63 81 0.21 0.27 93.114 1.5351 0.03740527
1.4865 1.5035 1.495 78 159 0.26 0.53 116.61 0.5746 0.004232887
1.5035 1.5205 1.512 74 233 0.24666667 0.776666667 111.888 0.71286667 0.006867282
1.5205 1.5375 1.529 47 280 0.15666667 0.933333333 71.863 1.25176667 0.033338719
1.5375 1.5545 1.546 16 296 0.05333333 0.986666667 24.736 0.69813333 0.030461884
1.5545 1.5715 1.563 2 298 0.00666667 0.993333333 3.126 0.12126667 0.007352802
1.5715 1.5885 1.58 2 300 0.00666667 1 3.16 0.15526667 0.012053869

10. TOTALES: 450.71 5.8786 0.170991667
media a= 1.50236667
desviacion media 0.01959533
varianza 0.00056997
desviacion estandar: 0.02387409

11. Sabemos que las clases o categorías se
refieren a las variaciones de la muestra:
1.4355≤ 1.4525 significa que hemos reunido
aquí los datos para cualquier perno de la
muestra que sea mayor que 1.4355 pero
menor o exactamente igual a 1.4525 en la
medida de su diámetro. De 1.4525 ≤1.4695
significa que encontramos alguna pieza que
esta en clase o grupo de pernos que tienen
un diámetro mayor de 1.4525 pero menos o
exactamente igual a 1.4695 cm de diámetro
y así sucesivamente.

12. En la siguiente columna que es la de
frecuencia, nos encontramos con que 5 piezas
tienen entre 1.4355 y 1.4525 cm de
diámetro, 13 piezas tienen entre 1.4525 y
1.4695 de diámetro, y, en conjunto, tenemos
datos de 300 piezas que abarcan toda muestra
que tomamos de piezas con diámetros entre
1.4355 y 1.5885.

13. Para calcular la media aritmética de datos agrupados, es necesario ampliar la
tabla anterior como sigue:
INTERVALOS REALES FRECUENCIAS punto
medio
de clase
Lim.inf. Lim.sup. Fi Fx
1.4355 1.4525 5 1.444 7.22
1.4525 1.4695 13 1.461 18.993
1.4695 1.4865 63 1.478 93.114
1.4865 1.5035 78 1.495 116.61
1.5035 1.5205 74 1.512 111.888
1.5205 1.5375 47 1.529 71.863
1.5375 1.5545 16 1.546 24.736
1.5545 1.5715 2 1.563 3.126
1.5715 1.5885 2 1.58 3.16
300 450.71

14. La media aritmética es
LA MEDIA ARITMETICA PARA DATOS AGRUPADOS= ∑fx = 450.71 = 1.502366667
n 300
Como podemos observar la media aritmética, o sea, el valor
medio de las medidas es 1.502366667 entonces estamos entre
un valor medio de 1.4355 a 1.5885 que es este.

15. La mediana es el valor medio del conjunto de datos que tenemos, se encuentra que la
media es relativamente fácil. En este ejercicio de los pernos podemos ver que hay un
total de 300 puntos de datos, un número par de puntos de datos. La clase media se pone
de relieve en la primera tabla que vimos al inicio. El cálculo de la mediana lo
obtendremos mediante la siguiente formula:
MEDIANA PARA DATOS AGRUPADOS: L + n/2-CF (i)
f
L = el límite inferior de la clase que contiene la mediana
n = número total de frecuencias
f = la frecuencia de la clase mediana
CF = el número total de frecuencias en las clases antes de la clase que contiene la
mediana
i = la anchura de la clase que contiene la mediana
Poniendo los números del ejemplo en la fórmula actual, vemos que el valor de la
mediana se representa de la forma siguiente:
Mediana de las medidas del diámetro de los pernos=1.4355+300/2-(5+13)(1.4525) =
63
1.4355+150-(18) *1.4525 = 4.47883333
63
Como podemos observar el valor de la mediana es 4.47883333 lo que nos muestra que
estamos en un buen punto de mejoría en cuanto a nuestras medidas estándar o al valor
deseado al cual no queremos sobrepasar. Podría decirse que el cliente puede estar
satisfecho con los valores que le estamos ofreciendo de acuerdo a los valores requeridos
y nuestra calidad no esta tan mal.

16. La moda es, simplemente, el punto f mediados de la clase
que contiene el mayor número de frecuencias de clase. En
este caso, observaremos que la moda es la medida que mas
se repite en nuestros datos, o sea, en las medidas obtenidas
en la muestra. Nos encontramos con el modo de
funcionamiento siguiente:
La clase que contiene el mayor número de frecuencias de las
clases:
1.4865 1.5035
Se destacan a continuación el punto medio de la clase modal
1.495
La moda de estos datos es de 1.495

17. En resumen:
 media aritmética de los datos agrupados
La
es 1.502366667 cm de diámetro.
 mediana de los datos agrupados es
La
4.47883333 cm de diámetro.
 moda de los datos agrupados es de 1.495
La
cm de diámetro.

18. CLASE MEDIANA
SUSTITUIR EN LA FORMULA:
1.4865
XI SIGNIFICA LIMITE INF EN LA CLASE MEDIANA
81
FRECUENCIA ACUMULADA DE LA CLASE ANTERIOR A LA CLASE MEDIANA
78
LIMITE SUPERIOR MENOS EL LIMITE INFERIOR 1.5035
0.0170 -
1.4865
MODA:
LA FRECUENCIA ABSOLUTA MAS GRANDE Y TOMAR LA MARCA DE CLASE
1.495
MEDIA ARITMETICA:
1.50236667

20. CUARTIL INICIAL
1.444 3
1.444 7
CUARTIL 1
1.4780 3
1.4780 7
LINEA 1
1.444 5
1.4780 5
CUARTIL 2
1.5120 3
1.5120 7
CUARTIL 3
1.5630 3
1.5630 7
LINEA 2
1.4780 7
1.5630 7
LINEA 3
1.478 3
1.5630 3
LIMITE SUPERIOR
1.5800 3
1.5800 7
LINEA 4
1.5630 5
1.5800 5

23. Los resultados son reinterpretados si las
especificaciones del cliente fuesen diferentes:
 a. 1.40±0.15
 b. 1.45±0.15
 c. 1.55±0.15
 d. 1.60±0.15
 e. 1.40±0.20
 f. 1.45±0.20
 g. 1.50±0.20
 h. 1.55±0.20
 i. 1.60±0.20

34. La estadística desde mi punto de vista es muy
importante ya que nos permite ver la cantidad
de mejoría, o, en su defecto, la disminución de
nuestra productividad, notar si estamos
haciendo bien las cosas, si en realidad estamos
aprovechando nuestros recursos y si vamos por
un buen camino.