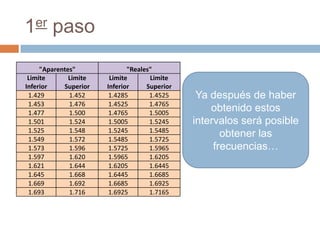
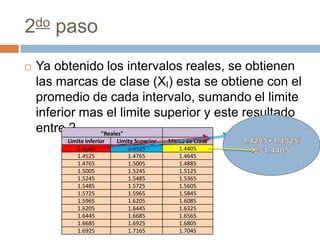
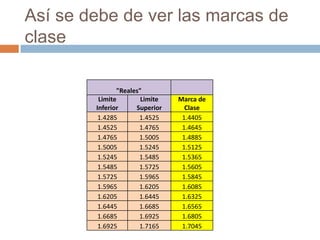
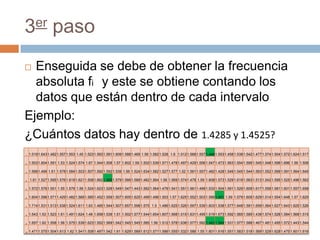
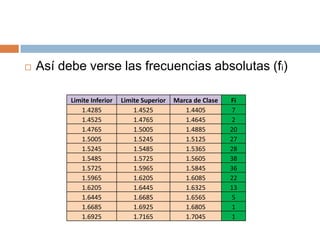
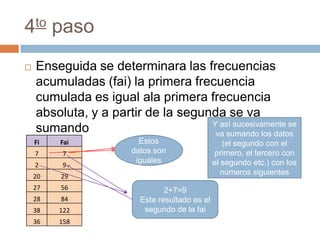
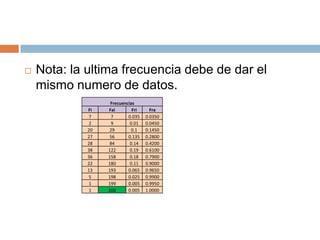
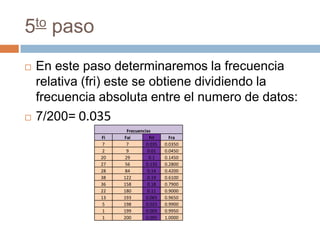
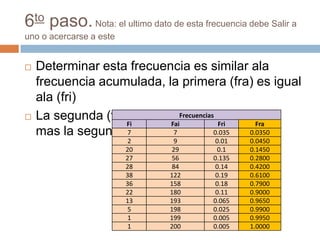
El documento explica cómo obtener las frecuencias de datos agrupados en intervalos. En primer lugar, se determinan los límites reales de cada intervalo y la marca de clase como promedio. Luego, se cuentan los datos en cada intervalo para obtener la frecuencia absoluta. A continuación, se calculan la frecuencia acumulada, relativa y relativa acumulada mediante sumas sucesivas de las frecuencias.

1. FRECUENCIAS
¿CÓMO OBTENER LAS
FRECUENCIAS:
FI,FAI,FRI,FRAI
Luis Alonso Gallegos Arias

2. Introducción:
 En estas diapositivas encontraras como
obtener las frecuencias de unos datos
agrupados con los ejemplos que se mostraran
enseguida.

3. 1er paso
"Aparentes" "Reales"
Limite Limite Limite Limite
Inferior Superior Inferior Superior
1.429 1.452 1.4285 1.4525 Ya después de haber
1.453 1.476 1.4525 1.4765
1.477 1.500 1.4765 1.5005
obtenido estos
1.501 1.524 1.5005 1.5245 intervalos será posible
1.525 1.548 1.5245 1.5485
1.549 1.572 1.5485 1.5725
obtener las
1.573 1.596 1.5725 1.5965 frecuencias…
1.597 1.620 1.5965 1.6205
1.621 1.644 1.6205 1.6445
1.645 1.668 1.6445 1.6685
1.669 1.692 1.6685 1.6925
1.693 1.716 1.6925 1.7165

4. 2do paso
 Ya obtenido los intervalos reales, se obtienen
las marcas de clase (XI) esta se obtiene con el
promedio de cada intervalo, sumando el limite
inferior mas el limite superior y este resultado
entre 2 "Reales"
Limite Inferior Limite Superior Marca de Clase
1.4285 1.4525 1.4405
1.4525 1.4765 1.4645
1.4765 1.5005 1.4885
1.5005 1.5245 1.5125
1.5245 1.5485 1.5365
1.5485 1.5725 1.5605
1.5725 1.5965 1.5845
1.5965 1.6205 1.6085
1.6205 1.6445 1.6325
1.6445 1.6685 1.6565
1.6685 1.6925 1.6805
1.6925 1.7165 1.7045

5. Así se debe de ver las marcas de
clase
"Reales"
Limite Limite Marca de
Inferior Superior Clase
1.4285 1.4525 1.4405
1.4525 1.4765 1.4645
1.4765 1.5005 1.4885
1.5005 1.5245 1.5125
1.5245 1.5485 1.5365
1.5485 1.5725 1.5605
1.5725 1.5965 1.5845
1.5965 1.6205 1.6085
1.6205 1.6445 1.6325
1.6445 1.6685 1.6565
1.6685 1.6925 1.6805
1.6925 1.7165 1.7045

6. 3er paso
 Enseguida se debe de obtener la frecuencia
absoluta fi y este se obtiene contando los
datos que están dentro de cada intervalo
Ejemplo:
¿Cuántos datos hay dentro de 1.4285 y 1.4525?
1 1.519 1.643 1.482 1.557 1.553 1.45 1.523 1.593 1.591 1.609 1.588 1.469 1.56 1.582 1.528 1.6 1.512 1.568 1.557 1.448 1.553 1.458 1.538 1.542 1.477 1.574 1.504 1.572 1.624 1.517
2 1.503 1.604 1.591 1.53 1.524 1.574 1.67 1.544 1.508 1.57 1.602 1.59 1.502 1.539 1.571 1.478 1.497 1.429 1.556 1.547 1.473 1.563 1.554 1.595 1.545 1.548 1.596 1.696 1.56 1.506
3 1.568 1.499 1.61 1.578 1.584 1.503 1.507 1.592 1.592 1.539 1.56 1.524 1.634 1.582 1.527 1.577 1.52 1.561 1.557 1.482 1.428 1.549 1.545 1.544 1.563 1.552 1.599 1.591 1.564 1.645
4 1.61 1.527 1.595 1.576 1.619 1.621 1.508 1.662 1.485 1.579 1.566 1.589 1.482 1.564 1.58 1.569 1.574 1.478 1.59 1.608 1.573 1.529 1.619 1.563 1.513 1.542 1.595 1.525 1.496 1.562
5 1.572 1.576 1.551 1.55 1.579 1.56 1.524 1.623 1.528 1.549 1.547 1.443 1.562 1.564 1.479 1.541 1.551 1.561 1.499 1.533 1.504 1.591 1.529 1.609 1.617 1.559 1.581 1.601 1.557 1.658
6 1.604 1.596 1.571 1.429 1.482 1.569 1.585 1.452 1.559 1.507 1.605 1.625 1.499 1.496 1.503 1.57 1.625 1.552 1.503 1.586 1.451 1.59 1.579 1.609 1.629 1.514 1.554 1.648 1.57 1.625
7 1.714 1.531 1.513 1.538 1.524 1.611 1.63 1.485 1.544 1.507 1.657 1.598 1.575 1.5 1.486 1.625 1.526 1.597 1.539 1.603 1.538 1.577 1.648 1.591 1.659 1.564 1.627 1.643 1.625 1.526
8 1.543 1.53 1.523 1.61 1.491 1.624 1.48 1.658 1.539 1.51 1.502 1.577 1.544 1.654 1.607 1.568 1.515 1.631 1.495 1.519 1.673 1.592 1.565 1.585 1.439 1.574 1.528 1.584 1.568 1.515
9 1.657 1.62 1.558 1.56 1.575 1.539 1.623 1.552 1.569 1.542 1.545 1.545 1.585 1.56 1.512 1.578 1.636 1.577 1.582 1.443 1.544 1.531 1.577 1.588 1.467 1.481 1.495 1.572 1.443 1.544
10 1.471 1.575 1.504 1.613 1.62 1.541 1.508 1.497 1.542 1.61 1.629 1.589 1.612 1.571 1.586 1.555 1.532 1.586 1.55 1.601 1.616 1.551 1.583 1.518 1.569 1.529 1.628 1.475 1.601 1.616

7.  Así debe verse las frecuencias absolutas (fi)
Limite Inferior Limite Superior Marca de Clase Fi
1.4285 1.4525 1.4405 7
1.4525 1.4765 1.4645 2
1.4765 1.5005 1.4885 20
1.5005 1.5245 1.5125 27
1.5245 1.5485 1.5365 28
1.5485 1.5725 1.5605 38
1.5725 1.5965 1.5845 36
1.5965 1.6205 1.6085 22
1.6205 1.6445 1.6325 13
1.6445 1.6685 1.6565 5
1.6685 1.6925 1.6805 1
1.6925 1.7165 1.7045 1

8. 4to paso
 Enseguida se determinara las frecuencias
acumuladas (fai) la primera frecuencia
cumulada es igual ala primera frecuencia
absoluta, y a partir de la segunda se va
Y así sucesivamente se
sumando va sumando los datos
Fi Fai Estos (el segundo con el
7 7 datos son primero, el tercero con
iguales el segundo etc.) con los
2 9
20 29
números siguientes
27 56 2+7=9
28 84 Este resultado es el
38 122 segundo de la fai
36 158

9.  Nota: la ultima frecuencia debe de dar el
mismo numero de datos.
Frecuencias
Fi Fai Fri Fra
7 7 0.035 0.0350
2 9 0.01 0.0450
20 29 0.1 0.1450
27 56 0.135 0.2800
28 84 0.14 0.4200
38 122 0.19 0.6100
36 158 0.18 0.7900
22 180 0.11 0.9000
13 193 0.065 0.9650
5 198 0.025 0.9900
1 199 0.005 0.9950
1 200 0.005 1.0000

10. 5to paso
 En este paso determinaremos la frecuencia
relativa (fri) este se obtiene dividiendo la
frecuencia absoluta entre el numero de datos:
 7/200= 0.035
Frecuencias
Fi Fai Fri Fra
7 7 0.035 0.0350
2 9 0.01 0.0450
20 29 0.1 0.1450
27 56 0.135 0.2800
28 84 0.14 0.4200
38 122 0.19 0.6100
36 158 0.18 0.7900
22 180 0.11 0.9000
13 193 0.065 0.9650
5 198 0.025 0.9900
1 199 0.005 0.9950
1 200 0.005 1.0000

11. 6to paso. Nota: el ultimo dato de esta frecuencia debe Salir a
uno o acercarse a este
 Determinar esta frecuencia es similar ala
frecuencia acumulada, la primera (fra) es igual
ala (fri)
 La segunda (frai) es igualFrecuencias
ala primer a(frai)
Fi Fai Fri Fra
mas la segunda 7(fri) 7 0.035 0.0350
2 9 0.01 0.0450
20 29 0.1 0.1450
27 56 0.135 0.2800
28 84 0.14 0.4200
38 122 0.19 0.6100
36 158 0.18 0.7900
22 180 0.11 0.9000
13 193 0.065 0.9650
5 198 0.025 0.9900
1 199 0.005 0.9950
1 200 0.005 1.0000