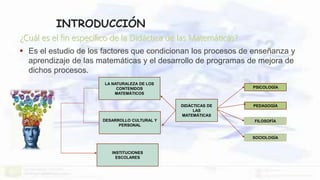
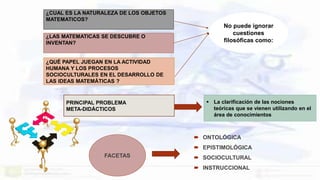
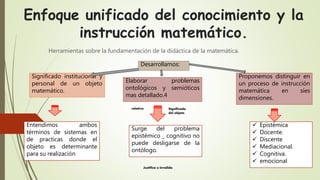
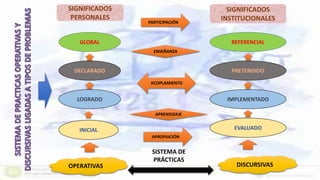
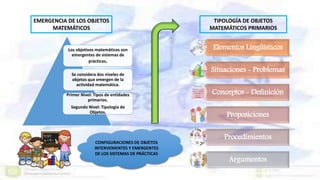
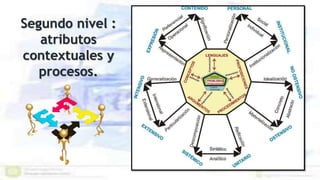
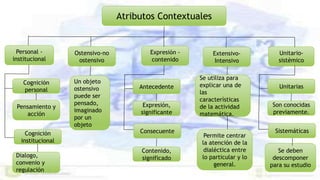
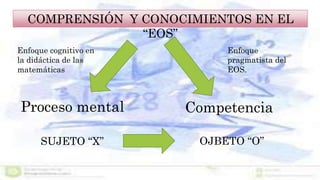
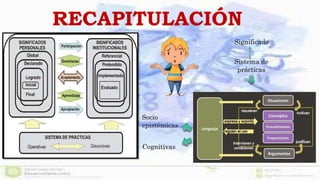
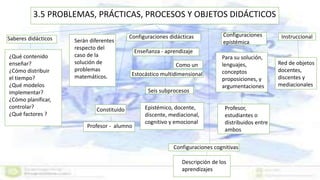
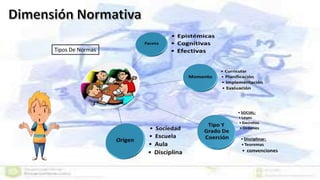
Este documento presenta un enfoque ontosemíotico para el estudio del conocimiento y la instrucción matemática. Propone analizar los procesos de enseñanza y aprendizaje de las matemáticas desde cuatro facetas: ontológica, epistemológica, sociocultural e instruccional. Además, sugiere distinguir cinco dimensiones en un proceso de instrucción matemática: epistémica, docente, discente, mediacional y cognitiva-emocional.