El documento presenta información sobre la coordinación y revisión técnica de un libro de texto de matemáticas para octavo grado en Nicaragua. Contiene los nombres de los profesores responsables de la coordinación general, revisión y asesoría técnica del libro. También incluye información sobre el diseño, ilustración y financiamiento del libro, así como agradecimientos a la Sociedad Matemática de Nicaragua y docentes que participaron en el proceso de validación.

2. Coordinación General, Revisión y Asesoría Técnica
Profesora María Elsa Guillén
Profesora Rosalía Ríos Rivas
Autor
Profesor Luis Adolfo Gámez Rodríguez
Revisión Técnica General
Profesora Rosalía Ríos Rivas
Revisión y Asesoría Técnica Científica
Profesor Francisco Emilio Díaz Vega
Profesor Humberto Antonio Jarquín López
Profesor Jorge Alberto Velásquez Benavidez
Sociedad Matemática de Nicaragua
Diseño y Diagramación
Ramón Nonnato Morales
Róger Alberto Romero
Miguel Ángel Mendieta Rostrán
Ilustración
Róger Alberto Romero
Fuente de Financiamiento
PASEN I - Recursos del Tesoro - PROSEN
Agradecemos los valiosos aportes de la Sociedad Matemática de Nicaragua y de los docentes
durante el proceso de validación.
Primera Edición___________
© Todos los derechos son reservados al Ministerio de Educación (MINED), de la República de
Nicaragua.
Este texto es propiedad del Ministerio de Educación (MINED) , de la República de Nicaragua.
Se prohíbe su venta y reproducción total o parcial.
«La presente publicación ha sido reproducida con el apoyo de la Unión Europea a través del
Programa de Apoyo al Sector Educación en Nicaragua (PROSEN). El contenido de la misma es
responsabilidad exclusiva del MINED y en ningún caso debe considerarse que refleja los puntos
de vista de la Unión Europea».

3. PRESENTACIÓN
El Gobierno de Reconciliación y Unidad Nacional, a través del Ministerio
de Educación (MINED), entrega a docentes y a estudiantes de Educación
Secundaria, el libro de texto de Matemática en el cual se desarrollan los
cinco pensamientos: aleatorio ,numérico ,variacional, métrico y espacial. La
Matemática es una herramienta esencial en campos como las ciencias de la
Tierra y la naturaleza, la medicina, las ciencias sociales, la computación, la
arquitectura, la ingeniería y en la vida cotidiana.
El propósito fundamental del texto, es propiciar en los estudiantes un papel
más activo en el proceso de aprendizaje para que puedan interactuar con
los conocimientos planteados en el libro, permitiéndoles que complementen
lo desarrollado en la clase, consolidar, comparar, profundizar en aquellos
aspectos que explicó su docente y prepararse para la evaluación.
El libro de texto a través de sus contenidos y actividades, contribuye a la
formación en valores individuales, comunitarios y sociales, los que se
reflejarán en el comportamiento de la o el estudiante dentro y fuera del Centro
Educativo.
El libro de texto es un tesoro valioso en las manos de cada estudiante, y
cuidarlo con esmero, permitirá que otros compañeros que están en los
grados que les anteceden también puedan hacer uso de él, en su proceso de
aprendizaje.
Esto significa que el libro de texto es una propiedad social por tanto se debe
cuidar porque no solo a usted le será de ayuda, sino que dependiendo del cuido
que le dé, también le será de provecho a otros, razón por la que le sugerimos
lo forre, no lo manche, no lo ensucie, no lo rompa, ni lo deshoje. Esa será
su contribución desinteresada y solidaria, con los próximos estudiantes que
utilizarán este libro.
Ministerio de Educación

4. INTRODUCCIÓN
El presente texto corresponde a los contenidos del área de Matemática del Octavo Grado
de la Educación Media.
El texto contiene 7 unidades con los siguientes contenidos:
En la Unidad I, se desarrollan los conceptos fundamentales de la Estadística Descriptiva
para datos agrupados. Se presenta un repaso de los temas de Estadística Descriptiva
para datos no agrupados, los cuales son abordados con detalle en el Libro de Texto de
Matemática de Octavo Grado.
En la Unidad II, se estudia el conjunto de los números reales y sus propiedades. Se hace
énfasis en la interpretación geométrica de las propiedades de los números reales. Se
hace un repaso de las propiedades fundamentales de los números naturales, enteros y
racionales.
En la Unidad III, se estudian los conceptos fundamentales de álgebra. Se abordan las
expresiones algebraicas tales como monomio, binomio y trinomio, y las operaciones en las
que intervienen. Se utiliza la geometría para la interpretación de las propiedades básicas
de las expresiones algebraicas y la construcción de modelos algebraicos basados en
situaciones de la realidad.
En la Unidad IV, se estudian las operaciones con polinomios: suma, resta, multiplicación y
división. Se introduce la división sintética (método de Ruffini) para la división de polinomios.
La geometría se utiliza para la interpretación de las propiedades de los polinomios. Se
desarrollan los productos notables y su interpretación geométrica.
En la Unidad V, se estudian las funciones. Se inicia con un repaso del concepto de relación,
que ya ha sido abordado con detalle en Séptimo Grado. Una característica fundamental
de esta unidad, es que las funciones que se estudian tienen como dominio el conjunto de
los números enteros o subconjuntos de números enteros. Estas funciones son llamadas
funciones discretas. Se abordan las funciones lineales con sus propiedades tratándolas
como funciones lineales discretas. Se presentan diferentes interpretaciones del concepto
de función a través de modelos basados en situaciones de la realidad cotidiana. También
se estudian en esta unidad las ecuaciones lineales de primer orden con una incógnita y
sus aplicaciones a situaciones de la realidad.
En la Unidad VI, se desarrollan los conceptos básicos de Geometría Euclidiana Plana a
partir del concepto de pentágono regular. Los conceptos básicos de Geometría se abordan
con detalle en el Séptimo Grado. En esta Unidad se hace un repaso de los conceptos
básicos hasta los cuadriláteros. Las demostraciones están presentes sin embargo, no
representan un peso específico significativo en el desarrollo de la teoría. Se concluye la
unidad con el concepto de circunferencia y círculo.

5. En la Unidad VII, se estudian perímetros y áreas de regiones poligonales. Se estudian
los perímetros de polígonos regulares y se presenta una clasificación de los polígonos
regulares. También se aborda el concepto de área de una región limitada por un polígono
regular y el área del círculo. Se concluye esta unidad con el tema “Construcciones
geométricas con regla y compás”.
El texto está estructurado a doble columna, siendo la columna izquierda dedicada a
temas sobre historia de la Matemática, reforzamiento, curiosidades matemáticas, juegos
matemáticos. Algunos conceptos sobre los cuales es necesario hacer especial énfasis.
En la columna derecha se desarrolla el contenido científico, ejemplo, trabajo en equipo y
actividaddes finales para cada unidad.
Los iconos utilizados en el texto tienen los siguientes significado:
Ma
tem
áti
ca
7
¿Sabías qué?
Lea, analice e interprete.
Refuerce sus conocimientos.

6. Primera Unidad: Estadística
Estadística.��������������������������������������������� 2
Introducción�������������������������������������� 2
Repaso de estadística descriptiva
para datos no agrupados.����������������� 2
Medidas de tendencia central para datos
no agrupados.���������������������������������������� 7
Estadística descriptiva para datos
agrupados.������������������������������������������� 13
Actividades Finales de la Primera Unidad
������������������������������������������������������������� 41
Segunda Unidad: El
Conjunto de los Números
Irracionales
El Conjunto de los Números Reales.
������������������������������������������������������������� 52
Introducción.����������������������������������� 52
El conjunto de los números
irracionales.������������������������������������� 53
Representación de números
irracionales en una recta numérica.56
Representación de un número real en
una recta numérica.������������������������ 58
Valor absoluto de un número real.�� 58
Suma de números reales.��������������� 53
Sumando dos números reales
utilizando la recta numérica real.���� 59
Propiedades de la suma de números
reales.��������������������������������������������� 60
Multiplicación de números reales.��� 62
Propiedad conmutativa del producto
de números reales.������������������������� 63
División de números reales������������� 65
Propiedades de la relación de orden
en el conjunto de los números
reales.��������������������������������������������� 68
Actividades Finales de la Segunda
Unidad��������������������������������������������� 73
Tercera Unidad:
Introducción al Álgebra
Introducción al álgebra.������������������������ 80
Expresiones algebraicas.���������������� 80
Dominio de una variable.���������������� 82
¿Qué es un monomio?������������������� 85
Monomios semejantes.������������������� 86
Tipos de monomios.������������������������ 87
Suma y resta de monomios.����������� 88
¿Qué es un binomio?���������������������� 92
¿Qué es un trinomio?��������������������� 95
¿Qué es un polinomio?������������������� 97
El término independiente de un
polinomio.���������������������������������������� 98
Concepto de polinomio ordenado.�� 99
Valor numérico de una expresión
algebraica.������������������������������������������ 100
Actividades Finales de la Tercera Unidad
����������������������������������������������������������� 104
Cuarta Unidad :
Operaciones con polinomios
Operaciones con polinomios.������������� 114
Indice

7. ¿Cómo se suman dos
polinomios?����������������������������������� 114
Propiedades de potenciación
(Repaso)��������������������������������������� 116
Multiplicación de monomios.�������������� 120
División de monomios.����������������������� 121
Suma y resta de polinomios.�������������� 122
Suma de polinomios.�������������������� 122
Resta de polinomios.�������������������� 124
Los signos de agrupación.����������������� 129
Multiplicación de polinomios.�������������� 131
Multiplicación de dos polinomios.� 132
Simplificación de expresiones
algebraicas que contienen productos
indicados.�������������������������������������� 134
División de polinomios.����������������������� 137
División sintética o Regla de​ Ruffini.
����������������������������������������������������������� 141
Productos notables.���������������������������� 144
Cubo de la suma de dos términos.148
Cubo de la diferencia de dos
términos.��������������������������������������� 149
Producto de la forma
(x + a)(x + b).��������������������������������� 150
Actividades Finales de la Cuarta Unidad
����������������������������������������������������������� 160
Quinta Unidad : Funciones
Funciones.����������������������������������������� 168
Introducción.��������������������������������� 168
Repaso de relaciones.������������������ 168
Concepto de función.������������������������� 175
Funciones discretas.�������������������������� 181
Concepto de función discreta.������ 181
Concepto de variable independiente y
de variable dependiente.��������������� 183
Funciones definidas por
ecuaciones.����������������������������������� 184
El criterio de la recta vertical para
identificar funciones.��������������������� 186
La función lineal.��������������������������� 187
Operaciones con funciones
lineales.����������������������������������������� 190
Ecuaciones lineales en una variable
(incógnita).������������������������������������������ 197
El concepto de igualdad.��������������� 197
Grado de una ecuación lineal con una
incógnita���������������������������������������� 199
Propiedades de las ecuaciones
lineales con una incógnita.������������ 199
Ecuaciones de la forma
ax = b (a ≠ 0).��������������������������������� 202
Ecuaciones de la forma
ax ± b = cx + d; (a ≠ 0).������������������� 203
Ecuaciones lineales con una incógnita
y coeficientes fraccionarios.���������� 204
Ecuación lineal con una variable�� 205
Procedimiento general para resolver
ecuaciones lineales con una
variable����������������������������������������� 206
Resolución de problemas modelados
por ax + b = c.�������������������������������� 207
Algunas ideas para resolver
problemas aplicados��������������������� 208
Actividades Finales de la Quinta Unidad
����������������������������������������������������������� 214

8. Sexta Unidad : Construcción
de Figuras Geométricas.
Construcción de figuras
geométricas.��������������������������������������� 222
Conceptos básicos de
Geometría.������������������������������������ 222
Regiones poligonales y polígonos
regulares�������������������������������������������� 226
Línea poligonal.����������������������������� 226
Región poligonal cerrada.������������� 227
El pentágono regular.�������������������� 228
Suma de las medidas de los ángulos
internos de un polígono.��������������� 232
Ángulo exterior de un polígono con
región interior convexa.����������������� 233
El hexágono regular.��������������������� 234
Propiedades de los ángulos externos
de un polígono regular.����������������� 242
La circunferencia y el círculo.������������� 244
La circunferencia.�������������������������� 244
Posiciones relativas de dos
circunferencias.����������������������������� 247
Propiedades de los arcos.������������ 249
El círculo.�������������������������������������� 250
Polígonos regulares inscritos y
circunscritos a una
circunferencia.������������������������������� 252
Nombres de algunos polígonos
regulares.������������������������������������������� 255
Curiosidades matemáticas.����������� 256
Séptima Unidad : Área
y perímetro de regiones
poligonales regulares. Área
del círculo.
Área y perímetro de regiones poligonales
regulares. Área del círculo.���������������� 260
Introducción.��������������������������������� 260
Área de una región poligonal.������������ 261
Áreas de círculos y sectores
circulares.�������������������������������������� 265
Ángulos notables en la
circunferencia.������������������������������� 266
Ejercicios resueltos.���������������������� 270
Construcciones geométricas con regla y
compás.���������������������������������������������� 275
Introducción. �������������������������������� 275
Construcciones básicas.��������������� 275
Actividades Finales de la Séptima Unidad
����������������������������������������������������������� 283

9. Estadística
Unidad 1
El Gobierno de Reconciliación y Unidad Nacional puso en funcionamiento el parque
eólico “Comandante Camilo Ortega” quien es considerado el Apóstol de la Unidad
Sandinista. “La unidad de todos los nicaragüenses, unidos por el Bien Común de este
país, en reconciliación y haciendo patria siempre para este pueblo”.
Este parque eólico cuenta con una capacidad para generar 40 megawatts (MW), y se
encuentra ubicado en el sureño departamento de Rivas. Con este se busca la
transformación de la matriz energética y la generación de energía renovable, lo cual
conlleva a un impacto de menos costos de producción y un mayor beneficio para las
familias.
Fuente: 19 digital
12 de Marzo 2 014
Altura de las cumbres de Nicaragua.

10. 2
Estadística.
Introducción
¿Qué temas sobre Estadística Descriptiva se estudiarán en
Octavo Grado?
En el libro de texto de Séptimo Grado se estudiaron los conceptos
básicos de Estadística Descriptiva para conjuntos de datos no
agrupados. Los conjuntos analizados contenían cantidades
pequeñas de datos.
En este texto se estudiarán los conceptos básicos de Estadística
Descriptiva para conjuntos de datos agrupados.
Repaso de estadística descriptiva para datos no
agrupados.
Lea, analice e interprete
Recordemos algunos conceptos.
Actividad
A continuación se presentan las calificaciones de Matemática
de 10 estudiantes varones y mujeres del 8vo
grado del Colegio
“Rafaela Herrera”, del municipio de Masaya, correspondientes al
primer semestre del año 2013.
85 91 78 78 85
78 90 80 90 91
Para el conjunto de datos dado realizar las siguientes actividades:
• Construir una tabla estadística para la frecuencias absoluta.
• Construir un diagrama de barras.
• Construir una tabla estadística para la frecuencias absoluta.
• Construir una tabla estadística que indique los porcentajes para la
frecuencias absoluta.
• Construir un diagrama de sectores circulares.
Fuéunprominentecientífico,
matemático y pensador, que
estableció la disciplina de la
estadística matemática.
Karl Pearson
(1 857 - 1 936 )
La estadística trata de la
recolección, organización,
presentación e
interpretación de datos
Estadística
Descriptiva
Estadística
Inferencial
Subdivisiones de
la Estadística
Recuerde
El Rango es la
diferencia entre sus
valores extremos; es
decir la diferencia entre
el valor máximo y el
valor mínimo.
Es importante recordar
los conceptos de
población, muestra,
distribución de
frecuencias, media
aritmética, mediana y
moda para datos no
agrupados.
Nota histórica

11. 3
Recordemos
Muchos problemas de
la vida real y toma de
decisiones se resuelven
utilizando métodos
estadísticos.
££ Construcción de una tabla estadística para la frecuencias
absoluta.
Calificaciones Frecuencias
85 2
91 2
78 3
90 2
80 1
n =10
Tabla 1
La tabla indica que:
• La calificación 85 la obtuvieron 2 estudiantes.
• La calificación 91 la obtuvieron 2 estudiantes.
• La calificación 80 la obtuvo sólo 1 estudiante.
Actividad
Observar la tabla de frecuencias y responda a las siguientes
preguntas:
• ¿Qué frecuencias corresponden a las calificaciones 78 y 90?
• ¿Cuál es la calificación de mayor frecuencia?
££ Construcción de un diagrama de barras.
¿Cómo se construye un diagrama de barras?
Un diagrama de barras se construye por medio de dos ejes que se
intersectan en un ángulo recto, es decir, un ángulo cuya medida
es 90º
• En el eje horizontal ubicamos las calificaciones.
• En el eje vertical ubicamos las frecuencias.
¿Qué es tabla de
frecuencias?
Tabla de frecuencias en
una variable cualitativa
es un resumen de los
datos obtenidos de
la muestra frente a la
variable que se quiere
caracterizar.
La frecuencia nos indica
el número de veces que
un dato se repite en el
conjunto.
¿Qué es diagrama
de barras de
frecuencias?
Diagrama de barras
de frecuencias es
un diagrama en el
que se representan
gráficamente los
datos de una tabla de
frecuencias.

12. 4
Matemático ruso. Uno
de los matemáticos
más brillantes del
siglo XX. Junto a
sus colaboradores
realizó importantes
aportes a la teoría
relacionada con el
análisis estadístico de
los textos, tanto en
prosa como en verso.
Realizó grandes
contribuciones
a la teoría de
probabilidades.
A.N. Kolmogórov
(1 903 - 1 987)
El diagrama de barras se construye con los datos de la tabla 1.
0
1
2
3
4
Calificaciones
85 91 78 90 80
2 2 2
1
3
Frecuencias
Fig. 1
Interpretar el diagrama de barras de frecuencias.
La calificación de 85 la obtuvieron 2 estudiantes.
La calificación de 91 la obtuvieron 2 estudiantes.
La calificación de 80 la obtuvo un estudiante.
Actividad
Observar el diagrama de barras de frecuencias y contestar las
siguientes preguntas:
¿Cuál es la calificación de mayor frecuencia?
¿Qué frecuencia corresponde a la calificación de 90?
Encuentre el número total de datos a partir del diagrama de barras.
££ Construcción de una tabla estadística de frecuencias relativas.
La frecuencia relativa fr
se obtiene dividiendo la frecuencia entre
el número total de datos n.
Verifique los valores para de acuerdo con los datos
presentados en la siguiente tabla:
Calificaciones fi
fr
85 2 2/10=0,2
91 2 2/10=0,2
78 3 3/10=0,3
90 2 2/10=0,2
80 1 1/10=0,10
n =10
Tabla 2
Nota histórica

13. 5
££ Construcción de una tabla estadística que indique los porcentajes
para la frecuencias absoluta.
Los porcentajes se obtienen multiplicando por 100 las frecuencias
relativas.
En el ejemplo y a partir de la tabla 2, obtenemos:
Calificaciones fi
fr
Porcentajes
85 2 2/10 = 0,2 0,2(100) = 20%
91 2 2/10 = 0,2 0,2(100) = 20%
78 3 3/10 = 0,3 0,3(100) = 30%
90 2 2/10 = 0,2 0,2(100) = 20%
80 1 1/10 = 0,10 0,1(100) = 10%
n = 10 Total = 100%
Tabla 3
Actividad
Observe la tabla de porcentajes y conteste las siguientes preguntas:
¿Qué calificación corresponde al 30% del total?
¿Qué calificación corresponde al 10% del total?
¿Cómo calcula el número total de datos a partir de cualquiera de
los porcentajes?
££ Construcción de un diagrama de sector circular.
¿Qué es un diagrama de sector circular?
El diagrama circular es una representación de las frecuencias en un
círculo.
Calificaciones Porcentajes Ángulo
85 0,2(100)= 20% 72°
91 0,2(100) = 20% 72°
78 0,3(100) = 30% 108°
90 0,2(100) = 20% 72°
80 0,1(100) = 10% 36°
Total = 100%
Tabla 4
Un diagrama circular se
construye de la siguiente
manera:
Recordemos que el
círculo corresponde a un
ángulo de 360º.
El ángulo para cada
frecuencia se obtiene
mediante una regla de
tres:
360°→100%
x → 20%
x = 72°
Por lo tanto, el 20%
corresponde a un ángulo
de 72°.
En el Séptimo Grado, el
ángulo se calcula así:
x = 360°fr
x = (0,20)(360°)
x = 72°
Ma
tem
áti
ca
7
¿Sabías qué?

14. 6
Actividad
Compruebe que el ángulo para el 30%
es de 108º y para el 10% es de 36º.
El diagrama de sector circular es el que
podemos apreciar a nuestra derecha.
¿Qué información brinda este
diagrama?
• El30%delosestudiantesobtuvieron
una calificación de 78.
• El 10% de los estudiantes obtuvieron una calificación de 80.
Actividad
Encuentre las calificaciones que corresponden al 20%.
Actividad
A continuación se presenta un gráfico de pastel (ver explicación
columna izquierda), correspondiente a un grupo de 50 estudiantes
varones y mujeres de la clase de Física de Décimo Grado.
Observe el gráfico y responda la pregunta:
Mujeres Varones
40 %
60 %
Fig. 3
¿Cuántas mujeres y cuántos varones hay en el grupo?
Actividad
Realice un gráfico de sector circular correspondiente al grupo de
estudiantes de su aula de clases.
Investigue el número total de estudiantes de su centro de estudios
o Instituto de clases y realice un gráfico de sector circular.
Nació en Londres.
Psicólogo de profesión,
estudió estadística
y logró desarrollar
notables aplicaciones
de la estadística en el
campo de la psicología.
Charles Edward
Spearman
(1 863 - 1 945)
Fig. 2
30 %
20 %
20 %
20 %
10 %
78 90 809185
¿Sabías qué?
Ma
tem
átic
a
7
Si el diagrama se dibuja de
esta forma, se le denomina
Diagrama de sectores circulares.
Noticias
Novelas
Películas
Documentales
Si se le dibuja de esta
otra forma, se le llama
Diagrama de pastel.
Noticias
Novelas
Películas
Documentales
Nota histórica

15. 7
Medidas de tendencia central para datos no
agrupados.
££ Cálculo de la media aritmética , para datos no agrupados.
Media aritmética x̅ =
Suma de todos los datos
Número de datos
¿Cómo se calcula la media aritmética o promedio?
Actividad
Las calificaciones obtenidas por 10 estudiantes en una prueba
parcial de Matemática son las siguientes:
72 78 80 84 85
87 90 90 90 91
Encontrando la media aritmética o promedio de estos datos.
• Calculando la suma de todas las calificaciones:
Suma = 72 + 78 + 80 + 84 + 85 + 87 + 90 + 90 + 90 + 91 = 847
Número de datos = 10
Efectuando la siguiente operación:
x̅ =
Suma de todos los datos
Número de datos
=
10
847
= 84,7
se obtiene que la media aritmética es 84,7
Actividad
Un estudiante necesita saber su calificación del tercer corte
evaluativo de Matemática. El docente de la disciplina le informa que
su promedio de entrada al cuarto corte evaluativo es de 75 y que
las calificaciones de primero y segundo corte son respectivamente
68 y 74. ¿Cuál es la calificación del tercer corte evaluativo?.
££ Cálculo de la mediana.
¿Cómo se calcula la mediana de un conjunto de datos no
agrupados?
• Si el número de datos es impar, entonces se suma 1 al número
de datos y el resultado se divide entre 2.
Considere un conjunto de 11 datos
86 91 84 80 86 64 81 86 86 84 92
El símbolo Σ (Sigma),
se utiliza para indicar
sumatorias en forma
abreviada.
x x x xi
i
k
k
=
∑ = + + +
1
1 2 ...
Si n = 4, entonces:
x x x x xi
i=
∑ = + + +
1
4
1 2 3 4
Símbolo de sumatoria
• La mediana de un
conjunto de datos,
es el dato que divide
al conjunto en dos
partes iguales. La
mediana se denota
por Me
.
Ma
tem
áti
ca
7
¿Sabías qué?

16. 8
Con este número de datos se procede de la siguiente manera:
• Sumar 1 al número de datos: 11 + 1 = 12.
• Dividir el resultado entre 2:
2
12 = 6.
Por lo tanto, la mediana se encuentra en la posición 6.
La mediana es 86.
1
64
2
80
3
81
4
84
5
84
6
86
7
86
8
86
9
86
10
91
11
92
5 datos 5 datos
Mediana
Observe que tanto a la izquierda como a la derecha de la mediana
hay 5 datos. La mediana está en el centro de la muestra y es 86.
¿Qué ocurre si el número de datos es par?
Ejemplo
El siguiente conjunto de datos corresponde a las calificaciones
finales de Matemática del primer semestre 2010 de 10
estudiantes del 11mo
Grado “B” del Colegio Público de Santa
Cruz, Departamento de Estelí. Se pide encontrar la mediana para
este conjunto de datos.
86 91 84 80 86 64 81 86 86 84
Se siguen los pasos siguientes:
• Ordenando los datos de menor a mayor.
1
64
2
80
3
81
4
84
5
84
6
86
7
86
8
86
9
86
10
91
El número de datos es par.
Si el número de datos es par, entonces se realizan los siguientes
pasos:
• Dividiendo el número de datos entre 2.
El número de datos es 10.
Dividiendo 10 entre 2, se obtiene 5.
Matemático británico. En
teoría de probabilidades
existe un teorema que
lleva su apellido y trata
sobre la probabilidad de
un suceso condicionado
por la ocurrencia de otro
suceso.
Thomas Bayes
(1 702 - 1 761)
Nota histórica

17. 9
• Se suma el dato que se encuentra en la posición 5 con el dato
que le sigue y se calcula el promedio de los dos. El resultado
del promedio será la mediana.
El dato que se encuentra en la posición 5 es 84 y el dato que le
sigue es 86,
La mediana será el promedio de 84 y 86.
Me
=
84 + 86
2
= 85
1
64
2
80
3
81
4
84
5
84
6
86
7
86
8
86
9
86
10
91
85
Observar que en este caso la mediana no pertenece al conjunto de datos.
Actividad
Calcular la mediana para el siguiente conjunto de datos ya ordenados de
menor a mayor:
43 70 76 76 77 78 80 81 82 85 87 90
££ Cálculo de la moda Mo
, para un conjunto de datos no agrupados
Ejemplo
En el primer corte evaluativo de Matemática 10 estudiantes de Octavo
Grado obtuvieron las calificaciones siguientes:
56 57 61 67 72 72 72 84 91 92
Observe que los datos están ordenados de menor a mayor.
El dato que más se repite es 72, por lo tanto la moda de este conjunto de
datos es: Mo
= 72.
Ejemplo
Se da un conjunto de datos correspondiente a las calificaciones de la
asignatura “Física” de 11vo
grado:
70 70 70 72 78
78 79 81 82 85
La moda es el dato que
más se repite en un
conjunto de datos.
No existe una fórmula
para calcular la moda
con datos no agrupados.
Lo único que se debe
hacer es encontrar el
dato que más se repite.
Un conjunto de datos
puede tener más de una
moda, en estos casos se
dice que la muestra es
bimodal, trimodal, etc.
Dr. Luis Adolfo Gámez
Rodríguez
(1 959 - 2 011)
Destacado profesor
universitario, nacido en
Estelí, con profundos
conocimientos en
Física Teórica y
Matemática. Fue
presidente de la
Sociedad Matemática
de Nicaragua y Realizó
sus estudios en la
Universidad Estatal
M.V. Lomonósov de
Moscú.
Ma
tem
áti
ca
7
¿Sabías qué?

18. 10
Actividad
Verifique los valores de la siguiente tabla de frecuencias absolutas,
frecuencias relativas y de porcentajes.
xi
fi
fr
%
70 3 3/10 = 0,30 30
72 1 1/10 = 0,10 10
78 2 2/10 = 0,20 20
79 1 1/10 = 0,10 10
81 1 1/10 = 0,10 10
82 1 1/10 = 0,10 10
85 1 1/10 = 0,10 10
Total = 10 1 100
Tabla 5
Ejemplo
La calificación 70 aparece 3 veces en el conjunto de datos, es
decir, que su frecuencia absoluta es 3. Su frecuencia relativa es
3
10
0 03= ,
Su frecuencia porcentual (o porcentaje) es 0,30(100) = 30%.
A continuación, se utilizarán los datos de la tabla 5 para construir
un diagrama de barras de porcentajes.
Diagrama de barras de porcentajes correspondiente a la Tabla 5.
En el eje horizontal se ubican la calificaciones y en el eje vertical
se ubican los porcentajes correspondientes a cada calificación.
Diagrama de barras para porcentajes
35 %
30 %
25 %
20 %
15 %
10 %
5 %
0 %
70 72 78 79 81
30
10 10 10 10 10
20 %
82 85
Calificaciones
Porcentaje
Fig. 4
• La frecuencia
absoluta fi
representa el
número de veces
que cada dato
aparece en el
conjunto de datos.
• La frecuencia relativa fr
es el cociente entre la
frecuencia absoluta y
el total de datos.
Ma
tem
áti
ca
7
¿Sabías qué?

19. 11
Ejemplo
Los datos a continuación corresponden a las calificaciones de la
asignatura Física de 12 estudiantes de 11mo
Grado:
60 62 63 63 64 65 68 70 70 70 81 85
• Para estos datos la tabla de frecuencias absolutas f, frecuencias
relativas fr y de porcentajes, es la siguiente:
xi
fi
fr
%
60 1 1/12 = 0,08333 8,33
62 1 1/12 = 0,08333 8,33
63 2 2/12 = 0,1666 1,66
64 1 1/12 = 0,08333 8,33
65 1 1/12 = 0,08333 8,33
68 1 1/12 = 0,08333 8,33
70 3 3/12 = 0,25 25
81 1 1/12 = 0,08333 8,33
85 1 1/12 = 0,08333 8,33
Total 12 1 100
Tabla 6
Actividad
1. Verifique que los valores contenidos en la Tabla 6 son correctos.
2. Un pelotero consigue 15 temporadas de 86, 75 , 91, 120,100, 75,
96, 102, 100, 96, 86, 97, 115, 88 y 75 hits.
a. Elabore una tabla de frecuencia absoluta con estos datos.
b. Determine las medidas de tendencia central:
££ Mediana
££ Media aritmética
££ Moda.
c. Elabore un histograma.
La frecuencia porcentual es
el resultado de multiplicar
cada frecuencia relativa por
100.
Ma
tem
áti
ca
7
¿Sabías qué?

20. 12
Actividad
Con ayuda del diagrama de barras presentado en la figura 5
Diagrama de barras
4
3
2
1
0
60 62 63 64 65
1 1 1 1 1
3
2
68 70
Calificaciones
Frecuencias
1 1
81 85
Fig. 5
Responda las preguntas:
a. ¿Cuántos estudiantes obtuvieron una calificación menor de
85?
b. ¿Cuántos estudiantes obtuvieron una calificación menor que
81 y mayor que 62?
c. Calcule la media aritmética, la mediana y la moda.
Trabajemos en equipo.
Para el conjunto de datos:
63 61 67 70 71 71 71 84 84 84 90 91 92 93 94
1. Construya:
a. Una tabla estadística que contenga frecuencias absolutas,
frecuencias relativas y porcentajes.
b. El histograma de barras.
c. El diagrama de sector circular.
d. Calcule la media aritmética y la mediana.
e. ¿Cuántas modas tiene este conjunto de datos?

21. 13
Estadística descriptiva para datos agrupados.
¿Qué ocurre cuando los datos a ser analizados son numerosos?
Para muestras que contienen una gran cantidad de datos, por
lo general 30 o más datos, existen métodos de la Estadística
Descriptiva que se basan en la agrupación de los datos de
la muestra. Estos métodos se conocen como métodos de la
Estadística Descriptiva para datos agrupados.
Lea, analice e interprete
££ Distribuciones de frecuencias.
Ejemplo
Los datos dados a continuación corresponden a las calificaciones
de Matemática de un grupo de 30 estudiantes del Octavo Grado de
un colegio del municipio de Managua.
73 50 52 76 70 72 75 76 51 53
79 72 74 70 54 55 70 52 51 74
71 77 57 53 84 76 77 76 86 89
¿Qué procedimiento será más fácil para analizar el conjunto de
datos presentado?
Ordenamos los datos de menor a mayor.
50 51 51 52 52 53 53 54 55 58
70 70 70 71 72 72 73 74 74 75
76 76 76 76 77 77 79 84 86 89
• A continuación se pueden dividir estos datos en grupos. A estos
grupos los llamaremos clases.
Clase o intervalo de clase.
Cuandoelnúmerodedatosenmuygrande,resultamásconveniente
dividir la muestra en intervalos de clase o clases.
¿Cuántas clases se deben tomar?
Para un conjunto de datos se tomará un mínimo de 4 clases y un
máximo de 12 clases.

22. 14
Para el conjunto dado tomaremos 5 clases.
50 51 51 52 52 53 53 54 55 58
70 70 70 71 72 72 73 74 74 75
76 76 76 76 77 77 79 84 86 89
££ Rango.
El Rango es la diferencia entre sus valores extremos; es decir la
diferencia entre el valor máximo y el valor mínimo.
Se calcula así:
Rango = Valor máximo – Valor mínimo
Retomando el ejercicio de grupo de 30 estudiantes de la página
13 el rango será:
R = 89 - 50 = 39
Se llama intervalo de clase a cada uno de los intervalos en que pueden
agruparse los datos de una variable estadística.
££ Amplitud de clase.
Es el número de datos contenidos en la clase.
La amplitud de clase es igual para todas las clases. Esto significa
que todas las clases contienen el mismo número de datos. La
amplitud de clase se calcula de la siguiente manera:
Amplitud de clase =
Rango
número de clases
En el ejemplo propuesto de los estudiantes de octavo grado:
Amplitud de clase =
Matemático suizo.
Introdujo la primera ley
de los grandes números,
que establece que, bajos
ciertas condiciones, un
promedio muestral se
aproxima al promedio de
la población de donde
se obtuvo la muestra,
si el tamaño de ésta es
grande.
Jakob Bernoulli
(1 654 - 1 705)
Nota histórica

23. 15
££ ¿Cómo construir una tabla de frecuencias para datos
agrupados?
Ordenamos los datos de menor a mayor, se determina el rango,
la amplitud de clase, se forman los intervalos, a continuación se
encuentra la frecuencia absoluta, frecuencia relativa, frecuencia
acumulada y otra información que se requiera.
Ejemplo
Con los siguientes datos ordenados de menor a mayor, construir
una tabla de frecuencias absolutas.
50 51 51 52 52 53 53 54 55 58
70 70 70 71 72 72 73 74 74 75
76 76 76 76 77 77 79 84 86 89
Se seguirán los siguientes pasos:
Paso 1. Se encuentran las clases.
El extremo superior de cada clase se obtiene sumando al extremo
inferior la amplitud de clase disminuida en (8 - 1).
El extremo inferior del primer intervalo es el dato más pequeño, en
este caso corresponde a 50.
Para obtener el extremo superior procedemos de la siguiente
manera:
Extremo superior = Extremo inferior + (Amplitud de clase menos 1)
Paso 2. Sumamos a 50 la amplitud de clase disminuida en uno,
es decir:
Extremo superior = 50 + (8 – 1) = 50 + 7 = 57
Extremo
inferior
Amplitud de clase
menos 1
Por lo tanto, el primer intervalo de clase es:
50 - 57
La simbología utilizada
en estadística es:
fi
: Es la frecuencia
absoluta.
fr
: Es la frecuencia
relativa.
%fr
: Porcentajes para
frecuencia relativa.
Fi
: Es la frecuencia
acumulada.
Fr
: Frecuencia
acumulada relativa.
%Fr
: Porcentaje para la
frecuencia acumulada
relativa
Xi
: Marca de clase.
N: Tamaño de la
población cuando es
finita.
n: Tamaño de la muestra
o total de datos.
Ma
tem
áti
ca
7
¿Sabías qué?

24. 16
El segundo intervalo de clase tiene como extremo inferior 58. El
extremo superior será:
Extremo superior = 58 + 7 = 65.
Por lo tanto, el segundo intervalo de clase es: 58 - 65
El tercer intervalo de clase tiene como extremo inferior 66. El
extremo superior será:
Extremo superior = 66 + 7 = 73.
Por lo tanto, el tercer intervalo de clase es: 66 - 73
El cuarto intervalo de clase tiene como extremo inferior 74. El
extremo superior será:
Extremo superior = 74 + 7 = 81.
Por lo tanto, el tercer intervalo de clase es: 74 - 81
El quinto intervalo de clase es: 82 - 89. Verifíquelo.
Observe que los extremos de cada clase no necesariamente
están contenidos en el conjunto de datos que se está analizando.
Describimos las clases con los siguientes esquemas:
Datos
de la clase
50-57
50 51 51 52 52 53 53 54 55 (9)
Datos
de la clase
58-65
58 (1)
Datos
de la clase
66-73
70 70 70 71 72 72 73 (7)
Datos
de la clase
74-81
74 74 75 76 76 76 76 77 77 79 (10)
Datos
de la clase
82-89
84 86 89 (3)
La amplitud de clase
no necesariamente
es igual al número de
datos en una clase. Por
ejemplo, la clase
58 - 65 contiene
solamente 1 dato y su
amplitud, igual que la
amplitud de todas las
clases, es 8.
Los números que van de
58 a 65 son:
58, 59, 60, 61, 62, 63, 64, 65
Son 8 cifras, lo que nos
indica que la amplitud de
clase es 8.
Límite
interior o
extremo
inferior.
Límite
superior o
extremo
superior.
Características de
una clase.
58 - 65
Ma
tem
áti
ca
7
¿Sabías qué?

25. 17
En la siguiente tabla se presentan los intervalos de clase y las
frecuencias absoluta correspondientes.
Tabla de frecuencias absoluta.
Clases fi
50 - 57 9
58 - 65 1
66 - 73 7
74 - 81 10
82 - 89 3
Total: 30
Tabla 7
££ El histograma de frecuencias absoluta.
Histograma de frecuencias absoluta
Frecuencias
Intervalos de Clase
(50 - 57)
0
5
10
15
9
1
10
3
7
(85 - 65) (66 -73) (74 - 81) (82 - 89)
Fig. 6
££ Interpretación del histograma de frecuencias absoluta.
• 9 estudiantes obtuvieron calificaciones entre 50 y 57.
• 1 estudiante obtuvo una calificación entre 58 y 65
• 7 estudiantes obtuvieron una calificación entre 66 y 73
• 10 estudiantes obtuvieron una calificación entre 74 y 81.
• 3 estudiantes obtuvieron una calificación entre 82 y 89.
Fue un matemático
ruso, estudiante de
Kolmogórov. Nació
en Simbirsk, Rusia y
murió en Moscú. Es
muy conocido por sus
trabajos con Kolmogórov
en el campo de la Teoría
de Probabilidades.
Boris Vladímirovich
Gnedenko.
(1 912 - 1 995)
Histograma: Se emplea
para ilustrar muestras
agrupadas en intervalos.
Está formado por
rectángulos unidos a
otros, cuyos vértices de
la base coinciden con los
límites de los intervalos y
el centro de cada intervalo
es la marca de clase, que
representamos en el eje
de las abscisas. La altura
de cada rectángulo es
proporcional a la frecuencia
del intervalo respectivo.
La frecuencia absoluta fi
representa el número de
observaciones (datos)
que se encuentran
ubicadas dentro de un
intervalo.
Ma
tem
áti
ca
7
¿Sabías qué?
Nota histórica

26. 18
Observe que el número total de datos se obtiene sumando
los valores correspondientes a las frecuencias absoluta.
En el ejemplo tenemos que:
9 + 1 + 7 + 10 + 3 = 30, que es el número de datos.
Recuerde que la amplitud de clase no necesariamente
coincide con el número de datos contenidos en la clase.
££ Construcción de un polígono de frecuencias.
El polígono de frecuencias es un gráfico de líneas que se construye
uniendo con segmentos de recta los puntos medios (o marcas
de clase) de los intervalos de clase.
El punto medio de la clase (o marca de clase) para la clase
50 - 57 es:
50 + 57
2
= 53,5 Marca de clase.
Clase Xi
: Marca de clase fi
50 - 57 53,5 9
58 - 65 61,5 1
66 - 73 69,5 7
74 - 81 77,5 10
82 - 89 85,5 3
n = 30
Tabla 8
Actividad
Verifique los valores para las marcas de clase correspondientes a
las siguientes clases presentadas en la Tabla 8:
58 - 65; 66 - 73; 74 - 81; 82 - 89
En el eje horizontal se ubican las marcas de clase y en el eje
vertical se ubican las frecuencias.

27. 19
Al unir los puntos medios de las bases superiores de los rectángulos
correspondientes al histograma de frecuencias absoluta, se obtiene
una figura conocida como Polígono de Frecuencias.
Polígono de Frecuencias
Frecuencias
Marcas de Clase
53,5
0
5
10
15
9
1
10
3
7
61,5 69,5 77,5 85,5
Fig. 7
££ Frecuencias acumuladas.
La frecuencia acumulada es igual al número de datos que hay
en el intervalo más las frecuencias de los datos anteriores.
Denotaremos las frecuencias acumulada por Fi
.
En la Tabla 8 se presentan los intervalos de clase con las
correspondientes frecuencias absolutas.
Clases Frecuencias absoluta (fi
)
50 - 57 9
58 - 65 1
66 - 73 7
74 - 81 10
82 - 89 3
n = 30
Tabla 9
Laprimerafrecuencia acumulada coincide conlaprimerafrecuencia
absoluta; es decir que la primera frecuencia acumulada es 9.

28. 20
La segunda frecuencia acumulada será:
9 + 1 = 10
El proceso continua en forma análoga, obtenemos entonces:
10 + 7 = 17
17 + 10 = 27
27 + 3 = 30
Los datos se presentan en la tabla siguiente:
Clases fi
Fi
50 - 57 9 9
58 - 65 1 9 + 1 = 10
66 - 73 7 10 + 7 = 17
74 - 81 10 17 + 10 = 27
82 - 89 3 27 + 3 = 30
n = 30
Tabla 10
££ Histograma de frecuencias acumuladas.
¿Cómo se construye un histograma de frecuencias acumuladas?
En el eje horizontal se ubican los intervalos de clase y en el eje
vertical las frecuencias acumuladas.
Histograma de Frecuencias Acumuladas
FrecuenciasAcumuladas
Intervalos de Clase
50 - 57
0
10
20
30
9 10
27
30
17
58 - 65 66 - 73 74 - 81 82 - 89
40
Fig. 8
¿Qué información nos brinda este histograma?
• 9 estudiantes obtuvieron calificaciones en el intervalo
50 - 57.
Es conocido por su
trabajo en el área de la
probabilidad y estadística.
La desigualdad de
Chebyshev se emplea para
demostrar la ley débil de los
grandes números
y el teorema de
Bertrand-Chebyshev
(1845-1850) que establece
que la cantidad p(n) de
números primos menores
que n es:
p(n) = n / log(n) + o(n)
Pafnuti Lvóvich
Chebyshev
(1 821 - 1 894)
Nota histórica

29. 21
• 10 estudiantes obtuvieron calificaciones menores o iguales
a 65.
• 17 estudiantes obtuvieron calificaciones menores o iguales
a 73.
• 27 estudiantes obtuvieron calificaciones menores o iguales
a 81.
• 30 estudiantes obtuvieron calificaciones menores o iguales
a 89.
££ Ojiva.
Una ojiva se construye tomando en cuenta que en el eje horizontal
aparecen los límites superiores y en el eje vertical las frecuencias
acumuladas. Las coordenadas formadas por ambos son unidas
por segmentos.
Clase xi
fi
Fi
50 - 57 53,5 9 9
58 - 65 61,5 1 9 + 1 = 10
66 - 73 69,5 7 10 + 7 = 17
74 - 81 77,5 10 17 + 10 = 27
82 - 89 85,5 3 27 + 3 = 30
n = 30
Tabla 11
Ojiva
FrecuenciasAcumuladas
Límite superior
57
0
20
(57,9)
(65,10)
(81,27)
(89,30)
(73,17)
40
65 7373 81 89
Fig. 9

30. 22
££ Frecuencia relativa fr
.
La frecuencia relativa se obtiene dividiendo la frecuencia absoluta
entre el número total de datos.
• El porcentaje % para la frecuencia relativa se obtiene
multiplicando cada frecuencia relativa por 100.
• La frecuencia acumulada se obtiene sumando a cada
frecuencia el acumulado de las frecuencias anteriores.
La primera frecuencia acumulada coincide con la primera
frecuencia absoluta.
• La frecuencia acumulada relativa se obtiene dividiendo cada
frecuencia acumulada entre el número de datos.
• El porcentaje para la frecuencia relativa acumulada se
obtiene multiplicando por 100 cada frecuencia acumulada
relativa.
Ejemplo
Verificar en la tabla 11 con relación a la frecuencia 10 lo siguiente:
• La frecuencia relativa.
• El porcentaje para las frecuencias relativas.
• La frecuencia acumulada.
• La frecuencia relativa acumulada.
• El porcentaje para las frecuencias relativas acumuladas.
Para la frecuencia con valor de 10 tenemos:
La frecuencia relativa es:
10
30
0 33= ,
El porcentaje para la frecuencia relativa es:
0,33(100) = 33%

31. 23
La frecuencia acumulada hasta la frecuencia de valor 10 es:
9 + 1 + 7 +10 = 27
o bien 9 + 10 + 17 = 27
La frecuencia relativa acumulada es:
27
30
0 9= ,
El porcentaje para la frecuencia relativa acumulada es:
0,9(100) = 90%
Intervalo de clase fi
fr
% fr
Fi
Fr
%Fr
50 - 57 9 9/30 =3/10
58 - 65 1 1/30
66 - 73 7 7/30
74 - 81 10 1/3 33 27 0,9 90
82 - 89 3 1/10
Total 30 30/30
Tabla 12
Actividad
Realizar los mismos cálculos del ejemplo anterior para las demás
frecuencias de la Tabla 12.
Intervalo de clase fi
fr
% fr
Fi
Fr
%Fr
50 - 57 9 9/30 =3/10
58 - 65 1 1/30
66 - 73 7 7/30
74 - 81 10 1/3 33 27 0,9 90
82 - 89 3 1/10
Total 30 30/30
Tabla 13

32. 24
Actividad
Los siguientes datos son de una cooperativa de taxis que midió
la cantidad de kilómetros recorridos por 40 vehículos por galón
consumido.
45 38 44 45 44 44 39 40
43 44 43 43 45 44 45 42
38 43 39 38 40 41 42 44
43 41 37 38 40 42 41 43
40 40 38 39 44 43 42 40
Tabla 14
Realice los siguiente:
a. Ordene los datos de menor a mayor.
b. Elabore una tabla de distribución de frecuencia con 5 intervalos.
c. Construya un histograma.
d. Construya una ojiva.
££ Medidas de tendencia central para datos agrupados.
Lea, analice e interprete.
Las medidas de tendencia central son valores numéricos en torno
a los cuales está concentrado el resto de la muestra.
Las medidas de tendencia central son: la media aritmética
(o promedio), la moda y la mediana.
££ Media aritmética para un conjunto de datos agrupados.
Para datos agrupados el cálculo de la media aritmética se realiza
utilizando la tabla de frecuencias absolutas y las marcas de clase
de acuerdo a los siguientes pasos:
Paso 1. Se multiplica cada marca de clase por la frecuencia
absoluta correspondiente.
Paso 2. Se suman los productos obtenidos en el paso 1.
La media aritmética para
datos no agrupados
es el valor obtenido al
sumar todos los datos y
dividir el resultado entre
el número total de datos.
Ma
tem
áti
ca
7
¿Sabías qué?

33. 25
Paso 3. Se divide el resultado de la suma obtenido en el Paso 2,
entre el número de datos de la muestra.
x i
k
k k
= =
+ +…+=∑ 1 1 1 2 2
f X
n
f X f X f X
n
i i
donde las Xi
son las marcas de clase (puntos medios de los
intervalos de clase) y las fi
son las frecuencias absoluta.
A través del ejemplo que se presenta a continuación, reconozca
los pasos para calcular la media aritmética con datos agrupados.
Ejemplo
Con los datos de la tabla dada a continuación, calcule la media
aritmética del conjunto de datos utilizando la fórmula para el cálculo
de la media aritmética para datos agrupados.
La tabla contiene las clases, las frecuencias absoluta, las marcas
de clase y los productos de las frecuencias absolutas con las
marcas de clase, fi
· Xi
Clases fi
Xi
fi
· Xi
50 - 57 9 53,5 (9)(53,5) = 481,5
58 - 65 1 61,5 (1)(61,5) = 61,5
66 - 73 7 69,5 (7)(69,5) = 486,5
74 - 81 10 77,5 (10)(77,5) = 775
82 - 89 3 85,5 (3)(85,5) = 256,5
Total n = 30 ∑
k
i = 1
fi
· Xi
= 2 061
Tabla 15
La fórmula es:
x i
k
k k
= =
+ +…+⋅=∑ 1 1 1 2 2
f X
n
f X f X f X
n
i i
Sumando los productos fi
. Xi
de la tabla:
481,5 + 61,5 + 486,5 + 775 + 256,5 = 2 061
Dividiendo este resultado entre el número total de datos que es
n = 30.
x i
= = =
⋅=∑ 1
5
2061
68 7
f X
n 30
i i
,
Por lo tanto, la media aritmética para este conjunto de datos es
68,7
Las marcas de clase son
los puntos medios de las
clases. Se encuentran
calculando la suma de
los extremos de cada
clase y dividiendo el
resultado entre 2.
La simbología empleada
en estadística será:
fi
: Es la frecuencia
absoluta.
Xi
: Marca de clase.
n: Tamaño de la muestra
o total de datos.
Ma
tem
áti
ca
7
¿Sabías qué?

34. 26
££ Mediana para un conjunto de datos agrupados.
La mediana de un conjunto de datos es el dato (o valor) que
se sitúa en el centro de la muestra (un 50% de los valores se
encuentran por debajo de la mediana y otro 50% por arriba).
Para calcular la mediana para datos agrupados se realizan los
siguientes pasos:
Paso 1. La mediana se encuentra en el intervalo de clase cuya
frecuencia acumulada llega hasta la mitad de la suma de las
frecuencias absolutas.
Es decir que la clase de la mediana tiene una frecuencia igual o
menor a
n
2
, donde n es la suma de las frecuencias absolutas.
Paso 2. Se encuentra la frecuencia acumulada antes de la clase
de la mediana.
Paso 3. Se encuentra el extremo o límite inferior de la clase de
la mediana.
La amplitud de clase es C.
Estos datos se sustituyen en la siguiente expresión:
Me L
n
F C
f
i
i
i
= +
−



−
2 1
Li
: es el extremo inferior del intervalo que contiene a la mediana.
n: es el número total de dato.
Fi - 1
: es la frecuencia acumulada anterior a la clase de la mediana.
C: es la amplitud de la clase que contiene a la mediana.
fi
: es la frecuencia de la clase de la mediana.

35. 27
Ejemplo
Utilizar los datos de la tabla 15 para encontrar la mediana Me del
conjunto de datos.
Paso 1. La mitad de la suma de las frecuencias absolutas es:
n
2
30
2
15= =
Por lo tanto, la clase de la mediana es la de frecuencia absoluta
menor o igual a 15. La frecuencia acumulada 17 es mayor que
15, por lo tanto la clase correspondiente a la mediana es la de
frecuencia absoluta 7, es decir la clase 66 - 73.
Paso 2. La frecuencia acumulada, hasta antes de la clase de la
mediana es 10.
Paso 3. El extremo inferior o límite inferior de la clase de la
mediana es 66.
La amplitud del intervalo de clase es 8.
M L
n
F
f
66
30
e i
i-1
= +
−




= +
−



2 2
10 8
7
C
i
Me = 71,7 ≈ 72
££ Moda para un conjunto de datos agrupados.
Moda. La moda en un conjunto de datos, es el dato que más se
repite; es decir el de mayor frecuencia. Se denota por Mo.
• Cálculo de la moda para datos agrupados.
Para calcular la moda para un conjunto de datos agrupados se
aplica la expresión siguiente:
M L Co i= +
∆
∆ + ∆






1
1 2
Li
: es el límite inferior de la clase que contiene a la moda que es
la de mayor frecuencia absoluta.
Para datos agrupados, la
moda esta en la mayor
concentración de datos
(mayor frecuencia),
la clase con mayor
frecuencia es la clase
modal. La moda si existe
puede ser no única y
sedenota por Mo.
Ma
tem
áti
ca
7
¿Sabías qué?

36. 28
Δ1
: Mayor frecuencia absoluta menos la inmediata anterior.
Δ2
: Mayor frecuencia absoluta menos la inmediata posterior.
C: es la amplitud de la clase.
A continuación se plantea un ejemplo del cálculo de la moda para
un conjunto de datos agrupados con la expresión indicada.
Ejemplo
Utilizar los datos de la tabla para encontrar la moda Mo del
conjunto de datos.
Clases f F
50 - 57 9 9
58 - 65 1 10
66 - 73 7 17
74 - 81 10 27
82 - 89 3 30
Total 30
Tabla 16
La clase que contiene a la moda es la de mayor frecuencia, en
este caso es 74 - 81. La frecuencia para esta clase es fi
= 10.
• El límite inferior es Li
= 74.
• La frecuencia anterior a la clase modal es 7.
• La frecuencia posterior a la clase modal f es 3.
• La amplitud de clase es 8.
La fórmula para al cálculo de la moda de dato agrupado es:
M L Co i= +
∆
∆ + ∆






1
1 2

37. 29
Entonces, sustituyendo los datos obtenemos:
Mo = +
−
−( )+ −( )





74
10 7
10 7 10 3
8
Mo
= 76,4 ≈ 76
Trabajemos en equipo.
Actividad
Los datos que se presentan a continuación corresponden a los
bonos productivos entregados por el gobierno de reconciliación y
unidad nacional a 30 municipios del país. Para este conjunto de
datos encuentre la media aritmética, la mediana y la moda.
80 99 125 113 117 142 131 103 111 123
135 97 109 86 117 107 125 94 121 90
117 128 120 130 129 98 90 82 81 95
Refuerce sus conocimientos.
Explique con sus palabras y ejemplifique los conceptos que usted
ha aprendido sobre media aritmética, mediana y moda para datos
agrupados.
1. En un conjunto de datos ¿Cuál es la moda?
2. El que divide al conjunto de datos en dos partes iguales es:
a. El que más se repite.
b. Es el promedio de los datos.
c. Tiene la menor frecuencia.
3. ¿La media aritmética de un conjunto de datos que contenga
sólo números enteros puede no ser un número entero?
4. ¿La mediana de un conjunto de datos que contenga sólo
números enteros puede no ser un número entero?
5. ¿La moda de un conjunto de datos que contenga sólo números
enteros, en el caso que exista, debe ser un número entero?
Durante la Cruzada
Nacional de
Alfabetización (CNA),
“Héroes y Mártires por la
Liberación de Nicaragua”,
que se realizó en el año
1 980, impulsado por
el gobierno sandinista
en su primera etapa,
el porcentaje de
analfabetismo pasó de
un 50,35 % al 12,86 % al
finalizar la Cruzada.
Ma
tem
áti
ca
7
¿Sabías qué?

38. 30
Aplico los conocimientos aprendidos.
1. A continuación se presenta el siguiente conjunto de datos
correspondientes a la presión sanguínea sistólica de 30
pacientes de un hospital:
129 117 128 135 122 128 143 122 143 128
120 128 140 160 150 120 129 130 140 120
150 170 140 120 124 130 140 130 124 126
2. Construya una tabla de frecuencias absolutas, frecuencias
relativas y de porcentajes.
3. Apartir de las tablas construidas en el ejercicio anterior, calcule
la media aritmética, la mediana y la moda.
4. El siguiente gráfico corresponde al número de habitantes por
vivienda en los Distritos de la Ciudad de Managua, según
datos del Censo Nacional del 2005.
Diagrama de Barras
Habitantesporvivienda
Distritos de la ciudad de Managua
4,6
4,8
5
5,2
5,4
5,6
Distrito II Distrito III Distrito IV Distrito V Distrito VI
5
5,2 5,25,2
5,5
Fig. 10
5. Observa el diagrama y contesta a las preguntas:
• ¿Cuántos habitantes por vivienda hay en el Distrito II?
• ¿Cuál es el Distrito con mayor número de habitantes por
vivienda?
El promedio de bateo
se calcula dividiendo el
número de imparables
conectados entre el
número de turnos
oficiales al bate.
Ejemplo: Si un bateador
conecta 3 imparables
en 10 turnos oficiales
al bate, entonces su
promedio de bateo será:
3
10
0 333= ,
Ma
tem
áti
ca
7
¿Sabías qué?

39. 31
6. A continuación se presentan los promedios de bateo de 30
jugadores del Campeonato de Beisbol Juvenil de Nicaragua en
el año 2 009 impulsado por el Gobierno de Reconciliación y
Unidad Nacional (GRUN)
0,559 0,500 0,488 0,474 0,447 0,417 0,412 0,410
0,405 0,395 0,370 0,350 0,340 0,340 0,333 0,333
0,330 0,300 0,300 0,300 0,298 0,290 0,290 0,285
0,280 0,280 0,277 0,270 0,270 0,260 0,222 0,220
Tabla 17
• Construir una tabla de frecuencias.
7. Considere los datos correspondientes a las calificaciones
obtenidas por 14 estudiantes en una prueba parcial Matemática
de Octavo Grado.:
58 62 63 64 64 68 70
70 70 72 78 79 81 85
El diagrama de sectores circulares para estos datos es el siguiente:
Diagrama de sectores circulares
58 62 63 64 68 70 78
21%
15%
7%
7%
7%
7%
7%7%
7%
7%
7%
72 79 81 85
Fig. 11
Interpretando el diagrama de sectores circulares.
• La calificación 70 aparece tres veces en el conjunto de datos,
por lo tanto representa un 21% del total. El 21% se obtiene
dividiendo 3 (número de veces que aparece 70) entre 14
(número total de datos).
3
14
0 21 21= =, %

40. 32
• La calificación 64 aparece dos veces, ¿Qué porcentaje
representa?
• Las calificaciones que aparecen una vez, qué porcentaje
representan?
• ¿Qué ángulos corresponden a cada porcentaje?
• Encuentre la media aritmética, la mediana y la moda
8. Recuerda que un pictograma es un gráfico con dibujos
alusivos al carácter que se está estudiando y cuyo tamaño es
proporcional a la frecuencia que representan; dicha frecuencia
se suele indicar.
Ejemplo
Árboles Plantados
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
Octubre
Noviembre
Diciembre
150
100
50
0
Fig. 12
¿En qué mes se plantaron menos árboles?,
¿En cuál se hicieron más plantaciones?
La cumbre de mayor
altura en Nicaragua
es el Mogotón, que se
encuentra en la Sierra
de Dipilto, con una altura
sobre el nivel del mar de
2 107 metros.
(Fuente: Jaime Íncer
Barquero. Geografía
iIustrada de Nicaragua,
pág. 55, Julio del 2,008)
9. En el cuadro se presenta el número de estudiantes que
practican deportes en un aula de clase
Deporte Número de Estudiantes
Fútbol 20
Básquetbol 15
Béisbol 10
Otros 5
Total 50
Tabla18
Ma
tem
áti
ca
7
¿Sabías qué?

41. 33
Construir un diagrama de sectores circulares.
Para representar el diagrama de sectores circulares, se debe
calcular qué área del círculo en grados corresponde a la frecuencia
absoluta de la variable estudiada. Así, para saber qué área
corresponde al fútbol que fue escogido como el deporte preferido
por 20 estudiantes de un total de 50, se realiza el siguiente
procedimiento.
N° de Estudiantes Grados
50 360°
20 x
x =
20 360
50
( )( )o
= 144°
Luego el área que corresponde al fútbol es 144°
Asimismo se calcula el área para cada uno de los otros deportes.
Básquetbol
N° de Estudiantes Grados
50 360°
15 x
x =
15 360
50
( )( )o
= 108°
El área que corresponde a básquetbol es de 108°
Béisbol
N° de Estudiantes Grados
50 360°
10 x
x =
10 360
50
( )( )o
= 72°
Nota: La suma de los grados de todos los deportes escogidos debe
dar 360º que es el área total del círculo.
Veamos:
Deporte Ángulo
Fútbol 144°
Básquetbol 108°
Béisbol 72°
Otros 36°
Total 360°
Tabla 19

42. 34
El diagrama de sectores circulares correspondiente es:
Basquetbol: 15
Fútbol: 20
Beisbol: 10
Otros: 5
Deporte Preferido
Figura 13
10. Toma en cuenta el siguiente histograma de los estudiantes de
7mo grado de un instituto y responde:
70
60
50
40
30
20
10
143 158153148
Clases
Estaturas en cm
A
B
S
O
L
U
T
A
F
R
E
C
U
E
N
C
I
A
Fig. 14
¿En cuántas clases se han agrupado los datos?
¿Cuántos estudiantes de 7o
grado hay en esta población?
¿Cuál es la clase de datos que tiene menor frecuencia?
¿En qué clase se concentra el mayor número de estudiantes?
Por lo tanto, se puede considerar que la mayor parte de dicha
población tiene una estatura regular entre:
• 146 y 150 cm
• 151 y 155 cm
• 141 y 145 cm
• 156 y 160 cm

43. 35
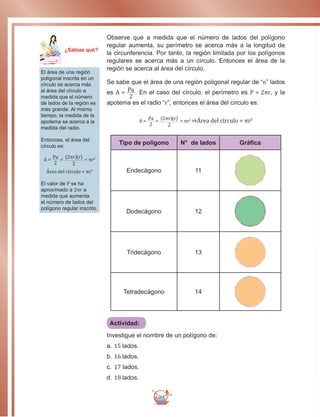
11. Dados los datos de las estaturas en centímetros de 30 personas,
represente gráficamente la distribución en un histograma.
175 147 160 167 167
170 157 164 158 162
168 166 158 166 169
169 169 154 163 165
162 168 162 168 163
150 165 166 163 165
Solución:
Por una parte, la variable que estamos estudiando es continua
(la estatura). Además, entre los datos que tenemos hay una gran
variedad. Por tanto, debemos agrupar los datos en intervalos.
El menor valor es 147 y el mayor es 175; su diferencia es
175 - 147 = 28.
Así, podemos tomar 6 intervalos de longitud 5, empezando por
146,5:
Intervalo fi
146,5 - 151,5 2
151,5 - 156,5 1
156,5 - 161,5 4
161,5 - 166,5 13
166,5 - 171,5 9
171,5 - 176,5 1
30
Tabla 20
0 146,5 151,5 156,5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Frecuencia
Estatura
176,5161,5 166,5 171,5
Histograma de la tabla de frecuencia anterior (Fig.15)
La notación de intervalos
de clase [ LI, LS ] o bien
[ Li, Ls ] expresa:
Li : Límite inferior de un
intervalo.
Ls : Límite superiorde un
intervalo.
Marca de clase (Xi ):
Se calcula sumando el
límite inferior y el límite
superior, luego dividimos
el resultado por 2.
X
L +L
i
i s
=
2
Límites reales:
Los límites reales se
determinan restando 0,5
o
1
2
al límite inferior y
al superior le sumamos
0,5 o
1
2
Ma
tem
áti
ca
7
¿Sabías qué?

44. 36
En algunos casos
dependiendo de la
cantidad de datos es
necesario organizar
los datos en una
representación gráfica
de doble tronco.
Diagrama de Tallo y Hoja
El diagrama de tallo y hoja es una herramienta que permite
obtener una representación visual informativa de un conjunto de
datos, para su elaboración es necesario separar para cada uno
de los datos el último dígito de la derecha (hoja) del bloque de
cifras restantes (tallo).
Los pasos para construir el diagrama son:
Paso 1: Paso opcional, ordenar de forma ascendente (de menor
a mayor) los datos. Este paso permite obtener una representación
ordenada del diagrama de tallo y hoja.
Paso 2: Seleccionar el último dígito de la derecha para el valor
de la hoja, siendo los dígitos iniciales los valores del tallo. Para
números mayores de cuatro dígitos es posible utilizar valores de
hojas de más de un dígito.
Paso 3: Hacer una lista de los valores de los tallos en una columna,
ordenados de forma ascendente (de menor a mayor).
Paso 4: Registrar las hojas por cada observación junto al valor
correspondiente del tallo.
También es posible agregar una columna de datos adicionales con
información complementaria como lo son la frecuencia relativa,
la frecuencia acumulada, un indicador del tallo que incluya la
mediana.
El número de tallos puede variar de un diagrama a otro, sin
embargo es recomendable que este número oscile entre 5 y 20
tallos ya que esto nos facilitará y permitirá:
1. Identificar el valor característico de la distribución de los datos.
2. Identificar la forma general de la distribución de los datos.
3. La dispersión de los datos.
Sin embargo lo anterior no será posible si la dispersión de los
datos es muy grande.
Ma
tem
áti
ca
7
¿Sabías qué?

45. 37
Ejemplo
Diámetro: Se presentan los diámetros (Tabla 21)
Diámetro, datos
ordenados
2,5 2,5 2,9 3,9 3,9 3,9 4,2 4,3 4,5
De cada dato, Tallo 2 2 2 3 3 3 4 4 4
Hoja 5 5 9 9 9 9 2 3 5
Diagrama de tallo y hojas (Tabla 22):
Tallo Hojas
2 5 5 9
3 9 9 9
4 2 3 5
5 3
Para completar la información se suele añadir una columna
delante del tallo en la que se cuentan las frecuencias de cada tallo
acumulándolas de arriba hacia abajo y viceversa, en el tallo donde
se encuentre el dato mediano se escribe solamente la frecuencia
de ese tallo.
Si se desea se pueden marcar las filas donde estén los cuartiles
colocando un asterisco a continuación de la frecuencia. Para los
datos anteriores:
frecuencias Tallo Hojas
3 2 5 5 9
3 3 9 9 9
3 4 2 3 5
1 5 3
Tabla 23
Actividad
1. Considere las siguientes calificaciones del primer corte evaluativo
en la disciplina de física aplicada a 20 estudiantes y construya un
diagrama de tallo y hojas.
69 84 52 93 61 74 79 65 88 63
57 64 67 72 74 55 82 61 68 77

46. 38
Trabajo en equipo
1. Considere las siguientes calificaciones del cuarto corte
evaluativo de 20 estudiantes. del octavo grado A del colegio
Primero de Mayo.
69 84 52 93 61
74 79 65 88 63
57 64 67 72 74
55 82 61 68 77
Determine lo que se le pide:
a. Elabore un diagrama de tallo y hojas.
b. Construye una tabla de distribución de frecuencias.
c. Calcule:
La media aritmética.
La mediana.
La moda.
d. Elabore dos gráficos estadísticos de los estudiados.
2. Al investigar los precios por habitación de 50 hoteles de la
cuarta región de Nicaragua se han obtenido los siguientes
resultados
700 300 500 400 500 700 400 750 800 500
500 750 300 700 1 000 1 500 500 750 1 200 800
400 500 300 500 1 000 300 400 500 700 500
300 400 700 400 700 500 400 700 1 000 750
700 800 750 700 750 800 700 700 1 200 800
Determíne:
a. La distribución de frecuencias de los precios.
• Agrupados en 5 intervalos de igual amplitud.
b. Porcentaje de hoteles con un precio superior a 750.
c. ¿Cuántos hoteles tienen un precio mayor o igual que 500 pero
menor o igual a 1 000?.

47. 39
Ejemplo
La tabla de datos correspondiente a las edades de 50 estudiantes
de la modalidad de secundaria a distancia del Instituto Experimental
México está dada a continuación:
Intervalo Marca de
clase: Xi
Frecuencia
absoluta:
fi
Frecuencia
absoluta
acumulada
Fi
Frecuencia
porcentual
fr
Frecuencia
porcentual
acumulada
%
[15,22) 18,5 37 37 0,74=74% 74%
[22,29) 25,5 5 42 0,10=10% 84%
[29,36) 32,5 3 45 0,06=6% 90%
[36,43) 39,5 4 49 0,08=8% 98%
[43,50) 46,5 0 49 0,00=0% 98%
[50,57) 53,5 0 49 0,00=0% 98%
[57,64) 60,5 1 50 0;02=2% 100%
Total n = 50 1,00=100%
La moda es la edad de 18,5 años que es la marca de clase que
corresponde a la mayor frecuencia absoluta 37
Me L
n
F C
f
i
i
i
= +
−



−
2 1
La mediana es la edad que se encuentra en el centro de todas las
edades para calcularla utilizaremos la fórmula
Donde:
Me
= Mediana, la cual se encuentra ubicada en el primer intervalo
pues
n
2
= =
50
2
25 y este dato se encuentra en la frecuencia
acumulada del primer intervalo.
Li
= Límite inferior del intervalo que contiene la mediana, es decir,
15
C = amplitud = 7 porque 22 - 15 = 7
n = Número de datos = 50
Tabla 24

48. 40
Fi - 1
= frecuencia acumulada anterior al intervalo que contiene la
mediana = 0 porque antes de este primer intervalo no hay datos
acumulados.
fi
= La frecuencia absoluta que corresponde al intervalo que
contiene la mediana = 37
Me = +
−




15
7
50
2
0
37
Me = +
[ ]15
7 25
37
Por tanto:
Me = +15
175
37
Me
= 15 + 4,73
Me
= 19,73
Lo cual significa que la mediana o la edad que se encuentra en
el centro de los datos recolectados es 19.
Actividad
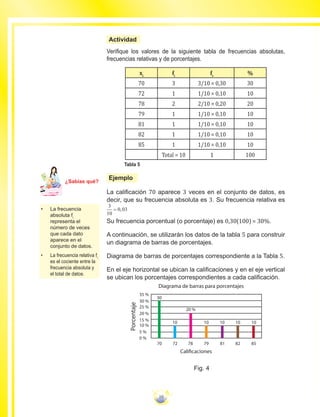
1. La tabla de frecuencias siguiente corresponde al número de consultas
realizadas por una brigada de médicos sandinistas en diferentes
comunidades del país. Calcular la media arítmetica, mediana y moda.
Intervalo Marca de
clase Xi
Frecuencia
absoluta
fi
Frecuencia
absoluta
acumulada
Fi
Frecuencia
porcentual
%
Frecuencia
porcentual
acumulada
%
[44,51) 47,5 16 16 10,67 10,67
[51,58) 54,5 19 35 12,67 23,33
[58,65) 61,5 24 59 16 39,33
[65 ,72) 68,5 31 90 20,67 60
[72,79) 75,5 23 113 15,33 75,33
[79,86) 82,5 15 128 10 85,33
[86,93) 89,5 13 141 8,67 94
[93,100) 96,5 9 150 6 100
150
Tabla 25

49. 41
Actividades Finales de la Primera Unidad
1. Se pregunta a 40 niñas y niños cuál de los siguientes deportes prefiere practicar:
básquetbol (B), natación (N), fútbol (F), tenis (T), ajedrez (A).
Estos son los resultados:
FFBFF FAFBT
NFFFA BBFFA
BFFFF BFBBT
FTFFB BFTTA
Realice la correspondiente tabla de frecuencias
2. Hemos preguntado a un grupo de 30 vecinos del barrio en el que vivimos sobre las
actividades realizadas en su tiempo libre. Éstas fueron las respuestas obtenidas:
baile baile cine baile baile deporte
baile música música baile amigos idiomas
baile amigos cine deporte baile cine
baile amigos música música baile baile
deporte baile amigos baile baile baile
Elabora: Una tabla de categoria y un gráfico de barras.
3. Encuentre el valor de la media aritmética, la mediana y la moda en las siguientes
situaciones:
a. El número de estrellas de los hoteles de una ciudad viene dado por la siguiente
serie:
3, 3, 4, 3, 4, 3, 1, 3, 4, 3, 3, 3, 2, 1, 3, 3, 3, 2, 3, 2, 2, 3, 3, 3, 2, 2, 2, 2, 2, 3, 2, 1, 1, 1, 2, 2, 4, 1.
b. Las calificaciones de 50 estudiantes en Matemática han sido las siguientes:
5, 2, 4, 9, 7, 4, 5, 6, 5, 7, 7, 5, 5, 2, 10, 5, 6, 5, 4, 5, 8, 8, 4, 0, 8, 4, 8, 6, 6, 3, 6, 7, 6, 6, 7, 6, 7, 3, 5,
6, 9, 6, 1, 4, 6, 3, 5, 5, 6, 7.
4. En un grupo de 30 personas se miden la estatura, en centímetros, de cada una de
ellas, obteniendo los siguientes resultados:
160 163 165 164 162 168 175 167 159 160
161 164 167 168 154 163 164 167 164 165
166 168 165 167 159 164 150 166 147 170
a. Elabore una tabla de frecuencias con cuatro intervalos.

50. 42
5. A continuación se presentan las alturas en metros sobre el nivel del mar de las
principales cumbres de Nicaragua.
Altura Nombre Ubicación Altura Nombre Ubicación
2 107 Mogotón Nueva Segovia 1 442 Apante Matagalpa
1 792 Jesús Sierra de Jalapa 1 421 Malacate Nueva Segovia
1 750 Kilambé Jinotega 1 410 Marimacho Nueva Segovia
1 745 Peñas Blancas Matagalpa 1 364 Zinica Jinotega
1 730 Pataste Madriz 1 348 El Fraile Estelí
1 700 Tepesomoto Madriz 1 345 Chagüitillo Matagalpa
1 680 Chimborazo Jinotega 1 338 Quirragua Matagalpa
1 675 Cúspide Jinotega 1 326 Arenales Nueva Segovia
1 652 Sazlaya Jinotega 1 305 Guabule Matagalpa
1 640 El Diablo Jinotega 1 250 Cuscawas Matagalpa
1 367 Quiabú Estelí 1 200 Baba Jinotega
1 550 Tisey Estelí 1 184 Cerro Alegre Boaco
1 053 El Variador Chinandega 1 120 Güisisil Managua
1 450 Musún Matagalpa 1 108 Masigüe Boaco
1 445 Tomabú Estelí 1 059 Mombachito Boaco
a. Construye una tabla de frecuencias absolutas, frecuencias relativas y de porcentajes.
b. Calcule:
££ La media aritmética
££ La mediana
££ La moda.

51. 43
6. Los datos que se dan a continuación corresponden a las alturas en metros sobre el
nivel del mar de los volcanes de Nicaragua.
Altura Volcán Ubicación Altura Nombre Ubicación
859 Cosigüina Chinandega 818 Asososca León
1 105 Chonco Chinandega 1 280 Momotombo León
1 745 San Cristóbal Chinandega 480 Chiltepe Managua
1 405 Casitas Chinandega 632 Masaya Masaya
1 061 Telica León 1 345 Mombacho Granada
834 San Jacinto León 629 Zapatera Granada
675 Cerro Negro León 1 610 Concepción Rivas
836 Rota León 1 394 Maderas Rivas
938 Pilas León 1 050 El Hoyo León
a. Construye una tabla de frecuencias absolutas, frecuencias relativas y de porcentajes.
b. Calcule:
££ La media aritmética
££ La mediana
££ La moda.
c. Elabora los gráficos estadísticos siguientes:
££ Diagrama de barra.
££ Gráfico de sector circular.

52. 44
7. El gobierno Sandinista desea saber si el número medio de hijos por familia ha descendido
respecto a la década anterior. Para ello ha encuestado a 50 familias respecto al número
de hijos y ha obtenido los siguientes datos:
2 4 2 3 1 2 4 2 3 0 2 2 2 3 2 6 2 3 2 2 3 2 3 3 4
3 3 4 5 2 0 3 2 1 2 3 2 2 3 1 4 2 3 2 4 3 3 2 2 1
a. Construye la tabla de frecuencias a partir de estos datos.
b. ¿Cuántas familias tienen exactamente tres hijos?¿qué porcentaje de familias tienen
exactamente 3 hijos?
c. ¿Qué porcentaje de las familias de la muestra tienen más de dos hijos? ¿Y menos
de 3?
d. Construye un diagrama de sector circular.
e. Construye un histograma
8. En un hospital se desea hacer un estudio sobre el peso en kilogramos de los recién
nacidos. Para ello, se recogen los datos de 40 bebés y se tiene:
3,2 3,7 4,2 4,6 3,7 3,0 2,9 3,1 3,0 4,5
4,1 3,8 3,9 3,6 3,2 3,5 3,0 2,5 2,7 2,8
3,0 4,0 4,5 3,5 3,5 3,6 2,9 3,2 4,2 4,3
4,1 4,6 4,2 4,5 4,3 3,2 3,7 2.1 3,1 3,5
a. Construir una tabla de frecuencias
b. Si sabemos que los bebés que pesan menos de 3 kilogramos nacen prematuramente
¿Qué porcentaje de niños prematuros han nacido entre estos 40?
c. Normalmente los niños que pesan más de 3 kilogramos y medio no necesitan estar
en la incubadora ¿qué porcentaje de niños está en esta situación?
d. Represente a través de un gráfico estadístico estudiado la información recogida.

53. 45
9. Los estudiantes del Instituto Nacional de Oriente fueron clasificados según sexo
(masculino - femenino) y si usan lentes (si o no). Estas variables forman parte de
un estudio que se realizó entre septiembre y octubre de 2 014 y tenía como objetivo
determinar los factores claves asociados con el rendimiento académico a fin de
proponer un plan de mejoras. A continuación la tabla de contingencia que resume los
datos relacionados con las dos variables.
SEXO
Usa lentes Total
Si No
Masculino (1) 350 90
Femenino (0) 40
Total 110 800
Una tabla de este tipo se llama de doble entrada o de contingencia. La tabla contiene
celdas, totales marginales fila, totales marginales columna y el total general.
££ Las dimensiones de una tabla de contingencia se especifican por el número de filas
multiplicadas por el número de columnas. En este caso la tabla es de 2 x 2 ya que
hay dos niveles de la variable “sexo” (filas) y dos niveles de la variable “usa lentes”
(columnas).
Responda:
a. Complete la tabla
b. ¿Cuántos estudiantes son del sexo masculino? ¿qué porcentaje del total
representa esto?
c. ¿Qué porcentaje de estudiantes usa lente?
d. ¿Del total de estudiantes, qué porcentaje son del sexo femenino y no usa lente?
e. ¿De los estudiantes del sexo masculino, qué porcentaje usa lente?
f. ¿De los estudiantes que usa lente, qué porcentaje es femenino?
g. Haga un gráfico estadístico que muestre la interacción entre ambas variables.
Describa una conclusión relevante

54. 46
10. Los datos son mediciones de intensidad solar directa (en watts/m2
) realizados en
distintos días en una localidad.
562 869 708 775 775 704 809
856 655 806 878 909 918 558
768 870 918 940 946 661 820
898 935 952 957 693 835 905
a) Construya una tabla de distribución de frecuencia con 4 frecuencias
b) Elabore un histograma, polígono de frecuencia u ojiva
c) Determine las medidas de tendencia central
• Media aritmética
• Mediana
• Moda
12. La gran variedad de factores a considerar en la compra de una vivienda, lugar,
precio, tasa de amortización, tipo de construcción y otros hacen que el tiempo que un
comprador tarda en llegar a su decisión final sea muy variable. Los siguientes datos
representan la duración de la búsqueda (en semanas) de 25 compradores de vivienda
en cierta población.
15 17 7 15 20
5 3 19 10 3
11 10 4 8 13
9 15 6 2 8
12 1 2 13 4
a. Construya un histograma de frecuencias que contenga 3 intervalos.
b. ¿A qué conclusión llega con esta descripción gráfica acerca del tiempo de búsqueda
que invierten los compradores de vivienda?

55. 47
13. Los datos a continuación son el número de bono productivo alimentario aprobado por
el gobierno sandinista en 28 municipios del país.
56 86 70 77 77 70 80
85 65 80 87 90 91 55
76 87 91 94 64 61 82
89 93 95 95 69 83 90
a. Construya una tabla de distribución de frecuencia con 3 intervalos.
b. Elabore un histograma.
c. Determine las medidas de tendencia central con datos agrupados:
££ Media aritmética
££ Mediana
££ Moda.
14. El responsable de una biblioteca de cierta Universidad ordenó un estudio del tiempo
que un estudiante tiene que esperar (en minutos) para que le sea entregado el libro
solicitado para consulta. Los datos fueron tomados durante un día normal a una muestra
de 20 estudiantes:
12 16 11 10 14 3 11 17 9 18 16 4 7 14 15 16 5 6 7 7
Hallar las medidas de tendencia central:
• La media aritmética
• La moda
• La mediana

56. 48
15. La tabla siguiente muestra la distribución por edades del cabeza de familia en el barrio
Hugo Chávez de Managua durante el año 2 014.
Edad fi
[20,25) 2
[25,30) 4
[30,35) 5
[35,40) 10
[40,45) 9
[45,50) 6
[50,55) 4
[55,60) 2
a. Determine la mediana y la moda.
b. ¿Por qué la mediana es una medida más adecuada que la media aritmética en este
caso?
16. En una empresa de transporte se tomaron 40 datos que significan el peso de carga por
viaje (en miles de libras)
60 55 80 72 75 63 48 79 82 72
58 60 74 80 53 61 80 68 76 75
63 65 72 81 64 78 62 83 79 61
63 62 77 76 51 74 78 50 79 55
Conteste:
a. ¿Cuántos camiones llevaron carga con menos de 60 000 libras?
b. ¿Qué porcentaje de camiones llevaban cargas entre 6 000 y 77 000 libras?
c. ¿Cuál es el peso promedio de los vehículos que cargaron entre 78 000 y 83 000 libras?

57. 49
17. Las siguientes son cantidades de óxido de azufre (en toneladas) emitidas por una
planta industrial en 60 días:
15 26 17 11 23 24 18 13 9 13
22 9 6 14 17 26 12 28 17 23
26 22 18 20 11 20 15 19 16 10
19 15 22 26 20 21 19 21 16 19
18 23 24 20 16 18 7 13 23 14
14 29 19 17 20 24 22 24 18 18
Elabore una tabla de frecuencia de 5 intervalos.
18. Las notas finales en la asignatura de matemática de 50 estudiantes de octavo grado en
el Colegio Carmela Noguera de la ciudad de Granada fueron las siguientes:
58 68 73 61 66 96 79 65 86 93
43 67 80 62 78 78 65 79 84 33
90 75 88 75 82 89 67 73 73 55
66 81 67 97 61 75 87 73 82 61
92 68 60 74 94 75 78 88 72 82
Conteste:
a. ¿Cuál es el promedio de las notas menores a 70?
b. ¿Cuál es el porcentaje de estudiantes que tienen notas mayores o iguales a 70?
c. Elabore un gráfico estadístico apropiado a estos datos,
19. A continuación se da la tabla de frecuencia correspondiente a las notas finales de un
curso en Ciencias Naturales, expresadas en la escala de 1 al 10:
Intervalo Frecuencia
1 - 2 8
3 - 4 15
5 - 6 7
7 - 8 13
9 - 10 7
Total 50
Elabore el histograma correspondiente a estos datos.

58. 50
20. Las siguientes cantidades reflejan el pago de 55 abonados de Enacal que cancelaron
sus recibos el día de hoy, correspondientes al mes de marzo de 2 014.
111 97 114 109 118
94 105 91 114 138
115 88 132 141 99
89 103 110 116 105
82 114 113 108 112
141 125 102 102 94
92 108 146 101 96
132 107 95 124 132
112 118 101 98 118
97 114 115 140 123
135 129 104 107 108
Elabore los una tabla de frecuencias con cuatro intervalos y un histograma.
Determine las medidas de tendencia central:
• Media aritmética
• Mediana
• Moda
21. El Ministerio de la Familia visitó la Penitenciaría de Estelí, con el objetivo de hacer un
estudio sobre las edades de los jóvenes comprendida entre los 15 y 17 años y que han
tenido problemas relacionados con el consumo de drogas. Estas edades fueron las
siguientes:
15 15 15 16 17 17 16 15 16 17
16 16 15 15 15 15 15 15 17 16
16 16 16 15 17 16 15 16 17 15
15 15 15 16 16 15 16 17 15 16
Determine las medidas de tendencia central:
• Media aritmética
• Mediana
• Moda

59. Unidad 2
El Gobierno de Reconciliación y Unidad Nacional ha impulsado un importante proyecto
como es la construcción del puente Santa Fe y paralelo a la construcción del puente
también se construyó la carretera ubicada en la costa Sur del Río San Juan de Nicaragua
hasta concluir en la frontera con Costa Rica, lo que facilitará que las exportaciones de la
zona central del país puedan salir en esa dirección hacia Puerto Limón en Costa Rica,
además de la entrada y salida de nicaragüenses hacia el país vecino del Sur.
Fuente: 19 digital.
Abril 2 014.
Conjunto de
Números Reales

60. 52
El Conjunto de los Números Reales.
Introducción.
En el Séptimo Grado fueron estudiados los siguientes conjuntos
numéricos:
• El conjunto de los números naturales que se denota por ℕ.
• El conjunto de los números enteros que se denota por ℤ.
Z = … − − …{ }, , , , , ,2 1 0 1 2
• El conjunto de los números racionales que se denota por ℚ.
Un número es racional si puede ser expresado como el cociente
de dos números enteros, siempre que el denominador sea
diferente de cero.
En notación de conjuntos se escribe así:
Q Z Z= = ∈ ∈ ≠






x x| , ,
p
q
donde p q y q 0
El símbolo “∈” se lee “pertenece a”.
El conjunto de los números naturales está contenido en el
conjunto de los números enteros y el conjunto de los números
enteros está contenido en el conjunto de los números racionales.
Utilizando la simbología de los conjuntos se escribe:
� ⊂ � ⊂ ℚ
El conjunto de los números naturales es subconjunto de los
números enteros y el conjunto de los números enteros es
subconjunto de los números racionales.
IMPORTANTE
La suma de dos
números irracionales
no necesariamente es
irracional.
Ejemplo:
2 2 0+ −( )=
Tanto 2 como − 2 son
números irracionales.
Sin embargo, su suma
da como resultado el
número cero que es un
número racional.
Lo mismo ocurre con el
producto y la división de
números irracionales.
Ejemplos:
3 12 36 6( )( )= =
2
2
1=
Tanto 6 como 1 son
números racionales
Fue un respetado
matemático y físico. Se
le considera el principal
matemático del siglo
XVIII y uno de los más
grandes de todos los
tiempos.
Leonhard Paul Euler
(1 707 - 1 783)
Nota histórica

61. 53
El conjunto de los números irracionales.
Lea, analice e interprete.
££ Introducción.
¿Qué conjuntos de números han sido estudiados?
Han sido estudiados el conjunto de los números naturales ℕ, el
conjunto de los números enteros ℤ y el conjunto de los números
racionales ℚ.
Actividad
Al efectuar las siguientes divisiones:
1
3
0 333333= , ...;
1
6
0 166666= …, ;
1
7
0 142857142= …,
se obtienen decimales periódicos. Los decimales periódicos se
pueden expresar como cociente de dos números enteros con
denominador distinto de cero. Esto significa que son números
racionales.
Surgen dos preguntas:
• ¿Existen desarrollos decimales que no sean periódicos?
• ¿Si existen, qué números representan?
Para contestar la primera pregunta consideremos los siguientes
números decimales:
0,20 200 2000 20000 200000 2…
5,7822 3222 42222 5222222 6…
Observe que los dos números decimales anteriores no son
periódicos y no se pueden expresar como cociente de dos números
enteros, por lo tanto no son números racionales.
Si usted intenta con una calculadora o por cálculo directo encontrar
el valor de 2 , observará que nunca obtendrá un decimal periódico.
El número 2 es un ejemplo de un número irracional.
¿Qué conjunto de números incluye a los números decimales no
periódicos?
El conjunto de los
números irracionales no
es cerrado respecto a
la suma ni respecto al
producto
Nota histórica
Números irracionales
famosos.
π
Pi es un número
irracional famoso. Se
han calculado más de
un millón de sus cifras
decimales sin repetirse.
Las primeras son:
3,1415926535897932384
626433832795...
e
Se han calculado muchas
cifras decimales de e sin
encontrar ningún patrón.
Los primeros decimales
son:
2,7182818284590452353
602874713527...
Φ
El número áureo o
número de oro es un
número irracional. Sus
primeros dígitos son:
1,6180339887498948
4820...
Ma
tem
áti
ca
7
¿Sabías qué?

62. 54
Analizaremos un ejemplo que tiene un significado histórico muy
importante en el surgimiento de los números irracionales.
Ejemplo
Se da un cuadrado cuyo lado tiene medida 1m. Se pide calcular
la medida de la diagonal del cuadrado.
De acuerdo con el teorema de Pitágoras la longitud o medida de
la diagonal es:
d AB BC= + = + =2 2 2 2
1 1 2
D C
BA 1
1
d = 2
El número 2 no se puede expresar como el cociente de dos
números enteros y por tanto no es un decimal periódico, o sea
que no es racional.
Se ha obtenido un número que no pertenece ninguno de los
conjuntos que se han estudiado.
££ El concepto de número irracional
Los números que no son decimales periódicos y no se pueden
expresar como el cociente de dos números enteros reciben el
nombre de números irracionales. Se denotarán los números
irracionales con el símbolo ℚ'
Ejemplo
Son números irracionales los siguientes:
2 3 5 7, , , ,...
Información importante.
• El número e ≈ 2,718281828449…es irracional.
El número e, que además de ser irracional es un número
trascendente, es la base de los logaritmos neperianos o logaritmos
naturales que serán estudiados en el Noveno Grado.
También aparece en los procesos de crecimiento y decaimiento,
en el estudio de la desintegración radiactiva, en la farmacología,
en el estudio de crecimiento de colonias de bacterias, en el
estudio de las epidemias, en arqueología, en la física nuclear, en
ciencias económicas, en ciencias ambientales, etc.
Fue un estudiante
de Pitágoras, quién
descubrió los números
irracionales intentando
escribir la raiz cuadrada
de 2 en forma de
fracción (se cree que
usando Geometría).
Pero en su lugar
demostró que no se
puede escribir como
fracción, así que es un
número irracional.
Muchas raíces cuadradas,
cúbicas, etc. también son
irracionales.
Ejemplos:
77 11 173 4
...
No todas las raíces son
irracionales.
4 2 27 33
= = ...
son números racionales.
Nota histórica

63. 55
• El número π ≈ 3,141592653589…es irracional.
El número π es el número irracional más famoso y probablemente
el más conocido.
La longitud de una circunferencia se calcula utilizando el número
π (Longitud = 2πr), el área de un círculo se calcula usando el
número π (Área = πr2
). También se calcula utilizando el número π:
el volumen de una esfera, el volumen de un cilindro, el volumen de
un cono, áreas de superficies, etc.
Calcule usted el valor aproximado del número π dividiendo la
longitud de cualquier circunferencia entre el diámetro de la misma.
• El número áureo o número de oro.
Φ =
+
≈
1 5
2
1 618033988749, ...
es un número irracional.
El número áureo o número de oro “Φ”,(Phi,se lee “fi”) es un número
irracional muy interesante. Aparece en la pintura, la arquitectura,
en las estructuras de la naturaleza. Luca Pacioli se refería a la
divina proporción, Leonardo de Vinci se refería a la perfección
áurea. En el estudio de los poliedros en Geometría también
aparece el número de oro.
Trabajemos en equipo.
Actividad
Mida con una cuerda la circunferencia de cualquier recipiente
que tenga forma cilíndrica. A continuación encuentre el diámetro
de la circunferencia. Con los datos obtenidos realice el siguiente
cálculo:
El valor que obtendrá es una aproximación al número π, cuyo
valor es aproximadamente 3,14159…
Si realiza esta misma actividad con
diferentes recipientes circulares, obtendrá
el mismo resultado. Esto justifica referirse al
número π como la relación entre la longitud
de la circunferencia y su diámetro.
Filósofo griego nacido
en la isla de Samos y
muerto en Metaponto.
Se le considera el primer
matemático puro. La
sociedad que lideró
estaba regida por códigos
secretos que hace que su
figura sea muy misteriosa.
El Teorema de
Pitágoras
El cuadrado de la medida
de la hipotenusa de un
triángulo rectángulo es
igual a la suma de los
cuadrados de las medidas
de los catetos.
c (Cateto)
a (Hipotenusa)
b (Cateto)
A
B
C
a2
= b2
+ c2
Pitágoras de Samos
(580 a. C.-520 a.C)
Diámetro
Circunferencia
Nota histórica

64. 56
Representación de números irracionales en una
recta numérica.
¿Cómo se ubica un número irracional en una recta numérica?
Trabajemos en equipo.
1. Dibuje un cuadrado de lado de longitud 1.
2. Trace la diagonal del cuadrado.
3. Calcule la medida de la diagonal del cuadrado.
D C
BA 1
1
La longitud de la diagonal se puede encontrar por medio del
teorema de Pitágoras.
AC AB BC AC AC AC2 2 2 2 2 2 2
1 1 2 2 2= + ⇒ = + = ⇒ = ⇒ =
La longitud de la diagonal AC es 2 . El número 2 no se puede
expresar como un cociente de dos números enteros y no es un
decimal periódico, luego no es un número racional.
¿Cómo se representa en una recta numérica el número irracional
3 ?
Usted puede utilizar la construcción de la diagonal de un cuadrado
de lado de longitud 1 para ubicar el número irracional 2 en la
recta numérica.
Ejemplo
Utilizando la figura realice la siguiente construcción:
• Prolongue el lado AB hacia la derecha.
• Con un compás, tomando como centro el punto D y con
radio DB trace una circunferencia.
• La circunferencia cortará a la prolongación del lado DC en
un punto que corresponde al número irracional 2 .
El símbolo ⟹
se lee
“si,…,entonces
Ma
tem
áti
ca
7
¿Sabías qué?

65. 57
Ha obtenido una figura como la que se muestra a continuación:
Por el teorema de Pitágoras se obtiene:
DB = + =1 1 22 2
DE = ( ) +2 1
2
2
DE = + =2 1 3
Observe que la medida del segmento DB = 2 y la medida del
segmento DE = 3 .
Trabajemos en equipo.
Siguiendo los mismos pasos que en el ejemplo anterior, encuentre
la ubicación sobre la recta real de los siguientes números
irracionales: 7 8 11, .
Sugerencia: 7 4 3 2 32
2
= + = + ( )
El conjunto de los números reales.
Lea, analice e interprete.
El siguiente esquema muestra los distintos conjuntos de números
La unión del conjunto de los números racionales con el conjunto
de los números irracionales, recibe el nombre de conjunto de
los números reales y se denota con la letra ℝ, simbólicamente
se escribe:
ℝ = ℚ ∪ ℚ'
Simbólicamente también se puede escribir el conjunto de los
números reales de está manera: ℝ = ℕ∪ℤ∪ℚ∪ℚ'. Véase el
esquema que sigue:
Números reales
Números racionales
Números irracionales
Números enteros
Números fraccionarios
Positivos
Negativos
Números naturales
Números enteros
negativos
Cero
A B
CD 1
1
E
Una construcción
alternativa de algunos
números irracionales
Paso 1. Dibujar un
triángulo ∆PAB rectángulo
en A y con catetos de
medida 1.
Paso 2. Trazar un
segmento perpendicular al
segmento BP en el punto
B, cuya medida sea 1.
Paso 3. Trazar un seg-
mento perpendicular al
segmento PC en el punto
C cuya medida sea 1.
Obtenemos la figura
siguiente:
A
B
C
D
P
2
3
5
1
1
1
1
Por el teorema de Pitágoras
aplicado al triángulo ∆PAB,
obtenemos:
BP2
= AP2
+ AB2
BP2
= 12
+ 12
BP2
= 2
BP = 2
De forma similar con el
∆PBC se obtiene que:
PC = ( ) + =2 1 3
2
2
Con un proceso similar se
obtienen:
5 6 7 ...

66. 58
Representación de un número real en la recta
numérica.
Consideremos una línea recta y ubiquemos en ella números
reales.
Cero
Números
reales
negativos
Números
reales
positivos
0 0,5 1,51 2-1-2 -1,5 -0,5
A la línea recta donde se ubican los números reales se le llama
recta numérica o recta real.
El número real cero “0” se llama origen de la recta real.
Valor absoluto de un número real.
En muchas actividades de la vida real es necesario trabajar con
números que siempre deben ser positivos. Ejemplo de esto son
las distancias entre puntos.
¿Qué es el valor absoluto de un número real?
Consideremos dos números reales ubicados sobre una recta
numérica, por ejemplo el número 3 y el número - 4.
La distancia
entre -4 y 0
es 4
La distancia
entre 0 y 3
es 3
0 1 2 3-1-2-3-4 4
Observe que la distancia siempre es un número positivo.
Ahora se presenta el concepto de valor absoluto.
Valor absoluto de un número real
Esladistanciaentreelorigenyelnúmeroreal.Representaremos
el valor absoluto de un número real a por |a|.
La siguiente tabla ilustra el concepto de valor absoluto.
Si a es un número positivo, entonces
|a| = a
Ejemplo: |3| = 3.
Si a es cero, entonces |a| = 0 Ejemplo: |0| = 0
Si a es un número negativo,
entonces |a| = −a.
Ejemplo: |−3|=−(−3)=3
La unión del conjunto
de los números
naturales, con el
conjunto de los
números enteros,
el conjunto de los
números racionales
y el conjunto de los
números irracionales,
se obtiene el conjunto
de los números reales.
El valor absoluto de un
número entero x se define:
x, si x es positivo (x 0)
│x│= 0, si x = 0
-x, si x es negativo (x 0)
Donde -x es el opuesto del número entero x.
Donde -x es el opuesto
del número entero x.
Ma
tem
áti
ca
7
¿Sabías qué?

67. 59
Importante: a a a2
= = ±
Ejemplo: 4 2 22
= = ±
Suma de números reales.
Al sumar dos números reales se obtiene un número real. Esta
propiedad de la suma de números reales se llama propiedad de
cerradura o de clausura.
Propiedad de clausura
Si a ∈ ℝ y b ∈ ℝ,entonces a + b ∈ ℝ, ∀ a, b ∈ ℝ
Ejemplos
a. 2 es número real y 0,5 es un número real, entonces la suma
2 + 0,5 = 2,5 es un número real.
b. 3 2 3 1 2 3 3 3+ = +( ) =
Sumando dos números reales utilizando la recta numérica
real.
Ejemplo
Encuentre la suma −3 + 7.
Solución: Contar 7 unidades hacia la derecha a partir de −3
El resultado de la suma será el número que se encuentra a 7
unidades a la derecha de - 3 en la recta numérica. El resultado
de la suma es 4.
Actividades
1. Encuentre la suma −2 + 6 utilizando la recta numérica.
2. Si a = 20, b = 10, c = 5 compruebe que (a ÷ b) ÷ c ≠ a ÷ (b ÷ c)
3. Determine el valor absoluto:
• |4 + (−100)|
• |−80 − 16 − 24|
• |−(−x)|
La división de números
reales en general no es
conmutativa
a ÷ b ≠ b ÷ a
Ejemplo.
6 ÷ 3 =
6
3
= 2
3 ÷ 6 =
3
6
= 0,5
2 ≠ 0,5
La división de números
reales en general no es
asociativa.
a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
Ejemplo.
16 ÷ (8 ÷ 4) = 16 ÷ 2 = 8
(16 ÷ 8) ÷ 4 = 2 ÷ 4= 1
2
8 ≠ 1
2
Símbolo Se lee
∀ Para todo
∈ Pertenece a
∉ No pertenece a
Ma
tem
áti
ca
7
¿Sabías qué?

68. 60
Propiedades de la suma de números reales.
¿El orden en que se sumen dos números reales alterará el
resultado?
Ejemplo
2 + 5 = 7 y 5 + 2 = 7. El resultado es el mismo.
Esta propiedad de los números reales se llama propiedad
conmutativa.
Propiedad conmutativa
Si a ∈ ℝ y b ∈ ℝ,entonces a + b = b + a, ∀ a, b ∈ ℝ
¿Qué ocurre cuando se suman 3 o más números reales?
Consideremos el siguiente ejemplo:
Ejemplo
Al efectuar la suma
2
3
5
4
7
2
3
39
7
14 117
21
131
21
+ +





 = + =
+
=
se obtiene el mismo resultado que al sumar
2
3
5
4
7
17
3
4
7
119 12
21
131
21
+





 + = + =
+
=
Esta propiedad se llama propiedad asociativa.
Propiedad asociativa
Si a ∈ ℝ, b ∈ ℝ y c ∈ ℝ, entonces a + (b + c) = (a + b) + c, ∀ a, b, c ∈ ℝ
Compruebe que:
1.
2.
0 8 0 057
4
3
0 08 0 057
3
4
, , , ,+ + = + +






Reforzamiento
Compruebe que:
8
20
6
15
6
15
8
20
+





 = +
10
10 10
7 7
10+ = +
6
7
1
8
2
9
6
7
1
8
2
9
+





 + = + +






0 8
20
8
20
8
0 8, ,+ −





 = − +

69. 61
Sumando tres números reales utilizando la recta
real.
Ejemplo
Encuentre la suma −3 + 5 + ( −6).
5 unidades hacia la
derecha a partir de -3
6 unidades hacia la
izquierda a partir de 2
-3 -1-2-6 -4-5 4 651 320
La distancia de cero al
extremo que indica la
punta de la flecha verde
es de -4
Entonces: −3 + 5 + ( −6) = ( −3 −6) + 5 = −9 + 5( 9 −6) = −4 .
¿Qué entenderemos por el opuesto o inverso aditivo de un número
real?
Dado un número real a cualquiera, el número −a se llama el
inverso aditivo u opuesto de a.
• El inverso aditivo u opuesto del número 2 es −2.
• El inverso aditivo u opuesto del número −2 es:
−(−2) = 2.
¿Qué ocurre si sumamos un número real cualquiera con su
opuesto o inverso aditivo?
Opuesto de un número real
Si a ∈ ℝ,entonces −a ∈ ℝ, ∀ a ∈ ℝ
El número −a se llama el opuesto o inverso aditivo del número a.
La suma de todo número real a con el número real 0 da como
resultado el mismo número a. Esta propiedad se llama propiedad
del idéntico aditivo y se dice que el cero es el elemento identidad
o elemento neutro para la suma de números reales.
Ejemplo
−0,289 + 0 = −0,289
¿Cómo se interpreta en un gráfico el opuesto de un número real?
El número real a y su opuesto (o inverso aditivo) el número real
−a, se encuentran a la misma distancia con respecto al origen.
También se dice que son simétricos.
• Un número par x se
denota como:
x = 2k, k ∈ ℤ
• Un número impar x
se denota como:
x = 2k + 1, k ∈ ℤ
Reforzamiento:
¿Cual de las siguientes
afirmaciones son
correctas?
• Los números
enteros son
subconjuntos de los
números racionales
• La intersección
de los números
racionales e
irracionales es el
conjunto vacio.
• El conjunto de los
números racionales
unido al conjunto
de los números
irracionales es el
conjunto de los
números reales.
Ma
tem
áti
ca
7
¿Sabías qué?

70. 62
Propiedad del opuesto de un número real.
Todo número real a sumado con su opuesto o inverso aditivo, da
como resultado el número cero.
a + (−a) = 0
Ejemplo
a) −





 + =
5
9
5
9
0 b) 10 10 0+ −( )=
Resta de números reales. a + (−b) = a − b; ∀ a, b ∈ ℝ
Cuando un número real se suma con el opuesto de otro número
real, obtenemos la resta de estos números reales.
Ejemplos
a. 5 + ( −3) = 5 −3 = 2
b. −10 + ( −3) = −10 − 3 = −13
c. 13 2 15 2 13 15 2 2 2− = −( ) = −
Multiplicación de números reales.
Propiedad de clausura del producto de números reales.
El producto de dos números reales es un número real.
Si a ∈ ℝ y b ∈ ℝ, entonces a · b ∈ ℝ, ∀ a, b ∈ ℝ
Ejemplo
1. 3(0,5) = 1,5 ∈ ℝ
2.
3
2
5
4
15
8





 −





 = − ∈ ℝ
3. (-0,2)(3,42) = - 0,684 ∈ ℝ
4.
1
2
2
3
3 4
6
7
6
+ =
+
= ∈ℝ
5. 2 5 10⋅ = ∈ℝ
En Matemática se
acostumbra utilizar un
punto · , el asterisco *
y también paréntesis ( )
para la multiplicación de
números reales.
Ejemplos:
El producto de un
número real a con el
número real b se puede
escribir así:
1) a·b
2) a*b
3) (a)(b)
La propiedad
conmutativa es de
gran importancia en el
estudio de los números
reales y el álgebra.
Ma
tem
áti
ca
7
¿Sabías qué?

71. 63
Propiedad conmutativa del producto de números reales.
No todas las operaciones definidas en un
conjunto cumplen con esta propiedad. En el
conjunto de los números reales, se cumple
la conmutatividad tanto para la suma como
para el producto.
Ejemplo
En la figura se presenta una región rectangular de base 5u y altura
3u.
Encontrar el área de esta región e ilustrar la propiedad conmutativa
del producto de números reales.
Área = (base)(altura) = (5u)(3u) = 15 u2
Área = (altura)(base) = (3u)(5u) = 15 u2
Propiedad asociativa de la multiplicación de números reales.
Propiedad asociativa de la multiplicación de números reales.
a ∙ (b ∙ c) = (a ∙ b) ∙ c, ∀ a, b, c ∈ ℝ,
Al multiplicar tres o más números reales, la forma en que éstos se
agrupan no cambia el resultado.
Ejemplo
3,5 ∙ (2,6 ∙ 4,7) = (3,5 ∙ 2,6) ∙ 4,7 ¡Compruébelo!
Propiedad del identico aditivo para la multiplicación de
números reales.
La multiplicación de un número real a por 1 da como
resultado el mismo número a.
1 ∙ a = a, ∀a ∈ ℝ
Propiedad anuladora o de la absorción del cero para la
multiplicación de números reales.
La multiplicación de un número real a por cero da como resultado
cero.
a ∙ 0 = 0,∀a ∈ ℝ
Matemático y filósofo
italiano. Ingresó en la
Universidad de Turín
en 1 876. Se graduó
en 1 880 con honores
y comenzó su carrera
académica. Conocido
por sus contribuciones
a la Teoría de Conjun-
tos. Peano publicó más
de doscientos libros y
artículos, la mayoría en
Matemática. La mayor
parte de su vida la dedi-
có a enseñar en Turín.
Falleció de un ataque
al corazón el 20 de abril
de 1 932 en Turín.
Giuseppe Peano
(1 858 –1 932)
5 u
3u
Nota histórica

72. 64
Propiedad del opuesto para la multiplicación de números
reales.
La multiplicación de un número real a por - 1 da como resultado
el opuesto del número a.
a ∙ ( - 1) = - a, ∀ a ∈ ℝ
Actividad
Utilizando números reales, verifique cada una de las propiedades
anteriores.
Propiedad distributiva de la suma respecto a la multiplicación
en los números reales.
a ∙ (b + c) = a ∙ b + a ∙ c
a ∙ (b - c) = a ∙ b - a ∙ c
(b + c) ∙ a = b ∙ a + c ∙ a
(b - c) ∙ a = b ∙ a - c ∙ a
∀a,b,c ∈ ℝ
La propiedad distributiva combina la suma de números reales
con el producto de números reales.
Ejemplo
2 ∙ (7 + 10) = 2 ∙ 7 + 2 ∙ 10 = 14 + 20 = 34
Ejemplo
Un ejercicio de áreas en el que se utiliza la propiedad distributiva.
El área de la región rectangular de la figura es:
x 2
3
Área = (x + 2)(3)
Por la propiedad distributiva obtenemos:
Área = (x + 2) ∙ 3 = x ∙ 3 + 2 ∙ 3 = 3x + 6
1. a . 0 = 0, ∀a ∈ ℝ ?
2. 0 + 0 = 0
3. a(a . 0) = a . 0
4. (a . 0) + (a . 0) = 0
5. (a . 0) + [(a . 0) + ( - a . 0)]
= a . 0 + (-a . 0) = 0
6. (a . 0) + 0 = 0
7.a . 0 = 0
Ma
tem
áti
ca
7
¿Sabías qué?

73. 65
Actividad
Utilice la propiedad distributiva para encontrar el área de la región
de la figura.
x
54
División de números reales
Todo número real a distinto de cero (a ≠ 0), tiene un recíproco que
se escribe
1
a
y cumple con la siguiente condición:
a
a
a a1 0R1 ∈ ≠= ∀
El resultado de multiplicar el número a por el recíproco del número
b (b ≠ 0), se llama cociente y se escribe:
a b a
b
a
b
b 0÷ = = ≠
1
La división de los números
b
y
d












a c se define de la siguiente
manera:
a
b
c
d
a
b
d
c
b c





 ÷





 = ≠, 0
Ejemplo
Efectuar la división
4
5
3
7





 ÷






Solución
4
5
3
7
4
5
7
3
4 7
5 3
28
15
÷ = =
( )( )
( )( )
=i
Otra forma de expresar la división de los números a y b y sus
opuestos es la siguiente:
1 2
3 4
. .
. .
−( )÷ −( )=
−
−
= −( )÷ =
−
= −
÷ −( )=
−
= − ÷ =
a b
a
b
a
b
a b
a
b
a
b
a b
a
b
a
b
a b
a
b
La división entre cero
no está definida
a
0
no está definida
Ley de los signos en la
multiplicación.
( + )( + ) = +
más por más da más
( - )( - ) = +
menos por menos da
más
( + )( - ) = -
más por menos da
menos
( - )( + ) = -
menos por más da
menos
Ma
tem
áti
ca
7
¿Sabías qué?

74. 66
Refuerce sus conocimientos.
££ Ejercicios resueltos.
1. Efectúe las siguientes divisiones:
a. −( )÷ −( )3 7 b. 3 7÷ −( ) c. −( )÷3 7
Soluciones:
• −( )÷ −( ) =
−
−
=3 7
3
7
3
7
. Si el numerador y el denominador
tienen el mismo signo, entonces el resultado es positivo.
• 3 7
3
7
3
7
÷ −( ) =
−
= − . Si el numerador y el denominador tiene
signos diferentes, entonces el resultado es negativo.
• −( )÷ =
−
= −3 7
3
7
3
7
2. Efectúe las siguientes divisiones:
a. −
÷
−
3
5
7
2
b. 9
4
3
5
÷
− c. −
÷
−
−
7
9
4
3
Soluciones:
a. −
÷
−
=
− −
=
−( ) −( )
( )( )
=
3
5
7
2
3
5
2
7
3 2
5 7
6
35
b. 9
4
3
5
9
4
5
3
9 5
4 3
45
12
15
4
÷
−
=
−
=
( )( )
( ) −( )
=
−
= −
c. −
÷
−
−
=
− −
−
=
−( ) −( )
( ) −( )
=
−
= −
7
9
4
3
7
9
3
4
7 3
9 4
21
36
7
12
3. Pensamiento crítico.
Verdadero o falso: El recíproco de 0,025 es 40.
Solución
Verdadero. El recíproco de 0,025 es:
1
0 025
40
,
= . Verifíquelo.
Verifique también que el recíproco de 40 es 0,025.
a
b c
a
b
a
c+
≠ +
Sin embargo:
a b
c
a
c
b
c
+
= +
Ten cuidado con la
división:
- (( - a)/( - b))
Observa que al dividir
dos números del mismo
signo obtenemos un
número positivo, luego:
−
−
−





 = −
a
b
a
b
No cometas el error de
pensar que:
a b a b2 2
+ = +
Lo correcto es
a b a b2 2
+ ≠ +
Ejemplo:
Determine 3 42 2
+ por
error algunos piensan
en hacer
3 4 3 42 2
+ ≠ + = 7 (esto es
incorrecto)
Lo correcto es:
3 4 9 162 2
+ = + = 5
Ma
tem
áti
ca
7
¿Sabías qué?

75. 67
• Encuentre el reciproco de cada número.
a. −8 b. 3 39
6
−
−
c. −
−
45
7
d. −
−
1
2
Soluciones de los incisos b y d.
El recíproco de
3 39
6
−
−
es
−
−
6
3 39
.
El recíproco de −
−
1
2
es −
−
= − − = −
2
1
2 2
Pensamiento crítico. Verdadero o falso:
El recíproco de 6 es 0,16161616…
Solución
Verdadero. El recíproco de 6 es:
1
6
0 161616= , ...
Encontrar el reciproco de cada número.
a.
− −
−
4
5
b. −
−
45
7
c.
6 24
5 6
−
− − −
d. −
− −
−
1
2
Soluciones de los incisos c y d.
c. El recíproco de
6 24
5 6
−
− − −
es
− − −
−
=
− −
−
=
−5 6
6 24
11
18
11
18
d. El recíproco de −
− −
−
1
2
es −
−
− −
= −
−
− −
= −
−
= − = −
2
1
2
1
2
1
2
1
2
• ¿Cuáles de las siguientes divisiones son posibles y cuáles no
lo son?
a. 3
0
; b.
−4
0 ; c. 0
5
; d.
7
2 2− ; e. 4 4
8
−
; f. −
−
3
1
2
1
2Soluciones de los incisos a y d
•
3
0
no es posible porque la división entre cero no está definida.
•
7
2 2−
no es posible. Observe que
7
2 2
7
0−
= y la división entre
cero no está definida.
El número 0 no tiene
recíproco
El recíproco de 0 es
1
0
que no existe.
No cometas este error
- | - 2| = 2
Lo correcto es:
- | - 2| = - 2
La justificación es la
siguiente:
| - 2| = + 2
Por lo tanto,
- | - 2| = - ( + 2) = - 2
Ma
tem
áti
ca
7
¿Sabías qué?

76. 68
Propiedades de la relación de orden en el conjunto
de los números reales.
Dos números reales cualesquiera se pueden comparar. Por
ejemplo, considere los números 3 y 7.
Ejemplo
El número 3 es menor que el número 7. Esto significa que 3 no
puede ser mayor que 7 y tampoco puede ser igual a 7.
Esta propiedad de cualquier par de números reales se conoce
como Propiedad de Tricotomía.
Un número mayor que otro no puede ser menor y no puede ser
igual a ese mismo número.
Interpretación de la relación de orden en la recta
numérica.
Ejemplo
Considere los números reales:
- 3 ; - 1; 0 ; 0,5 ; 1,5 ;2 ; 3.
Ubicamos estos números en la recta real:
-3 -2 -1 0 1 2 30,5 1,5
• - 3 - 1 ( - 3 está a la izquierda de - 1 en la recta)
• 0,5 - 3 (0,5 está a la derecha de - 3 en la recta)
• 0 - 3 (0 está a la derecha de - 3 en la recta)
• 0 3 (0 está a la izquierda de 3 en la recta)
Propiedad de tricotomía.
Dados dos números reales cualesquiera a y b, se cumple
una y sólo una de las siguientes expresiones:
a = b, a b ó a b
El símbolo “” se lee “mayor que”
El símbolo “” se lee “menor que”
El cero es mayor que
cualquier número
negativo y es menor
que cualquier número
positivo
¿Por qué menos por
menos da más?
b + ( - b) = 0
-a[b + ( - b)] = -a(0)
(-a)(b) + (-a)( - b) = 0
(-a)(b) + (-a)(-b) + (a)( b)
= 0 + (a)(b)
0 + (-a)(-b) = (a)(b)
(-a)(-b) = (a)(b)
Ma
tem
áti
ca
7
¿Sabías qué?

77. 69
Propiedad transitiva de la relación de orden
1. Si a b y b c, entonces a c.
Ejemplo
Si 5 3 y 3 2,entonces 5 2.
Ejemplo
Si Roberto tiene 14 años de edad, Juan tiene 13 años y Enrique
tiene 12 años. Entonces se puede afirmar que:
La edad de Roberto es mayor que la de Juan, la edad de Juan
es mayor que la de Enrique. Entonces se puede asegurar que la
edad de Roberto es mayor que la edad de Enrique.
Simbólicamente se puede escribir que:
Edad de Roberto Edad de Juan Edad de Enrique
14 13 12
Edad de Roberto Edad de Enrique
14 12
2. Si a b entonces - a - b.
Ejemplo
Si 5 3 entonces - 5 - 3.
-5 -2-4 -3 -1 0 1 2 3 4 5
Observe que 5 es mayor que 3 y se encuentra a la derecha del 3
en la recta numérica. También observe que - 5 se encuentra a la
izquierda de - 3 en la recta numérica.
Importante. El cero se encuentra a la izquierda de cualquier
número positivo y a la derecha de cualquier número negativo. Por
eso se afirma que el cero es mayor que cualquier número negativo
y menor que cualquier número positivo.
Losgriegosdemostraron
que el número 2 no es
un número racional.
¿Como lo hicieron?
Supongamos que:
p
q
es una expresión
racional simplificada,
es decir que p y q no
tengan factor común.
Además sea:
2 =
p
q
( 2 )2
= (
p
q
)2
2 =
p
q
2
2
p2
= 2q2
entonces p2
es
divisible por dos y
por consiguiente p es
divisible por 2 ,
sea p = 2R, siendo R un
entero puesto que:
p2
= 2q2
y p = 2R
entonces tenemos que:
(2R)2
= 2q2
4R2
= 2q2
2R2
= q2
Entoncesq2
es divisible por
2 y por lo tanto q también
es divisible por dos.
Entonces p y q tienen como
factor común al número 2
por ser ambos pares, lo
que contradice el hecho de
que p y q no tienen factor
común y por lo tanto 2 no
es racional.
Ma
tem
áti
ca
7
¿Sabías qué?

78. 70
3. Si a b entonces a + c b + c
Ejemplo
Si 7 4 entonces 7 + 3 4 + 3⇒10 7
0 31 2 4 5 6 7 8 9 10
Observe que 7 es mayor que 4 y se encuentra a la derecha del 4
en la recta numérica. También observe que 10 se encuentra a la
derecha de 7 en la recta numérica y por lo tanto es mayor que 7.
4. Si a b y c 0 entonces ac bc.
Ejemplo
8 4 y c = 3⟹(8)(3) (4)(3)⟹24 12
5. Si a b y c 0 entonces ac bc.
Ejemplo
9 5 y c = - 2⟹(9)( - 2) (5)( - 2)⟹ - 18 - 10
6. Si a b y b c, entonces a c
Ejemplo
13 15 y 15 17⟹13 17
7. Si a b entonces - a - b.
Ejemplo
24 36 ⟹ - 24 - 36
8. Si a b entonces a + c b + c
Ejemplo
12 14 ⟹12 + 7 14 + 7⟹19 21
9. Si a b y c 0 entonces ac bc.
Ejemplo
2 3 y 5 0 entonces 2(5) 3(5)
10. Si a b y c 0 entonces ac bc.
Ejemplo
2 3 y -2 0 entonces -2(2) -2(3)
Dados dos números
reales
a
b
y
c
d
se cumple
a
b
c
d
a d b c⋅ ⋅ ⇒
además
a
b
c
d
a d b c⋅ ⋅ ⇒
Ma
tem
áti
ca
7
¿Sabías qué?

79. 71
Refuerce sus conocimientos.
££ Ejercicios propuestos.
I. Encuentre los valores de las expresiones dadas a continuación.
a. 10
b. −2 8,
c. − −7 2 2 4, ,
d. − −− ( )3 9
e. 6 8+ −( )
f. − + −( )3 7 2 1, ,
g. − +2
5
6
3
1
4
II. Encuentre los productos y cocientes indicados.
a) −( )( )3 7 ; b) 90 18÷ − c) −( )( )8 4 100,
d) -63 7÷ −( ); e) − ÷
3
4
1
2
; f) − −( ) −( )




18 5
7
15
g) −











 −












1
2
3
5
2
3
5
8
; h) − ÷ −





7
4
5
3
10
III. Ubique los siguientes números reales en una recta numérica.
a) −5; b) −
1
3 ; c) −
3
4
; d) − 5 ; e) 7 ; f) 10 ; g) −
8
3
; h) 7
IV. Escriba en el espacio en blanco el símbolo que corresponda (, , = ).
Matemático alemán
conocido como el
«padre del análisis
moderno».
Nació en Ostenfelde,
Westfalia (actualmente
Alemania) y murió
en Berlín (Alemania).
Estudió Matemática
en la Universidad
de Münster. Además
de sus prolíficas
investigaciones cabe
señalar que fue
profesor de cátedra en
la Universidad de Berlín
en la cual tuvo entre
sus discípulos a Georg
Cantor, Ferdinand
Georg Frobenius,
Wilhelm Killing,
Leo Königsberger,
Carl Runge y Sofia
Kovalévskaya.
Karl Theodor Wilhelm
Weierstrass
(1 815 - 1 897)
Nota histórica
a. -1 ___ - 10
b. |- 1| ___ |- 10|
c.
−
−
1
2
1
2
___
d. ___
4
16
8
32
e. 5 6___
f. 16 5___
g. - | - ( - 2)| ___0
h. 0 25
1
4
, ___
i. 0 075 0 39, ___ ,
j. 0 72737475 0 73737373, ...___ , ...

80. 72
V. Encuentre el opuesto de los siguientes números reales:
a. 400
b. - | - 2|
c. 3−π
d. 1 2−
e. 10
7 2−
VI. ¿Qué propiedad de los números reales se ilustra en cada una
de las siguientes proposiciones?
a. 5 + 4 = 4 + 5
b. -7 + (4 + 2) = (-7 + 4) + 2
c.
d. 5 8 5 8∈ ∈ ⇒ ( )( )∈R R R
e. 5
3
7
2
9
5
3
7
5
2
9
+





 =





 +






f.
7
9
5
7
9
5+





 = +
g. −





 + = −
3
8
0
3
8
h. -0,78 + 0,78 = 0
i. 7
9
4
3
4
3
7
9











 =












j. 0,78 (-1) = -0,78
k. 0 5 3 6 0 5 3 0 5 6, , ,−( ) = ( )( )−( )( )
l. (37)(45) = (45)(37)
m. 17
1
17
1





 =
n. − ( ) =8 0 0
Reto Matemático:
Al número de 3 digitos
2a3 se le suma el
numero 326 y da el
número de tres digitos
5b9, se sabe que 5b9 es
divisible por 9, entonces
el valor de a + b es de:
a. 2
b. 4
c. 6
d. 8

81. 73
Actividades Finales de la Segunda Unidad
1. ¿Cuáles de las siguientes proposiciones son verdaderas y cuáles son falsas?
a. El recíproco un número entero distinto de cero es un número entero.
b. El opuesto de un número entero es un número entero.
c. Existe un número entero que no tiene recíproco.
d. Existe un número entero cuyo recíproco es un número entero.
2. Dé un ejemplo de dos números irracionales cuya suma sea un número racional.
3. Dé un ejemplo de dos números irracionales cuyo producto sea un número racional.
4. Dé un ejemplo de dos números irracionales cuyo cociente sea un número racional.
5. Ordene los siguientes números reales de menor a mayor.
3;−5
1
2
; - 7; 6 , - 6 ; 4/3; 2
6. Resuelva considerando las raíces cuadradas positivas y luego las negativas.
a. +( ) −( )+ − ( ) −( )+ −( )÷ −( ){ }5 4 64 3 2 40 8
b.
16 81 27
4
3
1
2
2
3
3
4
÷ + − −






+
c. 4 3 6 3 4 5 7 15 3 4 12 9
2
( ) ÷ − + ( )− ( )  ÷ −
d. 9 4 10 3 6 5 12 8 6 9 95 90−( )+ − +( )  + ( ) −( )  ÷ − +( ) −( ) −( ) 
7. El m.c.m de dos números, m y n es 360 y el m.c.d es 2 ¿Cuales son los números?

82. 74
8. Al calcular el producto L . H, sabiendo que: L = a + b + c y H = d + c = f + g , siendo que a,
b, c, d, e, f, g son números naturales y que:
• b . f = 91
• a . d = 18
• c . d = 16
• b . g = 39
La respuesta es:
a) 310
b) 280
c) 300
d) 100
9. Complete la siguiente tabla con los símbolos ∈ o ∉ según corresponda a cada caso.
ℕ ℤ ℚ ℚ'
9,3
24 ∉ ∉ ∉ ∈
1,3333…
2,101001000…
e
π
1 5
2
+
∉ ∉ ∉ ∈
-1/6
1000
0
- 43
6

83. 75
10. Sume 8 números de tal manera que la suma de cómo resultado 1000.
11. A partir de la unidad fraccionaria
1
3
, represente en la recta real:
1
3
4
3
6
3
2
3
, , , − .
12. Clasifique los siguientes números decimales en racionales o irracionales y explique
la razón:
a. 0,55555555...
b. 0,125689312...
c. 1,3525252...
d. 0,75
13. Clasifique los siguientes números decimales en racionales o irracionales y explique
la razón:
a. 1,3030030003...
b. 2,1245124512...
c. 4,18325183251...
d. 6,1452453454...
14. Represente los siguientes números en una recta real (utilice calculadora para realizar
cálculos aproximados)
a.
b. 3
c. 3
3

84. 76
15. Exprese en forma de una potencia que tenga como base un número primo:
a. 5 . 5 . 5 . 5
b. (-3)(-3)(-3)
c. 1
2 2 2 2 2⋅ ⋅ ⋅ ⋅
d. 81
e. 27
16. En las siguientes operaciones, aplique las propiedades correspondientes y expresa el
resultado como potencia única:
a. 6 63
2
4
⋅( ) ( )
−
62
2
b. -5 -5 -5
3 5 4
( )



⋅( ) ( )
2
17. Utiliza las propiedades adecuadas para expresar el resultado de la siguiente operación
como una única potencia:
18. Investigue y escriba las siguientes raíces como exponentes fraccionarios y simplifique
cuanto se pueda:
a. 3105
; b. 2147
; c. 76
19. ¿Cuáles de las afirmaciones siguientes son correctas?
a. El conjunto de los números irracionales es subconjunto de los números racionales.
b. El conjunto de los números enteros es subconjunto de los números irracionales.
c. El conjunto de los números enteros es subconjunto de los números racionales.
d. En el conjunto de los números enteros siempre hay un número anterior.
e. El conjunto de los números racionales está dentro de los números naturales.
f. Dado un número real, no se puede encontrar ni su anterior ni su sucesor.
g. El conjunto de los números reales es infinito y tiene un orden.

85. 77
20. Exprese como radical: Escriba dos ejemplos que contradigan las siguientes
afirmaciones:
a. La potencia de un racional es un irracional
b. El producto de irracionales es un irracional
c. El cociente de irracionales es un irracional
d. La adición de racionales no es un irracional
e. La sustracción de irracionales no es un irracional
21. Realize las siguientes operaciones:
a. 3 2
1
5
24 4
−
b. 3 3
2
5
5− −3 3
c. 4
5
5 7 3+ −5 5
d. 11 81 12 243 3
−
e. 3
1
5
4 4
50 18−
f. 3 3
2
5
7 5− − +3 2 7
g. -2
3
4
4 4
10 10 104
− +
h. 3 5
7
5
7 8− − +5 4 5
i. 3 2( )( )=
j. −( )( )=5 3
k. − ÷ =64
32
5
l. 0 5
1
5
, ÷ =

86. 78
22. Calcule la forma fraccionaria o decimal (identificando cada una de sus partes), según
corresponda:
a. 9,2777...
b. 14,371717...
c. 63
22
d. 28
160
23. Calcule las siguientes operaciones:
a. |-3| · |-2| ÷ (- 6) + |2 - (- 3) + 24
- 10 ÷ (- 2)|
b. (- 100) ÷ (- 4) · (- 3) + 3
c. 2 · (- 3) · 4 · (- 5) ÷ (- 6) + 22
24. Realice las siguientes operaciones
a. 1
2
1
4
2
6
3
8
+ − − =
b. 2
5
3
4
1
2
1
5
⋅ − ⋅ =
c.
4
3
1
3
2
6
3
4
÷ +





 − =
25. Realice las siguientes operaciones:
a. 3
2
3
4
1
3
9
16
+ ⋅





 − =
b. 6
10
2
3
4
5
4
3
1
3
3
4
3
7
÷ − ⋅





 +





 − ÷ =
26. Realice las siguientes operaciones:
a. 4
10
2
3
4
5
5
3
1
4
3
5
÷ − + −





 ÷ =
b. 2
3
7
2
5
6
1
4
4
3
2
3
1
62
2
− − +





 + − + −






=

87. Introducción
al Álgebra
Unidad 3
El Gobierno Sandinista a través de sus instituciones realizó durante el periodo de la Alerta Roja (Abril 2 014)
una serie de actividades encaminadas a fortalecer los mecanismos de enfrentamiento de las emergencias
sísmicas.
Las instituciones que conformaron el Gabinete de Seguridad Humana y Ciudadana, durante la Alerta Roja
dieron cumplimiento a un modelo de trabajo que estaba encaminado a salvaguardar la vida de las familias
y a brindar acompañamiento a los más afectados por los terremotos en los municipios de Managua,
Nagarote, Mateare, La Paz Centro.
Fuente: 19 digital
20 de Abril 2 014

88. 80
Introducción al álgebra.
Expresiones algebraicas.
Leo, analizo e interpreto.
££ Introducción.
En la Unidad II se han estudiado los diferentes conjuntos
numéricos: números naturales ℕ, los números enteros ℤ, los
números racionales ℚ, los números irracionales ℚ' y la unión de
todos ellos, el conjunto de los números reales ℝ.
ℝ = ℚ∪ℚ'
El Álgebra es una rama de la Matemática en la que se usan
letras para representar relaciones aritméticas. Al igual que
en la aritmética, las operaciones fundamentales del álgebra
son la adición y la multiplicación. La sustracción, la división,
la potenciación y cálculo de raíces también son estudiadas en
la Escuela Primaria y en la Secundaria. En la aritmética, sin
embargo, no se generalizan las relaciones matemáticas. Así, en
su forma más general, se dice que el álgebra es el idioma de la
Matemática.
££ Concepto de expresión algebraica.
Una expresión algebraica, es aquella que está formada por
números y letras unidos entre si por medio de una o varias
operaciones matemáticas (suma, resta, multiplicación, división,
potenciación y radicación).
Ejemplo
Son expresiones algebraicas, las siguientes:
a. 3x: esta expresión algebraica se lee “3 por x”. Usualmente,
al escribir una expresión algebraica, se omite el símbolo del
producto. Esto quiere decir que:
3x = 3 . x = (3)(x)
El símbolo “x” no se acostumbra para la multiplicación, para no
confundirlo con la letra “x”.
b. - 5x + 4y: se lee “menos cinco por “x” más cuatro por “y”.
De manera más simple se puede leer: “menos cinco “x” más
cuatro “y”.
Debemos a su
nombre las palabras:
álgebra, guarismo y
algoritmo. De hecho,
es considerado como
el padre del álgebra y
como el que introdujo el
sistema de numeración.
Al - Juarismi
Área de una región
rectangular en lenguaje
aritmético.
8 u
6 u
Área = (6u)(8u)
Área = 48u2
Área de una región
rectangular en lenguaje
algebraico
b
a
Área = ab
u: es la abreviatura para
unidades.
Nota histórica

89. 81
c.
8x - 4y + 4z
5x - 2y
. Se lee: “ocho x menos cuatro y más cuatro z”,
dividido entre cinco x menos dos y”.
d. 9 2x y+ . Se lee: “raíz cuadrada de nueve x más dos y.
Una expresión algebraica está formada por cantidades que no
varían llamadas constantes y por cantidades que varían llamadas
variables.
Las constantes son cantidades fijas, determinadas. Las cantidades
variables son cantidades desconocidas cuyo valor puede cambiar.
Ejemplos
En la expresión algebraica 12x - 17y, 12y 17 son constantes
(coeficientes numéricos). Las variables son x e y.
Constante o Coeficiente
12x - 7y
Variable o literal
En una expresión algebraica como - 4x2
+ 6x, las expresiones que
se suman (o sumandos) se llaman términos.
-4x2
+ 6x -4x2
Término Término
Coeficiente 6Coeficiente -4
Coeficiente
Término
Exponente
Signo
literal
Importante. En una expresión algebraica que tenga coeficiente 1,
éste no se escribe.
Ejemplos
La expresión algebraica x y z2
, tiene como coeficiente 1. Puede
escribirse así: 1x y 1z2
, sin embargo se acostumbra no escribir el
1.
Cuando en la expresión algebraica tiene coeficiente negativo
como, por ejemplo, - 1m2
np4
, entonces se acostumbra escribir sólo
el signo menos y se omite el 1. Así, la expresión se escribe - m2
np4
Reforzamiento
En las siguientes
expresiones determine
el coeficiente, la
variable y el exponente:
• -6a2
b
•
8
3
3 4
x y
• -0,5a2
m6
• m
• xy
Ma
tem
áti
ca
7
¿Sabías qué?
Clasificación de
las expresiones
algebraicas:
IrracionalesRacionales
Enteras Fraccionarias

90. 82
Dominio de una variable.
El dominio de una variable es el conjunto de valores que se le
pueden asignar a la variable. En este texto, el conjunto que se
tomará como referencia es el conjunto de los números reales ℝ.
¿Cómo se escriben en lenguaje algebraico expresiones de la
vida cotidiana?
Aquí se presentan algunos ejemplos:
1. La mitad de un número multiplicado por 3.
La expresión se refiere a un número cualquiera. Entonces se
representa el número con una letra, por ejemplo a. Entonces
tenemos que:
“a” es el número.
La mitad del número “a” es:
a
2
La mitad del número “a” multiplicado por 3 es:
a a
a
2
3 3
2
3
2





 =





 =
2. El triple de la suma de tres números diferentes.
Aquí se hace referencia a tres números distintos, entonces
estos números pueden ser a, b y c. Entonces tenemos que:
a + b + c, es la suma de los tres números.
3(a + b + c), es el triple de la suma de los tres números.
Para poder interpretar cada término deben identificarse sus
elementos: signo, coeficiente, variables y exponentes.
3. El cuadrado más el triple de un número.
Llamamos “n” al número. Entonces:
n2
, es el cuadrado del número n.
3n, es el triple del número n.
n2
+ 3n, es el cuadrado más el triple de un número n.
Para el dominio de una
variable tomaremos
el conjunto de los
números reales ℝ
Reto Matemático
Convierta en expresión
algebraica los
siguientes enunciados:
• El doble de 6.
• 7 menos un número
cualquiera.
• El triple de un
número más el
quintuple de otro.
• El cuadrado de la
diferencia de dos
números.
• La quinta parte de
la suma de dos
números.
• Ocho menos el
cubo de un número
cualquiera.
• Tres veces un
número disminuido
en 18.
Ma
tem
áti
ca
7
¿Sabías qué?

91. 83
Observe que la expresión algebraica se ordena en función de
los exponentes en forma descendente. (de mayor a menor).
1. La edad de Roberto hace cinco años sumada con la edad de
Jorge hace 4 años.
• Llamamos
a: la edad actual de Roberto y b a la edad actual de Jorge,
entonces tenemos que:
• a - 5, es la edad de Roberto hace cinco años.
• b - 4, es la edad de Jorge hace cuatro años.
Obtenemos la expresión algebraica: (a - 5) + (b - 4) : a + b - 9
2. El perímetro de un triángulo equilátero.
El perímetro de un triángulo cualquiera es igual a la suma de las
medidas de sus lados. Si el triángulo es equilátero, entonces
sus tres lados tienen la misma medida. Así, tenemos en el
triángulo ABC de la figura, que los lados son los segmentos
(AB),(BC) y (AC) y por ser equilátero, AB = BC = AC.
AB = BC = AC = l
C
A B
• Llamamos l a la longitud de cada lado.
• Como los tres lados tienen la misma medida, entonces el
perímetro es:
Perímetro = l + l + l = 3l
3. La raíz cuadrada de la suma de los cubos de dos números
reales diferentes.
Llamamos a los números a y b. Entonces:
• a3
el cubo del número a.
• b3
, el cubo del número b
• a b3 3
+ , esta expresión algebraica es la raíz cuadrada de
la suma de los cubos de los números reales a y b.
Un triángulo se dice que
es equilátero si y sólo si
sus tres lados tienen la
misma medida.
C
A B
El triángulo ABC es
equilátero, entonces
sus tres lados tienen la
misma medida.
AB = BC = AC
Hipatia
Hipatia nació en
Alejandría a mediados del
siglo IV, en 370, según
algunas referencias, y en
355, según otras.
Hija y discípula del
astrónomo Teón, Hipatia
es la primera mujer
matemática de la que
se tiene conocimiento
razonablemente seguro y
detallado. Escribió sobre
geometría, álgebra y
astronomía,
Nota histórica
Ma
tem
áti
ca
7
¿Sabías qué?

92. 84
1. Encontrar una expresión algebraica para determinar el área
de la región presentada en la figura.
x
x
5
y
En la figura se presentan dos regiones: Una región cuadrada con
lado de medida x y una región rectangular de dimensiones y y 5.
El área total es igual al área de la región cuadrada sumada con
el área de la región rectangular.
Entonces tenemos que:
• El área de la región cuadrada es: x2
• El área de la región rectangular es: 5y
Por lo tanto, el área total es: A = x2
+ 5y
Actividad
Traducir del lenguaje cotidiano al lenguaje algebraico cada uno
de los siguientes enunciados:
1. La suma de tres números diferentes elevada al cubo.
2. La raíz cúbica de la suma de tres números diferentes elevada
al cuadrado.
3. La edad que tendrá Juan dentro de 3 años sumada con la
edad que tenía Alejandro hace 4 años.
4. La mitad de la suma de las raíces cuadradas de dos números
enteros positivos diferentes.
5. La raíz cúbica del producto de tres números enteros positivos.
6. El producto de tres números enteros positivos dividido entre
la raíz cúbica de la suma de estos números.
7. La suma de dos números, cada uno de ellos elevado al
cuadrado.
Reforzamiento
Traducir del lenguaje
algebraico al lenguaje
ordinario:
• x + 4
• 16 - b
• 7n
• a3
- 3a
• 2(a + 5)
• 2a + 1
•
v
5
•
a b+
4
•
2
5
a
2

93. 85
¿Qué es un monomio?
££ Concepto de monomio.
Un monomio es una expresión algebraica formada por el
producto indicado de factores numéricos y factores literales
cuyo exponente es un número natural o cero.
££ Elementos de un monomio.
Parte LiteralCoeficiente
ExponentesSigno
- 4x2
y1
z3
• El signo de un monomio es el que indica si el monomio es
positivo ( + ) o negativo ( - ). Si el signo es positivo, el signo se
omite.
Ejemplo
• El monomio – 5m2
n3
, tiene signo negativo, m y n son sus
partes literales, -5 su coeficiente numérico y sus exponentes
son 2 y 3.
• El monomio
5
3
4 5
x y , tiene signo positivo, x e y son sus partes
literales,
5
3
4 5
x yes su coeficiente numérico y sus exponentes son
4 y 5.
££ El coeficiente numérico. Es la parte numérica de un monomio.
Ejemplo
• En el monomio 45m2
n3
, el coeficiente numérico es 45.
• En el monomio −
2
3
3
xyz , el coeficiente numérico es −
2
3
.
• En el monomio - mn3
p, el coeficiente numérico es - 1.
• En el monomio x4
y3
z5
, el coeficiente numérico es 1.
• En el monomio -3, el coeficiente numérico es el mismo.
La expresión:
2
2 1
x
x= −
No es un monomio ya
que el exponente de la
variable es (-1).
-1 ≠ ℕ
-1 ≠ 0
El área de un cuadrado
se determina por la
ecuación A = l
2
y que
está expresión es un
monomio.
El área de un triángulo
se determina por la
ecuación
b a⋅
2
y este
es un monomio.
Reforzamiento
Investiga la ecuación
para el área de un,
círculo, trapecio y
rectángulo luego
determine cual de ellos
es monomio.
Ma
tem
áti
ca
7
¿Sabías qué?

94. 86
££ La parte literal es la variable o variables presentes en un
monomio con sus respectivos exponentes.
Ejemplo
• En el monomio 2 xy3
z4
, la parte literal es xy3
z4
.
• En el monomio
2
9
5 7
m n , la parte literal es m5
n7
.
££ El grado de un monomio con respecto a una letra se llama
grado relativo.
Ejemplo
• En el monomio 2m3
n2
p4
, el grado relativo respecto a “m”
es 3, el grado relativo respecto “n” es 2 y el grado relativo
respecto a “p” es 4.
• En el monomio - 7x5
y7
, el grado relativo respecto a “x” es 5
y el grado relativo respecto “y” es 7.
££ El grado absoluto de un monomio es la suma de los
exponentes de las variables.
Ejemplo
• El grado absoluto del monomio x3
y1
z4
, es 3 + 1 + 4 = 8.
• El grado absoluto del monomio 7x5
y7
, es 5 + 7 = 12.
Dos monomios son homogéneos si sus grados absolutos
son iguales en caso contrario son heterogéneos.
Ejemplo
• x2
yz4
y 7p2
y2
z3
, son homogéneos porque sus grados absolutos
son iguales a 7.
• 2a2
m5
n3
y5pr3
t3
,sonheterogéneosporquesusgradosabsolutos
son 10 y 7 respectivamente, es decir, son diferentes.
Monomios semejantes.
Dos monomios se dice que son semejantes cuando tienen la
misma parte literal con iguales exponentes.
Reforzamiento:
1. ¿Cuál es la parte
literal del monomio
mn3
5
? _______
2. El grado relativo a x
en el monomio 2x3
y5
es: _______
3. El grado absoluto del
monomio x y z4 8 3
4es: __
4. Determine cual de las
siguientes parejas de
terminos son seme-
jantes:
a. 8x y 6x
b. −
1
5
ab y ab
c. 2m y 3mn
d. x2
y y xy2
e. b2
y 5b2
f. az4
y -6z4
Reto Matemático:
Hallar a y b si el grado
absoluto del monomio es
igual a 17, y su coeficiente
tiene el mismo valor que el
grado relativo con respecto
a x. Siendo el monomio
M = (a + b)x2(a - 1)
y3b

95. 87
Ejemplo
• 2x2
yz3
y 5x2
yz3
, son semejantes porque x2
yz3
es la parte literal en
ambos monomios.
• Los monomios tienen diferente parte literal, entonces no son
semejantes.
Diferente parte literal.
2x2
yz3
y 5a2
bc
Tipos de monomios.
Dos o más monomios se dice que son homogéneos, si tiene el
mismo grado absoluto. Dos o más monomios que tienen diferente
grado absoluto se dice que son heterogéneos.
Ejemplos
• Los monomios 5xy3
y - 4m2
n2
son homogéneos.
En efecto:
El monomio 5xy3
tiene un grado absoluto igual a 4.
El monomio - 4m2
n2
tiene un grado absoluto igual a 4.
• Los monomios 7xy3
z2
y - 3 mn2
p son heterogéneos.
En efecto:
El monomio 7xy3
z2
tiene un grado absoluto igual a 6.
El monomio - 3mn2
p tiene un grado absoluto igual a 4.
Actividad
Completar la tabla.
Expresión
algebraica
Grado absoluto
Grado relativo
respecto a:
17x4
y3
z2 x
- 24m2
n5
p p
3ab5
c7 b
7x9
y11
z2 z
Matemática alemana
muy influyente, conocida
por sus grandes
contribuciones al álgebra
abstracta y a la física
teórica. En opiniones
de David Hilbert,
Albert Einstein y otros
científicos, es la mujer
más importante en la
historia de la Matemática.
Revolucionó la teoría
de anillos, la teoría de
campos y álgebras.
En Física, el Teorema
de Noether explica la
conexión fundamental
entre las simetrías y las
leyes de conservación.
Amalie Emmy Noether.
(1 882 –1 935)
Reto Matemático:
¿Cuántas letras se deben
tomar en el siguiente
monomio
M = a6
b24
c60
d120
...
Para que su grado sea
6006?
Nota histórica

96. 88
Actividad
Transcribe en tu cuaderno la siguiente tabla, e indica con una H
cuando los monomios sean homogéneos y con una HT cuando
los monomios sean heterogéneos.
Monomios Homogéneo Heterogéneo
3x2
y3
z5
y 2mn7
p2
H
− 3 4 5 2
m n p y - 2mn5
p2 HT
p2
qr5
y x2
yz5
- 2a2
b3
c5
y 4mn3
p5
5 3
hk m y 2xy7
z3 HT
3x2
y3
z5
y - 2mn7
p2
3a5
b3
c2
y 2m3
n6
p H
- wz5
y10
y 2ab13
c3
Suma y resta de monomios.
¿Cuándo se pueden sumar o restar dos monomios?
Dos monomios se pueden sumar o restar solamente cuando
son semejantes.
La suma o resta de dos o más monomios es otro monomio que
tiene la misma parte literal y cuyo coeficiente es la suma o resta
de los coeficientes.
Ejemplos
• Los monomios 2x2
y3
z y 3x2
y3
z son semejantes, entonces su
suma y su resta es:
2x2
y3
z + 3x2
y3
z = (2 + 3) x2
y3
z = 5x2
y3
z
2x2
y3
z - 3x2
y3
z = (2 - 3) x2
y3
z = -1x2
y3
z
Nació en Alejandría, no
se conoce nada con
seguridad sobre su vida
salvo la edad a la que
falleció, gracias a este
epitafio redactado en
forma de problema y
conservado en la antología
griega:
Aquí yacen los restos de
Diofanto. Los números
lo pueden mostrar , ¡oh
maravilla! La duración de
su vida.
Cuya sexta parte
constituyó la tierna
infancia.
Había transcurrido además
una duadécima parte de
su vida cuando le creció su
barba.
A partir de ahí , la séptima
parte de su existencia
transcurrió en un
matrimonio estéril. Paso un
quinquenio y entonces le
hizo dichoso el nacimiento
de su primogénito.
Este entrego su existencia
a la tierra habiendo vivido
la mitad de lo que su
padre llego a vivir. Diofanto
descendió a la sepultura
habiendo sobrevivido
cuatro años a su hijo.
Dime , caminante , cuantos
años vivió Diofanto hasta
que llego a su muerte .
Nota histórica

97. 89
• Los monomios 2x2
y3
y 3x2
y3
z no son semejantes, entonces no
es posible sumarlos.
• Los monomios 7mn2
p3
y 3mn2
p3
son semejantes, entonces
podemos efectuar la sustracción:
7mn2
p3
- 3mn2
p3
= (7 - 3)mn2
p3
= 4mn2
p3
• Los monomios 6x2
y2
z3
y xy2
z3
no son semejantes, entonces no
es posible efectuar la sustración.
Actividad
Trancriba en su cuaderno la siguiente tabla, luego calcule y la
suma y diferencia de cada par de monomios. Observe el ejemplo
indicado en la siguiente tabla:
Ejemplo
- 2a2
b3
c5
- ( - 4a2
b3
c5
) = - 2a2
b3
c5
+ 4a2
b3
c5
= 2a2
b3
c5
- 2a2
b3
c5
+ ( - 4a2
b3
c5
) = - 2a2
b3
c5
- 4a2
b3
c5
= - 6a2
b3
c5
Monomios Suma Diferencia
3x2
y3
z5
y 2x2
y3
z5
3 4 5 2
m n p y −4 3 4 5 2
m n p
p2
qr5
y p2
qr5
- 2a2
b3
c5
y - 4a2
b3
c5
- 6a2
b3
c5
2a2
b3
c5
5 3
hk m y 2 3
hk m
- 3x2
y3
z5
y 2x2
y3
z5
3mn7
p2
y 2mn7
p2
az5
y10
y 2az5
y10
2xy y - 6xy
3m2
n y -0,5 m2
n
Interesante
Un matemático que no
es en algún sentido un
poeta no será nunca un
matemático completo.
Karl Weiertrass.
Matemático alemán
Reforzamiento:
Reduzca los siguientes
términos semejantes:
• 8x2
- 12x2
• 6x + 4x - 10x + 7x
• 2ax
+ 3ax
• 5x9
- 2x9
+ 4x9
• -x2
- x2
y - 2x2
y
• - 2b + 4b - 5b
• 9a2
+ 5a2
- 12a2
•
2
3
a2
b +
1
4
a2
b

98. 90
Interesante.
No hay rama de la
Matemática, por muy
abstracta que esta
sea, que no pueda ser
aplicada alguna vez a
un fenómeno del mundo
real.
Nicolai Ivanovich
Lovachevsky.
(Matemático Ruso).
Refuerce sus conocimientos.
££ Ejercicios resueltos sobre monomios.
1. Escriba en cada caso dos monomios que cumplan con las
condiciones indicadas.
a. El coeficiente numérico es un número entero positivo y la
parte literal tiene dos variables.
b. El coeficiente numérico es un número irracional positivo,
tiene tres variables y el grado relativo respecto a la variable
x es 3.
c. El coeficiente es número irracional negativo, tiene tres
variables y el grado absoluto es 9.
Solución:
a. 5xy, 7m3
n4
.
b. 2 3 5 4
x y z , 3 3 5 4
x y z .
c. − 3 3 4 2
x y z , − 7 3 4 2
x y z .
2. En la tabla dada a continuación, se muestran los elementos
de cada monomio.
Monomio Coeficiente
Parte
literal
Grado
absoluto
Grado relativo
respecto a:
3x2
yz3
3 x2
yz3
6
x es 2
y es 1
z es 3
- 7m3
n7
- 7 m3
n7
10
m es 3
n es 7
3 5 2
x y 3 x5
y2
7
x es 5
y es 2
3m3
np2
3 m3
np2
6
m es 3
n es 1
p es 2
− 3xy - 3 xy 2
x es 1
y es 1

99. 91
3. Enlatabladelejercicio2identifiquedosmonomioshomogéneos
y dos monomios heterogéneos.
Solución:
Los monomios 3x2
yz3
y 3m3
np2
tienen grado absoluto 6, entonces
son homogéneos.
Los monomios - 7m3
n7
y − 3xy son heterogéneos. Sus grados
absolutos son 10 y 2 respectivamente.
4. Escriba un monomio para cada una de las expresiones
siguientes:
a. La raíz cuadrada del triple del producto de tres variables.
b. La tercera parte de un número real elevado al cuadrado.
c. Cuatro veces x elevado al cubo por y elevado al cuadrado
por z elevado a la quinta.
Solución:
a. 3xyz , b. 1
3
x2, c. 4x3
y2
z5
.
5. Geometría. Encuentre una expresión
algebraica para el área de la región triangular
de la figura.
El área de la región triangular es:
Área =
1
2
(base)(altura)
Área =
1
2
(5)(h) =
5
2
h
6. Escriba una “V” si la afirmación es verdadera y una “F” si la
afirmación es falsa.
a. El monomio 4xy7
tiene grado absoluto 8. (V).
b. El monomio mnp2
no tiene coeficiente numérico. (F).
c. El grado relativo respecto a x del monomio x5
y es 5. (V).
h
5
Hace pocos años,
Nicaragua editó 10
sellos de correos
que contenían las 10
fórmulas matemáticas
que cambiaron la faz
de la Tierra. ¿No es
admirable que un
país respete tanto
la Matemática como
para dedicar una
serie de sellos a un
conjunto abstracto de
ecuaciones?. He aquí la
lista de Nicaragua:
1 + 1 = 2
F
Gm m
r
→
= 1 2
2
E = mc2
elnN
= N
a2
+ b2
= c2
S = klogW
V = Vc
lnm0
/m1
λ = h/mv
∇2
E =
ku
C t2
2
2






∂
∂






F1
x1
= F2
x2
(Fuente: Clifford A.
Pickover. La Maravilla
de los Números. 2 002.
Ediciones Robinbook,
s. I., Barcelona)
Ma
tem
áti
ca
7
¿Sabías qué?

100. 92
¿Qué es un binomio?
££ Concepto de binomio.
Un binomio es una expresión algebraica formada por la suma o
diferencia de dos monomios.
Ejemplos de binomios.
1) 8m3
- 27, 2) 16a2
- b2
, 3) a3
- b3
, 4) 7xyz2
+ 5x2
y2
z.
El grado absoluto de un binomio, es el mayor grado absoluto
de los términos (o monomios) que forman el binomio. El grado
relativo respecto a una variable de un binomio es el mayor
exponente de la variable.
Ejemplo
Encontrar el grado absoluto de los siguientes binomios:
a. 2m2
n + 5mn4
. El grado absoluto es el grado del término
5mn4
. Entonces, el grado absoluto es 4 + 1 = 5.
b. 8x4
y5
+ 6xy2
. El grado absoluto es el grado del término 8x4
y5
.
Entonces, el grado absoluto es 4 + 5 = 9.
Ejemplos
Encuentre el grado absoluto de cada uno de los siguientes
binomios:
a. x3
y3
- 2x3
y7
.
b. m4
n5
- 2m8
n3
.
c. a9
b7
- 4a5
b6
.
Solución:
a. En el binomio x3
y3
- 2x3
y7
el término de mayor grado absoluto
es 2x3
y7
. El grado absoluto de este término es: 3 + 7 = 10.
Entonces, el grado absoluto del binomio es 10.
b. En el binomio m4
n5
- 2m8
n3
el término de mayor grado
absoluto es - 2m8
n3
. El grado absoluto de este término es:
8 + 3 = 11. Entonces, el grado absoluto del binomio es 11.
c. En el binomio a9
b7
- 4a5
b6
el término de mayor grado absoluto
es a9
b7
. El grado absoluto de este término es: 9 + 7 = 16.
Entonces, el grado absoluto del binomio es 16.
Reforzamiento:
Para el binomio
2x2
y3
- xy2
a. El grado absoluto
es: _______
b. Ordenado en forma
descendente con
relación a y es:
______________
c. Ordenado en forma
ascendente con
relación a x es:
_____________
d. El coeficiente del
término de grado 5
es:____

101. 93
Ejemplo
1. Exprese cada una de las proposiciones siguientes como un
binomio.
a. Tres veces un número elevado al cubo más dos veces el
mismo número elevado al cuadrado.
b. El perímetro de un triángulo equilátero con lado de medida
x más el perímetro de un cuadrado con lado de medida y
c. La suma de los cuadrados de los números x e y.
Solución:
a. Sea x el número. Entonces, obtenemos:
Tres veces el número elevado al cubo es 3x3
.
Dos veces el número x elevado al cuadrado es 2x2
.
La suma de estos dos números se expresa mediante el binomio:
b. Un triángulo equilátero tiene sus tres lados de igual medida,
entonces si cada lado tiene medida x, el perímetro será 3x. Un
cuadrado tiene sus cuatro lados de igual medida, entonces si
cada lado tiene medida y, el perímetro será 4y.
x y
Entonces, la suma de los perímetros es el binomio:
3x + 4y
c. El número x elevado al cuadrado es x2
y el número y elevado
al cuadrado es y2
. Entonces, la suma de los cuadrados de los
números x e y está expresada por el binomio:
x2
+ y2
Era un joven
matemático francés
nacido en Bourg -
la - Reine. Siendo
un adolescente, fue
capaz de determinar
la condición necesaria
y suficiente para que
un polinomio sea
resuelto por radicales,
dando una solución
a un problema que
había permanecido sin
resolver. Su trabajo
ofreció las bases para
la teoría que lleva su
nombre, una rama del
álgebra abstracta. Fue
el primero en utilizar el
término grupo en un
contexto matemático.
La teoría constituye
una de las bases
matemáticas de las
herramientas utilizadas
en comunicaciones y,
especialmente, en los
sistemas de navegación
por satélite, como GPS.
Évariste Galois
(1 811 - 1 832)
Nota histórica

102. 94
2. Escriba una expresión algebraica para el perímetro de un
rectángulo si sus lados tienen medidas en metros x e y.
y
x
Solución:
El perímetro del rectángulo es:
P = 2x + 2y.
3. Misael va al mercado y realiza las siguientes compras: 4 libras
de frijoles y 5 libras de arroz. Si la libra de frijoles tiene un costo
x y la libra de arroz tiene un costo y, escriba una expresión
algebraica que indique el costo total de lo comprado.
Solución:
El costo de las 4 libras de frijoles es 4 multiplicado por el costo
de cada libra, entonces el costo de las 4 libras de frijoles es 4x.
El costo de las 5 libras de arroz es 5 multiplicado por el costo de
cada libra, entonces el costo de las 5 libras de arroz es 5y.
Entonces, el costo total de lo comprado esta dado por la expresión:
Costo = 4x + 5y
4. Una familia está formada por 5 personas, 2 adultos y 3 niños.
Si la familia va al cine y el costo de la entrada es de x Córdobas
para adultos y Córdobas para niños, escriba una expresión
algebraica para el costo de la entrada al cine para la familia.
Solución:
Como el número de adultos es 2, entonces el costo de la entrada
para los adultos es 2x.
El número de niños es 3, entonces el costo de la entrada para los
niños es 3y.
Entonces, el costo de la entrada al cine para la familia esta dado
por la expresión:
Costo = 2x + 3y
Reforzamiento:
Escriba de
forma algebraica
las siguientes
expresiones:
• Siete menos que el
triple de un número.
• La diferencia de dos
números.
• El doble del
cuadrado de un
número más el triple
del doble de otro.
• La suma de dos
números enteros
impares.
• La diferencia de dos
números enteros
impares.

103. 95
¿Qué es un trinomio?
££ Concepto de trinomio.
Un trinomio es una expresión algebraica formada por la
combinación de sumas o diferencias de tres monomios.
Ejemplos de trinomios:
1) 6x3
y + 5xy2
- 4x4
y7
, 2) a2
-2ab + b2
, 3) 2x2
+7x+ 6
££ El grado absoluto de un trinomio, es el mayor grado absoluto
de los términos (o monomios) que forman el trinomio. El grado
relativo respecto a una variable de un trinomio es el mayor
exponente de la variable.
Ejemplos
Encuentre el grado absoluto de cada uno de los siguientes
trinomios:
a. 6x3
y + 5xy2
- 4x4
y7
b. 6a7
b - 5ab2
+ 3a4
b6
.
c. 8mnp2
- 5mn3
p5
- 7m5
n7
p3
.
Solución:
a. En el trinomio 6x3
y + 5xy2
- 4x4
y7
, el término de mayor grado
absoluto es 4x4
y7
.
El grado absoluto de este término es: 4 + 7 = 11. Entonces, el
grado absoluto del trinomio es 11.
b. En el trinomio 6a7
b - 5ab2
+ 3a4
b6
, el término de mayor grado
absoluto es 3a4
b6
.
El grado absoluto de este término es: 6 + 4 = 10. Entonces, el
grado absoluto del trinomio es 10.
c. En el trinomio 8mnp2
- 5mn3
p5
- 7m5
n7
p3
, el término de mayor
grado absoluto es 7m5
n7
p3
.
El grado absoluto de este término es: 5 + 7 + 3 = 15. Entonces,
el grado absoluto del trinomio es 15.
Importante.
Si un binomio o un trinomio contiene sólo una variable, entonces
su grado absoluto es igual al exponente mayor de la variable.
Fue un niño prodigio.
Matemático, astrónomo
y físico alemán
que contribuyó
significativamente
en muchos campos,
incluida la teoría de
números, el análisis
matemático, la
geometría diferencial,
la geodesia, el
magnetismo y la
óptica. Considerado
el príncipe de las
matemáticas y el
matemático más grande
desde la antigüedad,
Gauss ha tenido una
influencia notable
en muchos campos
de la Matemática y
de la ciencia, y es
considerado uno de los
matemáticos con más
influencia en la historia.
Johann Carl Friedrich
Gauss
(1 777 – 1 855).
Nota histórica

104. 96
Ejemplo
a. El binomio 3x3
- 2x, tiene grado absoluto 3.
b. El binomio - 4m5
+ 5m2
, tiene grado absoluto 5.
c. El binomio 7a8
+ 6a5
, tiene grado absoluto 8.
d. El trinomio 2x4
+ x2
- x, tiene grado absoluto 4.
e. El trinomio 3m4
+ m7
- m, tiene grado absoluto 7.
f. El trinomio 4a6
- 2a2
- a, tiene grado absoluto 6.
Ejemplo
Geometría. Escriba una expresión algebraica para la suma de
las áreas de las regiones de la figura.
Ejemplo
g. Geometría. Encuentre la suma de los volúmenes de los
cubos de la figura en la cual se indica que las aristas son
respectivamente x, y, z.
El área de una región
cuadrada con lado de
medida x es:
A = x2
u2
El área de una región
rectangular con
dimensiones y y z es:
A = yz u2
El área de una región
triangular con base de
medida u y altura de
medida v es:
A =
1
2
uv u2
u2
significa unidades
cuadradas
Ma
tem
áti
ca
7
¿Sabías qué?

105. 97
¿Qué es un polinomio?.
Un polinomio es una expresión algebraica formada por uno o
más monomios. Cuando el polinomio está formado por más de
un monomio, entonces estos monomios aparecen sumados,
restados o en una combinación de sumas y restas. Los monomios
que forman el polinomio se llaman términos del polinomio
P(x) = an
xn
+ an - 1
xn - 1
+ ... + a1
x + a0
, n ∈ ℤ
+
, y cada coeficiente es un
número real.
Ejemplo
De acuerdo al número de términos (un término) las expresiónes
algebraicas siguientes se denominan monomios:
1) -2xy2
2) 3m4
n 3) 5a3
b2
c 4) 12x
De acuerdo al número de términos (dos términos) las expresiónes
algebraicas siguientes se denominan binomios.
x2
4
1
16
−2)x y2 2
−1) 3) h3
+ 125p3
De acuerdo al número de términos (tres términos) las expresiónes
algebraicas siguientes se denominan trinomios.
• r2
+ 2r + 1
• 3x2
- 5x - 7
• y2
- 7y + 10
Cuando el número de monomios es mayor que tres, entonces se
usa la palabra polinomio.
• 3y4
+ 5y3
- 14y + 5
• 5x8
- 3x7
+ 2x6
- x5
+ x5
-10
El grado absoluto de un polinomio, es el grado del término de
mayor grado.
El grado relativo de un polinomio respecto a una variable, es el
mayor exponente de la variable en el polinomio.

106. 98
Refuerce sus conocimientos.
Transcribe la tabla siguiente en tu cuaderno y completa
información solicitada.
Expresión Términos
Grado
absoluto
Grado
absoluto
del
polinomio
Grado
relativo
respecto
a una
variable
x7
y4
+ x4
y5
x7
y4
11 11
Con
respecto a x
7
x4
y5
9
2a2
b + a3
b2
- 2a2
b4
2a2
b 3 6
Con
respecto a b
4
a3
b2
5
- 2a2
b4
6
4mn2
- m2
n3
- 2m3
n4
4mn2
3 7
Con
respecto
a m
3
- m2
n3
5
- 2m3
n4
7
El término independiente de un polinomio.
Considere el siguiente polinomio:
2x3
- x2
+ x - 1
Observe que el número - 1, no acompaña a una variable. Este
número se conoce como término independiente o término de
grado cero.
El polinomio 2x3
- x2
+ x - 1, se puede escribir así:
2x3
- x2
+ x - 1x0
Término de grado cero o término independiente
El término independiente
de un polinomio tiene
grado cero porque se
puede escribir como
el producto de una
constante por una
variable elevada a la
cero.
Ejemplo:
1. 2 = 2(1) = 2x°
2. 3 = 3a°
3. 4 = 4z°
Reto Matemático:
Calcular m y n para que
el polinomio
P(x) = 3xm + 1
yn - 3
+ 7xm + 2
yn + 1
+ 11xm + 3
yn - 2
sea de grado absoluto 8 y
de grado relativo respecto
a y igual a 5.

107. 99
Cuandoseescribeunpolinomio,siéstetienetérminoindependiente
o término de grado cero, sólo se escribe el coeficiente numérico y
no se escribe la variable elevada a la cero.
Concepto de polinomio ordenado.
Un polinomio se dice que está ordenado en forma ascendente
con respecto a una de sus variables, si el exponente de esa
variable aumenta.
Ejemplo
Ordenar el polinomio 2xy - x5
y5
+ x3
y4
en forma ascendente
respecto a la variable x.
Solución:
El polinomio ordenado en forma ascendente respecto a la variable
x, se escribe:
Exponente 1 Exponente 3 Exponente 5
2xy + x3
y4
- x5
y5
Observe el orden ascendente 1,3,5 de los exponentes de la
variable x.
Un polinomio se dice que está ordenado en forma descendente
con respecto a una de sus variables, si el exponente de esa
variable disminuye.
Ejemplo
Ordenar el polinomio 2xy - x5
y5
+ x3
y4
en forma descendente
respecto a la variable y.
Solución:
El polinomio ordenado en forma descendente respecto a la
variable y, se escribe:
Exponente 5 Exponente 4 Exponente 1
- x5
y5
+ x3
y4
- 2xy
Observe el orden ascendente 5,4,1 de los exponentes de la
variable y.
Se la recuerda sobre
todo como matemática,
aunque también se la
califica de lingüista,
filósofa, y más raramen-
te teóloga. Su nombre
está asociado a la curva
llamada indebidamente,
Bruja de Agnesi; los dos
sustantivos son incier-
tos: Agnesi no descu-
brió esa curva, ni lo
pretendió, y el nombre
de bruja seguramen-
te lo aportó el azar de
una mala traducción al
inglés. Para la histo-
ria de la Matemática
Agnesi es importante
por su influencia en la
divulgación del cálculo.
También es uno de los
personajes más citados
en las reflexiones sobre
el papel histórico de la
mujer en la Matemática.
María Gaetana Agnesi
(1 718 - 1 799)
Nota histórica

108. 100
Valornuméricodeunaexpresiónalgebraica.
Leo, analizo e interpreto.
¿Qué significa el valor numérico de una expresión algebraica?
Cuando en una expresión algebraica se sustituyen las variables
por números, entonces se obtiene el valor numérico de la
expresión. También se dice que se ha evaluado la expresión
algebraica.
La evaluación de una expresión algebraica se realiza de acuerdo
a los siguientes pasos:
Paso 1. Se escribe la expresión algebraica.
Paso 2. Se sustituyen las variables por números.
Paso 3. Se simplifica la expresión numérica obtenida.
Paso 1
Se escribe la
expresión algebraica
Paso 2
Se sustituyen las
variables por números
Paso
3
Se simplifica la
expresión numérica
obtenida
Ejemplo
Encuentre el valor numérico del monomio 3x2
y3
, cuando x = 1 y y = 3.
Paso 1. Se escribe el monomio. En este caso es: 3x2
y3
.
Paso 2. Se sustituyen las variables por números.
Si x = 1, y = 3,entonces 3x2
y3
= 3(1)2
(3)3
Paso 3. Se simplifica la expresión numérica obtenida.
3(1)2
(3)3
= 3(1)(9) = 27
El valor numérico del monomio es 27.
Ejemplo
Encuentre el valor numérico de:
1
2
2
x z , si x = 2 y z = -3
Solución:
1
2
1
2
2 3
1
2
4 3
12
2
62 2
x z = ( ) −( )= ( ) −( )= − = −
El último teorema de
Fermat.
En teoría de números,
el último teorema de
Fermat, o teorema de
Fermat - Wiles, es uno
de los teoremas más
famosos en la historia
de la Matemática.
Utilizando la notación
moderna, se puede
enunciar de la
siguiente manera:
Si n es un número
entero mayor que 2,
entonces no existen
números naturales a, b
y c (a, b 0), tales que
se cumpla la igualdad:
an
+ bn
= cn
En el año 1 995 el
matemático inglés
Andrew Wiles, en un
artículo de 98 páginas
publicado en “Annals
of mathematics”
donde demostró el
último Teorema de
Fermat
Ma
tem
áti
ca
7
¿Sabías qué?

109. 101
Actividad
Trancriba en su cuaderno la tabla siguiente y complete la
información solicitada.
Expresión
algebraica
Valores
de las
variables
Cálculo del valor numérico
3x2
y3
x = 1
y = 2
2m3
n + 5mn2
m = - 1
n = 3
2(- 1)3
(3) + 5(- 1)(3)2
= - 6 - 45 = - 51
4ab - 3a2
b4
+ b2
a = - 2
b = - 1
2x4
y + 2x3
y2
- x2
y3
x = 1
y = - 1
Ejemplo
1. Escribir un polinomio que cumpla las condiciones dadas.
a. Un binomio con grado absoluto 10 y variables x, y y z.
b. Un trinomio con grado absoluto 6, variables m, n y p con
coeficientes - 1, 3
5
y - 2.
c. Un polinomio de 4 términos, variables m, n y p. El grado
relativo respecto a n igual a 3.
Solución:
a. El binomio xy2
z5
- x2
y4z4
tiene grado absoluto igual al grado
absoluto del término - x2
y4
z4
, que es 10.
b. El trinomio − − −mnp m n p m np
3
5
22 2 2 2 2
tiene grado absoluto
igual al del término - m2
n2
p2
, que es 6.
c. El grado relativo del polinomio 3mnp + 2m2
n3
p3
+ m2
np2
+
mn2
p, respecto a la variable n es 3.
Reforzamiento:
1. Ordene los
polinomios de
acuerdo a la
variable que se
indica en orden
creciente y
decreciente:
a) x5
-2x4
y + x3
y2
+ x2
y3
respecto a x
b) 7ab2
- 4a3
+ 3a2
b + b3
con respecto a b
c) 3mn + 2m4
n2
- 5m3
n4
respecto a m
d) 2x2
y3
+ xy2
+ 4x3
- y
respecto a x
2. Si a = 6, b = 4,
c = -2, d = -3,
encontrar el
valor numérico
de cada una de
las expresiones
dadas a
continuación:
a) 2a + 3b - 4c - 5d
b)
6
2
cd
a b+
c)
ab cd
ad
−
d) 3(a + b) - 4bc
e) (ad + 2)(bc - 10)

110. 102
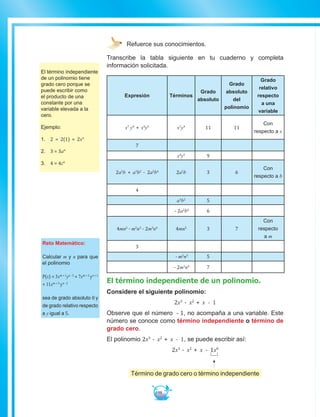
2. Encuentre el área de la región triangular de la figura base = 6u ;
altura = 4u; u = Unidades
El área de la región triangular está dada por:
Área ah u u u( )( )=
1
2
1
2
12 2
= = 6 4
El indice de masa corporal de una persona está dada por:
IMC =
masa en kilogramo
(Estatura en metro)2
Tabla del indice de masa corporal (IMC)
IMC Criterio
Menor de 18,5 Mala Nutrición
18,5 - 24,9 Normal
25 - 29,9 Sobrepeso
30 - 34,9 Obesidad Tipo I
35 - 39,9 Obesidad Tipo II
Mayor o Igual a 40 Obesidad Tipo III
Ejemplo
Resolvamos los siguientes ejercicios:
a. Si una persona tiene una masa corporal de 65 Kg y tiene una
estatura de 1,69 metros, entonces su IMC será:
IMC
Kg
m
Kg m=
( )
=
65
1 69
22 762
2
/ ;
este es un IMC normal
b. Si una persona tiene una masa corporal de 79 Kg y tiene una
estatura de 1,63 metros, entonces su IMC será:
IMC
Kg
m
Kg m=
[ ]
=
79
1 63
29 732
2
)
/
en este caso la persona de acuerdo a la tabla presenta sobrepeso.
Actividad:
Determine su propio indice de masa corporal. Luego diga en que
criterio de peso se encuentra.
h
a
Dos números enteros
positivos a y b se dice
que son consecutivos,
si uno de ellos se
obtiene sumándole 1
al otro. Es decir:
b = a + 1
Ejemplo: Los números
enteros 3 y 4 son
consecutivos:
4 = 3 + 1
Ma
tem
áti
ca
7
¿Sabías qué?

111. 103
El área de una región
cuadrada cuyos lado
miden x, es igual a:
Área = x2
.
El área de una región
rectangular con lados
de medida x e y es igual
a
Área = (x)(y).
El área de una región
triangular da base x y
altura h es:
Área =
1
2
(x)(h)
El volumen de un cubo
con arista de medida x
es:
Volumen = x3
Las expresiones algebraicas aparecen en diversas áreas del
conocimiento humano: economía, física, química, biología,
medicina, geometría, industria, agricultura, educación, etc. El
evaluar expresiones algebraicas es una actividad que realizamos
a cada momento, generalmente sin darnos cuenta.
Ejemplos
a. La superficie S de una persona se calcula usando la siguiente
formula, S=(0,1091) W0,425
h0,725
, con W en libras y hen pulgadas
¿Cuánto vale S para una persona que mide 5 pies y pesa 180
libras?
Solución:
S = (0,1091) W0, 425
h0, 725
= (0,1091)(180)0, 425
(60)0, 725
S = (0,1091)(9,08)(19,46) = 19,37
b. ¿Cuál es el volumen de agua que cabe dentro de un barril para
guardar agua potable. El barril tiene forma cilíndrica de 2 metros
de altura y radio de la base 0,5 m?
Solución:
Utilizamos el volumen de un cilindro
V = πr2
h = 3,1416(0,5)2
(2) = 0,7854 m3
c. Júpiter es el planeta más grande del Sistema Solar, y tiene un
diámetro aproximado de 142 880 000 m, y el más pequeño es
Plutón con un diámetro aproximado de 3 500 000 m. ¿Cuántas
veces cabe el volumen de pluton en Júpiter?
Solución:
Utilizamos el volumen de una esfera
Sea Vj
el volumen de Júpiter y sea Vp
el volumen de Plutón,
entonces:
V
V
R
r
R
r
j
p
= =





 =
⋅( )
⋅( )
=
4
3
4
3
1 4288 10
3 5 10
1 4288
3
3
3
3 8
6
3
3
π
π
,
,
,
,55
10
10
0 0680315
10
10
0 06803
3 8
6
3
24
18












≈






=, , 115 10 0 0680315 10 68 03124 18 6−
( )= ( )=, ,
Por tanto, Plutón cabe aproximadamente 68,031 en Júpiter.
Júpiter
Plutón
Ma
tem
áti
ca
7
¿Sabías qué?

112. 104
Actividades finales de la Tercera Unidad
1. Traduzca al lenguaje algebraico las siguientes expresiones:
a. El triple de un número entero a.
b. La raíz cuadrada del producto de tres números naturales a, b y c.
c. La diferencia de los cuadrados de dos números reales a y b.
d. La suma de dos números reales a y b elevada al cuadrado.
e. Cinco veces el cuadrado de un número real a menos cuatro veces el cuadrado de
un número real b.
f. La suma de los cubos de tres números enteros positivos m, n y n.
g. La mitad del número real m, más un tercio del número real n, menos la cuarta parte
de un número real p.
h. La mitad de la suma de cuatro números reales x, y, z y v.
i. La mitad de la suma de los cuadrados de tres números reales a, b y c.
j. La suma de tres números enteros pares consecutivos.
k. La suma de tres números enteros consecutivos.
l. La suma de tres números enteros impares consecutivos.
m. El triple de un número real a disminuido en dos.
2. Complete la siguiente tabla:
Expresión
algebraica
Variables Coeficientes Términos
- a2
bc2
m2
+ 2mn
5 - xy2
+ xy - x5
2
3
2 5
mn mn n+ −
x y xy x4 2 5
3 5− −

113. 105
3. Escriba una V si la afirmación es verdadera y una F si es falsa.
a. El grado absoluto de un polinomio es el grado absoluto del término de mayor grado.
b. El grado relativo de un polinomio respecto a una variable, es el menor exponente de
la variable.
c. El término independiente de un polinomio es el que tiene grado cero.
d. El grado relativo de un polinomio respecto a una variable es el mayor exponente de
la variable.
e. El monomio a2
bc, no tiene coeficiente numérico.
f. El grado absoluto del monomio 2xyz3
, es 6.
g. El monomio 4mn , tiene coeficiente racional.
h. El monomio
3
5
2 3 6
x y z , tiene 3 variables, coeficiente racional positivo y grado absoluto 12.
i. Existen polinomios con grado absoluto igual a 1.
j. Existen binomios con grado absoluto igual a cero.
4. Complete la siguiente tabla:
Expresión
algebraica
Tipo de
polinomio
Grado
absoluto
Grado relativo
respecto a:
- a2
bc2 b
m2
+ 2mn m
5 - xy2
+ xy - x5 x
2
3
2 5
mn mn n+ − n
x y xy x4 2 5
3 5− − y

114. 106
5. Clasifique los coeficientes (ℕ,ℤ,ℚ,ℚ') de los siguientes monomios:
a. 2πx2
, b. 3
4
2
xy , c. 2mn2
, d. - 4a3
b2
c, e.
1
2
2 3
x y z
6. Ordene los siguientes polinomios según las indicaciones.
a. x2
y3
- 3x3
y + 6xy2
. En forma ascendente respecto a x.
b. m2
n3
- 3m3
n + 6mn2
.En forma ascendente respecto a n.
c. ab + 2a3
b3
- 6a2
b2
– 1. En forma descendente respecto a a.
d. xy + 2x3
y3
- 6x2
y2
– 1. En forma descendente respecto a y.
e. 2x2
+ 2x - 3x3
+ 5x4
+ 4x5
- 3. En forma descendente.
f. 2x2
+ 2x - 3x3
+ 5x4
+ 4x5
- 3. En forma ascendente.
7. ¿Cuál de los siguientes polinomios está ordenado en forma descendente con respecto
a la variable x?
a. 2x2
y + 2xy2
- 3x3
y3
+ 5x4
y4
+ 4x5
y5
- 3.
b. 2x5
y + 2x4
y2
- 3x3
y3
+ 5x2
y4
+ 4xy5
- 3
8. Escriba una expresión algebraica para expresar el área de cada una de las regiones
presentadas a continuación:
b
h
x
y y
z z
REGIÓN CUADRADA
(SOMBREADA EN AMARILLO)
9. Escriba una expresión para el área de la región sombreada.
x x
z
yx x

115. 107
10. Escriba una expresión algebraica para el volumen de la figura. Los cubos tienen
aristas de medidas x, y y z.
z
y
x
z
y
11. Escribir los términos que faltan en los polinomios ordenados siguientes: Sugerencia:
Puede utilizar cualquier coeficiente numérico.
a. 3m4
- + m2
- + 1.
b. x5
- 6x4
+ - 4x2
- + 7.
c. - 6b2
+ - 7b4
- .
d. + m3
+ - 7m5
- .
12. Escriba una expresión algebraica para cada una de las situaciones descritas a
continuación:
a. Usted realiza en el mercado las compras siguientes: 10 libras de azúcar, 8 libras
de arroz, 6 libras de frijoles, 4 libras de papas y 3 litros de aceite. Si el precio de la
libra de azúcar es x, el de la libra de arroz es y, el de la libra de frijoles es z, el de
la libra de papas es z y el del litro de aceite es w, escriba una expresión algebraica
que indique el costo total de las compras.
b. Usted quiere pintar el interior y el exterior de su casa. El precio del galón de pintura
para interiores es x y el precio del galón de pintura para exteriores es y. Si se
necesitan 3 galones de pintura para el exterior y 4 galones de pintura para el
interior, escriba una expresión algebraica para el costo total de la pintura necesaria
para pintar la casa.
13. Ordenar los polinomios en forma ascendente:
a. 3a2
b - 5ab2
+ 6a3
b - 3a5
b4
££ Con relación a a
££ Con relación a b
b. m2
n2
+ 6m3
n - 5mn3
+11m5
n
££ Con relación a m
££ Con relación a n

116. 108
14. Escriba una expresión algebraica para cada una de las situaciones descritas a
continuación:
a. La ventana de una casa está diseñada como se muestra en la figura. Encuentre
una expresión algebraica para el área total de la región correspondiente.
a
b
c
b. El volumen de un cilindro circular recto está dado por la
expresión V = πr2
h, donde r es el radio de la base y h es
la altura. El volumen de un cono circular recto está dado por
la expresión 1
2
πr2
h, donde r es el radio de la base y h es su
altura. Encuentre una expresión para el volumen total de la
figura.
15. Determine el perímetro de cada figura:
m
m
p
a
a
a a
a a
b b
x
x
x x
16.Encuentre el valor numérico de las siguientes expresiones algebraicas:
a. 2x2
y3
z, para x =1; y = -1 y z = 2.
b. 2
3
mn2
+ m2
n, para m = 1
2
y n = -2
c. - 3a3
b2
+ 2a2
b - 5a, para a = - 1 y b = 2.
d. 2x4
- 3x3
+ x2
- 1, para x = 1.
h1
r
h2

117. 109
17. Hallar el valor numérico de las expresiones algebraicas siguientes si x = 1; y = -2;
z = -3
a. - 3x2
y + 4xy2
b. 2x3
+ 4x2
+ 1
c. - x2
y2
z + 4xyz2
d. x2
+ y - z
18. La expresión algebraica correspondiente al cálculo del IMC ya estudiado es:
IMC =
masa en kilogramos
estatura en metros
Verifique el IMC de los miembros de su hogar.
19. Clasificar las siguientes expresiones algebraicas.
a. 3x2
- x + 1
b. 3xy - 4
c. -2x5
+
x
5
-
1
7
d. xy - yz
d. a + b + c - d
d. -5x2
yz
20. Determinar el grado de los siguientes polinomios.
a. 4x3
y - 5x2
y5
+ 3y
b. 3xy - 5y4
+ y7
c. x2
+ 2xy + y2
21. Ordenar en sentido descendente, respecto de la variable x
a. 2xy3
- 7x2
y + 4x3
- 1
b. 2x - 6xy + x2
- x3
+ 2x5
c. x3
+ 3y2
x + y3
+ 3x2
y

118. 110
22. Asocie a cada uno de los enunciados la expresión algebraica correspondiente.
a. A un número se le quita siete 0, 2x
b. El doble de un numero más su cuadrado 2x + 1
c. Un múltiplo de 3 menos 1 2x + x2
d. El 20% de un número 1,1x
e. Cuatro veces un numero menos sus dos tercios 4x - 2
3
x
f. El precio de un pantalón aumentado en un 10% 3x - 1
g. Un número impar x - 7
23. Según la figura, exprese como un monomio:
x x
x
x
a. Perímetro
b. Área
c. Volumen
24. Traduce usando lenguaje algebraico:
• La suma de dos números.
• 10 más n.
• Un número aumentado en 3.
• Un número disminuido en 2.
• El producto de dos números.
• Uno restado a un número.
• 3 veces la diferencia de dos números.
• La diferencia de dos números.

119. 111
25. Traduce al lenguaje algebraico, utilizando solamente una variable.
a. Los tres quintos de un número menos 1.
b. La suma de tres números consecutivos.
c. Un múltiplo de 3 más su doble.
d. La suma de un número más su cuadrado.
e. El producto de dos números consecutivo.
26. Traduce al lenguaje algebraico, utilizando dos variables.
• Un número más la mitad de otro.
• El cuadrado de la suma de dos números distintos.
• La diferencia de los cuadrados de dos números distintos.
• El doble del producto de dos números distintos.
27. Traducir cada enunciado usando símbolos.
Lenguaje Ordinario
Lenguaje Matemático
(expresión algebraica)
1 La suma de dos lápices y una cantidad de lápices
2 Tres camisas más que un número de camisas
3 La diferencia entre un número de años y un año
4 Cuatro unidades menos que n unidades
5 Un número aumentado en uno
6 Un número disminuido en diez
7 El producto de dos números
8 Dos veces la suma de dos edades
9 Dos veces un número sumado a otro
10 Cinco veces el costo de la canasta básica
11 El cociente de dos números

120. 112
28. Resolver e interpretar los resultados obtenidos.
a. Traduzca al lenguaje algebraico, la siguiente conversación entre dos personas: “Un
novio le pregunta la edad a su novia y esta le contesta: tengo el doble de la edad
que tu tenías, cuando yo tenía la que tú tienes. Sabiendo que cuando tu tengas la
que yo tengo, nuestras edades sumaran 63 años”.
b. En un movimiento uniformemente acelerado, con velocidad inicial nula, el espacio
recorrido viene dado por la expresión . Calcular su valor, considerando
a = 4,92 m/s2
y t = 5 s
c. Una empresa constructora diseña piscinas tipo A y B, cuyas formas suponen tendrán
mucha. Discuta acerca de una fórmula para determinar la superficie de cada una,
según el largo, ancho y radios de las semicircunferencias.
Tipo A Tipo B
29. Escribe usando signos de operación y simplifica el resultado.
a. La suma de 24 y 19
b. 19 más que 33
c. Dos veces la diferencia de 9 y 4.
d. El producto de 6 y 16
e. 3 veces la diferencia de 27 y 21.
f. La diferencia de 9 al cuadrado y 4 al cuadrado
g. El cociente de 3 al cubo y 12 al cuadrado dividido por el producto de 8 y 12.

121. Operaciones
con Polinomios
Unidad 4
El Gobierno de Reconciliación y Unidad Nacional, a través de la Empresa Nicaragüense
de Alimentos Básicos (ENABAS) ha distribuido un total de 70 mil libras de frijoles en los
siete distritos de la capital, a través de los puestos de venta móviles que ha dispuesto el
Gobierno Sandinista mediante el Plan Especial de Frijoles Solidarios, con el objetivo de
brindar a la población un producto de calidad y a bajos precios, lo que representa un
ahorro económico considerable para los consumidores.
Fuente: 19 digital.
08 de Mayo 2 014.
a3
a2
b
ab2
b3

122. 114
Operaciones con polinomios.
££ Introducción.
Suma de Monomios (repaso)
En la unidad III, se estudiaron las condiciones para poder sumar
dos monomios.
Dos monomios se pueden sumar o restar sólo en el caso que
sean semejantes. Dos monomios son semejantes si tienen la
misma parte literal afectada de los mismos exponentes.
Al proceso de suma y resta de monomios se le llama reducción
de términos semejantes.
Ejemplos
Transcribe en tu cuaderno la siguiente tabla e indique con una x
qué pares de monomios son semejantes y cuáles no los son.
Pares de monomios Semejantes No semejantes
2x2
y3
z ; - 3x2
y3
z x
2x3
; - 5x2 x
4a2
bc3
; 5a2
bc3 x
− −
3
5
5
7
2 3 2 2
c; x
− −
7
3
5
8
4 2 4 2
p; x
Ejemplos
Efectúe las operaciones indicadas.
a. 2x2
y3
z + 3x2
y3
z
b. 2a3
- 5a3
c. 3m4
- 2m4
+ 7m4
- m4
d. 4a2
bc3
- 5a2
bc3
+ 3a2
bc3
- a2
bc3
Soluciones de los incisos a y d:
Operaciones indicadas
Suma de los
Coeficientes
Parte literal Resultado
2x2
y3
z + 3x2
y3
z 2 + 3 = 5 x2
y3
z 5x2
y3
z
4a2
bc3
– 5a2
bc3
+ 3a2
bc3
- a2
bc3
4 - 5 + 3 - 1 = 1 a2
bc3
a2
bc3
También conocido como
Fibonacci, nació en
Pisa, Italia en el año
1 170. Comienza con
los rudimentos de lo
que se conocía de los
números cuadrados
desde la antigua Grecia
y avanza gradualmente
resolviendo
proposiciones hasta dar
solución al problema de
análisis indeterminado
que le habían planteado
como desafío.
Murió en Pisa en el año
1 250.
Leonardo de Pisa
(1 170 - 1 250)
Nota histórica

123. 115
Actividad
Efectúe las operaciones indicadas en los incisos b y c del ejercicio
anterior.
Ejemplos
a. Dado el polinomio
2x6
- 7x5
+ 5x2
+ 4x - 3
Encuentre los términos que son semejantes al término - 6x2
.
Solución:
El término 5x2
, es semejante al término dado.
b. Reducir los términos semejantes:
a) 3x2
y 4x2
b) -5x y -x
Solución:
Al reducir los términos semejantes se obtiene:
3x2
y 4x2
, y su suma es: (3 + 4)x2
= 7x2
.También son semejantes los
términos - 5x y - x , y su suma es: ( - 5 - 1)x = - 6x.
c. Reducir los términos semejantes:
a) 2x4
y3
y - 3x4
y3
b) 5x3
y2
y - 2x3
y2
Solución:
Al reducir los términos semejantes se obtiene:
a) 2x4
y3
- 3x4
y3
= (2 - 3)x4
y3
= -x4
y3
b) 5x3
y2
- 2x3
y2
= (5 - 2)x3
y2
= 3x3
y2
Matemático, físico,
astrónomo y filósofo
alemán de origen
francés. Nació en
Mülhausen (ahora
Mulhouse, Alsacia,
Francia) y murió en
Berlín. Demostró
que el número π era
irracional, con lo que
cerró la posibilidad de
poder determinar una
cifra exacta (fracción
numérica) para este
número. También hizo
aportes al desarrollo de
la geometría hiperbólica.
Johann Heinrich Lambert
(1 728 - 1 777)
Nota histórica

124. 116
££ Propiedades de la potenciación (repaso)
La potenciación en los números reales cumple con las siguientes
propiedades:
Para multiplicar potencias que tienen la misma base, se escribe
la misma base y suman los exponentes.
En símbolo se escribe:
Suma de los exponentes
am
an
= am + n
Misma Base a
Ejemplo
( - 3x2
)(6x4
) = (- 3)(6) x2 + 4
= - 18x6
Para dividir potencias que tienen la misma base, se escribe la
misma base y se restan los exponentes.
En símbolo se escribe:
Misma Base (a)
Resta de los exponentes
a
a
a
m
n
m n
= −
Ejemplo
3
5
3
5
3
5
5
3
5 3 2x
x
x x= ( ) =
−
Matemático, físico,
filósofo y teólogo
francés, considerado
el padre de las
computadoras junto con
Charles Babbage
En 1 653, Pascal publica
el Tratado del triángulo
aritmético en el que
describe las propiedades
y aplicaciones del
triángulo aritmético o
triángulo de Pascal,
manera de presentar
coeficientes binomiales,
aunque los matemáticos
chinos conocían el
triángulo desde siglos
atrás.
Blaise Pascal
1 623 - 1 662
Nota histórica

125. 117
Recordar.
n - veces
an
= a∙a∙a.....a
Ejemplo:
34
= (3)(3)(3)(3) = 81
Para elevar una potencia a otra potencia, se escribe la misma
base y se multiplican los exponentes
En símbolo se escribe:
Se multiplican los exponentes m y n
(am
)n
= amn
Base (a)
Ejemplo
(2x4
)3
= (2)3
(x4
)3
= 8x12
La potencia de un producto es igual al producto de las potencias
de cada uno de los factores.
En símbolo se escribe:
Producto de las potencias de los factores
(a.b)n
= (a)n
(b)n
Ejemplo
(2x.y)4
= (2)4.x4.y4
= (2)(2)(2)(2) x4
y4
= 16x4
y4
Todo número real distinto
de cero elevado a la
cero, es igual a 1.
ao
= 1; a ≠ 0
También son muy impor-
tantes las siguientes pro-
piedades del 0 y del 1.
• a1
= a
• 0n
= 0; n ≠ 0
• 1n
= 1
Ma
tem
áti
ca
7
¿Sabías qué?

126. 118
La potencia de un cociente es igual al cociente de la potencia
del numerador entre la potencia del denominador, siempre que
el denominador sea diferente de cero.
En símbolo se escribe:
Potencia de un cociente
a
b
a
b
m
n
p m p
n p





 =
⋅
⋅
Cociente de las potencias
Ejemplos
7
8
7
8
7
8
49
64
2 2
2
2 2
2 2
2
2
x
y
x
y
x
y
x
y





 =
( )
( )
=
( )
( )
=
Las potencias negativas.
¿Qué ocurre cuando el exponente es negativo?
Por la propiedad del cociente de potencias que tienen la misma
base, tenemos:
a
a
a
m
n
m n
= −
Si m = 0, entonces:
a
a
a an
n n
0
0
= =− −
También, si m = 0, se cumple lo siguiente:
a
a a
a
a
m
n nn
= =
0
1
Por tanto, por la propiedad transitiva de la igualdad:
a
a
n
n
−
=
1
Ejemplo
a.
b. 1
2
25
5
= −
Reforzamiento:
Aplique las propiedades de
potencia para simplificar
los siguientes exponentes:
• 65
∙ 63
• (xy)5
• (8a2
b)5
• (3x4
)(2x3
)
• (-6xa
yb
)(-2xa
yb
)
• (3mn2
)5
(-4m5
n4
)
• (a2y
∙ a2
)3
•
• [(xnm
)m
]n

127. 119
Ejemplos
• Simplificar cada una de las siguientes expresiones utilizando
las propiedades de los exponentes.
a. (3x4
)(2x3
). Producto de dos potencias.
Solución:
(3x4
)(2x3
) = (3)(2)x4 + 3
= 6x7
.
b.
3
5
3 4
2 2
a b
a b
. Cociente de dos potencias.
Solución:
3
5
3
5
3
5
3 4
2 2
3 2 4 2 2a b
a b
a b ab= ( )( )=− −
c. ( - 3xy2
z3
)3
. Potencia elevada a otra potencia y un producto
elevado a una potencia.
Solución:
( - 3xy2
z3
)3
= ( - 3)3
(x1
)3
(y2
)3
(z3
)3
= - 27x3
y6
z9
d.
4
3
5 2 2
2
m n p





 . Potencia elevada a otra potencia y un producto
elevado a una potencia.
Solución:
4
3
4
3
16
9
5 2 2 5
2
2
2
2
2
10 4 4
2 2
m n p m n p m n p





 =





 =( ) ( ) ( )
Actividad
Resuelva y justifique la respuesta.
a. (8a2
b)(-5a4
b3
)(3a3
b5
)
b. (-6r5
s4
t7
)3
c. (8x2
y3
)5
d. 5
2
2
1
3
m
n−
−







128. 120
Multiplicación de monomios.
Para multiplicar monomios se utilizan las propiedades de los
exponentes.
Para multiplicar dos o más monomios, se multiplican los
coeficientes numéricos y las partes literales.
Recordar.
Al multiplicar varios factores negativos, si el número de factores
es par, el producto es positivo y si el número de factores es
impar, el resultado es negativo.
El producto de factores positivos siempre es positivo
independientemente del número de factores.
Ejemplos:
Efectuar las multiplicaciones siguientes:
a. ( - 2x5
y3
z4
)( - 7x2
y3
z5
)
Solución:
( - 2x5
y3
z4
)( - 7x2
y3
z5
) = ( - 2)( - 7)(x5
)(x2
)(y3
)(y3
)(z4
)(z5
)
( - 2x5
y3
z4
)( - 7x2
y3
z5
) = 14(x5 + 2
)(y3 + 3
)(z4 + 5
) = 14x7
y6
z9
b. (3a2
b3
c4
)( - 2ab4
c7
)(7ab5
c9
)
Solución:
(3a2
b3
c4
)( - 2ab4
c7
)(7ab5
c9
) = (3)( - 2)(7)(a2
)(a)(a)(b3
)(b4
)(b5
)(c4
)(c7
)(c9
)
= (3)( - 2)(7)(a2
)(a)(a)(b3
)(b4
)(b5
)(c4
)(c7
)(c9
)
= - 42(a2 + 1 + 1
)(b3 + 4 + 5
)(c4 + 7 + 9
) = - 42a4
b12
c20
c. −





 −





( )=
1
3
2
7
74 2 4 9 5 10
m n p m n p mn p
Solución:
−





 −





( )=
1
3
2
7
74 2 4 9 5 10
m n p m n p mn p
= −





 −





( )( )( )( )( )( )( )( )( )( )1
3
2
7
7 4 2 4 5 9 10
m m m n n n p p p
= ( )( )( )=+ + + + + +2
3
2
3
4 1 1 2 4 5 1 9 10 6 11 20
m n p m n p
El producto de dos
expresiones algebraicas se
escribe de cualquiera de
las siguientes maneras:
1. a ∙ b
2. a * b
3. (a)(b)
Reforzamiento:
Multiplique:
• x(-3x)(x2
)
• −





 −





 −






1
2
2
3
3
5
3 2 3
a ay y m
•
3
8
5
3
x t xy m m




 −






Ma
tem
áti
ca
7
¿Sabías qué?

129. 121
División de monomios.
Para dividir dos monomios se utilizan las propiedades de los
exponentes.
Recordar.
Al dividir dos cantidades de igual signo el cociente es positivo y al
dividir dos cantidades de diferente signo, el cociente es negativo.
Para dividir dos potencias que tienen la misma base, se escribe
la misma base y se restan los exponentes.
Ejemplo:
Efectuar las siguientes divisiones:
a.
−x y
x y
3 4
2 2 , el numerador y denominador tienen signos diferentes.
Solución:
−
= −( )( )= − = −− −x y
x y
x y x y xy
3 4
2 2
3 2 4 2 1 2 2
b.
−
−
3
5
4
5
2 5
3
m n
mn
, el numerador y el denominador tienen el mismo signo.
Solución:
−
−
=
−
−










=
( )( )
( )( )
( )( )=− −
3
5
4
5
3
5
4
5
3 5
5 4
3
4
2 5
3
2 1 5 3
m n
mn
m n mn 2
c. ab c
ab c
a b c a b c b c
4 3
2 2
1 1 4 2 3 2 0 2 1 2
= = =− − −
d. 8m2
n7
-2m6
n5
-4n2 - 7
m6 - 2 m4
-4n2
m4
4n2
Reforzamiento:
Resuelva las divisiones
indicadas:
• 16m6
n4
÷ 4n3
• 4m2
n3
÷ m2
n
• -4am
bn
÷ ax
bm
• xm - 3
÷ xm - 2

130. 122
Suma y resta de polinomios.
La forma en que se suman y se restan polinomios es similar
a la forma en que se suman y se restan números reales. Las
propiedades que se cumplen al realizar operaciones con números
reales, también se cumplen cuando se realizan operaciones con
polinomios.
Suma de polinomios.
Para sumar dos o más polinomios se siguen los pasos siguientes:
Paso 1. Se agrupan los polinomios.
Paso 2. Se eliminan los paréntesis.
Paso 3. Se agrupan los términos semejantes.
Paso 4. Se reducen los términos semejantes.
Ejemplos:
Efectuar la suma de los siguientes polinomios:
a. 2x - 3y + 1 y 5x + 4y - 2
Solución:
Paso 1. Se agrupan los polinomios:
(2x - 3y + 1) + (5x + 4y - 2)
Paso 2. Se eliminan los paréntesis.
2x - 3y + 1 + 5x + 4y - 2
Paso 3. Se agrupan los términos semejantes.
(2x + 5x) + (- 3y + 4y) + (1 - 2)
Paso 4. Se reducen términos semejantes.
7x + y - 1
Entonces 7x + y - 1 es el resultado de la suma.
Fue un matemático,
filósofo y enciclopedista
francés, uno de los
máximos exponentes del
movimiento ilustrado.
Es célebre por crear
—con Diderot—
L'Encyclopédie y por
su labor en el campo
de las matemáticas,
relativo a las ecuaciones
diferenciales y a las
derivadas parciales.
Jean Le Rond D’Alembert
1 717 - 1 783
Nota histórica

131. 123
b. - 3a + a2
- 2; a - 3a2
+ 2 y 4a2
- 6a
Solución:
Paso 1. Se agrupan los polinomios.
(- 3a + a2
- 2) + (a - 3a2
+ 2) + (4a2
- 6a)
Paso 2. Se eliminan los paréntesis.
- 3a + a2
- 2 + a - 3a2
+ 2 + 4a2
- 6a
Paso 3. Se agrupan los términos semejantes.
(- 3a + a - 6a) + (a2
- 3a2
+ 4a2
) + (- 2 + 2)
Paso 4. Se reducen los términos semejantes.
- 8a + 2a2
+ 0 = 2a2
- 8a.
Por tanto 2a2
- 8a. es el resultado de la suma de polinomios.
c.
1
2
3
4
22 2
a b− − ;
5
2
7
4
12 2
a a− +
Solución:
Paso 1. Se agrupan los polinomios.
1
2
3
4
2
5
2
7
4
12 2 2 2
a b a b− −





 +





+ −
Paso 2. Se eliminan los paréntesis.
1
2
3
4
2
5
2
7
4
12 2 2 2
a b a b− − ++ −
Paso 3. Se agrupan los términos semejantes.
1
2
5
2
3
4
7
4
2 12 2 2 2
a a b b+





 + − + −











 + − +( )
Paso 4. Se reducen términos semejantes.
1
2
5
2
3
4
7
4
2 1 3
10
4
12 2 2 2
+





 + − −





 + − +( )= + −





 + −( )a b a b
= 3
5
2
12 2
a b− −
Por tanto 3
5
2
12 2
a b− − es el resultado de la suma.
Reforzamiento:
1. Resuelva las
siguientes sumas de
polinomios:
• 3a2
- 2a ; a2
+ 1
• b2
c + 2 ; -2b2
c - 3bc2
- 5
• x2
- 4x + 2 ; 2x2
- 8 + 6x
• a4
+ 1 ; a3
+ 2 ; a3
- a2
+ 8
2. Un hotel de 3 pisos
está organizado asi:
El primer piso tiene m
habitaciones, el segundo
el doble de habitaciones
que el primero y el
tercero la mitad de
habitaciones que el
primero. ¿Cuántas
habitaciones tiene cada
piso, si el hotel tiene en
total 70 habitaciones?

132. 124
Otra forma de sumar dos o más polinomios consiste en
ordenarlos y escribir los términos semejantes en columnas.
Ejemplo:
Sumar los polinomios
7x4
- 2x2
+ 3x3
- x + 4 y - 6x + 4x3
- 7x2
- 1
Se ordenan los polinomios en orden descendente.
(7x4
+ 3x3
- 2x2
- x + 4) + (4x3
- 7x2
- 6x - 1)
Los términos semejantes se escriben en columnas para efectuar
la suma.
7 3 2 4
4 7 6 1
7 7 9 7 3
4 3 2
3 2
4 3 2
x x x x+ − − +
− − −
+ − − +
x x x
x x x x
Resta de polinomios.
Cuando se trabaja con números reales, la resta se define como la
suma de un número a con el opuesto de un número b.
a + ( - b) = a - b
El concepto de opuesto también se plantea para polinomios.El
siguiente ejemplo ilustra el concepto de opuesto para un polinomio:
Ejemplo:
Encuentre el polinomio opuesto al polinomio 3x2
- 4x + 3.
Solución:
El polinomio opuesto al polinomio 3x2
- 4x + 3, es:
- (3x2
- 4x + 3) = - 3x2
- ( - 4x) - ( + 3) = - 3x2
+ 4x - 3
Observe que: (3x2
- 4x + 3) + ( - 3x2
+ 4x - 3) = 0
(3x2
- 3x2
) + ( - 4x + 4x) + (3 - 3) = 0; por la propiedad del opuesto.
Para restar dos polinomios P(x) y Q(x) se suma P(x) con el
opuesto Q(x).
Reforzamiento:
1. Sumar 5
6
2
9
2 3
y + x con
− + −
1
2
3
8
52 2 3
y x yx x
2. Sumar xa + 2
- 5xa - 1
- 6x9
con xa + 3
- 8xa + 1
- 5
3. Sumar 3xa
y - 6x2
y2
- nxy2
- 10xy con 4x2
y2
- 3xy +1

133. 125
Ejemplo:
Restar al polinomio a3
- 2a2
+ 4a - 1 el polinomio 3a3
+ a2
- 5a - 4.
Solución:
Paso 1. Se encuentra el opuesto del polinomio que se va a restar
(sustraendo).
El opuesto del polinomio 3a3
+ a2
- 5a - 4, es el polinomio
- (3a3
+ a2
- 5a - 4) = -3a3
- a2
+ 5a + 4
Paso 2. Se suma el polinomio minuendo con el opuesto del
polinomio sustraendo.
(a3
- 2a2
+ 4a - 1) + ( - 3a3
- a2
+ 5a + 4)
Paso 3. Se eliminan los paréntesis.
a3
- 2a2
+ 4a - 1 - 3a3
- a2
+ 5a + 4
Paso 4. Se agrupan términos semejantes.
(a3
- 3a3
) + ( - 2a2
- a2
) + (4a + 5a) + ( - 1 + 4)
Paso 5. Se reducen los términos semejantes.
- 2a3
+ ( - 3a2
) + 9a + 3 = - 2a3
- 3a2
+ 9a + 3
Para restar polinomios se ordenan los polinomios y se escriben
los términos semejantes en columnas tomando en cuenta que
el sustraendo debe de ser su opuesto y finalmente se resuelven
igual que la suma de polinomios.
Ejemplo:
De 2x3
- 3x2
+4x-1 (minuendo) restar -x2
- 5x3
+ 6x - 3 (sustraendo).
Solución:
Se ordena el polinomio sustraendo - x2
- 5x3
+ 6x - 3. El polinomio
ordenado es:
- 5x3
- x2
+ 6x - 3
El polinomio opuesto del polinomio sustraendo - 5x3
- x2
+ 6x - 3 es
el polinomio:
- ( - 5x3
- x2
+ 6x - 3) = 5x3
+ x2
- 6x + 3.
Se escriben en columna los términos semejantes y se reducen los
términos semejantes.
2x3
- 3x2
+ 4x - 1
5x3
+ x2
- 6x + 3
7x3
- 2x2
- 2x + 2
Reforzamiento:
Realice las siguientes
operaciones:
De m + n restar m - n
Restar 2a - 3b de -a + 2b
Restar 5y2
- 3 de 4y2
- 13

134. 126
Refuerce sus conocimientos.
1. Sumar los siguientes polinomios:
a. 2a3
- 4a2
+ 7a - 1 y
1
2
2 73
a a− +
Solución:
Los polinomios ya están ordenados en forma descendente. Se
plantea la suma agrupando los polinomios.
(2a3
- 4a2
+ 7a - 1) +
1
2
2 73
a a− +






Se eliminan los paréntesis: 2a3
- 4a2
+ 7a - 1 +
1
2
2 73
a a− +
Se agrupan los términos semejantes.
2
1
2
4 7 2 1 73 3 2
a a a a a+





 + −( )+ −( )+ − +( )
Se reducen los términos semejantes.
(2 +
1
2
) a3
- 4a2
+ 5a + 6 =
5
2
a3
- 4a2
+ 5a + 6
a. 1
3
1
9
1
6
2 2
mn m n+ − y 3
4
1
9
3
2
2 2
n m n m mn− + −
Solución:
Se plantea la suma agrupando los polinomios.
1
3
1
9
1
6
3
4
1
9
3
2
2 2 2 2
mn m n n m n m mn+ −





 + − + −






Se eliminan los paréntesis.
1
3
1
9
1
6
3
4
1
9
3
2
2 2 2 2
mn m n n m n m mn+ − + − + −
Se agrupan los términos semejantes.
1
3
1
9
3
2
1
9
1
6
3
4
2 2 2 2
mn mn mn m m n n− −





 + +





 + − +






Los polinomios de Frits
Zernike, (científico
holandés, Premio Nobel
de Física en 1953),
nos ofrece un método
para descomponer
superficies complejas
en sus componentes
más simples. Este
método permite
investigar defectos
visuales como la miopía,
la hipermetropía y el
astigmatismo.
Ma
tem
áti
ca
7
¿Sabías qué?

135. 127
Se reducen los términos semejantes.
1
3
1
9
3
2
1
9
1
1
6
3
4
2 2
− −





 + +





 + − +





mn m n
6 2 27
18
1 9
9
2 9
12
2 2− −




 +
+




 +
− +




mn m n
Entonces
−
+ +
23
18
10
9
2 7
12
2mn m n es el resultado de la suma.
2. Efectuar las siguientes restas de polinomios:
a. Del polinomio - 11x5
y2
+ 13x3
y3
- 10 (minuendo) restar el
polinomio - 2x3
y3
- 11 - 17x5
y2
(sustraendo).
Solución:
Se plantea la resta agrupando los polinomios.
(11x5
y2
+ 13x3
y3
- 10) - ( - 2x3
y3
- 11 - 17x5
y2
)
Se eliminan los paréntesis.
11x5
y2
+ 13x3
y3
- 10 + 2x3
y3
+ 11 + 17x5
y2
Se agrupan los términos semejantes.
(11x5
y2
+ 17x5
y2
) + (13x3
y3
+ 2x3
y3
) + ( - 10 + 11)
Se reducen los términos semejantes.
(11 + 17)x5
y2
+ (13 + 2)x3
y3
+ ( - 10 + 11)
28x5
y2
+ 15x3
y3
+ 1
Entonces 28x5
y2
+ 15x3
y3
+ 1 es el resultado de la resta.
Célebre matemático
italiano del
Renacimiento, médico,
astrólogo. Nacido en
Pavía, Italia, fue amigo
de Leonardo Da Vinci.
Es conocido por sus
trabajos de álgebra.
En 1 539 publicó su
libro de aritmética
“Practica arithmetica et
mensurandi singulares”.
Publicó las soluciones
a las ecuaciones de
tercer y cuarto grado
en su libro “Ars magna”
datado en 1 545.
La solución a un caso
particular de ecuación
cúbica x3
+ ax = b (en
notación moderna).
Gerolamo Cardano
(1 501 - 1 576)
La otra forma de solución es:
11x5
y2
+ 13x3
y3
- 10
17x5
y2
+ 2x3
y3
+ 11
28x5
y2
+ 15x3
y3
+ 1
Nota histórica

136. 128
b. Del polinomio
3
8
2
3
1
3
232
m m p− + + restar el polinomio
− − + −
1
3
2
3
5
8
182
m p m
Solución:
Se plantea la resta agrupando los polinomios.
3
8
2
3
1
3
23
1
3
2
3
5
8
182 2
m m p m p m− + +





 − − − + −






Se eliminan los paréntesis.
3
8
2
3
1
3
23
1
3
2
3
5
8
182 2
m m p m p m− + + + + − +
Se agrupan los términos semejantes.
3
8
5
8
2
3
1
3
1
3
2
3
23 182 2
m m m m p p−





 + − +





 + +





 + +( )
3
8
5
8
2
3
1
3
1
3
2
3
412
−





 + − +





 + +





 +m m p
-
2
8
m3
+ (-
1
3
)m + p + 41 = -
1
4
m3
-
1
3
m + p + 11
c. Restar − + −a a b ab4 2 2 37
8
2
9
de
21
11
5
14
1
3
63 2 2 3
a b a b ab+ + − .
2
4
5
14
1
3
6
7
8
2
9
3 2 2 3 4 2 2 3
a b a b ab a a b ab+ + − − − + −






2
4
5
14
1
3
6
7
8
2
9
3 2 2 3 4 2 2 3
a b a b ab a a b ab+ + − + − −
Constatar que la respuesta es a a b a b ab4 3 2 2 32
11
29
56
1
9
+ − −
Resolver:
De: 8 - 6m2
Restar 15m2
- 60 + 4m
Reto matemático.
Empleando símbolos
matemáticos, ¿puedes
conseguir que cinco
nueves sean igual a mil?.
(Fuente: Clifford A.
Pickover. La Maravilla
de los Números. 2 002.
Ediciones Robinbook, s. I.,
Barcelona)

137. 129
Los signos de agrupación.
Los signos de agrupación se utilizan para efectuar operaciones
con polinomios que incluyen combinaciones de sumas y restas.
Los signos de agrupación más utilizados son: el paréntesis ( ), los
corchetes [ ] y las llaves { }.
Para suprimir los signos de agrupación en las operaciones con
polinomios, se utilizan las siguientes reglas:
1. Si la expresión que se encuentra dentro del signo de
agrupación está precedida por un signo menos (-), entonces
la expresión algebraica dentro del signo de agrupación
cambia de signo.
2. Si la expresión que se encuentra dentro del signo de
agrupación está precedida por un signo más (+), entonces
la expresión algebraica dentro del signo de agrupación
preserva su signo.
3. El orden para suprimir los signos de agrupación es a partir
del signo que se encuentra más al interior hasta llegar al que
está más externo.
Ejemplos:
Simplificar las expresiones algebraicas suprimiendo los signos de
agrupación y reduciendo los términos semejantes.
a. 9x - {4x - 2y + [ - 10x + 22y - (30x - 4y) ] }
Solución:
Primero se suprimen los paréntesis.
9x - {4x - 2y + [ - 10x + 22y - 30x + 4y] }
En segundo lugar se suprimen los corchetes.
9x - {4x - 2y - 10x + 22y - 30x + 4y}
En tercer lugar se suprimen las llaves.
9x - 4x + 2y + 10x - 22y + 30x - 4y
Se reducen los términos semejantes.
(9x - 4x + 10x + 30x) + (2y - 22y - 4y) = 45x - 24y
Reforzamiento:
De 8x2
– 2x + 1 restar 3x2
+ 5x – 8
Restar 2x3
– 3x2
+ 5x – 1
de x2
+ 1 – 3x
De la suma de 7x4
– 5x5
+
4x2
–7 con x3
– 3x2
– 5 + x
restar –3x4
+ 5 – 8x + 2x3

138. 130
b. - {2m2
+ 7n2
- [mn - 20m2
+ ( - 5m2
+ 12mn + 16n2
) - m2
] + 15mn}.
Solución:
Se eliminan los paréntesis.
- {2m2
+ 7n2
- [mn - 20m2
- 5m2
+ 12mn + 16n2
- m2
] + 15mn}
Se eliminan los corchetes.
- {2m2
+ 7n2
- mn + 20m2
+ 5m2
- 12mn - 16n2
+ m2
+ 15mn}
Se eliminan las llaves.
- 2m2
- 7n2
+ mn - 20m2
- 5m2
+ 12mn + 16n2
- m2
- 15mn
Se reducen términos semejantes.
( - 2m2
- 20m2
- 5m2
- m2
) + ( - 7n2
+ 16n2
) + (mn + 12mn - 15mn)
Entonces la respuesta es: - 28m2
+ 9n2
- 2mn
c. − + − − +


















x y x x y3 3 3 3 35
9
4
5
10
7
Solución:
Se eliminan los paréntesis: − + − − −












x y x x y3 3 3 3 35
9
4
5
10
7
Se eliminan los corchetes: − + − + +






x y x x y3 3 3 3 35
9
4
5
10
7
Se eliminan las llaves: − + − + +x y x x y3 3 3 3 35
9
4
5
10
7
Se reducen los términos semejantes.
(- x3
- 4
5
x3
+ 10
7
x3
)+ ( 4
9
y3
+ y3
)
Resolviendo las operaciones internas de cada parentesis se
obtiene:
- 13
35
x3
+ 14
9
y3
Matemático francés que
investigó en el campo
de la teoría de números,
sobre las formas
cuadráticas, polinomios
ortogonales, funciones
elípticas y en el álgebra.
Varias entidades
matemáticas se llaman
hermitianas en su honor.
También es conocido
por la interpolación
polinómica de Hermite
Charles Hermite
(1 822 - 1 901)
Nota histórica

139. 131
Multiplicación de polinomios.
Antes de estudiar la multiplicación de polinomios, se debe analizar
la multiplicación de un monomio por un polinomio.
Para multiplicar un monomio por un polinomio, se multiplica el
monomio por cada término del polinomio, aplicando la propiedad
distributiva de la multiplicación respecto a la adición y teniendo
en cuenta las reglas para la multiplicación de monomios.
££ Multiplicación de un monomio por un polinomio.
Ejemplos:
Efectuar las siguientes multiplicaciones:
a. x2
(2x3
- 3x2
+ x).
Solución:
x2
(2x3
- 3x2
+ x) = x2
(2x3
) - x2
(3x2
) + x2
(x)
x2
(2x3
- 3x2
+ x) = 2x2 + 3
- 3x2 + 2
+ x2 + 1
x2
(2x3
- 3x2
+ x) = 2x5
- 3x4
+ x3
a. m n m n m n m n2 2 3 4 2 5 33
4
5
1
3
2+ − +






Solución:
m n m n m n m n2 2 3 4 2 5 33
4
5
1
3
2+ − +





 =
=





 + ( )−





 + ( )m n m n m n m n m n m n m n2 2 3 2 2 4 2 2 2 5 3 2 23
4
5
1
3
2
= + − +
3
4
5
1
3
22 3 2 2 4 2 2 2 5 2 3 2 2
m m n n m m n n m m n n m n
= + − ++ + + + + +3
4
5
1
3
22 3 2 1 2 4 2 2 2 5 2 3 2 2
m n m n m n m n La respuesta final es:
3
4
m5
n3
+ 5m6
n4
- 1
3
m7
n5
+ 2m2
n2
Reforzamiento:
Resuelva los siguientes
ejercicios:
• a + b (b - a) + 2a - (a + b)
• (51 - 3w) + (w - 61 )
• (3x + 5) + (2x - 2)

140. 132
Multiplicación de dos polinomios.
Para multiplicar dos polinomios, se multiplica cada término
del primer polinomio por cada término del segundo polinomio,
utilizando las reglas para el producto de monomios y las
leyes de los exponentes. A continuación se reducen términos
semejantes.
Ejemplos:
1. Efectuar las multiplicaciones indicadas.
(3x2
- 2x + 2)(2x - 6).
Solución:
Se multiplica cada término del primer polinomio por el segundo
polinomio.
3x2
(2x - 6) - 2x(2x - 6) + 2(2x - 6)
Se efectúan las multiplicaciones de cada término del primer
polinomio por el segundo polinomio.
3x2
(2x) - 3x2
(6) - 2x(2x) + 2x(6) + 2(2x) - 2(6)
6x2 + 1
- 18x2
- 4x1 + 1
+ 12x + 4x - 12
6x3
- 18x2
- 4x2
+ 12x + 4x - 12
Se reducen términos semejantes.
6x3
- 22x2
+ 16x - 12
Otra forma de multiplicar es siguiendo los pasos que se describen
a continuación:
Paso 1. Se ordenan los polinomios.
Paso 2. Se escriben los polinomios ordenados uno debajo del
otro.
Paso 3. Se multiplican los polinomios término a término ubicando
los términos semejantes en columnas.
Paso 4. Se reducen los términos semejantes.
La multiplicación de
polinomios es una
operación algebraica
que tiene por objeto
hallar una cantidad
llamada producto,
dadas dos cantidades
llamadas multiplicando
y multiplicador de
modo que el producto
sea con respecto del
multiplicando en signo
y valor absoluto lo que
el multiplicador es con
respecto a la unidad
positiva.
Ma
tem
áti
ca
7
¿Sabías qué?

141. 133
Ejemplos:
Efectuar el producto de los polinomios:
a. (2x2
- 4x + 2)(x - 3).
Solución:
Paso 1. En este caso los polinomios ya están ordenados.
(2x2
- 4x + 2)(x - 3)
Paso 2. Se escriben los polinomios uno debajo del otro y se
multiplican término a término ubicando los términos semejantes en
columnas para luego reducirlos.
2 4 2
3
2 4 2
6 12 6
2
3 2
2
x x
x
x x x
x x
− +
−
− +
− + −
2x3
- 10x2
+ 14x - 6
b. (a2
- 3a + 4) (a2
+ 5a + 6)
Paso 1. En este caso los polinomios ya están ordenados.
Solución:
Paso 2. Se escriben los polinomios uno debajo del otro y se
multiplican término a término ubicando los términos semejantes en
columnas para reducirlos.
a2
- 3a + 4
a2
+ 5a + 6
a4
- 3a3
+ 4a2
5a3
- 15a2
+ 20a
6a2
- 18a + 24
a4
+ 2a3
- 5a2
+ 2a + 24 Se reducen los términos semejantes
Producto de a2
- 3a + 4 por 6
Producto de a2
- 3a + 4 por 5a
Producto de a2
- 3a + 4 por a2
Actividad:
Resuelva las siguientes multiplicaciones:
1. (a + 2)(a - 3)
2. (x2
+ 5)(x2
- 5)
3. (n2
- a - 1)(n2
+ a + 1)
2x2
- 4x + 2 por x
2x2
- 4x + 2 por -3
Se reducen los términos semejantes
Matemático francés.
Hizo importantes
contribuciones a la
estadística, la teoría
de números, el álgebra
abstracta y el análisis
matemático.
En 1 830 ofreció una
demostración del último
teorema de Fermat para
el exponente n = 5, casi
simultáneamente con
Dirichlet en 1 828.
Adrien - Marie Legendre
(1 752 –1 833)
Nota histórica

142. 134
Simplificación de expresiones algebraicas que
contienen productos indicados.
Para simplificar expresiones algebraicas que contienen productos
indicados, se realizan los pasos siguientes:
Paso 1. Se efectúan los productos indicados.
Paso 2. Se reducen los términos semejantes.
Paso 3. En caso que existan signos de agrupación, éstos se
eliminan siguiendo las propiedades de multiplicación de signos.
Los signos de agrupación se eliminan de adentro hacia fuera.
Ejemplos:
Simplificar las siguientes expresiones algebraicas:
a. 6a(b - 1) + 3b(a - 2) - 4c(b - 4).
Solución:
Efectuando los productos indicados.
6ab - 6a + 3ab - 6b - 4bc + 16c
Reduciendo los términos semejantes
(6 + 3)ab - 6a - 6b - 4bc + 16c
9ab - 6a - 6b - 4bc + 16c
b. - m2
+ 4{n2
+ [(m - 1)(m - 2) - 7m] }
Solución:
Efectuando los productos indicados.
- m2
+ 4{n2
+ [m2
- 2m - m + 2 - 7m] }
Eliminando los signos de agrupación.
- m2
+ 4n2
+ 4m2
- 8m - 4m + 8 - 28m
Reduciendo términos semejantes.
3m2
+ 4n2
- 40m + 8
Reforzamiento:
Resuelva las siguientes
operaciones:
• z(z - y) + 3z (y + 2z)
• 3(m + n)2
- 4(m - n)2
• [(x+y)(x-y) -x+y ](x-2y)

143. 135
c. {a2
- 2[b2
- (b - 1)(b - 1) - a2
] }
Solución:
Efectuando los productos indicados.
{a2
- 2[b2
- (b2
- b - b + 1) - a2
] }
Eliminando los paréntesis.
{a2
- 2[b2
- b2
+ b + b - 1 - a2
] }
Eliminando los corchetes.
{a2
- 2b2
+ 2b2
- 2b - 2b + 2 + 2a2
}
Eliminando las llaves y reduciendo términos semejantes.
3a2
- 4b + 2
d. x2
- [x - (x - 1)(x + 2) ]
Solución:
Se efectúan los productos indicados.
x2
- [x - (x2
+ 2x - x - 2) ]
Se eliminan los paréntesis.
x2
- [x - x2
- 2x + x + 2]
Se eliminan los corchetes.
x2
- x + x2
+ 2x - x - 2
Se reducen términos semejantes.
x2
+ x2
- x - x + 2x - 2 = 2x2
- 2x + 2x - 2
2x2
- 2x + 2x - 2 = 2x2
+ 0 - 2 = 2x2
- 2
e. Determinando el volumen del cubo de la figura.
Solución:
El volumen de un cubo es igual a la medida de la
arista elevada al cubo.
Volumen = (3x)3
= (3x)(3x)(3x)
Volumen = (3)(3)(3)(x)(x)(x)
Volumen = 27x3
Reto Matemático
Falacia algebraica
Considere dos números
reales a y b, tales que
a = b.
a = b ⟹ a2
= ab
a2
+ a2
⟹ a2
+ ab
2a2
= a2
+ ab
2a2
- 2ab = a2
+ ab - 2ab
2(a2
- ab) = a2
- ab
Dividiendo los lados de
la ecuación entre a2
- ab,
se obtiene:
2 = 1
¿Cuál es el error?
3x
3x
3x

144. 136
f. Geometría. Encontrando el perímetro de la siguiente figura
geométrica.
2a - b
2
2a - b
2
a
2
a a
bb b
Solución:
El perímetro P de la figura es la suma de las medidas de sus
lados:
P
a b a b
b b b a
a
a=
−
+
−2
2
2
2 2
+ + + + + +
Simplificando la expresión obtenida y se reduciendo términos
semejantes:
P = 1
2
(2a - b + 2a - b) + 3b + 5
2
a = 1
2
(4a - 2b )+ 3b + 5
2
a
P = 1
2
2 (2a - b) + 3b + 4a = (2a - b) + 3b + 5
2
a
P = 2a - b + 3b + 5
2
a = 9
2
a+ 2b
Actividad
Justifique cada paso de la solución del ejercicio anterior.
g. Geometría. Encontrar el perímetro de la figura.
Solución:
El perímetro es igual a la suma de las medidas
de los lados de la figura.
P = x + x + x + x + y + y + y + y + y + y + y + y
P = 4x + 8y
h. Geometría. Encontrar el área de la región
de color amarillo.
Solución:
El área de la región de color amarillo es:
Área = xy - y2
Justifique la respuesta.
xx
x
x
yy
y yy
yy
y
Reforzamiento:
1. Determine el área
y perimetro del
siguiente cuadrado:
2 + y
2. Encuentre el
producto de:
(3am
- bn
) (3am
+ bn
)
(x3
- y3
)(x3
+ y3
)
x
y
y
x

145. 137
División de polinomios.
La división de polinomios cumple con las propiedades de la división
de números reales.
Para dividir un polinomio entre un monomio, se aplica la
propiedad distributiva y la división de monomios.
££ División de un polinomio entre un monomio.
Ejemplo:
Dividir el polinomio 12x6
+ 2x5
- x4
- 8x2
entre el monomio 3x2
.
Solución:
Se plantea la división.
12x6
+ 2x5
- x4
- 8x2
3x2
Se aplica la propiedad distributiva y la división de monomios:
12x6
+ 2x5
- x4
- 8x2
3x2 =
12x6
3x2 +
2x5
3x2 -
x4
3x2 - 8x2
3x2
Se aplican las propiedades de las potencias.
3 2
x
12x6
+ 2x5
- x4
- 8x2
= +
3
2
4x6-2
x5-2
-
3
1
x4-2
-
3
8
x2-2
2
3
x4
+ 2
3
x3
- 1
3
x2
- 8
3
El resultado es: 2
3
x4
+ 2
3
x3
- 1
3
x2
- 8
3
Ejemplo:
Dividir el polinomio 2m6
+ 2m5
- m4
- 8m entre el monomio 4m.
Solución:
Se plantea la división.
2m6
+ 2m5
- m4
- 8m
4m
Se aplica la propiedad distributiva.
2m6
+ 2m5
- m4
- 8m
4m
=
2m6
4m
+
2m5
4m
-
m4
4m
-
8m
4m
• Para dividir potencias
que tienen la misma
base, se deja la
base y se restan los
exponentes.
a
a
a
m
n
m n
= −
• Para dividir dos mo-
nomios, se simplifi-
can los coeficientes,
si es posible, y se
dividen las partes
literales.
Ma
tem
áti
ca
7
¿Sabías qué?

146. 138
2m6
4m
+
2m5
4m
-
m4
4m
-
8m
4m
= 2
4
m6 - 1
+ 2
4
m5 - 1
- 1
4
m4 - 1
- 8
4
m1 - 1
= 1
2
m5
+ 1
2
m4
- 1
4
m3
- 8
4
m0
= 1
2
m5
+ 1
2
m4
- 1
4
m3
- ( 8
4
)(1)
La respuesta es 1
2
m5
+ 1
2
m4
- 1
4
m3
- 2
££ División de un polinomio entre otro polinomio.
Para dividir un polinomio entre otro polinomio, se siguen los pasos
siguientes:
Paso 1. Se ordenan los polinomios en forma decreciente con
respecto a una de las variables.
Paso 2. Se divide el primer término del dividendo entre el primer
término del divisor. El resultado es el primer término del cociente.
Paso 3. El primer término del cociente se multiplica por cada
término del divisor. Cada producto se resta de su término
semejante en el divisor. Si no tiene término semejante, entonces
se escribe en el lugar correspondiente de acuerdo con el orden
del dividendo.
Paso 4. Se baja el siguiente término del dividendo. Se divide el
primer término del dividendo parcial entre el primer término del
divisor. El resultado será el segundo término del cociente.
Paso 5. Este proceso se continúa hasta obtener un residuo de
menor grado que el divisor.
Si la división es exacta, entonces el residuo que se obtendrá al
efectuar la división es cero.
Ejemplo:
Efectuar la división del polinomio (10 - 4x2
+ x3
+ 5x) entre el
polinomio x - 2.
Solución:
Paso 1. Se ordenan los polinomios en orden descendente
respecto a la variable x.
• La división entre 0
no está permitida
(no está definida)
a
0
no está definida.
• a0
= 1;∀a ∈ �;
a ≠ 0
Todo número real
distinto de cero elevado
a la potencia 0 es igual
a uno.
Ma
tem
áti
ca
7
¿Sabías qué?

147. 139
x3
- 4x2
+ 5x + 10 x-2
Paso 2. Se divide x3
entre x. Este será el primer término del
cociente.
x3
- 4x2
+ 5x + 10 x-2
x2
Paso 3. Se multiplica x2
por x - 2. Cada resultado se resta del
dividendo.
x3
- 4x2
+ 5x + 10 x-2
x2
-x3
+ 2x2
0x3
- 2x2
Paso 4. Se baja el siguiente término del dividendo, 5x. Se divide
- 2x2
entre x. Se obtiene el segundo término del cociente.
x3
- 4x2
+ 5x + 10 x-2
x2
-x3
+ 2x2
-2x2
+ 5x
Se multiplica - 2x por cada término del divisor. Cada resultado se
resta del dividendo - 2x2
+ 5x.
x3
- 4x2
+ 5x + 10 x-2
x2
- 2x-x3
+ 2x2
-2x2
+ 5x
2x2
- 4x
x
Se divide x entre x. Se obtiene el tercer término del cociente.
x3
- 4x2
+ 5x + 10 x-2
x2
- 2x + 1-x3
+ 2x2
- 2x2
+ 5x
2x2
- 4x
x + 10
Se multiplica 1 por cada uno de los término de x - 2 y el resultado
se resta del dividendo x + 10.
x3
- 4x2
+ 5x + 10 x-2
x2
- 2x + 1-x3
+ 2x2
- 2x2
+ 5x
2x2
- 4x
x + 10
-x+ 2
12
Si al ordenar un
polinomio en forma
ascendente o
descendente con
respecto a un literal
este tiene todos sus
términos, es decir,
an
, an - 1
, an - 2
....a0
,
el polinomio está
completo.
Si al ordenar un
polinomio le falta uno
de sus términos , el
polinomio es incompleto,
los términos faltantes se
pueden reemplazar por
cero.
Ma
tem
áti
ca
7
¿Sabías qué?

148. 140
Se ha obtenido una contante. Una constante tiene grado cero que
es menor que el grado de x - 2, que es 1.
x3
- 4x2
+ 5x + 10 x - 2
-x3
+ 2x2
-2x2
+ 5x
2x2
- 4x
x+ 10
-x+ 2
12
x2
- 2x + 1
Dividendo Divisor
Cociente
Residuo
Observación importante.
El dividendo es igual al divisor por el cociente más el residuo.
x3
- 4x2
+ 5x + 10 (x2
- 2x + 1) (x - 2) + 12
Dividendo Divisor Cociente Residuo
Curiosidades matemáticas. El cuadrado mágico de orden 3.
Al sumar los números en cada fila, en cada columna y en las
diagonales, el resultado es 15 en todos los casos.
4 3 8
9 5 1
2 7 6
¿Puede encontrar tres soluciones diferentes a la presentada?
Un polinomio completo es: 3x3
- 5x2
+ 2x - 1
Un polinomio incompleto es: x4
- 2x2
+ 8
Escriba en su cuaderno dos polinomios completos y dos
incompletos.
Actividad
Resuelva la siguiente división.
x2
- xy +4y2
entre x + 2y
Matemático, físico y
astrónomo italiano que
después vivió en Prusia
y Francia. Lagrange
demostró el teorema
del valor medio,
desarrolló la mecánica
Lagrangiana y tuvo una
importante contribución
en astronomía.
Contribuyó al cálculo de
diferencias finitas con la
fórmula de interpolación
que lleva su nombre.
Sus tres trabajos
sobre el método de
interpolación de 1 783,
1 792 y 1 793, están
ahora en la misma fase
en que Lagrange los
dejó.
Joseph Louis Lagrange
(1 736 - 1 813)
=
Nota histórica
Polinomio completo con
respecto a una letra es
aquel que se caracteriza
porque todos los
exponentes de la letra
considerada existen,
desde el mayor hasta el
menor inclusive.
4x3
- 15x2
+ 12x - 11
Ma
tem
áti
ca
7
¿Sabías qué?

149. 141
División sintética o Regla de Ruffini.
Para aplicar el algoritmo o Regla de Ruffini se siguen los pasos
siguientes:
Ejemplo:
Dividir el polinomio - 3x3
+ x4
+ 4x - 2 entre el binomio x - 2.
Paso 1. Se ordena el dividendo en orden descendente.
x4
- 3x3
+ 4x - 2
Paso 2. Se escriben los coeficientes del polinomio. En caso
que una potencia no aparezca en el polinomio, el coeficiente
orrespondiente se sustituye por “0”.
Los coeficientes son: 1 - 3 0 + 4 - 2. El 0 se escribe en lugar de la
potencia que falta que es x2
.
Paso 3. En el lugar del divisor de escribe el término independiente
del divisor con signo contrario.
1 - 3 0 +4 -2 2
Paso 4. Se baja el primer coeficiente del dividendo y se multiplica
por el valor que se encuentra en el divisor. El resultado se escribe
debajo del segundo coeficiente del dividendo y se efectúa la
operación.
1 -3 0 + 4 -2 2
2
1 - 1
Paso 5. El resultado se multiplica por el divisor y el resultado se
escribe debajo del tercer coeficiente del dividendo y se efectúa la
operación.
1 -3 0 + 4 -2 2
2 - 2
1 - 1 - 2
El proceso se repite hasta que el residuo sea cero o un número
distinto de cero.
1 -3 0 + 4 -2 2
2 - 2 - 4
1 - 1 - 2 0 - 2
Reforzamiento:
Resuelva cada una de
las siguientes divisiones:
2x3
+ 5x2
+ 10x - 8 ÷ (x + 1)
x3
+ ax2
+ a2
x + a3
÷ (x + a)
m3
- 64 ÷ m - 4
2y3
- 3y2
- 5y3
-1 ÷ y - 2
Verifique las respuestas
obtenidas aplicando la
ley de Ruffini.
Reto Matemático
Hallar el número
de terminos en el
siguiente polinomio:
P(x) = (m - 1)xm - 6
+ (m - 2)
xm - 5
+ (m - 3)xm - 4
+ ... si es
completo

150. 142
Los coeficientes obtenidos corresponden a los coeficientes del
polinomio cociente. Este es un polinomio un grado menor que el
grado del dividendo. En el ejemplo, el grado del dividendo es 4,
entonces el grado del cociente es 3.
El resultado de la división es;
Coeficientes del
polinomio cociente
x3
- x2
- 2x
1 - 1 - 2 - 2 Residuo
El residuo de la división es - 2.
Ejemplo:
Dividir el polinomio x + 12 + 2x2
+ x3
entre el binomio x + 3
Se siguen los mismos pasos de resolución del ejemplo anterior.
Paso 1. Se ordena el dividendo en orden descendente.
x3
+ 2x2
+ x + 12
Paso 2. Se escriben los coeficientes del polinomio. En este caso
el polinomio está completo, contiene todas las potencias de x.
Los coeficientes son: 1 + 2 + 1 + 12.
Paso 3. En el lugar del divisor se escribe el término independiente
del divisor con signo contrario.
1 + 2 + 1 + 12 -3
Paso 4. Se baja el primer coeficiente del dividendo y se multiplica
por el valor que se encuentra en el divisor, El resultado se escribe
debajo del segundo coeficiente del dividendo y se efectúa la
operación.
1 + 2 + 1 + 12 -3
-3
1 - 1
Paso 5. El resultado se multiplica por el divisor y el producto se
escribe debajo del tercer coeficiente del dividendo y se efectúa la
operación.
1 + 2 + 1 + 12 -3
-3 3
1 - 1 4
El proceso se repite hasta que el residuo sea cero o un número
distinto de cero.
1 + 2 + 1 + 12 -3
-3 3 - 12
1 - 1 4 0
Las matemáticas,
consideradas
correctamente, poseen
no solamente verdad,
sino que suprema
belleza, una belleza fría
y austera, como la de
una escultura.
(Bertran Russel,
Misticismo y lógica,
1 918. Citado de:
“El Prodigio de los
números”. Clifford A.
Pickover, pág. 17)
Ma
tem
áti
ca
7
¿Sabías qué?

151. 143
Los coeficientes obtenidos corresponden a los coeficientes del
polinomio cociente. Este es un polinomio un grado menor que el
grado del dividendo. En el ejemplo, el grado del dividendo es 3,
entonces el grado del cociente es 2.
El resultado de la división es;
Coeficientes del
polinomio cociente
x2
- x + 4
1 - 1 4 0 Residuo
El residuo de la división es 0.
Actividad
I. Efectúe las siguientes divisiones, aplicando el método de Ruffini.
a. x3
- 2x2
+ 2x - 1 entre x - 1.
b. x3
- 4x2
+ 6x - 4 entre x - 2.
c. x4
- x3
- 2x2
+ 2x + 2 entre x + 1.
d. x5
- x4
- x + 1 entre x - 1.
e. x6
+ 3x5
- x2
- 4x - 3 entre x + 2.
f. x4
- x3
- x2
+ 4x + 5 entre x + 1.
II. Sean los polinomios:
A = 3x4
- 5x2
+ x - 1
B = 2x4
+ x3
- 2x + 3
C = 4x3
- x2
+ 7
D = 3x2
- 4x + 2
Resuelva :
1. (A + B + C + D) ÷ (x - 1)
2. (B - C + D) ÷ (x + 2)
3. (2a - 3B) ÷ (x + 1)

152. 144
Productos notables.
Los productos notables son casos particulares de la multiplicación
de polinomios, en los cuales no es necesario realizar todas las
operaciones propias de la multiplicación de polinomios, sino que
se realizan los cálculos en forma abreviada.
££ Cuadrado de la suma de dos términos.
Efectuando la multiplicación:
a + b
a + b
a2
+ ab
ab + b2
a2
+ ab + ab + b2
a2
+ 2ab + b2
Multiplicación de a por (a + b)
Multiplicación de b por (a + b)
Efectuando la suma
Reduciendo los terminos semejantes
En símbolos se escribe:
(a + b)2
= (a + b)(a + b) = a2
+ 2ab + b2
¿Cómo se puede interpretar el cuadrado de la suma de dos
términos?
Se ilustrará con un ejemplo, la interpretación geométrica del
cuadrado de la suma de dos términos.
Para la interpretación geométrica se utilizará el concepto de
área de regiones tales como regiones cuadradas y regiones
rectangulares.
El cuadrado de la suma de dos términos, (a + b)2
, es igual al
cuadrado del primer término a2
, más el doble producto del
primer término por el segundo término 2ab, más el cuadrado del
segundo término b2
.
Ejemplo:
Se pide encontrar el área de una región cuadrada con lado de
medida (a + b).
Solución:
El área de la región cuadrada es igual a
la medida del lado elevada al cuadrado.
El lado del cuadrado tiene medida
(a + b)
Con el desarrollo de
las computadoras,
los polinomios han
sido remplazados
por funciones spline
en muchas áreas del
análisis numérico. Las
splines se definen a
partir de polinomios y
tienen mayor flexibilidad
que los polinomios
ordinarios cuando
definen funciones
simples y suaves.
Éstas son usadas en
la interpolación spline
y en gráficos por
computadora.
Ma
tem
áti
ca
7
¿Sabías qué?
b
a
a
a + b
a + b
ab
ab
b
a2
b2

153. 145
Entonces, el área de la región cuadrada es: (a + b)2
Por otro lado, el área de la región cuadrada de la figura es también
igual a:
a2
+ ab + ab + b2
= a2
+ 2ab + b2
Entonces, hemos obtenido la siguiente igualdad:
(a + b)2
= a2
+ 2ab + b2
Esta expresión es conocida como el cuadrado de la suma de dos
términos.
Trabajo en equipo.
Utilizando cartulinas de diferentes colores, recorte figuras
geométricas según la interpretación geométrica del cuadrado de la
suma de dos términos
££ Cuadrado de la diferencia dos términos.
El cuadrado de la diferencia de dos términos, (a - b)2
, es igual
al cuadrado del primer término a2
, menos el doble producto del
primer término por el segundo término 2ab, más el cuadrado del
segundo término b2
.
En símbolos se escribe:
(a-b)2
= a2
- 2ab + b2
¿Cómo se puede interpretar el cuadrado de la diferencia de dos
términos?
Se presenta un ejemplo de Geometría.
Ejemplo:
Se pide encontrar el área de la región cuadrada de lado (a - b) de
la figura.
Solución:
El área de la región cuadrada de lado
(a - b) está dada por:
(a - b)2
Si al área de la región cuadrada de
lado a, que es a2
, le restamos las áreas
de las dos regiones rectangulares y el
área de la región cuadrada de lado b,
que es b2
, obtenemos el área buscada.
b
(a - b)
a
b
(a - b)(a - b)2
b2
Reforzamiento:
Resuelva aplicando
el producto notable
correspondiente:
(3x + 2y)2
(2a2
- 5b3
)2
(5 - 2x)2
(a4
+ 2b5
)2
( + 2x)
2
(5x2
- 3y2
)
1
2

154. 146
Entonces, el área es:
(a - b)2
= a2
- b(a - b) - b(a - b) - b2
Área
Buscada
Área de la
región
cuadrada.
Área de la
región
rectangular.
Área de
la región
cuadrada.
(a - b)2
= a2
- b(a - b) - b(a - b) - b2
(a - b)2
= a2
- ab + b2
- ab + b2
- b2
(a - b)2
= a2
- 2ab + b2
Área de la
región
rectangular.
Trabajemos en equipo.
Actividad.Utilizando cartulinas de diferentes colores, recorte
figuras geométricas según la interpretación geométrica del
cuadrado de la diferencia de dos términos.
££ Producto de la suma de dos expresiones algebraicas por
su diferencia.
El producto de las suma de dos términos por su diferencia, es
igual a la diferencia de sus cuadrados.
En símbolos se escribe:
(a + b)(a - b) = a2
- b2
Efectuando la multiplicación:
a + b
a - b
a2
+ ab
- ab + b2
a2
+ 0 - b2
a2
- b2
Multiplicación de “a” por (a + b)
Multiplicación de “-b” por (a + b)
Reduciendo los terminos semejantes
a2
+ 0 - b2
. Propiedad del neutro.
La propiedad del neutro para la suma de expresiones
algebraicas dice que toda expresión algebraica sumada con
“0” da como resultado la misma expresión algebraica.
En símbolos se escribe:
a + 0 = a
La ecuación cuadrática
(polinomio de segundo
grado)
x2
+ 1 = 0, a pesar de
su aparente simpleza,
no tiene solución en el
conjunto de los números
reales. Cuando tratamos
de resolver esta
ecuación, obtenemos
dos soluciones que
pertenecen al campo de
los números imaginarios
(complejos).
¿Cuál es la solución?
x2
+ 1 = 0 ⟹ x2
= -1 ⟹
x x i= ± −( ) ⇒ = ±1
La unidad “i” es la unidad
imaginaria.
i = −( )1
Ma
tem
áti
ca
7
¿Sabías qué?

155. 147
El siguiente ejemplo de Geometría ilustra una interpretación de
esta operación.
Ejemplo:
Considere la siguiente región cuadrada con lado de medida a y por
tanto con área a2
.
El área de la región cuadrada con lado de
medida b es:
Área = b2
El área de la región rectangular de
dimensiones a y a - b, es igual a:
Área = a(a - b) = a2
- ab
El área de la región rectangular de dimensiones a y a - b, es igual a:
Área = b(a - b) = ab - b2
Considere ahora la siguiente región rectangular:
a + b
a - b
El área de la región rectangular de la figura es:
Área = (a + b)(a - b)
A continuación se suman las áreas de las regiones rectangulares:
Suma de la áreas = a2
- ab + ab - b2
= a2
- b2
Finalmente obtenemos la igualdad:
(a + b)(a - b) = a2
- b2
Trabajando en grupo. Utilizando cartulinas de diferentes colores,
recorte figuras geométricas según la interpretación geométrica del
cuadrado de la suma de dos términos
Reto Matemático
Un jugador escribe un
número cualquiera sobre
un papel sin enseñárselo
al conductor del juego.
El conductor del juego
dice que:
Lo multiplique por 5 le
sume 6 lo multiplique
por 4 le sume 9 lo
multiplique por 5 y
finalmente, que diga el
resultado.
Al número que da el
jugador, se le resta 165
y el resultado de divide
entre 100.
Al final, el conductor
del juego le dice que el
número que escribió en
el papel es el resultado
final.
(Fuente: El Secreto de
los números, André
Jouette, pág. 52)
a
ba - b
bb2
a - b

156. 148
Cubo de la suma de dos términos.
El cubo de la suma de dos términos, es igual al cubo del primer
término, más el triple producto del cuadrado del primer término
por el segundo término, más el triple producto del primer término
por el cuadrado del segundo término, más el cubo del segundo
término.
En símbolos se escribe:
(a + b)3
= a3
+ 3a2
b + 3ab2
+ b3
Ejemplo:
En la figura se presenta un cubo
con arista de medida (a + b).
También se presentan las partes
componentes del cubo. Se pide
calcular el volumen del cubo y la
suma de los volúmenes de las
partes componentes.
Solución:
El volumen del cubo es igual a la medida de la arista elevada al
cubo. La arista tiene medida a. Entonces el volumen del cubo es:
Volumen = (a + b)3
b3
ab2
ab2
a2
b
ab2
a2
b a3
a2
b
Observe que:
1. Hay un cubo de arista de medida a. Entonces su volumen es
a3
.
2. Hay tres figuras que tienen el mismo volumen (a2
b), entonces
se tiene que:
Volumen de las tres figuras = 3a2
b
a + b
a + b
a
a
a
b
b
b
a + b
Reforzamiento:
Resuelva utilizando
el producto notable
correspondiente:
• (2x + 3y)3
• (3m - 4n)3
• (5m2
- 3n2
)3
• (x3
+ y2
)3

157. 149
3. Tambien hay tres figuras que tienen el mismo volumen (ab2
),
entonces se tiene que:
Volumen de las tres figuras = 3ab2
4. Finalmente, el cubo más pequeño tiene arista de medida b.
Entonces su volumen es:
Volumen del cubo más pequeño = b3
A continuación, sumamos los volúmenes encontrados y se obtiene:
Suma de volúmenes = a3
+ 3a2
b + 3ab2
+ b3
El volumen obtenido es el volumen del cubo de mayór tamaño (el
cubo original). El volumen del cubo original es (a + b)3
, entonces
igualando este volumen con la suma de los volúmenes obtenemos:
(a+b)3
= a3
+ 3a2
b + 3ab2
+ b3
Esta es la expresión para el cubo de la suma de dos términos.
Trabajo en equipo.
Utilizando cartulinas de diferentes colores, construya sólidos
geométricos que ilustren con modelos reales el cubo de la suma
de dos términos.
Cubo de la diferencia de dos términos.
El cubo de la diferencia de dos términos, es igual al cubo del
primer término, menos el triple producto del cuadrado del primer
término por el segundo término, más el triple producto del primer
término por el cuadrado del segundo término, menos el cubo del
segundo término.
En símbolos se escribe:
(a-b)3
= a3
- 3a2
b + 3ab2
- b3
Resuelva:
• (x + y)3
• (2a - b)3
• (5m -3n)3
Reto Matemático.
Operaciones
Piramidales.
(0)(9) + 1 = 1
(1)(9) +2 = 11
(12)(9) + 3 = 111
(123)(9) + 4 = 1 111
(1234)(9) + 5 = 11 111
• ¿Puedes continuar
con la pirámide?
• Determine la forma
generalizada:
Verifique los resultados.
(Fuente: El Secreto de los
números, André Jouette,
pág. 53)

158. 150
Producto de la forma (x + a)(x + b).
Cuando se multiplican dos binomios que tienen un término
común, se suma el cuadrado del término común con el producto
del término común por la suma de los términos no comunes, y
al resultado se le suma el producto de los términos no comunes.
En símbolos se escribe:
(x + a)(x + b) = x2
+ ax + bx + ab = x2
+ (a + b)x + ab
Término
común
elevado
al
cuadrado
Término
común
Acontinuación se presenta un ejemplo que ilustra la interpretación
geométrica de este producto.
Ejemplo:
Encuentre el área de una región rectangular cuyos lados tiene
medidas (x + a) y (x + b).
Solución:
Considere una región rectangular cuyos lados tienen medidas
(x + a) y (x + b).
x
ab
x + b
a
bx
ax
b
x + a
x
b
x x2
a
El área de la región rectangular de la figura es:
Área = (x + a)(x + b)
Reforzamiento:
Resuelva los siguientes
productos notables:
• (x - 2)(x - 7)
• (x + 2)(x + 7)
• (x + 2)(x - 7)
• (x - 2)(x + 7)

159. 151
La suma de las áreas de las regiones rectangulares que se
encuentran en el interior del rectángulo es:
+ + +Área = x2
ax bx
abbx
axx2
ab
+ + +
Área = x2
+ (a + b)x + ab
También el área es igual a: Área = (x + a)(x + b)
Entonces, finalmente se obtiene:
(x + a)(x + b) = x2
+ (a + b)x + ab
Trabajo en equipo.
1. Efectuar las operaciones indicadas aplicando los productos
notables estudiados.
• (2a + 3b)(2a - 3b)
• (x + 3y)2
• (2x - 5y)2
• (m + 2)(m + 3)
• (a + 3b)3
• (2m - 4n)3
• [(x + y) - z]2
• [(2a - b) - (a + 4b) ]2
• [(m - 2n + p) - (m + 4n - p) ]3
• [(x + y) - 1][(x + y) + 1]
• (a + b + c)3
• [(m + n) - (x + y) ][(m + n) + (x + y) ]
• (a + b)3
+ (a - b)3
• (m + n)3
- (m - n)3
La medalla Fields
fue constituida por el
matemático canadiense
Charles Fields y
fue concedida por
primera vez en 1 936.
Cada cuatro años la
Unión Matemática
Internacional selecciona
para el premio hasta
a cuatro de los
investigadores más
destacados del mundo,
que deben tener menos
de cuarenta años. El
premio consiste en una
medalla de oro y una
pequeña cantidad en
metálico (actualmente
unos 13 500 dólares),
pero por su prestigio se
considera equivalente
al premio Nobel. El rey
de Noruega entrega
el premio en una
ceremonia especial.
(Fuente: La cuadratura
del cuadrado, Ian
Stewart, pág. 139).
Ma
tem
áti
ca
7
¿Sabías qué?

160. 152
Reto. Efectuar las operaciones indicadas.
• (a + b + c + d + e)2
• (a + b + c + d + e)3
Refuerce sus conocimientos.
££ Ejercicios.
• Transcribe en tu cuaderno la siguiente tabla y completa la
informaciónescribiendo una “S” donde los monomios sean
semejantes y “NS” en el caso que nos sean semejantes.
Monomios Semejantes No semejantes
-2x3
yz2
y -7x3
yz2
S
3ab4
c y 6ab4
c2
NS
5mn3
p y -4mn3
p
7xy2
z3
y -9xyz3
NS
• Reducir los términos semejantes en las expresiones
algebraicas siguientes:
a. 2a - 6a
Solución:
2a - 6a = (2 - 6)a = - 4a
b. 2x2
y - 3xy2
+ 5x2
y + 3xy2
Solución:
2x2
y - 3xy2
+ 5x2
y + 3xy2
= (2x2
y + 5x2
y) + ( - 3xy2
+ 3xy2
).
(2x2
y + 5x2
y) + (- 3xy2
+ 3xy2
) = (2 + 5)x2
y + (- 3 + 3)xy2
.
(2 + 5)x2
y + (- 3 + 3)xy2
= 7x2
y + (0)xy2
.
7x2
y + (0)xy2
= 7x2
y + 0 = 7x2
y
Reto Matemático.
¿Sabrías escribir el
número 10 de dos
formas distintas
empleando cuatro
nueves?

161. 153
a. mn2
p3
+ 1
2
m2
n2
p3
- 1
4
mn2
p3
.
Solución:
mn2
p3
+ 1
2
m2
n2
p3
- 1
4
mn2
p3
= (m2
n2
p3
- 1
4
mn2
p3
) + ( 1
2
m2
n2
p3
)
(m2
n2
p3
- 1
4
mn2
p3
) + ( 1
2
m2
n2
p3
) = (1 - 1
4
)m2
n2
p3
+ 1
2
m2
n2
p3
(1 - 1
4
)m2
n2
p3
+ 1
2
m2
n2
p3
= 3
4
mn2
p3
+ 1
2
m2
n2
p3
• Indicar el tipo de polinomio y el grado de las expresiones
algebraicas siguientes:
a. 2x2
y - 3xy3
+ 6xy b. 2x2
c. 5
Solución:
Polinomio Tipo de polinomio Grado del polinomio
a.2x2
y - 3xy3
+ 6xy Trinomio
Es el grado del término
3x1
y3
, que es el de mayor
grado. El grado es 3 + 1 = 4
b. 2x2
Monomio 2
c. 5 x0
Monomio
El grado es cero, ya que
la variable tiene potencia
cero.
• Indique con una “” cuáles de las siguientes expresiones son
monomios. En caso afirmativo, indique su grado y coeficiente.
a. 13x3
b. 25x - 3 c. 3a + 1, d. mn2
, e. 3a- 1
f. 4a- 2
bc.
Soluciones:
Expresión
algebraica
Es
monomio
No es
monomio
Grado Coeficiente
13x3
 3 13
25x - 3 
3a + 1 
mn2
 2 + 1 = 3 1
3a-1

4a-2
bc  4
La fórmula más bella.
A veces aparecen
encuestas para decidir
cuál es la fórmula
matemática más bella
de todos los tiempos
(es verdad, no me estoy
inventando) y casi
siempre resulta vencedora
una famosa fórmula
descubierta por Euler, que
utiliza números complejos
para relacionar las dos
famosas constantes e y π.
La fórmula es:
eπi
= -1
Y es esencial en una
rama de la matemática
denominada análisis
complejo.
(Fuente: La cuadratura
del cuadrado, Ian
Stewart, pág. 201).
Ma
tem
áti
ca
7
¿Sabías qué?

162. 154
Explicación de las respuestas en los casos en que no son
monomios.
1. 25x - 3, no es monomio, ya que tiene dos términos.
2. 3a + 1, no es monomio, ya que tiene dos términos.
3. 3a- 1
= 3( 1
a
) = 3
a
; tiene un exponente negativo, es decir, una
variable en el denominador.
4. 4a- 2
bc = 4( 1
a2
)bc = 4
a2
bc, tiene un exponente negativo, es
decir, una variable en el denominador.
• Ordene los siguientes polinomios en forma descendente con
respecto a la variable que se indique:
a. a2
bc3
- 2
3
a3
b2
c4
+ 4a4
b3
c5
- 1
7
a5
b4
c6
, respecto a “a”.
Solución:
El polinomio se escribe en forma descendente con respecto a “a”
así:
- 1
7
a5
b4
c6
+ 4a4
b3
c5
- 2
3
a3
b2
c4
+ a2
bc3
Los exponentes de la variable “a” están escritos en forma
descendente: 5; 4; 3; 2.
b. x4
yz2
- 3
7
xy2
z4
+ 5x2
y3
z3
- 7
9
x5
y4
z, respecto a la variable z.
Solución:
El polinomio se escribe en forma descendente respecto a z, así:
- 3
7
xy2
z4
+ 5x2
y3
z3
+ x4
yz2
- 7
9
x5
y4
z
Los exponentes de la variable z están escritos en forma
descendente: 4; 3; 2,1.
££ Suma y resta de polinomios.
• Efectúe las operaciones indicadas.
a. 38ab – (- 8 ab)
b. – 8cde2
– 16 cde2
.

163. 155
a. (- 8x3
+ 3x – 2x2
) – ( - 2x3
+ 5x – 6x2
)
b. ( 3
5
x4
- 2x2
+ 3
4
x - 1) + (x4
4x2
- x + 7)
Soluciones:
a. 38ab – (- 8ab) = 38ab + 8ab = (38 + 8)ab = 46ab.
b. – 8cde2
– 16 cde2
= (- 8 - 16)cde2
= - 24cde2
c. (- 8x3
+ 3x–2x2
) – (- 2x3
+ 5x–6x2
)
= ( - 8x3
+ 2x3
) + (3x - 5x) + (–2x2
+ 6x2
)
= ( - 8 + 2)x3
+ (3 - 5)x + ( - 2 + 6)x2
= - 6x3
- 2x + 4x2
= - 6x3
+ 4x2
- 2x
Actividad
Justifique los pasos de la resolución de los ejercicios a, b, y c.
Los polinomios también se pueden sumar escribiendo uno de los
polinomios debajo del otro de acuerdo a los términos semejantes
de cada polinomio. La resolución del inciso d se presenta de esa
manera.
d. ( 3
5
x4
- 2x2
+ 3
4
x - 1) + (x4
+ 4x2
- x + 7)
Solución:
Se escribe uno de los polinomios debajo del otro, de acuerdo a los
términos semejantes.
3
5
x4
- 2x2
+ 3
4
x - 1
x4
+ 4x2
- x + 7
( 3
5
+1)x4
+ (- 2 + 4)x2
+ ( 3
4
- 1)x + (- 1 + 7)
(3 + 5
5 )x4
+ 2x2
+ (3 - 4
4 )x - 6
( 8
5 )x4
+ 2x2
+(- 1
5 )x - 6
8
5
x4
+ 2x2
- 1
5
x - 6

164. 156
Trabajo en equipo.
Actividad
Efectuar las siguientes divisiones:
a. x4
- y4
entre x - y
b. x4
- y4
entre x2
- y2
c. x3
+ y3
entre x + y
d. x3
- y3
entre x - y
££ Multiplicación de polinomios.
Efectúe las operaciones indicadas.
a. (2x3
) (5x3
).
b. 35(2m2
n3
p).
c. 4(5x2
2y3z)(2y2
z2
).
d. 5(8x3
3y2
z5
) (6x3
yz2
).
e. 6(- 2x3
) (- 5x)(- 3x2
).
Soluciones:
a. (2x3
)(5x3
) = (2)(5)(x3
)(x3
) = 10x3 + 3
= 10x6
b. 35(2m2
n3
p) = (35)(2)2m2
n3
p = 70m2
n3
p
c. 4(5a2
2b3c)(2b2
c2
) = (4)(5)(2)(3)(2)(a2
)(b)(b2
)(c)(c2
)
= 240(a2
)(b1 + 2
)(c1 + 2
)
= 240a2
b3
c3
d. 5(8x3
3y2
z5
)(6x3
yz2
) = (5)(8)(3)(6)(x3
)(x3
)(y2
)(y)(z5
)(z2
)
= 720(x3 + 3
)(y2 + 1
)(z5 + 2
)
= 720x6
y3
z7
e. 6( - 2x3
)(- 5x)(- 3x2
) = (6)(- 2)(- 5)(- 3)(x3
)(x)(x2
)
= (- 180)(x1 + 3 + 2
)
= - 180x6
El problema 14 del
Papiro de Moscú
En el problema 14
del papiro de Moscú
(1890 a. de C.) se pide
calcular el volumen de
un tronco de pirámide
cuadrangular. El escriba
expone los pasos:
eleva al cuadrado 2 y
4, multiplica 2 por 4,
suma los anteriores
resultados y multiplícalo
por un tercio de 6 (h);
finaliza diciendo: «ves,
es 56, lo has calculado
correctamente». En
notación algebraica
actual sería:
,
un polinomio de cuatro
variables
(V, h, t, b) que,
conociendo tres, permite
obtener la cuarta
variable.
Ma
tem
áti
ca
7
¿Sabías qué?

165. 157
Realice las multiplicaciones indicadas.
a. (7x2
)(– 2x3
+ 6x2
- 4)
Solución:
(7x2
)(– 2x3
+ 6x2
- 4) = (7x2
)(– 2x3
) + (7x2
)(6x2
) + (7x2
)(–4)
= (7)( - 2)(x2
)(x3
) + (7)(6)(x2
)(x2
) + (7)(–4)(x2
)
= - 14x2 + 3
+ 42x2 + 2
- 28x2
= - 14x5
+ 42x4
- 28x2
b. (6m – 6m2
+ 5) ( - 4 + 6m2
– 3m)
Solución:
Se ordenan los polinomios en orden descendente.
6m – 6m2
+ 5 = - 6m2
+ 6m + 5
- 4 + 6m2
– 3m = 6m2
– 3m - 4
Se escriben los polinomio uno debajo del otro.
–6m2
+ 6m + 5
6m2
- 3m - 4
-36m4
+ 36m3
+ 30m2
18m3
- 18m2
- 15m
24m2
- 24m - 20
-36m4
+ 54m3
+ 36m2
- 39m - 20
Producto de (6m2
) por (–6m2
+ 6m + 5)
Producto de (-3m) por (–6m2
+ 6m + 5)
Producto de (-4) por (–6m2
+ 6m + 5)
££ División de polinomios.
Realizar las divisiones indicadas.
a.
12x3
4x
= 3x3 - 1
= 3x2
b.
2(8x6
y2
z5
)
(6x3
yz2
)
=
8
3
x6 - 3
y2 - 1
z5 - 2
=
8
3
x3
yz3
c.
x4
- 2x3
- 11x2
x2
= x4
x2 - 2x3
x2 -
11x2
x2
= x4 - 2
- 2x3 - 2
- 11x2 - 2
= x2
- 2x1
- 11x0
= x2
- 2x - 11

166. 158
a.
x4
y2
- 3x3
y3
- 10x2
y4
x2
y2
=
x4
y2
x2
y2
-
3x3
y3
x2
y2
-
10x2
y4
x2
y2
= x4 - 2
y2 - 2
- 3x3 - 2
y3 - 2
- 10x2 - 2
y4 - 2
= x2
y0
- 3x1
y1
- 10x0
y2
= x2
(1) - 3xy - 10(1)y2
= x2
- 3xy - 10y2
££ División sintética. (Método de Ruffini).
Dividir el polinomio (x3
+ x2
- 3x - 2) entre el binomio (x + 2).
Solución:
Paso 1.Los polinomios están ordenados en forma descendente
(x3
+ x2
- 3x - 2).
Paso 2. Se escriben los coeficientes del polinomio. En caso
que una potencia no aparezca en el polinomio, el coeficiente
correspondiente se sustituye por 0.
Los coeficientes son: 1 1 - 3 - 2.
Paso 3. En el lugar del divisor de escribe el término independiente
del divisor con signo contrario.
1 1 - 3 - 2 - 2
Paso 4. Se baja el primer coeficiente del dividendo y se multiplica
por el valor que se encuentra en el divisor, El resultado se escribe
debajo del segundo coeficiente del dividendo y se efectúa la
operación.
1 1 - 3 - 2 - 2
- 2
1 - 1
Paso 5. El resultado se multiplica por el divisor y el producto se
escribe debajo del tercer coeficiente del dividendo y se efectúa la
operación.
1 1 - 3 - 2 - 2
- 2 + 2
1 - 1 - 1
Matemático y médico ita-
liano. Estudió Matemá-
tica, literatura, filosofía,
medicina y biología en la
Universidad de Módena.
Se graduó en 1788, y
fue nombrado rector de
la misma universidad
en 1814. Su principal
aporte fue el intento
de demostrar que las
ecuaciones polinómicas
de grado superior al
cuarto son irresolubles
por radicales, problema
que permanecía abierto
desde el siglo XVI y que
sería finalmente resuelto
por Évariste Galois.
Paolo Ruffini
(1 765 – 1 822)
Nota histórica

167. 159
El proceso se repite hasta que el residuo sea cero o un número
distinto de cero.
1 1 - 3 - 2 - 2
- 2 + 2 + 2
1 - 1 - 1 0
Los coeficientes obtenidos corresponden a los coeficientes del
polinomio cociente. Este es un polinomio un grado menor que el
grado del dividendo. En el ejemplo, el grado del dividendo es 3,
entonces el grado del cociente es 2.
El resultado de la división es;
Coeficientes
del polinomio
cociente
0 Residuo
x2
- x - 1
1 - 1 - 1
El residuo de la división es 0.
Trabajo en equipo.
1. Efectuar las siguientes divisiones de polinomios con el método
de Ruffini.
a. 3x4
- 2x2
+ 5x - 2 entre x - 1
b. - x4
+ 2x3
- 3x + 1 entre x + 3
c. 3x3
+ 2x2
- x - 2 entre x + 2
d. 3x3
- 27 entre x - 3
2. Escriba una V, si la afirmación es Verdadera y una F, si la
afirmación es falsa.
x4
- 8x3
+ 11m2
- 13m + 2 es divisible entre x3
+ 5x.
El binomio a - 2 divide en forma exacta al polinomio a2
- 4.
El trinomio x2
+ x + 1 es divisor del polinomio x3
- 1.
3. Geometría. Si se conoce que el volumen de un objeto de forma
cilíndrica es V = 2x3
+ 23x2
+ 78x + 72 y que la altura es igual a
h = x + 6, calcular el área de la base.
Sugerencia: El volumen de un objeto que tiene forma cilíndrica
está dado por la fórmula:
V = A.h
2
Donde A es el área de la base y h es la altura.
En la división:
P(x) ÷ Q(x)
P(x) se llama Polinomio
Dividendo.
Q(x) se llama Polinomio
Divisor.
C(x) se llama Polinomio
Cociente.
R se llama Residuo o
Resto de la división.
Si la división es exacta,
entonces el residuo es
igual a cero.
Ma
tem
áti
ca
7
¿Sabías qué?

168. 160
Actividades finales de la Cuarta Unidad
I. Efectúa las divisiones usando el método de Ruffini.
1. x3
+ 3 ÷ x + 1
2. 2x4
+ 3x2
- 5 ÷ x - 2
3. 2x3
- 18x2
+ 22x + 42 ÷ x - 7
4. 2x3
+ 6x2
- 3x + 1 ÷ x + 1
5. 5x3
+ 6x2
- 3x + 1÷ x + 1
6. 3x3
+ 15x2
- 3x - 15 ÷ x + 5
7. x4
+ x2
+ 1 ÷ x - 1
8. 3x4
+ 15 ÷ x + 3
9. x3
- 9x + 10 ÷ x - 3
II. Dados los polinomios p(x) = 3x2
+ 5x - 6; q(x) = 5x2
+ 8x - 9; r(x) = 3x + 4, calcule:
1. p(x) + q(x)
2. p(x) - q(x)
3. p(x) + q(x) - r(x)
4. p(x) - q(x) - r(x)
III. Dados los polinomios p(x) = x3
- 5x2
+ 7; q(x) = 2x3
- 7x + 6x - 3x + 1 calcule:
1. p(x) + q(x)
2. q(x) - p(x)
3. p(x) • q(x)

169. 161
IV. Dados los polinomios p(x) = 4x2
- 13x + 20; q(x) = 10x2
- 7x + 8; r(x) = 5x - 1 calcule:
1. p(x) + q(x)
2. p(x) - q(x)
3. p(x) + q(x) - r(x)
4. p(x) - q(x) - r(x)
V. Calcula los productos notables indicados :
1. (a - 2b)3
2. (3x + 2y)3
3. (-1 + 4h)3
4. (7x + 2y)(7x - 2y)
5. (-a + 5b)(a + 5b)
6. (4a - 6b)2
7. (5x + 8y) (5x - 8y)
8. (2 + 8h)2
9. (-3x - 4y)2
10. (x + 2y)2
11. (4x - 5y)3
12. (1 - xy)3
VI.Calcule el cuadrado del siguiente trinomio utilizando los productos notables y con la
definición de potencia y comprueba que se obtiene el mismo resultado:
(x - y + z)2
VII. Calcule las siguientes potencias de polinomios utilizando productos notables:
1. (3x - y)4
2. (-x + 5y)4

170. 162
VIII. Aplique productos notables y simplifica:
(2x2
- y + z - t )2
+ (3x - y)2
IX. Identifique de que producto notable proviene cada expresión:
1. 6x – 12 = ____( - )
2. _____( - ) = 24a + 12ab
3. 4x – 8y = _____( - )
4. _____( - ) = 10x - 15x2
5. _____( - ) = 14m2
n + 7mn
6. 6x4
- 30x3
+ 2x2
= _____( - + )
7. 4m2
+ 20 am = _____( + )
8. 4a3
bx + 4bx = _____( + )
9. ( + )2
= m2
- 2m + 1
10. x2
+ 26x + 25 = ( + )( + )
11. ( + )2
= y2
- 10y + 25
12. 4c2
– 20cd + 25d2
= ( - )2
13. ( + )2
= y2
+ 6y + 9
14. ( + )2
= h2
+ 4h + 4
15. ( - )2
= 9a2
- 12ab + 4b2
16. ( - )2
= 4x2
– 20xy + 25y2
17. ( - )2
= 49x2
- 14x + 1
18. 16m2
- 40mn + 25n2
= ( - )2
19. ( - )( + ) = y2
- 4

171. 163
20. ( - )( + ) = 4x2
- 9
21. ( - )( + ) = a2
- 1
22. ( - )( + ) = m2
- 25
23. 49x2
- 36y2
= ( + )( - )
24. ( + )( - ) = 121p2
- 400q2
25. ( - )( + ) = 16a2
b2
- 49
26. ( - )( + ) = m2
n4
- x8
27. ( + )( - ) =
1
4
- x4
28. ( - )( + ) =
n
y
a
x
2
2
2
2
4
9
−
29. _____( + - ) = 2ab + 4a2
b - 6ab2
30. _____( - + ) = b2
- 3b – 28
31. _____( - + - ) 20xy2
- 5xy + 10x2
y - 5x2
y2
32. _____( + + )= z2
+ 6z + 8
33. _____( + ) = 5a + 25ab
X. Dados los siguientes polinomios:
1. Determinar el grado absoluto de cada uno de ellos.
2. Expresarlos en forma ordenada: ascendente y descendente.
•
A x = -3+ 2x -
3
2
x5 2
( )
• B x =
5
3
x +
3
2
x -7x - 42 3
( )
• C x =
2
5
x -6x - 2x + 143 2
( )
• D x =
5
4
x - 3x -5- x3 4 2
( )

172. 164
XI.Ordene en forma descendente los siguientes polinomios:
1. 4x³ - 1 + 3x ²
2. 1
2
5 6
x x+
3. − + −2 3
2
3
x x x³ ²
XII. Realizar las siguientes multiplicaciones con monomios:
1. 3
7
5
3 3 2
xy x y( )⋅





 =
2. −( )⋅





⋅





⋅





 =9
7
3
1
2
2
5
3 4
x x x
3. 5ab y -3a x y
1
6
a b xy =2 3 3 3 2 2 3
( )⋅( )⋅






4. 9
2
2
3
3 52 3
x x x





⋅





 + −( )⋅( )=
XIII. Sumar los siguientes polinomios:
1. P(x) = 0,1x - 0,05x ² + 0,7 y Q(x) = 0,3x + 1 - x²
2. V(x) = 0,1 x - 0,05 x²
+ 0,7 y M(x) = 0,3x + 1 - x²
XIV. Realice los ejercicios indicados.
a. De x4
- x³ - x² + 2x + 2 restar 2x²
+ 3x³
+ 4x4
- 5x + 5
b. Restar 0,1x - 0,05x ² + 0,7 de 0,3x + 1 - x²

173. 165
c. Calcular el valor numérico de P(x)= para los siguientes valores:
1. x = 1
2. x = -1
3. x =
2
3
4. x = -3
d. Dados los polinomios: P(x) = 4x²
- x + 2; Q(x) = x³
+ x – 1; R(x) = 2x - 1
Hallar:
1) P(x) + Q(x)
2) P(x) + R(x)
3) Q(x) • R(x)
4) P(x) • R(x)
5) P(x) ÷ R(x)
6) Q(x) ÷ R(x)
e. Dividir por el método de Ruffini los siguientes polinomios:
1) P(x) = 3x³
+ 2x²
- x - Q(x) = x + 2
2) P(x) = x7
+ x5
- x³
- x Q(x) = x – 1
3) P(x) = 64x6
+ 64 Q(x) = x + 2
f. Determinar si:
1) P(x) = 2x²
- x - 1 es divisible por Q(x) = x – 2
2) P(z) = 2z²
- z - 1 es divisible por Q(z) = z – 1
XV. Desarrolle las siguientes expresiones y compruebe los resultados para x = 1.
1. 5(x + 4)2
2. (x + 5)2
3. (x - 4)2
4. (x + 3)3
5. (x + 1)2
6. (x+1)(x-1)
x
2
-3x + 4x -5x -
2x
3
+
5
4
2 3
4

174. 166
XVI. Sin realizar las multiplicaciones respectivas, obtenga los siguientes productos.
1. (x + 2)(x + 3)
2. (m + 6)(m + 4)
3. (y + 1)(x + 5)
4. (n + 2)(n - 2)
5. (k + 5)(k + 5)
6. (z - 1)(z - 1)
XVII. Complete los espacios vacios en el desarrollo de (x ± y)2
1. (x+___)2
= ____+ 4xy + ____
2. (____ - ___)2
= 9x2
- ____ + ____
3. (____ - ___)2
= x4
- 16x2
+ ____
4. (6 - ___)2
= _____-12x + x2
XVIII. Complete los espacios que faltan en el desarrollo de (x ± a)(x ± b)
1. (x + 5)(___ + 2) = ___ + 7x ___
2. (___+___)(___ + ___) = x2
+ 11x + 24
3. (x+___)(x+___) = ____ + 8x + 15
4. (x - ___)(x + 9)= ____ -2x - 99
5. (x - 7)(x - ___) = ____ -12x + ___
6. (___ + ___)(___ + ___) = m2
- 11m + 3
XIX. Obtener el término indicado en los siguientes productos notables.
1. Primero y último término de 1 3
3
+( )k
2. Tercer término de 3
1
2
m
n
+






3. Penúltimo término de a b2
1
2
3
3−






4. Encuentre el término que no contiene a x en el desarrollo de: 6
1
2
2
x
x
−







175. Funciones
Unidad 5
La Coordinadora del Consejo de Comunicación y Ciudadanía, compañera Rosario
Murillo, informó a través de los Medios del Poder de las Familias y Comunidades: “En el
modelo de alianzas gobierno nacional-gobierno local, Presidencia de la
República-Gobiernos Locales, estaremos haciendo por año, en los próximos tres años,
3 mil 21 cuadras en todos los municipios del país. Estas cuadras son trabajadas en
concreto hidráulico, adoquín y asfalto”.
Fuente: 19 digital.
21 de Mayo 2 014.
Función Lineal
f(x)= mx + b
m: pendiente de la recta
b: ordenada al origen
y = 2x + 1

176. 168
Funciones.
Lea, analice e interprete.
Introducción.
En el séptimo grado se estudiaron los conceptos de producto
cartesiano, par ordenado, sistema coordenadas cartesianas y el
concepto de relación.
Surge la pregunta: ¿Cuáles son las similitudes y diferencias
entre una relación y una función? O tal vez, ¿Porqué es que
todas las funciones son relaciones; pero, no todas las relaciones
son funciones? ¿Qué significa la prueba de la línea vertical
para identificar si una relación es o no una función?¿Podemos
distinguir una función discreta de una continua?
Los conocimientos que adquieras en esta unidad te permitirán
dar respuestas a todas estas preguntas. Podrás determinar el
dominio y el recorrido o rango. Se explica visualmente cómo
diferenciar la gráfica de una función de una relación.
Repaso de relaciones.
££ El concepto de producto cartesiano.
En la teoría de conjuntos el producto cartesiano de dos conjuntos
no vacíos A e B, denotado por A×B, es el conjunto de todos los
pares ordenados en los que la primera componente pertenece
al conjunto A y la segunda al conjunto B.
En símbolos se escribe: A × B = {(a,b)|a ∈ A ∧ B ∈ b) }
Ejemplo:
Dados los conjuntos A = {1,2,3} y B = {a,b,c}, encuentre el producto
cartesiano de los conjuntos A y B.
Solución
A × B = {(1,a);(1,b);(1,c)(2,a);(2,b);(2,c);(3,a);(3,b);(3,c) }
Par ordenado (1,a)
Primera componente Segunda componente
1 ∈ A
a ∈ B
Matemático francés,
considerado como el padre
de la filosofía moderna.
La influencia de Descartes
en la Matemática es
también evidente; el
sistema de coordenadas
cartesianas fue nombrado
en honor a él. Se le
considera el padre de
la geometría analítica,
permitiendo que formas
geométricas se expresaran
a través de ecuaciones
algebraicas.
René Descartes
(1 596-1 650)
Nota histórica
El par ordenado se
escribe (a,b). En el
caso del par ordenado
cuya componentes sea
u número decimal se
escribirá: (a;b)
Por ejemplo:
(3,5;4)
(0,2;0,5)
Ma
tem
áti
ca
7
¿Sabías qué?

177. 169
El producto cartesiano no cumple con la propiedad conmutativa.
A × B ≠ B × A
Para el ejemplo anterior tenemos:
B × A = {(a,1);(b,1);(c,1);(a,2);(b,2);(c,2);(a,3);(b,3);(c,3) }
Par ordenado (a,1)
1 ∈ A
a ∈ B
(a,1) ≠ (1,a) ; (b,1) ≠ (1,b) ; (c,1) ≠ (1,c); etc.
££ Concepto de relación.
Una relación es un subconjunto de un producto cartesiano. Una
relación se denotará con el símbolo ℛ.
Ejemplos:
Considere los siguientes conjuntos:
A = { - 1,2,5,7} y B = {8,9}
El producto cartesiano A × B de estos conjuntos es:
A × B = {( - 1,8);( - 1,9);(2,8);(2,9);(5,8);(5,9);(7,8);(7,9) }
El conjunto P = {( - 1,8);( - 1,9);(2,8) }, es un subconjunto del conjunto
A × B = {( - 1,8);( - 1,9);(2,8);(2,9);(5,8);(5,9);(7,8);(7,9) }
El conjunto P = {( - 1,8);( - 1,9);(2,8) } ⊂ (A × B) es una relación.
El conjunto T = {(2,8); (5,8); (5,9); (7,8); (7,9) }, es un subconjunto
del conjunto
A × B = {( - 1,8); ( - 1,9); (2,8); (2,9); (5,8); (5,9); (7,8); (7,9) }
El conjunto T = {(2,8); (5,8); (5,9); (7,8); (7,9) } ⊂ (A × B) es una
relación.
Reforzamiento:
Sea A = {1,3,5,7} y 3{a,b,c}
Pruebe que AxB ≠ BxA
Fue la primera
matemática rusa de
importancia y la primera
mujer que consiguió
una plaza de profesora
universitaria en Europa
(Suecia, 1 881).
Sofia Vasílievna
Kovalévskaya.
(1 850-1 891)
Nota histórica

178. 170
££ Dominio y recorrido (o rango) de una relación.
El conjunto formado por los primeros elementos de los pares
ordenados, se llama dominio de la relación. Se denotará el
dominio con la letra D. También se le llama conjunto de las
preimágenes.
Ejemplo:
Dada la relación ℛ = {(2,4);(3,5);(4,6);(5,7) }, indicar cuál es el
dominio.
Solución
El conjunto formado por los primeros elementos de los pares
ordenados forman el dominio de la relación:
D = {2,3,4,5 }
El conjunto formado por los segundos elementos de los pares
ordenados, se llama recorrido de la relación. El recorrido se
denotará con la letra I. También se le llama conjunto de las
imágenes.
Ejemplo:
Dada la relación ℛ = {(2,4);(3,5);(4,6);(5,7) }, indicar cuál es el
recorrido.
Solución
El conjunto formado por los segundos elementos de los pares
ordenados forman el recorrido de la relación:
I = {4,5,6,7 }
Ejemplo:
Dada la relación ℛ = {(2,5);(3,5);(4,5);(5,5) }, indicar cuál es el
dominio y el recorrido.
Solución
El dominio es el conjunto:
D = {2;3;4;5}
El recorrido es el conjunto:
I = {5}
Matemático alemán que
desarrolló con Dedekind
y Frege la teoría de
conjuntos, que es la
base de la matemática
moderna. Gracias a sus
investigaciones sobre
los conjuntos infinitos
fue el primero capaz de
formalizar la noción de
infinito bajo la forma de
los números transfinitos
(cardinales y ordinales).
Georg Ferdinand
Ludwig Philipp Cantor
(1 845-1 918)
Nota histórica

179. 171
££ Formas de representación de una relación.
(I) Diagrama de Sagital de una relación .
Ejemplo:
Considere la relación ℛ = {(2,5);(3,4);(4,6);(5,7) }
Su dominio es el conjunto D = {2;3;5;4;5} y su recorrido es el
conjunto I = {5;4;7;6}.
Conjunto
de las
preimágenes
Conjunto
de las
imágenes
2
3
4
5
5
4
7
6
Dominio
(Preimágen)
Recorrido
(Contradominio)
Diagrama Sagital
Otra forma de escribir una relación ente dos elementos de un par
ordenado es, en forma simbólica aℛb, que se lee a está relacionado
con b.
(II) Representación como un conjunto de pares ordenados.
La relación puede ser representada por el conjunto de pares
ordenados.
ℛ = {(2,5);(3,4);(4,6);(5,7) }
(III) Representación por medio de una tabla.
x y
2 5
3 4
4 6
5 7
El recorrido de una
relación también
se conoce como
contradominio o imagen.
El dominio también
se conoce como
preimagen.
Ma
tem
áti
ca
7
¿Sabías qué?

180. 172
(IV) Representación por una tabla de doble entrada.
Representar la relación ℛ = {(2,5);(3,4);(5,6);(4,7) } mediante una
tabla de doble entrada.
2 3 5 4
5 (2,5)
4 (3,4)
6 (5,6)
7 (4,7)
En la primera fila se ubican los valores de la primera componente
x y en la primera columna se ubican los valores de la segunda
componente y.
Observe que en la primera fila, no se repite ninguna de las
componentes.
• Representación gráfica. La representación gráfica consiste
en la ubicación en un sistema de coordenadas cartesianas de
los pares ordenados de la relación
ℛ = {(2,5);(3,4);(5,6);(4,7) }
En el eje horizontal se ubican las primeras componentes de
cada par ordenado y en el eje vertical se ubican las segundas
componentes.
(5,6)
(3,4)
(2,5)
(4,7)
1 2 3 4 5 6
1
2
3
4
5
6
x
y
0
7
Los gráficos de
funciones y relaciones
se presentan en un
sistema de coordenadas
cartesianas, llamadas
así en honor de Renato
Descartes. El sistema
consiste en dos rectas
perpendiculares
llamados ejes de
coordenadas. El eje
horizontal se llama eje
de las abscisas o “eje x”
y el eje vertical se llama
eje de las ordenadas o
“eje y”.
x
y
Ma
tem
áti
ca
7
¿Sabías qué?

181. 173
Refuerza tus conocimientos.
Ejercicios resueltos.
1. Encontrar el producto cartesiano de los siguientes conjuntos:
A = {1,2} y B = {3,5,7,9}
Solución
A×B = {(1,3);(1,5);(1,7);(1,9);(2,3);(2,5);(2,7);(2,9) }
2. Dada la relación ℛ = {(1,3);(2,3);(2,4);(3,5);(3,7)}, ¿Cuál es
son su dominio y recorrido?. Representar la relación con un
diagrama de sagital, con una tabla y con una gráfica.
Solución
• Representación con un diagrama de sagital.
Conjunto
de las
preimágenes
Conjunto de
las
imágenes
Dominio Recorrido o rango
1
2
3
3
4
5
7
• Representación como un conjunto de pares ordenados.
La relación puede ser representada por el conjunto de pares
ordenados
ℛ = {(1,3);(2,3);(2,4);(3,5);(3,7)}
Observar que los pares ordenados (2,3);(2,4) tienen la misma
primera componente, lo mismo que los pares ordenados (3,5);(3,7).
En el siglo XVII Gottfried
Wilthem Leibniz, uno
de los inventores del
calculo, introdujo el
término funciones
en el vocabulario
matemático.
Ma
tem
áti
ca
7
¿Sabías qué?

182. 174
(V) Representación por una tabla de doble entrada.
Representar la relación ℛ = (1,3);(2,3);(2,4);(3,5);(3,7) mediante
una tabla de doble entrada.
1 2 3
3 (1,3) (2,3)
4 (2,4)
5 (3,5)
7 (3,7)
En la primera fila se ubican los valores de la primera componente
x y en la primera columna se ubican los valores de la segunda
componente y.
Observe que hay dos pares ordenados que tienen la misma
primera componente.
(VI) Representación por medio de una gráfica.
En el eje horizontal se ubican las primeras componentes de
cada par ordenado y en el eje vertical se ubican las segundas
componentes.
1 2 3 4 5 6
1
2
3
4
5
6
7
x
y
0
(3,7)
(3,5)
(2,3)(1,3)
(2,4)
Observar que los pares ordenados que tiene la misma primera
componente, se encuentra en la misma línea vertical.
Físico, matemático
y astrónomo inglés,
formuló la Ley de
Gravitación Universal y
las leyes fundamentales
de la Mecánica, clásica
más conocidas como
“Leyes de Newton”.
Newton comparte con
Leibniz el crédito por el
desarrollo del cálculo
integral y diferencial,
que utilizó para formular
sus leyes de la física.
Contribuyó en otras
áreas de la matemática,
desarrollando el
teorema del binomio
y las fórmulas de
Newton-Cotes. Se le
considera como uno
de los protagonistas
principales de la llamada
«Revolución científica»
del siglo XVII.
Isaac Newton
(1 642 – 1 727)
Nota histórica

183. 175
Concepto de función.
Lea, analice e interprete.
El estudio de las funciones no es solamente una preocupación
contemporánea. La idea de función aparece implícita en variadas
disciplinas a través del tiempo. Se presenta en fórmulas, ecuaciones
o en el planteamiento de problemas.
La idea de función esta ligada con las palabras de relación o
dependencia, que desde la antigüedad se han utilizado para
explicar algún descubrimiento logrado en forma empírica o práctica.
Definición de función.
Una función es una relación en la cual a cada elemento del
dominio le corresponde un único elemento del recorrido o imagen.
A continuación se presentan diferentes relaciones, identifique
cuáles representan una función y cuáles no.
Ejemplo:
El conjunto A está formado por los nombres de los departamentos
del norte de Nicaragua y el conjunto B está formado por sus
cabeceras departamentales.
Utilice diagramas sagital para representar la relación entre los
conjuntos A y B y conteste las siguientes preguntas:
• ¿La relación presentada es una función?
• ¿Cuáles son los pares ordenados que forman la relación?
Solución
Los conjuntos descritos son:
A = {Nueva Segovia,Madriz,Estelí,Matagalpa,Jinotega}
B = { Estelí,Jinotega,Ocotal,Somoto,Matagalpa}
Relación es la
correspondencia de un
primer conjunto llamado
dominio con un segundo
conjunto llamado
recorrido.
Ma
tem
áti
ca
7
¿Sabías qué?

184. 176
El diagrama sagital es el siguiente:
A B
Estelí
Jinotega
Ocotal
Matagalpa
Somoto
Nueva
Segovia
Madriz
Estelí
Matagalpa
Jinotega
A B
Estelí
Jinotega
Ocotal
Matagalpa
Somoto
Nueva
Segovia
Madriz
Estelí
Matagalpa
Jinotega
f
Como se puede observar en el diagrama, a cada departamento
le corresponde una única cabecera departamental. Entonces, la
relación es una función
Los pares ordenados para la función presentada son:
{(Nueva Segovia,Ocotal); (Madriz,Somoto); (Estelí,Estelí) ;
(Matagalpa,Matagalpa); (Jinotega,Jinotega)}
Ejemplo:
En el diagrama se presenta una relación entre dos conjuntos A y
B.
Solución
Se puede observar que al elemento
0, que pertenece al conjunto A, le
corresponden dos elementos: el 1 y
el 3 que pertenecen al conjunto B. Por
tanto, el diagrama no representa una
función.
Los pares ordenados en esta relación son:
Dos pares ordenados tienen la misma primera
componente
{(-2,1);(0,1);(0,3);(6,5)}
Hay dos pares ordenados que tienen el mismo primer elemento,
es otra forma de determinar que la relación dada no es una
función.
La contribución de
Leibniz a la matemática
consistió en enumerar
en 1 675 los principios
fundamentales del
cálculo infinitesimal.
Esta explicación
se produjo con
independencia de los
descubrimientos del
científico inglés Isaac
Newton, cuyo sistema
de cálculo fue inventado
en 1 666. El sistema de
Leibniz fue publicado
en 1 684, el de Newton
en 1 687, y el método
de notación ideado por
Leibniz fue adoptado
universalmente. En
1 672 también inventó
una máquina de calcular
capaz de multiplicar,
dividir y extraer raíces
cuadradas.
-2
0
6
1
3
5
A Bℛ
Gottfried Wilhelm Leibniz
(1 646 –1 716)
Nota histórica

185. 177
Ejemplo:
El conjunto A está formado por las edades de los miembros de una
familia y el conjunto “B” está formado por sus nombres: Alfredo
es el padre y tiene una edad de 55 años, Martha es la madre y
tiene una edad de 50 años. Los hijos son: Enrique que tiene una
edad de 27 años, Jorge tiene una edad de 27 años y Susana tiene
una edad de 29 años. Sabiendo que Enrique y Jorge son gemelos
y utilizando un diagrama sagital, exprese la relación entre los
conjuntos A y B y conteste las siguientes preguntas:
• ¿Es o no una función la relación entre los conjuntos A y B?
• ¿Cuáles son los pares ordenados que forman la relación?
Solución
Los conjuntos A y B son:
A = {Alfredo,Martha,Enrique,Jorge,Susana}
B = {55,50,27,29}
El diagrama sagital se presenta en la figura de la derecha:
En el diagrama se puede observar
que hay un elemento del conjunto A
(el 27) al cual le corresponden dos
elementos del conjunto B (Enrique
y Jorge). Enrique y Jorge tienen la
misma edad porque son gemelos. En
consecuencia, la relación no es una
función.
Los pares ordenados que forman esta
relación son:
{(55,Alfredo);( 50,Martha);( 27,Enrique);(27,Jorge);(29,Susana)}
Dos pares ordenados que
tienen la misma primera
componente.
55
50
27
29
Alfredo
Martha
Enrique
Susana
Jorge
A B
ℛ
Reforzamiento:
Elija 10 nombres de sus
compañeros de clase,
pregunte la edad de
cada uno y construya un
diagrama sagital para
esta situación.

186. 178
Ejemplo:
A cada ciudadano nicaraguense (conjunto A) le corresponde un
número de cédula de identidad (conjunto B).
• ¿Es o no una función la relación entre los conjuntos A y B?
Solución
El conjunto A está formado por los nombres de los ciudadanos y
el conjunto B está formado por sus números de cédula.
Puesto que una misma persona no puede tener dos números
de cédula diferentes, entonces en esta relación no existirán dos
pares ordenados que tengan igual la primera componente. Por
tanto, esta relación es una función.
En un diagrama sagital, esta función se puede representar así:
Función de A a B
A B
f : A → BNombres
de los
ciudadanos
nicaraguense
Números de
cédulas
de identidad
Ejemplo:
A cada estudiante de una universidad pública que se presenta
al exámen de admisión le corresponde una calificación en
matemática. Diga si es o no una función la relación entre los
conjuntos.
Solución
Puesto que un mismo estudiante no puede tener dos calificaciones
diferentes, entonces en esta relación no existirán dos pares
ordenados que tengan igual la primera componente. Por tanto,
esta relación es una función.
Dominio y recorrido de una función.
Dada una función entre los conjuntos A y B, el conjunto A se
llama dominio de la función y el conjunto B se llama recorrido de
la función. El dominio de una función se denotará con la letra D
y el recorrido con la letra I.
Johann Peter Gustav
Lejeune Dirichlet
(1805- 1 859) fué un
matemático alemán
que tras graduarse,
fue profesor en las
universidades de
Breslau (1 826-1 828),
Berlín (1 828-1 855)
y Gotinga, en donde
ocupó la cátedra dejada
por Gauss tras su
muerte. En el campo
del análisis matemático
perfeccionó la definición
y concepto de función, y
en mecánica teórica se
centró en el estudio del
equilibrio de sistemas
y en el concepto de
potencial newtoniano.
Ma
tem
áti
ca
7
¿Sabías qué?

187. 179
La función entre el conjunto A y el conjunto B se denotará de la
siguiente manera:
f : A ⟶ B Recorrido de la función
Dominio de la función
Función
Los elementos del conjunto A se llaman preimágenes y los del
conjunto B imágenes.
Ejemplos:
Los siguientes son dos ejemplos de funciones:
a. La función tiene como dominio al conjunto A, cuyos elementos
son los nombres de los países de Centro América y como
recorrido al conjunto B, cuyos elementos son los nombres de
las capitales de estos países.
• Describa con un diagrama sagital la función descrita.
• Escriba los pares ordenados que componen esta función.
Solución
En la figura de la derecha
se presenta el diagrama de
sagital.
En el diagrama se puede
observar que a cada elemento
del conjunto A (el dominio)
le corresponde un único
elemento de conjunto B (el
recorrido).
Los pares ordenados de la función son:
{(Guatemala,Guatemala); (El Salvador,San Salvador); (Honduras,Tegucigalpa);
(Nicaragua,Managua); (Costa Rica,San José)}
b. Alejandro recibe de su padre 20 córdobas cada día de lunes a
viernes. Exprese la situación presentada como una relación y
diga si es una función e indique también los pares ordenados.
Guatemala
El Salvador
Honduras
Nicaragua
Costa Rica
Guatemala
San Salvador
Tegucigalpa
Managua
San José
BA
f
Leonard Euler es
considerado el principal
matemático del siglo
XVIII y como uno de los
mas grandes de todos
los tiempos. Introdujo
gran parte de la moderna
terminología y notación
matemática.
Fué el que denotó la
función como se conoce
actualmente: f(x)
Ma
tem
áti
ca
7
¿Sabías qué?

188. 180
Matemático ruso.
Hizo importantes
contribuciones a la
teoría de conjuntos
y a la topología.
Aleksándrov estudió en
la Universidad Estatal
de Moscú, donde
tuvo como profesores
a Dmitri Egórov y
Nikolái Luzin. Junto
con Pável Urysohn,
visitó la Universidad
de Göttingen en 1 923
y 1 924. Tras obtener
su doctorado en 1 927,
siguió trabajando en la
Universidad Estatal de
Moscú. Trabajó en el
instituto de Matemática
“Stekov”. Fue nombrado
miembro de la Academia
Rusa de Ciencias en
1 953.
Pável Sergéyevich
Aleksándrov
(1 896 –1 982)
Solución
Sea X el conjunto cuyos elementos son los días de la semana y
Y el conjunto cuyos elementos son las cantidades de dinero que
recibe Alejandro cada día de lunes a viernes. Entonces, se tiene:
Cada día de Lunes a Viernes Alejandro recibe 20 Córdobas,
Los elementos del conjunto X son los días de las semana.
X = {Lunes,Martes,Miércoles,Jueves,Viernes}
El conjunto Y está formado por la cantidad de dinero que recibe
Alejandro cada día de la semana.
Y = {20}
El diagrama sagital se presenta en la
figura de la derecha.
Como se puede observar en el
diagrama, todos los elementos del
conjunto X tienen la misma imagen,
que es el único elemento del Y, el
número 20.
Los pares ordenados de esta relación son:
{(Lunes,20); (Martes,20);(Miércoles,20);(Jueves,20);(Viernes,20)}
No hay dos pares ordenados que tengan igual la primera
componente. Por tanto, la relación dada es una función.
Actividad:
Seleccione 8 compañeros de clases y pregúnteles cuántos
hermanos tienen, luego cono los datos obtenidos realice un
diagrama sagital.
Si una torta se hace con tres huevos,¿Cuántos huevos son
necesarios para hacer 2, 3, 5, 7 y 10 tortas? Complete la tabla
con valores que correspondan.
2 3 5 7 10 Tortas
Huevos
Lunes
Martes
Miercoles
Jueves
Viernes
20
X
Y
f
Nota histórica

189. 181
Funciones discretas.
Lea, analice e interprete.
En los ejemplos de funciones que se han analizado, tanto el dominio
como el recorrido son conjuntos finitos. También se han analizado
funciones en las cuales tanto el dominio como el recorrido son
conjuntos de números naturales o bien conjuntos de números
enteros.
Concepto de función discreta.
Una función se dice que es discreta si su dominio es un
subconjunto del conjunto de los números enteros.
Analizaremos funciones cuyo dominio y recorrido sean el conjunto
de los números naturales o bien el conjunto de los números enteros.
En símbolos se escribe:
Dominio
Números
naturales
Recorrido
Números
naturales
f : ℕ ⟶ ℕ
Números
Enteros
Recorrido
Números
Enteros
f : ℤ ⟶ ℤ
Dominio
Ejemplo:
A cada número entero desde -1 hasta 5 le corresponde el doble del
mismo número.
Solución
Sea X el conjunto de los números enteros desde -1 hasta 5.
X = {-1,0,1,2,3,4,5}
El conjunto Y está formado por los elementos del conjunto X
multiplicados por 2. Entonces.
Y = {-2,0,2,4,6,8,10}
Una función discreta
tiene como dominio
el conjunto de los
números enteros ℤ o un
subconjunto de este.
El gráfico de una función
discreta no es una
línea continua, sino que
está formada sólo por
los pares ordenados
ubicados en un sistema
de coordenadas.
Ma
tem
áti
ca
7
¿Sabías qué?

190. 182
El la figura de la derecha se presenta el diagrama sagital.
El dominio de esta relación es:
D = x = {-1,0,1,2,3,4,5}
El recorrido es:
I = y = {-2,0,2,4,6,8,10}
En el diagrama sagital de puede observar
que a cada elemento del dominio le
corresponde un único elemento del
recorrido. Entonces la relación dada es
una función. Los pares ordenados de esta
función son:
{(-1,-2);(0.0);(1,2);(2,4);(3,6);(4,8);(5,10)}
En una tabla, los pares ordenados se escriben
así:
Los elementos del dominio serán denotados
por la letra x (minúscula) y los elementos
del recorrido serán denotados por la letra y
(minúscula).
Los elementos de la columna de la izquierda
de la tabla, son los elementos del dominio de
la función y los elementos de la columna de la
derecha de la tabla, son los elementos del recorrido de la función.
El gráfico de esta función discreta esta formada por puntos
ubicados en un sistema de coordenadas cartesianas.
(0,0)
(1,2)
(2,4)
(3,6)
(4,8)
(5,10)
(-1,-2)
1 2 3 4 5 6 7 8 9 10
2
4
6
8
10
-1-2
-2
y
x
Los puntos de la gráfica anterior no pueden ser unidos
debido a que la función es discreta, y su gráfica está formada
exclusivamente por los puntos que se indican en la tabla.
-2
2
4
6
8
10
0
-1
1
2
3
4
5
0
X Y
f
El gráfico de una función
es el conjunto de todos
los puntos (x,y) donde x
pertenece al dominio de
la función y y pertenece
al recorrido de la
función.
x y
-1 -2
0 0
1 2
2 4
3 6
4 8
5 10
Ma
tem
áti
ca
7
¿Sabías qué?

191. 183
Concepto de variable independiente y de variable
dependiente.
Se han estudiado los conceptos de relación y función. Las
relaciones y funciones están descritas por su dominio, recorrido y
ley de asiganción.
Puesto que se está trabajando con cantidades variables, es
necesario distinguir las variables dependientes de las variables
independientes.
Ejemplo:
Se sabe que el precio de un lapicero es de 4 córdobas. Si se quiere
comprar una cantidad x de lapiceros, entonces el costo total de
la cantidad x de lapiceros será igual al precio de cada lapicero
multiplicado por x.
Entonces, se obtiene:
Costo de los lapiceros = (Precio de cada lapicero) (El número de lapiceros)
El costo de los x lapiceros, depende del precio de cada lapicero.
Entonces denotamos por y el costo de los lapiceros, y obtenemos
la siguiente igualdad:
y = 8x
donde y es la variable dependiente y x es la variable independiente.
En Matemática se conoce como variable independiente, a
los elementos del dominio de una función y como variable
dependiente a los elementos del recorrido de una función.
Notación: La notación funcional es la siguiente:
que se lee: “ye igual a efe de equis” o bien “ f de x”
Es importante recordar que la notación f (x) no significa f
multiplicado por x.
Euler definió la
constante matemática
conocida como número
e en su honor.
El número e puede ser
representado como un
número real en varias
formas y la de mayor
uso es:
e = 2,7182818284...
Ma
tem
áti
ca
7
¿Sabías qué?

192. 184
Funciones definidas por ecuaciones.
En la notación funcional que se ha presentado y = f (x), y es la
variable dependiente y x es la variable independiente.
La variable y depende de la variable x.
Ejemplo:
Usted necesita comprar una cierta cantidad de cuadernos para
el inicio del año escolar 2 015. Si cada cuaderno tiene un costo
de 25 Córdobas, entonces el costo total de los cuadernos será
igual al número de cuadernos multiplicado por el precio de cada
cuaderno. ¿Cómo se describe la situación presentada en lenguaje
simbólico?
Solución
Se denota por x el número de cuadernos a comprar y se denota
por y el costo de los cuadernos, entonces obtenemos la igualdad:
y = f (x) = 25x
Si usted va a comprar 6 cuadernos, entonces el costo será de:
y = f (x) =25(6) = 150 Córdobas
Esta es una función que tiene como dominio el número de
cuadernos que se desea comprar y como recorrido el costo de
los cuadernos. El costo y depende del número de cuadernos x.
Este es un ejemplo de una función discreta cuyo dominio es
un subconjunto de los números naturales y su recorrido es un
subconjunto de los números naturales. En símbolos:
f : �⟶�
Ejemplo:
En el diagrama de la figura se presenta una
relación entre dos conjuntos:
El conjunto A = {-2,-1,0,1,2} y el conjunto B
formado por los cuadrados de los elementos del
conjunto A;
B = {0,1,4}
Una ecuación es una
igualdad que contiene
variables.
Ejemplo:
La expresión algebraica
x + y = 3
es una ecuación.
-2
-1
0
1
2
0
1
4
A B
ℛ
Ma
tem
áti
ca
7
¿Sabías qué?

193. 185
Diga si la relación presentada es o no una función. Encuentre el
dominio, el recorrido y la gráfica.
Solución
El dominio de la relación es:
Dominio = {-2,-1,0,1,2}
El recorrido de la relación es: I = {0,1,4}
Los pares ordenados de la relación son:
ℛ = {(-2,4);(-1,1);(0,0);(1,1);(2,4)}
Como se puede observar, no hay dos pares ordenados que tengan
la misma primera componente. Por tanto, la relación presentada
es una función.
La ecuación que describe a esta relación es: y = x2
Donde:
x ∈ {-2,-1,0,1,2} y y ∈ {0,1,4}.
Este es otro ejemplo de una función discreta.
La gráfica de la función se presenta a continuación:
(2,4)
(1,1)
(0,0)
(-1,-1)
(-2,4)
-1
-2
-3
-4
-5
-1-2-3-4-5 1 2
1
2
3 4 5
3
4
5
Reforzamiento:
Se sabe que una libra
de papas cuesta 10
cordobas, entonces
la función para saber
el costo total por libra
comprada es f(x) = 10x.
¿Cuánto cuestan 2,3,4,5
y 6 libras de papas?
Realice un gráfico de
esta función.

194. 186
El criterio de la recta vertical para identificar
funciones.
Una forma sencilla de determinar si una relación es o no una
función es el criterio de la recta vertical.
¿En qué consiste este criterio?
Considérese el ejemplo siguiente:
Ejemplo:
Una relación está dada por el siguiente conjunto de pares
ordenados:
ℛ = {(1,2);(2,1);(3,3);(3,4);(4,6);(5,6)}
Esta relación no es una función debido a que hay dos pares
ordenados que tiene igual la primera componente.
La gráfica de esta relación es la siguiente:
1 2 3 4 5 6
1
2
3
4
5
6
(6,6)(4,6)
(3,4)
(3,3)
(1,2)
(2,1)
En la gráfica se puede observar que hay dos puntos que se
encuentran sobre la misma recta vertical. Estos dos puntos tienen
igual la primera componente.
Si en una gráfica existe una recta vertical que contiene más de
un punto de la gráfica, entonces la relación que representa esa
gráfica no es una función.
En la gráfica la recta vertical se presenta punteada.
Este es el criterio que se conoce como el criterio de la recta
vertical.
Si al trazar una línea
vertical, ésta contiene
más de un punto de la
gráfica de una relación,
entonces la relación no
es una función.
Ma
tem
áti
ca
7
¿Sabías qué?

195. 187
La función lineal
Iniciaremos el estudio de las funciones lineales con el siguiente
ejemplo.
Ejemplo:
Según datos del INIDE (Instituto Nacional de Información y
Desarrollo) el precio del litro de leche fluida, al mes de septiembre
del año 2014, es de 16 Córdobas. En la siguiente tabla se presentan
los precios para diferentes cantidades de litros de leche.
Litros de leche 1 2 3 4 5
Precio 16 32 48 64 80
Como pares ordenados, estos datos se escriben como sigue:
{(1,16);(2,32);(3,48);(4,64);(5,80)}
Observe que los datos de la fila de los precios aumentan en
forma directamente proporcional. Además observe que no hay
dos pares ordenados que tengan la misma primera componente
y que por tanto, los pares ordenados representan una función.
Al ubicar estos pares ordenados en un sistema de coordenadas,
obtenemos el gráfico siguiente:
Cantidad de Litros
1 2 3 4 5
16
32
48
64
80
0
(1,16)
(2,32)
(3,48)
(4,64)
(5,80)
Observe que los puntos de la gráfica están orientados según una
línea recta. Sin embargo, esta línea recta no se puede trazar porque
la gráfica contiene exclusivamente los puntos que se muestran.
Esta esla gráfica de una función discreta.
Los puntos de la gráfica
de una función lineal
discreta, están ubicados
según una línea recta.
Ma
tem
áti
ca
7
¿Sabías qué?

196. 188
¿Cómo se puede escribir en forma simbólica la función anterior?
Si llamamos
x: Cantidad de litros de leche
y: Precio de x litros, entonces se obtiene la ecuación:
y = f(x) = 16x
Donde x ∈ {1,2,3,4,5} y y ∈ {16,32,48,64,80}
Observe que si:
x = 1,entonces f(1) = 16(1) = 16
x = 2,entonces f(2) = 16(2) = 32
x =3,entonces f(3) = 16(3) = 48
x = 4,entonces f(4) = 16(4) = 64
x = 5,entonces f(5) = 16(5)=80
En el ejemplo precedente, se puede observar que existe una
proporcionalidad directa entre la cantidad de litros de leche a
comprar y el precio de cada litro. La constante de proporcionalidad,
en este caso es el precio de un litro de leche; es decir, 16 Córdobas.
Las magnitudes cantidad de litros de leche y precio de cada
litro son directamente proporcionales. Hemos denotado por x la
cantidad de litros de leche y y el precio en Córdobas.
Por tanto, la relación y = 16x, es la ecuación asociada a la
proporcionalidad descrita en el ejemplo precedente.
Una proporcionalidad directa cuya expresión algebraica tiene la
forma:
y = mx
donde “m” es la constante de proporcionalidad, se llama
función lineal de proporcionalidad directa.
Ejemplo:
Dada la función y = f(x) = x, con dominio D = {-2,-1,0,1,2}, encuentre:
1. El recorrido o imágen.
2. Los pares ordenados.
3. La gráfica.
En esta unidad se
estudian funciones
discretas, por tanto el
dominio de la función
lineal será el conjunto de
los números enteros ℤ”
o bien un subconjunto
de los números enteros
como lo es el conjunto
de los números
naturales ℕ.
Ma
tem
áti
ca
7
¿Sabías qué?

197. 189
Solución
Los valores que están en el recorrido son los siguientes:
f (-2) = -2
(-2;-2)
f (-1) = -1
(-1,-1)
f (0) = 0
(0,0)
f (1) = 1
(1,1)
f (2) = 2
(2,2)
Por tanto, el recorrido es el conjunto:
ℛ = {-2,-1,0,1,2}
Los pares ordenados son los siguientes:
(-2,-2), (-1,-1), (0,0), (1,1), (2,2)
La gráfica es la siguiente:
(1,1)
(2,2)
(-1,-1)
(-2,-2)
(0,0)
1 2 3-3 -2 -1
1
2
3
-1
-2
-3
y
x
Es importante recordar que los puntos no se pueden unir debido
a que la gráfica está formada exclusivamente por los puntos que
representan los pares ordenados de la función.
Importante
En noveno grado se es-
tudiará el conjunto de los
número reales y una vez
conocida la función lineal
será graficada a través
de una recta continua.
Por ejemplo:
y = f (x)
(1,1)
(-1,-1)
(0,0)
1 2 3-3 -2 -1
1
2
3
-1
-2
-3
y
x
x -1 0 1
y -1 0 1
El dominio es D = �
La imagen es I = �
Ma
tem
áti
ca
7
¿Sabías qué?

198. 190
Operaciones con funciones lineales.
• Suma de funciones lineales
Dadas las funciones lineales f (x) y g(x), se cumple:
(f + g)(x) = f (x) + g(x)
Ejemplo:
Sea f x g x x= =2
1
2
( )x( ) , entonces:
f g x f x g x x x+ = + = + = +





 =2
1
2
2
1
2
5
2
( )( )( )( ) x x
(f + g)(x) = f (x) + g(x) = 5
2
x
• Diferencia de funciones lineales
Dadas las funciones lineales f (x) y g(x), se cumple:
(f - g)(x) = f (x) - g(x)
Ejemplo:
Sea f (x) = 10x y g(x) = 5x, entonces:
(f - g)(x) = f (x) - g(x) = 10x - 5x = (10 - 5)x = 5x
(f - g)(x) = f (x) - g(x) = 5x
• Producto de funciones lineales.
Dadas las funciones lineales f (x) y g(x), se cumple:
(f ∙ g)(x) = f (x) ∙ g(x)
Ejemplo:
Sea f (x) = 5x y g(x) = 7x, entonces:
(f ∙ g)(x) = f (x) ∙ g(x) = (5x)(7x) = 35x
(f ∙ g)(x) = f (x) ∙ g(x) = 35x²
Matemático inglés al
que históricamente
se le ha dado menos
mérito en su papel en
el desarrollo del cálculo
moderno. Isaac Newton
fue discípulo de Barrow.
En 1 675 publicó una
nueva edición con
numerosos comentarios
de los primeros cuatro
libros sobre “Secciones
cónicas” de Apolonio
de Pérgamo, y de otros
trabajos de Arquímedes
y de Teodosio.
Isaac Barrow
(1 630 -1 677)
Nota histórica

199. 191
• Cociente de funciones lineales.
Dadas las funciones lineales f(x) y g(x), se cumple:
(g
f
)(x) =
f (x)
g(x)
; g(x) ≠ 0
Ejemplo:
Sea f (x) = 24x y g(x) = 12x, entonces:
(g
f
)(x)=
f (x)
g(x)
=
24x
12x
= 2(1) = 2 ⟹ (g
f
)(x) =
f (x)
g(x)
= 2
La función constante.
En un ejemplo anterior se planteó la siguiente situación:
Alejandro recibe de su padre 20 córdobas cada día de lunes a
viernes. Exprese la situación presentada como una relación. Diga
si es una función constante.
En el diagrama sagital para esta relación
es:
Como se puede observar en el diagrama,
todos los elementos del conjunto X
tienen la misma imagen, que es el único
elemento del Y , el número 20.
El dominio de esta relación es el conjunto:
D = {Lunes,Martes,Miércoles,Jueves,Viernes} y el recorrido de la
relación es el conjunto I = {20}.
Cuando todos los elementos del dominio tienen la misma imagen,
entonces la función es una función constante.
Los pares ordenados de esta función constante son:
{(Lunes,20); (Martes,20);(Miércoles,20);(Jueves,20);(Viernes,20)}
Lunes
Martes
Miercoles
Jueves
Viernes
20
X
Y
f
Reforzamiento:
Sea f(x) = 3x y g(x) = 1
8
x
Calcular:
f(x) + g(x)
f(x) - g(x)
f(x) g(x)
f (x)
g(x)

200. 192
La gráfica de la función constante se presenta a continuación.
(Lunes;20) (Martes;20) (Miercoles;20) (Jueves;20) (Viernes;20)
30
20
10
Cantidad
de dinero
Días de
la semana
Lunes Martes Miercoles Jueves Viernes
0
Observe que todos los puntos deberian estar ubicados en una
línea recta. Esta línea recta no puede ser trazada porque la
función es discreta y la gráfica la componen exclusivamente los
puntos que representan los pares ordenados
Simbólicamente, la función constante del ejemplo, se expresa
con la ecuación:
y = f (x) = 20
Donde, 20 (variable dependiente) es la cantidad de dinero que
Alejandro recibe cada día y x (variable independiente) representa
a los días de la semana.
¿Qué ocurre si todos los pares ordenados tiene igual la primera
componente?
En este caso, todos los puntos de la gráfica estarán ubicados
según una línea recta vertical y la relación no es una función. La
expresión algebraica que representa a una relación de este tipo
es:
x = k, donde k es una constante.
Conclusión:
Una función f es constante si se presenta de la forma f (x) = k,
siendo k un número real y cuya representación será una línea de
puntos paralelos al eje x.
Refuerce tus conociemientos.
Ejercicios:
1. Sean las funciones reales f(x) = x + 5 y g(x) = x2
+ 3x -10 .
Hallar: a. (f + g) (x) b. (f - g) (x)
Reforzamiento:
Gráfique las siguientes
funciones:
• y = 2
• f (x) = 3
• y = -4
• f (x) =
1
2
• y = 0,8

201. 193
Solución
a. (x) = (x + 5) + (x2
+ 3x - 10) = x2
+4x – 5
b. (x) = (x + 5) - (x2
+ 3x -10) = -x2
-2x + 15
2. Sean las funciones f(x) = 3 x + 1, y g(x) = 2x – 4
Definir la función f + g y calcular las imágenes de los números 2,
-3 y
1
5
.
Solución
La función f + g se define como
(f + g)(x) = f (x) + g(x) = 3x + 1 + 2 x - 4 = 5 x - 3.
(f + g)(2) = 5(2) - 3 = 7
(f + g)(-3) = 5(-3) - 3 = -18
( f + g)
Obsérvese que si se calculan las imágenes de f y g por separado
y se suman, el resultado es el mismo.
Por ejemplo, para la imagen del 2,
f (2) = 3(2) + 1 = 7
|(f + g)(2) = 7 + 0 = 7
g(2) = 2(2) - 4 = 0
3. Dadas las funciones f (x) = x2
- 3, y g (x) = x + 3, definir la función
(f - g)(x).
Calcular las imágenes de
1
3
, -2 y 0 mediante la función (f - g)(x).
Solución
(f - g)(x) = f (x) - g(x) = x2
- 3 - (x + 3) = x2
- 3 - x - 3 = x2
- x - 6
(f - g)(
1
3
) = (
1
3
)2
-
1
3
- 6 = -
56
9
(f - g)(-2) = (-2)2
- (-2) - 6 = 4+4-6 = -2
(f - g)(0) = (0)2
- 0 - 6 = - 6

202. 194
Calculando las imágenes de los números mediante las funciones
f y g por separado y efectuando la resta se obtiene el mismo
resultado.
4. Dadas las funciones f (x) =
2
x
- 3 y g (x) = 2x + 1, definir la función
(f . g)(x).
Solución
(f . g)(x) = f(x) . g(x) =
2
x
- 3 . (2x + 1) = x2
-
2
11x - 3
Calculando las imágenes de los números mediante las funciones f
y g por separado y multiplicando despues se obtienen los mismos
resultado.
5. Dadas las funciones f (x) = -x - 1 y g(x) = 2x + 3, definir (g
f
)(x)
y (f
g
)(x)
Calcular las imágenes de los números -1, 2 y mediante g
f
Solución
f
g
x
f x
g x
x
x
x
x





 =






=
+( )
=
− +
+
1 1
2 3( )
( ) ( )− −
2 3
( )
( )
La función (g
f
)(x) está definida para todos los números reales,
salvo para x = -
2
3 , donde la función g se anula.
•
f
g





 −( )= =1
0
1
0
•
f
g





( )= −2
3
7
•
f
g











 =
−






= −
3
2
5
2
6
5
12
•
f
g
x
g x
f x
x
x
x
x x





 =
( )





=
+( )
− −( )
=
+
− +( )1 1
( )
( )
2 3 2 3
La función (f
g
)(x) está definida para los números reales, salvo
para x = -1, donde la función f se anula.
Calculando por separado las imágenes de los números mediante
las funciones f y g y después efectuando su cociente, se obtienen
los mismos resultados.

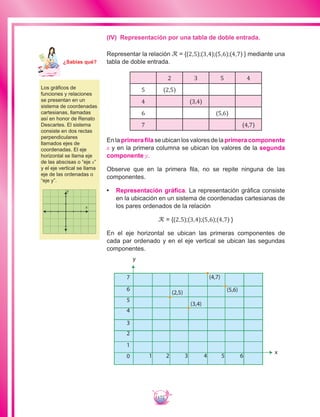
203. 195
6. Dada la función f (x) = x2
+ x - 2, calcular: 3f (x) y
1
3





 ( )f x .
Obtener las imágenes de los números 2, 1 y 0 mediante la
función 3f (x)
Solución
• 3f(x) = 3(x2
+ x - 2) = 3x2
+ 3x - 6
•
1
3
1
3
22




 ( )=





 + −( )f x x x
• 3f(2) = 3(2)2
+ 3(2) - 6 = 12
• 3f(1) = 3(1)2
+ 3(1) - 6 = 0
• 3f(0) = 3(0)2
+ 3(0) - 6 = - 6
COMPOSICION DE FUNCIONES
Dadas dos funciones reales de variable real, g y f, se llama
composición de las funciones g y f y se escribe g o f, a la función
definida de � en �, por (g o f )(x) = g[ f (x)]
La función (g o f )(x) se lee g compuesto con f aplicado a x.
Cálculo de la imagen de un elemento mediante una función
compuesta
Para obtener la imagen de la función compuesta (g o f )(x) aplicada
a un número x, se siguen estos pasos:
a. Se calcula la imagen de x mediante la función f (x).
b. Se calcula la imagen mediante la función g de f (x). Es decir, se
aplica la función g al resultado obtenido anteriormente.
Ejercicios
1. Sean las funciones f (x) = x + 3 y g(x) = x2
.
Calcular (g o f )(x) y la imagen mediante esta función de 1, 0 y -3.
Solución
(g o f )(x) = g . [f (x)] = (x + 3)2
= + +
1
3
1
3
2
3
2
x x

204. 196
Sobre el signo de
igualdad
Médico y matemático
galés que utilizó por
primera vez el signo
igual (=) en el año
1557. Se dedicó a la
enseñanza pública
de las matemáticas,
trabajo que ya había
hecho con anterioridad.
Robert Recorde
(1 510 - 1 558)
La imagen de los números 1, 0, -3, mediante la función (g o f )(x)
es:
• (g o f )(1) = g[f (1)] = (1 + 3)2
= 42
= 16
• (g o f )(0) = g[f (0)] = (0 + 3)2
= 32
= 9
• (g o f )(-3) = g[f (-3)] = (-3 + 3)2
= 02
= 0
2. Dadas las funciones f (x) = x2
+ 1, y g(x) = 3x - 2, calcular:
a. (g o f )(x)
b. (f o g)(x)
c. (g o f )(1) y (f o g)(-1)
Solución
a. La función (g o f )(x) está definida por:
g[f (x)] = g(x2
+ 1) = 3 . (x2
+ 1) - 2 = 3x2
+ 3 - 2 = 3x2
+ 1
b. La función (g o f )(x) está definida por:
f [g(x)] = (3x - 2)2
+ 1 = 9x2
+ 4 - 12x + 1 = 9x2
- 12x + 5
Obsérvese que (g o f )(x) ≠ (f o g )(x).
c. Aplicando los resultados de los apartados anteriores:
(g o f )(1) = 3(1)2
+ 1 = 3 + 1 = 4
(f o g)(-1) = 9(-1)2
- 12(-1) + 5 = 9 + 12 + 5 = 26
3. Resuelva:
Si f (x) = 2x - 5 y g(x) = 2x2
Calcule:
££ (g o f )(x)
££ (f o g )(x)
££ (f o g )(-3)
Nota histórica

205. 197
Ecuaciones lineales en una variable
El concepto de igualdad.
Una igualdad es una expresión que relaciona dos cantidades
mediante el signo “igual”. Si las cantidades relacionadas son
números, entonces se dice que la igualdad es una igualdad
numérica.
Ejemplo:
La igualdades 2 + 2 = 4, 25 = 5, 33
= 27 , son ejemplos de
igualdades numéricas.
Silascantidadesrelacionadassonvariables,entonceslaigualdades
se llaman igualdades algebraicas. Si una igualdad algebraica se
cumple para todos los valores de la o las variables que aparecen
en ella, entonces se llama identidad.
Ejemplo:
Son ejemplos de identidades las siguientes:
x2
- y2
= (x + y)(x - y), (x - y)2
= x2
- 2xy + y2
Actividad:
Verifique las identidades del ejemplo para x = 1 e y = -2.
Si una igualdad algebraica se cumple sólo para algunos valores de
la o las variables, entonces se llama ecuación.
Ejemplo:
Son ejemplos de ecuaciones las siguientes expresiones
algebraicas:
2x - 1 = 4x - 3 , -4x - 2 = 6x + 8
En el caso de la primera ecuación, se verifica para x = 1.
En efecto:
Si x = 1, entonces 2x - 1 = 4x - 3 ⟺ 2(1) - 1 = 4(1) - 3
2(1) - 1 = 4(1) - 3 ⇔ 2 - 1 = 4 - 3 ⇔ 1 = 1
La relación de igualdad
cumple con las siguientes
propiedades:
Propiedad de reflexividad.
a = a; ∀a
Propiedad de simetría.
a = b ⟹ b = a; ∀a,b
Propiedad de transitividad.
a = b y b = c⟹ a = c; ∀a,b,c
Cuando una relación
cumple con las tres
propiedades, se llama
relación de equivalencia.
Ma
tem
áti
ca
7
¿Sabías qué?

206. 198
Ejemplo:
Verifique que la igualdad -4x - 2 = 6x + 8, se cumple para x = -1.
En una ecuación, la variable o variables son cantidades
desconocidas que se llaman incógnitas.
Las expresiones que se encuentran en los lados de una ecuación
se llaman miembros de la ecuación. Al miembro que está a la
izquierda del signo de igualdad, se acostumbra llamarlo “primer
miembro” y al que está a la derecha del signo de igualdad
“segundo miembro”.
Los sumandos de cada uno de los miembros de una ecuación se
llaman términos de la ecuación.
Ejemplo:
En la ecuación 3x - 6 = 4x - 1
• La incógnita es la variable x.
• Los términos son: 3x, -6, 4x y -1. Los términos -1 y -6 se
llaman términos independientes.
• El primer miembro es: 3x - 6.
• El segundo miembro es: 4x - 1
3x - 6 = 4x - 1
Primer
miembro
Segundo
miembro
Término Término
Ejemplo:
En la ecuación 2y + 8 = 8y - 5 ,la incógnita es la variable y, los
términos son 2y + 8 y 8y - 5, los términos 8 y -5 son términos
independientes , el primer miembro es 2y+8y el segundo miembro
es 8y - 5.
Reforzamiento:
Encuentre el valor de x
en cada ecuación:
a. 3x - 2 = 8 - 4x
b. 2x + 3 = 3x -5
c. 5 - 4x = x - 8

207. 199
Grado de una ecuación lineal con una variable
El grado de una ecuación con una variable es el grado mayor de
la variable. En el caso de una ecuación lineal con una variable,
el grado de la variable es uno 1, y la ecuación recibe el nombre
de ecuación lineal de primer grado con una variable.
Ejemplo:
El siguiente, es un ejemplo de una ecuación lineal de primer grado
con una variable:
4x1
- 1 = 5 ⟹ 4x - 1 = 5
Una variable
Exponente 1
Propiedades de las ecuaciones lineales con una
variable.
1. Si se suma el mismo número a los dos miembros de una
ecuación, ésta no se altera.
Ejemplo:
Sumar 3 a los dos miembros de la ecuación
2x - 6 = 7x - 2.
Solución
Sumando 3 a los dos
miembros de la ecuación.
2x - 6 + 3 = 7x - 2 + 3
2x - 3 = 7x + 1
Ecuación equivalente a la ecuación
original 2x - 6 = 7x - 2
Lo que hoy conocemos
como ecuaciones
lineales, aparecían
en el papiro Rhind,
escrito por el sacerdote
egipcio Ahmes (2 000
años a. de C.), quien
representa la incógnita
con un ibis (ave tropical)
escarbando en el suelo.
Ma
tem
áti
ca
7
¿Sabías qué?

208. 200
2. Si se resta un mismo número a los dos miembros de una
ecuación, ésta no se altera.
Ejemplo:
Restar -2 a los dos miembros de la ecuación 5x - 7= 9x - 4.
Solución
Restando -2 a los dos
miembros de la ecuación
5x - 7 - 2 = 9x - 4 - 2
5x - 9 = 9x - 6
Ecuación equivalente a la ecuación
original 5x - 7 = 9x - 4
3. Si se multiplican por un mismo número los dos miembros de
una ecuación, ésta no se altera.
Ejemplo:
Multiplicar por -2 los dos miembros de la ecuación
-2x + 8 = -4x - 7.
Solución
Multiplicando por -2 los dos
miembros de la ecuación.
-2(-2x + 8) = -2(-4x - 7)
4x - 16 = 8x + 14
Ecuación equivalente a la
ecuación original -2x + 8 = -4x - 7.
4. Si se dividen entre un mismo número diferente de cero los dos
miembros de una ecuación, ésta no se altera.
Ejemplo:
Dividir entre -4 los dos miembros de la ecuación 4x + 16 = -8x - 4.
El uso de las letras x,
y, z para representar
incógnitas y las primeras
del abecedario para
valores conocidos, aparece
en el libro La Geometrie
de Descartes. Se cuenta
que cuando el libro se
estaba imprimiendo y
debido a la gran cantidad
de ecuaciones que tenía,
se quedaban sin letras,
el editor le preguntó
a Descartes si podía
emplear otras letras para
las ecuaciones. Descartes
le respondió que era
indiferente las letras que
utilizase en las ecuaciones.
El editor eligió la x porque
en francés esa letra se
utiliza poco.
Otros autores afirman
que la x se usó como
abreviatura de la palabra
árabe shei (cosa).
Ma
tem
áti
ca
7
¿Sabías qué?

209. 201
Solución
4 16
4
8 4
4
x x+
−
=
− −
−
4 16
4
8 4
4
4
4
16
4
8
4
4
4
4 2 1
x x x x
x x
+
−
=
− −
−
⇒
−
+
−
=
−
−
−
−
⇒ − − = +
Dividiendo entre -4 los dos miembros de la ecuación.
Ecuación equivalente a la ecuación original 4x + 16 = -8x -4
-x - 4 = 2x + 1
• Solución o raíz de una ecuación lineal con una variable.
Se llama solución o raíz de una ecuación al valor que la satisface
o la verifica
Ejemplo:
La ecuación lineal de primer grado con una variable x - 7 = 5, tiene
como solución el valor x = 12.
En efecto: Si x = 12, entonces:
x - 7 = 5 ⇒ 12 - 7 = 5 ⇒ 5 = 5
También se dice que 12 es raíz de la ecuación dada.
££ Ecuaciones de la forma x ± a = b.
Para resolver ecuaciones de la forma x ± a = b se suma o se resta
(según el caso) a los dos miembros de la ecuación el término
independiente a.
Simbólicamente se escribe:
x + a = b ⟹ x + a + (-a) = b + (-a) ⟹ x + 0 = b - a
Por tanto, x = b - a
x - a = b ⟹ x - a + a = b + a ⟹ x + 0 = b + a
Por tanto, x = b + a. La operación realizada se llama transposición
de términos.

210. 202
Para pasar un término de una ecuación de un miembro a otro, se
cambia el signo del término.
Ejemplo:
Encuentre la solución de la ecuación x + 5 = 8.
Solución
Restando 5 a los dos miembros de la ecuación,
x + 5 - 5 = 8 - 5 ⇒ x + 0 =3 ⇒ x = 3; la solución es x = 3
Ejemplo:
Encuentre la solución de la ecuación x − = −
5
7
3
4
Solución
Sumando
5
7
a los dos miembros de la ecuación, se obtiene:
x x x− + = − + ⇒ + = − ⇒ =
− +5
7
5
7
3
4
5
7
0 5
21 20
28
la solución es x = −
1
28
Ecuaciones de la forma ax = b(a ≠ 0).
Para resolver ecuaciones de la forma ax = b (a ≠ 0)se dividen los
dos miembros de la ecuación entre a. Simbólicamente se escribe:
ax b
ax
a
b
a
x
b
a
a= ⇒ = ≠; 0= ⇒
Por tanto, x
b
a
a= ≠; 0.
Para despejar la incógnita en la ecuación ax = b (a ≠ 0), basta
con pasar a dividir el coeficiente a al otro miembro de la
ecuación.
Ejemplo:
Encuentre la solución de las ecuación 3x = -7.
Solución
Se dividen los dos miembros de la ecuación entre 3
3 7
3
3
7
3
7
3
x
x
x= −
−
−⇒ =⇒ =
La solución es: x = −
7
3
Diofanto de Alejandría
Nacido alrededor del
(200 - 214) y fallecido
alrededor de (284 -
298), fue un antiguo
matemático griego. Es
considerado el padre
del álgebra.
Nota histórica

211. 203
Ejemplo:
Encuentre la solución de las ecuación
2
3
1
2
x = .
Solución
Se dividen los dos miembros de la ecuación entre
2
3
.
2
3
1
2
2
3
2
3
1
2
2
3
3
4
x
x
x= ⇒ = ⇒ =
La solución es: x =
3
4
.
Ecuaciones de la forma ax ± b = cx + d; (a ≠ 0).
Para encontrar la solución de una ecuación de la forma:
ax ± b = cx + d; (a ≠ 0)
se realizan los pasos siguientes:
Paso 1. Se efectúa la transposición de términos dejando en un
sólo miembro los términos que contienen a la incógnita.
Paso 2. Se reducen términos semejantes en los dos miembros de
la ecuación.
Paso 3. Se divide cada miembro de la ecuación, entre el coeficiente
de la incógnita. Este último paso consiste en el despeje de la
incógnita.
Ejemplo:
Encuentre la solución de la ecuación
5x - 6 = 2x - 1
Solución
Paso 1. Se efectúa la transposición de términos.
5x - 6 = 2x - 1 ⇒ 5x - 2x = -1 + 6
Paso 2. Se reducen términos semejantes en los dos miembros de
la ecuación.
5x - 2x = -1 + 6 ⇒ 3x = 5
Paso 3. Se divide cada miembro de la ecuación, entre el coeficiente
de la variable.
3 5
3
3
5
3
5
3
x
x
x= ⇒ == ⇒
La solución es: x =
5
3
Reforzamiento:
Resuelva las siguientes
ecuaciones lineales:
• 3x + 7 = 2x - 3
• 4x + 8 = 8
• 5x = 3
• 6 + 9x = -10x
•
11
5
8
3
5
6
x
x− = +
• 3 11
1
2
3
7
x x+ = +

212. 204
Ecuaciones lineales con una incógnita y
coeficientes fraccionarios.
Para resolver una ecuación con coeficientes fraccionarios, se
realizan los pasos siguientes:
Paso 1. Se encuentra el mínimo común múltiplo de los
denominadores.
Paso 2. Se multiplica el mínimo común múltiplo por cada uno de
los miembros de la ecuación.
Paso 3. Se efectúan los productos indicados, se reducen términos
semejantes y se despeja la incógnita.
Ejemplo:
Encuentre la solución de la ecuación
x x x x
2
2
3
5
4
7
6
1
12
− + = +
Solución
Paso 1. El mínimo común múltiplo de los denominadores es 12.
Paso2. Se multiplican los dos miembros de la ecuación por 12.
12
2
2
3
5
4
12
7
6
1
12
( ) − +





 = ( ) +






x x x x
Paso 3. Se efectúan los productos indicados, se reducen términos
semejantes y se despeja la incógnita.
12
2
24
3
60
4
84
6
12
12
6 8 15 14 1
x
x x x x
− +
= +− +
= +
x x x
6x - 8x + 15x - 14x = 1 ⇒ 21x - 22x = 1⇒ - x = 1
La solución de la ecuación es: x = -1.
Las ecuaciones lineales
se utilizan para resolver
problemas de la vida
cotidiana, por ejemplo,
un articulo escolar se
vende en 24 cordobas.
Si la ganancia es del
50% con relación al
precio, de mayoreo,
¿Cuál es el precio de
mayoreo?
x = precio de mayoreo.
Establecemos:
Precio de venta - precio
de mayoreo = ganancia.
24 - x = 50% x
24 - x = 0,5 x
-x - 0,5 x = -24
-1,5 x = -24
x = −
−
24
1 5,
x = 16
El precio de mayoreo
del artículo es de 16
córdobas.
Ma
tem
áti
ca
7
¿Sabías qué?

213. 205
Como sabemos una ecuación es una igualdad que contiene
cantidades conocidas llamadas coeficientes y cantidades
desconocidas llamadas variables o incógnitas (se designan por
cualquier letra del alfabeto, y en particular por: x,y,z). En el caso de
las ecuaciones con una variable, se catalogan según el exponente
más alto de la variable.
Ejemplo:
Ecuación lineal 2x + 4 = 10, ecuación cuadrática 2x2
+ x + 5 = 9, ecuación
cúbica 3x3
+ 5x2
– 2x + 1 = 8.
Ecuación lineal con una variable
Sean a,b,c constantes reales con a ≠ 0. Se llama ecuación lineal
o de primer grado con una variable a toda ecuación de la forma
ax + b = c
Ejemplos:
a. 3x + 2 = 0
b.
3
5
(x - 2) = 0
Si dos ecuaciones lineales con una variable tienen el mismo
conjunto solución, decimos que son equivalentes entre sí.
Ejemplo:
2y + 3 = 13 y 4y + 6 = 26 son equivalentes, tienen el mismo conjunto
solución S = {5}
Para resolver ecuaciones lineales usaremos el concepto de
ecuaciones equivalentes. Para esto transformaremos la ecuación
original en otras equivalentes a ella, hasta obtener una ecuación
de la forma x = c, donde x es una incógnita y c es una constante
real.
Las siguientes son algunas transformaciones que se pueden
usar para obtener ecuaciones equivalentes entre sí:
1. Permutar miembros de la ecuación ax + b = c
Es equivalente con c = ax + b
2. Sumar el mismo número a ambos miembros de la igualdad
ax + b = c
Es equivalente a ax + b + d = c + d
Reforzamiento:
Se entregan x cerdos en
bonos productivos que
impulsa el gobierno de
Reconciliación y Unidad
Nacional. El costo total
de los cerdos es de
52 000 cordobas y cada
uno de los cerdos costo
800 cordobas. Plantee
una ecuación y calcule
el número de cerdos
comprados

214. 206
3. Multiplicar ambos miembros de la igualdad por un mismo
número diferente de cero.
ax + b = c
Es equivalente a d(ax + b)= dc con d ≠ 0
Procedimiento general para resolver ecuaciones
lineales con una variable.
Elimine todas las fracciones multiplicando cada lado por el mínimo
común denominador.
a. Quitar paréntesis.
b. Simplifique los términos semejantes, usando la propiedad
aditiva de la igualdad para lograr que la ecuación tenga la
forma: ax = b
c. Despeje la variable mediante la propiedad multiplicativa de la
igualdad
d. Verifique el resultado con la ecuación original
Ejemplos:
a. 2x + 3 = 5
Simplificamos los términos semejantes usando la propiedad
aditiva
2x + 3 - 3 = 5 - 3 ⟹ 2x = 2
de donde resulta
x = 1
Comprobación
2(1) + 3 = 5 ⟹ 5 = 5
El conjunto solución es S = {1}
b. 12 = -2(2x - 6)
Primero quitamos paréntesis multiplicando por -
1
2
12(-
1
2
) = -2
1
2
(2x - 6) ⟹ -6 = 2x - 6
Mediante la propiedad aditiva.
-6 + 6 = 2x - 6 + 6 ⟹ 0 = 2x

215. 207
Usando propiedad multiplicativa.
0(
1
2
) = 2x(
1
2
) ⟹ 0 = x
Por la propiedad reflexiva.
x = 0
Comprobación
12 = -2[2(0) - 6] ⟹ 12 = 12
El conjunto solución es: S = {0}
Resolución de problemas modelados por ax + b = c.
La ciencia matemáticaz, así como el ejercicio de su enseñanza
siempre han tenido, como principal medio y fin, la resolución
de problemas matemáticos. Paul Richard Halmos expresó su
convencimiento de que los problemas son el corazón de la
Matemática. Desde esta perspectiva, en vista de que el contenido
determina el método, esto nos conduce a afirmar que los problemas
también son el corazón de la Didáctica de la Matemática. Al
respecto, otros matemáticos han aseverado que una clase de
matemática debe estar siempre centrada en resolver problemas,
y el papel del profesor debe ser el de ‘buscador’ de situaciones
reflexivas y significativas para el estudiante. Este hecho, por su
parte, supone la concepción del maestro como un profesional de
la educación innovador y creativo.
La resolución de problemas es considerada en la actualidad la
parte más esencial de la educación matemática ya que permite
combinar elementos de conocimiento, reglas, técnicas destrezas
y conceptos previamente adquiridos para dar una solución a una
situación nueva. Es una actitud cognitiva compleja que caracteriza
una de las actividades humanas más inteligentes.
Es a partir de la publicación de George Polya en 1 945 de su obra
How to solve it que se ilustra por primera vez un camino didáctico
hacia la enseñanza de la resolución de problemas. Redescubre
y desarrolla la heurística, y precisa una serie de estrategias que
deben constituir una herramienta fundamental en la enseñanza de
la resolución de problemas. Con su propuesta de las cuatro etapas
abrió el camino de una didáctica de la resolución de problemas:
(comprensión del problema, concebir el plan de solución, ejecutar
el plan de solución y evaluar la solución).
Fue un destacado matemá-
tico estadounidense, naci-
do en Budapest (Hungría).
Halmos se destacó tanto
por sus contribuciones
teóricas, en ramas como
en teoría de las probabili-
dades, estadística, teoría
de operadores, teoría er-
gódica y análisis funcional,
(especialmente sobre los
Espacios de Hilbert); así
como por haber redactado
una serie de libros de texto
excepcionalmente bien
escritos.
Paul Richard Halmos
(1 916 - 2 006)
Nota histórica

216. 208
Algunas ideas para resolver problemas aplicados
1. Si el problema se expresa por escrito, léalo con cuidado varias
veces y considere los datos junto con la cantidad desconocida
que ha de encontrarse.
2. Introduzcavariablesparadenotarlascantidadesdesconocidas.
Este es uno de los pasos más importantes en la solución.
3. Si es necesario haga un dibujo para darse una idea.
4. Liste los datos conocidos y sus relaciones con la cantidad
desconocida.
5. Formule una ecuación que describa con precisión lo que se
expresa en palabras.
6. Resuelva la ecuación formulada.
7. Compruebe las soluciones obtenidas consultando el enunciado
original del problema.
Ejemplos:
a. Un docente muy ingenioso, actuando de mago propone a sus
estudiantes lo siguiente:
Piensen un número, auméntenlo en 15, multipliquen por 3 el
resultado obtenido y a esta cifra réstenle 9, luego dividan entre 3
y resten 8. ¿Díganme el resultado final?, y yo les daré el número
que pensaron. Una estudiante le dice 32, y el docente le responde
instantáneamente; el número que pensaste fue 28. ¿Cómo
consigue el docente adivinar de prisa?
Comprobación
Sea x: el número que piensa la estudiante:
1. Aumentado en 15, x + 15
2. Se multiplica por 3, el resultado obtenido 3(x + 15)
3. A esta cantidad se le resta 9, 3(x + 15)-9
4. Luego se divide por 3
3 15 9
3
x +( )−
5. Y a la expresión anterior se le resta 8
3 15 9
3
8
x +( )−
−

217. 209
La expresión anterior simboliza el procedimiento planteado por el
docente, ahora vamos a realizar algunas operaciones indicadas
para simplificar dicha expresión.
3 15 9
3
8
3 15 3
3
8 15 3 8
x x
x
+ −
− ⇒
+ −  − ⇒ + − −
( ) ( )
( )
(x + 15) - 3 - 8 = x + 15 - 11 = x + 4
Interpretación
La expresión x + 4 representa el número pensado por la estudiante,
más cuatro. Por tanto el docente “adivina” el número pensado,
restando 4 a (x + 4), en otras palabras x + 4 - 4 = x.
b. Sobre la vida de Diofante (250 d. de C.) aparece en los siglos V
o VI un epigrama algebraico que constituye una ecuación lineal
y dice: “Transeúnte, ésta es la tumba de Diofante: es él quien
con esta sorprendente distribución te dice el número de años
que vivió. Su juventud ocupó su sexta parte, después durante la
doceava parte su mejilla se cubrió con el primer vello. Pasó aún
una séptima parte de su vida antes de tomar esposa y, cinco años
después, tuvo un precioso niño que, una vez alcanzada la mitad
de la edad de su padre, pereció de una muerte desgraciada. Su
padre tuvo que sobrevivirle, llorándole durante cuatro años. De
todo esto, deduce su edad.
Comprobación
Sea x: la edad que vivió Diofante.
Su juventud ocupo una sexta parte de su vida.
x
6
Después, durante la doceava parte su mejilla se cubrió de vello.
x x
6 12
+






Pasó una séptima parte de su vida antes de tomar esposa.
x x x
6 12 7
+





 +

218. 210
Cinco años después, tuvo un precioso niño.
x x x
6 12 7
5+





 + +
Una vez alcanzada la mitad de la edad de su padre, pereció de
una muerte desgraciada.
x x x x
6 12 7
5
2
+





 + +





 +
Su padre tuvo que sobrevivirle, llorándole durante cuatro años.
x x x x
6 12 7
5
2
4+





 + +





 + +
De todo esto, deduce su edad.
La expresión anterior representa en suma la vida de Diofante,
luego:
x x x x
x
6 12 7
5
2
4+





 + +





 + + =
x x x x x x x x
x
6 12 7 2
9
1
1 2 42 756
84
+ + + +
+ +
== ⇒x
4 7 1 + +
75 756
84
75 756 84 84 75 756
x
x x
+
⇒ − == ⇒x x + = x
9 756
756
9
84= =x x
Interpretación:
Ochenta y cuatro años fue la edad de Diofante.
Su juventud ocupo una sexta parte de su vida.
84
6
14= años.
Después, durante la doceava parte su mejilla se cubrió de vello.
84
6
84
12
14 7 21+ = + = años.
Pasó una séptima parte de su vida antes de tomar esposa.
84
6
84
12
84
7
14 7 12 33+ + = + + = años.

219. 211
Cinco años después, tuvo un precioso niño.
84
6
84
12
84
7
5 14 7 12 5 38+ + + = + + + = años.
Una vez alcanzada la mitad de la edad de su padre, pereció de
una muerte desgraciada.
84
6
84
12
84
7
5
84
2
14 7 12 5 42 80+ + + + = + + + + = años.
Su padre tuvo que sobrevivirle, llorándole durante cuatro años.
84
6
84
12
84
7
5
84
2
14 7 12 5 42 4 84+ + + + = + + + + + = años.
c. En un tratado del álgebra escrito por el célebre matemático
Leonhard Euler, publicado en 1770 aparece el siguiente
problema: “En un hotel se alojan 20 personas entre hombres
y mujeres. Cada hombre paga 8 monedas por su hospedaje
y cada mujer 7, del mismo valor, ascendiendo el total de la
cuenta a 144 monedas. Se pregunta: ¿Cuántos hombres y
cuántas mujeres hay en el hotel?”
Comprobación
Sea H: el número de hombres alojados en el hotel y (20 - H) el
número de mujeres
Tal que se cumple:
H+(20 - H) = 20
Según el valor del hospedaje, tenemos que:
8H + 7(20 - H) = 144 ⇒ 8H + 140 - 7H = 144
H = 144 - 140 = 4 ⇒ (20 - H) = 16
Interpretación:
4 hombres a 8 monedas resulta 32 monedas, 16 mujeres a 7
monedas resulta 112monedas, entonces 32+112=144 monedas.
d. Al preguntársele a Pitágoras por el número de sus estudiantes,
dio la siguiente respuesta: “La mitad de mis estudiantes estudia
Matemática, la cuarta parte estudia Física, la séptima parte
aprende Filosofía y aparte de éstos hay tres ancianos” ¿Puedes
deducir cuántos estudiantes tenía el famoso matemático
griego?

220. 212
Comprobación
Sea z el número total de estudiantes que tiene Pitágoras. La mitad
de sus estudiantes estudia Matemática, esto lo expresamos por Z
2
.
La cuarta parte estudia Física implica Z
4
.
La séptima parte estudia Filosofía sería Z
7
y tendríamos que añadir
a los tres ancianos.
z z z
z
2 4 7
3+ + + =
z z z
z
z z z z
2 4 7
3 0
28 14 8 168 56
56
0
+ + + − =
+ + + −
=
50 168 56
56
0
6 168
56
0
6 168
168
6
z z
z
z
z
+ −
=
− +
=
− = −
=
−
−
z = 28
Interpretación:
Estudian Matemática.
z
2
28
2
14= = ,
estudian Física
z
4
28
4
7= =
estudian Filosofía.
z
7
28
7
4= = .
Sumando tenemos: 14 + 7 + 4 + 3 = 28 estudiantes.

221. 213
Refuerce sus conocimientos.
1. Resuelva las siguientes ecuaciones lineales.
a. 3x - 6 = 6
b. 4x - 2=8.
c. 2x - 4 = 4
d. 3x - 10 = 2x - 30
e. 4x - 4 = 11x + 7
f. 8x = x - (4x - 12)
g. 4(x - 6)-2(x + 8) = x + 10
h. 14 - (5x - 1)(2x + 3) = 17 - (10x + 1)(x - 6)
i. (4 - 5x)(4x - 5) = (10x - 3)(7 - 2x)
j. -3(2x + 7) + (6 - 5x) - 8(1 - 2x) = (x - 3)
k. 184 - 7(2x + 5) = 301 + 6(x - 1) - 6
l. 14x - (3x + 2) - 10 = 10x - 1
m. (5 - 3x) - (-4x + 6) = 5x + 17
n. -[x - 1 - (2x + 5)] = x
o. x x+
=
−
+
2
4
2
8
1
p. 5
8 15
3
x
x
=
−
q. x +
=
2
5
2
r. x x+
=
−5
8
9
5
s. x x x
x
+ − − +
= − +
5 3 2
5
5 2x
( ) ( )
Matemático griego.
Estudió en Alejandría,
donde tuvo como
maestro a Conón
de Samos y entró
en contacto con
Eratóstenes; a
este último dedicó
Arquímedes su Método,
en el que expuso
su genial aplicación
de la mecánica a
la geometría. Es
muy conocido por el
famoso “Principio de
Arquímedes”, utilizado
ampliamente en la
Mecánica de fluidos. En
la obra sobre la esfera
y el cilindro utilizó el
método denominado de
exhausción, precedente
del cálculo integral, para
determinar la superficie
de una esfera y para
establecer la relación
entre una esfera y el
cilindro circunscrito en
ella.
Arquímedes
(287 a.C.- 212 a. de C.)
Nota histórica

222. 214
ACTIVIDADES FINALES DE LA QUINTA UNIDAD
I. Resuelva los siguientes problemas.
1. El área de una región rectangular que tiene 10 cm de largo y x cm de ancho es 120
cm2
. Encuentre el valor de x.
2. La suma de dos números enteros positivos consecutivos es igual a 45. Encuentre
los números.
3. La suma de dos números enteros pares consecutivos es 70. Encuentre los números.
4. Un triángulo tiene sus tres lados de diferente medida. El primer lado tiene una
longitud igual a 16u . Sabiendo que la longitud del tercer lado es 4u. mayor que la
longitud del segundo lado, encuentre las longitudes del segundo y tercer lados, si el
perímetro es igual a 48u.
5. Francisco se prepara para entrar al colegio. Visita una librería para realizar las
siguientes compras: 5 cuadernos, tres lapiceros, un lápiz y un borrador de leche.
El costo total de lo comprado es de C$159 Córdobas. Sabiendo que el precio de
un lapicero es 15 veces menor que el de un cuaderno, que el precio de un lápiz es
2 veces menor que el de un lapicero y que el precio de un borrador de leche es 2
veces mayor que el de un lápiz, encuentre el precio de cada artículo.
6. La edad de Enrique es el triple de la edad de Roberto. La edad que tenía Enrique
hace 7 años era el doble de la edad que tendrá Roberto dentro de 6 años. ¿Qué
edad tienen Enrique y Roberto?
7. La Edad de Humberto es cuatro veces mayor que la de su hija María. Si la suma de
sus edades es 65, ¿Qué edad tiene Humberto y su hija?
8. Miguel sale en su vehículo de Managua hacia Estelí a las 8:00am., a una velocidad
de 80 km/h. José sale en su vehículo de Estelí hacia Managua a la misma hora, a
una velocidad de 70km/h. Si la distancia entre Managua y Estelí es de 150km., ¿en
qué kilómetro se encontrarán y a qué hora?
9. En un mercado de Managua, Maria compra frijoles y azúcar para una semana. Si
compra 5 libras de frijoles y 7 libras de azúcar en C$132 Córdobas, y sabiendo que
el precio de la libra de frijoles es tres veces mayor que el precio de la libra de azúcar,
¿cuál es el precio de la libra de frijoles y el de la libra de azúcar?
10. Un estudiante de un curso de álgebra obtiene notas de 75, 82, 71 y 84 en los
exámenes. ¿Qué calificación en sus siguientes pruebas elevará su promedio a 80?

223. 215
11. En cierta prueba médica diseñada para medir la tolerancia a los carbohidratos,
un adulto ingiere 7 onzas (oz) de una solución glucosa al 30%; cuando la prueba
se aplica a un niño, la concentración de glucosa debe disminuir al 20%. ¿Cuánta
solución de glucosa al 30% y cuánta agua se necesita a fin de preparar 7 oz de una
solución de glucosa al 20%?
12. El doble de un número más el triple de su sucesor, más el doble del sucesor de éste
es 147. Hallar el número.
13. El dígito de las unidades de un número de 2 dígitos es 5 más que el dígito de las
decenas. Si el número original se divide por el número con los dígitos invertidos,
el resultado es
3
8
Encuentre el número original. Se cuenta que la legendaria
fundadora de Praga, la reina Libussa de Bohemia, eligió a su consorte entre tres
pretendientes, planteándoles el siguiente problema: ¿Cuántas ciruelas contenía un
canasto del cual ella sacó la mitad del contenido y una ciruela más para el primer
pretendiente, para el segundo la mitad de lo que quedó y una ciruela más y para
el tercero la mitad de lo que entonces quedaba y tres ciruelas más, si con esto el
canasto se vació. ¿Puedes calcularlo tú?
14. El agua cubre el 70,8% de la superficie terrestre, es decir, cerca de 3,61 x 106
Km2
.
Calcula aproximadamente la superficie total de Tierra.
15. Seiscientas personas asisten a presenciar el estreno de una película. Los boletos
para adultos cuestan C$ 50 y los niños C$ 20. Si la taquilla recibió un total de
C$ 24 000, ¿Cuántos niños asistieron al estreno?
16. Las edades de un matrimonio suman 62 años. Si se casaron hace 10 años y la edad
de la novia era de la edad del novio. ¿Qué edad tienen actualmente?
17. Miguel tiene el doble de dinero que Marlene y el triple que Meyling. Si Miguel regalara
C$ 14 a Marlene y C$ 35 a Meyling, los tres quedarían con igual cantidad. ¿Cuánto
dinero tiene cada uno?
18. Una persona puede pintar un muro en 5 horas, otra lo hace en 6 horas y una tercera
persona tarda 12 horas en pintar el mismo muro. ¿Cuánto tardarían si la pintaran
entre las tres personas?
19. Un trabajador percibe C$ 4 920 de salario después de restar las deducciones, las
cuales corresponden a 40% del sueldo bruto. ¿Cuál es el sueldo bruto?
20. Hallar dos números enteros pares consecutivos cuya suma sea 194.
21. La cabeza de un pez corresponde al tercio de su peso total, la cola a un cuarto del
peso y el resto del cuerpo pesa 4,6 kg ¿Cuánto pesa el pez?

224. 216
22. Un farmacéutico debe preparar 15 mililitros de gotas oftálmicas para un paciente con
glaucoma. La solución ha de tener un ingrediente activo de 2%, pero el farmacéutico
sólo tiene en existencia soluciones al 10% y 1%. ¿Cuánto de cada tipo de solución
requiere la elaboración de la receta?
23. Un preso dice a su carcelero: Hoy es mi cumpleaños y ni siquiera sé cuánto tiempo
me queda de condena. ¡Qué casualidad!, también es hoy mi cumpleaños. ¿Cuántos
años cumples? Veinticinco. Yo cumplo cincuenta y cuatro. Saldrás de la cárcel el
día que yo sea exactamente el doble de viejo que tú. ¿Cuántos años de condena le
quedan al preso?
II. Encierre en un circulo la respuesta correcta:
1. Antonio e Iveth limpiaron una huerta en cierto tiempo, si cada uno hubiera limpiado la
mitad, Antonio habría trabajado cinco días menos, mientras Iveth hubiera trabajado
siete días más. ¿En cuánto tiempo limpiaron la huerta Antonio y Iveth?
a. 7 días
b. 35 días
c. 12 días
d. 4 días
e. 10 días
2. La ruta 119 de transporte urbano colectivo de Managua, comienza su trayecto con
un cierto número de pasajeros. En la primera parada descienden
1
3
de los pasajeros
y suben 8. En la segunda parada descienden
1
2
de los pasajeros que quedaron y
subieron 2. En este momento el bus lleva la mitad de pasajeros de los que llevaba
al inicio del trayecto. ¿Cuántos pasajeros habia al principio del trayecto?.
a. 100
b. 50
c. 36
d. 18
e. 20

225. 217
3. El latón es un aleación de cobre y zinc; el bronce es una aleación de Cu, Zn y Sn, el
bronce es una aleación que contiene el 80% de cobre, 4% de zinc y 16% de estaño.
Analizando una masa fundida de latón y bronce vemos que contiene 74% de cobre,
16% de zinc y 10% de estaño. Hallar la razón del cobre al zinc en la composición del
latón.
a.
9
16
b.
9
4
c.
16
9
d.
4
9
e.
9
14
4. Si el lado de un cuadrado se duplica, su perímetro aumenta 40m. Calcule la medida del
lado del cuadrado.
a. 100
b. 20
c. 40
d. 10
e. 25
5. ¿Cuántos litros de alcohol al 90% habrá que mezclarlos con alcohol al 70% para obtener
10 litros de solución de alcohol al 85%?
a. 7 litros
b. 7,5 litros
c. 6 litros
d. 6,5 litros
e. 9 litros

226. 218
III. Los diagramas que se presentan a continuación, diga cuales representan una función
a
b
c
1
2
3
a
b
c
1
2
3
a
b
c
1
2
3
A B
A B A B
a
b
c
a + b
2b
c + b
a
b
c
1
2
3
4
A B
A
B
a
b
c
1
2
3
4
A
B
IV. Sean los conjuntos A = { 2, 4, 6 } y B = { 3, 5 }
1. Realizar el producto cartesiano.
2. Definir el dominio de la relación obtenida.
3. Definir el rango de la relación obtenida.
4. Representar las parejas ordenadas en un plano cartesiano.
V. Para f (x) = 3x2
+ 5x + 2; y g(x) = x2
+ x, obtener:
1. (f + g) (x) =
2. (f – g) (x) =
3. (f . g) (x) =
4. f x
g x
( )
( )
=

227. 219
VI. Para f x
x
x
( )=
−1
; y g x x( )= +1 2
, encuentre:
a. (f + g)(x)
b.
g
f
x





( )
c. (f . g)(x)
VII. Si f (x) = x2
- 5x + 3 y g(x) = x2
, calcule:
a. f [g(x)] y g [f (x)]
b. Calcula
££ f [g(4)]
££ g [f (4)]
££ g [f (-2)]
££ f [g(-2)]
££ ( f ∘ f ) (x)
££ (g ∘ g) (x)
VIII. Representa gráficamente las funciones:
a. y = 3x + 6
b. y = -2x - 4
c. y = 4x + 5
d. y = 8 - 3x
e. y = -3x

228. 220
IX. Representa las funciones lineales sabiendo que y es la variable dependiente:
a. 2x = 3y
b. 3y = 4x + 5
c. 2x = y - 1
d. 8x + 2y = 16
e. 6x - y = 2
f. 2x + 1 = 5y
g. x + y = 4x - 3
h. 1
2
x + 7 = y - 10
i. 8x + 6 = 2 - 3y
j. 6y - x = 0
X. Sean A = {1,2,3,4,5,6} y B = {1,3,5,7,9}
Calcule:
a. A x B
b. B x A
c. A x A
d. B x B
Determine el dominio y recorrido de los productos cartesianos anteriores.
XI. Determine el conjunto solución de las siguientes ecuaciones:
a. 3x + 1 = 10
b. 3x + 10 = -5x + 2
c. 8 - 10x + 9 = 6x - 3
d. 6 + 11x = 10x - 11
e. 3(4x - 3) = 2(x - 5)
f. 5 6 4
1
2
4 8−( )= −( )x x

229. Construcción de
Figuras Geométricas
Unidad 6
Pascual Rigoberto López Pérez, más conocido por Rigoberto López Pérez (1 929 – 1 956),
poeta nicaragüense e importante símbolo de la revolución, marcó el inicio del fin de la
tiranía, pasó a la inmortalidad el 21 de Septiembre de 1 956. En septiembre de 1 981,
Rigoberto López Pérez entró a la lista de héroes nacionales por la “gesta heroica llevada
a cabo al ajusticiar al tirano”. El Decreto fue aprobado el día en que se cumplieron 25 años
del asesinato de López Pérez.
Fuente: 19 digital.
20 de Septiembre 2 013.
pa



230. 222
Construcción de figuras geométricas.
Lea, analice e interprete.
En el séptimo grado fueron estudiados los conceptos básicos de
Geometría. Recordaremos los más importantes.
Conceptos básicos de Geometría.
La Geometría está construida de acuerdo con el sistema
axiomático. El punto de partida para el estudio de los entes
geométricos son los conceptos primitivos o no definidos de punto,
recta, plano y espacio.
Los términos no definidos o primitivos, sirven de base para
construir otros elementos de la Geometría.
Términos no definidos o primitivos
¿Cuáles son los elementos geométricos que se construyen con
ayuda de los términos no definidos?
Con ayuda de los términos primitivos se enuncian:
• Las definiciones.
• Los axiomas.
• Los teoremas.
Ejemplo:
La definición de puntos colineales es:
Definición
Un conjunto de puntos del espacio son colineales si y sólo si
pertenecen a la misma recta.
El dibujo a continuación, ilustra la definición:

P Q P
Los puntos P, Q y R son colineales porque pertenecen a la misma
recta .
Matemático griego.
Poco se conoce
de la biografía de
Euclides, pese a ser el
matemático más famoso
de la Antigüedad.
Euclides fue autor de
diversos tratados, pero
su nombre se asocia
principalmente a uno
de ellos, los Elementos,
que rivaliza por su
difusión con otras obras
como el Quijote. Se
trata, en esencia, de una
compilación de obras
de autores anteriores
(entre los que destaca
Hipócrates de Quíos),
que las superó de
inmediato por su plan
general y la magnitud de
su propósito.
Euclides
(330 a.C.- 275 a.C.)
Nota histórica

231. 223
Importante
Dos puntos siempre están situados en una misma recta. Por eso
no es correcto decir “dos puntos colineales”. Dos puntos siempre
son colineales.
Los términos primitivos son utilizados para formular los axiomas de
la Geometría.
Un axioma es una proposición cuya veracidad se admite sin
demostración.
Ejemplo:
La siguiente proposición es un axioma:
Dadas dos rectas diferentes en un
plano, si se intersectan, su intersección
es un único punto.
El siguiente dibujo, ilustra el axioma: La intersección de las rectas
 y m

es un único punto.
El siguiente esquema muestra la estructura de un sistema
axiomático en el estudio de la Geometría Euclidiana.
Términos no definidos
o primiƟvos
Axiomas
Definiciones
Teoremas
Geometría
Teoría
de conjuntos.
Leyes de la lógica
matemática.
A continuación se presenta la idea básica de figura geométrica.
Se llama figura geométrica a un subconjunto no vacío de puntos
de una recta, un plano o el espacio.
Arístocles de Atenas,
apodado Platón «el de
anchas espaldas», nace,
probablemente, el año
428-427 a. de C. en
Atenas.
Pertenecía a una familia
noble. Platón funda en el
año 387 la Academia, en
la cual se estudiaba un
conjunto de disciplinas
tales como geometría,
astronomía, música
y dialéctica. Platón
concedía mucha
importancia a los
estudios matemáticos.
De esto da cuenta la
leyenda que rezaba en
el frente de la Academia:
“que nadie entre aquí si
no sabe geometría”.
Platón murió en el 347
a. de C., a los (80 - 81)
años de edad.
m
Nota histórica

232. 224
La figura geométrica más simple es el
segmento.
En la figura de la derecha se presenta un segmento.
Dados dos punrtos P y Q, se llama segmento a la unión del
conjunto formado por P y Q con el conjunto formado por todos los
puntos X que se encuentran entre P y Q. Un segmento se denota
por: PQ
Los puntos P y Q se llaman extremos del segmento.
Se llama rayo a la unión del segmento PQ
con el conjunto de puntos que se encuentran
después de Q. El punto P se llama origen
del rayo. Se denota un rayo por PQ
Se llama ángulo a la unión de dos rayos no
colineales que tienen el mismo origen. El
punto Q, el origen común, se llama vértice del
ángulo. Los rayos QR y QP se llaman lados
del ángulo.
Un ángulo con vértice en el punto Q se denota
por: ∠PQR
Es importante recordar que los lados de un ángulo son rayos.
A continuación se presenta la figura de un triángulo.
Dados tres puntos no colineales A, B y C,
la unión de los segmentos AB, BC y CE se
llama triángulo. Los puntos A,B y C se llaman
vértices del triángulo y los segmentos AB ,
BC y CE se llaman lados del triángulo.
Todo triángulo tiene tres vértices, tres lados
y tres ángulos. En el triángulo de la figura,
los ángulos tienen vértices A, B y C
Dadas dos rectas diferentes en un plano, éstas se pueden
intersectar o no. En la figura mostrada al inicio de la pagina
siguiente se presenta dos rectas que no se intersectan.
P
X
Q
P
X
Q
P
Q
R
α
A B
C
Reforzamiento:
Utilizando una regla y
un compás dibuje:
• Un triángulo cuyos
lados miden 6 cm,
9 cm y 4 cm.
• Un triángulo
equilátero cuyos
lados miden 3 cm.
Tradicionalmente por
error se ha utilizado la
siguiente simbología
para indicar la medida
de un ángulo
∡A = 35° ó m∡A = 35°
En este texto se
trabajará suprimiendo
el símbolo grado (°) y
la medida del ángulo
anterior utilizando el
lenguaje matemático
internacional será
representado como:
∠A = 35 ó ∠A = 35

233. 225
Se dice que dos rectas diferentes son
paralelas, si y sólo si están contenidas
en un mismo plano y no se intersectan.
La teoría de las paralelas sirve de base
para el estudio de la semejanza de
triángulos, en la cual juega un papel muy importante el teorema
de Thales.
Dos consecuencias muy importantes del concepto de rectas
paralelas son los siguientes:
• La suma de las medidas de los ángulos
interiores de un triángulo es igual a 180.
• La suma de los ángulos interiores de
cualquier cuadrilátero es igual a 360.
La figura de la derecha representa un
cuadrilátero.
Dados cuatro puntos A, B, C y D, de los cuales no hay tres que
sean colineales, la unión de los segmentos AB, BC, CE y DA se
llama cuadrilátero. Los puntos A, B, C y D se llaman vértices del
cuadrilátero. Los ángulos con vértices en los puntos A, B, C y D
son los ángulos internos del cuadrilátero.
Actividad
• Conceptualice, elabore su representación gráfica e indique
como se denota simbólicamente:
a. Axioma
b. Ángulo.
c. Rayo.
d. Triángulo.
e. Cuadrilátero
La negación del
quinto postulado de
Euclides acerca de la
unicidad de la paralela
que se puede trazar
por un punto exterior
a una recta, sirvió
como fundamento
para la creación de
otras geometrías que
recibieron el nombre
de geometría no
euclidiana.
En la creación,
desarrollo y
fundamentación de las
geometría no euclidiana
jugaron un papel
fundamental Nicolai
Ivanovich Lovachevski
(matemático ruso),
Janos Bolyai
(matemático húngaro),
Karl Fiedrich Gauss
(matemático alemán,
conocido como
el Príncipe de la
Matemática).
Las geometrías
no euclidianas
representaron una
transformación radical
de las concepciones del
espacio-tiempo y en la
creación de una de las
teorías más importantes
de la física actual, la
teoría de la relatividad
creada por el genio de
Albert Einstein (físico
alemán).
m
A
B
CD
Ma
tem
áti
ca
7
¿Sabías qué?

234. 226
Regiones poligonales y polígonos regulares
Hasta el momento usted ha estudiado figuras geométricas como
recta, segmento, rayo, ángulos, triángulos y cuadriláteros.
En esta unidad se estudiarán polígonos regulares de más de
cuatro lados.
Un polígono que tiene todos sus lados de la misma medida se
llama polígono regular.
¿Qué polígonos regulares ha estudiado?
Ha estudiado en el séptimo grado polígonos regulares tales
como el triángulo equilátero (que es un polígono regular de tres
lados), el rombo (que es un cuadrilátero regular de cuatro lados
con ángulos opuestos de la misma medida), el cuadrado (que es
un cuadrilátero regular de cuatro lados de la misma medida y con
sus cuatro ángulos interiores de la misma medida igual a 90).
Línea poligonal.
Definición
Dado n puntos A1
, A2,
..., An
en el plano con, n ≥ 3, con la condición
de que no hay tres puntos consecutivos que sean colineales.
La unión de los segmentos A1
A2
, A2
A3
,…An - 1
An
se llama línea
poligonal. Si el punto A1
no coincide con An
la linea poligonal es
abierta.
Línea poligonal = A1
A2
∪ A2
A3
∪…∪ An - 1
An
Los puntos A1
, A2,
..., An
se llaman vértices de la línea poligonal.
Los segmentos A1
A2
, A2
A3
,…An - 1
An
,se llaman lados de la línea
poligonal.
A continuación se presenta la gráfica de una línea poligonal
abierta.
Lobachevski fue un
destacadísimo matemático
ruso del siglo XIX. Creador
de una de las geometrías
no euclideanas, la
geometría hiperbólica,
junto al húngaro J. Bolyai
y el matemático alemán
K.F. Gauss. Fue rector de
la Universidad de Kazán
durante dos décadas y un
trabajador infatigable. En
palabras de Clifford
(1 845-1 879), Lobachevski
era más que un
matemático, calificándole
como el Copérnico de la
geometría.
Nicolai I. Lobachevski
(1 792-1 856)
A1
A2
A3 An - 1
An
Vértice
Lado
Nota histórica

235. 227
La suma de las medidas de los segmentos que forman la línea
poligonal se llama perímetro de la línea poligonal.
Se denotará el perímetro con la letra P.
P = A1
A2
+ A2
A3
+ ... + An - 1
An
Los vértices A1
y A2
son vértices consecutivos de la poligonal. Los
vértices A1
y A3
son vértices no consecutivos de la línea poligonal.
Cuando el primer vértice de una línea poligonal coincide con el
último, entonces la línea poligonal se llama línea poligonal cerrada.
P2
P3
P1
P4
Lado
Línea poligonal
cerrada
Coinciden el primer
vértice y el último.
Región poligonal cerrada.
Se llama región poligonal cerrada al conjunto de puntos de un
plano limitado por una línea poligonal cerrada.
En la figura de la derecha se presenta una
región poligonal cerrada. La región poligonal
mostrada está limitada por la línea poligonal
formada por los puntos P1
, P2
, P3
y P4
.
Los puntos P1
, P2
, P3
y P4
son los vértices de la línea poligonal y
los segmentos P P1 2 ,P P2 3 , P P3 4 y P P4 1 se llaman lados de la región
poligonal.
¿Qué se entiende por región poligonal convexa?
Observe las siguientes figuras:
P2
P3
P4
P1
P5
a. Convexa
A
B
P2
P3
P4
P1
P5
b. Cóncava
A
B
P2
P3
P4
P1
Un polígono es simple si
solo tiene un borde que no
se cruza con el mismo.
Un polígono es complejo si
se interseca con el mismo.
Un polígono es convexo
si sus ángulos internos no
son mayores que 180.
Un polígono es cóncavo
si al menos un ángulo es
mayor que 180.
Ma
tem
áti
ca
7
¿Sabías qué?

236. 228
En la figura a) los puntos A y B están en el interior de la región
poligonal y el segmento que los une también está contenido en el
interior de la región poligonal. Cuando esto se cumple para dos
puntos cualesquiera del interior de una región poligonal, se dice
que la región es convexa.
En la figura b) los puntos A y B están en el interior de la región
poligonal, pero el segmento que los une no está totalmente
contenido en el interior de la región poligonal. Cuando esto ocurre
para al menos dos puntos del interior de una región poligonal, se
dice que la región es cóncava.
El pentágono regular.
A continuación se presenta la figura de un pentágono regular: los
lados del pentágono regular tienen la misma medida.
108° 108°
108° 108°
108°
B
A C
E D
Vértice
Lado
Ángulo Interno o Ángulo Interior
Se llama pentágono regular a un polígono regular de cinco lados
de igual medida y cinco ángulos internos de igual medida.
AB ≅ BC ≅ CD ≅ DE ≅ AE
Se llama perímetro de un pentágono regular, a la suma de las
medidas de sus lados. Se denotará el perímetro con la letra P.
P = AB + BC + CD + DE + EA = l + l + l + l + l = 5l
Si l es la longitud de un lado, entonces P = 5l
P = l + l + l + l + l = 5l
Número de lados Longitud de cada lado
Minkowski nació en
Aleksotas, Rusia
(actualmente Kaunas,
Lituania), y cursó sus
estudios en Alemania
en las universidades
de Berlín y Königsberg,
donde realizó su
doctorado en 1 885.
Durante sus estudios
en Königsberg en
1883 recibió el premio
de matemáticas de la
Academia de Ciencias
Francesa por un trabajo
sobre las formas
cuadráticas. Minkowski
impartió clases en las
universidades de Bonn,
Göttingen, Königsberg
y Zúrich. En Zúrich fue
uno de los profesores de
Einstein.
Hermann Minkowski
(1 864 - 1 909)
Nota histórica

237. 229
Ejemplo:
Encontrar el perímetro de un pentágono si el lado tiene medida 5u.
Solución
El perímetro es: P = 5 + 5 + 5 + 5 + 5 = 5(5) = 25u.
Ejemplo:
Si el perímetro de un pentágono regular es P = 45u, encontrar la
longitud del lado del pentágono.
Solución
El perímetro es P = 45u, entonces la longitud del lado del pentágono
es
P = 5l ⟹ l =
La longitud del lado es: l = 9u.
• Elementos del pentágono regular.
Lossegmentos AB ,BC,CD ,DEy EA sellaman ladosdelpentágono.
Los puntos A, B, C, D y E se llaman vértices del pentágono.
Los ángulos con vértices en los puntos A, B, C, D y E se llaman
ángulos internos del pentágono.
El segmento de recta que une dos vértices no consecutivos se
llama diagonal del pentágono. Por ejemplo, los vértices A y B son
consecutivos, los vértices A y C son no consecutivos y AC es una
diagonal.
En la figura de la derecha, los
segmentos CE , AD, BD, BE y
AC son diagonales del pentágono.
¿Cuántas diagonales tiene un
polígono regular de n lados?
A continuación se encontrará
una expresión para el número de
diagonales de un pentágono.
D
E C
BA

238. 230
• Número de diagonales de un pentágono regular.
En el pentágono regular de
la figura se pueden observar
las diagonales:
AD, CE, BE, BD y CA
Observe que la diagonal
AD es la misma que DA , la
diagonal BE es la misma que
la diagonal EB, esto mismo
sucede para las otras diagonales.
Lo anterior significa que, como de cada vértice parten dos
diagonales, entonces el número de diagonales es igual a:
5(2) = 10
Pero 2 es igual a (5 - 3). Es decir, el número de lados menos 3,
entonces, el número de diagonales es:
Número de diagonales = Nd =
−
=
5 5 3
2
5
( )
Se divide por 2 debido a que de las 10 diagonales, hay 5 pares de
diagonales que tienen los mismos extremos, por tanto el número
total de diagonales se divide por 2.
La expresión para encontrar el número de diagonales de un
pentágono sugiere que al número de lados (5) se multiplica por
el número de lados disminuido en 3 y el resultado se divide por
2. Entonces, se puede encontrar la expresión para el número de
diagonales de un polígono regular de n lados.
• Número de diagonales para un polígono regular de “n”
lados.
Razonando de manera similar que con el pentágono, se deduce la
expresión para encontrar el número de diagonales de un polígono
regular de n lados. Esta expresión es:
Número de diagonales = N
n n
d =
−( )3
2
donde n es el número de lados del polígono
Matemático francés, Se
doctoró en matemáticas
en 1 879. Fue nombrado
profesor de física
matemática en La Sorbona
(1 881). Antes de llegar a
los treinta años desarrolló
el concepto de funciones
automórficas. En 1 895
publicó su Analysis situs,
un tratado sistemático
sobre topología. En el
ámbito de las matemáticas
aplicadas estudió
numerosos problemas
sobre óptica, electricidad,
telegrafía, capilaridad,
elasticidad, termodinámica,
mecánica cuántica,
teoría de la relatividad y
cosmología.
Henri Poincaré
(1 854 - 1 912)
Nota histórica
D
E C
BA
Diagonal

239. 231
Ejemplo:
Si se aplica a un triángulo la expresión encontrada para el número
de diagonales de un polígono regular de n, a un triángulo (n = 3)
obtenemos
Nd =
−( ) = =
3 3 3
2
0
2
0
Es decir que un triángulo no tiene diagonales.
Ejemplo:
En el caso de un cuadrado, se tienen 4
lados, entonces el número de diagonales es
Nd =
−( ) =
4 4 3
2
2
Las diagonales son: CA y BD.
• Centro de un pentágono regular.
Se llama centro de un pentágono
regular a un punto del interior del
pentágono que equidista de sus
vértices.
En la figura de la derecha, el punto P
es el centro del pentágono. El punto P
equidista de los vértices del pentágono.
Los segmentos que unen el punto P con
los vértices tienen la misma medida r.
PA = PB = PC = PD = PE = r
• Apotema de un pentágono regular.
Se llama apotema de un pentágono
regularalsegmentoderectaperpendicular
que une el centro del pentágono con
cualquiera de sus lados.
En la figura de la derecha, el segmento
PF es la apotema. La letra a representa la
longitud de la apotema.
El pentágono regular
está formado por 5
triángulos isósceles con
base de igual medida r,
que es la distancia del
centro del pentágono a
cada vértice.
A B
CD
D
E C
BA F
a
P
r
D
E C
BA F
a
P
r
l
Ma
tem
áti
ca
7
¿Sabías qué?

240. 232
La apotema es perpendicular al lado
opuesto. En la figura el segmento PF (la
apotema) es perpendicular al lado AB . El
punto F es punto medio del segmento AB
, entonces AF ≅ FB .
Donde l
2
es la longitud de cada lado.
¿Cómo se calcula la longitud de la
apotema?
En la figura, el triángulo ∆PFA es rectángulo en el vértice F. Esto
quiere decir que el ángulo ∠PFA tiene medida 90. Entonces, se
puede aplicar el teorema de Pitágoras al triángulo rectángulo
∆PFA.
r a a r a r2
2
2 2 2
2
2
2
2 2 2
=





 + ⇒ = −





 ⇒ = −






l l l
Apotema = a r r= −





 = −2
2
2
2
2 4
l l
Donde “l” es la longitud del lado del pentágono.
Suma de las medidas de los ángulos interiores de
un polígono.
La suma de las medidas de los ángulos internos de un polígono
regular de “n” lados, cuya región interior es convexa, se calcula
con la expresión:
(n - 2)180
Ejemplo:
En el caso del triángulo (n = 3), la suma de las medidas de los
ángulos interiores es:
(3 - 2)180 = (1)(180) = 180
Ejemplo:
En el caso del cuadrado (n = 4), la suma de las medidas de los
ángulos interiores es:(4 - 2)180 = (2)(180) = 360
A
P
F
a
l
2
Bl
2
Un polígono regular
de tres lados se llama
triángulo equilátero
ó equiángulo y cada
ángulo interior mide 60
grados.
Un polígono regular
de 4 lados se llama
tetrágono y cada
ángulo interior mide 90
grados.
Un polígono regular
de 5 lados se llama
pentágono y cada
ángulo interior mide
108 grados.
Un polígono regular
de 6 lados se llama
hexágono y cada
ángulo interior mide
120 grados.
Un polígono regular
de 7 lados se llama
hectágono y cada
ángulo interior mide
128,571 grados.
Un polígono regular
de 8 lados se llama
octágono y cada
ángulo interior mide135
grados.
Un polígono regular
de nueve lados se
llama nonágono y cada
ángulo interior miden
140 grados.
Un polígono regular de
10 lados se llama cada
ángulo interior mide
144 grados.
Ma
tem
áti
ca
7
¿Sabías qué?

241. 233
Actividad:
a. Verificar que la suma de las medidas de los ángulos interiores
de un pentágono (n = 5), es 540.
b. Verificar que la suma de las medidas de los ángulos interiores
de un hexágono (n = 6), es 720.
c. Verificar que la suma de las medidas de los ángulos interiores
de un heptágono regular (n = 7), es 900.
Para encontrar la medida de un ángulo
interior de un polígono regular, con
región interior convexa, se divide la
suma de las medidas de todos los
ángulos interiores, por el número de
lados.
Así se tiene que:
Medida del ángulo interior
n
n
−( )2 180
En el caso del pentágono, se tiene:
Medida de un ángulo interior =
5 2 180
5
540
5
108
−( ) = =
Ángulo exterior de un polígono con región interior
convexa.
El la figura se muestra un ángulo exterior
de un pentágono regular.
Observe que la suma de las medidas
de un ángulo exterior con la medida
del ángulo interior adyacente es igual a
180. Forman un par lineal.
• Ángulo central de un pentágono.
En la figura se presenta un ángulo
central de un pentágono regular.
El ángulo central mostrado es:
∠APB = ∠α.
¿Cómo se calcula la medida de un
ángulo central de un pentágono regular
en función del número de lados?
Reforzamiento:
Un pentágono regular de
6 cm de lado, tiene un
radio de 5 cm. Calcule
su perímetro y apotema.
108° 108°
108° 108°
108°
B
A C
E D
Ángulo
Interno
108° 108°
108°
108°
108°
D
A C
E D
Ángulo
Interno
Ángulo
externo
E C
BA F
P
r
Ángulo
Central
α = 72°
• Ángulo central:
Es el ángulo
cuyo vértice es
el centro de la
circunferencia. El
∠CPD es un ángulo
central. A todo
ángulo central le
corresponde un arco
de circunferencia
comprendido entre
los lados del ángulo.
Así el ángulo ∠CPD
subtiende el. La
medida de un
ángulo central es
igual a la medida
del arco CD
comprendido entre
sus lados.
m∠CPD = mCD.
Gráfico de un
ángulo central
α = 72°
C
p
α = 72°
D
Ma
tem
áti
ca
7
¿Sabías qué?

242. 234
El pentágono tiene 5 ángulos
centrales con la misma medida.
La suma de las medidas de los
5 ángulos centrales es igual a
360. Entonces la medida de un
ángulo central es:
5(m∠α) = 360 ⟹ m∠α =
360
5
= 72
Entonces la medida del ángulo
central del pentágono regular
es 72. Se sabe que un ángulo
interno de un pentágono regular tiene una medida de 108. Esto
significa que la medida de un ángulo exterior es:
180 - 108 = 72
Por tanto se concluye que la medida del ángulo central del
pentágono regular es igual a la medida de un ángulo exterior del
pentágono regular.
El hexágono regular.
Se llama hexágono regular a un polígono
regular de seis lados de igual medida y
seis ángulos internos de igual medida.
En la siguiente figura se presenta un
hexágono regular:
• Elementos del hexágono.
Los segmentos AB , BC ,CD DE,EF y FA se llaman lados del
hexágono.
Los lados del hexágono regular tienen la
misma medida.
AB = BC = CD = DE = EF = FA
Los puntos A, B, C, D, E y F se llaman vértices
del hexágono.
Los ángulos con vértices en los puntos A, B, C, D, E y F se llaman
ángulos internos del hexágono.
Un segmento de recta que une dos vértices no consecutivos se
llama diagonal del hexágono.
¿Saben Matemática las
abejas?
Las abejas, cuando
guardan la miel, tienen
que resolver varios
problemas. Necesitan
guardar la miel en
celdillas individuales, de
tal manera que formen
un mosaico sin huecos
ni salientes entre las
celdillas, ya que hay que
aprovechar el espacio al
máximo.
Sólo podrían hacerlo con
triángulos, cuadrados y
hexágonos.
Eligieron los hexágonos
regulares, debido a
que entre todos los
polígonos regulares con
el mismo perímetro,
encierran mayor área
aquellos que tengan
mayor número de lados.
A B
C
DE
F
A B
C
DE
F
Ángulo
Interno
Diagonal
Lado
Ma
tem
áti
ca
7
¿Sabías qué?
α = 72°
B
A C
DE
α = 72°
α = 72°
α = 72°
α = 72°
α = 72°p

243. 235
Por ejemplo, Los vértices A y B son
consecutivos, los vértices A y C son no
consecutivos.
En la figura de la derecha, los segmentos
AC, AD, AE, BD y BE, son diagonales del
hexágono.
La suma de las
medidas de los lados del hexágono se llama
perímetro del hexágono.
P = l + l + l + l + l + l = 6 l
AB = BC = CD = DE = EF = FA = l
Perímetro = P = AB + BC + CD + DE + EF + FA
Número de lados Longitud de cada lado
Ejemplo:
Un hexágono regular tiene lado de medida 8u. (l = 8u.). Encontrar
su perímetro.
Ejemplo:
El perímetro es P = 6l = 6(8u) = 48u.
Ejemplo:
El perímetro de un hexágono regular (polígono de seis lados de
igual medida) es de 126u. Encontrar la medida del lado.
Ejemplo:
El perímetro es P = 126u., entonces la medida del lado es:
l = = =
u
u
6
126
6
21
P
A continuación se encontrará una expresión para calcular el
número de diagonales de un hexágono regular.
A B
C
DE
F
Ángulo
Interno
Diagonal
Lado
A B
C
DE
F
Lado
Un hexágono regular
tiene ángulos internos
congruentes de 120
cada uno.
Poseen ángulos
externos congruentes de
240.
Construcción
Geométrica
Dado un punto P
cualquiera trace una
circunferencia con
centro en P cuyo radio
sea igual al lado del
hexágono a construir.
Elegir un punto A sobre
la circunferencia y
trazar un diámetro que
cruce por A. Marcar el
otro punto donde este
diámetro interseca la
circunferencia como D.
Apoyando el compás en
el punto A trace un arco
que cruce O cortando
la circunferencia en dos
puntos marcados como
B y F.
Apoyando el compás
en D trace un arco
que cruce o cortando
la circunferencia en
dos puntos a los que
llamaremos C y E.
Una los puntos: A y B, B
y C, C y D, D y F, F y G,
E y A.
E F
D
CB
A
rr
r
Ma
tem
áti
ca
7
¿Sabías qué?

244. 236
• Número de diagonales de un hexágono regular.
En el hexágono regular de la figura se
pueden observar las diagonales:
AC, AD, AE, BD, BE, BF ,CE ,CF y DF
Observar que:
En total hay 18 diagonales, pero sólo
hay 9 diagonales diferentes.
El número de diagonales de un polígono regular de n lados se
calcula con la fórmula:
Número de diagonales = N
n n
d =
−( )3
2
Para el hexágono el número de lados es n=6. Entonces el número
de diagonales es:
Número de diagonales = Nd =
−
=
6 6 3
2
9
( )
Este es el número de diagonales que se obtuvo contando
directamente en la figura las diagonales del hexágono regular.
Ejemplo:
Encontrar el perímetro y el número de diagonales de los siguientes
polígonos regulares:
• Un heptágono regular con lado de medida 7u.
• Un octógono regular con lado de medida 8u.
• Nonágono con lado de medida 9u.
• Decágono con lado de medida 10u.
• Endecágono con lado de medida 11u.
Físico alemán. Uno de los
científicos más famosos
del siglo xx. Creador de
la Teoría Especial de la
Relatividad Probablemente,
la ecuación más conocida
de la física a nivel popular,
es la expresión matemática
de la equivalencia masa-
energía:
E = mc²
deducida por él como
una consecuencia lógica
de esta teoría. Por sus
explicaciones sobre el
efecto fotoeléctrico y sus
numerosas contribuciones
a la física teórica, en 1 921
obtuvo el Premio Nobel de
Física y no por la Teoría de
la Relatividad
Albert Einstein
(1 879 –1 955)
A B
C
DE
F
Nota histórica

245. 237
• Centro de un hexágono regular.
Se llama centro de un hexágono regular
a un punto del interior del hexágono que
equidista de los vértices del hexágono.
En la figura de la derecha, el punto P es el
centro del hexágono. El punto P equidista de
los vértices del hexágono. Los segmentos
que unen el punto P con los vértices tienen
la misma medida r.
PA = PB = PC = PD = PE = PF = r
Apotema de un hexágono regular.
Se llama apotema de un hexágono regular,
al segmento de recta perpendicular que une
el centro del hexágono con cualquiera de sus
lados.
En la figura de la derecha, el segmento PF es
la apotema. La letra a representa la longitud
de la apotema.
La apotema es perpendicular al lado
opuesto AB . En la figura el segmento PF
(la apotema) es perpendicular al lado AB .
El punto F es punto medio del segmento AB
, entonces AF
AB
= =
2 2
l . Donde l es la longitud
del lado.
¿Cómo se calcula la longitud de la apotema?
En la figura, el triángulo ∆PFA es rectángulo en
el vértice F. Esto quiere decir que el ángulo ∠PFA
tiene medida 90. Entonces, se puede aplicar el
teorema de Pitágoras al triángulo rectángulo
∆PFA.
r a a r a r2
2
2 2 2
2
2
2
2 2 2
=





 + ⇒ = −





 ⇒ = −






l l l
Apotema = a r r= −





 = −2
2
2
2
1
2 4
l
Donde l es la longitud del lado del hexágono.
Filósofo y matemático
griego.
Se atribuye a Pitágoras
haber transformado
la Matemática en
una enseñanza
liberal mediante la
formulación abstracta
de sus resultados, con
independencia del
contexto material en
que ya eran conocidos
algunos de ellos; éste
es, en especial, el caso
del famoso teorema que
lleva su nombre y que
establece la relación
entre las medidas de los
lados de un triángulo
rectángulo.
Pitágoras
(572 a.C. - 497 a.C.)
A B
C
DE
F
a
p
r
A B
C
DE
F
a
P
r
Lado
F
A B
C
DE
F
a
p
r
F
A P
F
r
Nota histórica

246. 238
• Suma de las medidas de los ángulos internos de un
hexágono regular.
La suma de las medidas de los ángulos internos de un polígono
regular de n lados, cuya región interior es convexa, se calcula con
la expresión:
(n - 2)180
En el caso del hexágono regular (n = 6), la suma de las medidas
de los ángulos interiores es:
(6 - 2)180 = (4)(180) = 720
La suma de las medidas de los ángulos internos de un hexágono
es 720 grados.
Para encontrar la medida de un ángulo interior de un polígono
regular, con región interior convexa, se divide la suma de las
medidas de todos los ángulos interiores, por el número de lados.
Así se tiene que:
Medida del ángulo interior =
n
n
−( )2 180
En el caso del hexágono regular:
Medida del ángulo interior
6 2 180
6
720
6
120
−( ) = =
• Ángulo central de un hexágono regular.
En la figura se presenta un ángulo central de
un hexágono regular.
El ángulo central mostrado es:
∠APB = ∠θ.
¿Cuál es la medida de un ángulo central de un hexágono regular?
El hexágono regular tiene 6 ángulos centrales con la misma
medida. La suma de las medidas de los 6 ángulos centrales es
igual a 360. Entonces la medida de un ángulo central es:
6 360
360
6
60m θ m θ∠ ∠= ⇒ = =
A B
C
DE
F
Ángulo Interno
A B
θ
El matemático griego
Pappus de Alejandría
fué el primero en
preguntarse porqué
las abejas guardan
la miel en hexágonos
cuando sería mas
sencillo construir
triángulos o cuadrados.
Él descubrió que al
construir hexágonos
las abejas utilizan el
mismo perímetro que
al construir triángulos
o cuadrados, pero el
área que encierra el
hexágono es mayor.
Por tanto eso les
permite almacenar
mayor cantidad de miel,
ahorrando al máximo la
producción de cera.
Ma
tem
áti
ca
7
¿Sabías qué?

247. 239
• Ángulo exterior de un hexágono regular.
El la figura se muestra un ángulo
exterior de un hexágono regular.
Observe que la suma de las medidas
de un ángulo exterior con la medida del
ángulo interior adyacente es igual a 180,
ya que un par lineal.
(Medida del ángulo exterior) + (Medida del
ángulo interior adyacente) = 180
Se sabe que un ángulo interno de un hexágono regular tiene una
medida de 120. Esto significa que la medida de un ángulo exterior
es de (180 - 120 = 60).
Por tanto se concluye que la medida de un ángulo central del
hexágono regular es igual a la medida de un ángulo exterior del
hexágono regular.
Medida de un ángulo central = Medida de un ángulo exterior
Una característica interesante del
hexágono regular es que está compuesto
por triángulos equiláteros.
¿Cómoseverificaque eltriángulo equilátero
es ∆PAB, es también isóceles?.
En el hexágono regular de la figura el
triángulo ∆PAB es isósceles porque tiene
dos lados de la misma medida.
(PA = PB = r)
Los ángulos de la base de un triángulo isósceles tienen la misma
medida, entones la medida del ángulo m∠α = m∠β es igual a la
medida del ángulo ∠y (m∠y).
Entonces tenemos que:
• m∠α = m∠β, son ángulos de la base de un triángulo isósceles.
• m∠α + m∠β + m∠θ = 180, suma de las medidas de los ángulos
interiores de un triángulo cualquiera.
• m∠θ = 60, por ser un ángulo central.
A B
α
θ
β
P
rr
C
DE
F
A B
C
DE
F
Ángulo Interior
Ángulo Exterior
Matemático alemán.
Entre 1 869 y 1870
cooperó estrechamente
con su colega
noruego Sophus Lie,
colaboración de la cual
se derivó el trabajo de
este último sobre los
denominados grupos
continuos, trabajo
que Klein incorporaría
posteriormente en
su propia obra. En
1 872, tras ingresar
como profesor en
la Universidad de
Erlangen, pronunció una
conferencia inaugural en
la que ofreció una visión
general de la geometría
desde el punto de vista
de la teoría de grupos,
que se conocería como
programa de Erlangen
y que había de ejercer
una poderosa influencia
en el desarrollo ulterior
de la disciplina.
Felix Klein
(1 849 - 1 925)
Nota histórica

248. 240
• m∠α + m∠β + 60 = 180 ⟹ m∠α + m∠α = 180 - 60
• m∠α + m∠α = 120 ⟹ 2m∠α = 120 ⟹ m∠α = 60.
• Como m∠α = m∠β, entonces m∠β = 60.
¿Qué se ha obtenido?
Se ha obtenido que m∠α = m∠β = m∠θ = 60, entonces el triángulo
∆PAB tiene sus tres ángulos de igual medida y es por lo tanto
equiángulo. Un triángulo equiángulo también es equilátero.
Entonces el triángulo ∆ABP es equilátero. Todos los triángulos
que forman el hexágono son equiláteros.
El lado del hexágono tiene medida igual al radio,(r = AB).
Donde r es la distancia del centro a cada vértice.
Ejemplo:
Encontrar la medida l del lado de un
cuadrado en función de la distancia r del
centro del cuadrado a cada vértice del
mismo.
Solución
Considérese un cuadrado de lado l como
el de la figura.
El triángulo ∆CEP es rectángulo en E.
Aplicando el teorema de Pitágoras
obtenemos:
r2
= (l
2
)
2
+ (l
2
)
2
⇒ r2
= 2l
2
4
⇒ r2
= l
2
2
Entonces:
2r2
= l
2
⇒ l
2
= 2r2
⇒ l= 2r2
⇒ l= 2 r
Ejemplo:
Encontrar la medida del lado de un hexágono regular en función
de la distancia r del centro del hexágono a cada vértice.
r
C
EP
l
2
l
2
A B
D C
P
r
l
2
E
l

249. 241
Solución
El hexágono está formado por triángulos
equiláteros, entonces, en particular, el triángulo
∆APB es equilátero, por tanto:
r = AB = l
Ejemplo:
Encontrar la medida del lado de un triángulo
equilátero en función de la distancia r del
centro del triángulo a cada vértice.
Solución
En el triángulo equilátero (∆ABC) de la
figura, los segmentos AB , AC y BC son medianas.
Entonces, la medida del segmento AD es AD
2
= l
2
.
Aplicando el teorema de Pitágoras a los triángulos
rectángulos ∆ADC y ∆ADP, obtenemos:
l
2
= (r + a)2
+ (l
2
)
2
ecuación(1) y r2
= a2
+ (l
2
)
2
ecuación((2)
De la ecuación (1) se obtiene:
l
2
= (r + a)2
+ (l
2
)
2
⇒ (r + a)2
= l
2
- l
2
4
(r + a)2
= 3l
2
4
⇒ (r+a)2
= 3l
2
4
a = 3
2
l - r
De la ecuación (2) se obtiene:
r a
a r
a r
2 2
2
2 2
2
2
2
2
4
4
= +






= −
= −
, de donde
A B
r
P
C
DE
F
F
r
r
P
a
C
A B
D
2
A D
P
C
r
a
l
r
l
2
Al trazar diagonales
desde un mismo
vértice de un polígono
se obtiene
(n - 2) triángulos.
Compruébelo en
un pentágono,
un hexágono, un
heptágono y un
octágono.
Ma
tem
áti
ca
7
¿Sabías qué?

250. 242
Igualando los resultados se obtiene:
3
2 4
3
2 4
2
2
2
2
2
− = − ⇒ −






= −r r r r
3
2
2
3
2 4
2
2 2
2






−





( )+ = −r r r
3
4
3
4
3
4 4
32 2 2
2
2
2
− + = − ⇒ + =r r r r
2
3 3= ⇒ =r r
Esta es la medida del lado del triángulo equilátero, en función de
la distancia r del centro a cada una de los vértices.
Actividad de grupo. Justifique cada paso del ejercicio precedente.
Propiedades de los ángulos externos de un
polígono regular.
En la figura de la derecha se presenta un hexágono regular. De
las propiedades del hexágono regular se sabe que el cuadrilátero
APEF es un paralelogramo.
Se sabe que los ángulos opuestos de un paralelogramo tiene la
misma medida. Además:
Los ángulos ∠α y ∠β forman un par lineal,
entonces se cumple:
m∠α + m∠β = 180 ecuación 1
Los ángulos ∠α y ∠θ forman un par lineal,
entonces se cumple:
m∠α + m∠θ =180 ecuación 2
Igualando las ecuaciones se obtiene:
m∠α + m∠β = m∠α + m∠θ
Simplificando se obtiene: m∠β = m∠θ.
Se ha obtenido que la medida del ángulo exterior es igual a la
medida del ángulo central.
Los radios de un
polígono regular son
congruentes.
Un radio de un polígono
regular biseca el ángulo
hacia el cual está
dibujado.
Para un polígono regular
de n lados se cumple:
El ángulo central mide:
360
n
Todo ángulo interno
mide:
n
n
−( )2 180
Todo ángulo externo
mide:
360
n
A B
F
E
α α
β θ
D
C
P
Ma
tem
áti
ca
7
¿Sabías qué?

251. 243
La suma de las medidas de los ángulos centrales de cualquier
polígono regular es igual a 360. Entonces se concluye que:
La suma de las medidas de los ángulos externos de cualquier
polígono regular es 360.
Los cálculos con las medidas de los lados y ángulos de cualquier
polígono regular se pueden realizar con las herramientas que
brinda la trigonometría, que será estudiada en Décimo Grado.
Sin hacer uso de la trigonometría, el proceso de resolución del
problema de la igualdad de medidas del ángulo central y el ángulo
externo de cualquier polígono regular es más extenso.
Se presenta el ejemplo del pentágono regular.
Ejemplo:
Un ángulo central de un pentágono regular tiene la misma medida
que un ángulo externo. Esta medida es igual a 72.
Solución
La medida del ángulo central de un pentágono
regular es: m∠x = 72
La suma de las medidas de los ángulos
internos de un pentágono regular es: 5(72)
= 540
La suma de las medidas de los 6 ángulos externos del pentágono
regular es: 5m∠y.
La suma de las medidas de los ángulos m ∠ y y m ∠ z es 180.
m∠y + m∠z = 180
Multiplicamos por el número de lados del `pentágono regular que
es 5.
5(m∠y + m∠z) = 5(180)
Pero m ∠ z = 108, entonces: 5(m∠y + 108) = 5(180)
5(m∠y + 108) = 5(180) ⟹ 5m∠y + 540 = 900
5m∠y + 540 = 900 ⇒ 5m∠y = 900 - 540 = 360
5 360
360
5
72m y m y∠ ∠= ⇒ = =
Por tanto, se ha obtenido que la medida del ángulo externo es:
m ∠ y = 72
Esta medida es igual a la medida del ángulo central.
z
y x
Nació en la ciudad de
Mileto, aproximadamente
en el 624 a. de C., y murió
en el 546 a. de C.
Fue maestro de
Anaximandro. Ninguno de
sus escritos sobrevivió,
por lo que es difícil saber
exactamente cuáles fueron
sus descubrimientos
matemáticos.
Probablemente se le
atribuyan descubrimientos
que no le corresponden.
Lo que sabemos de Thales
proviene de Aristóteles.
Primero fue a Egipto y
desde allí introdujo en
Grecia los estudios sobre
Geometría.
Inventó la matemática
deductiva.
Thales de Mileto
(624 a.C - 546 a. C.)
Nota histórica

252. 244
La circunferencia y el círculo.
Lea, analice e interprete.
¿Qué ideas tiene sobre los conceptos de circunferencia y el
círculo? ¿Cómo expresa los conceptos de circunferencia y círculo
en el lenguaje de la Matemática?
Iniciaremos con la definición de circunferencia.
La circunferencia.
En el medio que nos rodea se pueden encontrar con frecuencia
objetos que tiene forma de circunferencia. Las llantas de un
automóvil, la carátula de algunos tipos de relojes, etc. Todos estos
objetos tienen en común que representan a una circunferencia.
A continuación se presentan los conceptos geométricos que
justifican las propiedades de una circunferencia.
Definición. Se llama circunferencia, al conjunto de puntos del
plano que equidistan de un punto fijo llamado centro. La distancia
de cualquier punto de la circunferencia al centro se llama radio
El punto O es el centro. El punto C pertenece al
interior de la circunferencia pero no pertenece a
la circunferencia. El segmento OA cuya medida
es r, es el radio de la circunferencia. El punto A
pertenece a la circunferencia, el punto B es exterior
a la circunferencia.
Observaciones importantes.
• La circunferencia divide al plano en dos regiones, de manera
que todo punto del plano pertenece a una de estas regiones
o será un punto de la circunferencia.
• Se llaman puntos interiores, a todos aquellos puntos cuya
distancia al centro es menor que el radio de la circunferencia.
• Se llaman puntos exteriores, a todos los puntos cuya distancia
al centro sea mayor que el radio de la circunferencia.
Actividad:
Dibujar una circunferencia por medio de un compás y ubique:
Un punto interior.
Un punto exterior.
Un punto sobre la circunferencia.
C
A
B
r
O

253. 245
££ Curiosidad matemática.
Con un sólo corte recto puedes dividir un
pastel en dos partes. Un segundo corte que
atravieseelprimeroproduciráprobablemente
cuatro partes, y un tercer corte (ver la
ilustración) puede llegar a producir siete
partes. ¿Cuál es el mayor número de partes
que puedes lograr con seis cortes rectos?.
(Sugerencia: observa que los cortes pueden
ser: 2, 4,7,..)
(Fuente: Matemática para divertirse, Martin Gardner. Edición Original: Dover
Publications Inc., New York, 1 986, pág. 37.)
Elemento Concepto Gráfico
Cuerda
Segmento que une
dos puntos de la cir-
cunferencia.
Cuerda
B
A
Diámetro
Cuerda que pasa por
el centro
Diámetro
B
A
Arco
Cada una de los
conjuntosdepuntosen
que una cuerda divide
a la circunferencia. Se
suele asociar a cada
cuerda el menor arco
que delimita.
Arco B
A
Semicircunferencia
Es un arco que tiene
una longitud igual a la
mitad de la longitud de
la circunferencia.
El arco es una semi-
circunferencia.
Diámetro
B
A
Semicircunferencia
Semicircunferencia
Es considerado
el creador de la
Geometría Fractal, al
referirse al impacto
de esta disciplina
en la concepción
e interpretación de
los objetos que se
encuentran en la
naturaleza. En 1 982
publicó su libro Fractal
Geometry of Nature en
el que explicaba sus
investigaciones en este
campo. La geometría
fractal se distingue por
una aproximación más
abstracta a la dimensión
de la que caracteriza
a la geometría
convencional
Benoît Mandelbrot
(1 924 –2 010)
5
4 6
2
1
7
3
Nota histórica

254. 246
Actividad:
Dibuje una circunferencia con un compás y dibuje los elementos
de la misma. ¿Se puede decir que un diámetro es una cuerda?
Explique su respuesta.
• Posiciones relativas de un punto y una recta respecto a
una circunferencia.
Punto interior: Es un punto cuya distancia al centro
es menor que la medida del radio.
Punto de la circunferencia: Es un punto que
pertenece a la circunferencia. Su distancia al centro
es igual a la medida del radio.
Punto exterior a la circunferencia: Es un punto cuya distancia
al centro es mayor que la longitud del radio.
A
Recta secante: Corta a la circunferencia en dos puntos.
A
B
Recta tangente: Recta que tiene un punto en común con la
circunferencia.
A
Recta exterior: No tiene punto en común con la circunferencia
Interesante
Las nubes no son esferas,
las montañas no son
conos, las costas no son
círculos, y las cortezas de
los árboles no son lisas, ni
los relámpagos viajan en
una línea recta.
Benoît Mandelbrot
A
A

255. 247
Posiciones relativas de dos circunferencias.
Lea, analice e interprete.
• Circunferencias concéntricas: Dos circunferencias
son concéntricas, si la distancia entre sus centros es
cero, es decir, si tienen el mismo centro.
• Circunferencias congruentes: Dos
circunferencias son congruentes si
sus radios tiene la misma medida.
Radios de la misma medida:
r1
= r2
Sean las circunferencias O y O' con radios r y r', respectivamente
y r r'. Se llamará recta de los centros o línea de los centros a la
recta que contiene al segmento OO' y que une los centros de las
dos circunferencias.La distancia entre los centros O y O' es d.
• Circunferencias exteriores: Se
llaman circunferencias exteriores cuando
los puntos de cada una de ellas son
exteriores a la otra.
La distancia entre los radios es mayor que la suma de las medidas
de los radios.
OO' r + r'
• Circunferencias tangentes exteriormente.
Dos circunferencias son tangentes
exteriormente cuando tienen un
punto en común, (llamado punto
de tangencia P) siendo los demás
puntos de cada una exteriores a
la otra. La recta que pasa por los
puntos A y B es perpendicular a la
línea de los centros.
OO' = r + r'
0 = 0
r1
r2
0 0'M N
d
r r'
0 0'Pr r'
A
B
Dados tres puntos en
un mismo plano no
alineados existe una y
solo una circunferencia
que pasaría por ellos.
Si se dispone de tres
puntos A, B y C no
alineados en el mismo
plano, las mediatrices
de AB y BC se cortarán
en un punto y éste
es el centro de la
circunferencia que pasa
por A,B,C.
Compruébelo.
Ma
tem
áti
ca
7
¿Sabías qué?

256. 248
• Circunferencias tangentes interiormente.
Dos circunferencias son tangentes interiormente
cuando tiene un punto común, siendo los demás
puntos de una de ellas, interiores a la otra. A
es el punto de tangencia. OA = r, es el radio de
la circunferencia mayor. La distancia entre los
centros es:
OO' = r – r'.
• Circunferencias secantes.
Dos circunferencias son secantes si se
cortan en dos puntos A y B. La distancia
entre los centros OO' es menor que la
suma de las medidas de los radios.
OO' r + r'
• Las circunferencias son interiores.
Se dice que dos circunferencias son
interiores cuando todos los puntos de una
de ellas son interiores a la otra.
OO' = r – r'- AB
Definición. Normal a una circunferencia.
Se llama normal a una
circunferencia a la recta
perpendicular a la recta tangente
en el punto de tangencia. La
recta tangente y el radio son
perpendiculares en el punto de
contacto. La normal en cada
punto de la circunferencia pasa
por el centro.
Actividad:
Describa las posiciones relativas de dos circunferencias. Haga un
dibujo para cada caso.
0
0´
A
0
0´
A
B
r´
r
Actividad recreativa
El joven con turbante y
el gato.
¿Cuántos cuadrados
distintos puedes contar
en el dibujo del joven
con turbante?
¿Cuántos triángulos
distintos puedes contar
en el dibujo del gato?
(Fuente: Matemática
para divertirse, Martin
Gardner.Edición
Original: Dover
Publications Inc., New
York, 1986, pág. 38.)
0 0' A B
r'r
Tangente
Normal
A C
O

257. 249
Propiedades de los arcos.
• Arcos entre paralelas.
Los arcos de una circunferencia comprendidos entre paralelas,
son congruentes.
Caso I. Las dos paralelas AB y CD son secantes y
el segmento AB es paralelo al segmentoCD .El arco
PC tiene la misma medida que el arco PD. Cuando
dos arcos tienen la misma medida se dice que son
congruentes. El símbolo de congruencia es: ≅.
PC PD≅
Caso II. Una de las dos paralelas es secante CD
y la otra es tangente AB .
PC PD≅
CasoIII.Lasdosrectassonparalelasytangentes.
PMQ PNQ ≅
Actividad:
1. ¿Cómo encontrar la medida del radio de una
circunferencia si no se conoce el centro de la misma?
Sugerencia: Trazar dos rectas tangentes a la circunferencia
que sean paralelas.
2. Trazar una tangente a una circunferencia y verificar por medición
directa que es perpendicular al radio en el punto de contacto.
3. Complete:
a. ______________ cada mitad de la circunferencia.
b. ______________ segmento que une dos puntos de una
circunferencia.
c. ______________punto del cual todos los puntos de la
circunferencia
d. ______________ cuerda que pasa por el centro de la
circunferencia.
La medida s de un arco
de una circunferencia
es igual al producto de
la medida del radio r de
la circunferencia por la
medida del ángulo θ.
P
Q
r θ
La medida del PQ es
igual a:
s = rθ
Si el ángulo tiene una
medida igual a 2π
radianes
θ = 2π = 360
entonces el arco
se convierte en la
circunferencia
s = Lc
= r(2π)
Lc
= 2πr
Lc
es la longitud de la
circunferencia.
A
C
O
D
BP
P
O
A B
DC
P
O
A B
DC
NM
Q
Ma
tem
áti
ca
7
¿Sabías qué?

258. 250
El círculo.
Los círculos aparecen en diferentes estructuras del mundo que
nos rodea. Aparecen en las ciencias técnicas, en el arte y la
pintura. También se utiliza para nombrar regiones geográficas de
la Tierra. Las técnicas de construcción utilizan los círculos como
excelentes auxiliares para el diseño de obras de ingeniería y
arquitectura.
££ ¿Qué es un círculo?
Se llama círculo al conjunto de puntos del plano formado por
los puntos de la circunferencia unido con el conjunto de puntos
pertenecientes al interior de la circunferencia.
Esta definición describe un círculo cerrado, es decir que contiene
a su frontera que es la circunferencia.
El punto O es el centro. Este punto pertenece al círculo.
El punto E es exterior al círculo.
El punto A pertenece a la circunferencia, es decir,
a la frontera del círculo.
El punto B pertenece al círculo.
El segmento OA cuya medida es r, es el radio del círculo.
££ Observaciones importantes.
• Se llaman puntos interiores, a todos aquellos puntos cuya
distancia al centro es menor que la medida del radio.
• Se llaman puntos exteriores, a todos los puntos cuya
distancia al centro es mayor que la longitud del radio del
círculo. El punto E es exterior.
Actividad:
Enumere las semejanzas y diferencias entre una circunferencia y
un círculo.
B
A
E
r
O
El centro, radio
y diametro son
elementos comunes a
la circunferencia y al
circulo.
El diámetro equivale a
dos veces el radio:
D = 2r
por tanto el radio es la
mitad del diámetro
r
D
=
2
La longitud de la circun-
ferencia divide entre la
longitud de su diámetro
da como resultado el nú-
mero real π, cuyo valor
aproximado es:
π = 3,1415926535...
Ma
tem
áti
ca
7
¿Sabías qué?

259. 251
• Elementos de un círculo.
Segmento circular: Conjunto de puntos
del círculo limitado por una cuerda y el arco
correspondiente.
Semicírculo: Es el conjunto de puntos del
círculo limitado por un diámetro del círculo
Zona circular : Es el conjunto de puntos
del círculo limitado por dos cuerdas.
Sector circular: Conjunto de puntos del círculo
limitado por dos radios. Se acostumbra tomar
el área menor.
Corona circular: Conjunto de puntos del círculo
limitado por dos circunferencias concéntricas.
Trapecio circular: Un trapecio circular es la
porción de círculo limitada por dos radios y una
corona circular..
Propiedad
Todo diámetro perpendicular a una cuerda,
divide a ésta en dos segmentos congruentes.
CD AB AP PB⊥ ⇒ =
Propiedad
En una circunferencia o en circunferencias
congruentes, cuerdas congruentes
equidistan del centro.
AB ≅ CD ⇒ PO= QO
Un círculo está formado
por una circunferencia y
sus puntos interiores. El
círculo, a diferencia de
una circunferencia, es
una región.
C
r
A
A
B
A
B
A
B
C
D
A
B
A
B
C
D
A
B
C
P
D
A
B
C
P
D
Q
O
Ma
tem
áti
ca
7
¿Sabías qué?

260. 252
Propiedad
La recta tangente a una circunferencia es
perpendicular al radio en el punto de contacto.
La recta AB es tangente a la circunferencia en P y
el segmento OP es radio, entonces:
m∠APO = 90
Propiedad
Por cada punto de una circunferencia pasa una tangente y sólo
una. (Unicidad de la tangente).
En la figura se presenta la recta normal OP y la recta tangente AB
Estas rectas son mutuamente perpendiculares.
OP AB⊥
Actividad
Trabajemos en equipo.
Dibujamos una circunferencia con ayuda de un compás. Trazamos
una recta tangente a la circunferencia en un punto P y otra recta
tangente a la circunferencia en un punto Q (diferente de P). A
continuación trazamos una recta normal a la circunferencia en
cada punto P y Q. Las rectas normales se cortarán en punto O. El
punto O es el centro.
Polígonos regulares inscritos y circunscritos a una
circunferencia.
Lea, analice e interprete.
Un polígono se dice que está inscrito en
una circunferencia si sus vértices pertenecen a
la circunferencia. Un polígono se dice que está
circunscrito a una circunferencia, si sus lados son
tangentes a la circunferencia.
• Triángulo circunscrito a una circunferencia.
En un triángulo circunscrito a
una circunferencia, el punto de
intersección de las bisectrices, es
decir el incentro, es el centro de la
circunferencia inscrita.
A
B
P
O
Los puntos notables
en un triángulo son: el
baricentro, el ortocentro,
el incentro y el
circuncentro.
Cuadrado
Inscrito
Cuadrado
Circunscrito
Incentro
BisectrizBisectriz
Bisectriz
A
B
C
Ma
tem
áti
ca
7
¿Sabías qué?

261. 253
• Triángulo inscrito en una circunferencia.
En un triángulo inscrito
en una circunferencia, el
punto de intersección de
las mediatrices, es decir el
circuncentro, es el centro de
la circunferencia circunscrita
Importante
En un triángulo equilátero, los puntos notables: baricentro,
incentro, circuncentro y ortocentro coinciden.
• Cuadrado inscrito en una circunferencia.
Un cuadrado se dice que está inscrito en una circunferencia, si sus
cuatro vértices se encuentran en la circunferencia. En un cuadrado
inscrito en una circunferencia se cumple que:
r2
2 2 2 2
2 2
2
4 2
2=





 +





 = = ⇒ =
A
B
CO
l
l
2
l
2
• Pentágono inscrito en una circunferencia.
Un pentágono se dice que está inscrito en una circunferencia si
sus vértices pertenecen a la circunferencia.
En la figura, a es la apotema, los segmentos PA y PB son radios
de la circunferencia circunscrita.
A B
P
l
a
C
E
D
l
F
l
2
l
2
Circuncentro
Mediatriz
A
B
Mediatriz
Mediatriz
C
Reforzamiento:
Si un cuadrado
está inscrito en una
circunferencia de radio
de 1cm.¿Cuál es el valor
de cada lado?

262. 254
Por el teorema de Pitágoras, tenemos:
PA a r
a2
2
2 2
2 2
2
4
4
=





 + ⇒ =
+
; PA = r
l l2 2 2 2 2
4 4 2= − ⇒ = −r a r a
La apotema “a” se calcula como sigue:
4 4
2
2 2 2 2
2
a r a r= − ⇒ = −





l
l
Hexágono regular inscrito en una circunferencia.
Un hexágono está inscrito en una circunferencia si los vértices
pertenecen a la circunferencia.
En la figura, a es la apotema, r es el radio de la circunferencia
circunscrita, el segmento AB es el lado del hexágono y el
segmento FA tiene como medida la mitad de la medida del lado
FA =
l
2
. El triángulo ∆PAB es equilátero por lo que:
PA = PB = AB = l.
Por el teorema de Pitágoras, aplicado al triángulo rectángulo
∆PAF , tenemos:
FA r a a2
2
2 2
2
2 2
2 2
=





 = − ⇒





 = −
l l
l
l
l l
l
l
2
2
2
2
2
4
3
4
4
3
2 3
3
− = =
=
=
a
a
a
P
A B
C
l
DE
F
a
r
l
2
Se llama Ceviana, a
una recta que pasa
por un vértice de un
triángulo y corta en un
punto al lado opuesto o
a su prolongación. Las
Cevianas más conocidas
son: la que contiene
a la mediana, la que
contiene a la altura y
la que contiene a la
bisectriz. La mediatriz
no es considerada una
Ceviana, debido a que
no necesariamente
pasa por un vértice del
triángulo.
Ma
tem
áti
ca
7
¿Sabías qué?

263. 255
Nombres de algunos polígonos regulares.
Tipo de polígono N° de lados Gráfica
Triángulo 3
Cuadrilátero 4
Pentágono 5
Hexágono 6
Heptágono 7
Octógono 8
Nonágono 9
Decágono 10

264. 256
Tipo de polígono N° de lados Gráfica
Endecágono 11
Dodecágono 12
Tridecágono 13
Tetradecágono 14
Curiosidad matemática.
Observación importante.
A medida que los polígonos regulares inscritos tienen mayor
número de lados, sus perímetros se van acercando a la longitud
de la circunferencia. La longitud de una circunferencia es: Lc
=
2πr, donde r es la medida del radio.
Pastel pentagonal. Encontrar 5 maneras de
dividir un pastel pentagonal en triángulos. Una
de las posibilidades se presenta en la figura.
Refuerce sus conocimientos.
Actividad:
Realice las siguientes actividades:
a. Trace una recta tangente a una circunferencia en cualquiera de
sus puntos.
b. A partir del punto de contacto, trace un radio.
c. Mida con un transportador el ángulo que forma la recta tangente
con el radio.
d. ¿A qué conclusión llega?

265. 257
ACTIVIDADES FINALES DE LA SEXTA UNIDAD
I. Calcule:
a. La longitud de una circunferencia, sabiendo que su radio tiene una longitud de 5u.
b. El radio de una circunferencia sabiendo que su longitud es 24u.
c. La longitud de la apotema de un pentágono regular, sabiendo que su lado tiene una
medida 6u. y el radio de la circunferencia circunscrita tiene medida 4u.
d. La longitud del lado de un pentágono regular, sabiendo que su perímetro es igual a
25u.
e. El perímetro de un hexágono regular, sabiendo que la apotema mide 4u. y el radio de
la circunferencia circunscrita tiene longitud igual a 5u.
f. Verifique, realizando las mediciones correspondientes, que tres ángulos inscritos en
el mismo arco son congruentes; es decir, que tienen la misma medida.
g. Describa nuevos conceptos aprendidos, relacionados con la circunferencia y el
círculo
h. Enumere tres propiedades de la circunferencia y del círculo.
i. ¿Cuándo se dice que un polígono está inscrito en una circunferencia?
j. ¿Cuándo se dice que un polígono está circunscrito a una circunferencia?
k. Identifique objetos de la realidad circundante que ilustren los conceptos de
circunferencia y círculo
l. Haga un dibujo que ilustre la definición de línea poligonal.
II. Indique cuáles de las siguientes regiones poligonales son convexas y cuáles son
cóncavas.
(a) (b) (c) (d)

266. 258
III. En la figura dada a continuación se presenta una región poligonal no convexa. Divida
esta región en subregiones poligonales convexas. Utilice segmentos de recta para
realizar la división.
IV. Dibuje tres polígonos regulares diferentes y realice los siguientes cálculos:
a. El perímetro de cada polígono regular.
b. La suma de las medidas de los ángulos interiores de cada polígono regular.
V. Resuelva los siguientes problemas:
a. Calcule la apotema de un pentágono regular, sabiendo que el lado tiene medida 12u.
y el radio de la circunferencia circunscrita tiene una medida de 8 u.
b. Calcule la medida del radio de un hexágono regular, sabiendo que la apotema tiene
medida 13u. y el lado tiene medida 10u.
VI. Escriba los conceptos de:
a. Región poligonal convexa.
b. Polígono regular. Dé ejemplos de polígonos regulares.
c. Circunferencia.
d. Círculo.
VII. Construya:
a. Un segmento circular.
b. Un semícirculo de diámetro 5cm.
c. Una zona circular en un círculo de radio 1,5cm.
d. Una corona circular en dos circunferencias concéntricas de radios 2cm y 3cm.
e. Un trapecio circular en dos circunferencias concéntricas de radios 1cm y 2cm.

267. Área y Perímetro
de Regiones Poligonales
Unidad 7
Para Nicaragua, con la VIII Cumbre de Petrocaribe con sede en Managua, se ratificaron
los acuerdos sobre cooperación energética, programas sociales y productivos; en
especial, la construcción de la Refinería en Nicaragua; la inyección financiera para
impulsar la agricultura, mejorar la producción de arroz y café; y el desarrollo de mataderos
industriales y plantas procesadoras de leche y maíz.
Fuente: 19 digital.
02 de Julio 2 013.

268. 260
Área y perímetro de regiones poligonales
regulares. Área del círculo.
Introducción.
El concepto de área de una región aparece en muchos campos
de la ciencia y de la técnica.
En nuestro medio, es muy común escuchar frases como: área
ocupada por el territorio de Nicaragua, área del Lago Xolotlán,
área de un terreno de forma rectangular.
La idea de área de una región es una de las más utilizadas en la
Geometría y sus aplicaciones prácticas.
Históricamente la Geometría surge, precisamente, de la necesidad
de medir objetos geométricos y la medición de áreas representa
una de las actividades más importantes en la economía de
muchos países.
En esta unidad se dará continuidad al tema del cálculo de áreas
para polígonos regulares de más de cuatro lados. En el Séptimo
Grado fueron estudiadas las áreas de regiones triangulares y
áreas de regiones limitadas por cuadriláteros.
¿Qué se entiende por área de una región poligonal?
En la Unidad VI se ha estudiado el concepto de línea poligonal.
En esta unidad se estudiarán las regiones poligonales regulares
y sus áreas. Se concluirá la unidad con el estudio del área del
círculo y de sectores circulares.
• Región poligonal: Se llama región poligonal, al conjunto de
puntos de un plano limitado por una línea poligonal. La línea
poligonal se llama frontera o contorno de la región poligonal.
La Geometría tiene dos
grandes tesoros: uno es
el teorema de Pitágoras, y
el otro el número áureo. El
primero puede compararse
a una medida de oro, y
el segundo a una piedra
preciosa.
(Johannes Kepler).
Matemático alemán.
Hilbert nació en
Königsberg, en Prusia
Oriental (actual
Kaliningrado, Rusia).
El texto “Grundlagen
der Geometrie”
(Fundamentos de
la Geometría) que
Hilbert publicó en 1 899
sustituye los axiomas de
Euclides tradicionales
por un conjunto formal
de 21 axiomas, los
cuales evitan las
debilidades identificadas
en los de Euclides,
cuyos trabajos seguían
siendo usados como
libro de texto en aquél
momento. El enfoque de
Hilbert marcó el cambio
al sistema axiomático
moderno.
David Hilbert
(1 862 – 1 943)
El área es un concepto
que se refiere a regiones
poligonales.
Nota histórica
Frontera
P1
P2
P3
P4Región Polígonal
Vértice

269. 261
Área de una región poligonal.
En el caso de una región poligonal, el
área A se obtiene dividiendo en regiones
triangulares y sumando posteriormente
las áreas de las regiones triangulares
obtenidas. Sin perder generalidad,
presentamos el caso de una región
poligonal compuesta por cuatro regiones
triangulares. El área de la región
poligonal es:
A = A1
+ A2
+ A3
+ A4
Importante: Recordar que el área se calcula para regiones
poligonales. En algunos textos no se utiliza la frase “área de una
región poligonal”. En este texto se utilizará en todos los casos esta
frase.
• Área de una región limitada por un pentágono regular.
Considere la región pentagonal de la figura.
Observe que la región pentagonal está formada
por 5 regiones triangulares que tiene la misma
área cada una.
El área de cada región triangular es:
1
2
la ,
donde l es la medida del lado y “a” es la medida
de la apotema y también es la medida de la altura
de cada región triangular.
Como son 5 regiones triangulares, entones el área de la región
limitada por el pentágono es:
Área =





 = ( )5
1
2
1
2
5l la a
Pero 5l es el perímetro del pentágono regular. Se simboliza el
perímetro con la letra P. Entonces, el área buscada es:
Área =
Pa
2
El área es igual al perímetro por la medida de la apotema dividido
por 2.
• Una región poligonal
está limitada por
un polígono. La
región poligonal
está formada por
el conjunto de
puntos interiores del
polígono.
• Un pentágono
regular tiene 5 lados
de la misma medida
y cinco ángulos
interiores de la
misma medida.
• El perímetro de un
pentágono regular
es igual a la suma
de las medidas de
sus lados. Es decir:
Perímetro = P = 5l
Donde l, es la lon-
gitud de cada lado
P r
a
A B
C
D
E
F
A1
A2
A3
A4
P
A B
F
Ma
tem
áti
ca
7
¿Sabías qué?

270. 262
• Área de una región limitada por un hexágono regular.
Considere la región hexagonal de la figura.
Observe que la región hexagonal está formada
por 6 regiones triangulares que tiene la misma
área cada una.
El área de cada región
triangular es:
1
2
a donde l
es la medida del lado y a es la medida de la
apotema y también es la medida de la altura
de cada región triangular.
Como son 6 regiones triangulares, entones el área de la región
limitada por el hexágono es:
Área= 6
1
2
1
2
6a





 = ( )a
Pero 6l es el perímetro del hexágono regular. Se simboliza el
perímetro con la letra P. Entonces, el área buscada es:
Área = P.a
2
El área es igual al perímetro por la medida de la apotema dividido
entre 2.
Actividad:
Resolver cada uno de los problemas siguientes:
1. Un hexagono tiene 23,38m2
de área y 3 metros de lado.
Encuentre su apotema.
2. Encuentre el área y perímetro de un hexágono regular de
lado 1,49 cm y apotema 1,29 cm.
3. Calcule el perímetro y área de un pentágono regular,
sabiendo que su lado es 5,52 cm y apotema de 3,8 cm.
4. Un octágono regular tiene 40 cm2
de área y 60 cm de
perímetro. Halle el valor de cada lado.
A B
r
P
C
DE
F
F
a
Curiosidades
matemáticas
¿Qué relación existe
entre las áreas de los
triángulos equiláteros
de la figura?
Sugerencia: Rotar el
triángulo pequeño un
ángulo de 180.
P
A B
F
a
Importante
El área de un polígono
regular de l lados se
obtiene mediante la
formula:
Área = P.a
2
donde P es el
perímetro del polígono
y a su apotema.

271. 263
5. En las figuras dadas, encuentre la apotema y el área de cada
polígono regular dado.
6. Encuentre el área de un octágono regular con lados de
longitud 5 y apotema a.
7. Encuentre el área de un hexágono regular con apotema 3 3
8. Si el apotema de un hexágono regular es 5 m, ¿Cuáles son el
perímetro y el área?
9. Si el área de un hexágono regular es 36 3 2
cm , ¿cuáles son los
apotema y la longitud de cada lado?
10. Si un triángulo equilátero y un hexágono regular tiene el mismo
perímetro, demuestre que la razón entre sus áreas es 2 a 3.
11. El área de un hexágono regular es de 50 3 pies cuadrados.
¿Cuáles son el perímetro y la apotema?
12. La longitud de los lados de un octágono regular es 2. ¿Cuál es
su apotema?
13. Don Ramón quiere construir un corral con 100 metros de valla
y ha de decidir la forma del corral. Rellénese la siguiente tabla
y véase si se le puede hacer alguna recomedación al granjero.
Longitud Ancho Perímetro Área
48 m 100 m
45 m 100 m
40 m 100 m
35 m 100 m
30 m 100 m
25 m 100 m
a a a
1 2 3
a

272. 264
Observe que a medida que el número de lados del polígono
regular aumenta, su perímetro se acerca más a la longitud de
la circunferencia. Por tanto, la región limitada por los polígonos
regulares se acerca más a un círculo. Entonces el área de la
región se acerca al área del círculo.
Se sabe que el área de una región poligonal regular de “n” lados
es A = Pa
2
. En el caso del círculo, el perímetro es P = 2πr, y la
apotema es el radio “r”, entonces el área del círculo es:
A = Pa
2
= (2πr)(r)
2
= πr2
⇒Área del círculo = πr2
Tipo de polígono N° de lados Gráfica
Endecágono 11
Dodecágono 12
Tridecágono 13
Tetradecágono 14
Actividad:
Investigue el nombre de un polígono de:
a. 15 lados.
b. 16 lados.
c. 17 lados.
d. 18 lados.
El área de una región
poligonal inscrita en un
círculo se acerca más
al área del círculo a
medida que el número
de lados de la región es
más grande. Al mismo
tiempo, la medida de la
apotema se acerca a la
medida del radio.
Entonces, el área del
círculo es:
A = Pa
2
= (2πr)(r)
2
= πr2
Área del círculo = πr2
El valor de P se ha
aproxímado a 2πr a
medida que aumenta
el número de lados del
polígono regular inscrito.
Ma
tem
áti
ca
7
¿Sabías qué?

273. 265
Áreas de círculos y sectores circulares.
Área
Círculo A = πr2
r
Sector
circular
A
r
sc =
α2
360
r
α
Corona
circular
Área del círculo mayor
menos el Área del circulo
menor
A = πR2
- πr2
R
r
α
Trapecio
circular
α
r
R
Segmento
circular
área del sector circular
menos el área de la
región triangular
A
r
A A B
α2
360
∆ O( (= −
A
B
O
α
r
r
El área de un sector
circular es igual a la
mitad del producto de
la medida del radio “r”
elevada al cuadrado, por
la medida del ángulo θ.
P
Q
θ
r
En símbolos se escribe:
Área = 1
2
r2
θ
Si el ángulo tiene una
medida igual a 2π
radianes (θ = 2π = 360°),
entonces, el sector
circular se convierte en
todo el círculo. El área
es,
Área = 1
2
r2
(2π)
Área = πr2
Esta es la expresión para
calcular el área de un
círculo de radio “r”
Ma
tem
áti
ca
7
¿Sabías qué?

274. 266
Trabajemos en equipo.
Actividad:
Resolver los siguientes ejercicios:
a. Encontrar el radio de un círculo, si se conoce que su área es
igual a 25πu2
b. Encontrar el área de un sector circular, si se conoce que el
radio mide r = 4u y el ángulo central mide α =45.
c. Encontrar el área de una corona circular, si se conoce que el
radio r = 5u y el radio R = 10u.
d. Encontrar el área de un trapecio circular, si se conoce que el
radio r = 7u, el radio R = 9u y el ángulo central α = 60.
e. Encontrar el área de un segmento circular, si se conoce que
el radio r = 4u y el área de la región triangular es igual a 20u
α = 45.
Ángulos notables en la circunferencia.
• Ángulo central: Es el ángulo cuyo vértice
es el centro de la circunferencia. El ∠AOB
es un ángulo central. A todo ángulo central
le corresponde un arco de circunferencia
comprendido entre los lados del ángulo.Así
el ángulo ∠AOB subtiende el. La medida de
un ángulo central es igual a la medida del
arco AB comprendido entre sus lados.
m∠AOB = mAB.
• Ángulo inscrito: Es el ángulo formado
por dos cuerdas contenidas en los rayos
del ángulo y que tiene su vértice sobre
la circunferencia. El ∠A es un ángulo
inscrito que subtiende el arco BC.
A continuación se formulan algunas
propiedades de los ángulos notables en una circunferencia.
Propiedad. La medida de un ángulo inscrito es igual a la
mitad de la medida del arco subtendido. La demostración
de esta proposición se realiza más adelante.
Las regiones
sombreadas son las
regiones interiores de
los ángulos. Los ángulos
están formados por la
unión de dos rayos no
colineales con vértice u
origen común.
r
A
B
O r
Ma
tem
áti
ca
7
¿Sabías qué?
A
B
C

275. 267
• Ángulo interior: Es aquel que está determinado
por dos cuerdas que se cortan en el interior
de un círculo. El ∠ARC (o bien el ∠BRD) es un
ángulo interior. Los arcos comprendidos entre
sus lados son AC y BD .
Propiedad. Un ángulo interior (∠ARC) tiene por medida la
semisuma de las medidas de los arcos comprendidos entre
sus lados.
• Ángulo exterior: Es un ángulo
determinado por dos secantes que
se intersecan en un punto exterior a
la circunferencia. El ∠E es un ángulo
exterior, AC y BD son los arcos
comprendidos entre sus lados.
Propiedad. Todo ángulo exterior (∠E) tiene por medida la
semidiferencia de las medidas de los arcos comprendidos
entre sus lados.
D
• Ángulo semi-inscrito: Es aquel que tiene su
vértice en la circunferencia; uno de sus lados
es una secante y el otro es una tangente. El
∠A es semi-inscrito y se dice que AB es el arco
comprendido entre sus lados.
Propiedad. El ángulo semi-inscrito (∠A) tiene por medida la
mitad de la medida del arco subtendido.
m∠A =
2
mAB
Propiedad. Todo ángulo inscrito en una
circunferencia, tiene por medida la mitad
de la medida del arco comprendido entre
sus lados.
r
A
B
O
C D
R
A
C
O
D
B
E
Reto matemático.
Observa los siguientes
cálculos:
1 = 12
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7 = 42
1 + 3 + 5 + 7 + 9 = 52
Puedes continuar con
la secuencia. ¿A qué
generalización puede
llegar?
Este problema lo
resolvió el matemático
ruso A. N. Kolmogórov a
la temprana edad de 5
años.
A
O
B
C
O
B
A

276. 268
Para la demostración de la medida de un ángulo inscrito, se deben
considerar tres casos, de acuerdo con la posición relativa de las
cuerdas que forman el ángulo y el centro de la circunferencia.
Caso I. La figura representa el primer caso cuando uno de los
lados del ángulo inscrito contiene al diámetro.
Se traza un radio auxiliar OB, para que se forme el ∆AOB.
Hipótesis: ∠CAB es un ángulo inscrito en la circunferencia.
Tesis: ∠ARC =
2
mBC
Demostración. La demostración se basa en la siguiente figura:
C
O
B
A
Paso Afirmación Justificación
1 ∠CAB es un ángulo inscrito Por hipótesis
2 BO es un radio Por construcción
3 ∠A ≅ ∠ABO
El ∆AOB es
isósceles
4 m∠COB = mBC El ∠COB es central
5 m∠A + m∠ABO = m∠COB
Teorema del ángulo
externo
6 m∠A + m∠A = m∠COB Pasos 3 y 5
7 2m∠A = m∠COB Por el paso 6
8 ∠ARC =
2
mBC
Dividiendo entre 2
• El teorema del
ángulo externo
afirma que la
medida de un
ángulo externo de
un triángulo, es
igual a la suma de
las medidas de los
ángulos interiores no
adyacentes.
• Un triángulo que
tiene dos lados de
la misma medida,
se dice que es
isósceles. En un
triángulo isósceles,
los ángulos de
la base tienen la
misma medida.
Ma
tem
áti
ca
7
¿Sabías qué?

277. 269
Caso II. El centro de la circunferencia está en
el interior del ángulo inscrito ∠BAC.
Caso III. El centro de la
circunferencia está en el
exterior del ángulo inscrito ∠BAC.
Propiedad. Todos los ángulos inscritos en el
mismo arco, tienen la misma medida.
m∠BDA = m∠BCA
Propiedad. Todo ángulo inscrito en una semicircunferencia tiene
medida 90 grados es decir m∠ACB = m∠ADB = 90
Actividad:
Dibujar un semicírculo e inscribir diferentes
ángulos en él. Mida con un transportador cada
uno de los ángulos dibujados.
Actividad:
Demostrar que todo ángulo inscrito en un semicírculo tiene medida
90. m∠x + m∠y = 90.
Demostración
Proposición Justificación
1 AO ≅ OC y BO ≅ OC OB, OC y BO son radios.
2
Los triángulos ∆AOC y ∆BOC
son isósceles
Tiene dos lados de la misma medida.
3 m∠x = m∠z y m∠y = m∠v
Son ángulos de la base de un triángulo
isósceles.
4 m∠x + m∠y + m∠z + m∠v = 180
Suma de las medidas de los ángulos
interiores de un triángulo
5 m∠x + m∠y + m∠x + m∠y = 180 ∠z ≅ ∠x y ∠v ≅ y
6 2m∠x + 2m∠y = 180
m∠x + m∠x = 2m∠x
y
m∠y + m∠y = 2m∠y
7 m∠x + m∠y = 90
Dividiendo entre 2 ambos lados de la
igualdad
C
O
B
A D
C
O
B
A
x y
z u w v
O
A B
C
C D
A B
O

278. 270
Trabajemos en equipo.
Actividad:
Discutir con sus compañeros de clase la demostración precedente.
Justifique cada uno de los pasos de la misma.
Actividad:
Ilustrar con un dibujo los conceptos de: ángulo central, ángulo
inscrito, ángulo semi-inscrito, ángulo exterior a una circunferencia.
Actividad:
Verificar por medición directa, que todos los ángulos inscritos en
el mismo arco, tienen la misma medida.
Ejercicios resueltos.
Refuerce sus conocimientos.
1. Calcular el área de las regiones que se presentan a
continuación:
a.
8 cm
6 cm
b.
4 cm 3 cm
7 cm
4 cm
Solución:
a. La figura está formada por una región rectangular coronada en
sus extremos por una región semicircular. Entonces,
A cm cm cm= ( )( )+
( )( ) +
( )( ) = +( )8 6
3
2
3
2
48 9 2π π
π
2 2
b. Una de las posibles soluciones es la siguiente:
A = (4cm)(4cm) + (3cm)(4cm) + (3cm)(3cm)
A = 16cm2
+ 12cm2
+ 9cm2
= 37cm2
Recordar.
El área de una región
rectangular es igual a
la medida de la base
“b” multiplicada por la
medida de la altura h.
Área = b.h
El área de una región
cuadrada es igual a
la medida del lado l
elevada al cuadrado.
Área = l
2
El área de un
semicírculo es igual a
la mitad del producto
de la constante “π” por
la medida del radio r
elevada al cuadrado.
Área = π.r2
2
La medida del radio es
igual a la mitad de la
medida del diámetro.
r = d
2
Donde d es la medida
del diámetro de la
circunferencia.

279. 271
Actividad:
Discutir las soluciones del ejercicio anterior. Plantear otras variantes
de solución para cada uno de los incisos a y b.
2. ¿Cuál es el área de la parte sombreada en las siguientes
regiones? En el inciso a) se dan tres circunferencias y en el
inciso b) se da un cuadrado de lado de medida 10 cm.
a
6 cm 3 cm
b
10 cm
Solución: Para la región sombreada a)
tenemos:
A cm cm cm cm=
( ) −
( ) +
( ) =
π π π π4 5
2
3
2
1 5
2
27
4
2
2
2
2
2
2 2, ,
Actividad:
Resolver el inciso b).
3. Calcule el área de las siguientes regiones sombreadas:
4 cm
4 cm
4 cm
4 cm
6 cm
11 cm
a. b.
Soluciones:
a) A = (8cm)(4cm) = 32 cm2
b) A = (6)(4) cm2
+
1
2
(5)(4)cm2
-
(π)(2)2
2
= (34 - 2π)cm2
Reforzamiento:
El área de una piscina
circular incluyendo
el borde, es de 28,27
m2
¿Cuántos metros
cuadrados de baldosa
serán necesarios para su
construcción considerando
que el radio de la piscina
es 2,5 m?

280. 272
Actividad:
1. Calcular el área de las siguientes regiones suponiendo que
cada cuadrito representa 1cm2
.
a)
b)
c)
2. ¿Cuál es el perímetro de las siguientes figuras?
a. b.
Solución: del ejercicio 1 caso a:
1. Observar que cada cateto del triángulo rectangulo tiene por
medidas 3 y 4 cm respectivamente.
2. Por consiguiente, uno de los catetos es la altura y el otro es su
base, dependiendo de como se considere la figura.
3. El área del triángulo sombreado es : A =
4cm(5cm)
2
4. Entonces el área es 10 cm2
• El área de una
región limitada por
un trapecio es igual
al producto de la
suma de las bases
por la altura y el
resultado se divide
por 2.
área =
(B + b).h
2
• El área de una
región triangulares
igual a la mitad de
la medida del lado b
por la medida de la
altura h.
área =
b . h
2
• El área de una
región limitada por
un paralelogramo es
igual al producto de
la medida de la base
b por la medida de
la altura h.
Área = b.h
Ma
tem
áti
ca
7
¿Sabías qué?

281. 273
3. Resuelva:
Expresar el área de la región rectangular en
términos de R y x.
A = x . y
y
R
x R x
R x
2 2
4
4
1
2
42
2 2 2
2 2




 =
−
= −= −
A = x . y ⇒ A = x . 4R2
- x2
Justificar las operaciones realizadas para obtener la expresión
para el área.
Actividad:
Realizar en grupo las siguientes actividades:
a. Calcule el área de regiones poligonales existentes en el entorno.
(área de las regiones rectangulares representadas por las
paredes del salón de clase, del piso, del techo, etc.).
b. Calcule el área de la región ocupada por el piso del aula de
clase, calculando el número de ladrillos y multiplicando al área
de la región determinada por cada ladrillo por el número de
ladrillos.
c. Calcule el área de la región rectangular representada por la
pizarra.
d. Calcule el área da las regiones representadas por las ventanas
del salón de clase.
Trabajemos en equipo.
Resolver los siguientes ejercicios:
1. La longitud de una circunferencia es
43,96 cm. ¿Cuál es el área del círculo
limitado por la circunferencia dada?
2. En un parque de forma circular de 7 m
de radio hay situada en el centro una
fuente, también de forma circular, de 5
m de radio. Calcule el área de la zona
de paseo. La región sombreada.
y
x
R y
x1
2
1
2
• El teorema de
Pitágoras afirma
que, en un triángulo
rectángulo, el
cuadrado de la medida
de la hipotenusa es
igual a la suma de
los cuadrados de
las medidas de los
catetos.
a
c
b
A B
C
a2
= b2
+ c2
a: es la medida de la
hipotenusa.
b: es la medida de uno de
los catetos.
c: es la medida del otro
cateto.
r = 5 mR = 7 m
Ma
tem
áti
ca
7
¿Sabías qué?

282. 274
3. La superficie de una mesa está formada
por una región cuadrada de 1m de lado y
4 círculos inscritos en la región cuadrada.
Calcule el área de la región sombreada.
4. Encuentre el perímetro de un trapecio isósceles cuya base
mayor es 10 cm, base menor de medida 4 cm y altura de
medida “h”.
También encuentre el área de la región limitada por el trapecio
isósceles. Sugerencia: Aplique el teorema de Pitágoras para
calcular la medida de la altura “h”.
5 cm 5 cm
4 cm
10 cm
h
5. Un problema curioso.
¿Con qué rapidez puedes calcular la longitud de la diagonal
del rectángulo que va de la esquina A a la esquina B?
A
B6 4
6. Dibuje un octágono inscrito en un círculo .
Si cada lado del polígono mide 3 cm y su apotema es de 3,62
cm ¿Cuál es el aréa de la región fuera del octágono y que es
común al circulo?
7. Hallar el área de un dodecágono regular (12 lados) si cada
lado mide 10 cm y la apotema mide 18,66 cm.
8. Hallar el área de un heptágono regular si cada lado mide 8cm
y la apotema mide 8,31cm.
1u

283. 275
Construcciones geométricas con regla y
compás.
Lea, analice e interprete.
Introducción.
Las construcciones geométricas con regla y compás se remontan
a la época de Euclides y Platón. Es importante tener en cuenta que
la regla y el compás euclidianos son instrumentos sin graduación.
Platón consideraba la regla y el compás como instrumentos ideales,
en cambio consideraba los demás instrumentos como mecánicos.
Las construcciones geométricas juegan un papel muy importante
en el desarrollo del pensamiento lógico de los estudiantes. Los
conceptos y objetos que son construidos por los estudiantes, pasan
a formar parte de su formación, mientras que aquellos conceptos
que son sólo transmitidos al estudiante, pueden ser utilizados en
un número muy reducido de situaciones que tienen relación directa
sólo con los modelos resueltos en clase.
Construcciones básicas.
a. Construcción de un triángulo equilátero, conociendo el lado del
triángulo.
Sea AB un segmento cuya magnitud es a.
aA B
Paso 1. Con centro en el punto A, se
traza una circunferencia de radio a.
Paso 2. Con centro en el punto B, se
traza una circunferencia de radio a.
Las circunferencias se intersectarán
en los puntos C y D.
Los puntos A, B y C, determinan el triángulo equilátero ∆ACB, de
lado con medida a. (ver la figura 1).
El compás puede
trazar circunferencias
de cualquier radio
dado, no tiene ninguna
marca que permita
repetir una abertura
predeterminada. Sólo
puede abrirse entre
puntos que hayan
sido previamente
construidos, así que
en realidad su única
función es trazar
una circunferencia, o
parte de ella, con un
centro predeterminado
y un radio también
determinado por un
punto prefijado.
La regla carece de
marcas que permitan
medir con ella y sólo
tiene un borde, algo
imposible en las reglas
comunes. Puede usarse
para trazar una recta
entre dos puntos que
ya existen en el papel,
o bien prolongar una
recta.
A B
C
D
a
Figura 1
Ma
tem
áti
ca
7
¿Sabías qué?

284. 276
b. Construcción del punto medio de un segmento dado AB .
Los pasos de la construcción son
los mismos que en la construcción
anterior. Solamente resta trazar el
segmento de recta CD que corta al
segmento de recta AB en el punto E.
En la figura de la derecha, el punto E
es el punto medio del segmento AB
. La recta que pasa por los puntos C
y D es la mediatriz del segmento AB .
c. Construcción de una recta perpendicular a una recta dada por
un punto que pertenece a ella.
Sea  una recta y P un punto que pertenece a la recta.
A P B

Figura 3
Paso 1. Con centro en P trazamos una circunferencia que corte a
la recta  en dos puntos A y B. (Ver la figura 3)
Paso 2. Con centro en A se
traza una circunferencia de
radio mayor a la distancia
entre A y P, y con centro en B
se traza una circunferencia del
mismo radio que el anterior.
Sean Q y R los puntos de
intersección de estas dos
circunferencias. La recta m que
pasa por los puntos Q y R, es perpendicular a la recta  en el
punto P. (ver la figura 4).
Trabajemos en equipo.
Actividad:
Utilizando regla y compás, realice las tres construcciones
anteriores. ¿En el dibujo de la construcción del inciso c., qué tipo
de triángulos son los triángulos ∆AQB y ∆ARB?
• Se llama punto
medio de un
segmento, al
punto que divide al
segmento dado en
dos segmentos de
igual medida.
• Dos rectas
diferentes son
perpendiculares si al
cortarse forman un
ángulo de 90.
A B
C
D
E
Figura 2
A B
m
l
P
Figura 4
Ma
tem
áti
ca
7
¿Sabías qué?

285. 277
d. Construcción de una recta perpendicular a una recta  por un
punto P, fuera de ella.
Paso 1. Con centro en P se traza una circunferencia que intersecte
a la recta  en los puntos A y B.
Paso 2. Con centro en A y en B se trazan dos circunferencias del
mismo radio. Sea Q uno de los puntos de intersección de estas dos
circunferencias.
Figura 5
A B
m
l
P
La recta que une los puntos P y Q es perpendicular a la recta  (ver
la figura 5)
e. Construcción de la bisectriz de un ángulo dado.
Sea ∠AOB el ángulo dado.
Paso 1. Con centro en el punto
O se traza una circunferencia
que intersecte al segmento OA
en el punto P y al segmento OB
en el punto Q.
Paso 2. Con centro en el punto
P se traza una circunferencia de
radio PQ y con centro en el punto
Q se traza una circunferencia
con el mismo radio PQ. Sea R uno
de los puntos de intersección de
estas dos circunferencias. (ver
la figura 6).
El rayo que tiene origen en el punto O y pasa por el punto R, biseca
al ángulo ∠AOB (ver la figura).
Importante.
La recta que pasa
por los puntos de
intersección de dos
circunferencias, es
perpendicular a la
recta que contiene
a los centros de la
circunferencia. (ver el
dibujo de la construcción
d)
Se llama bisectriz de un
ángulo, al rayo que tiene
como origen el vértice
del ángulo y divide al
ángulo en dos ángulos
de la misma medida.
Figura 6
P
Q
R
O
Ma
tem
áti
ca
7
¿Sabías qué?

286. 278
f. Construcción de triángulo
escaleno (sus tres lados son de
diferente medida) conociendo
sus tres lados.
Suponer que los lados del triángulo
tienen medidas: a,b y c.
Paso 1. Se traza un segmento de
recta AB con medida a.
Paso 2. Con centro en el punto A, se traza una circunferencia con
radio de medida b.
Paso 3. Con centro en el punto B, se traza una circunferencia con
radio de medida c.
Paso 4. Las circunferencias trazadas se cortarán en los puntos C
y D. (ver la figura 7).
Al unir los segmentosAC , BC y AB , se obtiene el triángulo escaleno
∆ABC. Observar que también se puede trazar el triángulo ∆ABD
que tiene las mismas dimensiones y la misma forma que el
triángulo ∆ABC.
g. Construcción de una recta
paralela a una recta dada l
por un punto dado P.
Paso 1. Construir una recta n
perpendicular a la recta dada
l , que pase por el punto P. Las
rectas l y n se cortan en
el punto P.
Paso 2. Construir una recta m perpendicular a la recta n en el
punto P que pertenece a la recta n .
Las rectas l y m son paralelas.
h. Construcción de una circunferencia
circunscrita a un triángulo.
Se da un triángulo ∆ABC.
Paso1. Construir la mediatriz de dos de
los lados del triángulo. Basta con construir
dos mediatrices, ya que la tercera pasa por
el punto de intersección de las otras dos
mediatrices.
A
B
CO
Figura 9
n
P
m
Figura 8
A B
C
D
a
b
c
Figura 7

287. 279
El punto de intersección de las mediatrices, el punto O en la gráfica,
es el centro de la circunferencia circunscrita y se llama circuncentro.
El radio de la circunferencia circunscrita es el segmento que une
en centro de la circunferencia con cualquiera de los vértices del
triángulo. En la figura el radio es r.
i. Construcción de una circunferencia
inscrita en un triángulo.
Se da un triángulo ∆ABC.
Paso1. Construir la bisectriz de dos
de los ángulos del triángulo. Basta con
construir dos bisectrices, ya que la
tercera pasa por el punto de intersección
de las otras dos bisectrices.
El punto de intersección de las bisectrices y el punto O en la gráfica,
en el centro de la circunferencia inscrita y se llama incentro. El radio
de la circunferencia circunscrita es el segmento perpendicular que
va del punto O (el centro) al punto D.
Trabajemos en equipo.
Actividad:
Realice con regla y compás las construcciones indicadas en los
incisos anteriores (d, e, f, g, h, e i).
j. Construir una circunferencia que pase por tres puntos.
Paso 1. Trazar un triángulo por los tres puntos dados. Esto siempre
es posible cuando los tres puntos son no colineales.
Paso 2. Construir dos de las tres mediatrices de los lados del
triángulo. El punto de intersección de las mediatrices es el
circuncentro o centro de la circunferencia circunscrita. El radio de
la circunferencia circunscrita es el segmento que une el centro con
cualquiera de los vértices del triángulo.
Actividad:
Realizar la construcción de una circunferencia circunscrita a un
triángulo isósceles.
• Una circunferencia
está inscrita en un
triángulo, si sus tres
lados son tangentes a
la circunferencia.
• Por tres puntos no
colineales siempre
es posible trazar una
circunferencia.
BisectrizBisectriz
O
r
A B
C
D
Figura 10
Ma
tem
áti
ca
7
¿Sabías qué?

288. 280
k. Construcción de un pentágono regular.
Paso 1. Trazar una circunferencia con
una abertura cualquiera del compás
con centro en el punto O.
Paso 2. Trazar dos segmentos (AB) y
(CD) perpendiculares que se corten en
el centro de la circunferencia.
Paso 3. Construir el punto medio M
del segmento OC.
Paso 4. Trazar el segmento MA.
Paso 5. Con M como centro y con radio r = MA, trazamos una
circunferencia que corta al segmento CD en el punto N. El
segmento AN es el lado del pentágono regular.
Paso 6. Partiendo del punto A y con una abertura del compás
tomado los puntos A y N, marcar sobre la circunferencia cuatro
puntos que, con el punto A son los 5 vértices del pentágono
regular. (ver la figura 11).
Trabajemos en equipo.
Actividades:
a. Construcción de un hexágono regular.
Realizar la construcción de un hexágono regular siguiendo los
pasos siguientes:
Paso 1. Trazar una circunferencia con cualquier abertura del
compás.
Paso 2. Con el mismo radio y apoyándose en cualquier punto
de la circunferencia, trazar arcos sobre la circunferencia hasta
marcar los seis vértices del hexágono regular.
b. Construcción de un decágono regular.
Realizar la construcción de un decágono regular siguiendo los
pasos siguientes:
Paso 1. Construir un pentágono regular.
Paso 2. Construir el punto medio de cada uno de los lados del
pentágono.
A
C D
R Q
B
S P
M O N
Figura 11

289. 281
Paso 3. Trazar rectas que pasen por el centro de la circunferencia
y el punto medio de cada lado del pentágono. Los puntos de
intersección de estas rectas con la circunferencia, son los vértices
del decágono regular.
c. Construcción de un dodecágono regular.
Realizar la construcción de un dodecágono regular siguiendo los
pasos siguientes:
Paso 1. Construir un hexágono regular.
Paso 2. Construir el punto medio de cada uno de sus lados.
Paso 3. Trazar rectas que pasen por el centro de la circunferencia
y el punto medio de cada lado del hexágono. Los puntos de
intersección de estas rectas con la circunferencia, son los vértices
del dodecágono regular.
d. Realizar las siguientes construcciones con regla y compás.
• Un triángulo isósceles, conociendo la base y uno de los lados
que tiene la misma medida.
• Un cuadrado, conociendo el lado.
• Un ángulo de 45. (Sugerencia: construir la bisectriz de un
ángulo de 90).
• Una recta perpendicular en un extremo de un segmento dado.
• En un triángulo cualquiera construir el incentro.
• En un triángulo cualquiera construir el circuncentro..
Actividades:
1. ¿Cuántos triángulos se pueden contar en la siguiente figura?
Karl F. Gauss matemático
alemán conocido
como el “príncipe de la
Matemática” demostró
que el heptadecágono
(polígono regular de 17
lados) se puede construir
con regla y compás.
Los tres problemas de
construcción con regla y
compás imposibles.
1. Cuadratura del círculo.
Plantea la
construcción de
un cuadrado cuya
superficie interior
sea la misma de la
un círculo dado.
2. Duplicación del cubo.
Consiste en
construir el lado de
un cubo que tenga
el doble de volumen
que otro cubo cuyo
lado se da como
dato del problema.
3. Trisección del
ángulo
Partiendo de un
ángulo dado,
trisecarlo significa
construir un ángulo
que mida justo un
tercio del ángulo
dado.
Ma
tem
áti
ca
7
¿Sabías qué?
Nota histórica

290. 282
2. Investiga
Construye un círculo de cartón y mide la distancia del centro
al borde. Enrolla un trozo de cordel alrededor del contorno del
círculo. Desenróllalo después y mídelo también. Divide la segunda
cantidad entre la primera y anota el resultado. Puedes repetir el
experimento con círculos de distintos tamaños.
¿Qué puedes decir de los resultados que se obtienen?
3. En la figura dada hay 32 triángulos, nombre los vértices y diga cuales
son
4. En la siguiente figura acomode los números del 1 al 7, uno por círculo,
de modo que cada uno de los triángulos grandes y cada una de las
diagonales sumen igual.

291. 283
ACTIVIDADES FINALES DE LA SÉPTIMA UNIDAD
1. Define y elabora una gráfica donde se representen los conceptos siguientes:
a. Centro
b. Radio
c. Cuerda
d. Diámetro
e. Arco
f. Semicircunferencia
2. Dibuje con regla y compás una circunferencia de 3 cm de radio con centro en el punto
A y traza sobre ella los siguientes elementos: un radio, un diámetro, una cuerda y un
arco.
3. Lea las preguntas, haga un gráfico de ser necesario y responday responda.
a. ¿Cuándo un punto es exterior a la circunferencia?
b. ¿Cuándo un punto es interior a la circunferencia?
c. ¿Cuál es la condición que debe cumplir un punto para pertenecer a la circunferencia?
d. ¿Cuándo decimos que una recta y una circunferencia son secantes?
e. Cuando una recta y una circunferencia son exteriores, ¿qué relación existe entre el
radio y la distancia del centro a la recta?
f. ¿Cómo son una recta y una circunferencia si sólo tienen un punto en común?
g. ¿Cómo son una recta y una circunferencia si la distancia del centro a la recta coincide
con el radio?
h. ¿Cuántos puntos en común tienen una recta y una circunferencia que son exteriores?
4. Realice las siguientes actividades
a. Dibuje una circunferencia y una recta exterior. Traza un segmento desde el centro
a la recta de manera que su longitud determine la distancia del punto a la recta.
Compara este valor con el radio.

292. 284
b. Dibuje una circunferencia y una recta interior. Traza un segmento desde el centro
a la recta de manera que su longitud determine la distancia del punto a la recta.
Compara este valor con el radio.
c. Dibuje una circunferencia y una recta tangente. Traza un segmento desde el centro
a la recta de manera que su longitud determine la distancia del punto a la recta.
Compara este valor con el radio.
d. Dibuje dos circunferencias exteriores. Calcula la distancia entre los dos centros.
Compara este valor con la suma de los dos radios.
e. Dibuje dos circunferencias tangentes exteriores. Calcula la distancia entre los dos
centros. Compara este valor con la suma de los dos radios.
f. Dibuje dos circunferencias concéntricas.
5. Realice los siguientes ejercicios, consultando la teoría estudiada.
a. Indique si los siguientes puntos son interiores, exteriores o pertenecen a la
circunferencia.
A
B
B
0
D E
b. Indique cuáles de los puntos están a igual distancia del centro, cuáles se encuentran
a una distancia del centro mayor que el radio, cuáles están a distancia menor que el
radio y cuáles están a una distancia equivalente al doble del radio.
A
E
B
0
C
D
c. Indica la posición relativa de las rectas que aparecen en la figura, con respecto a
la circunferencia.

293. 285
t
s
u
v
d. Represente sobre la figura la distancia de cada una de las rectas al centro de la
circunferencia e indica en qué casos esa distancia es mayor que el radio, en qué
casos es menor y en cuáles es igual que el radio.
t
s
u
v
e. Dibuje dos circunferencias de radios 5cm y 3cm respectivamente que sean tangentes
interiores. ¿A qué distancia se encuentran sus centros?
f. Dibuje las mismas circunferencias anteriores, pero esta vez en posición de tangentes
exteriores. ¿A qué distancia se encuentran ahora sus centros?
6. Lee con atención y complete:
a. Un ángulo central es cualquier ángulo que tenga _______________ en el
_______________ de la circunferencia.
b. Todo ángulo central determina ________________ sobre la circunferencia.
c. Sellamaánguloinscritoalánguloquetiene__________________enlacircunferencia,
de forma que sus lados son __________________ con la circunferencia.
d. La medida de cualquier ángulo inscrito es _____________ de la medida del ángulo
central correspondiente.
e. Un diámetro de la circunferencia determina una ____________________, que se
corresponde con un ángulo central de __________.
f. Todo ángulo inscrito en una semicircunferencia es un ______________________.

294. 286
7. Resuelve los siguientes ejercicios
a. Identifique los siguientes tipos de ángulos, por su posición en la circunferencia.
b. Represente sobre la circunferencia de la figura un ángulo central recto y un ángulo
inscrito que coincida con el arco que lo subtiende. Calcule la medida del ángulo
inscrito.
c. Represente sobre la circunferencia de la figura un ángulo inscrito y un ángulo central
que subtienda su arco. Calcula la medida del ángulo central.

295. 287
d. En la siguiente figura indica la amplitud de los ángulos señalados, sin utilizar el
transportador, sabiendo que el ángulo m∠AOC mide 54.
• m ∠ AOB
• m ∠ ABC
• m ∠ OAB
• m ∠ BOC
e. Si partimos una pizza de forma circular en 18 trozos iguales, ¿qué ángulo corresponde
a cada ración? ¿En cuántos trozos habría que cortarla para que cada ración fuese
de 30?
8. Complete
a. La región del círculo determinada por dos radios se llama
___________________________
b. Llamamos ________________________________ a la región del círculo
determinada por una cuerda.
c. Laregiónlimitadapordoscircunferenciasconcéntricassedenomina______________
_________________
d. Si cortamos una corona circular por dos radios, obtenemos una figura
llamada:__________ ______________________
e. La fórmula para calcular la longitud de una circunferencia de radio R es____________
9. Resuelve los siguientes problemas
a. Calcule la longitud de una circunferencia que tiene 35 cm de radio.
b. Calcule la longitud de dos circunferencias que tienen 3 m de diámetro, la primera, y
2m de radio la segunda.
c. Halla la longitud de la circunferencia, sabiendo que su radio es 0,56 pies
d. Calcule la longitud del arco correspondiente a un ángulo de 60 en una circunferencia
de radio 2cm.

296. 288
e. Calcule el radio de una circunferencia sabiendo que tiene una longitud de 5 cm
f. Una piscina circular de 12 m de diámetro está rodeada por una acera de 1 m de
anchura. ¿Cuál será la longitud de la acera si la medimos exactamente por la mitad
de su anchura?
g. Calcule el área de un círculo de 0,8 m de radio.
10. Calcule el área de los sectores sombreados.
11. El segundero de un reloj mide 2 cm. Calcula la longitud del arco que describe esta
aguja en 30 segundos.
12. Si el minutero de un reloj mide 4 cm, calcula el área del sector circular que describe
esta aguja entre las 3:20 y las 4:00. Calcula el área del sector que describe en el mismo
intervalo de tiempo la aguja horaria, que mide 3 cm.
13. Resuelve el siguiente problema de área
Calcule el área y el perímetro de una puerta formada por un rectángulo de 10 pies de
anchura y doble altura, coronada por un semicírculo.
Figura 1
12 cm
Figura 2
4 cm
90°
60°
160°
Figura 3
3,3 cm
Figura 4
6 cm

297. 289
14. La rueda de un camión tiene 90 cm de radio. ¿Cuánto ha recorrido el camión cuando la
rueda ha dado 100 vueltas?
15. Un faro barre con su luz un ángulo plano de 128. Si el alcance máximo del faro es de 7
millas, ¿cuál es la longitud máxima en metros del arco correspondiente? Suponer que
un 1 milla = 1 690 m
16. La longitud de una circunferencia es 43,96 cm. ¿Cuál es el área del círculo?
17. El área de un sector circular de 90 es 4π cm. Calcule el radio del círculo al que pertenece
y la longitud de la circunferencia.
18. Determine el área de un sector circular cuya cuerda es el lado del triángulo equilátero
inscrito, siendo 2 cm el radio de la circunferencia.
19. Dadas dos circunferencias concéntricas de radio 8 y 5 cm respectivamente, se trazan
los radios OA y OB, que forman un ángulo de 60. Calcule el área del trapecio circular
formado.
20. En un parque de forma circular de 700 m de radio hay situada en el centro una fuente,
también de forma circular, de 5 m de radio. Calcule el área de la zona de paseo.
21. La superficie de una mesa está formada por una parte
central cuadrada de 1m de lado y dos semicírculos
adosados en dos lados opuestos. Calcule el área.
22. Calcule el área de la parte sombreada de la figura de
la derecha, si el radio del círculo mayor mide 6 cm y el
radio de los círculos pequeños miden 2 cm.
23. Calcule el área de la parte
sombreada de la figura
de la izquierda, siendo
AB = 10 cm, ABCD un cuadrado y APC Y AQC arcos de
circunferencia de centros B y D.
24. Calcule el área del sector circular cuyo ángulo central
mide 60º y el radio del círculo 5 cm.
25. Calcule el área del trapecio circular cuyas medidas son:
R = 3 cm, r = 1,5 cm, y el ángulo central 104.
Q
P
B C
DA

298. 290
26. De la figura, hallar α, si el área del sector S2
es la tercera parte del sector S1
S1
S2
3a 2aO
α
27. Un sector circular de radio R y longitud de arco L tiene un área S. Si incrementamos
su radio al doble y el área disminuye a la mitad, ¿en cuánto aumenta o disminuye la
longitud de arco con respecto al anterior?
28. El área y perímetro de un cuadrado y un sector circular son equivalentes. Hallar el
ángulo de dicho sector circular.
29. De la figura. Determine el área de la región sombreada.
A
B
C
D
O
12 16
3
θ
30. Un caballo está amarrado a un poste con un cuerda de longitud “L”, el caballo solo se
puede movilizar en el área que la cuerda se lo permita. Si incrementamos 10 metros la
longitud de la cuerda, el área por el cual se moviliza el caballo se cuadruplica. ¿Cuál es
la longitud de la cuerda original?
31. El péndulo de un reloj al balancearse describe un ángulo de 20 y una longitud de arco
de 3π. ¿Cuál es la longitud del péndulo?
32. La llanta de una bicicleta de radio 0,4 metros recorre 5 vueltas por minuto (5rpm)
¿calcular la distancia que recorrió la llanta en 30 minutos?

299. 291
GLOSARIO
Amplitud de clase. Es el número de datos contenidos en la clase y es igual al
rango entre el número de clases.
Ángulo. Es la unión de dos rayos no colineales que tienen el mismo origen.
Arco. Cada una de los conjuntos de puntos en que una cuerda divide a la
circunferencia.
Axioma. Es una proposición cuya veracidad se admite sin demostración.
Binomio. Es una expresión algebraica formada por la suma o diferencia de dos
monomios.
Círculo. Conjunto de puntos del plano formado por los puntos de la circunferencia
unido con el conjunto de puntos pertenecientes al interior de la circunferencia.
Circunferencia. Es un conjunto de puntos del plano que equidistan de un punto fijo
llamado centro.
Clase o intervalo de clase. Se llama intervalo de clase a cada uno de los intervalos
en que pueden agruparse los datos de una variable estadística.
Cuadrilátero. Dados cuatro puntos A, B, C y D, de los cuales no hay tres que sean
colineales, la unión de los segmentos y se llama cuadrilátero.
Cuerda. Segmento que une dos puntos diferentes de la circunferencia.
Diámetro. Cuerda que pasa por el centro de la circunferencia.
Dominio de una función. Dada una función entre los conjuntos A y B, el conjunto
“A” se llama dominio de la función.
Dominio de una relación. Es el conjunto formado por los primeros elementos de
los pares ordenados.
Dominio de una variable. El dominio de una variable es el conjunto de valores que
se le pueden asignar a la variable.
Ecuación. Es una igualdad algebraica que se cumple sólo para algunos valores de
la o las variables,

300. 292
Estadística. La estadística se ocupa de la recolección, organización, presentación
e interpretación de datos.
Expresión algebraica. Es aquella que está formada por números y letras
relacionados por medio de una o varias operaciones matemáticas.
Figura geométrica. Es un subconjunto no vacío de puntos de una recta, un plano
o el espacio.
Frecuencia acumulada relativa (Fr
). Es el cociente de dividir cada frecuencia
acumulada entre el número de datos.
Frecuencia relativa (fr). La frecuencia relativa es el cociente de dividir la frecuencia
absoluta entre el número total de datos.
Frecuencias acumulada (Fi). La frecuencia acumulada es el número de datos que
hay en el intervalo más las frecuencias de los datos anteriores.
Función discreta. Una función se dice que es discreta si su dominio es un
subconjunto del conjunto de los números enteros.
Función lineal de proporcionalidad directa. Es una expresión algebraica tiene la
forma y = mx, donde m es la constante de proporcionalidad.
Función. Es una relación en la cual a cada elemento del dominio le corresponde un
único elemento del recorrido o rango.
Grado absoluto de un binomio. Es el mayor grado absoluto de los términos (o
monomios) que forman el binomio.
Grado absoluto de un binomio. Es el mayor grado absoluto de los términos (o
monomios) que forman el trinomio.
Grado absoluto de un monomio. Es la suma de los exponentes de las variables.
Grado relativo de un monomio respecto a una variable. Es el mayor exponente
de la variable.
Grado relativo respecto a una variable de un binomio. Es el mayor exponente
de la variable.
Grado relativo respecto a una variable de un trinomio. Es el mayor exponente
de la variable.

301. 293
Grado. El grado de una ecuación con una incógnita es el grado mayor de la incógnita.
En el caso de una ecuación lineal con una incógnita, el grado de la incógnita es
uno, y la ecuación recibe el nombre de ecuación lineal de primer grado con una
incógnita.
Heptágono regular. Es un polígono regular de siete lados de igual medida y siete
ángulos internos de igual medida.
Hexágono regular. Es un polígono regular de seis lados de igual medida y seis
ángulos internos de igual medida.
Histograma de frecuencias. El histograma es un gráfico de barras. En el eje
horizontal se representan los intervalos de clase y en el eje vertical se representan
las frecuencias.
Identidad. Es una igualdad algebraica que se cumple para todos los valores de la
o las variables que aparecen en ella.
Igualdad. Es una expresión que relaciona dos cantidades mediante el signo “igual”.
Igualdad algebraica. Es una igualdad en la que las cantidades relacionadas son
variables.
Igualdad numérica. Es una igualdad en la que las cantidades relacionadas son
números.
Línea poligonal. Dados en el plano “n” puntos A1, A2,..., An, con n ≥ 3, con la
condición de que no hay tres puntos consecutivos que sean colineales. La unión de
los segmentos A1
A2
+ A2
A3
+ .... + An-1
An
, se llama línea poligonal.
Marca de clase. Es el punto medio de cada clase.
Monomio. Es una expresión algebraica formada por el producto indicado de factores
numéricos y factores literales con exponente natural o cero.
Monomios heterogéneos. Son aquellos que tienen diferente grado absoluto.
Monomios homogéneos. Son aquellos que tienen el mismo grado absoluto.
Monomios semejantes. Dos monomios se dice que son semejantes cuando tienen
la misma parte literal con iguales exponentes.

302. 294
Número irracional. Es un número que no es decimal periódico y no se pueden
expresar como el cociente de dos números enteros.
Número racional. Es el que puede ser expresado como el cociente de dos números
enteros, siempre que el denominador sea diferente de cero.
Números reales. La unión del conjunto de los números racionales con el conjunto
de los números irracionales, recibe el nombre de conjunto de los números reales.
Octógono regular. Es un polígono regular de ocho lados de igual medida y ocho
ángulos internos de igual medida.
Pentágono regular. Es un polígono regular de cinco lados de igual medida y cinco
ángulos internos de igual medida.
Perímetro de una línea poligonal. Es la suma de las mediadas de los segmentos
que forman la línea poligonal.
Porcentaje para la frecuencia relativa acumulada. Es el resultado de multiplicar
100 cada frecuencia acumulada relativa.
Producto cartesiano de dos conjuntos no vacíos A y B. Es el conjunto de todos
los pares ordenados en los que la primera componte pertenece al conjunto A y la
segunda al conjunto B. Se denota por A × B.
Radio de un circunferencia. Es el segmento que une cualquier punto de la
circunferencia con el centro.
Rayo . Es la unión del segmento con el conjunto de puntos que se encuentran
después de Q.
Recorrido de una función. Dada una función entre los conjuntos A y B, el conjunto
B se llama dominio de la función.
Recorrido de una relación. Es el conjunto formado por los segundos elementos
de los pares ordenados.
Recta secante. Corta a la circunferencia en dos puntos.
Recta tangente. Recta que tiene un punto en común con la circunferencia.
Rectas paralelas. Dos rectas diferentes son paralelas, si y sólo si están contenidas
en un mismo plano y no se intersectan.

303. 295
Región poligonal cerrada. Es el conjunto de puntos de un plano limitado por una
línea poligonal cerrada.
Relación. Es un subconjunto de un producto cartesiano. Una relación se denotará
con el símbolo ℛ.
Segmento. Es la unión del conjunto formado por los puntos P y Q con el conjunto
formado por todos los puntos X que se encuentran entre P y Q se representa por PQ.
Semicircunferencia. Es un arco que tiene una longitud igual a la mitad de la
longitud de la circunferencia.
Signo de un monomio. Es el que indica si el monomio es positivo (+) o negativo
(-). Si el signo es positivo, éste se omite.
Solución. Se llama solución o raíz de una ecuación al valor que la satisface o la
verifica.
Triángulo. Dados tres puntos no colineales A, B y C, la unión de los segmentos
y se llama triángulo.
Trinomio. Es una expresión algebraica formada por la suma o diferencia de tres
monomios.
Valor numérico de una expresión algebraica. Es el valor que obtiene cuando se
sustituyen las variables por números.
Variable dependiente. Se conoce como variable dependiente, a los elementos del
recorrido de una función.
Variable independiente. Se conoce como variable independiente, a los elementos
del dominio de una función.

304. 296
Bibliografía
a. Baldor Aurelio. Aritmética. México. Ed. Publicaciones Cultural S.A. de C.V., 1 983.
b. Baldor, Dr. Aurelio. Algebra. Madrid, Ed. y distribuciones Codice S. A., 1 963.
c. Bautista Ballén, Mauricio. Matemáticas 7. Bogotá. Ed. Santillana, 2 007.
d. Beltrán Luis, Rodríguez Benjamín y Dimaté Mónica. Matemáticas 7: con tecnología
aplicad, Colombia, Ed. Prentice Hall, 1 999.
e. Beristain Eloísa y Campos Yolanda. Matemáticas 1 y 2. Bogotá, Colombia. Ed. Mc
Graw-Hill Latinoamericana, S.A., 1 974.
f. Gobierno de Nicaragua. Ley 225. Norma sobre el sistema internacional de unidades.
Recomendaciones para el uso correcto del S.I. Nicaragua.
g. Jurgensen Ray, Donnelly, Alfred y Dolciani, Mary. Geometría Moderna, 1ra. ed. en
español, México D. F., 1 968.
h. Lipschutz Seymoour. Teoría de conjuntos y temas afines, teoría y problemas. México.
Ed. Libros Mc Graw-Hill, 1 969.
i. Londoño Nelson y Bedoya Hernández. Serie Matemática progresiva 6-7-8, 7ma. ed.
Bogotá, Colombia, 1 988.
j. Moise, E. y Downs, F. Geometría Moderna. Estados Unidos, Addison Wesley publishing
company, 1 966.
k. Neira Marina y otros. Matemática en construcción 7. 2da. ed. Colombia, Oxford University
Press, 1 996.
l. Rey Pastor y Babini José. Historia de la matemática, vol. 1 y 2. Barcelona. Ed. Gedisa
S.A., 2 000.
m. Rich Barnett. Geometría 2da. ed. México. Ed. Mc Graw Hill, 1 991.
n. Saenz Luis, Gutierrez Luis y Sequeira Francisco. Matemática 2, educación secundaria
SGS. Nicaragua. FARBEN grupo editorial NORMA, 1 997.
o. Ministerio de Educación, compendio de los Documentos Curriculares con enfoque de
competencias, Managua, Nicaragua, 2 005.
p. Programa de Estudio Educación Secundaria, Matemática 7°, 8° y 9° Grado,
MINED - Nicaragua.