Este documento presenta información sobre las fuerzas de fijación y momentos de empotramiento en vigas. Incluye biografías de los cuatro autores del libro, quienes son ingenieros civiles de México, Perú y Bolivia. También incluye datos sobre la publicación como título, edición, distribuidora virtual, y derechos de autor.




























![Fuerzas de fijación y momentos de empotramiento en vigas
7
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 + (1)(𝑥) = 0 ⇒ 𝑀1 = 𝑥
Viga 𝐸𝐶𝑢2, figura 1-g.
Las reacciones en el empotramiento 𝐵 equivalen a
+→ ∑ 𝐹𝑋 = 0 ⇒∴ 𝑅 𝐵𝑋 = 0
+↑ ∑ 𝐹𝑌 = 0 ⇒∴ 𝑅 𝐵𝑌 = 0
+ ∑ 𝑀𝐵 = 0 ⇒ −1 + 𝑀 𝐵 = 0 ⇒∴ 𝑀 𝐵 = 1
Se infiere el momento interno 𝑚2 a partir de la figura 1-k.
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − 1 = 0 ⇒ 𝑀1 = −1
Obsérvese que la coordenada 𝑥 seleccionada conlleva a que no haya necesidad de determinar las
reacciones con el fin de encontrar los momentos internos.
Enseguida se presenta el cálculo de las incompatibilidades geométricas, empleando las ecuaciones
(𝐼) y (𝐼𝐼).
𝑑1 =
1
𝐸𝐼
[∫ (0)(𝑥)𝑑𝑥 + ∫ (−𝑃𝑥 +
𝑃𝐿
2
) (𝑥)𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
] =
1
𝐸𝐼
∫ (−𝑃𝑥2
+
𝑃𝐿
2
𝑥) 𝑑𝑥
𝐿
𝐿
2⁄
=
1
𝐸𝐼
[−
𝑃
3
𝑥3
+
𝑃𝐿
4
𝑥2
]
𝐿
2⁄
𝐿
=
1
𝐸𝐼
[−
𝑃
3
(𝐿3
− (
𝐿
2
)
3
) +
𝑃𝐿
4
(𝐿2
− (
𝐿
2
)
2
)] =
1
𝐸𝐼
(−
7𝑃𝐿3
24
+
3𝑃𝐿3
16
) = −
5𝑃𝐿3
48𝐸𝐼
𝑑2 =
1
𝐸𝐼
[∫ (0)(−1)𝑑𝑥 + ∫ (−𝑃𝑥 +
𝑃𝐿
2
) (−1)𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
]
𝐴
𝑀1
𝑥
1
(j)
𝐴
𝑀1
𝑥
1
(k)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-29-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
8
=
1
𝐸𝐼
∫ (𝑃𝑥 −
𝑃𝐿
2
) 𝑑𝑥
𝐿
𝐿
2⁄
=
1
𝐸𝐼
[
𝑃
2
𝑥2
−
𝑃𝐿
2
𝑥]
𝐿
2⁄
𝐿
=
1
𝐸𝐼
[
𝑃
2
(𝐿2
− (
𝐿
2
)
2
) −
𝑃𝐿
2
(𝐿 −
𝐿
2
)]
=
1
𝐸𝐼
(
3𝑃𝐿2
8
−
𝑃𝐿2
4
) =
𝑃𝐿2
8𝐸𝐼
Ahora se muestra el cálculo de los coeficientes de flexibilidad, aplicando las ecuaciones (𝐼𝐼𝐼) hasta
(𝑉𝐼).
𝑓11 =
1
𝐸𝐼
∫ (𝑥)(𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ 𝑥2
𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
1
3
𝑥3
]
0
𝐿
=
1
3𝐸𝐼
(𝐿3
− 03) =
𝐿3
3𝐸𝐼
𝑓21 =
1
𝐸𝐼
∫ (𝑥)(−1)𝑑𝑥 = −
1
𝐸𝐼
∫ 𝑥𝑑𝑥
𝐿
0
= −
1
𝐸𝐼
[
1
2
𝑥2
]
0
𝐿
= −
1
2𝐸𝐼
(𝐿2
− 02) = −
𝐿2
2𝐸𝐼
𝐿
0
𝑓12 =
1
𝐸𝐼
∫ (−1)(𝑥)𝑑𝑥
𝐿
0
= −
1
𝐸𝐼
∫ 𝑥𝑑𝑥
𝐿
0
= −
1
𝐸𝐼
[
1
2
𝑥2
]
0
𝐿
= −
1
2𝐸𝐼
(𝐿2
− 02) = −
𝐿2
2𝐸𝐼
Obsérvese que como una consecuencia del teorema de Maxwell de los desplazamientos recíprocos,
se cumple que 𝑓12 = 𝑓21. De forma más generalizada, se tiene que 𝑓𝑖𝑗 = 𝑓𝑗𝑖, lo cual hace que mientras
más grande sea el grado de hiperestaticidad, más se evita el cálculo de varios coeficientes de
flexibilidad.
𝑓22 =
1
𝐸𝐼
∫ (−1)(−1)𝑑𝑥 =
1
𝐸𝐼
∫ 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[𝑥]0
𝐿
=
1
𝐸𝐼
(𝐿 − 0) =
𝐿
𝐸𝐼
𝐿
0
Cálculo de las redundantes
Al sustituir los coeficientes en el sistema simultáneo de ecuaciones (1 − 3) y (1 − 4), se tiene
−
5𝑃𝐿3
48𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (1 − 5)
𝑃𝐿2
8𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (1 − 6)
Despejando 𝑀𝐴 de las expresiones (1 − 5) y (1 − 6) respectivamente, resulta
𝑀𝐴 =
5𝑃𝐿3
48𝐸𝐼
−
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌
−
𝐿2
2𝐸𝐼
− − − (1 − 7) 𝑀𝐴 =
−
𝑃𝐿2
8𝐸𝐼
+
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌
𝐿
𝐸𝐼
− − − (1 − 8)
Igualando la ecuación (1 − 7) con la ecuación (1 − 8) y simplificando da
5𝑃𝐿3
48𝐸𝐼
−
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌
−
𝐿2
2𝐸𝐼
=
−
𝑃𝐿2
8𝐸𝐼
+
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌
𝐿
𝐸𝐼
⇒ (
𝐿
𝐸𝐼
) (
5𝑃𝐿3
48𝐸𝐼
−
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌) = (−
𝐿2
2𝐸𝐼
) (−
𝑃𝐿2
8𝐸𝐼
+
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌)
−
𝐿4
3(𝐸𝐼)2
𝑅 𝐴𝑌 +
𝐿4
4(𝐸𝐼)2
𝑅 𝐴𝑌 =
𝑃𝐿4
16(𝐸𝐼)2
−
5𝑃𝐿4
48(𝐸𝐼)2
⇒ −
1
12
𝑅 𝐴𝑌 = −
1
24
𝑃 ⇒ 𝑅 𝐴𝑌 =
1
24
𝑃
1
12
⇒∴ 𝑅 𝐴𝑌 =
𝑃
2](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-30-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
12
cual pasa la línea de acción de la resultante, o sea, se halla el punto de aplicación de la resultante
(para una carga uniforme distribuida se tiene que se ubica a la mitad de la longitud sobre la cual
actúa).
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − 𝑊(𝑥) (
𝑥
2
) = 0 ⇒ 𝑀1 = −
𝑊𝑥2
2
Luego, se retoman los momentos internos 𝑚1 y 𝑚2 de las figuras 1-j y 1-k.
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se calculan las incompatibilidades geométricas.
𝑑1 = ∫
𝑀𝑚1
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
∫ (−
𝑊𝑥2
2
) (𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (−
𝑊𝑥3
2
) 𝑑𝑥
𝐿
0
=
1
2𝐸𝐼
[−
𝑊𝑥4
4
]
𝐿
2⁄
𝐿
= −
𝑊𝐿4
8𝐸𝐼
𝑑2 = ∫
𝑀𝑚2
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
∫ (−
𝑊𝑥2
2
) (−1)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (
𝑊𝑥2
2
) 𝑑𝑥
𝐿
0
=
1
2𝐸𝐼
[−
𝑊𝑥3
3
]
𝐿
2⁄
𝐿
=
𝑊𝐿3
6𝐸𝐼
Evidentemente, los coeficientes de flexibilidad son los mismos que se tienen en la viga 1.
𝑓11 = ∫
𝑚1 𝑚1
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
𝐿3
3𝐸𝐼
𝑓21 = ∫
𝑚1 𝑚2
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
= −
𝐿2
2𝐸𝐼
𝑓12 = 𝑓21 = −
𝐿2
2𝐸𝐼
𝑓22 = ∫
𝑚2 𝑚2
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
𝐿
𝐸𝐼
Cálculo de las redundantes
Al reemplazar los resultados obtenidos en las ecuaciones (2 − 1) y (2 − 2), se obtiene
−
𝑊𝐿4
8𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (2 − 3)
𝑊𝐿3
6𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (2 − 4)
𝐴
𝑀1
𝑥
𝑊
𝑊(𝑥)
𝑥/2
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-34-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
13
Se resuelve el sistema simultáneo de ecuaciones (2 − 3) y (2 − 4), empleando el método de Cramer.
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 =
𝑊𝐿4
8𝐸𝐼
− − − (2 − 5)
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = −
𝑊𝐿3
6𝐸𝐼
− − − (2 − 6)
Con base en las ecuaciones (2 − 5) y (2 − 6), se tienen los siguientes determinantes
∆= ||
𝐿3
3𝐸𝐼
−
𝐿2
2𝐸𝐼
−
𝐿2
2𝐸𝐼
𝐿
𝐸𝐼
|| = [(
𝐿3
3𝐸𝐼
) (
𝐿
𝐸𝐼
)] − [(−
𝐿2
2𝐸𝐼
) (−
𝐿2
2𝐸𝐼
)] =
𝐿4
3(𝐸𝐼)2
−
𝐿4
4(𝐸𝐼)2
=
𝐿4
12(𝐸𝐼)2
∆ 𝑅 𝐴𝑌
= ||
𝑊𝐿4
8𝐸𝐼
−
𝐿2
2𝐸𝐼
−
𝑊𝐿3
6𝐸𝐼
𝐿
𝐸𝐼
|| = [(
𝑊𝐿4
8𝐸𝐼
) (
𝐿
𝐸𝐼
)] − [(−
𝐿2
2𝐸𝐼
) (−
𝑊𝐿3
6𝐸𝐼
)] =
𝑊𝐿5
8(𝐸𝐼)2
−
𝑊𝐿5
12(𝐸𝐼)2
=
𝑊𝐿5
24(𝐸𝐼)2
∆ 𝑀 𝐴
= ||
𝐿3
3𝐸𝐼
𝑊𝐿4
8𝐸𝐼
−
𝐿2
2𝐸𝐼
−
𝑊𝐿3
6𝐸𝐼
|| = [(
𝐿3
3𝐸𝐼
) (−
𝑊𝐿3
6𝐸𝐼
)] − [(
𝑊𝐿4
8𝐸𝐼
) (−
𝐿2
2𝐸𝐼
)] = −
𝑊𝐿6
18(𝐸𝐼)2
+
𝑊𝐿6
16(𝐸𝐼)2
=
𝑊𝐿6
144(𝐸𝐼)2
𝑅 𝐴𝑌 =
∆ 𝑅 𝐴𝑌
∆
=
𝑊𝐿5
24(𝐸𝐼)2
𝐿4
12(𝐸𝐼)2
=
𝑊𝐿
2
⇒∴ 𝑅 𝐴𝑌 =
𝑊𝐿
2
𝑀𝐴 =
∆ 𝑀 𝐴
∆
=
𝑊𝐿6
144(𝐸𝐼)2
𝐿4
12(𝐸𝐼)2
=
𝑊𝐿2
12
⇒∴ 𝑀𝐴 =
𝑊𝐿2
12
Ecuaciones de equilibrio
Por lo tanto, a partir del diagrama de cargas de la figura 2-e, resulta
𝐴 𝐵
𝐿
𝑊
𝑊𝐿
𝐿/2
𝑀 𝐴 =
𝑊𝐿2
12
𝑀 𝐵
𝑅 𝐴𝑌 =
𝑊𝐿
2
𝑅 𝐵𝑌
(e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-35-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
17
bajo el rectángulo y el triángulo), las cuales vienen aplicadas en el centroide de sus respectivas
áreas. Recuerde que para un área triangular, el centroide se ubica a las dos terceras partes de la
base, y tal distancia se mide desde el punto del “pico”.
El equilibrio estático del cuerpo libre implica que
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 −
(
(𝑥) (𝑊 − (𝑊 −
𝑊
𝐿
𝑥))
2
)
൬
2
3
𝑥൰ − (𝑥) ൬𝑊 −
𝑊
𝐿
𝑥൰ ൬
1
2
𝑥൰ = 0
−𝑀1 + ൬−
𝑊
2
𝑥 +
𝑊
2
𝑥 −
𝑊
2𝐿
𝑥2
൰ ൬
2
3
𝑥൰ + ൬−𝑊𝑥 +
𝑊
𝐿
𝑥2
൰ ൬
1
2
𝑥൰ = 0
−𝑀1 −
𝑊
3𝐿
𝑥3
−
𝑊
2
𝑥2
+
𝑊
2𝐿
𝑥3
⇒ 𝑀1 =
𝑊𝑥3
6𝐿
−
𝑊𝑥2
2
Por otra parte, de los ejercicios previos, se sabe que
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se calculan los desplazamientos y giros requeridos. Para las incompatibilidades geométricas
tenemos
𝑑1 = ∫
𝑀𝑚1
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
∫ (
𝑊𝑥3
6𝐿
−
𝑊𝑥2
2
) (𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (
𝑊𝑥4
6𝐿
−
𝑊𝑥3
2
) 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
𝑊𝑥5
30𝐿
−
𝑊𝑥4
8
]
0
𝐿
=
1
𝐸𝐼
[
𝑊
30𝐿
(𝐿5) −
𝑊
8
(𝐿4)] = −
11𝑊𝐿4
120𝐸𝐼
𝑑2 = ∫
𝑀𝑚2
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
∫ (
𝑊𝑥3
6𝐿
−
𝑊𝑥2
2
) (−1)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (−
𝑊𝑥3
6𝐿
+
𝑊𝑥2
2
) 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[−
𝑊𝑥4
24𝐿
+
𝑊𝑥3
6
]
0
𝐿
=
1
𝐸𝐼
[−
𝑊𝐿4
24𝐿
+
𝑊𝐿3
6
] =
𝑊𝐿3
8𝐸𝐼
𝐴𝐼𝐼
𝐴𝐼](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-39-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
18
Los coeficientes de flexibilidad son
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = −
𝐿2
2𝐸𝐼
𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
Reemplazando los valores previos en las ecuaciones (3 − 1) y (3 − 2) da
−
11𝑊𝐿4
120𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (3 − 3)
𝑊𝐿3
8𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (3 − 4)
Resolviendo el sistema de ecuaciones (3 − 3) y (3 − 4), resulta
∆= ||
𝐿3
3𝐸𝐼
−
𝐿2
2𝐸𝐼
−
𝐿2
2𝐸𝐼
𝐿
𝐸𝐼
|| =
𝐿4
12(𝐸𝐼)2
∆ 𝑅 𝐴𝑌
= ||
11𝑊𝐿4
120𝐸𝐼
−
𝐿2
2𝐸𝐼
−
𝑊𝐿3
8𝐸𝐼
𝐿
𝐸𝐼
|| = [(
11𝑊𝐿4
120𝐸𝐼
) ൬
𝐿
𝐸𝐼
൰] − [(−
𝐿2
2𝐸𝐼
) (−
𝑊𝐿3
8𝐸𝐼
)] =
11𝑊𝐿5
120(𝐸𝐼)2
−
𝑊𝐿5
16(𝐸𝐼)2
=
7𝑊𝐿5
240(𝐸𝐼)2
∆ 𝑀 𝐴
= ||
𝐿3
3𝐸𝐼
11𝑊𝐿4
120𝐸𝐼
−
𝐿2
2𝐸𝐼
−
𝑊𝐿3
8𝐸𝐼
|| = [(
𝐿3
3𝐸𝐼
) (−
𝑊𝐿3
8𝐸𝐼
)] − [(
11𝑊𝐿4
120𝐸𝐼
) (−
𝐿2
2𝐸𝐼
)] = −
𝑊𝐿6
24(𝐸𝐼)2
+
11𝑊𝐿6
240(𝐸𝐼)2
=
𝑊𝐿6
240(𝐸𝐼)2
𝑅 𝐴𝑌 =
∆ 𝑅 𝐴𝑌
∆
=
7𝑊𝐿5
240(𝐸𝐼)2
𝐿4
12(𝐸𝐼)2
=
7𝑊𝐿
20
⇒∴ 𝑅 𝐴𝑌 =
7𝑊𝐿
20
𝑀𝐴 =
∆ 𝑀 𝐴
∆
=
𝑊𝐿6
240(𝐸𝐼)2
𝐿4
12(𝐸𝐼)2
=
𝑊𝐿2
20
⇒∴ 𝑀𝐴 =
𝑊𝐿2
20](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-40-320.jpg)


![Fuerzas de fijación y momentos de empotramiento en vigas
21
Ecuaciones de compatibilidad
Con referencia al punto 𝐴 de la figura 4-b, se requiere
0 = 𝑑1 + 𝑓11 𝑅 𝐴𝑌 + 𝑓12 𝑀𝐴 − − − (4 − 1)
0 = 𝑑2 + 𝑓21 𝑅 𝐴𝑌 + 𝑓22 𝑀𝐴 − − − (4 − 2)
Como siempre, los momentos internos 𝑀 se obtienen a partir de la viga liberada con cargas reales.
Dado que la distribución de la carga que actúa a lo largo de esta viga presenta una discontinuidad
(en la mitad del claro 𝐴 − 𝐵), deben efectuarse dos cortes perpendiculares al eje de la viga.
Corte en el primer tramo. Se secciona la viga a una distancia 𝑥 de 𝐴 en un punto arbitrario antes de
𝐿/2, es decir, antes de que la intensidad de la carga con variación lineal alcance el valor de 𝑊. El
diagrama de cuerpo libre de la sección cortada se visualiza en la figura 4-c.
0 ≤ 𝑥 ≤ 𝐿
2⁄
Note que la intensidad de la carga de triangulo rectángulo se encuentra en proporción, es decir,
𝑊
𝐿
2
=
𝑊´
𝑥
⇒ 𝑊´ =
2𝑊
𝐿
𝑥
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − [
(
2𝑊
𝐿
𝑥) (𝑥)
2
] (
𝑥
3
) = 0 ⇒ 𝑀1 = −
𝑊𝑥3
3𝐿
Corte en el tramo segundo tramo. Se secciona la viga a una distancia 𝑥 de 𝐴 en un punto arbitrario
justo después de 𝐿/2. En la figura 4-d se observa el diagrama de cargas para este segmento de viga
con longitud 𝑥.
𝐿
2⁄ ≤ 𝑥 ≤ 𝐿
Con base en la figura 4-e, empleando conceptos básicos de trigonometría, se deduce el punto de
intensidad 𝑊´´ de carga.
𝑊
𝐿
2
=
𝑊´´
𝐿 − 𝑥
⇒ 𝑊´´ =
𝑊(𝐿 − 𝑥)
𝐿
2
= 2𝑊 −
2𝑊
𝐿
𝑥
𝐴
𝑊´ = 2
𝑊
𝐿
𝑥
𝑥
𝑀1
𝐴𝐼
𝑥/3
𝐴𝐼
(c)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-43-320.jpg)

![Fuerzas de fijación y momentos de empotramiento en vigas
23
Luego, los momentos internos de las vigas liberadas que soportan una unidad de las reacciones
redundantes son, respectivamente
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Entonces,
𝑑1 = ∫
𝑀𝑚1
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
[∫ (−
𝑊𝑥3
3𝐿
) (𝑥)𝑑𝑥 + ∫ (
𝑊
3𝐿
𝑥3
− 𝑊𝑥2
+
𝑊𝐿
2
𝑥 −
𝑊𝐿2
12
) (𝑥)𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
]
=
1
𝐸𝐼
[∫ (−
𝑊
3𝐿
𝑥4
) 𝑑𝑥 + ∫ (
𝑊
3𝐿
𝑥4
− 𝑊𝑥3
+
𝑊𝐿
2
𝑥2
−
𝑊𝐿2
12
𝑥) 𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
]
=
1
𝐸𝐼
{[−
𝑊
15𝐿
𝑥5
]
0
𝐿
2⁄
+ [
𝑊
15𝐿
𝑥5
−
𝑊
4
𝑥4
+
𝑊𝐿
6
𝑥3
−
𝑊𝐿2
24
𝑥2
]
𝐿
2⁄
𝐿
}
=
1
𝐸𝐼
{[−
𝑊
15𝐿
((
𝐿
2
)
5
)] + [
𝑊
15𝐿
(𝐿5
− (
𝐿
2
)
5
) −
𝑊
4
(𝐿4
− (
𝐿
2
)
4
) +
𝑊𝐿
6
(𝐿3
− (
𝐿
2
)
3
) −
𝑊𝐿2
24
(𝐿2
− (
𝐿
2
)
2
)]}
=
𝑊𝐿4
𝐸𝐼
(−
1
480
+
31
480
−
15
64
+
7
48
−
1
32
) = −
11𝑊𝐿4
192𝐸𝐼
𝑑2 = ∫
𝑀𝑚2
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
[∫ (−
𝑊𝑥3
3𝐿
) (−1)𝑑𝑥 + ∫ (
𝑊
3𝐿
𝑥3
− 𝑊𝑥2
+
𝑊𝐿
2
𝑥 −
𝑊𝐿2
12
) (−1)𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
]
=
1
𝐸𝐼
[∫ (
𝑊𝑥3
3𝐿
) 𝑑𝑥 + ∫ (−
𝑊
3𝐿
𝑥3
+ 𝑊𝑥2
−
𝑊𝐿
2
𝑥 +
𝑊𝐿2
12
) 𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
]
=
1
𝐸𝐼
{[
𝑊
12𝐿
𝑥4
]
0
𝐿
2⁄
+ [−
𝑊
12𝐿
𝑥4
+
𝑊
3
𝑥3
−
𝑊𝐿
4
𝑥2
+
𝑊𝐿2
12
𝑥]
𝐿
2⁄
𝐿
}
=
1
𝐸𝐼
{[
𝑊
12𝐿
((
𝐿
2
)
4
)] + [−
𝑊
12𝐿
(𝐿4
− (
𝐿
2
)
4
) +
𝑊
3
(𝐿3
− (
𝐿
2
)
3
) −
𝑊𝐿
4
(𝐿2
− (
𝐿
2
)
2
) +
𝑊𝐿2
12
(𝐿 −
𝐿
2
)]}
=
𝑊𝐿3
𝐸𝐼
(
1
192
−
5
64
+
7
24
−
3
16
+
1
24
) =
7𝑊𝐿3
96𝐸𝐼](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-45-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
24
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = 𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
En consecuencia, el sistema de ecuaciones de flexibilidades es
−
11𝑊𝐿4
192𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (4 − 3)
7𝑊𝐿3
96𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (4 − 4)
Que equivale a
𝐿3
3
𝑅 𝐴𝑌 −
𝐿2
2
𝑀𝐴 =
11𝑊𝐿4
192
− − − (4 − 5)
−
𝐿2
2
𝑅 𝐴𝑌 + 𝐿𝑀𝐴 = −
7𝑊𝐿3
96
− − − (4 − 6)
Por lo tanto,
∆= ||
𝐿3
3
−
𝐿2
2
−
𝐿2
2
𝐿
|| =
𝐿4
12
∆ 𝑅 𝐴𝑌
= ||
11𝑊𝐿4
192
−
𝐿2
2
−
7𝑊𝐿3
96
𝐿
|| = [(
11𝑊𝐿4
192
) (𝐿)] − [(−
𝐿2
2
) (−
7𝑊𝐿3
96
)] =
11𝑊𝐿5
192
−
7𝑊𝐿5
192
=
𝑊𝐿5
48
∆ 𝑀 𝐴
= ||
𝐿3
3
11𝑊𝐿4
192
−
𝐿2
2
−
7𝑊𝐿3
96
|| = [(
𝐿3
3
) (−
7𝑊𝐿3
96
)] − [(
11𝑊𝐿4
192
) (−
𝐿2
2
)] = −
7𝑊𝐿6
288
+
11𝑊𝐿6
384
=
5𝑊𝐿6
1152
𝑅 𝐴𝑌 =
∆ 𝑅 𝐴𝑌
∆
=
𝑊𝐿5
48
𝐿4
12
=
𝑊𝐿
4
⇒∴ 𝑅 𝐴𝑌 =
𝑊𝐿
4
𝑀𝐴 =
∆ 𝑀 𝐴
∆
=
5𝑊𝐿6
1152
𝐿4
12
=
5𝑊𝐿2
96
⇒∴ 𝑀𝐴 =
5𝑊𝐿2
96](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-46-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
28
𝑊1 − 𝑊2
𝐿
=
𝑌
𝐿 − 𝑥
𝑌 =
(𝑊1 − 𝑊2)(𝐿 − 𝑥)
𝐿
=
𝑊1 𝐿 − 𝑊1 𝑥 − 𝑊2 𝐿 + 𝑊2 𝑥
𝐿
= 𝑊1 − 𝑊2 +
𝑊2
𝐿
𝑥 −
𝑊1
𝐿
𝑥
𝑊´ = 𝑊2 + 𝑌 = 𝑊2 + 𝑊1 − 𝑊2 +
𝑊2
𝐿
𝑥 −
𝑊1
𝐿
𝑥 = 𝑊1 +
𝑊2
𝐿
𝑥 −
𝑊1
𝐿
𝑥
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − (𝑥) (𝑊1 +
𝑊2
𝐿
𝑥 −
𝑊1
𝐿
𝑥) (
1
2
𝑥) −
[
(𝑥) (𝑊1 − (𝑊1 +
𝑊2
𝐿
𝑥 −
𝑊1
𝐿
𝑥))
2
]
(
2
3
𝑥) = 0
−𝑀1 − (𝑥) (
𝑊1
2
𝑥 +
𝑊2
2𝐿
𝑥2
−
𝑊1
2𝐿
𝑥2
) − (
1
3
𝑥2
) (−
𝑊2
𝐿
𝑥 +
𝑊1
𝐿
𝑥) = 0
𝑀1 =
𝑊1 𝑥3
2𝐿
−
𝑊2 𝑥3
2𝐿
−
𝑊1 𝑥2
2
+
𝑊2 𝑥3
3𝐿
−
𝑊1 𝑥3
3𝐿
=
𝑊1 𝑥3
6𝐿
−
𝑊2 𝑥3
6𝐿
−
𝑊1 𝑥2
2
Los momentos internos de las otras dos vigas isostáticas son
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se necesita de los siguientes desplazamientos y pendientes
𝑑1 = ∫
𝑀𝑚1
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
∫ (
𝑊1 𝑥3
6𝐿
−
𝑊2 𝑥3
6𝐿
−
𝑊1 𝑥2
2
) (𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (
𝑊1 𝑥4
6𝐿
−
𝑊2 𝑥4
6𝐿
−
𝑊1 𝑥3
2
) 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
𝑊1 𝑥5
30𝐿
−
𝑊2 𝑥5
30𝐿
−
𝑊1 𝑥4
8
]
0
𝐿
= −
11𝑊1 𝐿4
120𝐸𝐼
−
𝑊2 𝐿4
30𝐸𝐼
𝑑2 = ∫
𝑀𝑚2
𝐸𝐼
𝑑𝑥
𝐿2
𝐿1
=
1
𝐸𝐼
∫ (
𝑊1 𝑥3
6𝐿
−
𝑊2 𝑥3
6𝐿
−
𝑊1 𝑥2
2
) (−1)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (−
𝑊1 𝑥3
6𝐿
+
𝑊2 𝑥3
6𝐿
+
𝑊1 𝑥2
2
) 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[−
𝑊1 𝑥4
24𝐿
+
𝑊2 𝑥4
24𝐿
+
𝑊1 𝑥3
6
]
0
𝐿
=
𝑊1 𝐿3
8𝐸𝐼
+
𝑊2 𝐿3
24𝐸𝐼
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = 𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
𝐴𝐼
𝐴𝐼𝐼](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-50-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
29
Al reemplazar los resultados en las ecuaciones (5 − 1) y (5 − 2), se tiene
− (
11𝑊1 𝐿4
120𝐸𝐼
+
𝑊2 𝐿4
30𝐸𝐼
) +
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (5 − 3)
(
𝑊1 𝐿3
8𝐸𝐼
+
𝑊2 𝐿3
24𝐸𝐼
) −
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (5 − 4)
Al resolver el sistema el sistema simultáneo de ecuaciones previo, se obtiene
∆= ||
𝐿3
3
−
𝐿2
2
−
𝐿2
2
𝐿
|| =
𝐿4
12
∆ 𝑅 𝐴𝑌
= ||
11𝑊1 𝐿4
120
+
𝑊2 𝐿4
30
−
𝐿2
2
− (
𝑊1 𝐿3
8
+
𝑊2 𝐿3
24
) 𝐿
|| = [(
11𝑊1 𝐿4
120
+
𝑊2 𝐿4
30
) (𝐿)] − [(−
𝐿2
2
) (− (
𝑊1 𝐿3
8
+
𝑊2 𝐿3
24
))]
=
11𝑊1 𝐿5
120
+
𝑊2 𝐿5
30
−
𝑊1 𝐿5
16
−
𝑊2 𝐿5
48
=
7𝑊1 𝐿5
240
+
𝑊2 𝐿5
80
∆ 𝑀 𝐴
= ||
𝐿3
3
11𝑊1 𝐿4
120
+
𝑊2 𝐿4
30
−
𝐿2
2
− (
𝑊1 𝐿3
8
+
𝑊2 𝐿3
24
)
|| = [(
𝐿3
3
) (− (
𝑊1 𝐿3
8
+
𝑊2 𝐿3
24
))] − [(
11𝑊1 𝐿4
120
+
𝑊2 𝐿4
30
) (−
𝐿2
2
)]
= −
𝑊1 𝐿6
24
−
𝑊2 𝐿6
72
+
11𝑊1 𝐿6
240
+
𝑊2 𝐿6
60
=
𝑊1 𝐿6
240
+
𝑊2 𝐿6
360
𝑅 𝐴𝑌 =
∆ 𝑅 𝐴𝑌
∆
=
7𝑊1 𝐿5
240
+
𝑊2 𝐿5
80
𝐿4
12
=
7𝑊1 𝐿
20
+
3𝑊2 𝐿
20
⇒∴ 𝑅 𝐴𝑌 = (
7𝑊1 𝐿
20
+
3𝑊2 𝐿
20
)
𝑀𝐴 =
∆ 𝑀 𝐴
∆
=
𝑊1 𝐿6
240
+
𝑊2 𝐿6
360
𝐿4
12
=
𝑊1 𝐿2
20
+
𝑊2 𝐿2
30
⇒∴ 𝑀𝐴 = (
𝑊1 𝐿2
20
+
𝑊2 𝐿2
30
)
Ecuaciones de equilibrio
Se dibuja un diagrama de cargas colocando las redundantes calculadas, figura 5-e. Si en él se
aplican las ecuaciones de la estática, se obtienen las reacciones faltantes, figura 5-f.
+↑ ∑ 𝐹𝑌 = 0 ⇒ (
7𝑊1 𝐿
20
+
3𝑊2 𝐿
20
) − (𝐿)(𝑊2) − [
(𝐿)(𝑊1 − 𝑊2)
2
] + 𝑅 𝐵𝑌 = 0 ⇒∴ 𝑅 𝐵𝑌 = (
3𝑊1 𝐿
20
+
7𝑊2 𝐿
20
)
𝐴1
𝐴2](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-51-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
33
𝑎 =
Δa
Δ
=
𝑊𝐿
−𝐿3
4
= −4
𝑊
𝐿2
𝑏 =
Δb
Δ
=
−𝐿2
𝑊
−𝐿3
4
= 4
𝑊
𝐿
𝑐 =
Δc
Δ
=
0
−𝐿3
4
= 0
En consecuencia, al sustituir estos valores en la expresión (𝐼), se tiene que
𝑦 = −4
𝑊
𝐿2
𝑥2
+ 4
𝑊
𝐿
𝑥
Como no hay discontinuidad de carga a lo largo de la estructura primaria, sólo se efectuará un corte
perpendicular al eje longitudinal de la viga, entonces, no importa si tal seccionamiento se hace antes
o después de que la carga distribuida alcanza una intensidad de 𝑊.
En la figura 6-c se proporciona un diagrama de cargas del segmento de viga con longitud 𝑥. Previo
a efectuar el equilibrio estático en el cuerpo libre para deducir la función del momento 𝑀, se
determina la carga concentrada equivalente 𝐴𝐼 de la fuerza distribuida y su punto de aplicación 𝑥̅ 𝐼.
0 ≤ 𝑥 ≤ 𝐿
La fuerza resultante de la carga distribuida seccionada es
𝐴𝐼 = ∫ 𝑑𝐴 = ∫ 𝑦𝑑𝑥
𝐿2
𝐿1
= ∫ (−4
𝑊
𝐿2
𝑥2
+ 4
𝑊
𝐿
𝑥) 𝑑𝑥 = −4
𝑊
𝐿2
∫ 𝑥2
𝑥
0
𝑑𝑥 + 4
𝑊
𝐿
∫ 𝑥𝑑𝑥
𝑥
0
𝑥
0
−4
𝑊
𝐿2
[
𝑥3
3
]
0
𝑥
+ 4
𝑊
𝐿
[
𝑥2
2
]
0
𝑥
= −
4𝑊
3𝐿2
[𝑥3
− 03] +
4𝑊
2𝐿
[𝑥2
− 02] = −
4𝑊
3𝐿2
𝑥3
+
2𝑊
𝐿
𝑥2
y su ubicación es
𝑥̅ 𝐼 =
∫ 𝑥̃ 𝑑𝐴
∫ 𝑑𝐴
=
∫ 𝑥𝑦𝑑𝑥
𝐿2
𝐿1
∫ 𝑦𝑑𝑥
𝐿2
𝐿1
=
∫ 𝑥 (−4
𝑊
𝐿2 𝑥2
+ 4
𝑊
𝐿
𝑥) 𝑑𝑥
𝑥
0
∫ (−4
𝑊
𝐿2 𝑥2 + 4
𝑊
𝐿
𝑥) 𝑑𝑥
𝑥
0
Como el denominador ya fue resuelto, se atiende al numerador.
∫ 𝑥
𝐿
0
(−4
𝑊
𝐿2
𝑥2
+ 4
𝑊
𝐿
𝑥) 𝑑𝑥 = −4
𝑊
𝐿2
∫ 𝑥3
𝐿
0
𝑑𝑥 + 4
𝑊
𝐿
∫ 𝑥2
𝑑𝑥
𝐿
0
𝐴
𝑥
𝑦 = −4
𝑊
𝐿2
𝑥2
+ 4
𝑊
𝐿
𝑥
𝑥̅ 𝐼 𝑥 − 𝑥̅ 𝐼
𝐴𝐼
𝑀1
(c)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-55-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
34
= −4
𝑊
𝐿2
[
𝑥4
4
]
0
𝑥
+ 4
𝑊
𝐿
[
𝑥3
3
]
0
𝑥
=
−4𝑊
4𝐿2
[𝑥4
− 04] +
4𝑊
3𝐿
[𝑥3
− 03] = −
𝑊
𝐿2
𝑥4
+
4𝑊
3𝐿
𝑥3
∴ 𝑥̅ 𝐼 =
−
𝑊
𝐿2 𝑥4
+
4𝑊
3𝐿
𝑥3
−
4𝑊
3𝐿2 𝑥3 +
2𝑊
𝐿
𝑥2
𝑎 𝑙𝑎 𝑑𝑒𝑟𝑒𝑐ℎ𝑎 𝑑𝑒 𝐴
Tomando momentos alrededor del punto del corte, se obtiene
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − (−
4𝑊
3𝐿2
𝑥3
+
2𝑊
𝐿
𝑥2
) (𝑥 −
−
𝑊
𝐿2 𝑥4
+
4𝑊
3𝐿
𝑥3
−
4𝑊
3𝐿2 𝑥3 +
2𝑊
𝐿
𝑥2
) = 0
−𝑀1 − (−
4𝑤
3𝐿2
𝑥4
+
2𝑤
𝐿
𝑥3
+
𝑤
𝐿2
𝑥4
−
4𝑤
3𝐿
𝑥3
) ⇒ 𝑀1 =
𝑊
3𝐿2
𝑥4
−
2𝑊
3𝐿
𝑥3
Además,
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Por consiguiente,
𝑑1 =
1
𝐸𝐼
∫ (
𝑊
3𝐿2
𝑥4
−
2𝑊
3𝐿
𝑥3
) (𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (
𝑊
3𝐿2
𝑥5
−
2𝑊
3𝐿
𝑥4
) 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
𝑊
18𝐿2
𝑥6
−
2𝑊
15𝐿
𝑥5
]
0
𝐿
=
𝑊𝐿4
18𝐸𝐼
−
2𝑊𝐿4
15𝐸𝐼
= −
7𝑊𝐿4
90𝐸𝐼
𝑑2 =
1
𝐸𝐼
∫ (
𝑊
3𝐿2
𝑥4
−
2𝑊
3𝐿
𝑥3
) (−1)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (−
𝑊
3𝐿2
𝑥4
+
2𝑊
3𝐿
𝑥3
) 𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[−
𝑊
15𝐿2
𝑥5
+
𝑊
6𝐿
𝑥4
]
0
𝐿
= −
𝑊𝐿3
15𝐸𝐼
+
𝑊𝐿3
6𝐸𝐼
=
𝑊𝐿3
10𝐸𝐼
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = 𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
De tal modo que el sistema simultáneo de ecuaciones (6 − 1) y (6 − 2) se convierte en
−
7𝑊𝐿4
90𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (6 − 3)
𝑊𝐿3
10𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (6 − 4)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-56-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
35
Entonces, las fuerzas correctivas son resultado de
∆= ||
𝐿3
3
−
𝐿2
2
−
𝐿2
2
𝐿
|| =
𝐿4
12
∆ 𝑅 𝐴𝑌
= ||
7𝑊𝐿4
90
−
𝐿2
2
−
𝑊𝐿3
10
𝐿
|| = [(
7𝑊𝐿4
90
) (𝐿)] − [(−
𝐿2
2
) (−
𝑊𝐿3
10
)] =
7𝑊𝐿5
90
−
𝑊𝐿5
20
=
𝑊𝐿5
36
∆ 𝑀 𝐴
= ||
𝐿3
3
7𝑊𝐿4
90
−
𝐿2
2
−
𝑊𝐿3
10
|| = [(
𝐿3
3
) (−
𝑊𝐿3
10
)] − [(
7𝑊𝐿4
90
) (−
𝐿2
2
)] = −
𝑊𝐿6
30
+
7𝑊𝐿6
180
=
𝑊𝐿6
180
𝑅 𝐴𝑌 =
∆ 𝑅 𝐴𝑌
∆
=
𝑊𝐿5
36
𝐿4
12
=
𝑊𝐿
3
⇒∴ 𝑅 𝐴𝑌 =
𝑊𝐿
3
𝑀𝐴 =
∆ 𝑀 𝐴
∆
=
𝑊𝐿6
180
𝐿4
12
=
𝑊𝐿2
15
⇒∴ 𝑀𝐴 =
𝑊𝐿2
15
Ecuaciones de equilibrio
Estas se aplican al diagrama de cargas de la figura 6-d. La carga concentrada equivalente de la
carga distribuida con intensidad parabólica es
𝐴1 = ∫ (−4
𝑊
𝐿2
𝑥2
+ 4
𝑊
𝐿
𝑥) 𝑑𝑥
𝐿
0
= −
4𝑊
3𝐿2
[𝐿3
− 03] +
4𝑊
2𝐿
[𝐿2
− 02] =
2
3
𝑊𝐿
y su línea de acción se ubica en
𝑥̅1 =
∫ 𝑥 (−4
𝑊
𝐿2 𝑥2
+ 4
𝑊
𝐿
𝑥) 𝑑𝑥
𝐿
0
∫ (−4
𝑊
𝐿2 𝑥2 + 4
𝑊
𝐿
𝑥) 𝑑𝑥
𝐿
0
=
−4𝑊
4𝐿2 [𝐿4
− 04] +
4𝑊
3𝐿
[𝐿3
− 03]
2
3
𝑊𝐿
=
−𝑊𝐿2
+
4
3
𝑊𝐿2
2
3
𝑊𝐿
=
𝑊𝐿2
3
2
3
𝑊𝐿
=
1
2
𝐿
Así que,
+↑ ∑ 𝐹𝑌 = 0 ⇒
𝑊𝐿
3
−
2
3
𝑊𝐿 + 𝑅 𝐵𝑌 = 0 ⇒∴ 𝑅 𝐵𝑌 =
𝑊𝐿
3
+ ∑ 𝑀𝐴 = 0 ⇒ −
𝑊𝐿2
15
+
2
3
𝑊𝐿 (
𝐿
2
) −
𝑊𝐿
3
(𝐿) + 𝑀 𝐵 = 0 ⇒∴ 𝑀 𝐵 =
𝑊𝐿2
15](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-57-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
39
Se secciona la viga primaria. Con base en la figura 7-c, se calcula 𝑀.
0 ≤ 𝑥 ≤ 𝐿
La fuerza resultante de la carga distribuida seccionada es
𝐴𝐼 = ∫ 𝑑𝐴 = ∫ 𝑦𝑑𝑥
𝐿2
𝐿1
= ∫ (
𝑊
𝐿2
𝑥2
) 𝑑𝑥 =
𝑥
0
𝑊
𝐿2
∫ 𝑥2
𝑑𝑥 =
𝑊
𝐿2
[
𝑥3
3
]
0
𝑥
=
𝑊
𝐿2
[
𝑥3
− 03
3
] =
1
3
𝑊
𝐿2
𝑥3
𝑥
0
y su punto de aplicación es
𝑥̅ 𝐼 =
∫ 𝑥̃ 𝑑𝐴
∫ 𝑑𝐴
=
∫ 𝑥𝑦𝑑𝑥
𝐿2
𝐿1
∫ 𝑦𝑑𝑥
𝐿2
𝐿1
=
∫ 𝑥 (
𝑊
𝐿2 𝑥2
) 𝑑𝑥
𝑥
0
1
3
𝑊
𝐿2 𝑥3
=
𝑊
𝐿2 ∫ 𝑥3
𝑑𝑥
𝑥
0
1
3
𝑊
𝐿2 𝑥3
=
𝑊
𝐿2 [
𝑥4
4
]
0
𝑥
1
3
𝑊
𝐿2 𝑥3
=
𝑊
𝐿2 [
𝑥4
− 04
4
]
1
3
𝑊
𝐿2 𝑥3
=
1
4
𝑊
𝐿2 𝑥4
1
3
𝑊
𝐿2 𝑥3
=
3
4
𝑥
Se calcula el momento interno 𝑀. La suma de momentos respecto del punto del corte para el
cuerpo libre de la figura 7-c conlleva a
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0 ⇒ −𝑀1 − (
1
3
𝑊
𝐿2
𝑥3
) (
1
4
𝑥) = 0 ⇒ 𝑀1 = −
𝑊𝑥4
12𝐿2
Luego, los momentos internos para las vigas liberadas sometidas a una unidad de las fuerzas
redundantes son
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se calculan las incompatibilidades geométricas.
𝑑1 =
1
𝐸𝐼
∫ (−
𝑊𝑥4
12𝐿2
) (𝑥)𝑑𝑥
𝐿
0
= −
𝑊𝐿4
72𝐸𝐼
𝐴
𝑥
𝑦 =
𝑊
𝐿2
𝑥2
𝑥̅ 𝐼 =
3
4
𝑥
𝐴𝐼 =
1
3
𝑊
𝐿2
𝑥3
𝑥
4
𝑀1
(c)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-61-320.jpg)




![Fuerzas de fijación y momentos de empotramiento en vigas
44
∫
𝑥2
1 + 𝑥2
𝑑𝑥 = ∫ 𝑥2(1 + 𝑥2)−1
𝑑𝑥
Esta última integral es del tipo:
∫(𝑥 𝑚)(𝑎 + 𝑏𝑥 + 𝑐𝑥2) 𝑛
𝑑𝑥 =
𝑥 𝑚−1(𝑎 + 𝑏𝑥 + 𝑐𝑥2) 𝑛+1
𝑐(2𝑛 + 𝑚 + 1)
−
𝑏(𝑛 + 𝑚)
𝑐(2𝑛 + 𝑚 + 1)
∫ 𝑥 𝑚−1(𝑎 + 𝑏𝑥 + 𝑐𝑥2) 𝑛
𝑑𝑥
−
𝑎(𝑚 − 1)
𝑐(2𝑛 + 𝑚 + 1)
∫ 𝑥 𝑚−2 (𝑎 + 𝑏𝑥 + 𝑐𝑥2) 𝑛
𝑑𝑥
En este caso, 𝑚 = 2, 𝑎 = 1, 𝑏 = 0, 𝑐 = 1 y 𝑛 = −1.
Sustituyendo y simplificando, se tiene
∫(𝑥2)(1 + 𝑥2)−1
𝑑𝑥 =
𝑥2−1(1 + 𝑥2)−1+1
1(2(−1) + 2 + 1)
−
(0)(−1 + 2)
1(2(−1) + 2 + 1)
∫ 𝑥2−1(1 + 𝑥2)−1
𝑑𝑥
−
1(2 − 1)
1(2(−1) + 2 + 1)
∫ 𝑥2−2 (1 + 𝑥2)−1
𝑑𝑥 = 𝑥 − ∫
𝑑𝑥
1 + 𝑥2
La integral obtenida, ∫
𝑑𝑥
1+𝑥2, ya es de solución obvia, pues directamente se sabe que
∫
𝑑𝑥
1 + 𝑥2
= 𝑎𝑟𝑐 tan(𝑥)
Por lo tanto,
∫
𝑥2
1 + 𝑥2
𝑑𝑥 = ∫ 𝑥2(1 + 𝑥2)−1
𝑑𝑥 = 𝑥 − 𝑎𝑟𝑐 tan(𝑥)
En consecuencia,
∫ 𝑙𝑛(1 + 𝑥2)𝑑𝑥 = 𝑥 ∙ 𝑙𝑛(1 + 𝑥2) + 2(𝑎𝑟𝑐 tan(𝑥) − 𝑥)
La integral definida resulta ser
∫ 𝑙𝑛(1 + 𝑥2)𝑑𝑥
𝑥
0
= [𝑥 ∙ 𝑙𝑛(1 + 𝑥2) + 2(𝑎𝑟𝑐 tan(𝑥) − 𝑥)]0
𝑥
= [𝑥 ∙ 𝑙𝑛(1 + 𝑥2) + 2(𝑎𝑟𝑐 tan(𝑥) − 𝑥)] − [(0)𝑙𝑛(1 + 02) + 2(𝑎𝑟𝑐 tan(0) − 0)]
= 𝑥 ∙ 𝑙𝑛(1 + 𝑥2) + 2(𝑎𝑟𝑐 tan(𝑥) − 𝑥)
Se determina la ubicación de la carga concentrada previa.
𝑥̅ 𝐼 =
∫ 𝑥̃ 𝑑𝐴
∫ 𝑑𝐴
=
∫ 𝑥𝑦 𝑑𝑥
𝐿2
𝐿1
∫ 𝑦 𝑑𝑥
𝐿2
𝐿1
=
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥
𝑥
0
∫ 𝑙𝑛(1 + 𝑥2)𝑑𝑥
𝑥
0
=
(𝑥2
+ 1)𝑙𝑛(𝑥2
+ 1)
2
−
𝑥2
2
𝑥 ∙ 𝑙𝑛(𝑥2 + 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝑥) − 𝑥)
El denominador de la expresión anterior, ya había sido resuelto. A continuación se detalla el
procedimiento para esclarecer la forma en que se obtuvo el valor del numerador.](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-66-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
45
La integral en forma indefinida es
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥
Esta se resuelve como sigue. Sea 𝑧 = 1 + 𝑥2
. Entonces 𝑑𝑧 = 2𝑥𝑑𝑥, y por tanto 𝑥𝑑𝑥 =
1
2
𝑑𝑧. Así, la
regla de sustitución da
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥 =
1
2
∫ 𝑙𝑛(𝑧)𝑑𝑧
La integral que obtuvimos, ∫ 𝑙𝑛(𝑧)𝑑𝑧, es más sencilla que la original pero todavía no es obvia, así
que aplicamos la regla del producto para derivación para resolverla.
Sea
𝑢 = 𝑙𝑛(𝑧) 𝑑𝑣 = 𝑑𝑧
Entonces
𝑑𝑢 =
1
𝑧
𝑑𝑧 𝑣 = 𝑧
Al integrar por partes tendremos ∫ 𝑢 𝑑𝑣 = 𝑢𝑣 − ∫ 𝑣 𝑑𝑢, es decir,
∫ 𝑙𝑛(𝑧)𝑑𝑧 = (𝑙𝑛(𝑧))(𝑧) − ∫ 𝑧 (
1
𝑧
𝑑𝑧) = 𝑧𝑙𝑛(𝑧) − ∫ 𝑑𝑧 = 𝑧 ∙ 𝑙𝑛(𝑧) − 𝑧 = 𝑧[𝑙𝑛(𝑧) − 1]
Por lo tanto,
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥 =
1
2
𝑧[𝑙𝑛(𝑧) − 1]
Sustituyendo 𝑧 = 1 + 𝑥2
en la ecuación anterior se obtiene
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥 =
1
2
(1 + 𝑥2)[𝑙𝑛(1 + 𝑥2) − 1]
Así, tenemos
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥
𝑥
0
= [
1
2
(1 + 𝑥2)[𝑙𝑛(1 + 𝑥2) − 1]]
0
𝑥
= [
1
2
(1 + 𝑥2)[𝑙𝑛(1 + 𝑥2) − 1]] − [
1
2
(1 + 02)[𝑙𝑛(1 + 02) − 1]] =
(𝑥2
+ 1)𝑙𝑛(𝑥2
+ 1)
2
−
𝑥2
2
Por consiguiente, la función del momento flector 𝑀 es
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-67-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
46
−𝑀1 − [𝑥 ∙ 𝑙𝑛(𝑥2
+ 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝑥) − 𝑥)] [𝑥 −
(𝑥2
+ 1)𝑙𝑛(𝑥2
+ 1)
2
−
𝑥2
2
𝑥 ∙ 𝑙𝑛(𝑥2 + 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝑥) − 𝑥)
] = 0
𝑀1 = −
𝑥2
∙ 𝑙𝑛(𝑥2
+ 1)
2
+
𝑙𝑛(𝑥2
+ 1)
2
− 2𝑥 ∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝑥) +
3
2
𝑥2
Los momentos internos de las dos vigas isostáticas restantes de la figura 8-b, son
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se calculan los desplazamientos necesarios empleando el método del trabajo virtual.
𝑑1 =
1
𝐸𝐼
∫ (−
𝑥2
∙ 𝑙𝑛(𝑥2
+ 1)
2
+
𝑙𝑛(𝑥2
+ 1)
2
− 2𝑥 ∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝑥) +
3
2
𝑥2
) (𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[−
𝐿4
∙ 𝑙𝑛(𝐿2
+ 1)
8
+
𝐿2
∙ 𝑙𝑛(𝐿2
+ 1)
4
+
𝑙𝑛(𝐿2
+ 1)
24
−
2𝐿3
∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝐿)
3
+
7𝐿4
16
−
𝐿2
24
]
𝑑2 =
1
𝐸𝐼
∫ (−
𝑥2
∙ 𝑙𝑛(𝑥2
+ 1)
2
+
𝑙𝑛(𝑥2
+ 1)
2
− 2𝑥 ∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝑥) +
3
2
𝑥2
) (−1)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
𝐿3
∙ 𝑙𝑛(𝐿2
+ 1)
6
−
𝐿 ∙ 𝑙𝑛(𝐿2
+ 1)
2
+ 𝐿2
∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) −
𝑎𝑟𝑐𝑡𝑎𝑛(𝐿)
3
−
11𝐿3
18
+
𝐿
3
]
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = −
𝐿2
2𝐸𝐼
𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
El sistema de ecuaciones de flexibilidades resulta en
Por lo tanto,
𝑅 𝐴𝑌 =
6(𝐿4
− 1)𝑙𝑛(𝐿2
+ 1) + 𝐿(24(𝐿2
+ 1)𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿(19𝐿2
+ 18))
12𝐿3
= 𝐴
𝑀𝐴 =
6(𝐿4
+ 6𝐿2
− 3)𝑙𝑛(𝐿2
+ 1) + 𝐿(96𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 13𝐿(𝐿2
+ 6))
72𝐿2
= 𝐵
Ecuaciones de equilibrio. Por último, se calculan las reacciones en el empotramiento 𝐵 aplicando
las ecuaciones de equilibrio en el diagrama de la figura 8-d.
1
𝐸𝐼
[−
𝐿4
∙ 𝑙𝑛(𝐿2
+ 1)
8
+
𝐿2
∙ 𝑙𝑛(𝐿2
+ 1)
4
+
𝑙𝑛(𝐿2
+ 1)
24
−
2𝐿3
∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝐿)
3
+
7𝐿4
16
−
𝐿2
24
] +
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 − − − (8 − 3)
1
𝐸𝐼
[
𝐿3
∙ 𝑙𝑛(𝐿2
+ 1)
6
−
𝐿 ∙ 𝑙𝑛(𝐿2
+ 1)
2
+ 𝐿2
∙ 𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) −
𝑎𝑟𝑐𝑡𝑎𝑛(𝐿)
3
−
11𝐿3
18
+
𝐿
3
] −
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (8 − 4)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-68-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
47
La carga concentrada equivalente de la carga distribuida con intensidad logarítmica es
𝐴1 = ∫ 𝐿𝑛(1 + 𝑥2)𝑑𝑥 = 𝐿 ∙ 𝑙𝑛(𝐿2
+ 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿)
𝐿
0
y su línea de acción se localiza a una distancia de
𝑥̅1 =
∫ 𝑥(𝑙𝑛(1 + 𝑥2))𝑑𝑥
𝐿
0
∫ (𝑙𝑛(1 + 𝑥2))𝑑𝑥
𝐿
0
=
(𝐿2
+ 1)𝑙𝑛(𝐿2
+ 1)
2
−
𝐿2
2
𝐿 ∙ 𝑙𝑛(𝐿2 + 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿)
𝑎 𝑙𝑎 𝑑𝑒𝑟𝑒𝑐ℎ𝑎 𝑑𝑒 𝐴
El equilibrio estático del cuerpo libre estriba en
+↑ ∑ 𝐹𝑌 = 0 ⇒
6(𝐿4
− 1)𝑙𝑛(𝐿2
+ 1) + 𝐿(24(𝐿2
+ 1)𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿(19𝐿2
+ 18))
12𝐿3
−[𝐿 ∙ 𝑙𝑛(𝐿2
+ 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿)] + 𝑅 𝐵𝑌 = 0
∴ 𝑅 𝐵𝑌 =
6(𝐿4
+ 1) ∗ 𝐿𝑛(𝐿2
+ 1) − 𝐿(24𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) + 𝐿(5𝐿2
− 18))
12𝐿3
= 𝐶
+ ∑ 𝑀𝐴 = 0 ⇒ − [
6(𝐿4
+ 6𝐿2
− 3)𝑙𝑛(𝐿2
+ 1) + 𝐿(96𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 13𝐿(𝐿2
+ 6))
72𝐿2
]
+[𝐿 ∙ 𝑙𝑛(𝐿2
+ 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿)] [
(𝐿2
+ 1)𝑙𝑛(𝐿2
+ 1)
2
−
𝐿2
2
𝐿 ∙ 𝑙𝑛(𝐿2 + 1) + 2(𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) − 𝐿)
]
− [
6(𝐿4
+ 1) ∗ 𝐿𝑛(𝐿2
+ 1) − 𝐿(24𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) + 𝐿(5𝐿2
− 18))
12𝐿3
] (𝐿) + 𝑀 𝐵 = 0
∴ 𝑀 𝐵 =
6(𝐿4
+ 3) ∗ 𝐿𝑛(𝐿2
+ 1) − 𝐿(48𝑎𝑟𝑐𝑡𝑎𝑛(𝐿) + 𝐿(7𝐿2
− 30))
72𝐿2
= 𝐷
𝐴 𝐵
𝐿
𝑦 = 𝑙𝑛(1 + 𝑥2)
𝑅 𝐵𝑌 = 𝐶
𝑀 𝐵 = 𝐷𝑀𝐴 = 𝐵
𝑅 𝐴𝑌 = 𝐴
𝐴1
𝑥̅1
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-69-320.jpg)

![Fuerzas de fijación y momentos de empotramiento en vigas
49
𝐿
2⁄ ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀2 − 𝑀 = 0 ⇒ 𝑀2 = 𝑀
Se toman momentos alrededor del punto del corte en cada seccionamiento para deducir las
funciones de los momentos 𝑀, figuras 9-c y 9-d.
Se retoman los siguientes momentos internos
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se requiere de
𝑑1 =
1
𝐸𝐼
[∫ (0)(𝑥)𝑑𝑥 + ∫ (𝑀)(𝑥)𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
] =
3𝑀𝐿2
8𝐸𝐼
𝑑2 =
1
𝐸𝐼
[∫ (0)(−1)𝑑𝑥 + ∫ (𝑀)(−1)𝑑𝑥
𝐿
𝐿
2⁄
𝐿
2⁄
0
] = −
𝑀𝐿
2𝐸𝐼
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = −
𝐿2
2𝐸𝐼
𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
Las ecuaciones de compatibilidad necesarias son
3𝑀𝐿2
8𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (9 − 1)
−
𝑀𝐿
2𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (9 − 2)
La solución del sistema de ecuaciones (9 − 1) y (9 − 2) corresponde a
𝑅 𝐴𝑌 = −
3𝑀
2𝐿
⇒∴ 𝑅 𝐴𝑌 =
3𝑀
2𝐿
𝑀𝐴 = −
𝑀
4
∴ 𝑀𝐴 =
𝑀
4
𝐴
𝐿/2
𝑥
𝑀
𝑀2
𝑥 − 𝐿/2
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-71-320.jpg)


![Fuerzas de fijación y momentos de empotramiento en vigas
52
0 ≤ 𝑥 ≤ 𝑎
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0 ⇒ 𝑀1 = 0
𝑎 ≤ 𝑥 ≤ 𝑎 + 𝑏
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀2 − 𝑃(𝑥 − 𝑎) = 0 ⇒ 𝑀2 = −𝑃𝑥 + 𝑃𝑎
Los momentos internos 𝑚1 y 𝑚2, corresponden a
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝑎 + 𝑏
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝑎 + 𝑏
Se calculan las incompatibilidades geométricas.
𝑑1 =
1
𝐸𝐼
[∫ (0)(𝑥)𝑑𝑥 + ∫ (−𝑃𝑥 + 𝑃𝑎)(𝑥)𝑑𝑥
𝑎+𝑏
𝑎
𝑎
0
] =
1
𝐸𝐼
[∫ (−𝑃𝑥2
+ 𝑃𝑎𝑥)𝑑𝑥
𝑎+𝑏
𝑎
] =
1
𝐸𝐼
[
−𝑃𝑥3
3
+
𝑃𝑎𝑥2
2
]
𝑎
𝑎+𝑏
=
1
𝐸𝐼
{(
−𝑃(𝑎 + 𝑏)3
3
+
𝑃𝑎(𝑎 + 𝑏)2
2
) − (
−𝑃(𝑎)3
3
+
𝑃𝑎(𝑎)2
2
)}
=
1
𝐸𝐼
{(−
𝑃
3
(𝑎3
+ 3𝑎𝑏2
+ 3𝑎2
𝑏 + 𝑏3) +
𝑃
2
𝑎(𝑎2
+ 2𝑎𝑏 + 𝑏2)) − (
𝑃
6
𝑎3
)}
=
1
𝐸𝐼
(−
𝑃
3
𝑎3
− 𝑃𝑎𝑏2
− 𝑃𝑎2
𝑏 −
𝑃
3
𝑏3
+
𝑃
2
𝑎3
+ 𝑃𝑎2
𝑏 +
𝑃
2
𝑎𝑏2
−
𝑃
6
𝑎3
) = −
𝑃𝑎𝑏2
2𝐸𝐼
−
𝑃𝑏3
3𝐸𝐼
𝑑2 =
1
𝐸𝐼
[∫ (0)(−1)𝑑𝑥 + ∫ (−𝑃𝑥 + 𝑃𝑎)(−1)𝑑𝑥
𝑎+𝑏
𝑎
𝑎
0
] =
1
𝐸𝐼
[∫ (𝑃𝑥 − 𝑃𝑎)𝑑𝑥
𝑎+𝑏
𝑎
]
=
1
𝐸𝐼
[
𝑃𝑥2
2
− 𝑃𝑎𝑥]
𝑎
𝑎+𝑏
=
1
𝐸𝐼
{(
𝑃(𝑎 + 𝑏)2
2
− 𝑃𝑎(𝑎 + 𝑏)) − (
𝑃(𝑎)2
2
− 𝑃𝑎(𝑎))}
𝐴
𝑀1
𝑥
𝐴
𝑎 𝑥 − 𝑎
𝑃
𝑥
𝑀2
(c)
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-74-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
53
Se determinan los coeficientes de flexibilidad.
𝑓11 =
1
𝐸𝐼
∫ (𝑥)(𝑥)𝑑𝑥 =
1
𝐸𝐼
𝑎+𝑏
0
∫ 𝑥2
𝑑𝑥
𝑎+𝑏
0
=
1
𝐸𝐼
[
𝑥3
3
]
0
𝑎+𝑏
=
(𝑎 + 𝑏)3
3𝐸𝐼
𝑓21 =
1
𝐸𝐼
∫ (𝑥)(−1)𝑑𝑥 =
1
𝐸𝐼
∫ −𝑥𝑑𝑥
𝑎+𝑏
0
=
1
𝐸𝐼
[
𝑥2
2
]
0
𝑎+𝑏
= −
(𝑎 + 𝑏)2
2𝐸𝐼
𝑎+𝑏
0
𝑓12 = 𝑓21 = −
(𝑎 + 𝑏)2
2𝐸𝐼
𝑓22 =
1
𝐸𝐼
∫ (−1)(−1)𝑑𝑥 =
1
𝐸𝐼
∫ 𝑑𝑥
𝑎+𝑏
0
=
1
𝐸𝐼
[𝑥]0
𝑎+𝑏
=
𝑎 + 𝑏
𝐸𝐼
𝑎+𝑏
0
Las ecuaciones de compatibilidad necesarias son
− (
𝑃𝑎𝑏2
2𝐸𝐼
+
𝑃𝑏3
3𝐸𝐼
) +
(𝑎 + 𝑏)3
3𝐸𝐼
𝑅 𝐴𝑌 −
(𝑎 + 𝑏)2
2𝐸𝐼
𝑀𝐴 = 0 − − − (10 − 1)
𝑃𝑏2
2𝐸𝐼
−
(𝑎 + 𝑏)2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝑎 + 𝑏
𝐸𝐼
𝑀𝐴 = 0 − − − (10 − 2)
Al resolver el sistema de ecuaciones (10 − 1) (10 − 2), se tienen los siguientes valores para las
fuerzas redundantes
𝑅 𝐴𝑌 =
(3𝑎 + 𝑏)𝑏2
𝑃
(𝑎 + 𝑏)3
=
(3𝑎 + 𝑏)𝑏2
𝑃
(𝐿)3
=
𝑃𝑏2
𝐿3
(3(𝐿 − 𝑏) + 𝑏) =
𝑃𝑏2
𝐿2
(
3𝐿 − 2𝑏
𝐿
)
= [
𝑃𝑏2
𝐿2
(3 − 2
𝑏
𝐿
)]
𝑀𝐴 =
𝑎𝑏2
𝑃
𝑎2 + 2𝑎𝑏 + 𝑏2
=
𝑃𝑎𝑏2
(𝑎 + 𝑏)2
=
𝑃𝑎𝑏2
𝐿2
Ecuaciones de equilibrio, figura 10-e. Por lo tanto,
+↑ ∑ 𝐹𝑌 = 0 ⇒
(3𝑎 + 𝑏)𝑏2
𝑃
(𝑎 + 𝑏)3
− 𝑃 + 𝑅 𝐵𝑌 = 0
𝑅 𝐵𝑌 =
𝑎2(𝑎 + 3𝑏)𝑃
(𝑎 + 𝑏)3
=
𝑃𝑎2(𝑎 + 3𝑏)
𝐿3
=
𝑃𝑎2
𝐿3
(𝑎 + 3(𝐿 − 𝑎)) =
𝑃𝑎2
𝐿3
(3𝐿 − 2𝑎)
=
1
𝐸𝐼
{(
𝑃
2
(𝑎2
+ 2𝑎𝑏 + 𝑏2) − (𝑃𝑎2
+ 𝑃𝑎𝑏)) − (−
𝑃
2
𝑎2
)} =
1
𝐸𝐼
(
𝑃
2
𝑎2
+ 𝑃𝑎𝑏 +
𝑃
2
𝑏2
− 𝑃𝑎2
− 𝑃𝑎𝑏 +
𝑃
2
𝑎2
) =
𝑃𝑏2
2𝐸𝐼](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-75-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
54
=
𝑃𝑎2
𝐿2
(
3𝐿 − 2𝑎
𝐿
) = [
𝑃𝑎2
𝐿2
(3 − 2
𝑎
𝐿
)]
+ ∑ 𝑀𝐴 = 0 ⇒ −
𝑃𝑎𝑏2
(𝑎 + 𝑏)2
+ 𝑃𝑎 −
𝑃𝑎2(𝑎 + 3𝑏)
(𝑎 + 𝑏)3
(𝑎 + 𝑏) + 𝑀 𝐵 = 0
𝑀 𝐵 =
𝑃𝑎2
𝑏
(𝑎 + 𝑏)2
=
𝑃𝑎2
𝑏
𝐿2
Las fuerzas de fijación y los momentos de empotramiento perfecto se muestran en la figura 10-f.
𝐴 𝐵
𝑎 𝑏
𝑃
𝐿 𝑅 𝐵𝑌
𝑀 𝐵
𝑅 𝐴𝑌 = [
𝑃𝑏2
𝐿2
(3 − 2
𝑏
𝐿
)]
𝑀𝐴 =
𝑃𝑎𝑏2
𝐿2
𝐴 𝐵
𝑎 𝑏
𝑃
𝐿𝑅 𝐴𝑌 = [
𝑃𝑏2
𝐿2
(3 − 2
𝑏
𝐿
)]
𝑀 𝐴 =
𝑃𝑎𝑏2
𝐿2
𝑅 𝐵𝑌 = [
𝑃𝑎2
𝐿2
(3 − 2
𝑎
𝐿
)]
𝑀 𝐵 =
𝑃𝑎2
𝑏
𝐿2
(e)
(f)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-76-320.jpg)

![Fuerzas de fijación y momentos de empotramiento en vigas
56
Ecuaciones de compatibilidad. Se calculan los momentos flexionantes 𝑀 a partir de las figuras
11-c y 11-d.
0 ≤ 𝑥 ≤ 𝑎
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝑀1 = 0
𝑎 ≤ 𝑥 ≤ 𝑎 + 𝑏
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀2 + 𝑀 = 0 ⇒ 𝑀2 = 𝑀
Se tienen siguientes momentos internos 𝑚1 y 𝑚2
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝑎 + 𝑏
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝑎 + 𝑏
El desplazamiento vertical y la pendiente en 𝐴 de la estructuras primaria son, respectivamente
𝑑1 =
1
𝐸𝐼
[∫ (0)(𝑥)𝑑𝑥 + ∫ (𝑀)(𝑥)𝑑𝑥
𝑎+𝑏
𝑎
𝑎
0
] =
(2𝑎 + 𝑏)(𝑏𝑀)
2𝐸𝐼
𝑑2 =
1
𝐸𝐼
[∫ (0)(−1)𝑑𝑥 + ∫ (𝑀)(−1)𝑑𝑥
𝑎+𝑏
𝑎
𝑎
0
] = −
𝑏𝑀
2𝐸𝐼
Por otra parte, los coeficientes de flexibilidad corresponden a
𝑓11 =
(𝑎 + 𝑏)3
3𝐸𝐼
𝑓21 = −
(𝑎 + 𝑏)2
2𝐸𝐼
𝑓12 = −
(𝑎 + 𝑏)2
2𝐸𝐼
𝑓22 =
𝑎 + 𝑏
𝐸𝐼
Se plantea el sistema de ecuaciones de compatibilidad geométrica y se calculan las reacciones
redundantes.
(2𝑎 + 𝑏)(𝑏𝑀)
2𝐸𝐼
+
(𝑎 + 𝑏)3
3𝐸𝐼
𝑅 𝐴𝑌 −
(𝑎 + 𝑏)2
2𝐸𝐼
𝑀𝐴 = 0 − − − (11 − 1)
𝐴
𝑀1
𝑥
𝐴
𝑎 𝑥 − 𝑎
𝑀
𝑥
𝑀2
(c)
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-78-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
60
Expresando la ecuación (12 − 1) en términos de la incógnita, se tiene
0 = 𝑑1 + 𝑓11 𝑅 𝐴𝑋 = 0 − − − (12 − 2)
Se determinan las fuerzas normales 𝑁 con base en las figuras 12-e y 12-f.
0 ≤ 𝑥 ≤ 𝑎
+→ ∑ 𝐹𝑋 = 0
𝑁1 = 0
𝑎 ≤ 𝑥 ≤ 𝑎 + 𝑏
+→ ∑ 𝐹𝑋 = 0
𝑁2 − 𝑃 cos 𝛼 = 0 ⇒ 𝑁2 = 𝑃 cos 𝛼
Se deduce la fuerza normal 𝑛 a partir de la figura 12-g.
0 ≤ 𝑥 ≤ 𝑎 + 𝑏
+→ ∑ 𝐹𝑋 = 0
𝑁1 + 1 = 0 ⇒ 𝑁1 = −1
Al emplear la ecuación para determinar la deformación axial, se tiene que la incompatibilidad
geométrica es
𝑑1 = ∫
𝑁𝑛
𝐴𝐸
𝐿2
𝐿1
𝑑𝑥 = ∫
(0)(−1)
𝐴𝐸
𝑎
0
𝑑𝑥 + ∫
(𝑃 cos 𝛼)(−1)
𝐴𝐸
𝑎+𝑏
𝑎
𝑑𝑥 = −
𝑃 cos 𝛼
𝐴𝐸
[𝑥] 𝑎
𝑎+𝑏
= −
𝑃 cos 𝛼
𝐴𝐸
[(𝑎 + 𝑏) − (𝑎)] = −
𝑃𝑏 cos 𝛼
𝐴𝐸
𝐴
𝑁1
𝑥
𝐴
𝑎 𝑥 − 𝑎
𝑥
𝑁2
𝑃 cos 𝛼
(e)
(f)
𝐴
𝑁1
𝑥
1
(g)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-82-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
61
o también
𝑑1 =
𝑁𝑛𝐿´
𝐴𝐸
=
(0)(−1)(𝑎)
𝐴𝐸
+
(𝑃 cos 𝛼)(−1)(𝑏)
𝐴𝐸
= −
𝑃𝑏 cos 𝛼
𝐴𝐸
Por otra parte, el coeficiente de flexibilidad es
𝑓11 = ∫
𝑁𝑛
𝐴𝐸
𝐿2
𝐿1
𝑑𝑥 = ∫
(−1)(−1)
𝐴𝐸
𝑎+𝑏
0
𝑑𝑥 =
1
𝐴𝐸
[𝑥] 𝑎
𝑎+𝑏
=
1
𝐴𝐸
[(𝑎 + 𝑏) − (0)] =
𝑎 + 𝑏
𝐴𝐸
o también
𝑓11 =
𝑛𝑛𝐿´
𝐴𝐸
=
(−1)(−1)(𝑎 + 𝑏)
𝐴𝐸
=
𝑎 + 𝑏
𝐴𝐸
Nota: Para las ecuaciones anteriores, 𝐿´ no es necesariamente la longitud de la viga, más bien hace
referencia a la longitud del tramo analizado.
A continuación se sustituyen los resultados obtenidos para los desplazamientos horizontales en el
punto 𝐴 de cada viga en la ecuación (12 − 2)
−
𝑃𝑏 cos 𝛼
𝐴𝐸
+
𝑎 + 𝑏
𝐴𝐸
𝑅 𝐴𝑋 = 0 − − − (12 − 3)
Al resolver la ecuación lineal (12 − 3), resulta
𝑅 𝐴𝑋 =
𝑃𝑏 cos 𝛼
𝐴𝐸
𝑎 + 𝑏
𝐴𝐸
=
𝑃𝑏 cos 𝛼
𝑎 + 𝑏
=
(𝑃 cos 𝛼)(𝑏)
𝐿
La reacción restante desconocida se obtiene de
+→ ∑ 𝐹𝑋 = 0 ⇒ −𝑃 cos 𝛼 +
(𝑃 cos 𝛼)(𝑏)
𝐿
+ 𝑅 𝐵𝑋 = 0 ⇒ 𝑅 𝐵𝑋 = (𝑃 cos 𝛼) ൬1 −
𝑏
𝐿
൰ = (𝑃 cos 𝛼) ൬
𝐿 − 𝑏
𝐿
൰
= (𝑃 cos 𝛼) (
(𝑎 + 𝑏) − 𝑏
𝐿
) =
(𝑃 cos 𝛼)(𝑎)
𝐿
Las reacciones de los empotramientos 𝐴 y 𝐵 para la viga 12-b3 se esquematizan en la figura 12-h.
𝐴 𝐵
𝑃 cos 𝛼
𝑎 𝑏
𝑅 𝐴𝑋 =
( 𝑃 cos 𝛼)( 𝑏)
𝐿 𝑅 𝐵𝑋 =
( 𝑃 cos 𝛼)( 𝑎)
𝐿
(h)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-83-320.jpg)


![Fuerzas de fijación y momentos de empotramiento en vigas
64
Ecuaciones de compatibilidad. Inicialmente se analiza la estructura primaria. Para el cálculo de
las reacciones en los soportes de esta estructura liberada sometida a las solicitaciones reales, se
sigue el siguiente procedimiento:
Se calcula la fuerza resultante de la carga distribuida cuya intensidad varía de forma senoidal
hallando el área bajo la curva.
𝐴 = ∫ 𝑑𝐴 = ∫ 𝑊𝑑𝑥
𝐿2
𝐿1
𝐴 = ∫ 𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)
𝐿
0
𝑑𝑥 = 𝑤𝑜 ∫ 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)
𝐿
0
𝑑𝑥
Primero se resuelve la integral previa de forma indefinida. Sea 𝑢 =
𝜋𝑥
𝐿
, entonces 𝑑𝑢 =
𝜋
𝐿
𝑑𝑥, en
consecuencia 𝑑𝑥 =
𝐿
𝜋
𝑑𝑢. Al aplicar la regla de sustitución, resulta
∫ 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥 = ∫ 𝑠𝑒𝑛 𝑢 ∙
𝐿
𝜋
𝑑𝑢 =
𝐿
𝜋
∫ 𝑠𝑒𝑛𝑢 𝑑𝑢 =
𝐿
𝜋
(−𝑐𝑜𝑠𝑢) = −
𝐿
𝜋
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)
Así, considerando la solución de la integral de forma definida, se tiene
𝐴 = −𝑤𝑜
𝐿
𝜋
[𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)]
0
𝐿
= −𝑤𝑜
𝐿
𝜋
[𝑐𝑜𝑠(𝜋) − 𝑐𝑜𝑠(0)] = −𝑤𝑜
𝐿
𝜋
(−1 − 1) = 2𝑤𝑜
𝐿
𝜋
Se determina el brazo de palanca de la resultante calculando el centroide de área.
𝑥̅ =
∫ 𝑥̃ 𝑑𝐴
∫ 𝑑𝐴
=
∫ 𝑥𝑊 𝑑𝑥
𝐿2
𝐿1
∫ 𝑊 𝑑𝑥
𝐿2
𝐿1
=
∫ 𝑥
𝐿
0
[𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)] 𝑑𝑥
∫ 𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)
𝐿
0
𝑑𝑥
El denominador ya fue resulto. Enseguida se resuelve el numerador. La integral en forma indefinida
es
∫ 𝑥 [𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)] 𝑑𝑥 = 𝑤𝑜 ∫ 𝑥𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥
Ahora se aplica la integración por partes, ∫ 𝑢𝑑𝑣 = 𝑢𝑣 − ∫ 𝑣𝑑𝑢. Aquí 𝑢 = 𝑥 y 𝑑𝑣 = 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥. Por
consiguiente, 𝑑𝑢 = 𝑑𝑥 y 𝑣 = ∫ 𝑑𝑣 = ∫ 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥 = −
𝐿
𝜋
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
). En consecuencia,
𝑤𝑜 ∫ 𝑥𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥 = 𝑤𝑜 (𝑥 (−
𝐿
𝜋
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)) − ∫ (−
𝐿
𝜋
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)) 𝑑𝑥)
= −𝑤𝑜
𝐿
𝜋
(𝑥𝑐𝑜𝑠 (
𝑥𝜋
𝐿
) − ∫ (𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)) 𝑑𝑥) = 𝑤𝑜
𝐿
𝜋
{[
𝐿
𝜋
𝑠𝑒𝑛 (
𝑥𝜋
𝐿
) − 𝑥𝑐𝑜𝑠 (
𝑥𝜋
𝐿
)]}
Finalmente, la solución de la integral de forma definida es
∫ 𝑥
𝐿
0
[𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)] 𝑑𝑥 = 𝑤𝑜
𝐿
𝜋
{[
𝐿
𝜋
𝑠𝑒𝑛 (
𝑥𝜋
𝐿
) − 𝑥𝑐𝑜𝑠 (
𝑥𝜋
𝐿
)]
0
𝐿
}](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-86-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
65
𝑤𝑜
𝐿
𝜋
{[
𝐿
𝜋
[𝑠𝑒𝑛(𝜋)] − (𝐿)[𝑐𝑜𝑠(𝜋)]] − [
𝐿
𝜋
[𝑠𝑒𝑛(0)] − (0)[𝑐𝑜𝑠(0)]]}
= 𝑤𝑜
𝐿
𝜋
(𝐿 − 0) = 𝑤𝑜
𝐿
𝜋
(𝐿 − 0) = 𝑤𝑜
𝐿2
𝜋
Entonces, el punto de aplicación de la fuerza resultante viene dado por
𝑥̅ =
𝑤𝑜
𝐿2
𝜋
2𝑤𝑜
𝐿
𝜋
=
𝐿2
2𝐿
=
1
2
𝐿
Se identifican las reacciones del empotramiento 𝐴. En la figura 13-c se observa el diagrama de
cargas de la viga primaria.
Al aplicar las ecuaciones de equilibrio, se obtiene
+ ∑ 𝑀𝐴 = 0 ⇒ (2𝑤𝑜
𝐿
𝜋
) (
𝐿
2
) − 𝑀𝐴 = 0 ⇒ ∴ 𝑀𝐴 = 𝑤𝑜
𝐿2
𝜋
+↑ ∑ 𝐹𝑌 = 0 ⇒ 𝑅 𝐴𝑌 − 2𝑤𝑜
𝐿
𝜋
= 0 ⇒ 𝑅 𝐴𝑌 = 2𝑤𝑜
𝐿
𝜋
⇒ ∴ 𝑅 𝐴𝑌 = 2𝑤𝑜
𝐿
𝜋
+→ ∑ 𝐹𝑋 = 0 ⇒∴ 𝑅 𝐴𝑋 = 0
Los resultados son presentados en la figura 1-14d. Dado que la carga distribuida no presenta
discontinuidad, la función de momento no será discontinua a lo largo de la estructura. El origen del
sistema coordenado se selecciona en el extremo empotrado 𝐴.
𝐴 𝐵
𝑥̅ = 𝐿/2 𝐿/2
𝑊 = 𝑤0 sen
𝜋𝑥
𝐿
𝑤0
𝐴 = 2𝑤0
𝐿
𝜋
𝑅 𝐴𝑌
𝑀 𝐴
𝑅 𝐴𝑋
(c)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-87-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
66
Se emplea el método de secciones para deducir el momento 𝑀. A continuación, en la figura 1-14e,
se proporciona un diagrama de cuerpo libre del segmento de viga con longitud 𝑥. Teniendo la función
que define a la carga armónica, la resultante de la distribución actuante y su punto de aplicación se
encuentran de la manera usual.
0 ≤ 𝑥 ≤ 𝐿
𝐴 𝐶 = ∫ 𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)
𝑥
0
𝑑𝑥 = 𝑤𝑜
𝐿
𝜋
[−𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)]
0
𝑥
= 𝑤𝑜
𝐿
𝜋
{− [𝑐𝑜𝑠 (
𝜋𝑥
𝐿
) − 𝑐𝑜𝑠(0)]}
𝐴 𝐵
𝑥̅ = 𝐿/2 𝐿/2
𝑥
𝑊 = 𝑤0 sen
𝜋𝑥
𝐿
𝑤0
𝐴 = 2𝑤0
𝐿
𝜋
𝑅 𝐴𝑌 = 2𝑤 𝑜
𝐿
𝜋
𝑀 𝐴 = 𝑤 𝑜
𝐿2
𝜋
(d)
𝐴
𝑥
𝑊 = 𝑤0 sen
𝜋𝑥
𝐿
𝑅 𝐴𝑌 = 2𝑤 𝑜
𝐿
𝜋
𝑀 𝐴 = 𝑤 𝑜
𝐿2
𝜋
𝑥 − 𝑥̅ 𝐶𝑥̅ 𝐶
𝐴 𝐶
𝑀1 (e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-88-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
67
= 𝑤𝑜
𝐿
𝜋
[1 − 𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)]
𝑥̅ 𝐶 =
∫ 𝑥̃ 𝑑𝐴
∫ 𝑑𝐴
=
∫ 𝑥𝑦 𝑑𝑥
𝐿2
𝐿1
∫ 𝑦 𝑑𝑥
𝐿2
𝐿1
=
∫ 𝑥
𝑥
0
[𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)] 𝑑𝑥
∫ 𝑤𝑜 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)
𝑥
0
𝑑𝑥
=
𝑤𝑜
𝐿
𝜋
{[
𝐿
𝜋
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) − 𝑥𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)]
0
𝑥
}
𝑤𝑜
𝐿
𝜋
[1 − 𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)]
𝑥̅ 𝐶 =
{[
𝐿
𝜋
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) − 𝑥𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)] − [
𝐿
𝜋
[𝑠𝑒𝑛(0)] − (0)[𝑐𝑜𝑠(0)]]}
1 − 𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)
=
𝐿
𝜋
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) − 𝑥𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)
1 − 𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)
Tomando momentos alrededor del punto del corte, tenemos
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − 𝑤𝑜
𝐿2
𝜋
− 𝑤𝑜
𝐿
𝜋
[1 − 𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)] [𝑥 −
𝐿
𝜋
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) − 𝑥𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)
1 − 𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)
] + 2𝑤𝑜
𝐿
𝜋
(𝑥) = 0
𝑀1 = −𝑤𝑜
𝐿2
𝜋
− 𝑤𝑜
𝐿
𝜋
[𝑥 −
𝐿
𝜋
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)] + 2𝑤𝑜
𝐿
𝜋
𝑥 = 𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) + 𝑤𝑜
𝐿
𝜋
𝑥 − 𝑤𝑜
𝐿2
𝜋
Se determina el momento 𝑚1 a partir de la estructura liberada sometida a la acción de una unidad
de la fuerza redundante 𝑅 𝐵𝑌 y el equilibrio interno de la misma, figuras 13-f y 13-g.
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝐿 − 1(𝑥) − 𝑀1 = 0 ⇒ 𝑀1 = 𝐿 − 𝑥
1
𝐴 𝐵
𝐿
𝑥
1
𝐿
(f)
𝐴
𝑀1
𝑥
1
𝐿
(g)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-89-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
68
Se calcula el momento 𝑚2 con base en la estructura liberada que soporta como carga al momento
redundante unitario, figura 13-f, y su correspondiente seccionamiento, figura 13-g.
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−1 − 𝑀1 = 0 ⇒ 𝑀1 = −1
Enseguida se determinan las incompatibilidades geométricas 𝑑1 y 𝑑2.
𝑑1 =
1
𝐸𝐼
[∫ (𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) + 𝑤𝑜
𝐿
𝜋
𝑥 − 𝑤𝑜
𝐿2
𝜋
) (𝐿 − 𝑥)𝑑𝑥
𝐿
0
]
=
1
𝐸𝐼
[∫ (𝑤𝑜
𝐿3
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)) 𝑑𝑥
𝐿
0
+ ∫ (𝑤𝑜
𝐿2
𝜋
𝑥) 𝑑𝑥
𝐿
0
− ∫ (𝑤𝑜
𝐿3
𝜋
) 𝑑𝑥
𝐿
0
]
+
1
𝐸𝐼
[− ∫ (𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)) 𝑥𝑑𝑥
𝐿
0
− ∫ (𝑤𝑜
𝐿
𝜋
𝑥2
) 𝑑𝑥
𝐿
0
+ ∫ (𝑤𝑜
𝐿2
𝜋
) 𝑥𝑑𝑥
𝐿
0
]
Para mayor facilidad, se resuelven las integrales previas de manera individual.
∫ (𝑤𝑜
𝐿3
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)) 𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿3
𝜋2
∫ 𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥
𝐿
0
= (𝑤𝑜
𝐿3
𝜋2
) (2
𝐿
𝜋
) = 2𝑤𝑜
𝐿4
𝜋3
∫ (𝑤𝑜
𝐿2
𝜋
𝑥) 𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿2
𝜋
∫ 𝑥𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿2
𝜋
[
𝑥2
2
]
0
𝐿
=
1
2
𝑤𝑜
𝐿4
𝜋
∫ (𝑤𝑜
𝐿3
𝜋
) 𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿3
𝜋
∫ 𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿3
𝜋
[𝑥]0
𝐿
= 𝑤𝑜
𝐿4
𝜋
∫ (𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)) 𝑥𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿2
𝜋2
∫ 𝑥𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) 𝑑𝑥
𝐿
0
= (𝑤𝑜
𝐿2
𝜋2
) (
𝐿2
𝜋
) = 𝑤𝑜
𝐿4
𝜋3
1
𝐴 𝐵
𝐿
𝑥
1
(f)
𝐴
𝑀1
𝑥
1
(g)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-90-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
69
∫ (𝑤𝑜
𝐿
𝜋
𝑥2
) 𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿2
𝜋
∫ 𝑥2
𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿
𝜋
[
𝑥3
3
]
0
𝐿
=
1
3
𝑤𝑜
𝐿4
𝜋
∫ (𝑤𝑜
𝐿2
𝜋
) 𝑥𝑑𝑥
𝐿
0
= 𝑤𝑜
𝐿2
𝜋
∫ 𝑥𝑑𝑥
𝐿
0
=
1
2
𝑤𝑜
𝐿4
𝜋
Por consiguiente,
𝑑1 =
1
𝐸𝐼
(2𝑤𝑜
𝐿4
𝜋3
+
1
2
𝑤𝑜
𝐿4
𝜋
− 𝑤𝑜
𝐿4
𝜋
− 𝑤𝑜
𝐿4
𝜋3
−
1
3
𝑤𝑜
𝐿4
𝜋
+
1
2
𝑤𝑜
𝐿4
𝜋
) =
1
𝐸𝐼
(−
𝑤𝑜
3
𝐿4
𝜋
+ 𝑤𝑜
𝐿4
𝜋3
)
= −
1
3𝐸𝐼
𝑤𝑜
𝐿4
𝜋3
(𝜋2
− 3)
𝑑2 =
1
𝐸𝐼
[∫ (𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) + 𝑤𝑜
𝐿
𝜋
𝑥 − 𝑤𝑜
𝐿2
𝜋
) (−1)𝑑𝑥
𝐿
0
]
=
1
𝐸𝐼
[∫ (−𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
) − 𝑤𝑜
𝐿
𝜋
𝑥 + 𝑤𝑜
𝐿2
𝜋
) 𝑑𝑥
𝐿
0
]
=
1
𝐸𝐼
[∫ (−𝑤𝑜
𝐿2
𝜋2
𝑠𝑒𝑛 (
𝜋𝑥
𝐿
)) 𝑑𝑥
𝐿
0
− ∫ (𝑤𝑜
𝐿
𝜋
𝑥) 𝑑𝑥
𝐿
0
+ ∫ (𝑤𝑜
𝐿2
𝜋
) 𝑑𝑥
𝐿
0
]
=
1
𝐸𝐼
[(−𝑤𝑜
𝐿2
𝜋2
) (2
𝐿
𝜋
) + (−𝑤𝑜
𝐿
𝜋
) (
𝐿2
2
) + (𝑤𝑜
𝐿2
𝜋
) (𝐿)] =
1
𝐸𝐼
(−2𝑤𝑜
𝐿3
𝜋3
−
1
2
𝑤𝑜
𝐿3
𝜋
+ 𝑤𝑜
𝐿3
𝜋
)
=
1
𝐸𝐼
(
1
2
𝑤𝑜
𝐿3
𝜋
− 2𝑤𝑜
𝐿3
𝜋3
) =
1
2𝐸𝐼
𝑤𝑜
𝐿3
𝜋3
(𝜋2
− 4)
Por otra parte, los coeficientes de flexibilidad 𝑓11 hasta 𝑓22 son resultado de
𝑓11 =
1
𝐸𝐼
∫ (𝐿 − 𝑥)(𝐿 − 𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ (𝐿 − 𝑥)2
𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
1
3
(𝐿 − 𝑥)3
]
0
𝐿
=
𝐿3
3𝐸𝐼
𝑓21 = 𝑓12 =
1
𝐸𝐼
∫ (𝐿 − 𝑥)(−1)𝑑𝑥 = −
1
𝐸𝐼
∫ (𝑥 − 𝐿)𝑑𝑥
𝐿
0
= −
1
𝐸𝐼
[
1
2
(𝑥 − 𝐿)2
]
0
𝐿
= −
𝐿2
2𝐸𝐼
𝐿
0
𝑓22 =
1
𝐸𝐼
∫ (−1)(−1)𝑑𝑥 =
𝐿
𝐸𝐼
𝐿
0
Se formula y se resuelve el sistema de ecuaciones de compatibilidad geométrica para la obtención
de los valores de las fuerzas sobrantes.
−
1
3𝐸𝐼
𝑤𝑜
𝐿4
𝜋3
(𝜋2
− 3) +
𝐿3
3𝐸𝐼
𝑅 𝐵𝑌 −
𝐿2
2𝐸𝐼
𝑀 𝐵 = 0 − − − (13 − 1)
1
2𝐸𝐼
𝑤𝑜
𝐿3
𝜋3
(𝜋2
− 4) −
𝐿2
2𝐸𝐼
𝑅 𝐵𝑌 +
𝐿
𝐸𝐼
𝑀 𝐵 = 0 − − − (13 − 2)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-91-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
73
considérese que la carga de par uniformemente distribuida se reemplaza por un momento resultante
igual al área del rectángulo cuyo punto de aplicación puede estar en cualquier parte de la estructura.
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝑊𝑥 − 𝑀1 = 0 ⇒ 𝑀1 = 𝑊𝑥
A partir de las vigas con fuerzas redundantes unitarias aplicadas, se conoce que
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se determinan las incompatibilidades geométricas y los coeficientes de flexibilidad.
𝑑1 =
1
𝐸𝐼
∫ (𝑊𝑥)(𝑥)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ 𝑊𝑥2
𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[
1
3
𝑊𝑥3
]
0
𝐿
=
𝑊𝐿3
3𝐸𝐼
𝑑2 =
1
𝐸𝐼
∫ (𝑊𝑥)(−1)𝑑𝑥
𝐿
0
=
1
𝐸𝐼
∫ −𝑊𝑥𝑑𝑥
𝐿
0
=
1
𝐸𝐼
[−
1
2
𝑊𝑥2
]
0
𝐿
= −
𝑊𝐿2
2𝐸𝐼
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = −
𝐿2
2𝐸𝐼
𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
Se calculan las fuerzas superabundantes con base en el siguiente sistema de ecuaciones de
flexibilidades:
𝑊𝐿3
3𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (14 − 1)
−
𝑊𝐿2
2𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (14 − 2)
(
𝑅 𝐴𝑌
𝑀𝐴
) =
(
𝐿3
3
−
𝐿2
2
−
𝐿2
2
𝐿
)
−1
(
−
𝑊𝐿3
3
𝑊𝐿2
2 )
= (
12
𝐿3
6
𝐿2
6
𝐿2
4
𝐿
)
(
−
𝑊𝐿3
3
𝑊𝐿2
2 )
= (
−𝑊
0
)
Puesto que se obtuvo una magnitud negativa para 𝑅 𝐴𝑌, el sentido de esta reacción es opuesto al
que se propuso en la figura 14-b.
∴ 𝑅 𝐴𝑌 = 𝑊
𝐴
𝑀1
𝑥
𝑊
𝑀 𝑅 = 𝑊𝑥
(c)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-95-320.jpg)



![Fuerzas de fijación y momentos de empotramiento en vigas
77
En consecuencia,
𝑅 = ∫ 𝑟 cos 𝜃
𝑥
0
𝑟 cos 𝜃 𝑑𝜃 = 𝑟2
∫ (cos 𝜃)2
𝑥
0
𝑑𝜃 =
𝑟2
2
∫ (𝜃 + sin 𝜃 cos 𝜃)𝑑𝜃
𝑥
0
=
𝑟2
2
[arcsin
𝑥
𝑟
+
𝑥
𝑟
√𝑟2 − 𝑥2
𝑟
]
0
𝑥
=
𝑟2
2
{[arcsin
𝑥
𝑟
+
𝑥
𝑟2
√ 𝑟2 − 𝑥2] − [arcsin
0
𝑟
+
0
𝑟2
√ 𝑟2 − 02]}
=
1
2
(𝑟2
arcsin
𝑥
𝑟
+ 𝑥√ 𝑟2 − 𝑥2)
Enseguida se calcula el centroide de área 𝑥ҧ.
𝑥ҧ =
∫ (𝑥)(√𝑟2 − 𝑥2)
𝑥
0
𝑑𝑥
1
2
(𝑟2 arcsin
𝑥
𝑟
+ 𝑥√𝑟2 − 𝑥2)
=
𝑟3
3
−
(𝑟2
− 𝑥2)
3
2⁄
3
1
2
(𝑟2 arcsin
𝑥
𝑟
+ 𝑥√𝑟2 − 𝑥2)
Se escribe la ecuación de momento 𝑀. Tomando momentos alrededor del punto del corte en la
porción de viga que se indica en la figura 15-c, tenemos
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
− [
1
2
(𝑟2
arcsin
𝑥
𝑟
+ 𝑥√ 𝑟2 − 𝑥2)] [𝑥 −
𝑟3
3
−
(𝑟2
− 𝑥2)
3
2⁄
3
1
2
(𝑟2 arcsin
𝑥
𝑟
+ 𝑥√𝑟2 − 𝑥2)
] − 𝑀1 = 0
𝑀1 = (−
1
2
𝑟2
arcsin
𝑥
𝑟
) (𝑥) −
1
2
𝑥2√ 𝑟2 − 𝑥2 +
𝑟3
3
−
(𝑟2
− 𝑥2)
3
2⁄
3
No obstante,
−
1
2
𝑥2√ 𝑟2 − 𝑥2 −
(𝑟2
− 𝑥2)
3
2⁄
3
= − (
1
2
𝑥2√ 𝑟2 − 𝑥2 +
1
3
(𝑟2
− 𝑥2) (√ 𝑟2 − 𝑥2))
= − (√ 𝑟2 − 𝑥2) (
1
2
𝑥2
+
1
3
𝑟2
−
1
3
𝑥2
) = − (√ 𝑟2 − 𝑥2) (
1
3
𝑟2
+
1
6
𝑥2
)
Por consiguiente,
𝑀1 = (−
1
2
𝑟2
arcsin
𝑥
𝑟
) (𝑥) +
𝑟3
3
− (√ 𝑟2 − 𝑥2) (
1
3
𝑟2
+
1
6
𝑥2
)
=
− ((3𝑟2
arcsin
𝑥
𝑟
) (𝑥) − 2𝑟3
+ (√𝑟2 − 𝑥2)(2𝑟2
+ 𝑥2))
6
Enseguida se deducen las funciones de momento 𝑚1 y 𝑚2 a partir de las figuras 15-e y 15-f.](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-99-320.jpg)




![Fuerzas de fijación y momentos de empotramiento en vigas
82
− [
𝑊
2𝐿
(𝐿2
arcsin
𝑥
𝐿
+ 𝑥√ 𝐿2 − 𝑥2)]
[
𝑥 −
−
((𝐿2
− 𝑥2)
3
2⁄
− 𝐿3
) (𝑊)
3𝐿
𝑊
2𝐿
(𝐿2 arcsin
𝑥
𝐿
+ 𝑥√𝐿2 − 𝑥2)
]
− 𝑀1 = 0
𝑀1 = −
𝑊𝐿𝑥 arcsin
𝑥
𝐿
2
+
𝑊(𝑥2
− 𝐿2)√𝐿2 − 𝑥2
3𝐿
−
𝑊𝑥2
√𝐿2 − 𝑥2
2𝐿
+
𝑊𝐿2
3
𝑀1 = −
𝑊 (3𝐿2
𝑥 arcsin
𝑥
𝐿
+ 2(𝐿2
− 𝑥2)
3
2⁄
+ 3𝑥2
√𝐿2 − 𝑥2 − 2𝐿3
)
6𝐿
Los momentos internos de las vigas con fuerzas redundantes unitarias aplicadas son
𝑚1 ⟹ 𝑀1 = 𝑥 0 ≤ 𝑥 ≤ 𝐿
𝑚2 ⟹ 𝑀1 = −1 0 ≤ 𝑥 ≤ 𝐿
Se calculan las incompatibilidades geométricas.
𝑑1 =
1
𝐸𝐼
∫ (−
𝑊 (3𝐿2
𝑥 arcsin
𝑥
𝐿
+ 2(𝐿2
− 𝑥2)
3
2⁄
+ 3𝑥2
√𝐿2 − 𝑥2 − 2𝐿3
)
6𝐿
) (𝑥)𝑑𝑥
𝐿
0
= −
(15𝜋 − 26)𝑊𝐿4
180𝐸𝐼
𝑑2 =
1
𝐸𝐼
∫ (−
𝑊 (3𝐿2
𝑥 arcsin
𝑥
𝐿
+ 2(𝐿2
− 𝑥2)
3
2⁄
+ 3𝑥2
√𝐿2 − 𝑥2 − 2𝐿3
)
6𝐿
) (−1)𝑑𝑥
𝐿
0
=
(15𝜋 − 32)𝑊𝐿3
96𝐸𝐼
Los coeficientes de flexibilidad se presentan enseguida.
𝑓11 =
𝐿3
3𝐸𝐼
𝑓21 = −
𝐿2
2𝐸𝐼
𝑓12 = −
𝐿2
2𝐸𝐼
𝑓22 =
𝐿
𝐸𝐼
Se formula el sistema de ecuaciones de flexibilidades.
−
(15𝜋 − 26)𝑊𝐿4
180𝐸𝐼
+
𝐿3
3𝐸𝐼
𝑅 𝐴𝑌 −
𝐿2
2𝐸𝐼
𝑀𝐴 = 0 − − − (16 − 1)
(15𝜋 − 32)𝑊𝐿3
96𝐸𝐼
−
𝐿2
2𝐸𝐼
𝑅 𝐴𝑌 +
𝐿
𝐸𝐼
𝑀𝐴 = 0 − − − (16 − 2)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-104-320.jpg)




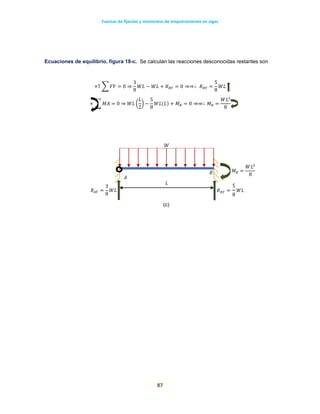









![Fuerzas de fijación y momentos de empotramiento en vigas
97
Incompatibilidades geométricas y coeficientes de flexibilidad
El siguiente paso consiste en calcular las reacciones y escribir las ecuaciones de momentos internos
para todas las vigas isostáticas que se muestran en la figura 23-b. Para la estructura primaria
𝑅 𝐴𝑌 = 𝑊𝑎 (1 −
𝑎
2𝐿
), para la primera complementaria 𝑅 𝐴𝑌 =
1
𝐿
y para la segunda también 𝑅 𝐴𝑌 =
1
𝐿
.
Nótese que solamente se están considerando las reacciones en 𝐴, esto es porque el cálculo de la
acción interna se realizará empleando una coordenada 𝑥 de izquierda a derecha, siendo innecesaria
la participación de las reacciones en 𝐵 para este fin. Para determinar los momentos 𝑀, se tienen dos
regiones a analizar y se requiere de realizar dos cortes, figuras 23-c y 23-d. Enseguida se deducen
los momentos internos 𝑚1 y 𝑚2 con base en las figuras 23-e y 23-f.
0 ≤ 𝑥 ≤ 𝑎
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − 𝑊(𝑥) (
𝑥
2
) + 𝑊𝑎 (1 −
𝑎
2𝐿
) (𝑥) = 0
𝑀1 = 𝑊 [𝑎 (1 −
𝑎
2𝐿
) (𝑥) −
𝑥2
2
]
𝑎 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀2 − 𝑊(𝑎) (𝑥 −
𝑎
2
) + 𝑊𝑎 (1 −
𝑎
2𝐿
) (𝑥) = 0
𝑀2 = 𝑊𝑎 [(1 −
𝑎
2𝐿
) (𝑥) − (𝑥 −
𝑎
2
)]
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 − 1 +
1
𝐿
(𝑥) = 0 ⇒ 𝑀1 =
𝑥
𝐿
− 1
W
𝑥/2
A
𝑊(𝑥)
𝑊𝑎 (1 −
𝑎
2𝐿
)
𝑀1
𝑥
W
a
𝑥
A 𝑀2
𝑊(𝑎)
𝑊𝑎 (1 −
𝑎
2𝐿
)
𝑥
A
1
d
𝑀1
1
𝐿
(c)
(d)
(e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-119-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
98
0 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 +
1
𝐿
(𝑥) = 0 ⇒ 𝑀1 =
𝑥
𝐿
Las incompatibilidades geométricas son resultado de
𝑑1 = ∫
(𝑊 [𝑎 (1 −
𝑎
2𝐿
) (𝑥) −
𝑥2
2
]) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝑎
0
+ ∫
(𝑊𝑎 [(1 −
𝑎
2𝐿
) (𝑥) − (𝑥 −
𝑎
2
)]) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝐿
𝑎
=
𝑊𝑎2
6𝐸𝐼
(𝑎 − 𝐿 −
𝑎2
4𝐿
)
𝑑2 = ∫
(𝑊 [𝑎 (1 −
𝑎
2𝐿
) (𝑥) −
𝑥2
2
]) (
𝑥
𝐿
)
𝐸𝐼
𝑑𝑥
𝑎
0
+ ∫
(𝑊𝑎 [(1 −
𝑎
2𝐿
) (𝑥) − (𝑥 −
𝑎
2
)]) (
𝑥
𝐿
)
𝐸𝐼
𝑑𝑥
𝐿
𝑎
=
𝑊𝑎2
12𝐸𝐼
(𝐿 −
𝑎2
2𝐿
)
Luego, los coeficientes de flexibilidad, 𝑓𝑖𝑗, son
𝑓11 = ∫
(
𝑥
𝐿
− 1) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝐿
0
=
𝐿
3𝐸𝐼
𝑓12 = ∫
(
𝑥
𝐿
− 1) (
𝑥
𝐿
)
𝐸𝐼
𝑑𝑥
𝐿
0
= −
𝐿
6𝐸𝐼
𝑓21 = ∫
(
𝑥
𝐿
) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝐿
0
= −
𝐿
6𝐸𝐼
𝑓22 = ∫
(
𝑥
𝐿
) (
𝑥
𝐿
)
𝐸𝐼
𝑑𝑥
𝐿
0
=
𝐿
3𝐸𝐼
Cálculo de redundantes y reacciones faltantes
Las ecuaciones (23 − 1) y (23 − 2) se convierten en
0 =
𝑊𝑎2
6𝐸𝐼
(𝑎 − 𝐿 −
𝑎2
4𝐿
) +
𝐿
3𝐸𝐼
𝑀𝐴 −
𝐿
6𝐸𝐼
𝑀 𝐵 − − − (23 − 3)
0 =
𝑊𝑎2
12𝐸𝐼
(𝐿 −
𝑎2
2𝐿
) −
𝐿
6𝐸𝐼
𝑀𝐴 +
𝐿
3𝐸𝐼
𝑀 𝐵 − − − (23 − 4)
En consecuencia,
𝑀𝐴 =
𝑊𝑎2
12
[6 +
𝑎
𝐿
(3
𝑎
𝐿
− 8)]
𝑀 𝐵 = −
𝑊𝑎3
12𝐿
(3
𝑎
𝐿
− 4)
𝑥
A 𝑀1
1
𝐿
(f)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-120-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
99
Las demás reacciones se calculan de manera sencilla con aplicación de las ecuaciones de la
estática, colocando los valores de las redundantes ya calculadas, figura 23-g.
+↑ ∑ 𝐹𝑌 = 0 ⇒ 𝑅 𝐴𝑌 + 𝑅 𝐵𝑌 − 𝑊𝑎 = 0
+ ∑ 𝑀𝐴 = 0 ⇒ −
𝑊𝑎2
12
[6 +
𝑎
𝐿
(3
𝑎
𝐿
− 8)] +
𝑊𝑎2
2
−
𝑊𝑎3
12𝐿
(3
𝑎
𝐿
− 4) − 𝑅 𝐵𝑌 𝐿 = 0
∴ 𝑅 𝐵𝑌 =
𝑊𝑎3
2𝐿2
(2 −
𝑎
𝐿
)
∴ 𝑅 𝐴𝑌 = 𝑊𝑎 −
𝑊𝑎3
𝐿2
+
𝑊𝑎4
2𝐿3
=
𝑊𝑎
2
[2 −
𝑎2
𝐿2
(2 −
𝑎
𝐿
)]
W
a
L
A B
𝑀 𝐴 =
𝑊𝑎2
12
[6 +
𝑎
𝐿
(3
𝑎
𝐿
− 8)] 𝑀 𝐵 = −
𝑊𝑎3
12𝐿
[3
𝑎
𝐿
− 4]
𝑅 𝐴𝑌 =
𝑊𝑎
2
[2 −
𝑎2
𝐿2
(2 −
𝑎
𝐿
)] 𝑅 𝐵𝑌 =
𝑊𝑎3
2𝐿2
(2 −
𝑎
𝐿
)
(g)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-121-320.jpg)
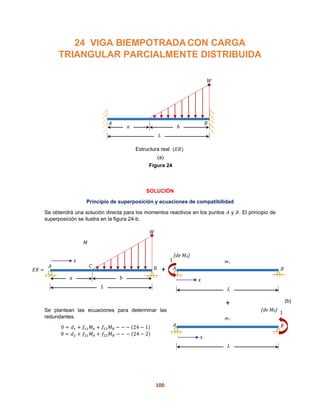
![Fuerzas de fijación y momentos de empotramiento en vigas
101
Incompatibilidades geométricas y coeficientes de flexibilidad
Con relación a la estructura primaria, se tiene que 𝑅 𝐴𝑌 =
𝑊𝑏2
6𝐿
. El análisis para el cálculo de las
funciones de momento 𝑀 se realiza con base en la coordenada 𝑥 con origen en 𝐴 y positiva hacia la
derecha. Puesto que esta viga no está cargada en toda su longitud, sino que solamente en una parte
(longitud 𝑏), se requiere de seccionar a la estructura en un sitio intermedio en cada tramo (𝐴𝐶̅̅̅̅ y 𝐶𝐵̅̅̅̅),
tal como se muestra en las figuras 24-c y 24-d.
0 ≤ 𝑥 ≤ 𝑎
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀1 +
𝑊𝑏2
6𝐿
(𝑥) = 0 ⇒ 𝑀1 =
𝑊𝑏2
6𝐿
(𝑥)
𝑎 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
−𝑀2 −
𝑊
6𝑏
(𝑥 − 𝑎)3
+
𝑊𝑏2
6𝐿
(𝑥) = 0
𝑀2 =
𝑊𝑏2
6𝐿
(𝑥) −
𝑊
6𝑏
(𝑥 − 𝑎)3
Las incompatibilidades geométricas se calculan enseguida.
𝑑1 = ∫
(
𝑊𝑏2
6𝐿
(𝑥)) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝑎
0
+ ∫
(
𝑊𝑏2
6𝐿
(𝑥) −
𝑊
6𝑏
(𝑥 − 𝑎)3
) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝐿
𝑎
=
𝑊𝑏2
12𝐸𝐼
(
𝑏2
10𝐿
−
𝐿2
3
)
𝑑2 = ∫
(
𝑊𝑏2
6𝐿
(𝑥)) (
𝑥
𝐿
)
𝐸𝐼
𝑑𝑥
𝑎
0
+ ∫
(
𝑊𝑏2
6𝐿
(𝑥) −
𝑊
6𝑏
(𝑥 − 𝑎)3
) (
𝑥
𝐿
)
𝐸𝐼
𝑑𝑥
𝐿
𝑎
=
𝑊𝑏2
360𝐸𝐼
[
20𝐿2
+ 3𝑏2
− 15𝐿𝑏
𝐿
]
A
x𝑊𝑏2
6𝐿
𝑀1
𝑊
𝑏
(𝑥 − 𝑎)
(𝑥 − 𝑎)
A
a
C
𝑀2
𝑊𝑏2
6𝐿
𝑥 − 𝑎
3
𝑊
2𝑏
(𝑥 − 𝑎)2
𝑥
(c)
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-123-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
102
Se retoman los coeficientes de flexibilidad obtenidos en la resolución de viga que se muestra en la
figura 23-a.
𝑓11 =
𝐿
3𝐸𝐼
𝑓12 = −
𝐿
6𝐸𝐼
𝑓21 = −
𝐿
6𝐸𝐼
𝑓22 =
𝐿
3𝐸𝐼
Cálculo de redundantes y reacciones faltantes
Al sustituir los valores en el sistema de ecuaciones (24 − 1) y (24 − 2), da
0 =
𝑊𝑏2
12𝐸𝐼
(
𝑏2
10𝐿
−
𝐿2
3
) +
𝐿
3𝐸𝐼
𝑀𝐴 −
𝐿
6𝐸𝐼
𝑀 𝐵 − − − (24 − 3)
0 =
𝑊𝑏2
360𝐸𝐼
[
20𝐿2
+ 3𝑏2
− 15𝐿𝑏
𝐿
] −
𝐿
6𝐸𝐼
𝑀𝐴 +
𝐿
3𝐸𝐼
𝑀 𝐵 − − − (24 − 4)
Teniendo en cuenta que 𝐿 − 𝑎 = 𝑏, resulta
𝑀𝐴 =
𝑊𝑏3
60𝐿
(5 − 3
𝑏
𝐿
) 𝑀 𝐵 = −
𝑊𝑏2
60𝐿
(10𝐿2
+ 3𝑏2
− 10𝐿𝑏)
Sin embargo, la expresión que define a 𝑀 𝐵 puede reducirse de la siguiente manera, considerando
que 𝑏 = 𝐿 − 𝑎:
𝑀 𝐵 = −
𝑊𝑏2
60
(3
𝑏2
𝐿2
+ 10
𝑎
𝐿
)
Empleando los resultados previos y al aplicar las ecuaciones de equilibrio en el plano, figura 24-e,
tenemos
+↑ ∑ 𝐹𝑌 = 0 ⟹ 𝑅 𝐴𝑌 + 𝑅 𝐵𝑌 =
𝑊𝑏
2
+ ∑ 𝑀 𝐵 = 0 ⟹ 𝑅 𝐴𝑌 𝐿 +
𝑊𝑏2
60
(3
𝑏2
𝐿2
+ 10
𝑎
𝐿
) −
𝑊𝑏
2
(
𝑏
3
) −
𝑊𝑏3
60𝐿
(5 − 3
𝑏
𝐿
) = 0
∴ 𝑅 𝐴𝑌 =
𝑊𝑏3
20𝐿2
(5 − 2
𝑏
𝐿
) ∴ 𝑅 𝐵𝑌 =
𝑊𝑏
20
[10 −
𝑏2
𝐿2
(5 − 2
𝑏
𝐿
)]
W
b
L
A B
a
𝑅 𝐴𝑌 =
𝑊𝑏3
20𝐿2
(5 − 2
𝑏
𝐿
) 𝑅 𝐵𝑌 =
𝑊𝑏
20
[10 −
𝑏2
𝐿2
(5 − 2
𝑏
𝐿
)]
𝑀 𝐴 =
𝑊𝑏3
60𝐿
5 + 3
𝑏
𝐿
൨ 𝑀 𝐵 =
𝑊𝑏2
60
[3
𝑏2
𝐿2
− 4
𝑎
𝐿
]
𝑊𝑏
2
𝑏
3
(e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-124-320.jpg)
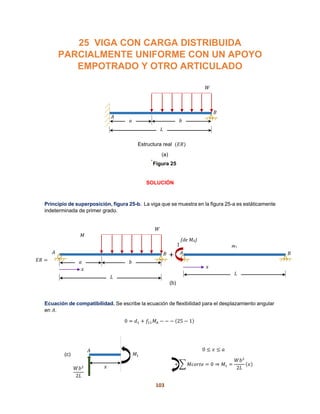
![Fuerzas de fijación y momentos de empotramiento en vigas
104
𝑎 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝑀2 =
𝑊𝑏2
2𝐿
(𝑥) −
𝑊
2
(𝑥 − 𝑎)2
Se escriben los momentos 𝑀 a partir de las figuras 25-c y 25-d. En consecuencia,
𝑑1 = ∫
(
𝑊𝑏2
2𝐿
(𝑥)) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝑎
0
+ ∫
(
𝑊𝑏2
2𝐿
(𝑥) −
𝑊
2
(𝑥 − 𝑎)2
) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝐿
𝑎
=
𝑊
24𝐸𝐼
(
𝑏4
− 2𝐿2
𝑏2
𝐿
)
𝑓11 =
𝐿
3𝐸𝐼
Al reemplazar los valores de 𝑑1 y 𝑓11 en la ecuación (25 − 1), obtenemos
0 =
𝑊
24𝐸𝐼
(
𝑏4
− 2𝐿2
𝑏2
𝐿
) +
𝐿
3𝐸𝐼
𝑀𝐴 ⇒∴ 𝑀𝐴 =
𝑊𝑏2
8𝐿
(2𝐿2
− 𝑏2)
Ecuaciones de equilibrio, figura 25-e.
+↑ ∑ 𝐹𝑌 = 0 ⟹ 𝑅 𝐴𝑌 + 𝑅 𝐵𝑌 = 𝑊𝑏
+ ∑ 𝑀 𝐵 = 0 ⟹ 𝑅 𝐴𝑌 𝐿 −
𝑊𝑏2
8𝐿
(2𝐿2
− 𝑏2) − 𝑊𝑏 (
𝑏
2
) = 0
∴ 𝑅 𝐴𝑌 =
𝑊𝑏2
8𝐿
(6 −
𝑏2
𝐿2
) ∴ 𝑅 𝐵𝑌 =
𝑊𝑏
8
[8 −
𝑏
𝐿
(6 −
𝑏2
𝐿2
)]
W
b
L
A
a
B𝑀𝐴 =
𝑊𝑏2
8𝐿
(2𝐿2
+ 𝑏2)
𝑅 𝐴𝑌 =
𝑊𝑏2
8𝐿
(6 −
𝑏2
𝐿2
) 𝑅 𝐵𝑌 =
𝑊𝑏
8
[8 −
𝑏
𝐿
(6 −
𝑏2
𝐿2
)]
𝑊𝑏
𝑏
2
W
𝑥 − 𝑎
𝑥
A
a
𝑊(𝑥 − 𝑎)
𝑀2
𝑊𝑏2
2𝐿 𝑥 − 𝑎
2
(d)
(e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-126-320.jpg)

![Fuerzas de fijación y momentos de empotramiento en vigas
106
0 ≤ 𝑥 ≤ 𝑎
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝑀1 =
𝑊𝑏2
3𝐿
(𝑥)
𝑎 ≤ 𝑥 ≤ 𝐿
+ ∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝑃1 =
𝑊
2𝑏
(𝑥 − 𝑎)2
𝑃2 = 𝑊(𝑥 − 𝑎) [1 −
𝑥 − 𝑎
𝑏
]
𝑀2 =
𝑊𝑏2
3𝐿
(𝑥) −
𝑊
2
(𝑥 − 𝑎)2
[1 −
𝑥 − 𝑎
𝑏
] −
𝑊
3𝑏
(𝑥 − 𝑎)3
Se calcula la incompatibilidad geométrica.
𝑑1 = ∫
(
𝑊𝑏2
3𝐿
(𝑥)) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝑎
0
+ ∫
(
𝑊𝑏2
3𝐿
(𝑥) −
𝑊
2
(𝑥 − 𝑎)2
[1 −
𝑥 − 𝑎
𝑏
] −
𝑊
3𝑏
(𝑥 − 𝑎)3
) (
𝑥
𝐿
− 1)
𝐸𝐼
𝑑𝑥
𝐿
𝑎
=
𝑊𝑏2
90𝐸𝐼
(
3𝑏2
− 5𝐿2
𝐿
)
El coeficiente de flexibilidad es
𝑓11 =
𝐿
3𝐸𝐼
Entonces,
0 =
𝑊𝑏2
90𝐸𝐼
(
3𝑏2
− 5𝐿2
𝐿
) +
𝐿
3𝐸𝐼
𝑀𝐴 − − − (26 − 1)
∴ 𝑀𝐴 =
𝑊𝑏2
30
(5 − 3
𝑏2
𝐿2
)
W
𝑥 − 𝑎
L
A
a
𝑊
𝑏
(𝑎 + 𝑏 − 𝑥)
𝑊𝑏2
3𝐿
𝑃1 𝑃2
𝑀2
A
𝑊𝑏2
3𝐿
𝑀1
𝑥
(c)
(d)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-128-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
107
Ecuaciones de equilibrio, figura 26-e.
+↑ ∑ 𝐹𝑌 = 0 ⟹ 𝑅 𝐴𝑌 + 𝑅 𝐵𝑌 =
𝑊𝑏
2
+ ∑ 𝑀 𝐵 = 0 ⟹ 𝑅 𝐴𝑌 𝐿 −
𝑊𝑏2
30
(5 − 3
𝑏2
𝐿2
) −
𝑊𝑏
2
(
2𝑏
3
) = 0
∴ 𝑅 𝐴𝑌 =
𝑊𝑏2
10𝐿
(5 −
𝑏2
𝐿2
)
∴ 𝑅 𝐵𝑌 =
𝑊𝑏
10
[5 −
𝑏
𝐿
(5 −
𝑏2
𝐿2
)]
W
b
L
A
B
a
𝑅 𝐴𝑌 =
𝑊𝑏2
10𝐿
(5 −
𝑏2
𝐿2
)
𝑅 𝐵𝑌 =
𝑊𝑏
10
[5 −
𝑏
𝐿
(5 −
𝑏2
𝐿2
)]
𝑀𝐴 =
𝑊𝑏2
30
(5 − 3
𝑏2
𝐿2
)
𝑊𝑏
2
2
3
𝑏
(e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-129-320.jpg)
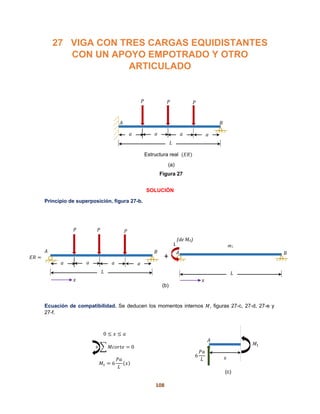





![Fuerzas de fijación y momentos de empotramiento en vigas
114
Se determinan los momentos 𝑚2, figura 28-e.
Cálculo del desplazamiento 𝑑1.
𝑑1 =
1
𝐸𝐼
∫ (−2𝑞𝑐2
− 2𝑞𝑐𝑥) ∙ (𝑐 +
𝐿
2
+ 𝑥) 𝑑𝑥
𝐿
2
−𝑐
0
+
1
𝐸𝐼
∫ (−
𝑞
2
𝑥2
) ∙ (−𝑐 +
𝐿
2
+ 𝑥) 𝑑𝑥
2𝑐
0
+
1
𝐸𝐼
∫ 0 ∙ 𝑥𝑑𝑥
𝐿
2
−𝑐
0
Desarrollando los productos por separado, se tiene
(−2𝑞𝑐2
− 2𝑞𝑐𝑥) ∙ (𝑐 +
𝐿
2
+ 𝑥) = −2𝑞𝑐3
− 𝑞𝑐2
𝐿 − 2𝑞𝑐2
𝑥 − 2𝑞𝑐2
𝑥 − 𝑞𝑐𝐿𝑥 − 2𝑞𝑐𝑥2
(−2𝑞𝑐2
− 2𝑞𝑐𝑥) ∙ (𝑐 +
𝐿
2
+ 𝑥) = −2𝑞𝑐3
− 𝑞𝑐2
𝐿 − (4𝑞𝑐2
+ 𝑞𝑐𝐿)𝑥 − 2𝑞𝑐𝑥2
(−
𝑞
2
𝑥2
) ∙ (−𝑐 +
𝐿
2
+ 𝑥) = (
𝑞𝑐
2
−
𝑞𝐿
4
) 𝑥2
−
𝑞
2
𝑥3
En consecuencia,
𝑑1 =
1
𝐸𝐼
∫ [−2𝑞𝑐3
− 𝑞𝑐2
𝐿 − (4𝑞𝑐2
+ 𝑞𝑐𝐿)𝑥 − 2𝑞𝑐𝑥2]𝑑𝑥
𝐿
2
−𝑐
0
+
1
𝐸𝐼
∫ [(
𝑞𝑐
2
−
𝑞𝐿
4
) 𝑥2
−
𝑞
2
𝑥3
] 𝑑𝑥
2𝑐
0
𝑑1 =
1
𝐸𝐼
[−(2𝑞𝑐3
+ 𝑞𝑐2
𝐿)𝑥 − (
4𝑞𝑐2
+ 𝑞𝑐𝐿
2
) 𝑥2
−
2𝑞𝑐
3
𝑥3
]
0
𝐿
2
−𝑐
+
1
𝐸𝐼
[(
𝑞𝑐
6
−
𝑞𝐿
12
) 𝑥3
−
𝑞
8
𝑥4
]
0
2𝑐
𝑑1 =
1
𝐸𝐼
[−(2𝑞𝑐3
+ 𝑞𝑐2
𝐿) (
𝐿
2
− 𝑐) − (
4𝑞𝑐2
+ 𝑞𝑐𝐿
2
) (
𝐿
2
− 𝑐)
2
−
2𝑞𝑐
3
(
𝐿
2
− 𝑐)
3
]
+
1
𝐸𝐼
[(
𝑞𝑐
6
−
𝑞𝐿
12
) (2𝑐)3
−
𝑞
8
(2𝑐)4
]
𝑑1 =
1
𝐸𝐼
[−𝑞𝑐3
𝐿 + 2𝑞𝑐4
−
𝑞𝑐2
𝐿2
2
+ 𝑞𝑐3
𝐿 − (
4𝑞𝑐2
+ 𝑞𝑐𝐿
2
) (
𝐿2
4
− 𝑐𝐿 + 𝑐2
)
−
2𝑞𝑐
3
(
𝐿3
8
−
3𝑐𝐿2
4
+
3𝑐2
𝐿
2
− 𝑐3
)] +
1
𝐸𝐼
[
4𝑞𝑐4
3
−
2𝑞𝑐3
𝐿
3
− 2𝑞𝑐4
]
𝑑1 =
1
𝐸𝐼
[2𝑞𝑐4
−
𝑞𝑐2
𝐿2
2
−
𝑞𝑐2
𝐿2
2
+ 2𝑞𝑐3
𝐿 − 2𝑞𝑐4
−
𝑞𝑐𝐿3
8
+
𝑞𝑐2
𝐿2
2
−
𝑞𝑐3
𝐿
2
−
𝑞𝑐𝐿3
12
+
𝑞𝑐2
𝐿2
2
− 𝑞𝑐3
𝐿 +
2𝑞𝑐4
3
+
4𝑞𝑐4
3
−
2𝑞𝑐3
𝐿
3
− 2𝑞𝑐4
] =
1
𝐸𝐼
[−
𝑞𝑐3
𝐿
6
−
5𝑞𝑐𝐿3
24
]
𝐿 2Τ
A D
𝐿 2Τ
𝑐 𝑐
B C
1
d
𝑀1 = 1
𝑀2 = 1
𝑀3 = 1
(e)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-136-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
115
Cálculo del desplazamiento 𝑑2.
𝑑2 =
1
𝐸𝐼
∫ (−2𝑞𝑐2
− 2𝑞𝑐𝑥) ∙ 1𝑑𝑥
𝐿
2
−𝑐
0
+
1
𝐸𝐼
∫ (−
𝑞
2
𝑥2
) ∙ 1𝑑𝑥
2𝑐
0
+
1
𝐸𝐼
∫ 0 ∙ 1𝑑𝑥
𝐿
2
−𝑐
0
𝑑2 =
1
𝐸𝐼
[−2𝑞𝑐2
𝑥 − 𝑞𝑐𝑥2]0
𝐿
2
−𝑐
+
1
𝐸𝐼
[−
𝑞
6
𝑥3
]
0
2𝑐
𝑑2 =
1
𝐸𝐼
[−2𝑞𝑐2
(
𝐿
2
− 𝑐) − 𝑞𝑐 (
𝐿
2
− 𝑐)
2
] +
1
𝐸𝐼
[−
𝑞
6
(2𝑐)3
]
𝑑2 =
1
𝐸𝐼
[−2𝑞𝑐2
(
𝐿
2
− 𝑐) − 𝑞𝑐 (
𝐿2
4
− 𝑐𝐿 + 𝑐2
)] +
1
𝐸𝐼
[−
4𝑞𝑐3
3
]
𝑑2 =
1
𝐸𝐼
[−𝑞𝑐2
𝐿 + 2𝑞𝑐3
−
𝑞𝑐𝐿2
4
+ 𝑞𝑐2
𝐿 − 𝑞𝑐3
−
4𝑞𝑐3
3
] =
1
𝐸𝐼
[−
𝑞𝑐3
3
−
𝑞𝑐𝐿2
4
]
Cálculo del desplazamiento 𝑓11.
𝑓11 =
1
𝐸𝐼
∫ 𝑥 ∙ 𝑥
𝐿
0
𝑑𝑥 =
1
𝐸𝐼
[
𝑥3
3
]
0
𝐿
=
𝐿3
3𝐸𝐼
Cálculo de los desplazamientos 𝑓12 𝑦 𝑓21.
𝑓12 = 𝑓21 =
1
𝐸𝐼
∫ 𝑥 ∙ 1
𝑥2
𝑥1
𝑑𝑥 =
1
𝐸𝐼
[
𝑥2
2
]
0
𝐿
=
𝐿2
2𝐸𝐼
Cálculo del desplazamiento 𝑓22 .
𝑓22 =
1
𝐸𝐼
∫ 1 ∙ 1
𝐿
0
𝑑𝑥 =
1
𝐸𝐼
[𝑥]0
𝐿
=
𝐿
𝐸𝐼
Cálculo de las reacciones redundantes
Reemplazando los valores de 𝑑1, 𝑑2, 𝑓11, 𝑓12, 𝑓21 y 𝑓22 en las ecuaciones (28 − 1) y (28 − 2), da
1
𝐸𝐼
[−
𝑞𝑐3
𝐿
6
−
5𝑞𝑐𝐿3
24
] + 𝑅 𝐷𝑌 (
𝐿3
3𝐸𝐼
) + 𝑀 𝐷 (
𝐿2
2𝐸𝐼
) = 0 − − − (28 − 3)
1
𝐸𝐼
[−
𝑞𝑐3
3
−
𝑞𝑐𝐿2
4
] + 𝑅 𝐷𝑌 (
𝐿2
2𝐸𝐼
) + 𝑀 𝐷 (
𝐿
𝐸𝐼
) = 0 − − − (28 − 4)
Despejando 𝑀 𝐷 de la ecuación (28 − 4), resulta
𝑀 𝐷 =
𝑞𝑐3
3𝐿
+
𝑞𝑐𝐿
4
− (
𝐿
2
) 𝑅 𝐷𝑌 − − − (28 − 5)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-137-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
116
Sustituyendo la en la ecuación (28 − 3), se llega a
(−
𝑞𝑐3
𝐿
6
−
5𝑞𝑐𝐿3
24
) + (
𝐿3
3
) 𝑅 𝐷𝑌 + (
𝐿2
2
) [
𝑞𝑐3
3𝐿
+
𝑞𝑐𝐿
4
− (
𝐿
2
) 𝑅 𝐷𝑌] = 0
−
𝑞𝑐3
𝐿
6
−
5𝑞𝑐𝐿3
24
+ (
𝐿3
3
) 𝑅 𝐷𝑌 +
𝑞𝑐3
𝐿
6
+
𝑞𝑐𝐿3
8
− (
𝐿3
4
) 𝑅 𝐷𝑌 = 0
(
𝐿3
12
) 𝑅 𝐷𝑌 =
𝑞𝑐𝐿3
12
⟹∴ 𝑅 𝐷𝑌 = 𝑞𝑐
De modo que
𝑀 𝐷 =
𝑞𝑐3
3𝐿
+
𝑞𝑐𝐿
4
− (
𝐿
2
) 𝑞𝑐 ⟹∴ 𝑀 𝐷 =
𝑞𝑐3
3𝐿
−
𝑞𝑐𝐿
4
Ecuaciones de equilibrio
Las demás reacciones se calcularán con las ecuaciones de equilibrio estático. Los resultados finales
se muestran en la figura 28-f.
+↑ ∑ 𝐹𝑌 = 0 ⇒ 𝑅 𝐴𝑌 + 𝑅 𝐷𝑌 − 2𝑞𝑐 = 0
𝑅 𝐴𝑌 = 2𝑞𝑐 − 𝑞𝑐 ⟹∴ 𝑅 𝐴𝑌 = 𝑞𝑐
+ ∑ 𝑀𝐴 = 0 ⇒ 𝑀𝐴 + 2𝑞𝑐 (
𝐿
2
) − 𝑅 𝐷𝑌 𝐿 − 𝑀 𝐷 = 0
𝑀𝐴 + 𝑞𝑐𝐿 − 𝑞𝑐𝐿 − (
𝑞𝑐3
3𝐿
−
𝑞𝑐𝐿
4
) = 0
∴ 𝑀𝐴 =
𝑞𝑐3
3𝐿
−
𝑞𝑐𝐿
4
𝑞
𝐿 2Τ
A D
𝐿 2Τ
𝑐 𝑐
B C
𝑀𝐴 =
𝑞𝑐3
3𝐿
−
𝑞𝑐𝐿
4
𝑅 𝐴𝑌 = 𝑞𝑐
𝑅 𝐷𝑌 = 𝑞𝑐
𝑀 𝐷 =
𝑞𝑐3
3𝐿
−
𝑞𝑐𝐿
4
(f)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-138-320.jpg)

![Fuerzas de fijación y momentos de empotramiento en vigas
118
Ecuación de compatibilidad. Retomando los resultados obtenidos para la incompatibilidad
geométrica 𝑑1 y el coeficiente de flexibilidad 𝑓11 de la viga mostrada en la figura 28-a, obtenemos
𝑑1 + 𝑅 𝐷𝑌 𝑓11 = 0 − − − (29 − 1)
1
𝐸𝐼
[−
𝑞𝑐3
𝐿
6
−
5𝑞𝑐𝐿3
24
] + 𝑅 𝐷𝑌 (
𝐿3
3𝐸𝐼
) = 0 − − − (29 − 2)
Despejando 𝑅 𝐷𝑌 de la ecuación (29 − 2), se llega a
𝑅 𝐷𝑌 =
𝑞𝑐3
2𝐿2
+
5𝑞𝑐
8
Ecuaciones de equilibrio, figura 29-c. Las reacciones faltantes son
+↑ ∑ 𝐹𝑌 = 0 ⇒ 𝑅 𝐴𝑌 + 𝑅 𝐷𝑌 − 𝑞2𝑐 = 0
𝑅 𝐴𝑌 = 2𝑞𝑐 −
𝑞𝑐3
2𝐿2
−
5𝑞𝑐
8
⟹∴ 𝑅 𝐴𝑌 = −
𝑞𝑐3
2𝐿2
+
11𝑞𝑐
8
+ ∑ 𝑀𝐴 = 0 ⇒ 𝑀𝐴 − 𝑞2𝑐 (
𝐿
2
) + 𝑅 𝐷𝑌 𝐿 = 0
𝑀𝐴 − 𝑞𝑐𝐿 + (
𝑞𝑐3
2𝐿2
+
5𝑞𝑐
8
) 𝐿 = 0
𝑀𝐴 − 𝑞𝑐𝐿 +
𝑞𝑐3
2𝐿
+
5𝑞𝑐𝐿
8
= 0
∴ 𝑀𝐴 = −
𝑞𝑐3
2𝐿
+
3𝑞𝑐𝐿
8
𝑞
𝐿 2Τ
A
D
𝐿 2Τ
𝑐 𝑐
B C
𝑅 𝐷𝑌 =
𝑞𝑐3
2𝐿2
+
5𝑞𝑐
8
𝑅 𝐴𝑌 = −
𝑞𝑐3
2𝐿2
+
11𝑞𝑐
8
𝑀𝐴 = −
𝑞𝑐3
2𝐿
+
3𝑞𝑐𝐿
8
(c)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-140-320.jpg)

![Fuerzas de fijación y momentos de empotramiento en vigas
120
SOLUCIÓN
Principio de superposición, figura 30-b. Se han seleccionado como fuerzas redundantes a las
reacciones del empotramiento derecho.
Ecuaciones de compatibilidad
Las ecuaciones de flexibilidad para el sistema estructural son las siguientes:
𝑑1 + 𝑅 𝐶𝑌 𝑓11 + 𝑀 𝐶 𝑓12 = 0 − − − (30 − 1)
𝑑2 + 𝑅 𝐶𝑌 𝑓21 + 𝑀 𝐶 𝑓22 = 0 − − − (30 − 2)
Cálculo de las incompatibilidades geométricas y de los coeficientes de flexibilidad
Se emplea una primera coordenada 𝑥 para analizar el segmento 𝐶 − 𝐵 con origen en 𝐶 y una
segunda coordenada 𝑥 para comprender el tramo 𝐵 − 𝐴 con origen situado en el punto 𝐵.
Se determinan los momentos 𝑀 con base en las figuras 30-c y 30-d.
𝑀1 = 0
𝑀2 +
𝑞(𝑎 − 𝑥)
𝑎
∙ 𝑥 ∙
𝑥
2
+ [𝑞 −
𝑞(𝑎 − 𝑥)
𝑎
] ∙
𝑥
2
∙
2𝑥
3
= 0
𝑀2 = −
𝑞𝑥2
2
+
𝑞𝑥3
2𝑎
−
𝑞𝑥2
3
+
𝑞𝑥2
3
−
𝑞𝑥3
3𝑎
= −
𝑞𝑥2
2
+
𝑞𝑥3
6𝑎
Se escriben las ecuaciones de momento 𝑚1 a partir de las figuras 30-e y 30-f.
C
𝑥
𝑀1
q
B
𝑥 b
C
𝑞(𝑎 − 𝑥)
𝑎
𝑀2
(c)
(d)
C
𝑥
𝑀1
1
B
𝑥 b
C𝑀2
1
(e) (f)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-142-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
121
𝑀1 − 1 ∙ 𝑥 = 0 ⇒ 𝑀1 = 𝑥
𝑀2 − 1 ∙ (𝑥 + 𝑏) = 0 ⇒ 𝑀2 = 𝑏 + 𝑥
Se deducen los momentos internos 𝑚2 de acuerdo con las figuras 30-g y 30-h.
𝑀1 = 1 𝑀2 = 1
Se calcula el desplazamiento 𝑑1.
𝑑1 =
1
𝐸𝐼
∫ (−
𝑞𝑥2
2
+
𝑞𝑥3
6𝑎
) ∙ (𝑏 + 𝑥)𝑑𝑥
𝑎
0
+
1
𝐸𝐼
∫ 0 ∙ 𝑥𝑑𝑥
𝑏
0
No obstante,
(−
𝑞𝑥2
2
+
𝑞𝑥3
6𝑎
) ∙ (𝑏 + 𝑥) = −
𝑞𝑏𝑥2
2
−
𝑞𝑥3
2
+
𝑞𝑏𝑥3
6𝑎
+
𝑞𝑥4
6𝑎
De modo que
𝑑1 =
1
𝐸𝐼
∫ (−
𝑞𝑏𝑥2
2
−
𝑞𝑥3
2
+
𝑞𝑏𝑥3
6𝑎
+
𝑞𝑥4
6𝑎
) 𝑑𝑥
𝑎
0
=
1
𝐸𝐼
[−
𝑞𝑏𝑥3
6
−
𝑞𝑥4
8
+
𝑞𝑏𝑥4
24𝑎
+
𝑞𝑥5
30𝑎
]
0
𝑎
𝑑1 =
1
𝐸𝐼
(−
𝑞𝑏𝑎3
6
−
𝑞𝑎4
8
+
𝑞𝑏𝑎3
24
+
𝑞𝑎4
30
) =
1
𝐸𝐼
(−
𝑞𝑏𝑎3
8
−
11𝑞𝑎4
120
)
Se calcula el desplazamiento 𝑑2.
𝑑2 =
1
𝐸𝐼
∫ (−
𝑞𝑥2
2
+
𝑞𝑥3
6𝑎
) ∙ 1𝑑𝑥
𝑎
0
+
1
𝐸𝐼
∫ 0 ∙ 1𝑑𝑥
𝑏
0
=
1
𝐸𝐼
[−
𝑞𝑥3
6
+
𝑞𝑥4
24𝑎
]
0
𝑎
𝑑2 =
1
𝐸𝐼
(−
𝑞𝑎3
6
+
𝑞𝑎3
24
) =
1
𝐸𝐼
(−
𝑞𝑎3
8
)
Se calcula el desplazamiento 𝑓11.
𝑓11 =
1
𝐸𝐼
∫ 𝑥 ∙ 𝑥
𝐿
0
𝑑𝑥 =
1
𝐸𝐼
[
𝑥3
3
]
0
𝐿
=
𝐿3
3𝐸𝐼
Se calculan los desplazamientos 𝑓12 𝑦 𝑓21.
𝑓12 = 𝑓21 =
1
𝐸𝐼
∫ 𝑥 ∙ 1
𝐿
0
𝑑𝑥 =
1
𝐸𝐼
[
𝑥2
2
]
0
𝐿
=
𝐿2
2𝐸𝐼
C
𝑥
𝑀1
1
B
𝑥 b
C𝑀2
1
(h)
(g)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-143-320.jpg)
![Fuerzas de fijación y momentos de empotramiento en vigas
122
Se calcula el desplazamiento 𝑓22 .
𝑓22 =
1
𝐸𝐼
∫ 1 ∙ 1
𝐿
0
𝑑𝑥 =
1
𝐸𝐼
[𝑥]0
𝐿
=
𝐿
𝐸𝐼
Cálculo de las reacciones redundantes
Al sustituir los valores de 𝑑1, 𝑑2, 𝑓11, 𝑓12, 𝑓21 y 𝑓22 en las ecuaciones (30 − 1) y (30 − 2), se llega a
1
𝐸𝐼
(−
𝑞𝑏𝑎3
8
−
11𝑞𝑎4
120
) + 𝑅 𝐶𝑌 (
𝐿3
3𝐸𝐼
) + 𝑀 𝐶 (
𝐿2
2𝐸𝐼
) = 0 − − − (30 − 3)
1
𝐸𝐼
(−
𝑞𝑎3
8
) + 𝑅 𝐶𝑌 (
𝐿2
2𝐸𝐼
) + 𝑀 𝐶 (
𝐿
𝐸𝐼
) = 0 − − − (30 − 4)
Al despejar 𝑀 𝐷 de la ecuación (30 − 4), resulta
𝑀 𝐶 =
𝑞𝑎3
8𝐿
− (
𝐿
2
) 𝑅 𝐶𝑌 − − − (30 − 5)
Combinando la expresión (30 − 5) con la expresión (30 − 3), tenemos
[−
𝑞𝑏𝑎3
8
−
11𝑞𝑎4
120
] + 𝑅 𝐶𝑌 (
𝐿3
3
) + [
𝑞𝑎3
8𝐿
− (
𝐿
2
) 𝑅 𝐶𝑌] (
𝐿2
2
) = 0
−
𝑞𝑏𝑎3
8
−
11𝑞𝑎4
120
+ 𝑅 𝐶𝑌 (
𝐿3
3
) +
𝑞𝑎3
𝐿
16
− (
𝐿3
4
) 𝑅 𝐶𝑌 = 0 ⇒ (
𝐿3
12
) 𝑅 𝐶𝑌 =
𝑞𝑏𝑎3
8
−
𝑞𝑎3
𝐿
16
+
11𝑞𝑎4
120
𝑅 𝐶𝑌 =
3𝑞(𝐿 − 𝑎)𝑎3
2𝐿3
−
3𝑞𝑎3
4𝐿2
+
11𝑞𝑎4
10𝐿3
= 𝑅 𝐶𝑌 =
3𝑞𝑎3
2𝐿2
−
3𝑞𝑎4
2𝐿3
−
3𝑞𝑎3
4𝐿2
+
11𝑞𝑎4
10𝐿3
⟹∴ 𝑅 𝐶𝑌 =
3𝑞𝑎3
4𝐿2
−
2𝑞𝑎4
5𝐿3
Reemplazando 𝑅 𝐷 en la ecuación (30 − 5), se obtiene
𝑀 𝐶 =
𝑞𝑎3
8𝐿
− (
𝐿
2
) (
3𝑞𝑎3
4𝐿2
−
2𝑞𝑎4
5𝐿3
) =
𝑞𝑎3
8𝐿
−
3𝑞𝑎3
8𝐿
+
𝑞𝑎4
5𝐿2
⟹∴ 𝑀 𝐶 = −
𝑞𝑎3
4𝐿
+
𝑞𝑎4
5𝐿2
Ecuaciones de equilibrio, figura 30-i.
+↑ ∑ 𝐹𝑌 = 0
𝑅 𝐴𝑦 + 𝑅 𝐶𝑌 −
𝑞𝑎
2
= 0 ⇒∴ 𝑅 𝐴𝑌 =
𝑞𝑎
2
−
3𝑞𝑎3
4𝐿2
+
2𝑞𝑎4
5𝐿3
+ ∑ 𝑀𝐴 = 0 ⇒ 𝑀𝐴 − (
𝑞𝑎
2
) (
2𝑎
3
) + 𝑅 𝐶𝑌 𝐿 + 𝑀 𝐶 = 0
𝑀𝐴 −
𝑞𝑎2
3
+ (
3𝑞𝑎3
4𝐿2
−
2𝑞𝑎4
5𝐿3
) 𝐿 −
𝑞𝑎3
4𝐿
+
𝑞𝑎4
5𝐿2
= 0](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-144-320.jpg)

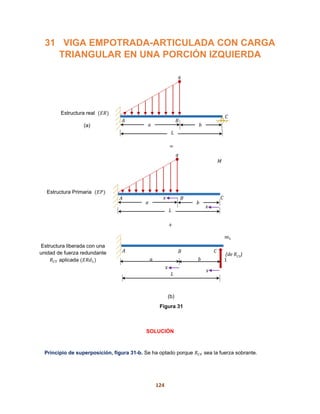


![Fuerzas de fijación y momentos de empotramiento en vigas
127
𝑀1 = 0
𝑀2 + 𝑚 = 0 ⇒ 𝑀2 = −𝑚
Se escriben las ecuaciones de momento 𝑚1 a partir de las figuras 30-e y 30-f.
𝑀1 − 1 ∙ 𝑥 = 0 ⇒ 𝑀1 = 𝑥
𝑀2 − 1 ∙ (𝑥 + 𝑏) = 0 ⇒ 𝑀2 = 𝑏 + 𝑥
Se determina el desplazamiento 𝑑1.
𝑑1 =
1
𝐸𝐼
∫ (−𝑚) ∙ (𝑥 + 𝑏)𝑑𝑥
𝑎
0
+
1
𝐸𝐼
∫ 0 ∙ 𝑥𝑑𝑥
𝑏
0
=
1
𝐸𝐼
∫ −(𝑚𝑥 + 𝑚𝑏)𝑑𝑥
𝑎
0
𝑑1 =
1
𝐸𝐼
[−
𝑚𝑥2
2
− 𝑚𝑏𝑥]
0
𝑎
=
1
𝐸𝐼
[−
𝑚𝑎2
2
− 𝑚𝑏𝑎]
Se determina el desplazamiento 𝑓11.
𝑓11 =
1
𝐸𝐼
∫ 𝑥 ∙ 𝑥
𝐿
0
𝑑𝑥 =
1
𝐸𝐼
[
𝑥3
3
]
0
𝐿
=
𝐿3
3𝐸𝐼
La ecuación de flexibilidad queda del siguiente modo:
1
𝐸𝐼
[−
𝑚𝑎2
2
− 𝑚𝑏𝑎] + 𝑅 𝐶𝑌 (
𝐿3
3𝐸𝐼
) = 0 − − − (32 − 1)
C
𝑥
𝑀1
B
𝑥 b
C
𝑀2
𝑚
(c)
(d)
C
𝑥
𝑀1
1
B
𝑥 b
C𝑀2
1
(e) (f)](https://image.slidesharecdn.com/librodevigascompleto-200514005530/85/Libro-de-vigas-completo-149-320.jpg)




