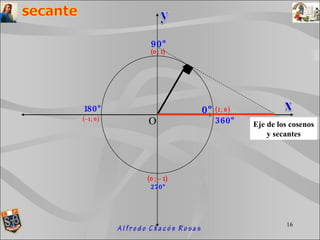
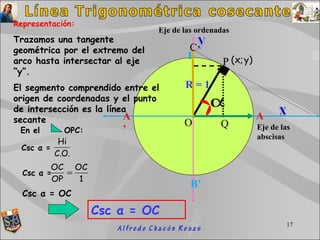
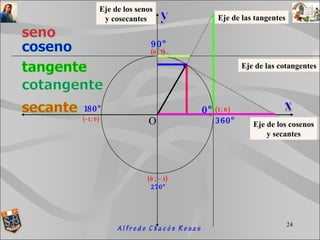
El documento describe las líneas trigonométricas y su representación en el círculo trigonométrico. Define las líneas seno, coseno, tangente y cotangente y explica cómo se representan en el círculo trigonométrico, cuyo radio es igual a 1. También indica los ejes asociados con cada línea trigonométrica.

3. Alfredo Chacon Rosas

4. Tema: Actitud:

5. O Eje de las ordenadas Eje de las abscisas A B B’ P Definición : Es un circulo geométrico cuyo centro “O” coincide con el origen del sistema cartesiano. Esta circunferencia tiene como característica fundamental, que el valor del radio es igual a UNO ( R = 1 ) A’ Donde : A: Origen de arcos. B: Origen de complementos. A’: Origen de suplementos. B’: Sin nombre especial R = 1

6. Se llaman líneas trigonométricas a los diferente segmentos de recta que representan a las razones trigonométricas de un ángulo trigonométrico y entre ellas tenemos:

7. Sen α = y O Eje de las ordenadas Eje de las abscisas A B B’ A’ Representación: Se representa por la perpendicular trazada desde el extremo del arco, hacia el diámetro horizontal. P R = 1 Q Sen α = Sen α = Sen α = PQ En el OQP:

8. O Eje de los senos y cosecantes Q Sen  La l ínea trigonométrica seno es un segmento de recta vertical orientado. P

9. O Eje de las ordenadas Eje de las abscisas A B B’ P A’ R = 1 Representación: Se representa por la perpendicular trazada desde el extremo del arco, hacia el diámetro vertical. Q En el OQP: Cos α = x Sen α = OQ Cos α = Cos α =

10. O Eje de los cosenos y secantes

11. O Eje de las tangentes A B B’ P A’ R = 1 Representación: Es una parte de la tangente geométrica trazada por el origen de arcos A(1;0), Se empieza a medir de este origen y termina en la intersección de la tangente geométrica con el radio prolongado que pasa por el extremo del arco. En el OQP: Tan α = AT Tan α = AT Tan α = Tan α = T Q

12. O Eje de las tangentes

13. O Eje de las cotangentes A B B’ P A’ R = 1 Representación: Es una parte de la tangente geométrica trazada por el origen de complementos de arcos A(0;1), Se empieza a medir de este origen de complementos y termina en la intersección de la tangente geométrica con el radio prolongado que pasa por el extremo del arco. En el OQP: Ctn α = BC Ctn α = BC Ctn α = Ctn α = C Q

14. O Eje de las cotangentes

15. O Eje de las ordenadas Eje de las abscisas A B B’ P A’ R = 1 Representación: Trazamos una tangente geométrica por el estremo del arco hasta intersectar al eje “x”. El segmento comprendido entre el origen de coordenadas y el punto de interseccion es la línea secante Q En el OPS: Sec α = OS Sec α = OS Sec α = Sec α = S

16. O Eje de los cosenos y secantes

17. O Eje de las ordenadas Eje de las abscisas A B B’ P A’ R = 1 Representación: Trazamos una tangente geométrica por el extremo del arco hasta intersectar al eje “y”. El segmento comprendido entre el origen de coordenadas y el punto de intersección es la línea secante Q En el OPC: Csc α = OC Csc α = OC Csc α = Csc α = C

18. O Eje de los senos y cosecantes

20. O Eje de los senos y cosecantes

21. O Eje de los senos y cosecantes Eje de los cosenos y secantes

22. O Eje de los senos y cosecantes Eje de las tangentes Eje de los cosenos y secantes

23. O Eje de los senos y cosecantes Eje de las tangentes Eje de las cotangentes Eje de los cosenos y secantes

24. O Eje de los senos y cosecantes Eje de las tangentes Eje de las cotangentes Eje de los cosenos y secantes

25. O Eje de los senos y cosecantes Eje de las tangentes Eje de las cotangentes Eje de los cosenos y secantes ¿Qué color tiene cada línea trigonométrica?

27. Ejercicio Nº 1 O U S P V Q R T A B B’ A’ PQ RP SA OU OV

28. Ejercicio Nº 2

29. Ejercicio Nº 3

30. Ejercicio Nº 4 Cos 53º Sen 30º Sen 100º Cos 200º Cos 315º 315º 30º 0º 360º 270º 200º 180º 100º 53º 90º 0

31. Ejercicio Nº 5 180º 360º 0º 90º 270º X Y O  

33. EVALUACIÓN COGNITIVA

35. Ejercicio Nº 1

36. El Señor es mi pastor nada me faltará. En verdes praderas me hace descansar, junto a tranquilas aguas me pastorea. Sal. 23 : 1-2