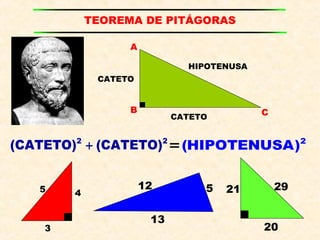
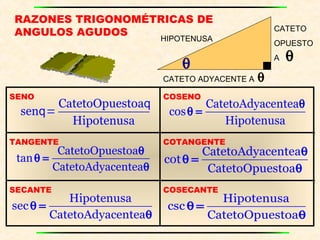
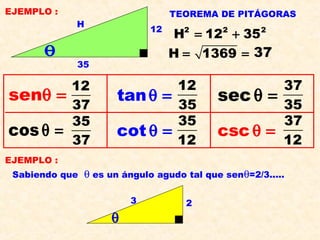
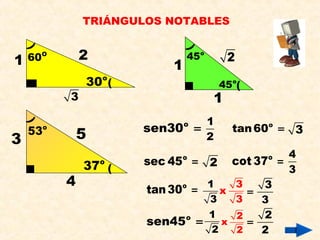
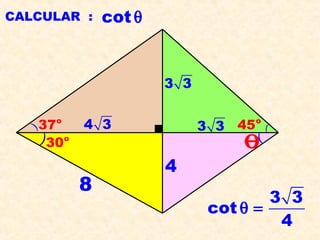
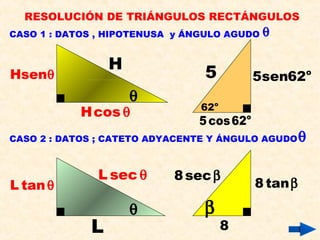
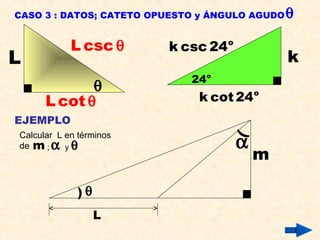
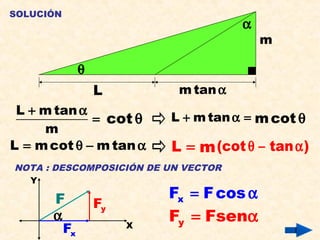
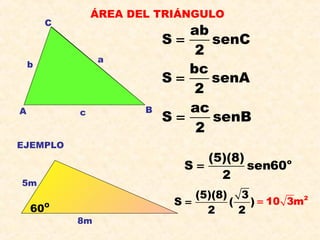
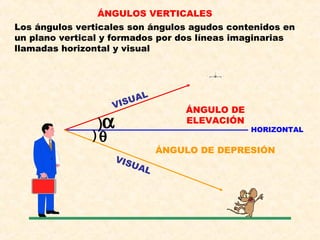
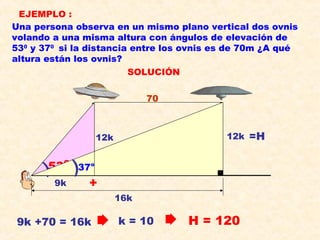
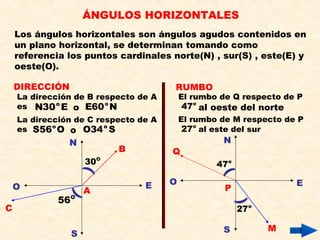
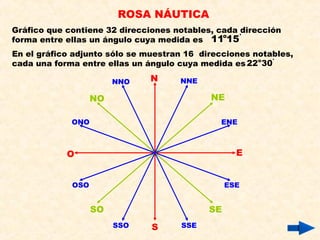
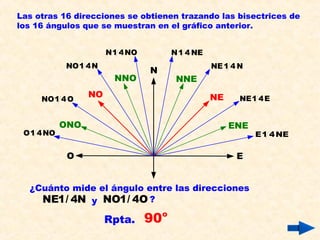
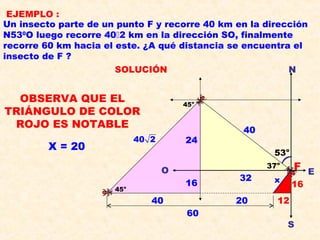
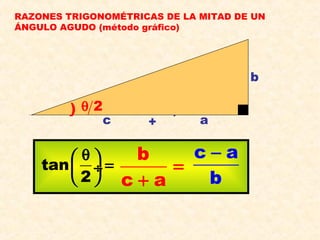
Este documento presenta información sobre conceptos básicos de trigonometría como el teorema de Pitágoras, las razones trigonométricas de ángulos agudos y sus propiedades, triángulos notables, resolución de triángulos rectángulos, área de triángulos, ángulos verticales y horizontales, rosa náutica y razones trigonométricas de la mitad de un ángulo agudo. Incluye ejemplos y ejercicios resueltos para ilustrar los diferentes temas.

1. RUBÉN ALVA CABRERARUBÉN ALVA CABRERA
rubalva@hotmail.com

3. TEOREMA DE PITÁGORAS
A
B C
CATETO
CATETO
HIPOTENUSA
2 2
(CATETO) (CATETO)+ = 2
(HIPOTENUSA)
3
45 512
13
20
21 29

4. RAZONES TRIGONOMÉTRICAS DE
ANGULOS AGUDOS
q
=q
CatetoOpuestoa
sen
Hipotenusa
θ
θ =
CatetoAdyacentea
cos
Hipotenusa
θ =
θ
Hipotenusa
sec
CatetoAdyacentea
θ =
θ
Hipotenusa
csc
CatetoOpuestoa
θ
θ =
θ
CatetoAdyacentea
cot
CatetoOpuestoa
θ
θ =
θ
CatetoOpuestoa
tan
CatetoAdyacentea
CATETO
OPUESTO
A
θCATETO ADYACENTE A
θ
HIPOTENUSA
θ
SENO COSENO
TANGENTE COTANGENTE
SECANTE COSECANTE

5. 12
35
H
2 2 2
H 12 35= +
TEOREMA DE PITÁGORAS
H 1369= = 37
senθ =
cosθ =
tanθ =
12
37
35
37
12
35
cot θ =
sec θ =
csc θ =
35
12
37
35
37
12
EJEMPLO :
EJEMPLO :
Sabiendo que θ es un ángulo agudo tal que senθ=2/3.....
23
θ
θ

6. RAZONES TRIGONOMÉTRICAS RECÍPROCAS
PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
1
sen
csc
θ =
θ
1
cos
sec
θ =
θ
1
tan
cot
θ =
θ
EJEMPLOS
o
1
A)
sen36
o
csc 36= o
1
B)
cos17
o
sec17=
sen csc 1θ θ = cos sec 1θ θ = tan cot 1θ θ =
D)sen2 csc2θ θ 1=o o
C)tan49 cot 49 1=
o
E)cos63 sec θ 1= o
63θ =
F)tan2 cot 1φ θ = 2φ = θ

7. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
A LAS RAZONES TRIGONOMÉTRICAS SENO Y COSENO
TANGENTE Y COTANGENTE ;SECANTE Y COSECANTE
SE LES DENOMINA :CO-RAZONES TRIGONOMÉTRICAS
PROPIEDAD :
“LAS RAZONES TRIGONOMÉTRICAS DE TODO ÁNGULO AGUDO
SON RESPECTIVAMENTE IGUALES A LAS CO-RAZONES
TRIGONOMÉTRICAS DE SU ÁNGULO COMPLEMENTARIO”
θ
φ senθ = cos φ
cos θ =
tanθ =
senφ
cotφ
a
b c
cot θ =
secθ =
cscθ =
tanφ
cscφ
sec φ

8. EJEMPLOS
o
A)sen25 =
o
B)tan43 =
o
C)sec60 =
o
cos65
o
cot 47
o
csc30
...............
...............
...............
o o O
25 65 90+ =
o o O
43 47 90+ =
o o O
60 30 90+ =
o
D)sen cos20θ =
o O
20 90θ + = o
70θ =
E)tan5 cotα = α
o
5 90α + α =
o
15α =
F)sen
5
π  = ÷
 
cos θ
5 2
π π
θ + =
2 5
π π
θ = −
3
rad
10
π
θ =

9. TRIÁNGULOS NOTABLES
1 2
3
o
30 (
)
O
60
1
1
2
o
45
o
45
(
)
3
4
5
o
37
o
53
(
)
o
sen30 =
1
2
o
tan60 = 3
o
sec 45 = 2
o
cot 37 =
4
3
o
tan30 =
1
3
3
x
3
3
3
=
o
sen45 =
1
2
2
x
2
2
2
=

10. )
)
(
(o
30
o
37 o
45
θ
4 3
4
3 3
3 3
CALCULAR : cotθ
8
3 3
cot
4
θ =

11. RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
θ
θ
H
Hsenθ
Hcos θ
L sec θ
L tanθ
L
5
o
62
o
5sen62
o
5cos62
8
β
8 tanβ
8secβ
CASO 1 : DATOS , HIPOTENUSA y ÁNGULO AGUDO θ
CASO 2 : DATOS ; CATETO ADYACENTE Y ÁNGULO AGUDOθ

12. L
θ
L cot θ
L csc θ
k
o
24
o
k csc 24
o
k cot 24
EJEMPLO
α
θ)
)
m
Calcular L en términos
de m α y θ;
L
CASO 3 : DATOS; CATETO OPUESTO y ÁNGULO AGUDOθ

13. SOLUCIÓN
α
θ
m
m tanαL
L m tan
m
+ α
= cot θ L m tan+ α = mcot θ
L mcot m tan= θ − α L = m(cot tan )θ − α
NOTA : DESCOMPOSICIÓN DE UN VECTOR
α
F
yF
xF X
Y
xF Fcos= α
yF Fsen= α

14. ÁREA DEL TRIÁNGULO
A B
C
a
b
c
ab
S senC
2
=
bc
S senA
2
=
ac
S senB
2
=
EJEMPLO
5m
8m
O
60
o(5)(8)
S sen60
2
=
(5)(8) 3
S ( )
2 2
= 2
10 3m=

15. ÁNGULOS VERTICALES
Los ángulos verticales son ángulos agudos contenidos en
un plano vertical y formados por dos líneas imaginarias
llamadas horizontal y visual
α
θ
ÁNGULO DE
ELEVACIÓN
ÁNGULO DE DEPRESIÓN
HORIZONTAL
VISUAL
VISUAL
)
)

16. Una persona observa en un mismo plano vertical dos ovnis
volando a una misma altura con ángulos de elevación de
530
y 370
si la distancia entre los ovnis es de 70m ¿A qué
altura están los ovnis?
EJEMPLO :
SOLUCIÓN
) ) o
37
O
53
70
12k 12k
)
O
53
9k
) o
37
16k
+
9k +70 = 16k k = 10 H = 120
=H

17. ÁNGULOS HORIZONTALES
Los ángulos horizontales son ángulos agudos contenidos en
un plano horizontal, se determinan tomando como
referencia los puntos cardinales norte(N) , sur(S) , este(E) y
oeste(O).
DIRECCIÓN
La dirección de B respecto de A
es E30N o
N60E o
La dirección de C respecto de A
es o
S56 O S34O o
o
o
RUMBO
El rumbo de Q respecto de P
o
47
El rumbo de M respecto de P
o
27 al este del sur
al oeste del norte
N
S
EO
O
30
O
56
A
B
C
EO
S
N
P
Q
o
47
o
27
M
)
(
(
)

18. ROSA NÁUTICA
Gráfico que contiene 32 direcciones notables, cada dirección
forma entre ellas un ángulo cuya medida es
'o
1511
En el gráfico adjunto sólo se muestran 16 direcciones notables,
cada una forma entre ellas un ángulo cuya medida es 'o
3022
N
S
EO
NNE
ENE
NNO
ONO
OSO
SSO
ESE
SSE
NENO
SO SE

19. Las otras 16 direcciones se obtienen trazando las bisectrices de
los 16 ángulos que se muestran en el gráfico anterior.
E
NE
N
NNE
ENE
NE41E
E41NE
NE41N
N41NE
NNO
NO41N
N41NO
NOO41NO
ONO
NO41O
O
¿Cuánto mide el ángulo entre las direcciones
NE1/ 4N y NO1/ 4O ?
Rpta.
o
90

20. Un insecto parte de un punto F y recorre 40 km en la dirección
N530
O luego recorre 402 km en la dirección SO, finalmente
recorre 60 km hacia el este. ¿A qué distancia se encuentra el
insecto de F ?
EJEMPLO :
SOLUCIÓN N
S
EO
o
53
)
o
45
o
45
40
40 2
60
x
o
37
24
32
16
40 20 12
16
OBSERVA QUE EL
TRIÁNGULO DE COLOR
ROJO ES NOTABLE
X = 20
F

21. RAZONES TRIGONOMÉTRICAS DE LA MITAD DE UN
ÁNGULO AGUDO (método gráfico)
θ2
θ
2
θ
a
bc
c
))
(
) 2θ
tan
2
θ  = ÷
 
b
c a
=
+
c a
b
−
+

22. EJEMPLO :
Sabiendo que : tan 8θ=24/7, calcula tan2θ
SOLUCIÓN
8θ
24
7
25
4θ
25
24
tan4
25 7
θ =
+
24
tan4
32
θ =
3
tan4
4
θ =
4θ 2θ
3
4
5
5
3
tan2
9
θ = 1
tan2
3
θ =
(

23. Te recomiendo adquirir mi libro
TRIGONOMETRIA
TEORÍA Y PRÁCTICA
COLECCIÓN UNICIENCIA
EDITORIAL SAN MARCOS ,940 PÁGINAS
rubalva@hotmail.com