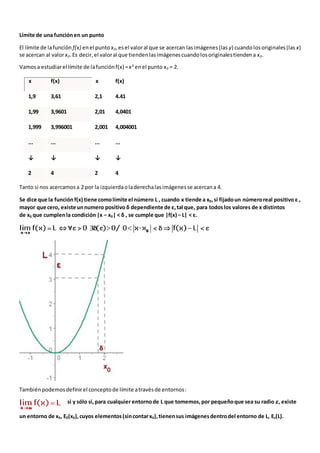
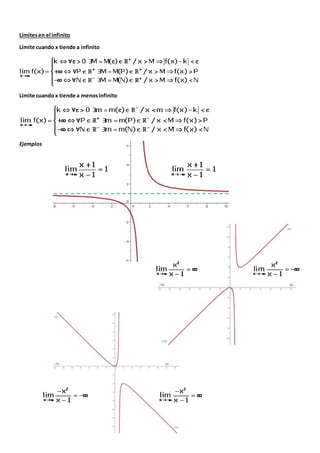
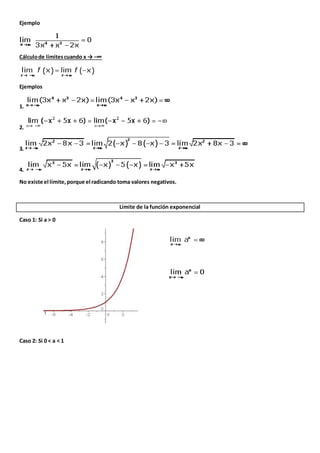
Este documento trata sobre los límites de funciones. Explica conceptos como límites laterales, límites infinitos, propiedades de los límites, cálculo de límites, indeterminaciones y la regla de L'Hôpital para resolver indeterminaciones. Contiene ejemplos y ejercicios de límites de funciones.

1. Límite de una función
Índice
Teoría
1. Limite de una función enun punto.
2. Límiteslaterales.
3. Limitesinfinitos.
4. Límitesen el infinito.
5. Propiedadesde los límites.
6. Operacionescon infinito.
7. Cálculo de límites.
8. Cálculo de límitescuando x tiende a ∞.
9. Límite de la funciónexponencial.
10. Límite de la funciónlogarítmica.
11. Indeterminaciones.
12. Comparación de infinitos.
13. Límite de un número partido por cero.
14. Indeterminacióninfinitopartido por infinito.
15. Indeterminacióninfinitomenosinfinito.
16. Indeterminacióncero partido por cero.
17. Indeterminacióncero por infinito.
18. Regla de L'Hôpital
19. Indeterminaciónuno elevadoa infinito.
Ejerciciosde límitesde funciones
2.1 EjerciciosI
2.2 EjerciciosII

2. Límite de una funciónen un punto
El límite de lafunción f(x) enel punto x0,esel valoral que se acercan lasimágenes(las y) cuandolosoriginales(las x)
se acercan al valorx0.Es decir,el valoral que tiendenlasimágenescuandolosoriginalestiendena x0.
Vamosa estudiarel límite de lafunciónf(x) =x2
enel punto x0 = 2.
x f(x) x f(x)
1,9 3,61 2,1 4.41
1,99 3,9601 2,01 4,0401
1,999 3,996001 2,001 4,004001
... ... ... ...
↓ ↓ ↓ ↓
2 4 2 4
Tanto si nos acercamosa 2 por la izquierdaoladerechalasimágenesse acercana 4.
Se dice que la función f(x) tiene comolímite el número L , cuando x tiende a x0,si fijadoun númeroreal positivo ε ,
mayor que cero, existe unnumero positivo δ dependiente de ε,tal que, para todoslos valores de x distintos
de x0 que cumplenla condición |x − x0| < δ , se cumple que |f(x) − L| < ε.
Tambiénpodemosdefinirel conceptode límite atravésde entornos:
si y sólo si,para cualquier entornode L que tomemos,por pequeñoque sea su radio ε, existe
un entorno de x0, Eδ(x0),cuyos elementos(sincontarx0),tienensus imágenesdentrodel entorno de L, Eε(L).

3. Límiteslaterales
Diremosque el límite de una funciónf(x) cuando x tiende hacia a por la izquierdaesL, si y sólosi para todo ε >
0 existe δ> 0 tal que si x (a − δ,a) , entonces|f(x) − L| < ε .
Diremosque el límite de una función f(x) cuando x tiende hacia a por la derechaes L , si y sólosi para todo ε >
0 existe δ> 0 tal que si x (a, a + δ),entonces|f (x) - L| <ε .
El límite de una funciónenun punto si existe,esúnico.
Ejemplos
1.
En este caso vemosque el límite tantopor la izquierdacomo por la derecha cuando x tiende a 2 es4.
El límite de lafunciónes4 aunque lafunciónnotengaimagenenx = 2.
Para calcular el límite de una funciónen un punto, no nos interesaloque sucede endicho punto sinoa su
alrededor.
2.
Comono coincidenlos límiteslaterales,lafunciónnotiene límite enx = 0.

4. Limitesinfinitos
Límite infinito
Una funciónf(x) tiene por límite +∞ cuando x → a, si fijado un númeroreal positivo K > 0 se verifica que f(x) >
k para todos los valorespróximos a a.
Ejemplo
Límite menosinfinito
Una funciónf(x) tiene por límite -∞ cuando x a, si fijado un númeroreal negativo K < 0 se verificaque f(x) <
k para todos los valorespróximos a a.
Ejemplo

5. Límitesen el infinito
Límite cuando x tiende a infinito
Límite cuando x tiende a menosinfinito
Ejemplos

6. Propiedadesde los límites
Límite de una constante
Límite de una suma
Límite de un producto
Límite de un cociente
Límite de una potencia
Límite de una función
g puede ser una raíz, un log, sen,cos, tg, etc.
Límite de una raíz
Límite de un logaritmo
Operacionescon infinito
Debemosseñalarque estasindicacionesnosonoperacionespropiamente dichas,sinosimplemente unrecursopara
ayudarnosa resolverlímites.
Debemostenerclaroque infinitonoesun número.
No distinguimosentre+∞y −∞ para no alargar excesivamente lalista.Nosbastaconsaber:
La reglade los signosy que a-n
= 1/a n
Sumas con infinito
Infinitomás un número Infinitomás infinito

7. Infinitomenosinfinito
Productos con infinito
Infinitopor un número Infinitopor infinito Infinitopor cero
Cocientescon infinitoycero
Cero partido por un número
Un númeropartido por cero
Un númeropartido por infinito
Infinitopartido por un número
Cero partido por infinito
Infinitopartido por cero
Cero partido por cero
Infinitopartido por infinito
Potenciascon infinitoy cero
Un númeroelevadoa cero
Cero elevadoa cero
Infinitoelevadoa cero
Cero elevadoa un número
Un númeroelevadoa infinito
Cero elevadoa infinito
Infinitoelevadoa infinito
Uno elevadoa infinito
Límites
Cálculodel límite enun punto
Si f(x) esuna funciónusual (polinómicas,racionales,radicales,exponenciales,logarítmicas,etc.)yestádefinidaenel
puntoa, entoncesse suele cumplirque:
Es decir:para calcular el límite se sustituye enlafunciónel valoral que tiendenlasx.

8. No podemoscalcular porque el dominiode definiciónestáenel intervalo[0,∞),portantono puede
tomar valoresque se acerquena−2.
Sinembargosí podemoscalcular , porque aunque 3 nopertenezcaal dominio,D= − {2, 3}, sí
podemostomarvaloresdel dominiotanpróximosa3 como queramos.
Cálculodel límite enuna funcióndefinidaa trozos
En primerlugar, tenemosque estudiarloslímiteslateralesenlospuntosde uniónde losdiferentestrozos.
Si coinciden,este esel valordel límite.
Si no coinciden,el límite noexiste.
.
En x = −1, loslímiteslateralesson:
Por laizquierda: Por laderecha:
Comoen amboscasos coinciden, el límite existe yvale 1.
En x = 1, loslímiteslaterales son:
Por laizquierda: Por laderecha:
Comono coincidenloslímiteslateralesnotiene límite enx =1.
Cálculode límitescuando x tiende a ∞
Para calcularel límite de una funcióncuandox → ∞ se sustituyenlasx por∞.
Límite de funcionespolinómicasenel infinito
El límite cuando x → ∞ de una funciónpolinómicaes +∞ o −∞ segúnque el términode mayor grado sea positivoo
negativo.
Ejemplos
1.
2.
Límite de la inversade un polinomioen el infinito
Si P(x) esun polinomio,entonces:
.

9. Ejemplo
Cálculode límitescuando x → −∞
Ejemplos
1.
2.
3.
4.
No existe el límite,porque el radicando toma valores negativos.
Límite de la función exponencial
Caso 1: Si a > 0
Caso 2: Si 0 < a < 1

10. 1.
2.
3.
4.
Límite de la función logarítmica
Caso 1: Si a > 0
Caso 2: Si 0 < a < 1

11. Ejemplo
Indeterminaciones
Una indeterminaciónnosignificaque el límite noexistaonose puedadeterminar, sinoque laaplicaciónde las
propiedadesde loslímitestal comolashemosenunciadasnosonválidas.

12. En estoscasos hayque efectuaroperacionesparticularespararesolvercadauna de las indeterminaciones.
Tipos de indeterminación
1. Infinitopartido por infinito
2. Infinitomenosinfinito
3. Ceropartido por cero
4. Ceropor infinito
5. Ceroelevadoa cero
6. Infinitoelevadoa cero
7. Unoelevadoa infinito
Comparación de infinitos
1. f(x) esun infinitode orden superiora g(x) si:
2. f(x) esun infinitode orden inferiora g(x) si:
3. f(x) esun infinitode igual ordena g(x) si:
Dadas dos potenciasde x,la de mayor exponente esuninfinitode orden superior.
Dadas dos funcionesexponencialesde base mayor que 1, la de mayor base es un infinitode ordensuperior.
Cualquierfunciónexponencial de base mayor que 1 esun infinitode ordensuperiora cualquierpotencia de x.
Las potenciasde x soninfinitosde orden superiora las funcioneslogarítmicas.
Dos polinomiosdel mismogrado o dos exponencialesde lamisma base son infinitosdel mismoorden.
Ejemplos
Hallarlos límitesporcomparaciónde infinitos:

13. 1.
2.
3.
Límite de un número partido por cero
El límite puede ser+∞, −∞ o no tenerlímite.
Ejemplos:Calcularel límite:
1.
Tomamosloslímiteslateralesparadeterminarel signode ∞.
Si le damos a la x un valorque se acerque a −1 por laizquierdacomo−1,1; tantoel numeradorcomodenominador
son negativos,porlotantoel límite porla izquierdaserá:+∞.
Si le damos a la x un valorque se acerque a −1 por laderechacomo −0,9. El numeradorseránegativoyel
denominadorpositivo,porlotantoel límite por laderechaserá:−∞.
Como no coincidenloslímiteslaterales,la funciónno tiene límite cuandox → −1.
2.

14. 3.
Indeterminación infinito partido infinito
Para resolverlaindeterminacióninfinitopartido porinfinitopodemosutilizarunode estosdosmétodos:
1. Por comparación de infinitos
1. El numeradortiene mayorgradoque el denominador.
El límite es ∞
2.El denominadortienemayorgrado que el numerador.
El límite es 0
3.Numeradory denominadortienenel mismogrado.
Al tenerel mismogradoel límite esel cociente entre los coeficientesde mayorgrado.
Ejemplos
1.
2.
3.

15. 4.
5.
2º Método
1. Si se trata de funcionespotencialesdividimostodoslossumandos por la x elevadaal mayor exponente.
2. Si son funcionesexponencialesdividimosporlaexponencial de mayor base.
Indeterminación infinito menos infinito
Para resolverlaindeterminación∞−∞ tenemosvariosmétodos:
1. Por comparación de infinitos
2. Con funcionesracionales
Ponemosacomún denominador,para llegara la indeterminación∞/∞.

16. 3. Con funcionesirracionales
Cuandose trata de funcionesirracionales podemosmultiplicarydividirporel conjugado.
Indeterminación cero partido por cero
Vamosa estudiarlaindeterminación0/0endoscasos:
Caso 1. Funciónracional
Se descomponenenfactoreslos polinomiosy se simplificala fracción.
1.
El límite es 0.
2.
Tomamoslímiteslaterales:

17. No tiene límite enx =−1
Caso 2. Funcióncon radicales
En primerlugar, multiplicamosnumeradory denominadorpor el conjugado de la expresiónirracional.
Realizamoslasoperacionesysimplificamosla fracción.
Indeterminación cero por infinito
La indeterminación∞·0 se transformaenotras indeterminaciones
como ∞/∞ o 0/0, que ya hemosvistocomose resuelven.
Ejemplo
Regla de L'Hôpital
Si endonde f y g son derivablesen unentornode a y existe ,
entonceseste límite coincide con

18. Para aplicarla reglade L'Hôpital hay que tenerunlímite de la forma,
 
 
0
lim
0x a
f x
g x
 donde a puede serunnúmero
o infinito,yaparecerlasindeterminaciones:
Las cuálespuedenserllevadas alaforma
0
0
Las indeterminacionesdel tipo0. ,aparecenenlímitesde productosde funciones f(x).g(x) cuandounade ellas,
p.ej.laf(x) tiende a0,y la otra, la g(x),tiende a .En este casonosotrosexpresaremosel límite enlaforma:
   
 
 
lim . lim
1x a x a
f x
f x g x
g x
 

y como 1/g(x) tenderáa0, se obtiene laformatípica 0/0, a lacual se puede aplicardirectamentelareglade
L'Hôpital.
Otro tipode indeterminaciónsusceptiblede realizarse porlareglade L'Hôpital esla forma - , que aparece en
límitesde unaresta,es decir,cuandotenemos: f(x)- g(x), yambasfuncionesenx=a se hacen+ . Para este caso
hay que tenerencuentala siguienteidentidad:
1 1 1 1
. . 1 1 0
. . lim
1 1 0
. .
x a
g f g ff g g f
f g f g
g f g f
f g f g

   
    
             
 
y si en x = a lasfunciones f yg son infinito,laexpresiónconsusinversasserá0,por loque f - g equivaldráa0/0; no
obstante, paraaplicarla reglade L'Hôpital,eneste caso deberemostransformar f - g como una expresión que
incluyauncociente.
Ejemplo:Hallarel límite de
Este límite tiene laforma - ,y antesde aplicarlareglade L'Hôpital debemosponerloenformade cociente:
así expresadoel cociente tiene laforma0/0,y se puede aplicar laregla:
0 . -

  


19. Ejemplos
Hallarel límite de:
este límite tiene laformaindeterminada0/0,por tanto,podemosaplicarlareglade L'Hôpital:
límite que sigue teniendolaformaindeterminada0/0,peroa la cual se puede volveraaplicarlareglade L'Hôpital:
que esen definitivael valordel límite.
Perola reglade L'Hôpital esmucho más general,puesesaplicable nosóloala indeterminación0/0,sinotambiéna
lasindeterminaciones: / ,0× , - .
Por ejemplo,unaindeterminacióndeltipo / ,provendráde unlímite de laforma:
endonde lasdos funciones f(x) yg(x) tiendanainfinitoen x=a,yeste límite obviamente novaríasi lo expresamosen
la forma:
y ahora sí tiene laforma0/0. En definitiva,laindeterminación / noes
diferente de la0/0.
Hallarel límite:
Este límite enprincipiotomalaforma indeterminada / ,yloresolvemosaplicandodirectamente lareglade
L'Hôpital:
OBSERVACIÓN: Noes necesariopasarel límite ala indeterminación0/0antesde aplicarla reglade L'Hôpital.Si
bien (f '/g') es distintode (1/g)'/(1/f '),encambionosondiferentesparanuestrocasode límitesenel punto x=a.
En cuantoa lasindeterminacionesdel tipo0× ,aparecenenlímitesde productosde funciones f(x)×g(x)cuando
una de ellas,p.ej.laf(x) tiende a0,y la otra, lag(x),tiende a .En este caso nosotrosexpresaremosel límite enla
forma:
y como 1/g(x) tenderáa0, se obtiene laformatípica 0/0, a lacual se puede aplicardirectamentelaregla de
L'Hôpital.
Hallarel límite de:
Este límite tiene laforma0× , porlo tanto,operamoscomohemosdicho:

20. habiendoexpresado lainversade latangente comolacotangente,cuyaderivadaes: - 1/(seno)²,estoes:
Ejemplosde límitesque dan
𝟎
𝟎
:
1)
2)
3)
4)
Indeterminaciones
30
lim
x
x sen x
x

30
0
lim
0x
x sen x
x


3 20 0 0 0
1 cos cos 1
lim lim lim lim
3 6 6 6x x x x
x sen x x sen x x
x x x   
 
   

21. En las indeterminacionesceroelevado a cero,infinitoelevadoa cero y uno elevadoa infinito;se realizanen
primer lugar las siguientesoperaciones:
Ejemplos
1) Este límite tiene laformaindeterminada0°,y tal como hemosdicho,puede expresarse:
 
 
0
lim 3 .ln3 3 .ln
0 0
lim lim x
x xx x x
x x
x e e 
 
 
enel interiordel paréntesis(laexponencial) tenemosunaindeterminación0× ,y ahora procederemosasí:
 
 
 
000
2
0 0
3
3.ln '3.ln limlimlim
111
'lim 3 .ln lim 3 0
1
xxx
x x
x xx
x x x
xx x
e e e e e e

 
       
 
          
     
     
2)
3)
ln
lim ln ln ln lnv v v v u
x a
u A u A u A v u A e

       
 lim lnln
lim lim x a
v uv u
x a x a
A e e 
 
 
 
   
 
2 202
2
0 0 0
3.ln cos 2 3.ln cos 23 lim
0 0
3. 2 3.tan2
lim lim lim 6. 1 tan 2
.cos2
lim cos 2 lim
6
x
x x x
x x
x xx
x x
sen x x
x
x x x
x e e
e e e

  
 
    
 
 
    
   
 ln cotg x
cosec x
0
limln cotg x
0 0
lim cotg x lim x
esen x sen x
x x
e e 
 
  

22. 2
2 2
0 0
2 200
cosec
1cotanlim lim
cos cosec . cos
limlim cos .
0cos .cotan cos
1
x x
xx
x
x
x sen xx sen x x
x
sen x x x sen x x
e e e e e
 



    
Indeterminaciónunoelevadoa infinito
Se resuelve transformandolaexpresión enuna potenciadel númeroe.
1er
Método
Ejemplo:
En la expresión sumamosy restamos1, y queda
Operandoconlosdos últimostérminosqueda: y ahora invertimos
el numeradordel últimotérmino: finalmentemultiplicamosydividimosal
exponenteporx+2 y x-1:
2º Método
Realizandolasiguiente transformación:
Ejemplo
1 1
.2 2 1
1
11 1
.
2 1
1 1 1
1
lim 1 lim lim
2
1
x
x x x
x
xx
x x
x x x
e e
x
x

  


 
  
 
  
      
  
   
1
.
2 1x x 
1 1
32 3
1
lim x
x
e e e

  

23. Ejerciciosde límitesde funciones
Nota: Infinitono es un número,las operaciones
que realizamos con ∞ son simplemente unrecurso
para ayudarnos a resolverlímites.
1 - Aplicandoladefiniciónde límite,probarque:
2 - Observarlagráficade estafunciónf(x) ycalcular
estoslímites.
Calcular los siguienteslímites
1.
2.
3.
4.
9.
10.
11.
12.
5.
6.
7.
13.
14.
8.
15.
Calcular:

24. 1)
2)
5)
6)
3) 7)
4) 8)
Ejerciciosde límitesde funcionesII
1 - Aplicandoladefiniciónde límite,probarque:
tiene límite igual a−1 cuando x 0
Calcular los límites:
2 -
3 -
4 -
5 -
6 -
Determinar loslímitesde: