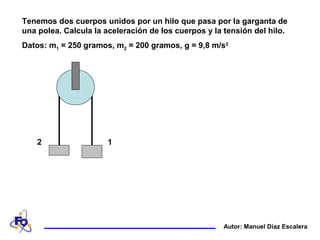
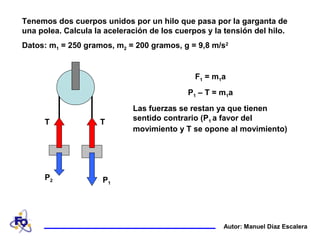
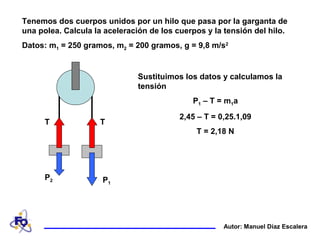
Dos cuerpos de masas 250g y 200g están unidos por un hilo que pasa por una polea. El documento explica cómo calcular la aceleración de los cuerpos (1.09 m/s2) y la tensión en el hilo (2.18 N) aplicando la segunda ley de Newton al sistema formado por los dos cuerpos y el hilo, y considerando las fuerzas que actúan sobre cada cuerpo de manera individual.

1. Problemas de fuerzas
Cuerpos enlazados por hilos
2 1
Autor: Manuel Díaz Escalera

2. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
2 1
Autor: Manuel Díaz Escalera

3. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
Paso 1 Dibujamos las fuerzas que
actúan sobre los dos cuerpos
P1 (peso del cuerpo 1)
P2 (peso del cuerpo 2)
T (Tensión del hilo)
P2P2
T TTT T
P1
2 1
Autor: Manuel Díaz Escalera

4. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
Aclaración
La tensión del hilo T es la misma
sobre los dos cuerpos y no es
necesario escribir T1 y T2
Autor: Manuel Díaz Escalera

5. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
Paso 2 Después de dibujar las fuerzas
podemos analizar el movimiento de los
cuerpos:
Los dos cuerpos unidos por un hilo se
mueven con la misma aceleración a (no
es necesario utilizar a1 y a2)
El cuerpo 1 (el más pesado) baja y el
cuerpo 2 sube.
Autor: Manuel Díaz Escalera

6. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
Paso 3 Si se considera que los dos
cuerpos y el hilo forman un único
cuerpo que se mueve con aceleración a
podemos aplicar la segunda ley de
Newton a dicho sistema:
F = m.a
Siendo F la fuerza resultante sobre los
dos cuerpos, m la masa de los cuerpos
y a la aceleración.
Autor: Manuel Díaz Escalera

7. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
F = m.a
P1 – P2 = (m1 + m2) .a
Los pesos se restan ya que tienen
sentido contrario (P1 a favor del
movimiento y P2 se opone al
movimiento).
Para el sistema formado por los cuerpos
y el hilo la tensión T es una fuerza
interna que no afecta a la aceleración.
Autor: Manuel Díaz Escalera

8. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
Paso 4 Sustituimos los datos y
calculamos la aceleración:
P1 = m1g = 0,25.9,8 = 2,45 N
P2 = m2g = 0,20.9,8 = 1,96 N
m1 + m2 = 450 gramos = 0,45 Kg
P1 – P2 = (m1 + m2) .a
2´45 – 1´96 = 0,45.a
a = 1,09 m/s2
Autor: Manuel Díaz Escalera

9. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
Paso 5 Para calcular la tensión del hilo
T aplicamos la segunda ley de Newton a
uno de los dos cuerpos. Por ejemplo al
número 1:
F1 = m1a
Siendo F1 la fuerza resultante sobre el
cuerpo 1, m1 la masa y a la aceleración
Autor: Manuel Díaz Escalera

10. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
F1 = m1a
P1 – T = m1a
Las fuerzas se restan ya que tienen
sentido contrario (P1 a favor del
movimiento y T se opone al movimiento)
Autor: Manuel Díaz Escalera

11. Tenemos dos cuerpos unidos por un hilo que pasa por la garganta de
una polea. Calcula la aceleración de los cuerpos y la tensión del hilo.
Datos: m1 = 250 gramos, m2 = 200 gramos, g = 9,8 m/s2
T T
P1
P2
Sustituimos los datos y calculamos la
tensión
P1 – T = m1a
2,45 – T = 0,25.1,09
T = 2,18 N
Autor: Manuel Díaz Escalera