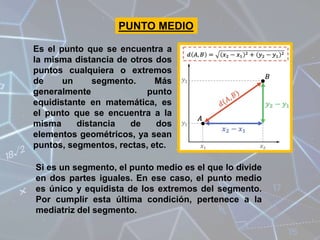
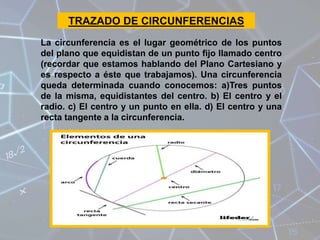
El documento presenta información sobre varios temas de geometría analítica como el plano cartesiano, distancias, puntos medios, ecuaciones de planos, trazado de circunferencias, parábolas, elipses, hipérbolas y representación gráfica de ecuaciones cónicas. Incluye ejemplos y ecuaciones para ilustrar cada concepto.

1. República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación
Universidad Politécnica Territorial “Andrés Eloy blanco”
Barquisimeto – Edo. – Lara
Alumna: Genesis Rodríguez
Sección: IN0114
Profesora: Wilmar Marrufo
PLANO NUMERICO

2. Se conoce también como
plano cartesiano,
coordenadas cartesianas
o sistema cartesiano, a
dos rectas numéricas
perpendiculares, una
horizontal y otra vertical,
que se cortan en un punto
llamado origen o punto
cero.
La finalidad del plano cartesiano es describir la
posición o ubicación de un punto en el plano, la cual
está representada por el sistema de coordenadas.
PLANO NUMERICO

3. La menor distancia entre dos puntos recorrida sobre la
superficie de una esfera es un arco de círculo máximo: la
ortodrómica. En las matemáticas, la distancia entre dos
puntos del espacio euclídeo equivale a la longitud del
segmento de la recta que los une, expresado numéricamente.
En espacios más complejos, como los definidos en la
geometría no euclidiana, el «camino más corto» entre dos
puntos es un segmento recto con curvatura llamada
geodésica. En física, la distancia es una magnitud escalar, que
se expresa en unidades de longitud.
DISTANCIA

4. Es el punto que se encuentra a
la misma distancia de otros dos
puntos cualquiera o extremos
de un segmento. Más
generalmente punto
equidistante en matemática, es
el punto que se encuentra a la
misma distancia de dos
elementos geométricos, ya sean
puntos, segmentos, rectas, etc.
Si es un segmento, el punto medio es el que lo divide
en dos partes iguales. En ese caso, el punto medio
es único y equidista de los extremos del segmento.
Por cumplir esta última condición, pertenece a la
mediatriz del segmento.
PUNTO MEDIO

5. ECUACIONES
La ecuación de un plano es una ecuación que permite
expresar matemáticamente cualquier plano. De modo que
para hallar la ecuación de un plano solo se necesita un
punto y dos vectores linealmente independientes que
pertenezcan a dicho plano.
(1) ECUACION VECTORIAL DE UN PLANO:
Dados un punto y dos vectores directores de un plano:
.

6. La formula de la ecuación vectorial de un plano es:
O, equivalentemente:

7. Se puede determinar a partir de su ecuación vectorial
Primero operamos y realizamos los productos de vectores por
los escalares:
2) ECUACIONES PARAMETRICAS DE UN PLANO:

8. Y, finalmente, conseguimos las ecuaciones paramétricas del
plano igualando las coordenadas correspondientes a cada
variable por separado:

9. se obtiene resolviendo el siguiente determinante e igualando el
resultado a 0:
De modo que la ecuación implícita o general del plano
resultante será de la siguiente forma:
(3) ECUACION IMPLICITA O CARTESIANA DE UN
PLANO:

10. La fórmula de la ecuación canónica o segmentaria de
un plano es la siguiente:
(4) ECUACION CANONICA O SEGMENTARIA DE UN
PLANO:

11. La ecuación canónica (o ecuación segmentaria) del
plano, también se puede obtener a partir de su
ecuación general:

12. Luego dividimos toda la ecuación del plano entre el valor
del parámetro D cambiado de signo:
Y, mediante las propiedades de las fracciones, llegamos a
la siguiente expresión:

13. En consecuencia, para poder formar esta variante
de las ecuaciones del plano es necesario que los
coeficientes A, B y C sean diferentes de cero,
evitando de esta manera las indeterminaciones de
las fracciones.
Por lo tanto, de esta expresión se deducen las
fórmulas para calcular directamente los
términos de la ecuación canónica o segmentaria
de un plano:

14. La circunferencia es el lugar geométrico de los puntos
del plano que equidistan de un punto fijo llamado centro
(recordar que estamos hablando del Plano Cartesiano y
es respecto a éste que trabajamos). Una circunferencia
queda determinada cuando conocemos: a)Tres puntos
de la misma, equidistantes del centro. b) El centro y el
radio. c) El centro y un punto en ella. d) El centro y una
recta tangente a la circunferencia.
TRAZADO DE CIRCUNFERENCIAS

15. Dados un punto FF (foco) y una recta rr (directriz), se
denomina parábola al conjunto de puntos del plano que
equidistan del foco y de la directriz. Simbólicamente:
P={P(x,y)|d(P,r)=d(P,F)} El eje focal es el eje perpendicular a la
directriz que pasa por el foco. Es el eje de simetría de la
parábola.
El punto de la parábola que pertenece al eje focal se llama
vértice. Para el esquema que realizamos, las coordenadas del
vértice sonV(0,0)V(0,0), las del foco F(c,0)F(c,0) y la recta
directriz está dada por r:x=–cr:x=–c.
Las coordenadas de un punto genérico QQ que pertenece a la
directriz son (– c,y)(–c,y).
PARABOLAS

17. La elipse es el lugar geométrico de los puntos del plano
cuya suma de distancias a dos puntos fijos llamados
focos es constante. Elementos de la elipse Focos Son
los puntos fijos F y F'. Eje focal Es la recta que pasa por
los focos. Eje secundario Es la mediatriz del segmento
FF'. Centro Es el punto de intersección de los ejes.
Radios vectores Son los segmentos que van desde un
punto de la elipse a los focos: PF y PF'.
ELIPSE

18. La hipérbola es el lugar geométrico de los puntos del
plano cuya diferencia de distancias a los puntos fijos
llamados focos es constante en valor absoluto. En la
gráfica anterior, esto significa que para cualquier punto
P de la Hipérbola Elementos de la hipérbola:
HIPERBOLA

19. Una superficie cónica esta engendrada por el giro de una
recta g, que llamamos generatriz, alrededor de otra recta e,
eje, con el cual se corta en un punto V, vértice. Elementos de
las cónicas Superficie - una superficie cónica de revolución
está engendrada por la rotación de una recta alrededor de
otra recta fija, llamada eje, a la que corta de modo oblicuo.
Generatriz - la generatriz es una cualquiera de las rectas
oblicuas. Vértice - el vértice es el punto central donde se
cortan las generatrices. Hojas - las hojas son las dos partes
en las que el vértice divide a la superficie cónica de
revolución. Sección - se denomina sección cónica a la curva
intersección de un cono con un plano que no pasa por su
vértice. En función de la relación existente entre el ángulo de
conicidad y la inclinación del plano respecto del eje del cono
pueden obtenerse diferentes secciones cónicas.
REPRESENTAR GRAFICAMENTE LAS
ECUACIONES DE LAS CONICAS

21. Basado en "Punto medio entre 2 puntos:
A( -6,8) B (2,4)
EJERCICICO DE PRACTRICA
EVALUACION

22. http://www.ehu.eus/juancarlos.gorostizaga/apoyo/geometr0.htm
https://www.profesorenlinea.cl/geometria/Ecuacion_Circunferenci
a.html
https://aga.frba.utn.edu.ar/parabola/
https://www.superprof.es/diccionario/matematicas/analitica/elipse
s.html
https://www.superprof.es/apuntes/escolar/matematicas/analitica/c
onica/hiperbola.html
https://www.superprof.es/apuntes/escolar/matematicas/analitica/c
onica/conicas.html
BIBLIOGRAFIAS
https://www.geometriaanalitica.info/ecuaciones-del-plano-
en-el-espacio/