Matematicas 1° 2012 2013

Matemáticas I
TS-matematicas1.indb 1 17/04/12 16:35
Versióndeevaluación23/04/12

Matemáticas I. Telesecundaria fue elaborado por la Dirección General de Materiales Educativos (dgme) de la Subsecretaría de Educación Básica,
Secretaría de Educación Pública.
Coordinación técnico-pedagógica
Dirección de Desarrollo e Innovación de Materiales Educativos,
dgme/sep
María Cristina Martínez Mercado, Gabriel Calderón López,
Alexis González Dulzaides
Autores
Diana Karina Hernández Castro, José Alfredo Rutz Machorro,
Citlali Yacapantli Servín Martínez, Eladio Escobedo Trujillo,
Francisco Ángel Vela Sánchez, Leonardo Jiménez Hernández,
Adriana Rodríguez Domínguez, Olga Leticia López Escudero,
Manuel García Minjares, Jesús Manuel Hernández Soto, Víctor Manuel
García Montes, Ana María López Avilés, Mauricio Héctor Cano Pineda,
Jesús Miguel Buendía Solorio
Revisión técnico-pedagógica
Ángel Daniel Ávila Mujica
Coordinación editorial
Dirección Editorial dgme/sep
Alejandro Portilla de Buen, Olga Correa Inostroza
Cuidado editorial
Anne Alberro Semerena
Producción editorial
Martín Aguilar Gallegos
Primera edición, 2012 (ciclo escolar 2013-2014)
D.R. © Secretaría de Educación Pública, 2012
Argentina 28, Centro,
06020, México, D.F.
ISBN: 978-607-514-022-3
Impreso en México
Distribución gratuita-Prohibida su venta
Servicios editoriales
Rocío Mireles Gavito
Diseño y diagramación
Rocío Mireles Gavito, Bruno Contreras, Fernando Villafán
Investigación iconográfica
Cynthia Valdespino, Erandi Alvarado
Corrección de textos
Eduardo Méndez Olmedo
Ilustraciones
Leonardo Olguín Landa (pp. 20b, 73, 75, 83, 107, 129, 159, 169, 180,
183, 184, 185, 191c, 194, 203, 211, 212, 220, 244, 250, 259).
Créditos iconográficos
Adam Wiseman (p. 239); Bruno Contreras (pp. 27, 28, 50, 53, 57, 59,
60, 147, 191b, 214-216, 271a); Cynthia Valdespino (pp. 8, 12, 14, 63,
78, 81, 93, 96, 99, 118, 119, 131, 134, 157, 160, 164, 176, 189, 207,
227, 234); Fernando Villafán (pp. 20a, 33, 62, 67, 166, 191a, 210, 242,
278); Rocío Mireles Gavito (pp. 98, 243); iStockphoto (pp. 22, 23, 29,
66, 71, 88, 94, 101, 103, 104, 105, 124, 128, 150, 151, 162, 175, 208,
248, 249, 252, 271, 279, 282)
TS-MATE-1-LEGAL.indd 2 25/04/12 14:44

Presentación institucional
Presentación
En el marco del Acuerdo 592, por medio del cual se establece la Articulación
de la Educación Básica, así como del Acuerdo 593 que señala los programas
de estudio de la asignatura de Tecnología para la educación secundaria, la
Secretaría de Educación Pública ha consolidado una propuesta de libros de
texto, a partir de un nuevo enfoque centrado en la participación de los alumnos
en su proceso de aprendizaje y en el desarrollo de las competencias básicas
para la vida y el trabajo. Especialmente en el contexto de la Telesecundaria,
el libro de texto se complementa con las Tecnologías de la Información
y Comunicación (tic), con los objetos digitales de aprendizaje, los materiales y
equipos audiovisuales e informáticos que, junto con las bibliotecas escolares,
representan el soporte pedagógico de los niños mexicanos en su proceso de
adquisición del conocimiento escolarizado.
Esta nueva generación de libros de texto para Telesecundaria responde al
principiodemejoracontinua,porloquehapuestoatenciónenelreplanteamiento
de las cargas de contenido para centrarse en estrategias innovadoras para el
trabajo escolar, incentiva habilidades orientadas al aprovechamiento de distintas
fuentes de información, busca que los estudiantes adquieran habilidades para
aprender de manera autónoma incentivando el uso intensivo de la tecnología
informática. Asimismo, con la intención de dar continuidad a la propuesta
editorial iniciada en los libros de texto de primaria, en este libro se ha fortalecido
la línea editorial que promueve una lectura integral capaz de interpretar tanto
el discurso textual como el visual. Se ha incluido en sus páginas una muestra
representativa de géneros y técnicas plásticas, así como propuestas iconográficas
que no sólo complementan el contenido textual, sino lo enriquecen y conforman
por sí mismos una fuente de información para el alumno.
En la preparación de este libro confluyen numerosas acciones de colaboración
de organismos y profesionales, entre los que destacan asociaciones de padres
de familia, investigadores del campo de la educación, instituciones evaluadoras,
maestros, editores y expertos en diversas disciplinas. A todos ellos la Secretaría
de Educación Pública les extiende un agradecimiento por el compromiso
demostrado con cada niño residente en el territorio nacional y con aquellos
mexicanos que se encuentran fuera de él.
Secretaría de Educación Pública

Bloque 2
Bloque 1
Índice
Conoce tu libro 6
8
Secuencia 1 De fracción a número decimal 10
Secuencia 2 Fracciones y decimales en la recta 18
Secuencia 3 Sumas y restas de fracciones 26
Secuencia 4 Sucesiones de números y figuras 31
Secuencia 5 Literales en fórmulas geométricas 40
Secuencia 6 Trazo de triángulos y cuadriláteros 50
Secuencia 7 Alturas, medianas, mediatrices y bisectrices en los triángulos 56
Secuencia 8 Reparto proporcional 62
Secuencia 9 Juegos de azar 68
78
Secuencia 10 Criterios de divisibilidad 80
Secuencia 11 MCD y mcm 88
Secuencia 12 Sumas con fracciones y decimales 93
Secuencia 13 Multiplicación y división con fracciones 98
Secuencia 14 Propiedades de la mediatriz y bisectriz 106
Secuencia 15 Fórmulas para calcular área y perímetro 112
Secuencia 16 Proporcionalidad directa 118

Bloque 5
Bloque 4
Bloque 3 124
Secuencia 17 Multiplicación con decimales 126
Secuencia 18 División con decimales 130
Secuencia 19 Ecuaciones de primer grado 134
Secuencia 20 Construcción de polígonos regulares 142
Secuencia 21 Cálculo de área y perímetro 149
Secuencia 22 Factor de proporcionalidad 154
Secuencia 23 Registro de una experiencia aleatoria 162
Secuencia 24 Análisis de frecuencia absoluta y relativa 170
178
Secuencia 25 Números positivos y negativos 180
Secuencia 26 El círculo y cómo construirlo 189
Secuencia 27 Pi en el círculo 196
Secuencia 28 Regla de tres 203
Secuencia 29 Proporcionalidad utilizando escala 210
Secuencia 30 Problemas de conteo 214
Secuencia 31 Tipos de gráficas 225
234
Secuencia 32 Sumas y restas con enteros 236
Secuencia 33 Notación exponencial 244
Secuencia 34 Raíz cuadrada 252
Secuencia 35 Sucesiones con progresión aritmética 262
Secuencia 36 Área y perímetro del círculo 269
Secuencia 37 Proporcionalidad múltiple 278
Hoja para las familias 284

6
Bloque 1
• Convertir números fraccionarios a decimales y viceversa.
• Conocer y utilizar las convenciones para representar
números fraccionarios y decimales en la recta numérica.
• Representar sucesiones de números o de figuras a partir
de una regla dada y viceversa.
TS_MAT1_B1_S01.indd 8-9 3/21/12 11:46 AM
Bloque 2
• Resolver problemas utilizando el máximo común divisor
y el mínimo común múltiplo.
• Resolver problemas geométricos que impliquen
el uso de las propiedades de las alturas, las medianas,
las mediatrices y las bisectrices en triángulos
y cuadriláteros.
TS_MAT1_B2_S10.indd 78-79 3/21/12 11:47 AM
Bloque 3
• Resolver problemas en los que se tengan que efectuar
multiplicaciones y/o divisiones con fracciones y números
decimales.
• Resolver problemas que impliquen el uso de ecuaciones
de las formas: x + a = b; ax = b y ax + b = c, donde
a, b y c son números naturales y/o decimales.
• Resolver problemas que impliquen el cálculo de
cualquiera de las variables de las fórmulas para encontrar
el perímetro y el área de triángulos, cuadriláteros y
polígonos regulares. Explicar la relación que existe entre
el perímetro y el área de las figuras.
TS_MAT1_B3_S17.indd 124-125 3/21/12 11:47 AM
Bloque 4
• Construir círculos y polígonos regulares que cumplan con
ciertas condiciones establecidas.
• Leer información presentada en gráficas de barras
y circulares. Utilizar estos tipos de gráficas para
comunicar información.
TS_MAT1_B4_S25.indd 178-179 3/21/12 11:47 AM
Bloque 5
• Resolver problemas aditivos que impliquen el uso de
números enteros, fraccionarios o decimales positivos
y negativos.
• Resolver problemas que impliquen el cálculo de la raíz
cuadrada y potencias de números naturales y decimales.
• Resolver problemas de proporcionalidad directa del tipo
“valor faltante”, en los que la razón interna o externa es
un número fraccionario.
TS_MAT1_B5_S32.indd 234-235 3/21/12 11:48 AM
Has estudiado Matemáticas durante toda la primaria. Ahora que inicias la se-
cundaria, uno de los propósitos del plan de estudios es que uses lo que ya sa-
bes para aprender los nuevos conocimientos que te serán presentados. Tu
profesor, con el apoyo de este libro y con el uso de algunos recursos tecnológi-
cos, te ayudará a que lo logres.
Lo primero será conocer tu libro y familiarizarte con los elementos que lo forman.
Tu libro de Matemáticas consta de cinco bloques. Cada uno contiene varias secuencias de
aprendizaje. En cada secuencia estudiarás un tema del programa de Matemáticas a través de
varias sesiones. Una sesión está diseñada para que la trabajes en una clase, aunque en oca-
siones será necesario que le dediques un poco más de tiempo.
Conoce tu libro

7
En cada secuencia de aprendizaje podrás encontrar los apartados siguientes:
196
Secuencia27
Pi en el círculo
Justificación de la fórmula para calcular la longitud
de la circunferencia y el área del círculo (gráfica
y algebraicamente). Explicación del número π (pi)
como la razón entre la longitud de la circunferencia
y el diámetro.
Sesión 108
En esta sesión medirás el perímetro de una circunferencia.
 ¿Qué sabes tú?
Observa la siguiente imagen.
Formen parejas y propongan cómo calcular la longitud de la circunferencia (perímetro) y el área
del círculo de la imagen anterior.
¿Qué métodos se les ocurrieron y qué resultados obtienen utilizándolos?
círculo
circunferencia
radio
diámetro
B3
176
Sesión 98
Evaluación
Aplica lo aprendido y selecciona la respuesta correcta a cada problema.
1. Jacinto requiere comprar 150.45 dólares para pagar un artículo que se ofrece en una tienda
en internet. ¿Cuántos pesos debe juntar para poder pagar, si el tipo de cambio está en
$14.30?
a) $ 2 152.534
b) $ 2 152.354
c) $ 2 152.435
d) $ 2 152.4035
2. Considera la ecuación 9x = 270.
¿Cuál de los siguientes problemas se puede resolver con la ecuación anterior?
a) El volumen de un eneágono regular mide 270 cm.
b) El área de un eneágono regular mide 270 cm.
c) El perímetro de un eneágono regular mide 270 cm.
d) El perímetro de un eneágono irregular mide 270 cm.
3. Un corredor tarda cierta cantidad de minutos para recorrer diferentes distancias, como se
muestra en la tabla.
Tiempo (minutos) 21 min 42 min 55 min 84 min
Distancia 7 km 14 km 28 km
Si corre durante 55 minutos, ¿qué distancia recorrió?
a) 15.00 km
b) 20 km
c) 18.33 km
d) 22 km
4. Un rollo higiénico contiene 43.7 metros de papel. Si cada hoja mide 10.4 cm, ¿cuántas
hojas higiénicas contiene el rollo?
a) 300.23
b) 499.10
c) 400.51
d) 420.19
5. ¿En cuál d
2 cm
6. En una ca
2 amarillos
a) Hay má
b) Hay má
c) Hay má
d) Hay má
La siguiente
de energía elé
4 casas duran
7. ¿En qué m
gía eléctric
a) Enero
b) Febrero
c) Diciemb
d) Marzo
9. ¿Qué políg
a) Dodecá
b) Undecá
c) Pentad
d) Icoságo
TS_MAT1_B3_S24.indd 176-177
B1
76
3. Comparen sus resultados con los obtenidos por otras parejas que seleccionaron la misma
bolsa. ¿Obtuvieron los mismos resultados?
Si algún equipo eligió la bolsa 4, pregúntenle ¿cuál fue el color de canica que más veces salió?
¿Por qué consideran que se obtuvieron esos resultados?
¿Consideran que inﬂuye el hecho de que hay igual número de canicas azules que de blancas?
Al considerar todos los resultados que obtuvieron en el grupo, ¿qué color ha salido con más
frecuencia?
¿Se puede saber el color de la canica que sale en una extracción?
Comparen los cálculos que hicieron y vean quiénes se acercaron más.
Si el juego se gana cuando se saca más veces una canica azul, ¿qué bolsa conviene elegir?
Autoevaluación
Responde lo siguiente.
1. Describe un juego que sea de azar.
2. Si se lanza una canica por cada laberinto, ¿en cuál de ellos es más probable que salga la
canica por la salida 1?
a)
1 1 112 2 223 33 4
b) c) d)
En los juegos de azar no podemos predecir quién ganará porque no se puede controlar los resultados. Sin
embargo, al registrar y analizar sus resultados podemos encontar alguna estrategia de juego.
TS_MAT1_B1_S09.indd 76 16/04/12 18:53
B4
230
Sesión 129
En esta sesión resolverás problemas utilizando gráficas circulares.
 Manos a la obra
1. La siguiente información se refiere a la distribución porcentual de horas a la semana que los
integrantes del hogar de 12 y más años de edad dedican a actividades de esparcimiento.
Convivencia social
Asistencia a eventos
culturales, deportivos
y de entretenimiento
Deportes y ejercicio físico
Participación en juegos
y aficiones
Utilización de medios
masivos de comunicación
59.0
4.2
2.1
6.7
28.1
Fuente: INEGI, Encuesta Nacional de Uso del Tiempo 2009.
¿A qué actividad le dedican más tiempo?
¿A qué actividad le dedican menos tiempo?
A la gráfica circular se le llama también “de pastel”, o diagrama de sectores, y se
construye empleando la frecuencia relativa (fracción o número decimal) de cada dato.
Al sumar los porcentajes de todos los sectores siempre da como resultado 100%.
Consulta en…
Explora los siguientes sitios para conocer otras interesantes gráficas de estadísticas:
<http://eleconomista.com.mx/industrias/2012/01/26/buen-fin-impulsa-ventas-minoristas-mexico>
<http://revistadelconsumidor.gob.mx/wp-content/uploads/2011/05/estudio-cereales2.pdf>
<http://revistadelconsumidor.gob.mx/wp-content/uploads/2011/11/bebidas-hidratantes.pdf>
<http://cuentame.inegi.org.mx/poblacion/default.aspx?tema=P>
<http://www.imcine.gob.mx/informes-y-estadsticas.html>
B2 S14
110 111
La bisectriz de un ángulo es la recta que lo divide en dos
ángulos iguales.
También es el lugar geométrico de los puntos del plano que
están a la misma distancia (equidistan) de las semirrectas
de un ángulo.
Sólo en un triángulo equilátero la bisectriz de sus tres
ángulos internos es también la mediatriz de los lados
opuestos.
Sesión 60 Sesión 61
En esta sesión continuarás aplicando las propiedades
de la bisectriz de un ángulo.
Formen equipos, analicen el siguiente problema y contesten.
Un dato interesante…
Un problema que interesó durante mucho tiempo a los griegos fue trisecar (dividir en tres
ángulos iguales) un ángulo, utilizando sólo regla y compás. En el siglo XIX se demostró que
esto es imposible.
Elige un punto sobre la primera bisectriz trazada, y con
ayuda de tus escuadras dibuja rectas perpendiculares de
este punto a los lados del ángulo. Mídelas.
¿Qué observas?
En grupo, y con ayuda de su profesor, concluyan las pro-
piedades de la bisectriz que utilizaron en la solución y tra-
zo de esta situación.
Dibujen en su cuaderno tres ángulos de diferentes tama-
ños y amplitudes, tracen la bisectriz a cada uno y señalen
con color rojo las partes en las que se observen las propie-
dades de dicho lugar geométrico.
En la figura de la derecha podemos observar un triángulo
rectángulo. Si el segmento BC representa el pilar central
de un puente, el segmento AB el tirante principal, y se
pretenden colocar tres tirantes más que salgan del vérti-
ce B dividiendo al ángulo en partes iguales, ¿en qué pun-
tos deben colocarse los extremos de los tirantes sobre
el puente?
b
c
a
A
B
C
¿En cuántas partes es necesario dividir el ángulo B para
colocar las tres cuerdas?
¿Los extremos sobre el segmento “b” quedan a la misma
distancia uno del otro?
¿Cuántas veces se puede dividir un ángulo?
En esta sesión resolverás distintos problemas geométricos que implican el uso de
las propiedades de la mediatriz de un segmento y de la bisectriz de un ángulo.
1. Resuelve lo siguiente.
a) Une los puntos y traza la mediatriz al segmento PQ.
b) Traza los ejes de simetría de cada figura. Marca con
un color los que, además de ser ejes de simetría,
también sean mediatrices de algún lado de las figu-
ras, y con otro color los que sean bisectrices de
algún ángulo de las figuras.
c) Encuentra un punto que esté a la misma distancia
de los tres lados del siguiente triángulo (pista: re-
cuerda que cualquier punto de la bisectriz de un
ángulo está a la misma distancia de los dos lados
que lo forman).
 Autoevaluación
Traza en tu cuaderno un segmento, su mediatriz, marca dos puntos sobre ella y traza con
color rojo las distancias de los puntos a los extremos del segmento. Define la propiedad.
Traza en tu cuaderno un ángulo, su bisectriz, marca puntos sobre la bisectriz y traza con
color rojo las distancias de los puntos a los lados del ángulo. Define la propiedad.
Consulta en…
Para conocer más sobre este tema busca en las bibliotecas escolares y de aula el siguiente
libro: Carlos Bosch y Claudia Gómez, “Construcciones básicas” y “Paralelas con doblado de
papel”, en Una ventana a las formas, México, sep-Santillana, 2003 (Libros del Rincón).
P Q
TS_MAT1_B2_S14.indd 110-111 3/21/12 11:49 AM
B4
200
Sesión 111
En esta sesión encontrarás una fórmula para calcular el área de un círculo.
Lleva a cabo las siguientes actividades.
1. Observa la imagen.
Mide y calcula el perímetro y el área de los polígonos. Anótalos abajo de cada uno.
¿Qué sucede con los perímetros conforme aumenta el número de lados del polígono?
¿Y con el área?
¿Qué relación hay entre el perímetro de los polígonos y el perímetro de la circunferencia?
¿Qué relación hay entre el área de los polígonos y el área del círculo?
2. En equipos, analicen las construcciones de la sesión anterior.
Evaluación
Se te presentarán tanto ejercicios como
problemas en los que podrás elegir la
respuesta correcta entre cuatro opcio-
nes, aunque en algunos casos tendrás
que escribir una respuesta breve.
Consulta en…
Son sugerencias para que revises otros ma-
teriales, de modo que puedas ampliar y
ejercitar tus aprendizajes por medio de vi-
deos, libros de la biblioteca y sitios de in-
ternet, entre otros.
En cada bloque encontrarás:
Es una información curiosa y a veces poco
conocida.
 Autoevaluación
Su propósito es que valores los aprendi-
zajes, tanto de conocimientos como de
habilidades, que desarrollaste durante la
secuencia, contestando una pregunta o
completando alguna información.
Inicia con una breve introducción, la cual continúa
con una actividad en la que hallarás preguntas que
te ayudarán a construir tu conocimiento y a analizar
lo que estés aprendiendo. Algunas veces trabajarás
individualmente y otras en equipo o con todo el gru-
po. En esta sección también encontrarás las conclu-
siones sobre los conceptos estudiados.
Es una actividad que te permitirá diagnosticar
y rescatar las ideas previas. Aquí se relaciona
el nuevo conocimiento que aprenderás con
algo que ya hayas estudiado.

Bloque 1

• Convertir números fraccionarios a decimales y viceversa.
• Conocer y utilizar las convenciones para representar
números fraccionarios y decimales en la recta numérica.
• Representar sucesiones de números o de figuras a partir
de una regla dada y viceversa.

10
Secuencia 1
De fracción
a número decimal
Conversión de fracciones decimales y no decimales
a su escritura decimal y viceversa.
Sesión 1
En esta sesión identificarás lo que es una fracción decimal.
Reúnete con un compañero y organicen en la tabla las fracciones siguientes, considerando si
son decimales o no.
3
4
3
7
1
2
3
10
5
9
31
100
1
6
5
8
23
1000
92
10
4
11
Fracciones decimales Fracciones no decimales
Escriban en la tabla dos ejemplos más en cada columna.
Comenta con tu compañero cómo establecieron cuáles son las fracciones decimales.
Recuerda que toda expresión de la forma a
b
,
donde b es diferente de cero, recibe el
nombre de fracción común.

11
1. Junto con tu compañero, revisen la tabla donde clasificaron las fracciones.
Contesten lo siguiente:
Las que se encuentran en la columna denominada fracciones decimales, ¿son también
fracciones comunes?
Observen las fracciones siguientes:
3
10
31
100
23
1000
¿Qué pueden comentar sobre los denominadores?
2. En equipos, contesten lo que se les pide.
Escriban una fracción decimal que sea equivalente a 2
5
=
¿Cómo obtuvieron esa fracción decimal equivalente?
Encuentren una fracción decimal que sea equivalente a 2
3
=
¿Pudieron obtenerla?
¿Por qué?
Completen el siguiente enunciado:
Una fracción común puede expresarse como fracción decimal cuando…
A las fracciones comunes que tienen
como denominador una potencia de
10, es decir 10, 100 y 1 000… se les
conoce como fracciones decimales.

B1
12
Sesión 2
En esta sesión representarás fracciones comunes en su notación decimal.
1. En parejas, resuelvan el problema siguiente.
Adrián compró cuatro carretes de listón de 15 m cada uno, necesita hacer moños de dife-
rentes tamaños y para ello cortará un carrete en 10 trozos iguales, un segundo en 30, el
tercero en 5 y el cuarto en 2.
¿Cuánto medirá cada trozo?
Del primer carrete Del segundo carrete
Del tercer carrete Del cuarto carrete
¿Cómo determinaron lo que debe medir cada tramo de listón?
¿Realizaron alguna operación?
¿Cuál?
¿Cuáles trozos se pueden representar con una fracción decimal?
2. En equipos, realicen las divisiones que indican las fracciones comunes siguientes. Aproxi-
men sus resultados a dos o tres cifras decimales.
a) 4
5
= b) 3
10
= c) 21
4
= d) 35
100
=
e) 5
7
= f) 4
9
= g) 7
15
= h)
3
2 =
Pongan atención en los residuos de las divisiones que efectuaron y contesten lo siguiente:
¿En cuáles casos pudieron calcular el cociente exacto, es decir, obtuvieron como residuo 0?
¿Qué observan en los cocientes donde no se obtuvo residuo 0?
Con la participación de todo el grupo y con la guía de su profesor concluyan cómo
obtener la notación decimal de una fracción común. Anótalo en tu cuaderno.
En algunas ocasiones, las fracciones comunes
representan divisiones como en el problema
anterior, donde el numerador es el dividendo
y el denominador es el divisor, esto es
n
d
= d n
Una fracción se puede
escribir también con nota-
ción decimal.

S1
13
En esta sesión obtendrás la representación de números decimales como
fracciones comunes.
Sesión 3
Al dividir ciertos números enteros entre una potencia de 10 (por ejemplo 10, 100 o 1 000)
Noemí obtuvo los siguientes cocientes: 0.4, 0.45, 0.125, 0.564, 2.6 y 13.567. Indiquen un
posible divisor y un posible dividendo correspondiente a cada cociente.
Cociente 0.4: divisor , dividendo
Comparen sus respuestas con las de otros equipos.
Obtengan las fracciones decimales correspondientes a las divisiones anteriores.
2. En parejas, contesten las preguntas siguientes.
a) En una clase de telesecundaria Martín dice que 0.4 corresponde a 4
10
, y Héctor que a 2
5
.
¿Quién de los dos tiene la razón?
b) Salvador afirma que 0.45 corresponde a 9
20
, y Guadalupe que a 45
100
.
¿Quién de los dos está en lo correcto?
¿Sonequivalenteslasfracciones 9
20
y 45
100
? ¿Porqué?
c) Rosa dijo que al transformar ciento veinticinco milésimas a una fracción decimal y sim-
plificarla, obtuvo 1
8
. ¿Es correcto lo dicho por Rosa?
Expliquen brevemente por qué.
d) ¿Cómo se convierte un número decimal a fracción?
e) Describe en tu cuaderno cómo se puede simplificar una fracción a su mínima expresión.
Comparen sus respuestas con las de otras parejas y con ayuda del profesor determinen un
procedimiento para escribir un número decimal como fracción común representada en su
mínima expresión.

B1
14
3. Relacionen los números decimales con su respectiva fracción.
0.9
0.58
0.276
0.75
0. 840
a) 69
250
b) 3
4
c) 21
25
d) 9
10
e) 29
50
4. Resuelvan los siguientes problemas.
a) Víctor pidió 1 3
4
kg de tortillas, el encargado colocó en su báscula digital una pila de
tortillas y en la pantalla apareció 1.750 kg. Expliquen si le despacharon correctamente
o no las tortillas a Víctor.
b) La mamá de Rubén quiere cambiar en el banco unos cheques que le dieron, por las si-
guientes cantidades:
Ya en la ventanilla, la cajera le dijo que una cantidad está mal representada.
¿Cuál es la cantidad incorrecta?
Expliquen en su cuaderno por qué.
Comenta con tu grupo y con tu profesor un procedimiento que permita representar un
número decimal como fracción común.
Su Banco Fecha:
Pague por este cheque a: $
CHEQUE 0000101 Firma
15 de agosto 2013
Luz María Archundia 2 538. 68
Dos mil quinientos treinta y ocho pesos 68
100
M.N.
Su Banco Fecha:
10 de agosto 2013
Luz María Archundia 561. 220
Quinientos sesenta y un pesos
220
100
M.N.
Su Banco Fecha:
11 de agosto 2013
Luz María Archundia 5 000. 06
Cinco mil pesos
6
100
M.N.

S1
15
En esta sesión representarás números decimales como
fracciones no decimales.
Sesión 4
1. Reúnete con dos compañeros para realizar lo que se plantea a continuación.
a) Sumen el número que quieran en ambos lados de la siguiente igualdad:
8 = 6 + 2
Expliquen brevemente en su cuaderno por qué el resultado es otra igualdad.
b) Resten el número que quieran en ambos lados de la siguiente igualdad:
750 = 500 + 250
c) Multipliquen por el número que quieran en ambos lados de la siguiente igualdad:
15 = 20 − 5
d) Dividan entre el número que quieran distinto de 0, en ambos lados de la
siguiente igualdad:
1000 = 500 × 2
Después de haber conocido algunas propiedades de las igualdades, las cua-
les usarás en este tema de fracciones, retoma el estudio sobre cómo repre-
sentar las fracciones en su forma común o decimal.
2. Con tu mismo equipo, identifiquen un decimal o un grupo de decimales (periodo) que se
repiten varias veces en los cocientes siguientes y enciérrenlo con color rojo.
2
9
= 0.2222… 3
11
= 0.27272727… 41
333
= 0.123123123123… 1
6
= 0.16666…
Al expresar una fracción común en su forma decimal, en ocasiones el cociente se repite
indefinidamente, se dice entonces que el cociente es periódico y esto se representa colo-
cando un segmento sobre dicho periodo. Por ejemplo,
2
9
= 0.2 3
11
= 0.27 41
333
= 0.123 1
6
= 0.16
De los números decimales anteriores:
a) ¿Cuál es el decimal periódico del primer cociente?
b) ¿Cuál de las fracciones tiene un cociente periódico de tres dígitos?
Cuando se tiene una igualdad,
al operar en ambos lados de
ésta con un mismo número,
sumando, restando, multipli-
cando o dividiendo se obten-
drá otra igualdad.

B1
16
3. Continúa con tu equipo para analizar el siguiente procedimiento que permite obtener la
fracción común de los números decimales periódicos.
Se quiere encontrar la fracción común correspondiente al número decimal 0.3
Como no se conoce la fracción, se dejará el espacio, representado por un cuadrado.
Para encontrar cuánto vale se iguala con el número decimal periódico:
= 0.3 Se multiplican ambos términos de la igualdad por 10 para tener una
nueva igualdad, porque el periodo está formado por un decimal que
se repite. Si el periodo tuviera dos dígitos que se repiten, se multipli-
caría por 100, si tuviera 3 por 1 000, y así consecutivamente.
Entonces:
= 0.333 1
10 × = 10 × 0.333
10 × = 3.333 2
Para eliminar los decimales periódicos se resta la igualdad 1 de la igualdad 2 :
10 × − = 3.333 − 0.333
9 × = 3
Se dividen entre nueve los dos lados de la igualdad para dejar al sólo de un lado de la igualdad:

9 ×
9 = 3
9
Entonces, como 9
9
= 1 se tiene:
= 3
9
Esto quiere decir que, 0.3 = = 3
9
Como 3
9
se puede expresar como 1
3
, se concluye que 0.3 = 1
3
4. Identifiquen el decimal periódico de los números decimales siguientes y con el procedi-
miento anterior obtengan las fracciones comunes correspondientes.
a) 0.6666...
b) 0.36363636...
c) 0.135135135135135...

S1
17
Consulta en…
Busca en las bibliotecas escolares y de aula el siguiente libro para conocer más sobre el
tema: Luz María Marván, “Escritura decimal infinita” y “Otros símbolos para números no
enteros”, en Representación numérica, México, SEP-Santillana, 2003 (Libros del Rincón).
Entra al sitio: http://www.thatquiz.org/es-e/matematicas/fracciones/reducir/. Elige en el
recuadro de la izquierda las opciones “Fracción a decimal” y “Decimal a fracción”. Selecciona
el nivel en el que quieras practicar estas conversiones.
 Autoevaluación
Escribe en tu cuaderno lo siguiente.
• Un procedimiento para expresar una fracción común como número decimal.
• Un procedimiento para expresar un número decimal como fracción común.
5. En equipos, contesten lo siguiente.
a) ¿Qué tipo de fracción da como resultado un número decimal periódico?
b) ¿Cuál es el denominador de las fracciones que obtuvieron en cada inciso del ejercicio
anterior?
c) ¿Qué relación encuentran entre la cantidad de nueves que tiene el denominador y la
cantidad de cifras que tiene el periodo?
d) Si se expresan 0.3 y 0.3 como fracción común, ¿se obtiene la misma fracción?
¿Por qué?
Comparen sus resultados y sus respuestas con otros equipos.
6. Relaciona ambas columnas escribiendo den-
tro del paréntesis la letra que corresponda.
( ) 0.7
( ) 0.45
( ) 0.405
a) 5
11
b) 15
37
c) 7
9

18
Secuencia 2
Fracciones y decimales
en la recta
Representación de números fraccionarios
y decimales en la recta numérica a partir
de distintas informaciones, analizando
las convenciones de esta representación.
Sesión 5
En esta sesión aprenderás que en la recta numérica se pueden representar
números enteros, fracciones comunes y decimales, lo cual es muy útil porque
permite comparar números o comprobar equivalencias.
Gradúa las siguientes rectas numéricas según se te indique, es decir, marca las partes que
corresponden a cada división.
En cuartos.
0 1
En quintos.
0 1
En décimos.
0 1

19
1. En equipos de a lo más tres integrantes, escriban los números que hagan falta para com-
pletar la graduación de cada recta.
a)
0 2
10
5
10
9
10
b)
0 0.3 0.8
c)
0 0.4 5
10
0.9
2. Expliquen por qué en una recta se pueden ubicar tanto fracciones comunes como decimales.
3. En la siguiente recta escriban la fracción común o el número decimal correspondiente al
punto donde se ubica cada letra.
0 a c b = 1
2
d
Ahora comenten qué es lo que deben considerar para representar en una recta numérica
una fracción común y un número decimal.

B1
20
Sesión 6
En esta sesión observarás cómo se puede representar en la recta numérica
una fracción si se conoce la ubicación de otro par de fracciones.
1. En una escuela telesecundaria realizaron
competencias atléticas para conmemo-
rar el 40 aniversario de su fundación.
En la tabla se muestran las tres mejores mar-
cas obtenidas en salto de longitud por distin-
tos alumnos:
En la siguiente recta se ha representado el
salto de Erik López.
4 4 3
5
Reúnete con un compañero y representen en la recta anterior los saltos de los otros dos
alumnos.
Considerando que el ganador es el que realizó el salto más largo, ¿cómo otorgarías las
medallas?
Alumno Longitud aproximada del salto (metros)
Juan Godínez 4 1
2
José Sandoval 4 2
3
Erik López 4 3
5

S2
21
2. En parejas, ubiquen en la siguiente recta los números 7
3
, 1
3
, 12
6
, 0, 1 1
6
y 2
5
.
5
6
1
¿Qué hicieron para ubicar el 0?
¿Cuántos sextos se representan en la marca de 1
3
?
¿Qué otro número representa 12
6
?
¿Qué hicieron para ubicar a 2
5
?
Comparen sus respuestas con las de otros equipos y escriban en su cuaderno un procedi-
miento que les permita ubicar cualquier fracción cuando se tienen como referencia otras
dos fracciones.
3. Localiza las fracciones que se indican en cada inciso.
a) En la siguiente recta numérica ubica las fracciones 2
3
, 7
9
y 9
6
.
0 1
3
4
6
b) En la siguiente recta numérica ubica el 0 y las fracciones 3
2
, 3
10
y 11
5
.
2
5
c) En la siguiente recta numérica ubica las fracciones 1
4
, 3
5
y 5
12
.
1
3
1
2
Comenta con un compañero qué deben hacer cuando en una recta hay previamente locali-
zadas al menos dos fracciones que no tienen un denominador común y se desea ubicar otra.

B1
22
Sesión 7
En esta sesión representarás números decimales en la recta numérica.
1. En parejas, completen la graduación de las siguientes rectas.
a)
5 5.5 6

¿Cuánto representa cada segmento de la recta?
b)
7.2 7.24 7.29 7.3

¿Cuánto representa cada segmento de la recta anterior?
2. En parejas, lean la información siguiente y realicen lo que se indica.
Entre las competencias atléticas, la carrera de 100 m planos es considerada la reina de las
pruebas. Para determinar quién es el ganador se requiere manejar números decimales. Para
tal efecto, consideren la siguiente tabla de resultados obtenidos por las tres alumnas más
rápidas en las competencias conmemorativas del aniversario de su telesecundaria.
Alumna Tiempo (en segundos)
Ana Juárez 13.6
Sonia Martínez 13.3
Claudia Pérez 13.4
Ubiquen cada una de las marcas en la recta numérica siguiente.
12 14

S2
23
3. Lee la siguiente situación y realiza lo que se pide.
En la escuela también se hizo un torneo de salto de altura, en la tabla de abajo se registra-
ron los diez mejores saltos.
Competidor Altura del salto (m) Competidor Altura del salto (m)
Braulio 1.43 Alexa 1.55
Efrén 1.50 Antonia 1.43
Teresa 1.45 Jesús 1.49
Daniel 1.48 Emmanuel 1.54
Reyna 1.51 Aline 1.40
a) Ubica en la recta numérica los saltos registrados.
1.3 1.7
b) Contesta las preguntas.
¿Por qué la recta numérica no inicia en 0?
Para ubicar saltos como 1.45, 1.48 y 1.49, ¿en cuántas partes se tendrá que dividir el
espacio que hay entre 1.4 y 1.5?
c) Compara tus resultados con los de tus compañeros de grupo y contesten.
¿Hay saltos que estén ubicados en el mismo lugar en la recta numérica?
Andrea dice que 1.06 y 1.60 se ubican en el
mismo punto de la recta. Expliquen si es co-
rrecta o no la afirmación de Andrea.
¿Qué otro decimal se ubica en el punto 1.5?
1.5 1.51 1.52 1.53 1.54 1.55 1.56 1.57 1.58 1.59 1.6
1.52 1.521 1.522 1.523 1.524 1.525 1.526 1.527 1.528 1.529 1.530
1.4 1.5 1.6
Para ubicar números decimales en la recta, como
1.5, 1.52, 1.524, etcétera, es necesario dividir cada
segmento en 10 partes iguales y cada una de éstas
en otras 10, y así sucesivamente.

B1
24
Consulta en…
Entra al sitio: http://miayudante.upn.mx/ficha.html?rgrado=5rconsul=4numfich=42,
ahí encontrarás más información sobre la ubicación de números en la recta numérica.
Sesión 8
En esta sesión continuarás trabajando con la ubicación de fracciones
y decimales en la recta numérica.
1. Realiza lo que se te indica y contesta.
a) Ubica 1
2
, 3
5
, 1
4
y 7
8
en la recta numérica.
0 1
b) Ubica 0.75, 0.5, 0.6 y 0.25.
0 1
Al comparar las rectas numéricas de los incisos a y b, ¿qué fracciones comunes y números
decimales se ubican en el mismo punto?
¿Cómo puedes usar una sola recta numérica para ubicar fracciones comunes y números
decimales?
2. En parejas, ubiquen en la recta numérica 3
10
, 0.5, 1
4
, 0.75 y 3
4
.
0 1
¿Cómo ubicaron fracciones y decimales en la misma recta?
a) ¿Cómo graduaron la recta?
b) En una recta graduada con fracciones, ¿es posible ubicar también decimales?
c) ¿Cómo se haría?

S2
25
 Autoevaluación
Responde en tu cuaderno lo siguiente.
• ¿Cómo se ubica una fracción en la recta numérica cuando ya están localiza-
das otras dos?
• Describe una estrategia que te permita ubicar fracciones y números decima-
les en la misma recta numérica.
3. Expresa las siguientes fracciones en notación decimal y ubícalas en la siguiente recta.
a) 38
100
= b) 3
8
= c) 2
5
=
d) 7
20
= e) 365
1000
=
0 1
Explica cómo ubicaste las fracciones anteriores en la recta.
Para ubicar una fracción común en una recta numérica graduada con decimales, ¿qué im-
portancia tiene expresarla en notación decimal?
4. Ubica 0.25, 0.3, 0.2 y 0.295 en la siguiente recta.
0 1
2
¿Qué hiciste para ubicar en la recta los números decimales?
Compara tus respuestas con las de otros compañeros y escriban un procedimiento que les
permita ubicar fracciones comunes y decimales en la misma recta numérica.

26
Secuencia 3
Sumas y restas
de fracciones
Resolución y planteamiento de problemas
que impliquen más de una operación de suma
y resta de fracciones.
Sesión 9
En esta sesión identificarás cuándo un problema se puede resolver
con una adición, y para solucionarlo aplicarás tus conocimientos sobre
números fraccionarios.
En la vida cotidiana no siempre se emplean cifras exactas; por ejemplo, al comprar ciertos
productos es común el uso de fracciones para señalar la cantidad que se desea adquirir, por
lo que es habitual escuchar expresiones como: “quiero un cuarto de queso, y medio de jamón”.
Otro caso similar es indicar el nivel de combustible con el que cuenta un vehículo en términos
fraccionarios, al decir: “le queda un cuarto de gasolina”, o alguna otra expresión semejante.
1. En parejas, resuelvan lo siguiente.
En carpintería, es habitual expresar las medidas en
fracciones de pulgada. Observa la siguiente ima-
gen y escribe abajo de cada clavo su medida en
pulgadas.
Compara tus medidas de los clavos con las de otro compañero.
¿Cuál de los clavos mide 7
8
de pulgada?
¿Cuál clavo mide 2
3
de pulgada?
¿Cuántos clavos miden más de 1
2
pulgada?
¿Cuáles clavos miden menos de 3
4
de pulgada?
1 pulgada
1
2
pulgada

27
1. En parejas, resuelvan los siguientes problemas.
a) En el esquema de al lado se presentan pa-
res de clavos de distinta medida, calculen
cuál sería el tamaño total de cada pareja de
clavos. Consideren las medidas de los cla-
vos anteriores.
¿Cómo realizan una suma de fracciones con
diferente denominador?
b) Las distancias entre la telesecundaria y las
casas de Juan, Laura y María se ilustran en
el siguiente esquema.
Con base en la información que se presenta
contesten lo siguiente:
¿Cuál es la distancia total que recorrerá
Juan si primero va por María y después van
juntos a la telesecundaria?
¿Qué distancia recorrerá Juan para ir a la
telesecundaria si previamente va por Laura y
luego por María?
Comparen sus respuestas con las de otras
parejas.
c) Con base en la información del ejercicio an-
terior resuelvan en equipos las siguientes
preguntas.
Si consideramos el recorrido más corto de
sus casas a la telesecundaria, ¿cuál es la
distancia que recorren los tres estudiantes
en total?
Indiquen la ruta que muestra la siguiente
suma de fracciones y elaboren un enunciado
que describa el problema.
1
2
+ 1
4
+ 3
4
Para llevar a cabo la suma de números fraccionarios con
denominadores distintos se emplean fracciones equivalen-
tes. Por ejemplo, para efectuar la operación 2
3
+ 3
4
se
deben buscar fracciones equivalentes para ambos térmi-
nos, con la consigna de que tengan el mismo denominador.
Algunas fracciones equivalentes de 2
3
son 4
6
, 6
9
, 8
12
y 10
15
,
y de 3
4
son 6
8
, 9
12
y 12
16
.
Para este problema las fracciones que tienen el mismo
denominador son 8
12
y 9
12
.
De esta manera:
2
3
+ 3
4
= 8
12
+ 9
12
= 17
12
1 1
2
km
3
4
km
1
2
km
3
4
km
1
4
km
4
5
km
TELEsecundariaCasa
María
Casa
Juan
Casa
Laura
Distancias entre las casas de Juan, Laura y María con la telesecundaria

B1
28
Sesión 10
En esta sesión aplicarás tus conocimientos sobre sustracción de fracciones
para resolver problemas.
Para resolver una sustracción
de fracciones con diferentes
denominadores deben buscarse
fracciones equivalentes
con el mismo denominador.
Un problema que se soluciona
con una sustracción de fraccio-
nes responde a preguntas
como: ¿cuánto falta?, ¿cuánto
sobra?, ¿por cuánto es mayor?,
¿por cuánto es menor?,
¿cuál es la diferencia?
1
2
pulgada
1. Resuelve el problema que se plantea.
En la siguiente imagen se muestra un conjunto de clavos que
se van a clavar en un bloque de madera. Considerando las
medidas de los clavos de la sesión anterior, indica qué longitud
de cada clavo quedará fuera de la madera.
¿Hay algún clavo cuya longitud coincida con el
grosor de la madera?
¿Cómo resolviste el problema?
a) A una madera de 3
8
de pulgada se le colocó un clavo de 3
4
de pulgada. Si la punta del
clavo llega exactamente al otro lado de la madera, ¿qué longitud del clavo quedó sin
ser clavado?
b) La señora Julia compró 2 3
4
kilogramos de guayabas y 1 kilogramo y medio de naranjas,
¿qué cantidad de guayabas compró más que de naranjas?
c) Una jarra contiene 3 1
4
litros de agua de tuna. Si Marisol, Sara, Ángel,
Alejandro y Sofía se sirvieron cada quien un vaso con 1
2
litro de agua,
¿qué cantidad de agua queda en la jarra?
d) En parejas, planteen un problema que se resuelva con la operación
3
4
− 5
12
y resuélvanlo.
¿Cuál es el resultado?
Comparen su problema con el de otras parejas y revisen que éste impli-
que una sustracción de fracciones.
e) Para que un problema pueda resolverse mediante una sustracción,
¿qué tipo de preguntas se deben hacer?

S3
29
Sesión 11
En esta sesión aplicarás tu conocimiento sobre adición y sustracción de
fracciones para resolver problemas.
1. En parejas, resuelvan los problemas que se plantean.
a) El siguiente cuadro presenta el total de litros de agua embotellada que consumen al día
los alumnos de la telesecundaria 10 en los tres grados que la integran, divididos entre
hombres y mujeres.
Género
Grado
Primero Segundo Tercero
Masculino 6 1
4
L 7 1
8
L 7 3
4
L
Femenino 5 1
2
L 7 1
2
L 9 1
4
L
¿Qué cantidad total de agua toman los alumnos de la telesecundaria 10?
¿Quiénes toman más agua, los hombres o las mujeres?
¿Cuál es la diferencia en litros?
¿Cuál es la diferencia de la cantidad total de agua ingerida por las alumnas de segundo
respecto de las de primer grado?
La fracción 3
8
es resultado de sustraer…
9 1
4
− 7 3
4
7 1
2
− 7 1
8
De acuerdo con este contexto, escribe una pregunta que se resuelva con la operación
del inciso anterior.
b) En cierta población, el canal XW es visto por 1
3
de los hombres y por 1
2
de las mujeres,
mientras que el canal XZ es visto por 1
5
de los hombres y por 5
8
de las mujeres.
¿Qué canal es más visto por la población?
¿En qué medida es más visto este canal?
Hasta aquí has aprendido a determinar cuándo aplicar una adición o una sustracción
para resolver problemas de fracciones.

B1
30
Sesión 12
En esta sesión aprenderás a identificar cómo resolver problemas,
cuáles y cuántas operaciones son necesarias para su solución.
1. En parejas, resuelvan los problemas que se plantean.
a) Andrea compró y puso en una bolsa 1
2
kg de jamón, 3
4
kg de queso y 1
4
kg de salchi-
chas, y en otra bolsa lleva 1
2
kg de cebollas, 1
2
kg de jitomates, 1
4
kg de chile de árbol,
1
2
kg de tomates y 1
4
kg de aguacates. ¿Cuál de las dos bolsas pesa más?
b) El tiempo que destinó un joven para visitar a su novia la semana pasada fue: el lunes
3
4
de hora, el martes 1 hora 15 minutos, el miércoles 1
4
de hora, el viernes 2 horas 1
2
,
el sábado 4 horas y media, y finalmente el domingo, 2 horas 3
4
.
¿Cuál fue el tiempo total que dedicó el joven a visitar a su novia?
¿Cuál fue el tiempo total de visita el fin de semana?
¿Qué diferencia hubo entre el tiempo total de viernes, sábado y domingo respecto del
resto de la semana?
2. En equipos, comparen sus resultados de los problemas anteriores y describan una estrate-
gia para identificar cuándo deben utilizar la adición y cuándo la sustracción.
 Autoevaluación
• Indica la operación + o −, según corresponda en cada inciso.
2
4
2
8 =
6
8
1
3
1
9 =
2
9

Secuencia 4
Sucesiones de números
y figuras
31
Construcción de sucesiones de números o de figuras
a partir de una regla dada en lenguaje común.
Formulación en lenguaje común de expresiones generales
que definen las reglas de sucesiones con progresión
aritmética o geométrica, de números y de figuras.
Sesión 13
En esta sesión estudiarás la relación que existe entre varias figuras que se
forman con un patrón, lo cual te permitirá conocer la formación de otras
figuras que tengan las mismas características.
Cuando al analizar una colección de figuras ordenadas es posible encontrar un patrón o una
regla a partir de la cual se pueden generar cada uno de los elementos de dicha colección, se
dice que conforman una sucesión.
Observa la siguiente sucesión y en tu cuaderno complétala hasta la figura 6.
Figura 1 Figura 2 Figura 3
Escribe con tus propias palabras una regla para encontrar cada figura de la sucesión.

B1
32
1. En parejas, analicen la siguiente sucesión de figuras y realicen lo que se indica en cada
inciso.
a) En su cuaderno, completen la sucesión dibujando hasta el término 10.
Término 1 Término 2 Término 3 Término 4
b) Completen la tabla con la información obtenida de la sucesión anterior y contesten las
preguntas.
Número de término 1 2 3 4 5 6 7 8 9 10
Número de puntos 1 3 5

¿Cuántos puntos debe tener el término 15?
¿Cuántos puntos tendrá el término 22?
¿Y cuántos el término 27?
¿Cómo determinaron el número de puntos en cada término?
c) Agreguen a su tabla una fila en la que puedan calcular la diferencia entre el número de
puntos que tiene cada término.
Número de término 1 2 3
Número de puntos 1 3 5
Diferencia 3 − 1= 2 5 − 3 = 2
¿Cuántas puntos hay de diferencia entre cada término?
Escriban una regla que permita calcular la cantidad de puntos que tiene cada término.
d) Subrayen la regla que permite determinar el número de puntos que tendrá cada término
de la sucesión.
• Los números impares.
• Se multiplica por dos el número de cada término.
• A partir del segundo término se agrega dos al número de puntos del término anterior.
• Se multiplica por dos el número de cada término y se le resta uno.

S4
33
2. A continuación se muestran algunos elementos de una sucesión.
a) Dibujen en su cuaderno los primeros diez términos de esta sucesión.
Término 5Término 2Término 1
b) Completen las siguientes tablas.
Número de término 1 2 3 4 5 8 10
Número de cerillos
Diferencia

Número de término 15 21 26 30
Número de cerillos

¿Cuántos cerillos hay de diferencia entre una figura y la siguiente?
c) Contesten las siguientes preguntas.
¿Cuál será el término con 51 cerillos?
¿Cuál será el término que tenga 63 cerillos?
¿Habrá algún término con 100 cerillos?
Explica tu respuesta.
Una sucesión de figuras es una colección de las
mismas que está determinada por una regla de
formación o de crecimiento, de tal manera que si se
identifica la regla podemos generar los elementos
de esa sucesión.

B1
34
Sesión 14
En esta sesión estudiarás sucesiones con progresión aritmética.
1. Realiza lo siguiente.
a) Completa la sucesión
15, 27, , 51, 63, , 87, , 111, , , 147,…
Una sucesión numérica es una secuencia de números que siguen una regla. Se llama término
a cada uno de los números que la componen.
b) Encuentra una regla para obtener cualquiera de los términos de la sucesión anterior.
c) Completa la siguiente tabla.
Término 1 2 3 4 5 6 7 8 9
Número de la sucesión 15 27 51 63 87 111
Diferencia 27 − 15 =

d) Encuentra una regla para obtener cualquier término de la sucesión anterior y completa
la tabla siguiente, que es su continuación.
Término 21 22 23 24 25 30 40 50
Número de la sucesión 375 519
e) De las siguientes reglas, ¿cuáles son equivalentes a la que encontraste para obtener los
términos de la sucesión?
•• Sumar 12 al término anterior.
•• Calcular algunos múltiplos del 12.
•• Multiplicar por 12 el término y sumar 15.
•• Multiplicar por 12 el término y sumar 3.
Compara las respuestas que obtuviste con las de tus compañeros.

S4
35
2. Relaciona ambas columnas escribiendo dentro del paréntesis la letra que contenga la regla
de formación correspondiente a cada sucesión.
Términos de la sucesión Reglas de formación de la sucesión
( ) 7, 11, 15, 19, 23,…
( ) 8, 13, 18, 23, 28, 33,…
( ) 2, 6, 10, 14, 18, 22,…
( ) 3, 8, 13, 18, 23, 28,…
( ) 7, 16, 25, 34, 43, 52,…
( ) 9, 14, 19, 24, 29, 34, 39, 45,…
a) Sumar 4 al término anterior
b) Multiplicar el término por 5 y quitarle 2
c) A cuatro veces el término agregarle 3
d) Multiplicar el término por 5 e incrementarle 3
e) Multiplicar el término por 5 y sumar 4
f) Nueve veces el término y 2 unidades menos
Compara tus respuestas con las de tus compañeros.
3. Escribe un ejemplo de una sucesión numérica que sea progresión aritmética.
4. Crea una sucesión cuya regla de formación no genere una progresión aritmética.
5. Intercambia con un compañero las sucesiones que crearon en los incisos 3 y 4 y pídele que
identifique cuál es la progresión aritmética. En caso de que su respuesta no sea correcta,
explícale la regla de formación de tu progresión aritmética. Si no logran un acuerdo, consul-
ten con su profesor.
Una sucesión numérica es una progresión aritmética si para obtener cada
uno de sus términos se suma una cantidad constante, llamada diferencia, al
término anterior.
Las reglas que permiten obtener los términos de una sucesión se pueden dar
a partir del lugar que ocupa un término y la diferencia (es decir, la cantidad
constante) que hay entre dos términos consecutivos.

B1
36
Sesión 15
En esta sesión estudiarás cómo se forman las sucesiones de figuras con
progresión geométrica.
1. En equipos, analicen la siguiente sucesión.
a) Dibujen las dos figuras siguientes.
b) Respondan las siguientes preguntas.
¿Cuántos y de qué color serán los triángulos que forman la séptima figura?
¿Cuántos triángulos tendrá la octava figura?
¿De qué color serán los triángulos que forman la décima figura?
c) Completen la tabla.
Figura Número de triángulos Diferencia
1 2
2 4 4 – 2 = 2
3 8 8 – 4 = 4
4 16
5
6
¿Es constante la diferencia entre los triángulos que forman cada figura?
¿Encuentran alguna relación entre el número de triángulos de cada figura nueva respec-
to de la que le precede?
¿Cómo obtuvieron los triángulos que conforman la quinta y la sexta figura?
¿Cómo obtendrían el número de triángulos de cualquier figura de esta sucesión?
d) Andrea afirma que la regla es: El número de triángulos de cada figura se genera duplican-
do el total de triángulos de la figura anterior. Expliquen si es o no correcta su afirmación.
Figura 4Figura 3Figura 2Figura 1

S4
37
2. Analiza la siguiente sucesión y completa la tabla.
Figura 2Figura 1 Figura 3
Figura 1 2 3 4 5 6
Cantidad de
triángulos
Azules 1 4 16 36
Naranjas
Total 108 324
¿Cómo estableciste la cantidad de triángulos de la cuarta figura?
¿Cómo determinaste el número de triángulos azules de cada figura?
¿Y de los triángulos naranjas?
¿Y el total de triángulos de cada término?
¿Cuál es la regla que determina la cantidad total de triángulos de cada figura (o término) de
esta sucesión?
3. Lee las siguientes afirmaciones con respecto a la regla de formación anterior.
•• Raúl afirma que para obtener el número total de cada término se debe triplicar la canti-
dad de triángulos del término anterior.
•• Guadalupe dice que se obtiene multiplicando por 3 la cantidad de triángulos del término
que le antecede.
•• Ángel, por el contrario, dice que se suman 8 triángulos al término que le antecede.
De estas tres afirmaciones, ¿cuál es correcta?

B1
38
Sesión 16
En esta sesión estudiarás sucesiones numéricas con progresión geométrica.
Contesta lo que se te pide.
1. Con la siguiente regla dibuja las estrellas para cada uno de los términos que se marcan en
la sucesión.
El quíntuple del anterior.
Término 1 Término 2 Término 3
Completa la tabla.
Término 1 2 3 4 6 9
Cantidad de estrellas 3

¿Es constante la diferencia de la cantidad de estrellas entre los términos consecutivos de
esta sucesión?
2. Completa los términos que hacen falta en cada sucesión.
a) 2, 6, , 54, , ,…
¿Cuál es la regla para esta sucesión?
b) 2, 12, , 432, , ,…
Explica por qué la regla de esta sucesión es: El séxtuple del término anterior.
c) 3, , 48, 192, , ,…
Escribe la regla para esta sucesión
d) Encuentra el cociente entre cada par de términos consecutivos de la última sucesión.
3 =
48 =
192
48
= 192
=
¿Cómo son los cocientes de dos términos consecutivos?

S4
39
 Autoevaluación
1. Si se conocen dos términos consecutivos de una progresión aritmética, ¿cómo se obtiene la
regla de toda la sucesión?
2. Si se conocen dos términos consecutivos de una progresión geométrica, ¿cómo se obtiene la
regla para generar la sucesión?
3. Indica con una A si la sucesión es una progresión aritmética, con una G si es una progresión
geométrica, y con una X si no es ninguna de las dos.
5, 10, 15, 20, 25,… 15, 18, 17, 20, 19, 22
4, 6, 9, 13.5, 20.25 0, 3, 6, 9, 12,…
3. En parejas, organicen las piezas para crear dos sucesiones cuyas reglas son:
a) Cuatro veces el término anterior.
b) El triple del término anterior.
Las piezas son las siguientes:
20
80
270
90 12805
320 1030
810
Sucesión A: , , , , .
Sucesión B: , , , , .
¿Cuál es la razón de la sucesión A?
¿Y de la B?
4. En parejas, escriban la regla para generar una sucesión con progresión geométrica e inter-
cámbienla con la de otra pareja. Obtengan los primeros cinco términos de la sucesión y
revisen que sea correcta la construcción de los mismos.
Una sucesión numérica se denomina progresión
geométrica cuando cada término se obtiene multipli-
cando al anterior por una constante llamada razón.

Secuencia 5
Literales en fórmulas
geométricas
40
Explicación del significado de fórmulas geométricas,
al considerar a las literales como números generales
con los que es posible operar.
Sesión 17
En esta sesión representarás números por medio de literales,
con las que realizarás operaciones.
4 cm
Figura 1
4 cm
4 cm 4 cm
3 cm
Figura 2
3 cm3 cm
2.5 cm
Figura 3
2.5 cm2.5 cm
2.5 cm 2.5 cm
¿Cuánto mide el perímetro de la figura 1?
¿Y el de la figura 2?
¿Y el de la 3?

41
1. En parejas, calculen el perímetro de los siguientes triángulos equiláteros.
3 cm
Figura 1
3 cm3 cm
4 cm
Figura 2
a
Figura 3
¿Cuánto mide el perímetro de la figura 1?
Expliquen cómo calcularon el perímetro de las figuras, en particular el de las figuras 2 y 3,
en las que solamente se conoce la medida de uno de sus lados.
Un triángulo equilátero mide b por lado, ¿cuál de las siguientes expresiones pueden utilizar
para calcular su perímetro? Subrayen sus respuestas.
b + b + b b + 3 3b b 3

B1
42
2. Completen la tabla.
3 cm3 cm
3 cm
Figura 1
5 cm
Figura 2 Figura 3
Figura geométrica Longitud de sus lados Perímetro
Figura 1
Figura 2
Figura 3
¿Cómo representaron la longitud de los lados de la figura 3?
¿Cómo calcularon el perímetro de la figura 3?
Comparen sus respuestas con las de otras parejas.
3. Usa literales para expresar el perímetro de las siguientes figuras.
Perímetro Perímetro Perímetro
3 cm3 cm

S5
43
Sesión 18
En esta sesión trabajarás con figuras geométricas que se parecen en su forma
y en sus propiedades, así como en la manera en que se calcula su perímetro.
1. En parejas, contesten las preguntas.
A algunos estudiantes les pidieron utilizar literales para indicar las longitudes de un rectán-
gulo. Observen sus respuestas.
b
Figura 2
a
b
a
a
Figura 1
aa
a
Figura 3
ca
a
Figura 4
b
b
a
a) ¿En cuál de los rectángulos expresaron correctamente la longitud de los lados?
b) Expliquen por qué es o no correcta la forma en que se señalaron las longitudes en los
rectángulos anteriores.
c) ¿Cuántos pares de lados de la misma longitud tiene el rectángulo?
d) ¿Cómo se calcula el perímetro de un rectángulo?
e) Para calcular el perímetro de un rectángulo se puede emplear alguna de las siguientes
expresiones algebraicas:
a + b + a + b 2a + 2b 2(a + b)
¿Por qué son correctas estas expresiones algebraicas?

B1
44
2. En parejas, empleen cualquier literal para expresar la longitud de los lados de los siguientes
romboides.
Usen las letras que anotaron y escriban una expresión algebraica para calcular el perímetro
de cada romboide.
¿Es posible calcular el perímetro del romboide con la misma expresión algebraica que em-
plearon para el rectángulo? ¿Por qué?

S5
45
Sesión 19
En esta sesión trabajarás con las fórmulas para calcular el perímetro
de triángulos y trapecios isósceles.
1. En parejas, asignen una letra a la longitud de los lados de las figuras siguientes, tomen en
cuenta que son triángulos isósceles. Completen la tabla.
Figura Longitud de los dos lados iguales Longitud del tercer lado Perímetro
1
2
3
Una expresión algebraica que permite obtener el perímetro de un triángulo isósceles es:
¿Es la única? , ¿por qué?
Un triángulo escaleno tiene todos sus lados de diferente longitud, ¿cómo se puede expresar
su perímetro?
2. Observa el siguiente trapecio isósceles.
B (base mayor)
b (base menor)
ll
¿Cómo se puede expresar su perímetro?
En una figura geométrica señalamos con la misma lite-
ral los lados que tienen igual longitud, y si éstos tuvie-
ran longitudes diferentes se emplearían más literales.
Por ejemplo, en un rectángulo, el perímetro se puede
expresar como:
P = a + a + b + b, o bien P = 2a + 2b o P = 2(a + b)

B1
46
Para calcular el perímetro de un
polígono regular se debe conocer el
número de lados que lo forman y
multiplicarlo por su longitud.
Sesión 20
En esta sesión trabajarás con las fórmulas de los perímetros
de polígonos regulares.
1. En grupo, contesten las preguntas que se plantean.
¿Qué figuras regulares conocen?
¿Cómo se calcula el perímetro de una figura geométrica que tiene todos sus lados iguales?
Escriban una expresión algebraica que les permita calcular el perímetro de una figura
regular.
¿Cómo se calcularía el perímetro de un polígono regular de 38 lados?
2. Completa la tabla.
Nombre de la figura
Longitud
de sus lados
Número
de lados
Perímetro
Pentágono regular a
Hexágono regular b
Octágono regular m
Decágono regular h
Heptadecágono x 17
Triacontágono s 30
Observa que en la tabla anterior la letra m representa una literal, sin embargo, la misma
letra también es el símbolo de “metro”. Por ejemplo:
5m = m + m + m + m + m,
mientras que 5 m representa 5 metros.
Lo mismo ocurre con otras letras que también son utilizadas como sím-
bolos de unidad de medida, tales como s (segundo), h (hora), etcétera.

S5
47
Sesión 21
En esta sesión trabajarás con las fórmulas para calcular el área
de distintas figuras.
1. Lee la siguiente información y contesta.
Un ejemplo de unidad de superficie es un centímetro cuadrado, que es de este tamaño:
y se abrevia cm2
.
Observa los siguientes rectángulos y mide su área.
6 cm
Rectángulo A
5 cm
1 cm
Rectángulo B
3 cm
s
Rectángulo C
t
El área del rectángulo B es:
Del rectángulo A es:
Del rectángulo C es:
2. Si e es el largo de un rectángulo y f el ancho, subraya de las siguientes expresiones alge-
braicas cuáles son equivalentes y permiten calcular el área del rectángulo con resultados
iguales.
A = e × f = e f A = 2(e + f) A = (2 e) (2 f)
A = 2 e + 2 f A = f e

B1
48
3. Subraya la fórmula que te permita calcular el área del siguiente cuadrado.
x
x
x
x
Expresiones algebraicas.
4 x x + x ( x )( x )( x )( x ) x + x + x + x ( x )( x ) 4 + x x 2
4. En parejas, observen las siguientes figuras y contesten.
b
a
b
a
a
¿Cuál es la fórmula para calcular el área de un cuadrado?
¿Y la del rectángulo?
¿Cómodeterminaneláreadelapartenaranjadelcuadrado?
¿Y la parte naranja de los rectángulos?
¿Qué fracción representa el área naranja con respecto a toda la figura?
a

S5
49
Sólo una de las siguientes expresiones no determina el área del triángulo azul, ¿cuál es?
Márquenla.
A = 1
2
(a × b) A = a
2
× b
2
A = a
2
× b A = a × b
2
De manera grupal expliquen por qué la fórmula que comunmente usamos para calcular el
área de un triángulo es: A = b h
2
, donde b es la base y h es la altura.
b
h
 Autoevaluación
• ¿Qué representan las letras o literales en una expresión algebraica?


50
Secuencia 6
Trazo de triángulos
y cuadriláteros
Trazo de triángulos y cuadriláteros mediante el uso
del juego de geometría.
Sesión 22
En esta sesión aprenderás a trazar cuadriláteros y triángulos a partir de líneas
paralelas, utilizando escuadras.
¿Cómo puedes trazar líneas paralelas y perpendiculares con tu juego de geometría? Realiza tus
trazos en hojas blancas.
Observa la imagen de la derecha. Sobre una hoja blanca
coloca de la misma manera tu regla y tu escuadra y traza
líneas paralelas y perpendiculares. Mueve la escuadra
como lo indican las flechas.
Ahora observa las siguientes imágenes para trazar las lí-
neas perpendiculares y paralelas que se obtienen al mover
la escuadra.
Compara tus trazos con los de tus compañeros.

51
1. Realiza las siguientes construcciones y responde las preguntas.
Usa las escuadras y el compás para trazar en una hoja blanca dos líneas rectas paralelas
de 20 cm cada una. Las líneas deben tener una distancia de 5 cm entre ellas.
Traza las siguientes figuras geométricas, considerando que dos de sus lados deben estar
sobre las líneas paralelas que ya trazaste.
•• Un cuadrado.
•• Un rectángulo, uno de sus lados mide 3 cm.
•• Un romboide cuya base mide 7 cm.
•• Un romboide, dos de sus lados miden 4 cm y uno de sus ángulos mide 60º.
Contesta en tu cuaderno las siguientes preguntas.
a) ¿Cuánto mide cada lado del cuadrado?
b) ¿Cuánto miden los otros lados del rectángulo?
c) ¿Cuánto mide la altura de cada romboide?
2. Formen parejas y, en una hoja blanca, tracen un par de líneas paralelas para construir sobre
ellas los trapecios que se enlistan a continuación.
•• Trapecio recto.
•• Trapecio isósceles.
•• Trapecio escaleno.
Cada uno de los trapecios debe cumplir con las siguientes condiciones: la base mayor mide
8 cm; la base menor, 6 cm, y la altura, 4 cm.
¿A qué distancia deben trazarse las líneas paralelas?
¿Qué tienen en común los tres trapecios que trazaste, el perímetro o el área?
¿Por qué?
3. En una hoja blanca, y a partir de dos líneas paralelas, traza tres triángulos diferentes cuya
base mida 6 cm y su altura mida 5 cm.
¿Cuánto mide el área de cada triángulo?
4. En grupo, construyan un romboide, un trapecio y un triángulo cuyas áreas sean iguales.

B1
52
Sesión 23
En esta sesión construirás triángulos utilizando el juego de geometría.
1. Lee con atención las siguientes instrucciones y en una hoja blanca construye lo que se indica.
•• Con tu regla traza una línea recta y marca en ella dos puntos; de esta manera has tra-
zado un segmento. Los puntos son sus extremos.
•• Ahora utiliza tu compás, su apertura debe ser mayor a la longitud del segmento que
marcaste.
•• Coloca la punta de metal del compás en uno de los puntos extremos del segmento y
traza un círculo.
•• Sin cambiar la apertura del compás y colocando la punta metálica en el otro extremo,
traza otro círculo.
De las construcciones de la izquierda, marca con una palomita ( ) la que se parece a la
que tú trazaste.
¿En cuál de las construcciones anteriores obtienes un triángulo equilátero al unir los extre-
mos del segmento con uno de los puntos de intersección de las circunferencias?
¿Qué tipo de triángulo se obtiene con las instrucciones que seguiste?
2. Reúnete con un compañero y en sus cuadernos escriban las instrucciones para obtener un
triángulo equilátero.
Lean sus instrucciones a otra pareja para verificar que sí se obtiene ese triángulo. Es impor-
tante que solamente digan en voz alta lo que ustedes escribieron.
Hagan las correcciones necesarias para que sus instrucciones sean claras, de modo que
cualquiera pueda construir un triángulo equilátero al seguirlas.
3. Identifiquen en cuál de las cuatro construcciones anteriores se obtiene un triángulo isósce-
les. Trácenlo.
Comparen sus construcciones y sus respuestas con las de otras parejas.
4. En grupo, comenten qué cambios deben hacer al seguir las instrucciones para construir un
triángulo equilátero que mida 3 cm por lado.
5. Con regla y compás, traza en tu cuaderno un triángulo escaleno cuyos lados midan 3 cm,
4 cm y 2 cm.
a) Al trazar la primera línea, ¿cuál es la apertura del compás con respecto a la distancia
que hay entre los dos puntos que se marcan en ella?
Compara tu construcción con la de otros compañeros.
Construcción 1
Construcción 2
Construcción 3
Construcción 4

S6
53
Sesión 24
En esta sesión seguirás construyendo triángulos
y cuadriláteros utilizando el juego de geometría.
1. Considera las cuatro construcciones que aparecen en
la sesión anterior e identifica aquellas dos en las que
al unir los puntos extremos del segmento con los dos
puntos de intersección de las circunferencias se traza
un rombo. ¿Cuáles son esas construcciones? Subraya
tu respuesta.
•• Construcción 1
2. Traza los rombos y marca en cada uno la diagonal me-
nor y la diagonal mayor.
¿Qué tipo de ángulo se forma en el punto donde se
cortan?
3. En tu cuaderno escribe las instrucciones para cons-
truir un rombo.
Intercámbialas con algún compañero y comprueba si
al seguir tus instrucciones logra construir esa figura.
Si es necesario hacer correcciones, anótalas y com-
prueba nuevamente el procedimiento, pero ahora con
la ayuda de otro compañero.
4. Observa los pasos de la columna de la derecha para
trazar un triángulo cuyos lados miden 5 cm, 3.5 cm y
4.5 cm. Síguelos y traza en tu cuaderno ese triángulo.
5. En tu cuaderno traza un triángulo con un lado de 6 cm
y otro de 5 cm.
Compara el triángulo que construiste con los de tus
compañeros y contesten las siguientes preguntas.
¿Por qué los triángulos no son todos iguales?
¿Qué dato hay que determinar para que todos los
triángulos sean iguales?
Paso 3. Abrir el compás a 4.5 cm y apoyarlo en el
otro extremo del segmento, trazar otro arco que corte
al primero.
Paso 2. Abrir el compás a 3.5 cm y colocarlo en un
extremo del segmento, trazar un arco.
Paso 1. Trazar un segmento de 5 cm.
Paso 4. Unir cada extremo del segmento con el punto
de corte de los arcos para obtener el triángulo.

B1
54
Sesión 25
En esta sesión trazarás cuadriláteros que cumplan con ciertas condiciones.
1. Utiliza tu juego de geometría para completar los trazos y construir las figuras que se piden
en cada inciso.
a) Traza un rectángulo a partir del siguiente segmento. b) Traza un cuadrado.
c) El segmento siguiente es la base de un rectángulo. d) El segmento siguiente es una diagonal de un cuadrado.
2. En equipos, comparen los cuadrados y rectángulos que trazaron. Contesten las siguientes
preguntas.
¿Cuáles de las figuras trazadas son iguales? ¿Por qué?
En el caso del rectángulo a), ¿qué datos habría que definir para que todos los rectángulos
que construyeron fueran iguales?
¿Y en el caso del rectángulo c)?
3. Utilicen el juego de geometría para trazar de manera individual lo que se indica a continuación.
a) Un rombo con una diagonal de 3 cm y la otra de 7 cm.
b) Un romboide de base 7 cm y altura de 4.5 cm.
Comparen sus trazos con los de sus compañeros, ¿todas las figuras fueron iguales?

S6
55
Sesión 26
En esta sesión trazarás triángulos y cuadriláteros a partir
de ciertas condiciones.
1. En equipos, contesten en sus cuadernos las preguntas
siguientes.
a) ¿Se puede trazar un trapecio con 10 cm de base
mayor y 5 cm de base menor?
Si se puede trazar, ¿cuántas soluciones tiene?
Si se puede trazar más de una figura, ¿qué otro
dato o datos se tienen que definir para que sea
única la solución?
b) ¿Se puede trazar un romboide con base de 7 cm?
dato o datos se tienen que especificar para que
sea única la solución?
c) ¿Se puede trazar un triángulo con lados de 3 cm,
2 cm y 4 cm, y un ángulo de 90º?
dato o datos se tienen que dar para que sea única
la solución?
d) ¿Se puede trazar un rombo con una diagonal de
5 cm?
la solución?
e) ¿Se puede trazar un cuadrado que tenga diagona-
les de 4 cm?
la solución?
2. En seguida, verifiquen sus respuestas trazando las fi-
guras en su cuaderno.
3. En grupo, y con ayuda de su profesor, comparen sus
respuestas. Si se requiere, hagan las correcciones ne-
cesarias.
 Autoevaluación
1. Utiliza tu regla y tus escuadras para trazar en tu cuaderno un cuadrado que tenga 3 cm
por lado y un rectángulo que mida 7 cm de largo y 4 cm de altura.
2. ¿Cuántos rombos diferentes pueden construirse si se da la medida de sus lados?
Consulta en…
Entra al sitio: http://www.rena.edu.ve/TerceraEtapa/dibujoTecnico/trazadodetriangulos.html,
donde encontrarás animaciones que muestran paso a paso procedimientos interesantes para
que, dadas ciertas condiciones, construyas triángulos o cuadriláteros empleando solamente
regla y compás.

56
Secuencia 7
Trazo y análisis de las propiedades de las alturas,
medianas, mediatrices y bisectrices en un triángulo.
Sesión 27
En esta sesión aprenderás a trazar las alturas de cualquier tipo de triángulo,
y sus propiedades.
Relaciona las imágenes con el nombre de la recta correspondiente.
( ) Altura
( ) Mediana
( ) Mediatriz
1 2 3
A
B
C
1. En equipos, observen que en el siguiente
triángulo se marcaron con rojo las alturas.
Contesten las preguntas en su cuaderno.
¿De dónde a dónde van los segmentos
que indican las alturas del triángulo?
Alturas, medianas, mediatrices
y bisectrices en los triángulos

57
a) ¿Qué tipo de ángulo se forma entre el segmento AB y su altura?
b) ¿Y entre el segmento BC y su altura?
c) Sin medirlo, ¿qué tipo de ángulo crees que se formará entre el segmento AC y su altura?
Utiliza tu juego de geometría para comprobarlo.
d) ¿Cómo pueden trazar una altura en un triángulo empleando las escuadras?
e) ¿A qué se le llama altura en un triángulo?
f) Comparen sus respuestas con las de otros equipos y elijan la técnica más práctica para
encontrar las alturas en diferentes triángulos.
2. Encuentra el punto en que se unen las alturas en los siguientes triángulos.
La altura en un triángulo es el segmento de recta que va desde el vértice de un ángulo hasta el lado
opuesto, formando un ángulo de 90º con el mismo. Las escuadras son un buen recurso para trazar la
altura: se coloca la escuadra de 60° sobre el segmento al que se le va a trazar la altura, se desliza
la otra escuadra, usando su ángulo de 90°, hasta encontrar el vértice opuesto a dicho segmento
y se traza la altura.
altura
Paso 1. Paso 2. Paso 3.
Dado un triángulo, sus alturas siempre se intersecan en un único punto, llamado ortocentro.

B1
58
A B
C
A B
C
A B
C
La mediana es el
segmento que une
un vértice de un
triángulo con el
punto medio del
lado opuesto.
Las medianas se
intersecan siempre
en un único punto
llamado baricentro.
Sesión 28
En esta sesión conocerás otra recta notable de los triángulos: la mediana.
1. En equipos, analicen el segmento azul trazado en el triángulo ABC. A este segmento se le
denomina mediana.
a) ¿Cuánto mide la distancia de A a D?
b) ¿Cuánto mide la distancia de D a B?
c) ¿Desde dónde hasta dónde va la mediana que lle-
ga al segmento AB?
d) Comparen sus respuestas con las de otros equipos
y contesten.
e) ¿Cuáles son las características de una mediana?
f) ¿Cuáles son los pasos a seguir para trazar una me-
diana en un triángulo?
g) Tracen las medianas sobre los segmentos BC y CA
de tal forma que tengan las mismas propiedades
que el trazo de color azul.
h) ¿Las medianas tienen algún punto de intersección?
2. Traza las medianas en los siguientes triángulos y observa dónde se intersecan.
D
A
C
B

S7
59
Sesión 29
En esta sesión te presentamos otra recta notable de los triángulos, llamada
mediatriz, y sus propiedades.
1. En equipos, observen la secuencia de trazo de la mediatriz en un segmento y coloquen en
el recuadro una instrucción que describa claramente lo que se hace en cada paso.
A
P
BA B A B
El segmento trazado en color rojo se llama mediatriz.
Respondan las siguientes preguntas.
a) ¿Cómo son los segmentos AP y PB?
b) ¿Qué ángulo forman la mediatriz y el segmento AB?
c) ¿De qué otra forma se podrá trazar la mediatriz de un segmento?
d) Comparen sus respuestas con las de otros equipos y describan el procedimiento para
trazar una mediatriz sin usar el compás.
e) Explica brevemente qué es una mediatriz
2. Ahora dibuja en tu cuaderno tres triángu-
los de diferentes formas y tamaños y traza
las mediatrices de los lados de cada uno
de ellos.
Llamen O al punto en el que se cortan las
mediatrices.
En un triángulo, la mediatriz es la recta perpendicular
a uno de sus lados que pasa por su punto medio.
El punto en el que siempre se intersecan las tres
mediatrices de un triángulo se llama circuncentro.

B1
60
Sesión 30
En esta sesión trazarás las bisectrices de un triángulo.
Formen equipos de tres personas y desarrollen las actividades que se indican.
1. Tracen las diagonales en la siguiente figura.
A
BD
C
¿Cómo quedaron divididos los ángulos por las diago-
nales que trazaron?
Observen ahora la siguiente figura.
BD
C
Midan los ángulos en los que quedó dividido el án-
gulo C.
¿Qué hace la recta roja al ángulo C?
Dividan los ángulos D y B de la misma forma en que
está dividido el ángulo C.
Las rectas que trazaron se llaman bisectrices.
2. Observen detenidamente los pasos a seguir para trazar la bisectriz de un ángulo y escriban
en cada recuadro una instrucción clara para realizar dicho trazo.

S7
61
3. Dibuja en tu cuaderno un triángulo equilátero de 5 cm, un triángulo escaleno de 3 cm, 5 cm
y 7 cm respectivamente, y un triángulo isósceles cuyos lados iguales midan 5 cm y el lado
diferente, 3 cm. Traza las bisectrices de los ángulos interiores de cada triángulo con el
método anterior.
Resalta en color rojo el punto de intersección de las bisectrices de
cada uno de los triángulos. ¿Todas las bisectrices tienen un mismo
punto en común?
Ahora traza un triángulo cualquiera y sus bisectrices. Observa qué
sucede con el punto que tienen en común las bisectrices.
Comenta tus observaciones con tus compañeros.
La bisectriz es la recta que divide a
un ángulo en dos ángulos iguales.
En un triángulo las bisectrices
siempre se intersecan en un solo
punto, llamado incentro.
 Autoevaluación
• ¿Cómo se puede diferenciar la altura de la mediana en cualquier triángulo?
• ¿En qué tipo de triángulo coinciden las alturas, las medianas, las mediatrices y las
bisectrices?
Consulta en…
Para conocer más sobre este tema busca en las bibliotecas escolares y de aula el libro:
Carlos Bosch y Claudia Gómez, “Construcciones básicas” y “Paralelas con doblado de papel”,
en Una ventana a las formas, México, sep-Santillana, 2003 (Libros del Rincón).
La recta de Euler
En un triángulo, el ortocentro, el circuncentro y el baricentro se encuentran en una misma
recta (son colineales), a la que se denomina recta de Euler. Se llama así en honor del
matemático suizo Leonhard Euler, quien descubrió este hecho a mediados del siglo XVIII.
alturas H: ortocentro
medianas G: baricentro
mediatrices O: circuncentro
H
G
O

62
Secuencia 8
Reparto proporcional
Resolución de problemas de reparto proporcional.
Sesión 31
En esta sesión aprenderás a repartir basándote en ciertos criterios o en
determinados factores.
a) Don Ernesto tiene un terreno de 94.5 hectáreas, él quiere repartirlo por partes iguales
a sus hijos: Salvador, Martín, Héctor, Ricardo y Jesús, y a sus hijas: Rosa, Juana, Guada-
lupe y Carmen. ¿Qué cantidad de terreno le corresponde cada uno?
b) Tres amigos ganaron un premio de lotería de $100 000.00 con un boleto que costó
$40.00. Para comprar el boleto Raúl aportó $8.00, Andrés colaboró con 4 pesos más
que Raúl, y Braulio pagó el resto. Si reparten el premio de acuerdo con lo que aportaron,
¿a quién le corresponde la mayor cantidad del premio y a quién la menor?
¿Por qué?
¿Cómo resolvieron el primer problema?
¿Y el segundo? Versióndeevaluación23/04/12

63
1. En parejas, de acuerdo con el problema del premio, contesten.
¿Qué cantidad de dinero le corresponde a Andrés?
¿Y cuánto a Braulio?
¿Y a Raúl?
Registren en su cuaderno las operaciones que realizaron para obtener sus respuestas.
Comparen sus procedimientos con los de otras parejas, verifiquen que las cantidades ob-
tenidas sean las mismas.
Si hay algún procedimiento diferente al suyo, explíquenlo.
2. Lee el siguiente problema y resuélvelo.
De los 24 metros de listón que trae un carrete, María ocupó 8 metros para hacer una tarea
escolar, Ramiro empleó 11 metros, y Javier, el resto. El carrete les costó $60.00. Si se re-
parten el costo del carrete de acuerdo con la cantidad de listón que cada quien utilizó,
¿quién de ellos deberá aportar $20.00? ¿Por qué?
¿Con cuánto dinero deberá contribuir Javier?
Verifica tu respuesta con un procedimiento diferente al que empleaste.
Reflexionen sobre cuáles son las diferencias que hay entre un reparto proporcional y un
reparto equitativo.
De manera grupal escriban en su cuaderno las características que tiene un problema de
reparto proporcional.

B1
64
Sesión 32
En esta sesión continuarás con la solución de problemas de reparto
proporcional, sólo que ahora utilizarás tus conocimientos sobre fracciones.
Albañil
Cantidad de m2
construidos
Fracción que
representan del
total de m2
Cantidad de
dinero que le
corresponde
Alberto
Flavio
Gonzalo
Total
1. En parejas, resuelvan el siguiente problema.
a) Tres albañiles levantaron una barda de 30 m2
. Al-
berto levantó 10 m2
, Flavio 5 m2
y Gonzalo 15 m2
.
Por esta construcción les pagaron $2 100.00, y se
repartieron el dinero de acuerdo con el número de
metros cuadrados que cada quien levantó. Comple-
ten la tabla.
¿Cómo obtuvieron la cantidad de dinero que le co-
rresponde a cada uno?
2. De acuerdo con el problema del premio de lotería de la
sesión anterior, contesten las siguientes preguntas.
¿Quién de los tres contribuyó con la mitad del costo
del boleto?
¿Qué fracción del total del boleto aportó Raúl?
¿Qué cantidad del premio le habría tocado a Braulio si
hubiera colaborado con la cuarta parte del costo del
boleto?
Comparen sus respuestas con las de otras parejas y en
su cuaderno empleen fracciones para comprobar las
cantidades que corresponden a cada uno de los tres
amigos.
Expliquen si obtuvieron o no los mismos resultados
que en la sesión anterior.
3. En equipos, resuelvan los siguientes problemas.
a) Para completar un pedido que deben exportar, cin-
co artesanos de una comunidad juntaron los suéte-
res de lana que tejen. Hortensia fabricó 24 prendas;
Alonso, 40; Tomás, 30; Guadalupe, 16, y Blanca 10
piezas. Por este pedido les pagaron $22 200.00,
que repartieron proporcionalmente de acuerdo con
la cantidad de prendas que cada uno confeccionó.
¿Qué cantidad de dinero le corresponde a cada
uno de los artesanos?
b) Entre Angélica, Mónica y Francisco sacaron 400 co-
pias fotostáticas de una invitación. El costo total lo
pagaron en proporción a las invitaciones que cada
uno quiere repartir. Angélica pagó $22.00 por la
cuarta parte de las copias; Mónica, 3
5
partes, y lo
demás lo aportó Francisco.
¿Cuánto pagó Francisco?
¿Cuánto se pagó en total por todas las copias?
¿Cómo obtuvieron la respuesta de la pregunta an-
terior?
Comparen sus respuestas con las de otros compañeros y verifiquen que sean correctas.
Reflexionen sobre el empleo de fracciones en los problemas de reparto proporcional. Ex-
pliquen en qué situaciones de reparto proporcional es conveniente emplear fracciones.

S8
65
Sesión 33
En esta sesión resolverás problemas de reparto proporcional
considerando el valor unitario.
1. Lean la siguiente información y contesten.
¿Recuerdan que en el problema del boleto de lotería Raúl aportó $8.00 para comprar el
boleto, Andrés, cuatro pesos más que Raúl, y el resto lo pagó Braulio?
¿Cuánto aportó cada uno de ellos?
Si se repartieron los $100 000.00 de acuerdo con lo que pusieron, ¿cuánto le habría toca-
do a Raúl si únicamente hubiera aportado un peso de los $40.00 que costó el boleto?
¿Qué importancia crees que tiene saber la cantidad del premio que corresponde por cada
peso invertido?
a) Cuatro campesinos rentaron un camión por la can-
tidad de $4 200.00 para llevar al mercado las
2.5 toneladas de aguacate que recolectaron y que
transportan en 120 cajas de madera. Observa el
registro que realizaron y completa la tabla.
¿A quién de ellos le conviene más que se reparta el
pago del camión de acuerdo con la cantidad de
cajas?
¿Cuál reparto le conviene más a Efrén?
¿Emplearon fracciones para resolver este problema? ¿Por qué?
¿Cuánto se pagó por cada caja que se transportó?
¿Y cuánto por kilogramo de aguacate transportado?
b) Yolanda pagó $2 280.00 por los 60 m2
de barda
que pintaron entre Ernesto, Lorena y José. El prime-
ro pintó 28 m2
, Lorena, 19 m2
, y José el resto. De
acuerdo con el trabajo que cada uno realizó, ¿cuán-
to se le debió pagar? Para responder, completa la
siguiente tabla y en la última fila escribe la canti-
dad de metros cuadrados que pintó José.
Comparen sus respuestas con las de otras parejas y comprueben con algún otro procedi-
miento sus resultados.
Nombre
Cantidad
de cajas
Peso
(kilogramos)
Cantidad de dinero
a pagar por el flete, de
acuerdo con:
Cajas Peso
Irma 30 605
Lorena 45 945
Armando 20 450
Efrén 25 500
Total 120 2 500
Metros cuadrados pintados Cantidad de dinero a pagar
60
1
28
19
El valor unitario
se refiere a la
cantidad que
le corresponde
a una pieza,
objeto o unidad.

B1
66
Sesión 34
En esta sesión aplicarás tus conocimientos sobre las diferentes formas
aprendidas del reparto proporcional y resolverás diversos problemas
que lo involucran.
1. Resuelve los problemas siguientes.
a) A Marina le pagaron $300.00 por podar la quinta parte de los 60 m2
de césped de un
jardín. ¿Cuánto le pagaron a Anselmo si podó únicamente una cuarta parte de todo el
césped?
b) Cuatro amigos fueron al cine. Para pagar el total del costo de los boletos, Noemí aportó
$80.00, Abraham, $50.00 y Jesús dio $70.00. Adriana dijo que a la salida los recom-
pensaría. En agradecimiento por haber pagado su entrada, Adriana les obsequió
$500.00 para los tres, con la condición de que se repartieran conforme a lo que cada
uno de ellos aportó para su boleto.
¿Qué cantidad de dinero de los $500.00 le corresponde a cada uno?
c) El dueño de una fábrica de calzado quiere repartir un bono de $15 000.00 entre los
cuatro vendedores que tiene. Para ello cuenta con la información de las siguientes grá-
ficas, que corresponden a las ventas del tercer bimestre; además se sabe que en junio
se vendieron 140 unidades.
35
30
25
20
15
10
5
0
Andrés Ana Lizbeth José
Ventas de mayo
Unidadesvendidas
Andrés
50%
Ana
28%
Lizbeth
10%
José
12%
Ventas de junio

S8
67
 Autoevaluación
• ¿Cómo se calcula el valor unitario?
• ¿Qué diferencia hay entre el reparto proporcional y el reparto equitativo?
• ¿Cómo se debe interpretar el cociente de dividir 2 500 kilogramos entre $4 200.00?
Además, observamos que un problema de reparto
proporcional también se puede resolver a través de
fracciones, al determinar la fracción de la cantidad
a repartir. Por ejemplo, Braulio aportó $20.00 de
los $40.00 que costó el boleto, él aportó la mitad,
por lo que le corresponde la mitad del premio, es
decir, $50 000.00.
Para resolver un problema de reparto proporcional deben tomarse en cuenta
distintos criterios a fin de llevar a cabo la distribución correcta. Entre otras
formas, se puede resolver calculando el valor unitario, es decir, lo que le corres-
ponde a una unidad; por ejemplo, en el problema del premio de lotería se gana-
ron $100 000 y el boleto costó $40, por lo que por cada peso aportado a una
persona le corresponde el cociente de 100 000
40
, es decir, 2 500.
Si el bono se reparte de acuerdo con la cantidad de unidades vendidas, ¿qué cantidad
del bono le corresponde a Andrés?

68
Secuencia 9
Juegos de azar
Identificación y práctica de juegos de azar
sencillos, y el registro de los resultados.
Elección de estrategias en función del análisis
de resultados posibles.
Sesión 35
En esta sesión aprenderás a identificar cuándo un juego es de azar.
¿Alguna vez has jugado “gato”? Si es así, describe en qué consiste y cómo se determina al ganador.
¿Alguna vez has jugado “volados”? Describe en qué consisten y cómo se determina al ganador.
1. Reúnete con un compañero para jugar “gato” cin-
co veces. Uno de los jugadores inicia marcando
una cruz en una de las casillas. Luego, el siguiente
jugador marca un círculo en otra casilla. Gana el
primero que logra completar una fila, una columna
o una diagonal.
Antes de empezar, contesta de manera individual las siguientes preguntas.
¿Quién ganará el primer juego?
¿Quién va a ganar más juegos?
¿Cuántos juegos ganará cada jugador?

69
Después de jugar, contesta en tu cuaderno las siguientes preguntas.
¿Es cierto que en el juego del “gato”, el que inicia siempre gana?
¿Existe una estrategia para no perder en el juego? ¿Cuál es?
¿Conoces algún otro juego parecido al “gato”? ¿Cómo se llama y en qué consiste?
¿Hay alguna estrategia para ganar?
Compara tus respuestas con las de tus compañeros y lleguen a una conclusión grupal
con la guía de su profesor.
2. Reúnete con un compañero para jugar el juego de la “es-
calera”. Cada jugador deberá escribir su nombre en un
extremo de la escalera. Coloquen una ficha sobre el centro
de la escalera. Utilicen una moneda para hacer los lanza-
mientos por turnos; cuando sale águila, la ficha se baja un
escalón, y cuando sale sol, se sube uno. Gana el jugador
cuyo nombre está escrito en el escalón al que llega antes
la ficha.
Antes de empezar, contesta:
¿Quién consideras que va a ganar el juego?
Después de jugar, contesta las siguientes preguntas.
¿Consideras que existe una manera de ganar siempre en el juego de la escalera?
¿Es cierto o no que en el juego de la escalera el que pide primero siempre gana?
Si en un “volado” la moneda cae águila, ¿es seguro que en el siguiente “volado” no caerá águila?
¿Qué puede ocurrir?
¿Conoces algún otro juego, parecido al de la escalera, en el que
antes de empezar no se sepa quién va a ganar? ¿Cómo se llama
y en qué consiste?
¿Es el juego del “gato” un juego de azar? Justifica tu respuesta.
En un juego de azar, como el de la
escalera, no se puede saber con
anterioridad cuál será el resultado,
por lo que no se tiene seguridad de si
se va a ganar o se va a perder.

B1
70
Sesión 36
En esta sesión continuarás identificando si un juego es de azar o no.
1. En parejas, jueguen a “adivina el número”.
Tienes que pensar un número mayor que 0 y menor que 50. Lo anotas en un papelito, sin
que lo vea tu compañero. Él debe adivinar el número que pensaste, y para ello puede ha-
certe hasta seis preguntas. Tú sólo puedes contestar sí o no. Anoten las preguntas y res-
puestas en la siguiente tabla.
Preguntas Respuestas
¿Tu compañero o compañera adivinó el número que pensaste?
¿Qué número pensaste? ¿Cuántas preguntas te hizo?
Ahora es tu turno, ¿podrás adivinar el número que piense tu compañero con menos de seis
preguntas? Inténtalo.
Si este juego lo realizan muchas veces más, ¿podrían encontrar una manera segura de
adivinar el número? ¿Cuál?

S9
71
2. En equipos, jueguen a la “oca”. Necesitan un par de dados y una ficha por jugador. Todos
salen de Inicio y por turnos avanzan lo que sumen los dados. Gana el primero que logra
llegar a 63.
¿Ganó quien avanzó primero?
Realicen el juego una vez más.
¿Consideran que hay una manera segura de ganar el juego?
Comparen sus respuestas con las de sus compañeros y con su profesor. Comenten cuál de los
dos juegos anteriores es de azar y cuál no lo es, y por qué. Si encontraron estrategias para
ganar en cada juego, pruébenlas para ver si lo logran.

B1
72
Sesión 37
En esta sesión identificarás las principales características de un juego de azar.
1. Reúnete con un compañero para jugar “carrera al 10”. Las reglas del juego son las siguientes:
Se requieren dos jugadores. El jugador que inicia el juego puede anotar sólo el número 1 o
el 2. El otro jugador puede sumar 1 o 2 al número que anotó el primer jugador. En los si-
guientes turnos, siempre se le suma 1 o 2 al número que anotó el jugador anterior. Gana el
juego el primero que llegue a 10. Observa lo siguiente:
Toño Manuel Los jugadores son Toño y Manuel:
Toño inició el juego y anotó el número 1.
Manuel decidió sumar dos y anotó el 3.
1
5
8
3
7
10
¿Qué número anotó después Toño? ¿Quién ganó?
Ahora juega con tu compañero y anota en cada caso quién ganó.
Jugador 1 Jugador 2 Jugador 1 Jugador 2 Jugador 1 Jugador 2 Jugador 1 Jugador 2
Ganador: Ganador: Ganador: Ganador:
Jueguen varias veces hasta que encuentren alguna estrategia para ganar.
Comenten con sus compañeros si este juego es de azar o no y por qué. Versióndeevaluación23/04/12

S9
73
2. Observa las siguientes tres cajas con canicas. Debes extraer una canica de una de las ca-
jas, sin ver; ganas si la canica es blanca.
Caja A Caja B Caja C
¿De qué caja prefieres hacer la extracción?
Utiliza canicas y una caja o una bolsa para realizar varias extracciones. Recuerda que no
debes ver la canica hasta que esté afuera, y después de registrar su color debes regresarla
a la caja para seguir jugando.
Realicen el juego varias veces más, ¿hay una manera segura de ganar el juego?
Comenten en grupo y con su profesor si este juego es de azar o no y digan por qué.
3. Completa la siguiente tabla contestando Sí o No, para ello deberás tomar en cuenta los seis
juegos que has realizado en esta secuencia.
Juego
Se puede anticipar
quién ganará
Se puede encontrar una
estrategia para ganar
Se puede controlar
el resultado
Es un juego
de azar
Gato
Volados
Adivina el número
Oca
Carrera a 10
Extracción de canicas

Comparen sus respuestas con las de sus compañeros de grupo, y con ayuda de su profesor
contesten las siguientes preguntas.
¿Al lanzar un dado, se puede determinar el número de puntos que se mostrarán en la cara
superior? ¿Por qué?
¿Se puede determinar la cara que quedará a la vista al lanzar una moneda al aire?
¿Por qué?
¿Se puede determinar el color de la canica que se extrae de una caja o urna, sin ver?
¿Por qué?

B1
74
Sesión 38
En esta sesión aprenderás a registrar los resultados posibles
de un juego de azar.
1. En parejas, lleven a cabo la siguiente actividad, que consiste en lanzar varias veces
un dado.
a) Primero contesten las siguientes preguntas.
Antes de lanzar un dado, ¿saben en qué número caerá?
Si lanzan un dado muchas veces, ¿qué número saldrá más veces?
b) Ahora, lancen su dado veinte veces y registren sus resultados en la siguiente tabla.
Número de
lanzamiento
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Puntos que
marca el dado
¿Cuál es el número de puntos que más veces salió?
¿Qué número de puntos no salió?
¿Los resultados coinciden con lo que predijeron antes de lanzar el dado?
2. Comparen los resultados obtenidos por las diferentes parejas del grupo.
Concentren en una gráfica como la siguiente los resultados de cada equipo.
Númerodevecesquesalió
Número de puntos
1 2 3 4 5 6
Si elaboraron una tabla, cópienla en el pizarrón
y comparen los resultados con los de la gráfica.
¿Qué número se repitió más veces?
¿Quénúmeroserepitiómenosveces?
¿Hubo algún número de puntos que no saliera al
lanzar el dado?
Si se realiza un nuevo lanzamiento, y quieren ga-
nar, ¿qué número escogerían?
Hagan el lanzamiento, ¿ganó el número que es-
cogieron?

S9
75
Sesión 39
En esta sesión encontrarás alguna estrategia para jugar un juego
de azar en función del análisis de los resultados posibles.
1. En parejas, seleccionen una bolsa de canicas del siguiente grupo.
Bolsa 1 Bolsa 2 Bolsa 3 Bolsa 4
Consideren que utilizan esa bolsa para realizar el experimento de sacar canicas al azar,
devolviendo cada vez la canica que se saca antes de la siguiente extracción. Si se realizan
veinte extracciones, ¿cuántas canicas azules y blancas estiman que van a salir? Anoten sus
predicciones en el siguiente cuadro.
Predicciones
Azules
Blancas
2. Utilicen una bolsa no transparente y canicas, de acuerdo con el número de bolsa que se-
leccionaron, para realizar el experimento. Uno por uno deberá extraer una canica. Registren
en sus cuadernos los resultados; por ejemplo, anoten A cuando sale una canica azul, y una
B cuando sale una blanca. No olviden regresar la canica a la bolsa. Realicen cada uno
veinte extracciones.
Después de hacer el experimento completen el cuadro con el total de canicas azules y
blancas que salieron.
Resultado de veinte extracciones
Azules
Blancas


B1
76
3. Comparen sus resultados con los obtenidos por otras parejas que seleccionaron la misma
bolsa. ¿Obtuvieron los mismos resultados?
¿Por qué consideran que se obtuvieron esos resultados?
¿Consideran que influye el hecho de que hay igual número de canicas azules que de blancas?
Al considerar todos los resultados que obtuvieron en el grupo, ¿qué color ha salido con más
frecuencia?
¿Se puede saber el color de la canica que sale en una extracción?
Comparen los cálculos que hicieron y vean quiénes se acercaron más.
Si el juego se gana cuando se saca más veces una canica azul, ¿qué bolsa conviene elegir?
 Autoevaluación
1. Describe un juego que sea de azar.

2. Si se lanza una canica por cada laberinto, ¿en cuál de ellos es más probable que salga la
canica por la salida 1?
a)
1 1 112 2 223 33 4
b) c) d)
En los juegos de azar no podemos predecir quién ganará porque no se puede controlar los resultados. Sin
embargo, al registrar y analizar sus resultados podemos encontrar alguna estrategia de juego.

S9
77
Sesión 40
Evaluación
Aplica lo aprendido y selecciona la respuesta a cada problema.
1. ¿Qué notación decimal corresponde a 5
10
?
a) 0.50 b) 0.050 c) 0.0050 d) 0.00050
2. ¿Qué punto corresponde a la ubicación de la fracción 21
6
?
0 a b c d 4
a) d b) c c) b d) a
3. Dos tablas, una de 3
4
de pulgada y otra de 7
8
de
pulgada, son unidas por un clavo de 2 pulgadas,
¿qué parte del clavo sobresale de las tablas?
a) 1
4
b) 3
8
c) 1
8
d) 3
4
4. La sucesión numérica 2, 4, 8, 16, 32, 64, 128, 256,
512,…
a) Aumenta de dos en dos.
b) Disminuye de dos en dos.
c) Cada término es el doble del anterior.
d) Cada término es el cuadrado del anterior.
5. ¿Qué expresión algebraica se puede usar para
calcular el perímetro de un triángulo isósceles?
a) P = a + b + c c) P = 2(a + b)
b) P = 2a + b d) P = 3(a + b)
6. Dos mujeres compraron 80 gallinas en $3 200;
Andrea aportó $1 420 y Susana el resto. ¿Cuántas
gallinas corresponden al dinero que aportó Susana?
a) 50 b) 48 c) 42 d) 36
7. Utilizando sólo un compás marca los cuatro vértices
que definen a un cuadrado. Toma como una de las
aristas del cuadrado el segmento de recta siguiente.
A
B
8. ¿Cómo se llama la recta que divide a un ángulo en
dos ángulos iguales?
a) Mediatriz c) Bisectriz
b) Mediana d) Altura
9. Se lanzaron dos dados, gana Alberto si la suma es
menor a 7; Gonzalo si cae 7; Carmen si cae una suma
mayor de 10, y Ximena si cae 8, 9 o 10. ¿Quién de
ellos tiene más posibilidades de ganar?
a) Alberto c) Gonzalo
b) Carmen d) Ximena

Bloque 2

• Resolver problemas utilizando el máximo común divisor
• Resolver problemas geométricos que impliquen
el uso de las propiedades de las alturas, las medianas,
las mediatrices y las bisectrices en triángulos
y cuadriláteros.

80
Secuencia 10
Criterios de divisibilidad
Formulación de los criterios de divisibilidad
entre 2, 3, 5 y 7. Distinción entre números primos
y compuestos.
Sesión 41
En esta sesión determinarás los criterios para distinguir cuándo
un número es divisible entre 2 o entre 3.
Trabaja con un compañero para resolver el problema siguiente.
Beatriz quiere repartir los productos que se muestran en la tabla, de tal forma que al número
de personas que se indica les toque exactamente la misma cantidad entera.
Escriban en la tabla la cantidad que le corresponde a cada persona, cuando esto sea posible,
o pongan una cuando no se pueda dividir exactamente. Si tienen dudas con alguna reparti-
ción, pueden hacer una división para comprobar.
Número de
personas
$1 140 125
naranjas
77
manzanas
439
nueces
56
huevos
181
hojas de
papel
48
lápices
12
gomas
14
sacapuntas
2
3
5
7
¿Pudieron realizar la repartición de todos los productos
entre el número de personas señalado en cada renglón?
De las cantidades que se repartieron:
¿Cuáles son divisibles entre 2, esto es, que se pudieron
dividir exactamente entre 2?
¿Cuáles son divisibles entre 3?
¿Podrían establecer un procedimiento para determinar
cuándo un número es divisible entre 2, 3, 5 o 7, sin realizar
la división?
¿Todas las cantidades se podrán dividir exactamente entre
el 1 y ellas mismas? ¿Por qué?

81
En parejas, realicen las actividades siguientes.
1. En un deportivo se van a dar clases de seis deportes en los que se requiere repartir
a los participantes en dos o tres grupos. Con la información de alumnos inscritos
que se muestra en la siguiente tabla contesten en qué disciplinas es posible formar
dos o tres grupos con el mismo número de integrantes. Escriban SÍ en el caso de
que sea posible, y NO cuando no lo sea. Si tienen dudas, hagan las divisiones.
Especialidad Inscritos
¿Es posible formar 2 grupos
con el mismo número de
integrantes?
¿Es posible formar 3 grupos
con el mismo número de
integrantes?
Natación 220
Futbol 213
Beisbol 111
Volibol 146
Tenis 98
Atletismo 132
¿En qué deportes sí fue posible formar 2 grupos exactos?
¿En cuáles fue posible formar 3 grupos exactos?
Escriban los números que se pudieron dividir exactamente entre 2, es decir que son divisi-
bles entre 2. ¿Qué característica tienen en común estos números?
Expliquen brevemente cómo es posible determinar, sin realizar la división, cuándo un núme-
ro es divisible entre 2.
Escriban los números que se pudieron dividir exactamente entre 3, es decir que son divisi-
bles entre 3. ¿Qué característica tienen en común estos números?
¿Tiene algo que ver la terminación de los números para que sean divisibles entre 3?
¿Por qué?

B2
82
2. En la siguiente tabla hay diez números que al dividirlos entre 3 dejan residuo cero. Subráyenlos.
123 528 111 923 611
326 327 259 405 102
420 936 639 412 984
Busquen alguna característica que tengan en común los números divisibles entre 3.
Pueden realizar operaciones (suma, resta, multiplicación, división) con los dígitos de cada
número y ver si hay alguna característica común.
Comparen sus observaciones en el grupo y saquen una conclusión respecto a cómo deter-
minar cuándo un número es divisible entre 3 sin realizar la división.
Los números cuya última cifra es un número par son divisibles entre 2.
Por ejemplo:
458 es divisible entre 2, porque la última cifra es par.
1 080 es divisible entre 2, porque la última cifra es 0.
Son divisibles entre 3 los números en los que la suma de los dígitos que lo forman es un
múltiplo de 3.
Ejemplos:
285 es divisible entre 3, porque la suma de 2 + 8 + 5 es 15, y 15 es múltiplo de 3.
542 319 es divisible entre 3, porque la suma de 5 + 4 + 2 + 3 + 1+ 9 es 24, y 24 es
múltiplo de 3.
Un número natural a es divisible entre otro natural b distinto de cero,
cuando puede dividirse exactamente entre éste, es decir que existe un
natural c, de tal forma que bc = a. b a = c

S10
83
Sesión 42
En esta sesión conocerás los criterios para determinar cuándo
un número es divisible entre 5 o 7.
En parejas, lleven a cabo las actividades siguientes.
1. Catalina quiere comprar unas estampas para repartirlas entre sus cinco hijos, pero quiere
que a cada uno le toque un número exacto de estampas y que no sobre ninguna. ¿Qué
paquetes puede comprar para que se cumplan estas condiciones?
Escriban qué paquetes cumplieron con las condiciones marcadas.
Escriban qué características tienen en común los paquetes que sí cumplieron las condiciones.
2. Encierren los números que sean divisibles
entre 5.
¿Qué característica observan en los nú-
meros que pueden dividirse entre 5?
3. Analicen el procedimiento siguiente, que permite saber cuándo un número es divisible
entre 7.
a) ¿El número 386 es divisible entre 7?
Separen el dígito de las unidades: 38 6
Dupliquen el dígito de las unidades: 6 × 2 = 12
Resten el producto a las cifras de la izquierda: 38 − 12 = 26
Si el resultado es cero o múltiplo de 7 el número será divisible entre 7. Como 26
no es múltiplo de 7, entonces 386 no es divisible entre 7. Realicen la división y
compruébenlo.
123 365 258 415 780 965
589 333 200 555 145 789
235 350 625 380 415 100

B2
84
b) ¿El número 875 es divisible entre 7?
Resten el producto a las cifras de la izquierda: 87 − 10 = 77
Como el 77 es múltiplo de 7, entonces el 875 es divisible entre 7. Realicen la
división y compruébenlo.
c) Cuando el número es mayor, por ejemplo 2 982, el proceso se repite tantas ve-
ces como sea necesario. Analicemos si 2 982 es múltiplo de 7.
Dupliquen el dígito separado: 2 × 2 = 4
Resten el producto a las cifras que quedaron a la izquierda: 298 − 4 = 294
Se repite el procedimiento con el número obtenido en el paso anterior, para ver
si es múltiplo de 7, es decir, el 294.
Resten el producto a las cifras que quedaron a la izquierda: 29 – 8 = 21
El 21 es múltiplo de 7, entonces el 2 982 es divisible entre 7.
907 2520
875
787
602
644
339
337
Se cree, pero no se ha demostrado, que todo número par mayor que 2 se puede escribir
como suma de dos números primos. Este resultado se conoce como la conjetura de
Goldbach.
Ejemplos:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
4. Analiza los siguientes números. Emplea el procedi-
miento anterior para determinar si el número es divisi-
ble entre 7, y si el número es divisible, subráyalo.
Si tienen resultados distintos, comprueben realizando
la división.

S10
85
Sesión 43
En esta sesión conocerás qué son los números primos
y los números compuestos.
¿Qué tipos de números conoces?
1. En parejas, escriban qué tipos de números son los siguientes:
1°, 2°, 3°…
1, 2, 3, 4,…
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0, 2, 4, 6, 8…
2. Escriban qué otro tipo de números conocen y den un ejemplo de ellos.
Comparen sus respuestas con las de otra pareja y en caso de duda comenten con su maestro.
3. En equipos, resuelvan el problema siguiente.
Fátima tiene un pasatiempo: le gusta analizar números y
determinar cuáles son sus divisores. Ella sabe que un
número es divisor de otro cuando lo divide exactamente.
Ayúdale a completar la tabla.
¿Entre qué números fue divisible el 43?
¿y el 47?
Esta fue la forma en que Jorge analizó los números 43 y 47.
No son divisibles entre 2 porque no terminan en número par. No son divisibles entre
3 porque sus dígitos no suman un múltiplo de 3. No son divisibles entre 5 porque
no terminan en 0 o en 5. No son divisibles entre 7 porque al duplicar el dígito
de las unidades y restarlo a lo demás no da un múltiplo de 7. ¡No son divisibles
entre esos números!
¿Qué opinan del análisis que hizo Jorge?
Número Divisible entre…
240 1, 2, 3, 4, 5, 6,
43
246
47

B2
86
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
•• En la siguiente tabla tachen el 1 porque
no es número primo.
•• Encierren con un círculo el 2 y tachen to-
dos sus múltiplos (4, 6, 8, etcétera).
•• Encierren con otro círculo el siguiente nú-
mero que no esté tachado, en este caso el
3, y tachen todos sus múltiplos (6, 9, 12,
etcétera).
•• Encierren con un nuevo círculo el siguiente
número que no esté tachado, ahora sería
el 5, y tachen todos sus múltiplos (5, 10,
15, etcétera).
•• Encierren con un círculo el siguiente nú-
mero que no esté tachado, que será el 7,
y tachen todos sus múltiplos.
•• Busquen el siguiente número sin tachar y
enciérrenlo en un círculo. Después tachen
todos sus múltiplos.
•• Continúen así hasta que todos los núme-
ros estén tachados o encerrados.
En su cuaderno dividan los números 43 y 47 entre sí mismos y comenten lo que sucede.
¿Pudieron dividirse entre sí mismos? ¿Qué cociente obtuvieron?
Ahora dividan entre 1 los números señalados.
¿Qué cociente obtuvieron?
¿Qué pueden concluir?
De acuerdo con la definición anterior, ¿el número 1 es un
número primo?
4. En equipos, realicen la actividad siguiente.
La criba de Eratóstenes
Eratóstenes (276-194 a.n.e.) fue un matemático griego que ideó una forma para reconocer
cuáles números son primos. Háganla ustedes también.
Hay números que sólo tienen dos divisores
diferentes: ellos mismos y la unidad. Los
números que sólo tienen dos divisores diferentes
se llaman números primos.
1 13 , 13 13 ; 1 43 , 43 43 ; 1 47 , 47 47

S10
87
 Autoevaluación
• Determina entre qué números primos son divisibles los siguientes números:
210, 105, 77, 184, 91.
Consulta en…
Entra a los sitios: http://mimosa.pntic.mec.es/jgomez53/matema/conocer/primos.htm
y http://thales.cica.es/cadiz2/ecoweb/ed0898/recursos/sabiasque.htm,
donde encontrarás otros aspectos interesantes de los números primos.
Los números encerrados en círculo, es decir, los que quedaron sin tachar, son los números
primos menores de 100. Escríbanlos a continuación.
Todos los números que fueron tachados, a partir del 4 reciben el nombre de números com-
puestos.
Escriban con sus propias palabras lo que entienden por número compuesto.
Comparen su texto con el de otros equipos, y si tienen alguna duda coméntenla con el
maestro.

88
Secuencia 11
MCD y mcm
Resolución de problemas que impliquen
el cálculo del máximo común divisor
1. Reúnete con un compañero para resolver el problema siguiente.
Se inscribieron 240 personas en un curso de idiomas. Todas deben pertenecer a algún
grupo. Si se forman grupos con el mismo número de integrantes, cuántas personas habrá
en cada uno si se tienen:
Cinco grupos
Seis grupos
Ocho grupos
Doce grupos
¿Qué hicieron para saber cuántas personas correspondían a cada grupo?
Comprueben si 240 tiene como divisores a 5, 6, 8 y 12.
Sesión 44
En esta sesión resolverás problemas efectuando el cálculo del máximo común
divisor.

89
1. En equipos, resuelvan los problemas siguientes.
En la tabla se muestran los participantes que se han inscrito para las distintas disciplinas
de las pruebas de atletismo.
Disciplina Número de participantes
Carreras 60
Salto 48
Lanzamientos 30
Marcha 120
a) Se trata de formar equipos de manera que haya el mismo número de participantes de
cadadisciplina.¿Cuáleselmayornúmerodeequiposquesepuedencrear?
¿Cuántos integrantes de cada prueba habrá por equipo?
b) Diana dice que para contestar las preguntas la operación que se necesita emplear es la
división. ¿Tiene razón? ¿Qué números son los que hay que dividir?
¿Entre qué número habría que dividir?
c) Pedro dice que hay que multiplicar. ¿Tiene razón? ¿Qué números son los que
hay que multiplicar? ¿Por qué número habría que mul-
tiplicar?
d) Escriban en la tabla todos los divisores que tiene cada número
Número Divisores
60
48
30
120
¿Cuáles divisores son comunes a todos los números?
e) Comenten lo siguiente.
De los divisores comunes, ¿cuál es el mayor?
¿Cómo se relaciona este número con la solución del problema?

B2
90
El máximo común divisor (mcd) de varios números corresponde al
divisor que es común para todos los números dados y además
es el mayor.
Por ejemplo:
El mcd de los números
108 132 120 144
Números Divisores
108 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108
132 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132
120 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
144 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
Los divisores comunes son: 1, 2, 3, 4, 6 y 12, y el mayor es el 12.
Por lo tanto, el mcd de 108, 132, 120 y 144 es 12, esto quiere
decir que el número 12 es el número mayor que puede dividir
exactamente a todos los números mencionados.
Sesión 45
En esta sesión resolverás problemas encontrando el mínimo común múltiplo.
1. En parejas, resuelvan los problemas siguientes.
a) Rosa, Raúl y Rita juegan a la pulga y las trampas en una tira que llega hasta el 50.
Rosa dice que su pulga saltará de 3 en 3 empezando en el 1, Raúl dice que su pulga
saltará de 5 en 5 empezando en el 2, Rita podrá poner 2 trampas.
¿Lospodráatraparconlasdostrampasonecesitarámás?
¿Podríaatraparlosconunatrampaonecesitarálasdos?
Escriban los números por los que pasará la pulga de cada uno.
Rosa:
Raúl:
¿En qué números le conviene a Rita poner sus trampas para atrapar a sus compañeros?
Comparen sus respuestas con las de otros compañeros, y en caso de duda pidan que
justifiquen sus respuestas.
2. En equipos, resuelvan el problema siguiente.
Edna horneó galletas de diferentes sabo-
res: nuez, 216 piezas; vainilla, 264; cho-
colate, 240; fresa, 288, y con azúcar,
144. Quiere empacarlas en bolsas distri-
buidas equitativamente.
¿Cuál es el número máximo de bolsas que
puede llenar sin que le sobren o le falten
galletas? ¿Cuántas galletas
de cada sabor deberá poner en cada bol-
sa?
Comparen sus respuestas con las de otro
equipo, y en caso de duda pidan que jus-
tifiquen su respuesta y analicen cuál con-
sideran que es el procedimiento correcto.

S11
91
b) Luis, Leti, Luci y Lalo juegan a la pulga y las trampas en una tira que llega hasta el 100.
Todos iniciarán en el cero. Luis saltará de 4 en 4, Leti de 6 en 6, Luci de 3 en 3, y Lalo
solamente tendrá oportunidad de colocar una trampa.
¿Bastará una trampa para atraparlos a todos?
¿En dónde le conviene a Lalo colocar la trampa para atrapar al mayor número de com-
pañeros?
Si quiere atraparlos a todos lo antes posible, ¿en qué casilla deberá poner la trampa?
Escriban los números por los que pasará la pulga de cada uno.
Luis:
Leti:
Luci:
Observen los números por los que pasarán las pulgas y contesten:
¿Cuáles son los números comunes a todos?
¿Cuál es el número menor por el que pasarán todas las pulgas?
¿En qué número le conviene a Lalo poner la trampa?
Comparen sus respuestas con las de otro equipo, y en caso de duda pidan que las
justifiquen.
El mínimo común múltiplo (mcm) de varios números corresponde al múltiplo positivo que es común para
todos los números dados y además es el menor.
Por ejemplo:
El mcm de los números
18 12 10
Números Divisores
18 36, 54, 72, 90, 108, 126, 144, 162, 180, 198, 216, 234,…
12 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204,…
10 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180,…
El primer múltiplo común es 180.
Por lo tanto, el mcm de 18, 12 y 10 es 180. Esto quiere decir que el número 180 es el menor múltiplo
común y que puede ser dividido exactamente entre todos los números mencionados.

B2
92
Sesión 46
 Autoevaluación
• Escribe una forma de calcular el mínimo común múltiplo de varios números.
• Escribe una forma de calcular el máximo común divisor de varios números.
• Usando los números 18, 12 y 36, inventa dos problemas, uno que involucre el cálculo del
mínimo común múltiplo y otro que requiera el cálculo del máximo común divisor.
Avenida Central
parada
paradaparada
Enrique
En esta sesión resolverás problemas realizando el cálculo del máximo común
divisor o del mínimo común múltiplo.
a) Carlos tiene los dulces que se enlistan a continuación: 40 higos, 56 alegrías,
48 pepitorias y 24 calabazas. Los quiere empacar en cajas para su venta, de
tal forma que use el mayor número de cajas y que en cada una haya la misma
cantidad de cada tipo de dulces. ¿Cuántas cajas usará y cuántos dulces de
cada tipo habrá en cada una?
b) Para cubrir una ruta de 60 cuadras hay tres líneas de autobuses que suben o
bajan pasaje al final de las cuadras de la siguiente forma: la línea verde hace
parada cada 3 cuadras; la azul, cada 4 cuadras, y la rápida solamente se
detiene cada 6 cuadras.
Si Enrique vive en la esquina del final de la cuadra 7 y quiere caminar hasta
la calle más próxima en la que hagan parada las tres líneas, para que pueda
tomar cualquiera de ellas, ¿cuál es la cuadra a la que debe caminar?
Mónica vive en la esquina del principio de la calle 15 y quiere caminar a su
casa desde cualquier cuadra en la que pare una de las líneas. ¿Cuál parada
le queda más cerca? ¿De qué línea de autobús es?
Comparen sus respuestas con las de otro equipo, y en caso de duda pidan
que las justifiquen.

93
Secuencia 12
Sumas con fracciones
y decimales
Resolución de problemas aditivos en los que
se combinan números fraccionarios y decimales
en distintos contextos, empleando los algoritmos
convencionales.
Sesión 47
En esta sesión resolverás problemas utilizando la equivalencia
entre fracciones.
Trabajen en parejas para resolver la siguiente actividad.
Al comienzo del año, doce personas participan en una tanda, que es una modalidad de ahorro
en la que todos aportan al mes la misma cantidad de dinero, la cual se entrega en su totalidad
en cada ocasión a una persona diferente. En el mes de agosto un integrante salió de viaje y
otro tuvo un accidente, lo que les impidió hacer su aportación.
¿Qué fracción de la tanda recibió la persona en turno?
a) Hoy en la mañana Luis Adrián tomó medio litro de leche antes de ir a la escuela. Por la
tarde, al regresar a su casa, tomó otro vaso de leche, equivalente a un cuarto de litro, y
finalmente, antes de irse a dormir bebió leche en un vaso con capacidad de tres cuartos
de litro. Si consideramos que un vaso equivale a un cuarto de litro, ¿cuántos vasos de
leche tomó el día de hoy Luis Adrián?
b) El señor López utiliza la tercera parte de su día de trabajo en contestar llamadas; asi-
mismo, durante la mitad de la jornada laboral se encuentra en juntas con clientes. El
tiempo restante lo considera como su momento productivo. Conforme a la percepción
del señor López, ¿a cuántos momentos productivos es equivalente el tiempo destinado
a atender llamadas y a estar en juntas con clientes?
Comenta tus resultados con el grupo.
Cuando dos o más fracciones representan la
misma cantidad, entonces son equivalentes;
es decir, 1
2
= 2
4
.

B2
94
Para sumar o restar dos o más fracciones que
tienen diferente denominador se deben obtener
fracciones equivalentes con denominador común.
Sesión 48
En esta sesión resolverás problemas que implican el empleo de fracciones.
En equipos, resuelvan los siguientes problemas.
a) Tres hermanos reciben cada uno de sus papás la misma cantidad de dinero para utilizarla
en lo que quieran durante la semana. Pasados tres días los niños deciden juntar la cantidad
de dinero con que cuentan en ese momento porque quieren comprar un juguete que vale
1 1
3
veces lo que recibió alguno de ellos. Si al primero le queda la mitad de lo que recibió,
al segundo 2
6
y al tercero 7
8
, ¿será posible que les alcance el total de su dinero para com-
prar el juguete que quieren?
b) La señora Tina decidió hacer la dieta de la luna para bajar de peso. Al terminarla pesaba
9
10
de lo que tenía al comienzo de su dieta, sin embargo, debido a que tuvo una descom-
pensación estuvo en el hospital una semana. Al salir pesaba 1
8
menos que cuando inició la
dieta. ¿Qué fracción de peso perdió en total la señora Tina?

Un denominador común es cualquier múltiplo común de los denominadores de las fracciones,
así que por conveniencia utilizaremos el mínimo común múltiplo. Por ejemplo, en el caso de
3
2
+ 5
3
− 1
6
el mínimo común múltiplo de los denominadores es 6, de forma que las fracciones
equivalentes son 9
6
, 10
6
y 1
6
, siendo el resultado de la operación
18
6 = 3.

S12
95
Sesión 49
En esta sesión compararás fracciones.
En parejas, resuelvan los problemas siguientes.
a) En el siguiente cuadro se muestra la fracción que representan los maestros de secundaria
con respecto al número de alumnos de ese nivel en siete países. Esto es, la tabla nos dice
cuántos maestros hay por número de alumnos.
País Maestros por número de alumnos
Argentina
3
50
Brasil
3
50
Chile
1
25
Corea
1
20
España
2
25
Estados Unidos
7
100
México
1
20
Fuente: Elaboración propia con base en información del INEE.
Panorama educativo de México 2009, p. 40.
¿Qué países superan a México en mayor número de maestros por número de alumnos?
¿Por cuánto más?
¿Qué país es el que tiene mayor número de maestros por número de alumnos?
b) La familia Pérez fue a Acapulco, realizando el trayecto en un tiempo de 6 1
8
horas. Estando
allí se encontraron a la familia López, quienes llegaron por otro camino, empleando un
tiempo de 3 2
3
horas.
¿Cuánto tiempo se hubiera ahorrado la familia Pérez de haber tomado el mismo camino que
la familia López?
Para hacer una suma o una resta de números mixtos se acostumbra convertirlos a
fracciones impropias. Luego, las fracciones impropias se transforman en fraccio-
nes equivalentes con denominador común para poder efectuar la operación.

B2
96
Para realizar la adición o la sustracción con números decimales se
escriben los números en forma vertical, de manera tal que las cifras
queden alineadas a partir del punto decimal, esto permite sumar
décimos con décimos, centésimos con centésimos, y así sucesivamente.
Ejemplo:
9.05
+ 12.50
25.00
46.55

Sesión 50
En esta sesión verás cómo se trabaja con números decimales en ciertas
actividades cotidianas.
Trabajen en equipos la actividad siguiente.
Los precios de algunos productos que se venden en la papelería “La Goma” son los siguientes:
Producto Precio
Lápiz de 2 1
2
$ 3.00
Cuaderno profesional $ 17.80
Goma $ 6.20
Bolígrafo $ 4.20
Fotocopia $ 0.60
Fólder $ 1.50
Encuentren el costo de:
Diez copias, un fólder y un bolígrafo
Un cuaderno profesional, lápiz de 2
1
2 y una goma
80 copias, dos fólderes y tres cuadernos
Si una persona que va a “La Goma” tiene destinado pagar $100.00, ¿qué podría comprar?
Escriban una opción.

S12
97
Sesión 51
En esta sesión resolverás problemas utilizando tanto fracciones como decimales.
a) En un grupo de secundaria la mitad de los hombres está en el taller de electrónica,
mientras que la tercera parte de las mujeres cursa el de computación, ¿cuál es la diferen-
cia entre la fracción de hombres que estudian electrónica y la de mujeres que cursan
computación?
b) Una persona tiene que trabajar 40 horas a la semana. Si el lunes laboró 7
1
4 h, el mar-
tes 9
1
2 h, el miércoles 10
2
3 h, y el jueves 6
5
6 h, ¿cuánto tiempo tendrá que laborar el
viernes?
c) En una tlapalería, el señor Robles pagó por un kilogramo de cemento la cantidad de $35.60,
y por dos kilogramos de estopa, $15.06. Al pagar con un billete de $200, el encargado le
dice que no cuenta con centavos, por lo que el señor Robles acepta que no le dé los centavos
de cambio. ¿Cuánto recibió de cambio?
d) En el refrigerador de la casa de Juan hay un recipiente con 3.5 litros de leche; si él toma
1
4 L de leche por día, ¿para cuántos días le alcanza la leche que hay?
e) En un frutero hay 2 1
2
kg de fruta; si hay 0.125 kg de melón, 1
4
kg de manzana y medio
kilogramo de sandía, ¿qué cantidad de kilogramos hay de otras frutas?
 Autoevaluación
• ¿Cómo resolverías la siguiente operación?
3
5 + 7
2
10 + 0.85
• ¿Cuál es el resultado expresado en fracción?
• ¿Cuál es el resultado expresado con número decimal?

98
Secuencia 13
Multiplicación y división
con fracciones
la multiplicación y la división con números
fraccionarios en distintos contextos,
utilizando los algoritmos usuales.
Sesión 52
En esta sesión resolverás problemas cotidianos empleando la multiplicación
y la división de fracciones.
1. Contesta lo siguiente.
Óscar compra 1
2
kg de carne, 3
4
kg de cebolla, 3
4
kg de tortillas, 1 1
2
kg de jitomate y
verdura que pesó 2 1
2
kg, y todo lo pone en una bolsa, ¿cuánto peso lleva la bolsa?
Si su hermana le ayuda con la verdura y la carne, ¿cuánto peso lleva cada uno?

99
1. En parejas, completen la tabla y contesten las preguntas.
Una persona compró en el mercado las siguientes mercancías para su despensa.
Mercancías
Cantidad
de kilogramos
Precios
por kilogramo
Cantidad de dinero
a pagar
Cebollas 3 $6
Azúcar 1 1
2
$18
Carne
3
4
$80
Huevo
1
4
$24
¿Por cuál de las cuatro mercancías pagó más?
¿Cuánto pagó en total?
Si compran tres veces esa cantidad de cebollas, ¿cuánto deben pagar?
¿Cuánto cuesta 1
2
kg de azúcar?
Si compran 2 kg de carne, ¿cuánto deben pagar?
¿Y si compran 1
2
kg de huevo?
¿Cómo calculan cuánto pagó esa persona por la carne?
Si por 1
4
de kg de huevo paga 6 pesos, ¿cuánto dinero pagará por 3
4
kg?
2. Resuelve el problema siguiente.
El señor Pedro compró una pieza de 15 m de tela. Va a utilizar 4 1
2
m para hacer sus pan-
talones. El resto de la tela lo va a repartir en partes iguales a sus tres hijos.
¿Cuántos metros de tela le corresponden a cada hijo?
Pedro va a confeccionar dos pantalones con la tela que tiene, ¿cuántos metros utilizará
para cada pantalón?
Analiza con un compañero la estrategia seguida para resolver los problemas anteriores.

B2
100
Sesión 53
En esta sesión seguirás aplicando la multiplicación y la división de fracciones
en diferentes contextos, ahora las estudiarás para calcular áreas.
¿Cuánto tendrá de área un espejo rectangular que mide 2 m de alto y 5 m de largo?
alto
largo
2. En parejas, realicen la actividad siguiente y anoten los resultados en su cuaderno.
Una persona necesita comprar tres hojas de triplay con las siguientes medidas:
Hoja 1: 1
3
m × 1
6
m Hoja 2: 1 1
2
m × 3
5
m Hoja 3: 5
6
m × 3 m
La hoja de triplay que mide 6.10 m × 1.83 m vale $250.00.
Calculen el área y el costo de las hojas 1, 2 y 3.
Describan brevemente el método que siguieron para calcular el costo de las hojas.
Si se necesita una hoja de triplay que mida 3 m de largo y 1
4
m de ancho, ¿cuánto medirá
su área?, ¿y cuál será su costo?
Comparen sus respuestas y los procedimientos que emplearon con los de otras parejas.
Don José tiene una parcela de forma cuadrada. Si aró las 3
4
partes de su parcela y sembró
2
3
partes de la parte arada, ¿qué parte de la parcela sembró?
En la parte de la parcela que está sin arar construyó un corral que ocupa la mitad de ésta.
¿Qué parte de la parcela ocupa el corral?
Si el terreno mide de largo 1
5
de kilómetro, ¿cuál es el área en metros cuadrados de la
parcela de don José?
4. Comenten en grupo cómo se obtiene el producto y el cociente de dos fracciones.

S13
101
Sesión 54
En esta sesión resolverás problemas de multiplicación de fracciones.
En el museo Universum de la unam, en la ciudad de México, se tienen simuladores en los que
se representa la fuerza de gravedad de los planetas de nuestro sistema solar.
Los planetas atraen a los objetos con distinta intensidad.
La fuerza de gravedad en la Tierra es 5
6
veces la fuerza en Neptuno. Esto significa que en Nep-
tuno una persona saltaría 5
6
veces menos alto de lo que salta en la Tierra, y que su peso sería
6
5
veces mayor.
Si en la Tierra el récord de salto de altura es cercano a 2.5 m, ¿cuál sería la altura de este
récord en Neptuno?
Una persona que pesa 80 kg en la Tierra, ¿cuánto pesaría en Neptuno?
1. En equipos, completen la tabla siguiente.
Integrantes
del equipo
Peso en la Tierra
(en kg)
Peso en la Luna
(1
6
del peso en la Tierra)
Peso en Marte
(2
5
del peso en la Tierra)
Peso en
Neptuno
Cuando se multiplica cualquier número por una fracción menor que 1, el producto es menor
que ese número, porque se toma sólo una parte de él:
5
6
× 9 = 45
6
= 7 3
6
= 7 1
2
; 7 1
2
es menor que 9;
5
6
× 1
2
= 5
12
; 5
12
es menor que 1
2
.
Y cuando se multiplica cualquier número por una fracción mayor que 1, el producto es mayor
que ese número, porque se toma más de una vez:
5
2
× 4 = 20
2
= 10; 10 es mayor que 4;
5
2
× 2
3
= 10
6
; 10
6
es mayor que 2
3
.

B2
102
Sesión 55
En esta sesión resolverás problemas de división de fracciones en
distintos contextos.
Si en una papelería tienen un rollo de hule para forrar de 12 m y necesitan cortar trozos
de 2
3
m cada uno, ¿cuántos trozos se obtienen?
Si el rollo tuviera 15 1
2
m y necesitaran cortar trozos de 1
4
m cada uno, ¿cuántos trozos
se obtendrían?
2. En equipos, realicen las siguientes actividades.
La siguiente figura representa un rollo de hule de 12 m de largo.
Marquen la medida del largo de los trozos (2
3
m) tantas veces como se pueda a lo
largo del hule.
¿Cuántos trozos obtuvieron?
1 m 1 m 1 m 1 m 1 m 1 m 1 m 1 m 1 m 1 m 1 m 1 m
La fracción recíproca o inversa de una fracción es otra frac-
ción que se obtiene al invertir sus términos. Por ejemplo:
de 2
3
su recíproca o inversa es 3
2
.
¿Cuál será el resultado de multiplicar una fracción por su
recíproca?
Consulta en…
Entra al sitio http://www.universum.unam.mx/
y analiza la información que contiene acerca
de los planetas y la fuerza de gravedad.

S13
103
Dividir un entero entre una fracción es equivalente a multiplicar el
entero por el recíproco de la fracción. Por ejemplo:
12 ÷ 3
4
= 12 × 4
3
= 12
1
× 4
3
= 48
3
= 16
12 ÷ 1
2
= 12 × 2
1
= 12
1
× 2
1
= 24
1
= 24
Dividir cualquier fracción (dividendo) entre otra (divisor) es equivalente
a multiplicar el dividendo por el recíproco del divisor.
Por ejemplo:
9
5
÷ 3
4
= 9
5
× 4
3
= 36
15
= 12
5
Completen la siguiente tabla.
Cantidad de hule
disponible
12 m 12 m 12 m 12 m 12 m 12 m 12 m
Medida del largo
de los trozos
12 m 6 m 3 m 11
4
m 13
4
m 1
6
m 1
8
m
Número de trozos
que se obtienen
Si el rollo de hule mide 12 m y cortan trozos de 1
3
de m, ¿cuántos trozos se obtienen?
Escriban la división que corresponde a cada situación:
Si el rollo de hule mide 15 1
2
m y cortan trozos de 1
6
m, ¿cuántos trozos se obtienen?
Escriban la división que modela esta situación:
÷ =
Si tienen 10 trozos de 1
2
m y los unen, ¿cuántos metros de hule tienen en total?

B2
104
Sesión 56
En esta sesión estudiarás problemas de multiplicación y división de fracciones
en diversos contextos.
a) En una planta lechera se tienen distintas presentaciones de un mismo producto. Un
tanque de leche deslactosada tiene 36 000 L, con los que se llenarán 20 000 garrafo-
nes, sin que sobre leche.
¿De qué capacidad deben ser los garrafones?
¿Qué operación realizaron para encontrar la respuesta?
b) Se van a repartir 6 3
4
L de leche light en 27 envases. Se quiere que en cada envase haya
la misma cantidad de líquido y que no sobre.
Encierra la operación que resuelve correctamente el problema.
6 3
4
÷ 27 27 ÷ 6 3
4
27
4
× 18
4
6 3
4
× 27
¿Qué cantidad de leche quedará en cada envase?
2. En parejas, analicen las siguientes divisiones y, sin resolverlas, escriban frente a cada una:
cociente entero, resultado menor que el dividendo o resultado mayor que el dividendo, se-
gún sea el caso. Resuelvan las operaciones en su cuaderno y corroboren sus cálculos.
3 ÷ 2
4
= 2 1
3
÷ 3=
5 3
4
÷ 3 2
3
= 2
7
÷ 3
5
=
4
7
÷ 3
4
= 24
3
÷ 14
7
=

S13
105
 Autoevaluación
En una escuela presentaron examen 240 alumnos.
1. Si 3
6
de los alumnos que aprobaron son mujeres, ¿cuántas mujeres aprobaron?
a) 82 b) 104 c) 98 d) 72
2. Del total de alumnos que presentaron el examen, 5
12
están en primer grado, y de éstos,
4
5
lo aprobaron. ¿Cuántos alumnos de primer grado aprobaron?
a) 80 b) 65 c) 102 d) 78
a) Se tienen 9 litros de miel y se van a envasar en botellas de 3
4
, ¿cuántas botellas se
llenarán?
b) El rendimiento de gasolina de un automóvil A es de 11 1
2
km/L, y el del automóvil B es
de 15 1
4
km/L. Si con el tanque lleno el automóvil A recorre 690 km, ¿cuál es la capa-
cidad del tanque A? ¿Cuánto recorre el automóvil B
con la misma cantidad de gasolina?
Comparen sus procedimientos con los de otras parejas.

106
Secuencia 14
Propiedades de la mediatriz
y la bisectriz
Resolución de problemas geométricos que impliquen
el uso de las propiedades de la mediatriz de un
segmento y de la bisectriz de un ángulo.
Sesión 57
En esta sesión conocerás las aplicaciones que tienen las diferentes
propiedades de la mediatriz de un segmento.
En temas del bloque anterior viste el trazo de la mediatriz de un segmento y de la bisectriz de
un ángulo. Algunos problemas y situaciones generales en geometría implican el conocimiento
y análisis de las propiedades de dichos lugares geométricos.
El maestro de Matemáticas de 1°B ha organizado un concurso de construcción de papalotes
entre sus alumnos, con la condición de que los papalotes sean diseñados con figuras geomé-
tricas y que contengan representaciones de la mediatriz de un segmento y de la bisectriz de un
ángulo. El papalote ganador será premiado.
Chucho y su amigo entraron al concurso e investigaron algunos esquemas de figuras que cum-
plen con las condiciones solicitadas.
¿Qué necesitan saber Chucho y su amigo acerca de la mediatriz y la bisectriz para armar el
papalote y ganar el concurso?
Dibuja algunas figuras geométricas que conozcas, con las condiciones que puso el profesor.

107
1. En equipos, analicen el siguiente problema y contesten.
En un concurso de tiro con arco se colocan cinco blancos frente al tirador en turno; a éste
se le indica que debe situarse en el centro de la línea de tiro y desde ahí efectuar sus
disparos.
Localiza el punto P sobre la línea de tiro desde donde su disparo al punto C sea una per-
pendicular. Dibuja ahora los segmentos que parten del centro de la línea de tiro hacia cada
uno de los blancos marcados con las letras A, B, D y E.
¿Cuántos pares de segmentos iguales hay y cuáles son?
Siacercamoslalíneadetiro,¿cuántosparesdesegmentosigualesquedan?
En caso de que se decida alejar la línea de tiro, ¿cuántos pares de segmentos iguales
quedan?
¿Cuál es el segmento que tiene diferente medida que los demás?
¿Qué lugar geométrico representa dicho segmento si pasa por el punto medio de la línea
de blancos?
C
A
B
D
E

B2
108
Sesión 58
En esta sesión definiremos las propiedades de la mediatriz
que nos ayuden a resolver ciertas situaciones de la vida cotidiana.
1. Lee la información siguiente y contesta.
Al padre de Pepe, que es
herrero, le solicitaron una
puerta que tenga un diseño
como el que se muestra en
la siguiente figura:
Largo
Alto
Por la carga de trabajo, el papá le encargó a Pepe que realizara los cortes para la construc-
ción de la puerta, considerando su diseño y el ahorro de material. Reúnanse en equipos y
contesten las siguientes preguntas para ayudar a Pepe con el trabajo. Pueden hacer trazos
en su cuaderno para explicar sus procedimientos.
•• ¿Cómo son entre sí las varillas que forman el contorno de cada figura?
•• Si se pretende utilizar dos varillas para el centro de cada figura, ¿cuántas se necesitan
para armar la secuencia?
•• ¿Qué condición deben cumplir las dos varillas centrales para que la figura se arme co-
rrectamente?
•• Observa la secuencia de figuras, ¿cuántas mediatrices encuentras?
¿Cuál es la propiedad de la mediatriz que se usa en el armado del centro de cada rombo?
¿Cuál es la propiedad de la mediatriz que se usa en el armado del contorno de cada
figura?
En equipos, y con ayuda de su profesor, concluyan qué tipo de propiedades de la mediatriz y
su correcto trazo hemos analizado, y que podrían ayudar al padre de Pepe a entregar un mejor
diseño en su trabajo.
Para finalizar, tracen en su cuaderno un diseño
parecido al que debe entregar el padre de Pepe
con las medidas que ustedes determinen, y mar-
quen con color rojo la distancia de la mediatriz a
los extremos del segmento que divide y con color
azul el ángulo recto que forma la mediatriz con el
segmento que divide.
La mediatriz es la recta perpendicular a un segmento que
lo corta en su punto medio.
La mediatriz tiene una importante propiedad: la distancia
de cualquier punto de esa recta a cada uno de los dos
extremos del segmento al que divide es la misma.

S14
109
Sesión 59
En esta sesión resolverás algunos problemas usando las propiedades
1. En parejas, analicen el siguiente problema y contesten.
El maestro de Matemáticas del 1ºC propuso al grupo construir relojes de manecillas para
analizar las propiedades de la bisectriz de un ángulo , y luego procedió a plantear lo siguiente:
¿Qué hora exacta será cuando el minutero esté en las doce, el horario en las cuatro y el
segundero sea la bisectriz que forman las dos anteriores?
¿Quétuvieronquehacerparaencontrarlarespuestamásadecuada?
¿Cómoesladistanciaquehayentrecadamanecillaaesahora?
2. Realiza lo que se indica.
Traza en tu cuaderno tres círculos de 5 cm de radio, marca la división de las horas como si
fuera un reloj de manecillas y determina tres ángulos con sus bisectrices, como se hizo en
la actividad anterior.
Compara tus trazos con los de tus compañeros.

B2
110
La bisectriz de un ángulo es la recta que lo divide en dos
ángulos iguales.
También es el lugar geométrico de los puntos del plano que
están a la misma distancia (equidistan) de las semirrectas
de un ángulo.
Sólo en un triángulo equilátero la bisectriz de sus tres
ángulos internos es también la mediatriz de los lados
opuestos.
Sesión 60
En esta sesión continuarás aplicando las propiedades
1. Formen equipos, analicen el siguiente problema y contesten.
Un problema que interesó durante mucho tiempo a los griegos fue trisecar (dividir en tres
ángulos iguales) un ángulo, utilizando sólo regla y compás. En el siglo XIX se demostró que
esto es imposible.
Elige un punto sobre la primera bisectriz trazada, y con
ayuda de tus escuadras dibuja rectas perpendiculares de
este punto a los lados del ángulo. Mídelas.
¿Qué observas?
En grupo, y con ayuda de su profesor, concluyan las pro-
piedades de la bisectriz que utilizaron en la solución y tra-
zo de esta situación.
Dibujen en su cuaderno tres ángulos de diferentes tama-
ños y amplitudes, tracen la bisectriz a cada uno y señalen
con color rojo las partes en las que se observen las propie-
dades de dicho lugar geométrico.
En la figura de la derecha podemos observar un triángulo
rectángulo. Si el segmento BC representa el pilar central
de un puente, el segmento AB el tirante principal, y se
pretenden colocar tres tirantes más que salgan del vérti-
ce B dividiendo al ángulo en partes iguales, ¿en qué pun-
tos deben colocarse los extremos de los tirantes sobre
el puente?
b
c
a
A
B
C
¿En cuántas partes es necesario dividir el ángulo B para
colocar las tres cuerdas?
¿Los extremos sobre el segmento “b” quedan a la misma
distancia uno del otro?
¿Cuántas veces se puede dividir un ángulo?

S14
111
Sesión 61
En esta sesión resolverás distintos problemas geométricos que implican el uso de
las propiedades de la mediatriz de un segmento y de la bisectriz de un ángulo.
a) Une los puntos y traza la mediatriz al segmento PQ.
b) Traza los ejes de simetría de cada figura. Marca con
un color los que, además de ser ejes de simetría,
también sean mediatrices de algún lado de las figu-
ras, y con otro color los que sean bisectrices de
algún ángulo de las figuras.
c) Encuentra un punto que esté a la misma distancia
de los tres lados del siguiente triángulo (pista: re-
cuerda que cualquier punto de la bisectriz de un
ángulo está a la misma distancia de los dos lados
que lo forman).
 Autoevaluación
Traza en tu cuaderno un segmento, su mediatriz, marca dos puntos sobre ella y traza con
color rojo las distancias de los puntos a los extremos del segmento. Define la propiedad.
Traza en tu cuaderno un ángulo, su bisectriz, marca puntos sobre la bisectriz y traza con
color rojo las distancias de los puntos a los lados del ángulo. Define la propiedad.
Consulta en…
Para conocer más sobre este tema busca en las bibliotecas escolares y de aula el siguiente
libro: Carlos Bosch y Claudia Gómez, “Construcciones básicas” y “Paralelas con doblado de
papel”, en Una ventana a las formas, México, sep-Santillana, 2003 (Libros del Rincón).
P Q

112
Secuencia 15
Fórmulas para calcular
el área y el perímetro
Justificación de las fórmulas del perímetro y del área
de polígonos regulares, con apoyo de la construcción
y transformación de figuras.
Sesión 62
En esta sesión trabajarás con los perímetros y las áreas de triángulos
y rectángulos.
Calcula el perímetro y el área de las siguientes figuras.
Cuadrado
3 cm
Triángulo
3 cm
4 cm
Rectángulo
4 cm
3 cm
Hexágono
2 cm
Compara tus respuestas con las de otro compañero, y comenten los métodos utilizados para
obtenerlas.

113
Realiza las siguientes actividades.
a) Dibuja y recorta dos triángulos rectángulos cuyos lados midan 3 cm, 4 cm y 5 cm res-
pectivamente (igual al de la figura anterior).
Luego pégalos sobre el rectángulo de la figura anterior.
¿Cuál es la relación entre el área del rectángulo y la de cada uno de los triángulos?
¿Qué puedes decir del perímetro del rectángulo y de los triángulos?
b) Ahora dibuja en tu cuaderno un triángulo, con las medidas que desees. Haz dos copias
de tu triángulo y recórtalas.
Recorta cada uno de estos triángulos en dos partes por la altura del lado más largo. Con
las cuatro piezas obtenidas forma dos rectángulos. Describe cómo los acomodaste.
b
h hh
a c
Pega los rectángulos en tu cuaderno, a un lado del triángulo original.
¿Qué tienen en común estos rectángulos?
¿Qué relación hay entre el área de tu triángulo original y la suma de las áreas de los
rectángulos obtenidos?
c) Compara y comenta tus respuestas con las de otro compañero.

B2
114
Sesión 63
En esta sesión trabajarás con las áreas de rombos, romboides y trapecios.
Realiza las actividades siguientes.
1. Dibuja en tu cuaderno un rombo del tamaño que desees. Después haz una copia del rombo
y recórtala.
Dibuja en ambos rombos su diagonal mayor y su diagonal menor. Ahora recorta la copia a
través de sus diagonales para que obtengas cuatro triángulos.
Utiliza los triángulos para formar un rectángulo, y pégalo a un lado del rombo original.
¿Qué relación tienen las medidas de las diagonales del rombo con los lados del rectángulo
formado?
¿Cuál es la relación entre el área del rombo y la del rectángulo?
2. Dibuja un romboide en tu cuaderno. Haz una copia del romboide y recórtala.
Recorta la copia en dos partes, de modo que con éstas formes un rectángulo. Pega el rec-
tángulo formado a un lado del romboide original.
¿Qué relación tienen las medidas del romboide y las del rectángulo?
¿Cuál es la relación entre sus respectivas áreas?

S15
115
3. Dibuja en tu cuaderno un trapecio. Haz dos copias del trapecio y recórtalas.
Con las dos copias recortadas forma un romboide y pégalo a un lado del trapecio original.
¿Qué relación hay entre las medidas del trapecio y las del romboide?
¿Qué relación hay entre las áreas respectivas?
Compara y comenta tus resultados con los de otro compañero.
Los ejercicios realizados en esta sesión justifican estas fórmulas. Comenten en grupo sus aná-
lisis y con ayuda del profesor establezcan una conclusión.
En la siguiente tabla se anotan las fórmulas para calcular el área del rombo,
el romboide y el trapecio.
Área
d
D
(diagonal mayor × diagonal menor)
2
h
b
base × altura
h
b
B
(base mayor + base menor) × altura
2
Rombo
Romboide
Trapecio

B2
116
Cualquier polígono regular se puede dividir en tantos triángulos como lados tenga, uniendo
cada vértice del polígono con su centro. La altura de los triángulos que va de un lado del
polígono al centro se llama apotema.
El centro de un polígono regular es el punto que equidista de cada uno de sus vértices; por
lo tanto, el centro del polígono es el centro de la circunferencia que circunscribe al polígono.
Sesión 64
En esta sesión trabajarás con las áreas de polígonos regulares.
1. Realiza las actividades siguientes.
a) Dibuja y recorta seis triángulos equiláteros con lados de 2 cm.
Utiliza los triángulos para cubrir el hexágono que aparece al principio de esta secuencia
(pág. 112).
¿Qué relación hay entre el área del hexágono y la de uno de los triángulos?
¿Cómo calculas el perímetro del hexágono?
b) Dibuja un pentágono regular en tu cuaderno y ubica su centro.
Une cada uno de los vértices del pentágono con el centro mediante una línea recta.
¿En cuántos triángulos queda dividido el pentágono?
¿Qué tienen en común los triángulos?
¿Qué relación hay entre el área del pentágono y la de los triángulos?
2. En parejas, comenten lo siguiente.
¿Es posible hacer algo similar a lo realizado en el ejercicio anterior con un polígono regular
de más de seis lados?
¿Y con un polígono regular de menos de cinco lados?

S15
117
Sesión 65
En esta sesión continuarás trabajando las áreas de polígonos regulares.
1. Realiza la siguiente actividad.
Dado un polígono regular de n lados, se puede calcular su área mediante la siguiente
fórmula:
Área =
perímetro × apotema
2
a) ¿Cómo calculas su perímetro? Da una fórmula.
b) Justifica la fórmula del área de un polígono regular.
2. Calcula el área de la siguiente figura.
Compara y comenta tus resultados con los de otro compañero.
 Autoevaluación
Completa la siguiente tabla con las fórmulas para calcular las áreas y los perímetros que se
piden.
Perímetro Área
Triángulo
Rombo
Romboide
Polígono regular de n lados

118
Secuencia 16
Proporcionalidad directa
Identificación y resolución de situaciones de
proporcionalidad directa del tipo “valor faltante”
en diversos contextos, con factores constantes
fraccionarios.
Sesión 66
En esta sesión comenzarás a utilizar las nociones de proporcionalidad.
Para el cumpleaños de Mario se esperan veinte invitados. A cada uno le darán dos tamales
oaxaqueños preparados con la receta de la abuelita Carlota.
Tamales oaxaqueños (para 10 porciones)
4 hojas de plátano grandes lavadas y hechas rollo
1 Pollo mediano
1
4
kg de pierna de puerco
1
2
kg de mole negro
250 g de manteca de cerdo
1 kg de masa blanca para tortillas
Cebolla, ajo y sal al gusto
¿Para cuántos tamales es la receta?
¿Cuántos tamales necesitan preparar?
Escribe a continuación las cantidades adecuadas para
preparar los tamales que se necesitan.
Tamales oaxaqueños (40 porciones)
hojas de plátano grandes lavadas y hechas rollo
pollo mediano
kg de pierna de puerco
kg de mole negro
g de manteca de cerdo
kg de masa blanca para tortillas
Cebolla, ajo y sal al gusto
Si disminuimos la cantidad de porciones, ¿qué sucederá con la cantidad de hojas de plátano
que se requiere?
Si aumentan las porciones, ¿qué sucederá con la cantidad de manteca de cerdo que se requiere?

119
1. Con la información de la receta de la abuelita Carlota resuelve el siguiente problema. Como
gustaron tanto los tamales oaxaqueños, la mamá de Mario decidió abrir su propio negocio
de tamales. Mario desea elaborar una tabla para ayudarle a calcular la cantidad de ingre-
dientes que requiere, de acuerdo con el número de porciones que va a preparar. Ayúdale a
completarla.
Ingredientes
(en kg)
Números de Porciones
4 10 15
Masa blanca
Carne de cerdo
3
8
Mole negro
1
2
Para 12 porciones, Ana dice que se necesita 1
2
kg de carne de cerdo. Explica si ella tiene o
no razón.
Verifica con otro compañero tus respuestas.
a) Para hornear 25 donas se requiere 1
4
kg de harina, ¿cuántas donas se hornearán con
7 kg de harina?
b) En la construcción de una casa, con 3
4
partes de un bulto de mortero se pueden pegar
300 tabiques. Si se solicitaron 2 millares de tabiques, ¿qué cantidad de mortero se
necesita para pegar todo ese material?
Expliquen cómo encontraron la solución de cada problema.
Comparen sus procedimientos con los de otras parejas y reflexionen sobre lo siguiente.
Expliquen la importancia de conocer el valor unitario para resolver este tipo de problemas.
Verifiquen sus respuestas empleando el valor unitario.

B2
120
Sesión 67
En esta sesión aplicarás la constante de proporcionalidad para resolver
problemas de proporcionalidad directa.
1. En parejas, realicen la siguiente actividad con las figuras que se muestran.
a) Contesten las preguntas.
¿Cuánto miden los lados del cuadrado naranja en el A?
¿Cuánto miden en el B?
¿Cuánto mide el lado más largo del triángulo azul en A?
¿Cuánto mide el lado más largo del triángulo azul en B?
¿Cuál es la constante de
proporcionalidad, es de-
cir, cuántas veces es ma-
yor el Tangram B del A
respecto a los lados?
A
B

S16
121
Uno de los lados del triángulo rosa en el Tangram A mide 3 cm, conociendo la constan-
te de proporcionalidad y sin medir el triángulo rosa en el Tangram B, ¿cómo podrían
saber la longitud de su lado?
En el Tangram B la base del romboide mide 6 cm, sin medirla en el Tangram A y usando
la constante de proporcionalidad, ¿cómo obtendrían la longitud de la base del romboide?
Comparen sus respuestas con las de otros compañeros, comprueben que sean correctas.
2. En parejas, resuelvan lo siguiente.
a) Una estatuilla de madera que se talló en una telesecundaria mide 36 cm de altura y
13 cm de ancho. La estatuilla ha gustado tanto que se mandará reproducir de manera
tal que el ancho mida 87.75 cm. ¿Cuánto medirá la altura de dicha reproducción?
b) En una telesecundaria de Guanajuato se tiene la maqueta del taller de carpintería, el
cual mide 28 cm de largo y 12 cm de ancho. Si realmente el taller mide de ancho 14 m
y 3.2 m de altura, ¿cuántos centímetros mide la altura del taller en la maqueta?
¿Cuántos metros de ancho mide el taller?
Comparen sus respuestas con las de otros compañeros.
Cuando una cantidad aumenta o disminuye en la misma
constante de proporcionalidad respecto de otra, se dice
que están en proporción directa.

B2
122
3. Resuelve los siguientes problemas.
a) Para ilustrar una revista se va a utilizar una foto-
grafía original de 16 cm de largo por 8 cm de alto.
La ilustración para la portada se obtendrá de re-
ducir la fotografía original a la mitad, ¿cuáles se-
rán las medidas de la reproducción?
Si la ilustración de un reportaje se obtendrá de redu-
cir la fotografía de la portada a la cuarta parte, ¿cuá-
les serán las medidas de esta reproducción?
b) Óscar sabe que requiere 4.5 litros de gasolina
para recorrer aproximadamente una distancia de
42.75 km, ¿qué cantidad de gasolina requiere
para llegar a cada uno de los lugares menciona-
dos en la tabla?
Distancia
recorrida (km)
Cantidad de
gasolina (l)
San Juan
de los Lagos
38
Arandas 60.05
Tepatitlán 70.63
Tonalá 130

 Autoevaluación
• ¿Cómo se puede identificar un problema de proporción directa?
• ¿Qué es la constante de proporcionalidad y cómo se emplea?
Consulta en…
Entra al sitio http://recursostic.educacion.es/descartes/web/materiales_didacticos/
Proporcionalidad_lbc/magdirectprop.htm, y consulta acerca de la proporcionalidad directa.
¿Cuántos litros de gasolina necesita para recorrer
la distancia de un kilómetro?
¿Cuántos kilómetros recorrerá con un litro de ga
solina?
c) Para limpiar un terreno de tres hectáreas, Andrés y
María emplearon 22 jornadas de trabajo de 6 horas
cada una. Si ellos trabajan al mismo ritmo, ¿cuán-
tas horas se tardarán en limpiar un terreno de 7.5
hectáreas?
Comparen sus respuestas con las de otros compañeros y
comprueben que sean correctas empleando un método
diferente al que usaron.
Planteen en su cuaderno un problema de proporcionalidad
directa, resuélvanlo e intercámbienlo con otro compañero.
A lo largo de esta secuencia hemos visto que los proble-
mas de proporción directa se pueden resolver empleando
el valor unitario o la constante de proporcionalidad, esta
última se determina al comparar dos magnitudes; por
ejemplo, en el problema del Tangram, como cada lado del
A mide 6 cm y el del B 12 cm, la constante de proporcio-
nalidad es 6
12
, o bien 1
2
. La constante se multiplica o se
divide según se quiera determinar una cantidad mayor o
una menor a la que se tiene.

S16
123
Sesión 68
Evaluación
Aplica lo aprendido a lo largo del bloque y selecciona la respuesta a cada problema.
1. La respuesta a la siguiente operación 3
4
+ 1
9
– 0.8 es:
a) 11
180
b) 11
360
c) 11
18
d) 22
18
2. La distancia de cada uno de sus puntos a los lados del
ángulo que divide siempre es la misma:
a) mediana b) mediatriz c) recta d) bisectriz
3. Juan desea comprar un vidrio para cubrir una mesa
rectangular, cuyos lados miden 1 m y 1.5 m. Si el me-
tro cuadrado de vidrio cuesta $70, ¿cuánto le costara
el vidrio a Juan?
a) $75 b) $85 c) $95 d) $105
4. Entre qué números primos son divisibles los siguientes
números: 945, 735, 525.
a) 2, 3 b) 2, 3, 5 c) 3, 5, 7 d) 3, 7
5. Una línea de autobuses viaja a tres ciudades distintas,
A, B y C. Rumbo a la ciudad A sale un camión cada 3
horas, a la ciudad B cada 4, y a la ciudad C cada 5. Si
a las 7 de la mañana del lunes salieron los 3 camiones
al mismo tiempo, ¿qué día y a qué hora volverán a
salir al mismo tiempo los camiones?
a) El mismo lunes a las 7 p.m.
b) El mismo lunes a las 10 p.m.
c) El martes a las 3 a.m.
d) El miércoles a las 7 p.m.
6. Se tiene un terreno de forma irregular, como el de la
imagen. Si se desea saber cuál es su superficie, ¿con
cuál de los procedimientos siguientes se puede obte-
ner esa información?
a) Se mide la longitud de los lados del terreno y se
suman.
b) Se divide el terreno en cuadrados y la suma de las
superficies de cada cuadrado será la superficie del
terreno completo.
c) Se encuentra el centro del terreno, se calcula el
apotema y se multiplica por el número de lados del
terreno.
d) Se segmenta el terreno en triángulos, se calcula la
superficie de cada uno, se suman las superficies
obtenidas y esa es la superficie del terreno.
7. Mariana y Adriana sembraron 280 arbolitos. Si trabaja-
ron 5 horas diarias durante 4 fines de semana sem-
brando arbolitos, ¿cuántas horas se tardarán en
sembrar 1 400 arbolitos?
a) 280 horas c) 56 horas
b) 200 horas d) 25 horas

Bloque 3

• Resolver problemas en los que se tengan que efectuar
multiplicaciones y/o divisiones con fracciones y números
decimales.
• Resolver problemas que impliquen el uso de ecuaciones
de las formas: x + a = b; ax = b y ax + b = c, donde
a, b y c son números naturales y/o decimales.
• Resolver problemas que impliquen el cálculo de
cualquiera de las variables de las fórmulas para encontrar
el perímetro y el área de triángulos, cuadriláteros y
polígonos regulares. Explicar la relación que existe entre
el perímetro y el área de las figuras.

126
Secuencia 17
Multiplicación con decimales
Resolución de problemas que impliquen la
multiplicación de números decimales en distintos
contextos, utilizando el algoritmo convencional.
Sesión 69
En esta sesión realizarás multiplicaciones de números decimales
para resolver problemas de escalas.
En una fotografía las medidas son proporcionales a las reales. La imagen de una persona en
una foto está a escala 1 a 35, es decir que cada centímetro en la foto corresponde a 35 cm
en la realidad.
Si en la foto la persona mide 5 cm, ¿cuánto mide en la realidad?
1. En parejas, observen la siguiente imagen y reprodúzcanla a escala en su cuaderno, de ma-
nera que su dibujo sea 4 1
5
veces más grande que el original.
6 cm
4 cm
8.24 cm

127
2. Completen la tabla.
Multiplicación Producto (resultado de la multiplicación)
4.2 × 4
4.2 × 6
4.2 × 8.24

3. Calculen las medidas de los lados que miden 4 cm y 8.24 cm con los factores de escala
que aparecen en la tabla.
Factor de escala Medida del lado de 4 cm Medida del lado de 8.24 cm
0.15 0.6 cm 1.236 cm
0.7
1
2.2
3.4
8.3

Con base en la información de la tabla, contesten lo siguiente.
¿Qué tienen en común las escalas que amplifican el dibujo?
¿Qué tienen en común las escalas que reducen el dibujo?
4. Calcula mentalmente lo siguiente.
1.25 × 4 =
0.5 × 0.5 =
1.4 × 10 =
0.7 × 0.3 =
0.125 × 8 =
1.52 × 5 =
Comenten con otras parejas qué sucede cuando se multiplica un número natural por un
factor menor que la unidad.

B3
128
Sesión 70
En esta sesión multiplicarás números decimales en diferentes contextos.
1. En parejas, contesten lo siguiente.
a) El papá de Pedro, que trabaja en California, manda 75 dólares semanalmente para el
gasto familiar. Si el tipo de cambio es 1 dólar = 13.80 pesos…
¿Cuánto reciben a la semana en pesos?
¿Cuánto reciben al mes en pesos?
b) Una lámina de acero mide 6 × 20 pies. Si 1 pie = 30.48 cm, ¿cuáles son las medidas
de la lámina en centímetros?
¿Cuál es el área en metros cuadrados?
c) En un almacén están estibadas cajas A y B de 45.3 cm y 25.4 cm de altura respectiva-
mente. Si en una primera estiba hay 4 cajas A y 8 cajas B, ¿qué altura alcanza esta
estiba?
Si en otra estiba se encuentran 6 cajas B y 7 cajas A, ¿qué altura alcanza esta otra estiba?
d) En la telesecundaria 11 se organiza un campamento que durará tres días, con un costo
de $125.50 por día. ¿Cuánto pagará cada alumno por el campamento?
Si asistirán 79 alumnos, ¿cuánto dinero se recaudará?
e) A la semana, un automóvil consume 32.8 L de gasolina. Si el costo del litro de gasolina
es de $10.48, ¿cuánto dinero se gasta cada quincena en gasolina?
Comparen sus resultados con los de otra pareja y corrijan de ser necesario. Versióndeevaluación23/04/12

S17
129
Sesión 71
En esta sesión pondrás en práctica los conocimientos aprendidos en las
sesiones anteriores.
I. Adriana quiere cambiar el piso de la sala de su
casa por duela. Si las dimensiones de la sala
son 3.50 m por 4.80 m.
a) ¿Cuántos metros cuadrados de duela com-
prará?
b) Si el metro cuadrado de duela cuesta
$435.50, ¿cuánto invertirá?
c) La mano de obra del carpintero le va a
costar $160.00 por metro cuadrado, ¿cuánto le
pagará?
d) ¿Cuánto gastará en total Adriana?
 Autoevaluación
• Leonardo debe comprar cuatro y medio manojos de espinacas; si el manojo cuesta $7.75,
¿cuánto pagará Leonardo en total?
Consulta en…
Entra al sitio http://www.sectormatematica.cl/educbasica.htm y da clic en “Multiplicando
con decimales” y en “Multiplicando decimales menores que 1”.
II. En la clase de Tecnología se va a elaborar una con-
serva de frutas de la región. Para ello se utilizan
0.450 kg de pulpa de fruta, 0.225 kg de azúcar y
0.125 L de agua. ¿Cuántos gramos de pulpa de
fruta, azúcar y agua se requieren para elaborar tres
y media veces la cantidad de conserva?
III. En el año 2011 México sufrió un fuerte problema de
sequía en la mayoría de los estados, lo que afectó
a un total de 974.92 mil hectáreas de cultivo. Del
total de hectáreas afectadas, Coahuila, Chihuahua
y Zacatecas concentran 1
3
parte. ¿Cuántas hectá-
reas fueron afectadas en dichos estados?
Comenta con un compañero tus estrategias de solución y compara los procedimientos que sean diferentes.

130
Secuencia 18
División con decimales
Resolución de problemas que impliquen la división
de números decimales en distintos contextos,
utilizando el algoritmo convencional.
Sesión 72
En esta sesión resolverás problemas de contextos cotidianos utilizando
la división de números decimales.
Resuelve el problema siguiente.
Jugando futbol, los compañeros del grupo de primer grado rompieron un cristal de la ventana
del salón. Si el costo del cristal es de $55.20 y deben pagarlo entre los 12 alumnos que esta-
ban jugando, ¿cuánto pagará cada uno?
Comenten con sus compañeros los procedimientos que siguieron.
1. En parejas, lleven a cabo las actividades siguientes.
a) Para asistir a un paseo se alquiló un autobús en $1 820.00 y cada niño pagó $45.50,
¿cuántos niños asistieron?
Si el alquiler hubiera costado $2 755.00 y cada niño hubiese pagado $72.50, ¿cuántos
niños habrían asistido?
b) Un alumno dedica 12 1
2
horas a la semana para estudiar 8 asignaturas, dedicando el
mismo tiempo a cada una. ¿Cuántas horas a la semana dedica a cada asignatura?
¿Cuántos minutos?

131
2. Resuelve mentalmente las divisiones siguientes.
3 ÷ 1.5 = 3 ÷ 0.25 =
6 ÷ 0.1 = 13.5 ÷ 0.5 =
2.5 ÷ 0.125 = 4 ÷ 0.1 =
16. 5 ÷ 0.3 = 6 ÷ 0.2 =
Comenta con tus compañeros qué sucede cuando se divide un número natural entre un
número decimal menor que la unidad.
Algunas divisiones entre números con punto decimal pueden resolverse con una multiplica-
ción, convirtiendo el decimal a fracción. Por ejemplo, 5 ÷ 0.2 puede escribirse como 5 ÷ 1
5
que, como estudiaron en la división de fracciones, equivale a multiplicar 5 × 5 = 25.
Raúl va a leer un libro que tiene 184 páginas. Si al día lee 40 páginas, ¿en cuántos días
leerá el libro?
Si lee las 40 páginas en 2 horas, ¿en cuántos minutos lee una página?
Si el libro costó $335.60 y lo compraron entre 4 amigos, ¿con cuánto cooperó cada uno?
Observa la división que se realizó para resolver el problema.
8 3 . 9 0
4 3 3 5 . 6 0
3 2
1 5
1 2
3 6
3 6
0 0
A cada uno le tocarán $83.90.
El algoritmo para dividir un decimal entre un natural es el mismo que cuando se dividen dos
naturales, sólo debe conservarse la posición del punto decimal, es decir que se sube el punto
al cociente.

B3
132
Sesión 73
En esta sesión resolverás problemas de cambio de dinero utilizando
la división de números decimales.
Pedro pagó $67.50 por varias copias de una guía; si cada juego de copias le costó $7.50,
¿cuántos juegos de copias sacó?
Describan un procedimiento para poder realizar la división que resuelve el problema.
7.50 67.50
Expliquen a sus compañeros cómo resolvieron la división anterior y por qué lo hicieron así.
2. Resuelvan las siguientes divisiones:
5 6 50 60 500 600 5000 6000
a) ¿Cómo son los resultados que obtuvieron?
b) Observen que el dividendo (6) y el divisor (5) de la primera división se multiplicaron por
10 para obtener la segunda división (60 y 50).
c) ¿Por qué número se multiplicaron el dividendo y el divisor de la primera división para
obtener la cuarta división?
3. Consideren que se tiene la siguiente división:
3.4 17
Multipliquen dividendo y divisor por 10, ¿qué división obtienen? Anótenla y resuélvanla.
Esta división es más sencilla que 17 ÷ 3.4, y por la propiedad utilizada en el ejercicio anterior
saben que el resultado de esta división es el mismo para ambas.

S18
133
 Autoevaluación
Selecciona la respuesta correcta al problema.
1. Daniela cuenta con $420.00 y desea comprar trompos para regalarlos a sus sobrinos. Si
cada trompo cuesta $21.50, ¿cuántos trompos podrá comprar?
a) 21 b) 18 c) 19 d) 15
2. ¿Cuánto dinero le sobrará?
a) $13.00 b) $11.50 c) $12.50 d) $10.50
Consulta en…
Entra al sitio http://www.sectormatematica.cl/educbasica.htm y da clic en “Dividiendo
con decimales”. Aprenderás sobre la división de números decimales.
Una división con punto decimal en el divisor se resuelve:
1º Se transforma la división en otra que no tenga punto decimal en el divisor, para ello se
multiplican el dividendo y el divisor por 10, 100, 1 000,... según el divisor tenga 1, 2, 3,...
cifras decimales.
2º Se resuelve la división equivalente una vez que el divisor está expresado como un
número natural.
Por ejemplo, para resolver:
0.25 4.217
Se multiplican por 100 el dividendo y el divisor, porque el divisor tiene dos cifras decima-
les, para obtener la división:
25 4.217
Y se resuelve.
El resultado de dividir 421.7 ÷ 25 es el mismo que el de dividir 42.17 ÷ 2.5 o 4.217 ÷ 0.25.
Compruébenlo con una calculadora.

134
Secuencia 19
Ecuaciones de primer grado
el planteamiento de ecuaciones de primer grado
de las formas x + b = c; a x = b; a x + b = c,
utilizando las propiedades de la igualdad,
con a, b y c números naturales, decimales
o fraccionarios.
Sesión 74
En esta sesión resolverás problemas mediante ecuaciones
de primer grado de la forma x + b = c.
Si tengo $80.00, ¿cuánto dinero debo ahorrar para reunir $225.00?
a) En este problema hay dos números que sí se conocen, ¿cuáles son?
b) ¿Cuál es el número que al sumarle 80 da como resultado 225?
Comenten con sus compañeros cómo resolvieron el problema.

135
1. Pedro desea saber qué cantidad tenía inicialmente en su cuenta de ahorros si efectuó un
depósito de $150.00 y al final le quedaron $750.00.
a) ¿Cuál es el valor desconocido en este problema? Subráyenlo.
La cantidad que depositó
La cantidad ahorrada que tenía
El saldo final de su cuenta
b) En el problema hay dos valores que sí se conocen, ¿cuáles son?
c) En la siguiente igualdad el valor desconocido del problema es el número que debe estar
en el recuadro. Encuéntralo.
+ 150 = 750
d) ¿Qué operación hicieron con los valores conocidos para encontrar el número que va en
el recuadro?
e) ¿Qué cantidad tenía Pedro inicialmente en su cuenta de ahorros?
2. Representen con una igualdad el problema siguiente.
¿Cuál es el número que al sumarle 85 da como resultado 220?
a) ¿Cuál es la igualdad algebraica que representa el problema?
b) ¿Qué operación deben hacer para encontrar el resultado?
En Matemáticas se emplean letras para representar los valores desconocidos
o incógnitas. Para representar estos valores comúnmente se usan las últimas
letras del abecedario en minúsculas, siendo x la más utilizada.

B3
136
3. El problema anterior podemos representarlo como:
x + 85 = 220, donde x representa el valor desconocido.
a) ¿Cuánto vale x ? x =
b) Comprueben su resultado sustituyendo el valor obtenido en lugar de x en la igualdad
anterior.
+ 85 = 220
La ecuación x + 85 = 220 se resuelve de la manera siguiente.
Se resta 85 a ambos lados de la igualdad:
x + 85 − 85 = 220 − 85
x + 0 = 135
x = 135
4. Ana realizó dos depósitos, uno de $300.00 y otro de $200.00. Ella desea saber cuánto
tenía ahorrado antes de realizarlos, si su saldo actual es de $ 1 400.00.
a) ¿Cuáles de las siguientes ecuaciones representan el problema?
x − 300 – 200 + 1 400 x − 300 + 200 = 1 400 x + 300 + 200 = 1 400 x + 500 = 1 400
b) Resuelvan la ecuación, es decir, encuentren el valor de x.
x =
c) ¿Qué cantidad tenía ahorrada al principio?
d) Hay dos ecuaciones que representan el problema, comprueben la solución sustituyendo
la x en ambas.
+ 500 = 1400 + 300 + 200 = 1400
5. Luis reparte volantes de publicidad. Sale de su casa con una cantidad y recoge 1 200 vo-
lantes antes de empezar su labor. Reparte 450 en la mañana, 680 en la tarde y al final le
sobran 260 volantes.
a) En este problema hay cuatro valores conocidos, ¿cuáles son?
, , ,
b) La ecuación x + 1200 − 450 − 680 = 260 permite representar el problema. Resuélvanla.
c) ¿Cuántos volantes tenía al salir de casa?
Las igualdades en las que hay un valor
desconocido o incógnita reciben
el nombre de ecuaciones.

S19
137
Sesión 75
En esta sesión resolverás problemas utilizando ecuaciones
de primer grado de la forma ax = b.
En parejas, realicen lo que se les pide a continuación.
1. Una persona tiene un empleo y recibe un salario mensual. Al final de 9 meses ha ganado
$40 500.00. ¿Cuál es su salario mensual?
a) ¿Cuál es el valor desconocido? Subráyenlo.
El número de meses trabajados
El salario de los 9 meses
El salario que cobró cada mes
b) Usando la letra z para representar la incógnita (valor desconocido) escriban una ecua-
ción que represente el problema.
c) Encuentren el valor de z.
d) ¿Cuál es la ecuación que representa el problema anterior? Subráyenla.
40 500 z = 9 40 500 + z = 9 z + 9 = 40 500 9 z = 40 500
e) ¿Cuál de las siguientes operaciones permite encontrar el valor de z ? Subráyenla.
9 ÷ 40 500 40 500 ÷ 9 40 500 – 9 9 × 40 500
f) Usando la operación que señalaron, encuentren el valor de z .
z =
g) ¿Cuánto ganó cada mes?
Recuerden que 9z es lo mismo que 9 × z, pues
usualmente en las expresiones algebraicas
no se utiliza el signo × para evitar confundirlo
con otro número desconocido o incógnita
representado con la letra x.

B3
138
2. El perímetro de un cuadrado es igual a 50 cm, ¿cuál es la longitud de cada lado?
a) ¿Cuál de las siguientes ecuaciones corresponde a este problema? Se usa la letra L para
representar la longitud de cada lado. Subráyenla.
4 L = 50 L ÷ 4 = 50 L ÷ 50 = 4 4 + L = 50
b) ¿Cuánto mide cada lado?
c) Comprueben la solución en la ecuación que eligieron.
d) ¿Qué operación hicieron para encontrar la longitud?
3. Completen la tabla siguiente, que presenta algunos problemas. Escriban las ecuaciones
correspondientes y las operaciones con las que se pueden resolver hasta obtener el valor
de la incógnita.
Problema Ecuación Operación Valor de la incógnita
¿Cuál es el número
que al multiplicarlo
por 11 da 132?
¿Cuál es el número
que al dividirlo
entre 9 da 172?
Comparen con sus compañeros las respuestas de los problemas de esta sesión y comenten
qué estrategias siguieron para resolverlos.
La ecuación 6 x = 36 se resuelve de la siguiente manera:
Como 6 multiplica a la incógnita x, multiplicamos ambos miembros de la ecuación por 1
6
,
que es el recíproco del 6.
1
6
× 6 x = 1
6
× 36
1
6
× 6 × x = 1
6
× 36
6
6
× x = 36
6
1 × x = 6,
por lo que x = 6
Compruébenlo sustituyendo el valor de x en la ecuación.

S19
139
Sesión 76
En esta sesión continuarás analizando diferentes tipos de ecuaciones y la
forma de resolverlas. Ahora trabajarás con ecuaciones de la forma ax + b = c.
1. Cristina ha leído un libro más que el doble de los que ha leído Antonio. Si Cristina ha leído
19 libros, ¿cuántos ha leído Antonio?
a) ¿Cuál es la incógnita en este problema?
Subráyenla.
Libros que ha leído Cristina
Libros que ha leído Antonio
Total de libros leídos por los dos
b) Escriban una ecuación para representar el proble-
ma. Usen la letra L para representar la incógnita.
c) Resuelvan la ecuación y escriban un enunciado con
su respuesta.
Comenten en grupo qué operaciones efectuaron para resolver la ecuación.
2. En parejas, completen el proceso para resolver la ecuación 2 x + 1 = 19.
Observen que hay expresadas dos operaciones: primero se multiplica 2 por x, y después al
resultado se le suma 1.
2 x + 1 = 19
2 x + 1 − = 19 −
2 x + =
× 2 × x = × 18
1 × x =
Por lo que x =
Comparen sus procedimientos con los de otras parejas.
El papá de Julia le dio cierta cantidad de dinero para que la repartiera equitativamente
entre ella y sus tres hermanos, después le dio $6.00 más. Cuando Julia hizo el reparto final,
a cada uno le tocaron $11.00.
a) ¿Qué tuvo que hacer Julia para
repartir el dinero?
b) Escribe una ecuación que repre-
sente lo anterior.
c) ¿Qué cantidad de dinero recibió
inicialmente Julia?
Comprueben la solución y compárenla con la de otras parejas.

B3
140
Sesión 77
En esta sesión resolverás problemas que se pueden representar
con las ecuaciones vistas anteriormente.
En el rectángulo que se muestra en la figura, la medida de la base es igual al triple de la
medida de la altura menos 1 cm.
a
9.5 cm
De las siguientes ecuaciones, subrayen las que sirven para encontrar la altura.
a × 3 + 9.5 = 1
3a − 1 = 9.5
(a ÷ 3 ) − 1 = 9.5
a ÷ 3 + 1 = 9.5
Con la ecuación seleccionada calculen el valor de la altura y comprueben su respuesta
sustituyéndolo en la ecuación.
2. La tercera parte del número de alumnos que hay en el grupo A, más 15, es igual a 29.
a) Escriban una ecuación para resolver este problema.
b) ¿Cuántos alumnos hay en el grupo A?
3. Asombra a tus compañeros adivinando su edad por medio de las ecuaciones algebraicas
que has aprendido.
Les dices: “Multiplica tu edad por 3, agrega 10 al resultado, réstale el doble de tu edad y a
lo que te resulte quítale 6”. A continuación pregúntales qué número obtuvieron. Su edad
será ese resultado menos 4.
Escriban una ecuación que les permita resolver este problema.
Comenten en grupo si obtuvieron la edad de sus compañeros.

S19
141
 Autoevaluación
Resuelve el siguiente problema planteando una ecuación.
• De una caja de mangos, Luis vendió 6 en la mañana. A media tarde vendió el doble que
en la mañana y por la tarde sólo vendió 8. Si en la noche sólo le quedaban 10 piezas,
¿cuántos mangos había en la caja?
Consulta en…
Entra al sitio http://www.librosmaravillosos.com/hombrecalculaba/capitulo37.html. Juega
y aprende “Cómo se adivina un objeto” utilizando ecuaciones.
En las bibliotecas escolares y de aula busca los libros con las siguientes referencias para
conocer más sobre este tema:
Carlos Bosch y Claudia Gómez, Una ventana a las incógnitas, México, sep-Santillana, 2003
(Libros del Rincón).
Malba Tahan, El hombre que calculaba, trad. Basilio Lozada, México, sep-Limusa, 2005
Para la clase siguiente debes traer recortados
30 triángulos, 10 de cada uno de los modelos
de la página 144.
4. Encuentra el valor de x en las siguientes ecuaciones. Resuélvelas en tu cuaderno y después
comprueba tus resultados sustituyendo el valor obtenido en la ecuación.
a) 5x + 0.5 = 12
b) ( x ÷ 4 ) + 38 = 120
c) x + 32 − 21 = 45.7
d) 7 x − 14 = 28
En grupo, den a conocer sus resultados, y en caso de
tener resultados diferentes analícenlos con su profesor.

142
Secuencia 20
Construcción de polígonos
regulares
Construcción de polígonos regulares a partir de distintas
informaciones (medida de un lado, del ángulo interno, del
ángulo central). Análisis de la relación entre los elementos
de la circunferencia y el polígono inscrito en ella.
Sesión 78
En esta sesión trabajarás con polígonos regulares.
Describecontuspropiaspalabrasquéesunpolígono.
Comenten en grupo sus descripciones.
Con los triángulos que recortaste, de cada uno de los siguientes modelos,
trata de armar los polígonos siguientes:
1 2 3

143
¿Qué polígono se puede formar con triángulos como el 1?
¿Cuántos triángulos utilizarías?
¿Qué polígono se puede formar con triángulos como el 2?
¿Qué polígono se puede formar utilizando triángulos como el 3?
Calca los triángulos y verifica tus respuestas.
¿Se pueden formar otros polígonos?
¿Qué relación encuentras entre el número de lados y el número de triángulos que forman cada
polígono?
¿Cómo es la medida de los ángulos de los triángulos cuyo vértice coincide con el centro del
polígono?
Un polígono es regular cuando sus lados son iguales y la medida de sus ángulos es la misma.
Formen equipos, realicen la siguiente actividad y contesten las preguntas.
1. En hojas blancas o de color tracen tres diferentes polígonos regulares de 5 cm, 8 cm
y 10 cm por lado respectivamente.
¿Cómo trazaron cada polígono para que todos sus lados fueran iguales?
¿Cuántos polígonos más se pueden trazar con las medidas que tienen?
¿Se puede trazar el mismo polígono de tres tamaños diferentes?
Comenten en grupo sus respuestas, y con apoyo de su profesor determinen cómo influye la
medida de los lados de un polígono regular en su construcción.

144
B3
Sesión 79
En esta sesión estudiarás las propiedades del ángulo interior
de un polígono regular.
En parejas, realicen la siguiente actividad.
1. En los siguientes polígonos regulares marquen con un color los ángulos interiores.
¿Cuántos ángulos tienen cada uno de los polígonos regulares?
Organizados en equipos:
2. Midan con ayuda del transportador y anoten la medida de los ángulos interiores de los
siguientes polígonos regulares.
Como habrás observado, el ángulo interior de un polígono regular es la
abertura que forman los lados consecutivos de la figura.

145
S20
3. Escriban en la tabla los datos que obtuvieron.
Nombre del polígono regular Medida de cada ángulo interior

4. Contesten lo siguiente.
a) ¿Cómo podemos construir un polígono regular a partir de la medida de su ángulo interior?
b) ¿Cuánto mide el ángulo interior de un decágono regular?
¿Y el de un dodecágono regular?
Analicen en grupo y con su profesor cómo se puede construir un polígono regular a partir de
la medida de su ángulo interior.
5. Tracen en su cuaderno un polígono para cada ángulo interior proporcionado.
a) 90°
b) 108°
c) 120°
Comparen sus trazos con los de sus compañeros.

146
B3
Sesión 80
En esta sesión estudiarás las propiedades del ángulo central
de un polígono regular.
En parejas, realicen la siguiente actividad.
1. En los siguientes polígonos regulares marquen con un
color los ángulos centrales.
¿Cuántos ángulos marcaron en cada uno de los polígo-
nos regulares?
Como habrán observado, los ángulos centrales de un
polígono regular son los que tienen su vértice en el
centro del polígono.
Organizados en equipos, lleven a cabo las actividades si-
guientes.
2. Tracen en su cuaderno al menos dos polígonos regulares utilizando la medida de los ángu-
los de las escuadras de su juego de geometría y contesten las siguientes preguntas.
¿Qué procedimiento siguieron para trazar sus polígonos?
¿Cómo son los ángulos centrales de los polígonos trazados en relación con el vértice de la
escuadra que usaron?
3. El número de ángulos centrales en un polígono regular es el mismo que el número de lados
de la figura.
Con base en esta información, completen la siguiente tabla.
Nombre del polígono Número de lados
Número de ángulos
centrales
Medida de cada
ángulo central
Suma de los ángulos
centrales
Cuadrado
Pentágono
Hexágono
Octágono
Dodecágono


147
S20
Sesión 81
4. Contesten las preguntas siguientes.
a) ¿Cuál es el resultado de multiplicar el número de lados de un polígono regular por la
medida de su ángulo central?
b) Si el número de lados de un polígono regular es 10, ¿cuál es la medida de su ángulo
central?
c) La medida de cada ángulo central de un polígono regular es 40°, ¿cuántos lados tiene
ese polígono?
d) ¿Qué polígono regular tiene un ángulo central de 90°?
Comenten en grupo sus respuestas.
En esta sesión construirás polígonos regulares a partir de la medida
de su ángulo interno, de su ángulo central o de la medida de uno de sus lados.
En el trazo de polígonos regulares inscritos en una circun-
ferencia podemos identificar algunos elementos importan-
tes de la misma.
1. En equipos, realicen lo siguiente.
Ordenen la secuencia de construcción de un pentágo-
no regular y pongan dentro de los recuadros la instruc-
ción que corresponde al trazo realizado.
Contesten lo siguiente.
¿Cuál es la relación entre el total de grados de la
circunferencia y los ángulos centrales de un polígono
regular?

¿Qué procedimiento deben seguir si quieren saber la
medida del ángulo central de un polígono regular con n
número de lados?

Utilicen su procedimiento para construir un eneágono.
Comenten sus respuestas con el grupo y con su profesor.
72 °
B
72 °
A
B
72 °
A
B
72 °
A

148
B3
 Autoevaluación
1. ¿Cuántos lados tiene un polígono regular con un ángulo interior de 150º?
a) 15 b) 14 c) 13 d) 12
2. ¿Qué polígono regular tiene un ángulo central de 40º?
a) Pentágono b) Octágono c) Undecágono d) Eneágono
Consulta en…
En las bibliotecas escolares y de aula busca el libro con la siguiente referencia para
conocer más sobre este tema: Carlos Bosch y Claudia Gómez, “Nombre de los polígonos”,
“La miel de los hexágonos”, “Recubrimientos”, “Los reflejos del caleidoscopio”
y “Construcción de un caleidoscopio”, en Una ventana a las formas, México, sep-Santillana,
2003 (Libros del Rincón).
2. En parejas, completen lo que se les pide.
A partir del siguiente triángulo isósceles, cuyo ángulo desigual es de 72º, formen el polígo-
no regular.

149
Secuencia 21
Cálculo de área y perímetro
Resolución de problemas que impliquen calcular
el perímetro y el área de polígonos regulares.
Sesión 82
En esta sesión resolverás problemas que implican calcular el perímetro
y el área del triángulo y del cuadrado.
En la siguiente imagen aparece el tablero de un juego de mesa llamado
“damas chinas”.
El tablero está dividido en pequeños triángulos equiláteros, los cuales
señalan los posibles movimientos de las piezas. Cada uno de estos
triángulos tiene lados de 1 cm y una altura
aproximada de 0.866 cm.
En parejas, contesten las siguientes preguntas.
¿Cuánto mide el perímetro del tablero?
¿Cuánto mide el área del tablero?
¿Cómo calcularon el perímetro y el área?
Comenten sus respuestas con el grupo y con su profesor.

150
B3
1. Contesta lo que se te pide.
El ajedrez y las damas son otros juegos de mesa muy populares, los cuales emplean un
tablero cuadrado dividido a su vez en 64 casillas cuadradas, como se muestra en la si-
guiente imagen.
A B C D E F G H
8
7
6
5
4
3
2
1
8
7
6
5
4
3
2
1
A B C D E F G H
Si cada casilla del tablero de ajedrez mide 1 cm, ¿cuánto miden el área y el perímetro del
tablero?
2. Ahora, junto con otro compañero, construirán un tablero de damas que tenga un área de
256 cm2
.
¿Cuánto medirán los lados del tablero y los lados de las casillas?
Investiguen las reglas para que puedan jugar con su tablero de damas.

151
S21
Sesión 83
En esta sesión realizarás cálculos relacionados con el perímetro
y el área de polígonos regulares de cinco y seis lados.
Resuelve los siguientes problemas.
1. Regresando al tablero de damas chinas, observa que puedes dividirlo en un hexágono y seis
triángulos equiláteros, los cuales forman las puntas de la estrella de seis picos. Conside-
rando las medidas del tablero de damas chinas, ¿cuánto mide el área de cada uno de los
triángulos que forman los picos de la estrella?
¿Cuánto miden el perímetro y el área del hexágono?
2. Si se quisiera un tablero de damas chinas cuyo perímetro fuera de 96 cm, ¿cuánto mediría
cada lado del hexágono?
¿Cuál sería el perímetro del hexágono?
3. Si en lugar de hexágono tuviéramos un pentágono con un área igual a 17.32 cm y lados de
4 cm, ¿cuánto mediría el apotema del pentágono?
Si sólo conocieras el área y el apotema del pentágono, ¿cómo calcularías su perímetro?
Coméntalo con un compañero.
Un lugar en la naturaleza donde puedes encontrar hexágonos es en una colmena de
abejas. Sobre este hecho, Pappus de Alejandría dijo:
Las abejas…, en virtud de una cierta intuición geométrica…, saben que el hexágono posee
una superficie mayor que el cuadrado y que el triángulo, y que podrá contener más miel
con el mismo gasto de material.1
1
http://www.arrakis.es/~mcj/abejas.htm

152
B3
Sesión 84
En esta sesión calcularás el área y el perímetro de polígonos regulares
de siete o más lados.
1. Considera los siguientes polígonos.

153
S21
Haz las mediciones necesarias y completa la siguiente tabla.
Polígono regular Medida de lado Apotema Perímetro Área
Heptágono
Octágono
Decágono
Dodecágono
Pentadecágono

Como se observa en la tabla, el perímetro de los polígonos depende del número de lados.
2. Resuelve los ejercicios siguientes.
a) Calcula el área de un octágono cuyo lado mide 6.2 cm y su apotema 7.48 cm.
¿Cuánto mide su perímetro?
b) José quiere saber si con un pliego de papel china de 40 cm de ancho y 60 cm de largo
puede hacer una cometa con forma de decágono regular, con lados iguales a 4 cm
y apotema de 6.15 cm. ¿Logrará José realizar la cometa?
¿Qué cantidad de papel china utilizará? ¿Se puede hacer más
grande la cometa?
c) ¿Cuánto medirán los lados de un dodecágono con un área de 100 cm2
, si su apotema
mide 5.5 cm?
El perímetro de un polígono regular se puede calcular con la fórmula P = n × L
donde P es el perímetro, n el número de lados y L lo que mide el lado de la figura con que se está trabajando.
La fórmula para encontrar el área es la misma para todos los polígonos regulares, es decir:
Área = P × a
donde a es el apotema de la figura a la que se le está calculando el área.
 Autoevaluación
1. ¿Cuánta malla se necesita para cercar un jardín en forma de hexágono, con un apotema
de 2 m y un área de 13.85 m2
?
a) 2.30 m b) 13.85 m c) 16 m d) 11.74 m

154
Secuencia 22
Factor de proporcionalidad
Formulación de explicaciones sobre el efecto
de la aplicación sucesiva de factores constantes de
proporcionalidad en situaciones dadas.
Sesión 85
En esta sesión observarás qué sucede al aplicar sucesivamente
un factor de proporcionalidad entero.
1. En una clase de Artes Plásticas el profesor pidió a sus estudiantes organizarse en equipos
para dibujar la siguiente imagen, de acuerdo con estas indicaciones:
c
d
f
e
a
“Elaboren dos copias del dibujo original.
• Las medidas de la copia 1 son dos veces
mayores que las medidas del dibujo original.
• Las medidas de la copia 2 son tres veces
mayores que las medidas de la copia 1.”

155
a) Dibuja las copias 1 y 2 en papel cuadriculado.
b) Anota en la tabla las medidas que faltan. Comprueba tus respuestas dibujando las
copias.
Medida Original Copia 1 Copia 2
a
b
c
d
e
f
c) ¿Cuántas veces son más grandes las medidas de la copia 2 con respecto a las medidas
del original?
d) Completa el esquema. Escribe en cada recuadro el número por el que se deben multi-
plicar las medidas de un dibujo para conocer las medidas de otro dibujo.
Medidas
del dibujo
Medidas
de la copia 1
Medidas
de la copia 2
×3
2. Compara tus resultados con los de tus compañeros, y con ayuda de su profesor completen
las siguientes afirmaciones.
•• Aplicar el factor de escala ×3 a un dibujo, y después, a la copia resultante aplicarle el
factor ×2, equivale a aplicar al dibujo original el factor .
•• Al aplicar un factor de escala ×p y después ×q es equivalente a aplicar un solo factor,
que es igual .
El número por el cual se multiplica cada medida de un
dibujo para producir otro se llama factor de escala.

B3
156
Sesión 86
En esta sesión determinarás el efecto que produce la aplicación
sucesiva de un factor de proporcionalidad fraccionario.
1. En la clase de Artes Plásticas continúan dibujando. Ahora el profesor ha dado las siguientes
indicaciones:
a) En tu cuaderno dibuja las copias 3 y 4.
b) Escribe en la tabla las medidas que faltan.
a
b
c
d
e
f
c) Completa el esquema y anota el factor de escala que se aplica en cada di-
bujo. Luego determina el factor que al aplicarlo en el dibujo original produce
la copia 4.
Medidas
del dibujo
Medidas
de la copia 3
Medidas
de la copia 4
2. Compara tus respuestas con las de tus compañeros. Comenten qué ocurre cuando cambian
el orden en que se aplican los factores, ¿la nueva copia es igual o diferente a la copia 4?
Completen la siguiente tabla.
×2 × 1
3
a
b
c
d
e
f
Recuerda que dividir entre un
número, por ejemplo entre 2,
equivale a multiplicar por
1
2 .
• “Las medidas de la copia 3
son tres veces menores que
las del dibujo original.
• Las medidas de la copia 4
son dos veces mayores que
las de la copia 3.”

S22
157
3. Observa la copia 5, sus medidas son 2
3
de las del dibujo
original. Anótalas sobre la copia.
¿A las de qué copia son iguales esas medidas?
Por lo tanto, aplicar el factor de escala × 2
3
equivale a
primero obtener la reducción × 1
3
y después obtener la
ampliación ×2. También se cumple si primero se produce
la ampliación ×2 y luego se reduce × 1
3
.
c
d
b
f
e
a
Copia 5
Sesión 87
En esta sesión resolverás problemas que implican aplicar
un factor de proporcionalidad fraccionario.
1. Andrés quiere preparar un postre. Observa los ingredientes que
necesita.
Si Andrés lo desea preparar para 6 porciones, ¿qué cantidades
de cada ingrediente debe tener? Completa:
de azúcar
de leche
yemas de huevo
cucharadas de harina de maíz
cáscara de limón
palito de canela
Compara tus respuestas con las de otros compañeros y co-
menten cómo determinaron cada cantidad.
Natilla
Ingredientes para 4 porciones:
100 g de azúcar
500 ml de leche
3 yemas de huevo
1 1
2
cucharadas rasas de harina de maíz
1 cáscara de limón
1 palito de canela
canela en polvo al gusto

B3
158
2. Observa la manera en que Andrés determinó la cantidad que requiere de cada ingrediente.
“Primero calculó los ingredientes para una porción y luego multiplicó por 6”.
Por ejemplo:
Ingredientes para
4 porciones
Ingredientes para
una porción
Ingredientes para
6 porciones
100 g de azúcar
100 g de azúcar
4 porciones = 25 g de azúcar por porción. 25 g de azúcar por porción × 6 porciones =
150 g de azúcar.
a) Utiliza el procedimiento anterior para calcular la cantidad que se requiere de los otros
ingredientes.
Ingredientes para
4 porciones
Ingredientes para
una porción
Ingredientes para
6 porciones
500 ml de leche
3 yemas de huevo
1 1
2
cucharadas de harina de maíz
b) Para calcular la cantidad de cada ingrediente por porción, ¿por cuál número se divide?
Completa el siguiente esquema.
Ingredientes para
4 porciones
Ingredientes para
1 porción
Ingredientes para
6 porciones
×
c) Considerando la receta original, ¿cuál es el número por el que se multiplica o divide
para calcular de manera directa la cantidad de cada ingrediente, es decir, de 4 a 6
porciones?
Ingredientes para
4 porciones
Ingredientes para
6 porciones
Compara tus respuestas y utiliza el número que encon-
traste para verificar la cantidad que se requiere de cada
ingrediente para preparar el postre.
El número que te permite calcular la
cantidad requerida de cada ingrediente
es la constante de proporcionalidad.

S22
159
Sesión 88
En esta sesión determinarás qué factor de proporcionalidad se aplica.
Con tres engranes de diferente tamaño se forma una
maquinaria. Observen la imagen.
a) Si el engrane A da 2 vueltas, ¿cuántas vueltas da
el engrane B? y ¿cuántas
vueltas da el C?
b) Completen la tabla, deben calcular los valores que
faltan.
Engrane A Engrane B Engrane C
1
2 1
1 2
3
2 4
2 1
2 5
6 15
4
30
c) Anoten los factores de proporcionalidad en el si-
guiente esquema.
Número de vueltas
del engrane A
Número de vueltas
del engrane B
Número de vueltas
del engrane C
A
B
C

B3
160
Sesión 89
2. Otra maquinaria está formada de la siguiente
manera: el engrane A da cuatro vueltas mien-
tras el B completa una y el C da tres.
a) Completen la tabla, y en el esquema ano-
ten los factores de proporcionalidad.
b) ¿Cuál de los engranes es el menor? ¿Por
qué?
c) ¿Cuántos dientes tendrá cada engrane?
Hay más de una respuesta, anoten dos
Comparen sus respuestas con las de sus
compañeros y verifíquenlas con ayuda de su
profesor.
En esta sesión resolverás problemas que implican la aplicación
de factores de proporcionalidad.
1. La siguiente tabla muestra las medidas reales de un automóvil deportivo y algunas de las
medidas que tendrían sus modelos a escala. Organizados en equipos, complétenla.
Medidas Medidas reales Modelo A Modelo B Modelo C
Largo 4.2 m 4.83 cm
Ancho 2.2 m 5.12 cm 9.17 cm
Altura 1.5 m 6.25 cm
a) ¿Cuál es el factor de escala de cada modelo?
b) ¿Qué factor de proporcionalidad produjo las longitudes más pequeñas?
c) Los tres factores de proporcionalidad son fraccionarios. Analizando las operaciones que
realizaron, contesten: ¿de qué manera influye el denominador del factor de proporciona-
lidad?
Número de vueltas
del engrane A
Número de vueltas
del engrane B
Número de vueltas
del engrane C
4 1
2 6

S22
161
 Autoevaluación
La mamá de Ernesto tiene una fotografía rectangular que mide 10 cm × 15 cm. Ernesto y
sus hermanas quieren reproducirla en diferentes tamaños. En el estudio fotográfico, él pide
una reproducción a 4 ×. Rosaura pide que su copia sea a
1
2 × de la de su hermano, mientras
que Laura pide que su copia sea 3 × de la copia de su hermana.
a) ¿La fotografía de Ernesto es más grande o más pequeña que la original?

b) ¿Cuál de las tres fotografías es la de mayor tamaño?
c) ¿Cuáles son las dimensiones de la copia de Laura?
2. En la siguiente tabla se muestran las medidas que tiene un modelo de automóvil (A) con un
factor de escala de 1
64
. A partir de esas medidas y del factor de proporcionalidad comple-
ten la tabla.
Medidas Medidas reales Modelo A Modelo B
Largo 4.47 m 6.98 cm cm
Ancho m 2.66 cm cm
Altura m 2.42 cm cm
a) ¿Cuántas veces es más grande la medida real del largo del automóvil que la medida en
el modelo B?
b) ¿Cuál es la constante de proporcionalidad que te permite pasar de una medida real del
automóvil a su medida en el modelo B?
Comparen sus respuestas y verifiquen que hayan aplicado correctamente los factores de
proporcionalidad.
Cuando se refiere al factor de escala de una ampliación o reducción de una
fotografía, la equis representa la cantidad de aumentos (o de reducciones)
con respecto al original.
1
64
× 2

162
Secuencia 23
Anticipación de resultados de una experiencia aleatoria,
su verificación al realizar el experimento y su registro
en una tabla de frecuencias.
Registro de una experiencia
aleatoria
Sesión 90
En esta sesión estimarás el resultado de un juego de azar.
En Matemáticas decimos que una situación es de azar o aleatoria si presenta varios resultados
posibles y no se puede asegurar cuál de ellos se obtendrá.
a) Si lanzas una moneda al aire, ¿caerá al piso?
¿Es posible asegurar que siempre pasará lo mismo?
Menciona por qué.
Esta situación, ¿es de azar? ¿Por qué?
b) Si la moneda cae al piso, ¿qué cara quedará hacia arriba? ¿Por qué?
Esta situación, ¿es de azar? ¿Por qué?
Si lo que se quiere es observar la cara que queda hacia arriba al lanzar una moneda, ¿cuá-
les son los resultados posibles?
Si se lanza una moneda y se observa la cara que queda hacia arriba, ¿puedes afirmar qué
ocurrirá en un siguiente lanzamiento? ¿Por qué?
Si lanzas diez veces una moneda al aire, ¿caerán más águilas o más soles?

163
En una situación de azar, la frecuencia es el
número de veces que ocurre un resultado.
1. Formen equipos y cada integrante, por turnos, lanzará una moneda al aire diez veces. Regis-
tren en la siguiente tabla los resultados de cada uno. Tachen A si cae águila y S si cae sol.
Primer juego
Jugador
Número de volado Total por resultado
1º 2º 3º 4º 5º 6º 7º 8º 9º 10º
1
A A A A A A A A A A
S S S S S S S S S S
2
A A A A A A A A A A
S S S S S S S S S S
3
A A A A A A A A A A
S S S S S S S S S S

(Si su equipo tiene más de tres integrantes, copien la tabla en su cuaderno, agregando
tantos jugadores como sea necesarios.)
Contesten las siguientes preguntas.
a) ¿Cuántas águilas cayeron por jugador? b) ¿Cuántos soles por jugador?
c) Si vuelven a jugar, ¿obtendrán los mismos resultados?
Al número de veces que cae águila al lanzar diez veces una
moneda al aire se le identifica como su frecuencia. Tam-
bién se puede referir a la frecuencia con que cae sol en
diez lanzamientos.
2. Consideren los resultados que obtuvieron y compárenlos con los de otros equipos. Descri-
ban cuál es el comportamiento de los resultados. ¿La frecuencia es mayor que la que re-
gistraron en su equipo? ¿Es menor? ¿Es igual?
Si los equipos ganan cuando caen más águilas, ¿cuántos equipos ganaron?
En la siguiente tabla escriban los resultados obtenidos por todo el grupo.
Resultados de lanzar una moneda al aire en el grupo
Resultado Frecuencia
Caer águila
Caer sol
Total de lanzamientos
¿Cuál es la diferencia entre el número total de águilas y de soles?
¿Cuál de los siguientes resultados tiene más posibilidades de ocurrir en una serie de diez
lanzamientos de moneda?
a) AAASSAAASS b) SSSSSSAAAA c) SASASASAAS d) Cualquiera de las series puede ocurrir

164
B3
Sesión 91
En esta sesión registrarás los resultados de otro juego de azar. Analizarás
dichos resultados para poder proponer alguna manera de ganar.
1. En equipos de seis compañeros jueguen a las carreras. Cada jugador elige un carrito y co-
loca una ficha sobre él. Por turnos, cada quien lanza el dado, y avanza una casilla el jugador
cuyo carrito corresponde al número que se muestra en la cara superior del dado. Gana
el jugador que llegue primero a la meta.
Número de carrito META
1
2
3
4
5
6

(Si su equipo tiene menos integrantes pueden elegir más de un carrito.)
¿Quién ganó?
Si se realiza nuevamente el juego, ¿crees que tienes más posibilidades de ganar? ¿Por qué?
Realicen una vez más el juego.

165
S23
2. En la siguiente tabla anoten el número de carrito que ganó en cada equipo.
Número de equipo
Número de carrito que ganó
en la primera carrera
Número de carrito que ganó
en la segunda carrera

¿Cuál es el número de carrito que más veces aparece como ganador en la primera carrera?
¿Cuál es el número de carrito que más veces aparece como ganador en la segunda carrera?
¿Cuál es el número de carrito que más veces aparece como ganador al considerar ambas
carreras?
De acuerdo con los resultados obtenidos, si vuelven a jugar a las carreras, ¿existe algún
número que tenga ventaja sobre los demás?
Si así lo consideran, pruébenlo jugando una carrera más.
3. En un grupo, al analizar los resultados obtenidos, un equipo propuso que para ganar una
carrera conviene apostar por los carritos que tienen un número par.
¿Creen que tienen razón? ¿Por qué?
Otro equipo propuso apostarle a los carritos con el número 3 o más.
Organicen una carrera más y observen los resultados.
Describan una estrategia en la cual tengan más posibilidades de ganar una carrera.

166
B3
Sesión 92
En esta sesión anticiparás el resultado de una extracción y lo verificarás.
Para ello deberás anotar los resultados en una tabla de frecuencias.
1. Recorta cuatro cuadritos de papel iguales y escribe en cada uno de ellos una de las letras
de la palabra AZAR. Dóblalos, colócalos en una bolsa o en una caja y revuélvelos.
Si sacas de la caja uno de los papelitos doblados, ¿qué letra es más posible que saques?
¿Por qué?
¿Qué letras tienen las mismas posibilidades de salir?
¿Por qué?
2. Repite el experimento cincuenta veces. En cada extracción, registra una rayita en la columna
de conteo que corresponde a la letra que sale. Luego debes doblar de nuevo el papelito que
sacaste y regresarlo a la caja. Anota los resultados en la siguiente tabla de frecuencias.
Letras Conteo Frecuencia
A
Z
R
Total de extracciones 50
¿Qué letra fue la más frecuente? ¿Era lo que esperabas?
¿Por qué?
A
Z
A
R

167
S23
3. Compara tus resultados con los de tus compañeros, ¿cuál fue la letra que se extrajo con
mayor frecuencia?
¿Para qué letras la frecuencia fue la misma?
¿Por qué consideras que los resultados no son siempre los mismos?
¿Qué esperas que ocurra si repiten el experimento otras cincuenta veces?
4. Ahora reúnete con un compañero o compañera para realizar el experimento con la palabra
ALEATORIO.
Al sacar de la caja uno de los papelitos, ¿qué letra es más posible que saquen?
¿Por qué?
¿Qué letras consideran que tienen las mismas posibilidades de salir?
¿Por qué?
Elaboren en su cuaderno una tabla de frecuencias como la que utilizaron para registrar los
resultados del experimento con la palabra AZAR, pero ahora para las letras de la palabra
ALEATORIO.
5. Comparen sus resultados con los de sus compañeros y contesten las siguientes preguntas.
¿Qué letra fue la más frecuente? ¿Era lo que esperaban?
¿Por qué?
¿Alguna vez se han preguntado cuál es la letra que más se utiliza en nuestro idioma? ¿Cuál
letra suponen que es?
Propongan una manera de averiguarlo, llévenla a cabo y registren sus resultados en una
tabla de frecuencias. Después muestren sus resultados al grupo.

168
B3
Sesión 93
En esta sesión anticiparás y registrarás los resultados al extraer
una canica de una bolsa.
1. Lee y realiza lo siguiente.
Dos compañeros, María y Joel, colocan dos canicas en una urna; una de las canicas es azul
y la otra es blanca. Después de remover las canicas extraen una, sin mirar, y resulta ser
blanca. Regresan la canica a la bolsa, la remueven y hacen una extracción más. ¿De qué
color piensas que será la canica en esta ocasión?
Haz el experimento varias veces y comprueba si aciertas. ¿Qué piensas que es más fácil,
sacar la canica blanca o la azul?
María y Joel hicieron el experimento diez veces. Para registrar sus resultados, anotan una A
si sale azul, y una B si sale blanca. Observa sus resultados:
A B B A B A B B A B
¿Cuántas canicas azules sacaron?
¿Y cuántas canicas blancas?
2. Reúnete con un compañero y lleven a cabo el experimento descrito en el problema anterior,
pero primero anoten sus estimaciones en la siguiente tabla.
Estimaciones
Canicas azules que salen en 20 extracciones Canicas blancas que salen en 20 extracciones

Registren en una tabla de frecuencias sus resultados. Pueden anotar una rayita o escribir
una A si sale azul y una B si sale blanca.
Color Conteo Frecuencia
Azul
Blanco
Total

Comparen los resultados obtenidos en la estimación que hicieron previamente, ¿acertaron?
3. Comparen sus respuestas con las de otros compañeros y comenten:
¿Qué color de canica es más frecuente de obtener?
¿Podrían adivinar el color de la canica que saldrá en la próxima extracción?

169
S23
4. Repitan el experimento, pero esta vez pongan en la bolsa tres canicas: dos azules y una
blanca.
¿Consideran que ahora será más fácil obtener una canica blanca o una azul?
Cálculo
Canicas azules que salen en
30 extracciones de la bolsa 2
Canicas blancas que salen en
Resultados de 30 extracciones
Canicas azules que salen en
Canicas blancas que salen en
¿Qué color de canica es más frecuente sacar en esta situación?
¿Podrían adivinar el color de la canica que saldrá en la próxima extracción?
 Autoevaluación
Observa las cuatro bolsas que se muestran a continuación:
bolsa 1 bolsa 2 bolsa 3 bolsa 4
Contienen canicas de color azul (A) y blanco (B).
Marca con una palomita ( ) las frases que son verdaderas.
Es más fácil obtener una canica azul de la bolsa 1 que de la bolsa 2.
Consulta en…
Entra al sitio http://www.acanomas.com/Biblioteca.php y consulta la información sobre
otros juegos de azar.

170
Secuencia 24
Análisis de frecuencia
absoluta y relativa
Lectura y comunicación de información mediante
el uso de tablas de frecuencia absoluta y relativa.
Sesión 94
En esta sesión utilizarás tablas de frecuencia absoluta
para obtener la información resumida en ellas.
El manejo y la interpretación de información dependen de la cantidad de datos que se tengan;
por ejemplo, si se cuenta con un conjunto de diez datos, sólo bastaría enlistarlos y ordenarlos
para poder describir su comportamiento. Sin embargo, para el análisis de un número mayor de
datos se recomienda utilizar una tabla de frecuencia, la cual concentra y organiza la información.
A continuación se muestran las horas a la semana que cada alumno de tercer grado de la es-
cuela A invierte en estudiar después de clase. El grupo se compone de 50 estudiantes.
4 9 1 10 4
6 3 6 3 1
1 2 2 6 10
5 2 10 10 6
6 2 0 4 6
7 0 8 5 7
8 7 0 10 9
6 0 9 6 0
7 0 4 10 7
1 4 6 2 8
a) ¿Cuál es el mayor número de horas de estudio invertidas por un alumno?
b) ¿Cuál es la diferencia entre el alumno que invierte menos horas de estudio con respecto al
que invierte más horas?
c) ¿Cuántas horas estudian la mayoría de los alumnos?
e) ¿Cómo organizaron los datos para responder las preguntas?

171
1. En parejas, completen la siguiente tabla de frecuencias y contesten las preguntas.
Número de
horas invertidas
Conteo
Frecuencia
absoluta
0
4
6
3
a) ¿Cuántas horas diferentes se registraron?
b) ¿Cuáles fueron esas horas?
2. Usen la información que proporciona la tabla para contestar las preguntas
siguientes.
a) ¿Cuántos alumnos invierten 4 horas de estudio?
c) ¿Cuántos alumnos invierten 10 horas de estudio?
d) ¿Cuántos alumnos no invierten tiempo en estudiar?
En este ejemplo, el total de datos es de 50 alumnos.
En una tabla de frecuencias,
la columna de frecuencia
absoluta se refiere a la cantidad
de veces que aparece un dato
en toda la información, por lo
que al sumar dicha columna
nos dará el total de datos
u observaciones registrados.

B3
172
Sesión 95
En esta sesión utilizarás tablas de frecuencia relativa
para obtener información.
1. Continuaremos trabajando con los datos de la tabla de la sesión anterior. Agregaremos a
nuestra tabla de frecuencias las columnas de frecuencia relativa y el porcentaje referente
a cada dato.
En parejas, completen la siguiente tabla (realicen los cálculos que sean necesarios).
Número de
horas invertidas
Conteo
Frecuencia
absoluta
Frecuencia relativa Porcentaje
Cálculo Resultado Cálculo Resultado
0
4 4
50
0.08 0.08 × 100 8%
6
3 3
50
0.06 0.06 × 100 6%
Total 50 50
50
1 1 × 100 100%
Al dividir la frecuencia absoluta de cada dato entre el número total de datos se obtiene la
frecuencia relativa.
Al sumar los valores de la columna de frecuencia relativa el resultado debe ser igual a
uno. Al multiplicar por 100 la frecuencia relativa de cada dato, obtendremos el porcentaje
que representa ese dato con respecto al total.
2. Con base en los datos de la tabla, contesta las siguientes preguntas.
a) ¿Qué número de horas invertidas en estudiar tiene el mayor porcentaje?
b) ¿Cómo comprobarías que la columna de frecuencia relativa es correcta?

S24
173
Sesión 96
En esta sesión continuarás trabajando con tablas de frecuencia relativa.
1. Se realizó un concurso entre 30 telese-
cundarias del país para ver cuál reunía
la mayor cantidad de material reciclado
en kilogramos, los resultados se muestran
a continuación.
Con la información del cuadro anterior completa la tabla siguiente.
Cantidad de material reciclado
(kg)
Conteo
Frecuencia
absoluta
Frecuencia relativa Porcentaje
Cálculo Resultado Cálculo Resultado
1
34
40 3
3
30 0.10 0.1 × 100 10%
2
98
1
114
116
Total 30 1 × 100 100%
En equipos, comparen los resultados y contesten las preguntas siguientes.
a) La telesecundaria que ganó, ¿qué cantidad de material reciclado reunió?
b) ¿Qué cantidades de material reciclado reunieron las telesecundarias que quedaron
en segundo y tercer lugar?
c) ¿Cuál fue la menor cantidad de material reciclado que se recolectó?
34 34 115 52 106 72 52 40 89 116
114 110 89 67 115 80 96 89 40 89
89 62 40 98 80 46 111 111 29 25

B3
174
Sesión 97
En esta sesión interpretarás la información que se presenta en
distintas tablas.
1. La siguiente tabla muestra el número de viviendas particulares habitadas, por entidad
federativa, con disponibilidad de computadora en los años 2000, 2005 y 2010.
Entidad federativa 2000 2005 2010
Aguascalientes 25 927 61 954 99 579
Baja California 84 377 188 340 374 234
Baja California Sur 11 793 32 352 72 319
Campeche 8 532 27 061 55 160
Coahuila de Zaragoza 52 571 129 265 230 582
Colima 11 813 29 665 58 737
Chiapas 22 018 63 584 135 322
Chihuahua 72 885 183 005 312 615
Distrito Federal 451 553 825 157 1 171 631
Durango 21 445 59 870 105 076
Guanajuato 67 668 163 484 301 818
Guerrero 19 619 59 908 129 170
Hidalgo 23 971 72 311 134 561
Jalisco 163 935 371 642 652 230
Estado de México 289 186 697 749 1 162 156
Michoacán de Ocampo 46 557 118 615 221 817
Morelos 31 704 73 340 137 530
Nayarit 11 795 36 568 78 882
Nuevo León 127 178 261 981 468 025
Oaxaca 20 482 65 558 134 557
Puebla 64 339 166 162 287 815
Querétaro 38 673 86 444 153 832
Quintana Roo 18 557 47 916 115 058
San Luis Potosí 32 387 87 448 151 052
Sinaloa 37 781 104 451 220 665
Sonora 53 505 135 318 267 201
Tabasco 20 729 59 110 117 126
Tamaulipas 54 062 136 969 256 467
Tlaxcala 9 042 28 374 53 921
Veracruz de Ignacio de la Llave 72 247 202 314 405 608
Yucatán 28 494 69 669 129 964
Zacatecas 16 610 49 343 84 909
Estados Unidos Mexicanos 2 011 425 4 694 927 8 279 619
Nota: Cifras correspondientes a las siguientes fechas censales: 14 de febrero (2000), 17 de octubre (2005),
y 12 de junio (2010).
Fuente: http://www.inegi.org.mx/sistemas/sisept/default.aspx?t=mviv41s=estc=26573

S24
175
 Autoevaluación
• ¿Qué significaría que el total de la columna de frecuencia relativa fuera mayor a uno?
Consulta en…
Entra a la página del INEGI para conocer otros interesantes datos estadísticos sobre
nuestro país.
En parejas, utilicen la información anterior y calculen el porcentaje por año para cada enti-
dad con respecto al total nacional.
a) Cada uno explique a su compañero, con sus propias palabras, qué información muestra
la tabla.
b) ¿A qué años corresponde la información que presenta la tabla?
c) ¿Qué entidad muestra el mayor porcentaje y en qué año?
d) Indiquen por cada año las entidades que tienen los tres primeros lugares en porcentaje.
1º año
2º año
3º año
e) ¿Qué entidades mantienen el mismo porcentaje durante los tres años de análisis?
f) En cada año aumentó el número de computadoras en las viviendas particulares. ¿En qué
año hubo un mayor aumento?

B3
176
Sesión 98
Evaluación
Aplica lo aprendido y selecciona la respuesta correcta a cada problema.
1. Jacinto requiere comprar 150.45 dólares para pagar un artículo que se ofrece en una tienda
en internet. ¿Cuántos pesos debe juntar para poder pagar, si el tipo de cambio está en
$14.30?
a) $ 2 151.354
b) $ 2 151.4035
c) $ 2 151.435
d) $ 2 151.536
2. Considera la ecuación 9 x = 270.
¿Cuál de los siguientes problemas se puede resolver con la ecuación anterior?
a) El volumen de un eneágono regular mide 270 cm.
b) El área de un eneágono regular mide 270 cm.
c) El perímetro de un eneágono regular mide 270 cm.
d) El perímetro de un eneágono irregular mide 270 cm.
3. Un corredor tarda cierta cantidad de minutos para recorrer diferentes distancias, como se
muestra en la tabla.
Tiempo (minutos) 21 min 42 min 55 min 84 min
Distancia 7 km 14 km 28 km
Si corre durante 55 minutos, ¿qué distancia recorrió?
a) 15.00 km
b) 18.33 km
c) 20 km
d) 22 km
4. Un rollo higiénico contiene 43.7 metros de papel. Si cada hoja mide 10.4 cm, ¿cuántas
hojas higiénicas contiene el rollo?
a) 300.23
b) 400.51
c) 420.19
d) 499.10

S24
177
5. ¿En cuál de los siguientes polígonos regulares el área es de 20 m2
?
2 cm
a = 4
2 cm
a = 1.37
2 cm
a = 2.61
2 cm
a = 5.00
6. En una caja se colocan 12 lápices del mismo tamaño y textura, 3 son azules, 3 rojos,
2 amarillos, 2 negros, 1 verde y 1 morado. ¿Cuál de las siguientes frases es verdadera?
a) Hay más posibilidades de sacar un lápiz color morado que uno verde.
b) Hay más posibilidades de sacar un lápiz color azul que uno rojo.
c) Hay más posibilidades de sacar un lápiz color rojo que uno amarillo.
d) Hay más posibilidades de sacar un lápiz color amarillo que uno negro.
La siguiente tabla ilustra el consumo
de energía eléctrica en kilowatts (kW) de
4 casas durante 5 meses.
Mes Noviembre Diciembre Enero Febrero Marzo
Casa 1 86 95 105 88 102
Casa 2 78 89 110 80 97
Casa 3 76 98 89 78 114
Casa 4 89 100 65 117 76
7. ¿En qué mes se consumió la mayor cantidad de ener-
gía eléctrica?
a) Enero
b) Febrero
c) Diciembre
d) Marzo
8. ¿Qué casa consumió menos energía durante los cinco
meses?
a) Casa 1
b) Casa 2
c) Casa 3
d) Casa 4
9. ¿Qué polígono regular se puede generar a partir del ángulo mostrado?
a) Dodecágono
b) Undecágono
c) Pentadecágono
d) Icoságono
156°
a) b) c) d)

Bloque 4

• Construir círculos y polígonos regulares que cumplan con
ciertas condiciones establecidas.
• Leer información presentada en gráficas de barras
y circulares. Utilizar estos tipos de gráficas para
comunicar información.

180
Planteamiento y resolución de problemas
que impliquen la utilización de números enteros,
fraccionarios o decimales positivos y negativos.
Secuencia 25
Números positivos y negativos
Sesión 99
En esta sesión resolverás problemas que implican utilizar números enteros.
En equipos, cada uno de los integrantes escoja un objeto de la ilustración. Luego describan en
un trozo de papel la ubicación de los objetos que eligieron y muéstrenlo a uno de sus compa-
ñeros; pueden emplear números y símbolos para la descripción, pero no palabras. Cada uno
debe interpretar el mensaje de su compañero para saber qué objeto eligió. Anoten en el papel
el nombre del objeto y devuélvanlo a su compañero. Finalmente revisen si interpretaron correc-
tamente la descripción y pudieron identificar el objeto. Si hubo equivocaciones, deben encon-
trar en dónde estuvo la falla y corregirla.
40 m
10 m
4 m
1 m
1 m
10 m
4 m
22 m
40 m
60 m
ESCUELA

181
1. En otra telesecundaria,
un equipo elaboró un
mensaje que fue co-
rrectamente interpreta-
do. Observen y analicen
cómo lo hicieron.
Objetos que se eligieron: La persona que recibió el mensaje cree que es:
60 m Helicóptero
1 m
Tubería de gas
4 m Rata
a) Utilicen ese mismo
sistema y comple-
ten la tabla.
Ubicación Dibujo
Carro del metro
4 m
Tubería de agua potable
10 m
b) Hay objetos sobre el nivel del suelo, como el helicóptero, y por debajo de su nivel, como
el metro.
En esta propuesta ¿cómo se representaron los objetos que están ubicados sobre el
nivel del suelo?
¿Y los que se encuentran bajo el nivel del suelo?
Con este sistema, escriban cómo representarían la ubicación de un bache sobre la calle.
2. En parejas, contesten las siguientes preguntas.
En la primera actividad de la sesión, ¿cómo representaron ustedes los objetos que están
sobre el nivel del suelo? ¿Por qué?
¿Cómo lo hicieron con los objetos que están ubicados bajo
el nivel del suelo?
¿Por qué?
Comparen sus mensajes con los de otros equipos. ¿Cuáles
les parecen más claros y por qué?
Como hay distintas maneras de comunicar
la ubicación de los objetos, se debe establecer
un acuerdo. En este ejemplo podríamos repre-
sentar el nivel del suelo con el cero, lo que está
sobre el nivel del suelo con signo positivo +
y lo que está bajo el nivel del suelo con signo
negativo − .

B4
182
Sesión 100
En esta sesión localizarás números enteros en un recta númerica.
1. En parejas, completen la siguiente tabla usando los signos + y – según corresponda.
Objeto Ubicación
Palomas a 20 m sobre el nivel del suelo. + 20 m
Una señal de tránsito a nivel del suelo.
Un cable de la luz a 4 m de altura.
Una estación del metro a 15 m bajo el nivel del suelo.

2. En parejas, localicen en la siguiente recta numérica los objetos que se mencionan en la
tabla anterior. Cada división equivale a 5 unidades.
3. Localicen los siguientes números en la recta numérica. Cada división equivale a una unidad.
1, 3, 7, –1, –5, –6, 0
Los números con signo positivo, o simplemente positivos, se ubican a la derecha del cero en
la recta numérica y se escriben con el signo + o sin él; por ejemplo, el 1 positivo se escribe +1
o sólo 1.
Los números negativos se ubican a la izquierda del cero en la recta numérica y siempre se
escriben anteponiéndoles un signo −; por ejemplo, el 16 negativo se escribe −16.
El cero no es ni positivo ni negativo, es neutro, por lo que se escribe sin signo (no se le pone
+ ni –).
Los números enteros están formados por los enteros positi-
vos, los enteros negativos y el cero. Se pueden representar
en la recta numérica tal y como se hizo con las fracciones
y los decimales. Para ubicarlos, primero se determina
el lugar del cero, a continuación se sitúan a su derecha los
números con signo + (enteros positivos) y a su izquierda
los números con signo – (enteros negativos).

S25
183
Sesión 101
En esta sesión identificarás el orden que tienen los números enteros.
Conocer la temperatura ambiental es importante para realizar nuestras actividades cotidianas.
Para medirla se emplean los termómetros ambientales, como el de la ilustración, que muestran
tanto temperaturas sobre cero o temperaturas positivas, como temperaturas bajo cero o tem-
peraturas negativas. Las temperaturas bajo cero se acostumbra representarlas anteponiéndo-
les el signo –.
Conocer los cambios o las variaciones de la temperatura nos permite, entre otras cosas, tener
un mayor control de las cosechas y cuidar mejor nuestra salud.
1. En parejas, contesten las preguntas con los datos de la tabla.
El 16 de enero de 2012 el Servicio Meteorológico Nacional publicó un aviso de las heladas
que se esperaban para ese día en distintas ciudades.
Ciudad Estado
Temperatura máxima
(°C)
Temperatura mínima
(°C)
La Rosilla Durango 16.0 –8.5
El Vergel Chihuahua 14.0 –5.0
Creel Chihuahua 22.0 –4.0
La Ascensión Nuevo León 23.0 –3.0
¿Qué temperaturas máximas se esperaban en La Rosilla y El Vergel?
¿Cuál es mayor?
¿Cuál de las temperaturas mínimas que se esperaban en Creel y La Ascensión es menor?
¿De cuánto se esperaba la variación de temperatura en El Vergel?
¿Y en Creel?
2. En grupo, comparen sus resultados y comenten sus procedimientos.
En el equipo 1 señalaron que la variación de temperatura que se esperaba en El Vergel es
de 9 °C, porque 14 − 5 = 9.
En el equipo 2 utilizaron el termómetro ambiental para localizar las temperaturas y dijeron
que la variación es de 19 °C, porque es el número de grados que hay entre ambas tempe-
raturas.
¿Cuál de los dos equipos obtuvo la variación de temperatura correcta?

B4
184
La variación de temperatura es el número de grados que hay entre dos tempe-
raturas dadas.
Por ejemplo,
Máxima Mínima Diferencia
Guapoca 21.3 –2.9 24.2
La variación de temperatura también la podemos interpretar como la distancia
que hay entre dos números en una recta numérica horizontal.
Por ejemplo: entre −12° y 7° hay una distancia de 19 unidades.
Es decir, la distancia entre dos números es igual a la longitud del segmento
que los une.
−12 −11 −10 −9 −8 −7 −6 −5 −4 −3 −2 −1 0 1 2 3 4 5 6 7
19
3. En equipos, empleen la imagen del termómetro para contestar las preguntas siguientes.
a) En un cierto día, la temperatura máxima en Toluca fue de 25 °C y la temperatura mínima
fue de −1.5 °C. ¿De cuánto fue la variación de temperatura en esa ciudad?
b) La temperatura mínima de Pachuca fue de −2.9 °C. Si se sabe que la variación de tem-
peratura es de 23.4 °C, ¿cuál fue la temperatura máxima de dicha ciudad?
c) ¿Cuántos grados hay de −9 °C a −26 °C?
d) ¿Cuántos grados hay de −1.5 °C a −15.5 °C?
e) En el termómetro ubiquen las temperaturas 13 °C y 4 °C, ¿cuál de las dos es menor?
f) ¿Cuál es la variación entre estas temperaturas?
g) Ahora ubiquen las temperaturas –13 °C y –4 °C, ¿cuál de las dos es menor?
h) ¿Cuál es la variación entre estas temperaturas?
i) Entre –13 °C y 4 °C, ¿cuál de las dos temperaturas es menor?
j) Analicen sus respuestas en grupo y en caso de controversia consulten con su profesor.
24.2

S25
185
4. Calcula la distancia que hay entre cada par de
marcas del mismo color.
Distancia entre marcas naranjas
Distancia entre marcas azules
Distancia entre marcas verdes
Distancia entre marcas rojas
Distancia entre marcas azules
Distancia entre marcas verdes
Consulta en…
Entra al sitio http://www.librosvivos.net/smtc/homeTC.asp?TemaClave=1025, ahí encon-
trarás más información sobre los números enteros.
-15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
20°C
16°C
1°C
−1°C
−8°C
−29°C

B4
186
Sesión 102
En esta sesión conocerás el valor absoluto y el simétrico
de los números con signo.
La distancia que hay entre un número dado y el cero se conoce como valor absoluto. Observa
que este valor es siempre positivo porque corresponde a la longitud del segmento que une
a dicho número con el cero.
El valor absoluto de un número se representa por medio de dos barras paralelas.
Por ejemplo: la longitud entre el –11 y el 0 es 11, es decir, el valor absoluto de –11 es 11
y se escribe |–11| = 11.
La longitud entre el 7 y el 0 es 7, es decir, el valor absoluto de 7 es 7 y se escribe |7| = 7.
1. En la recta numérica se han representado algunos números.
−8 −7 −6 −5 −4 −3 −2 −1 0 1 2 3 4 5 6 7 8
−7.5 −6.5 −1
1
2

1
2
1
1
2
3.5
a) ¿Qué número positivo tiene el mismo valor absoluto que −6.5?
b) ¿Qué número negativo tiene el mismo valor absoluto que 1
2
?
c) ¿Cuáles números tienen valor absoluto 5?
Compara tus respuestas con las de tus compañeros y comenten los procedimientos que em-
plearon.
2. Contesta las siguientes preguntas.
a) ¿Qué número negativo tiene el mismo valor absoluto que 11?
b) ¿Qué valor absoluto tienen los números 18 y −18?
c) ¿Qué número positivo tiene el mismo valor absoluto que −7.5?

S25
187
3. En parejas, contesten las siguientes preguntas.
a) ¿Cuál es el simétrico del 5?
b) ¿Cuál es el simétrico del −3?
c) ¿Cuál es el simétrico del −18.9?
d) ¿Cuál es el simétrico del 16.1?
e) ¿Son simétricos los números 3
2
y − 3
2
?
f) ¿Cuál es el simétrico de − 1
4
?
Comparen sus respuestas con las de sus compañeros.
El valor absoluto de los números positivos y negativos siempre es un número positivo.
Por ejemplo: |–10.2| = 10.2 y |10.5| = 10.5
Dos números que están a la misma distancia del cero se llaman números simétricos.
Por ejemplo: +3 y –3 son números simétricos.
-3 0 3
|-3|=3 |3|=3

B4
188
Sesión 103
 Autoevaluación
1. Ubica sobre la recta numérica los números siguientes: –1.5,
1
2
, –0.25, –
1
3
, 2.25
-3 -2 -1 0 1 2 3
2. Abajo de cada uno de los números anteriores escribe su valor absoluto.
3. Encuentra el simétrico del mayor número positivo y del menor número negativo.
Consulta en…
Busca en las bibliotecas escolares y de aula las siguientes referencias con lecturas interesantes sobre este tema:
Carlos Bosch y Claudia Gómez, “Números enteros”, en Una ventana al infinito, México, sep-Santillana, 2002
Luz María, Marván, “Números simétricos”, “Números con signo”, “¿Mayor o menor?” y “El valor absoluto”,
en Representación numérica, México, sep-Santillana, 2002 (Libros del Rincón).
En esta sesión resolverás ejercicios aplicando lo que estudiaste anteriormente.
1. En una recta numérica, ¿de qué lado del cero se ubican los siguientes números?
28 –27 33
–18 –16 8
2. ¿Qué distancia hay entre los siguientes pares de números?
a) −6 y 10 b) 10.3 y 26 c) −9 y −0.5
d) −15 y 3.9 e) −6.1 y 0 f) 0.9 y 8.1
g) −4.25 y 0.5
3. Escriban mayor que () o menor que () según corresponda.
a) 14.7 6.1 b) −9.5 5 c) −4.3 −15.7
d) –0.98 –0.1 e) –15.6 10.6

Secuencia 26
El círculo y cómo construirlo
189
Construcción de círculos a partir de diferentes datos
(el radio, una cuerda, tres puntos no alineados, etc.)
o que cumplan condiciones dadas.
Sesión 104
En esta sesión reconocerás la diferencia entre círculo y circunferencia.
1. Completa la siguiente definición.
Una línea curva cerrada, que cumple con la condición de que todos sus puntos mantienen
la misma distancia con el centro es
2. Organizados en equipos lleven a cabo la siguiente actividad y contesten las preguntas.
Para permitirle a Víctor salir a jugar futbol con sus amigos, su mamá le puso como condición
que armara el siguiente rompecabezas de un círculo, en cuyas piezas se han señalado
algunas rectas notables y ciertos puntos sobre la circunferencia.
A
B
C
En una hoja, calquen el rompecabezas de Víctor, recórtenlo y ármenlo.
¿Cuánto tiempo les tomó armarlo?

B4
190
Responde las preguntas siguientes.
1. En la imagen del rompecabezas, los puntos A, B y C ¿están sobre la circunferencia o dentro
del círculo?
2. ¿Es lo mismo círculo que circunferencia? . Si consideras que son distin-
tos, escribe con tus propias palabras una definición de círculo y una de circunferencia.
3. En las siguientes imágenes escribe el nombre de los elementos del círculo y su definición.
Comenten en grupo las respuestas que dieron.

S26
191
Sesión 105
En esta sesión trazarás circunferencias a partir de dos puntos dados.
1. Organizados en equipos, observen la siguiente situación y contesten
las preguntas.
Javi y Ale jugaban con una cuerda en el patio de su casa. Ale perma-
necía firme mientras Javi daba vueltas manteniendo tensa la cuerda.
a) ¿Qué figura describe el movimiento de Javi?
b) ¿Qué elemento representa en la figura descrita el punto donde
se paró Ale?
c) ¿Qué elemento de la circunferencia representa la cuerda con la
que jugaban?
d) ¿Se puede trazar una circunferencia conociendo la longitud
de su radio?
3. Don Cheto amarró un chivo a una estaca
con una cuerda, como se muestra en la
figura de la derecha.
Cuando está completamente extendida,
la cuerda mide 6 metros.
Colorea la región de pasto que puede co-
mer el chivo mientras está amarrado.
2. Observa la siguiente figura y escribe un
procedimiento para trazar una circunfe-
rencia, con ayuda del compás, conocien-
do la longitud de su radio.
a) Si se traza otro segmento del centro a
un punto cualquiera de la circunferen-
cia dibujada, ¿cómo es en relación al
radio?
b) ¿Cuántos radios tiene una circunfe
rencia?
10 m
5 m

B4
192
Sesión 106
En esta sesión encontrarás un procedimiento para trazar una circunferencia
a partir de su diámetro o de una cuerda de la misma.
1. En parejas, resuelvan la siguiente actividad.
Para una obra de teatro de la asignatura de Artes se nece-
sitan unas máscaras de cartulina de forma circular. Para
hacerlas, cada alumno midió la distancia de su frente a su
barbilla. A continuación están los segmentos que indican
las distancias obtenidas por dos alumnas.
Conociendo estas distancias, ¿cómo construirán la base de las máscaras?
¿Qué elemento del círculo representarán estos segmentos?
Ahora midan la distancia que hay entre su frente y su barbilla y hagan su propia máscara.
Compartan con el grupo el procedimiento que siguieron para elaborar su máscara y elijan
la mejor máscara (recuerden que debe tener forma circular).
2. Realiza lo siguiente.
a) Marca un punto en tu cuaderno y traza una circunferencia de 5 cm de radio.
b) Señala dos puntos sobre la misma y únelos, procurando que no definan el diámetro.
¿Cómo se llama este segmento?
c) Traza la mediatriz del segmento resultante.
18 cmYoyis
20 cmArucha
Observa que al trazar la mediatriz del segmento
que definen dos puntos sobre la circunferencia,
el centro está sobre dicha mediatriz.
El segmento que determina la unión de dos
puntos dentro de la circunferencia se llama
cuerda.
Responde las siguientes preguntas.
¿Cómo son las distancias del centro a los puntos mar-
cados sobre la circunferencia?
¿Es posible trazar otras circunferencias que pasen por
los mismos puntos que elegiste?
Comenta tus respuestas con tus compañeros.

S26
193
Como ya viste, la mediatriz de un segmento que une dos puntos de la circunferencia pasa por
el centro de la misma; por lo tanto, conociendo dos puntos y tomando un punto sobre la me-
diatriz como centro, se puede trazar una circunferencia que pase por ellos.
Mediatriz
B
A
3. Encuentra el centro de las circunferencias aplicando los conceptos que manejamos en la
sesión.
Analicen en grupo lo que sucede en el caso de la figura 3.

B4
194
Sesión 107
En esta sesión trazarás circunferencias a partir de tres puntos dados.
En parejas, resuelvan lo que se les solicita.
1. La tienda de ropa Mores tiene tres sucursales ubicadas en diferentes puntos de la ciudad.
Si se decide colocar una bodega a la misma distancia de cada una de las tres sucursales,
¿en qué lugar se debe ubicar la bodega? Señálenlo en el croquis.
Los puntos marcados con rojo son los sitios donde se localizan las tiendas.
a) ¿Es posible determinar un punto que se encuentre a la misma distancia de los puntos
rojos?
b) Describan el procedimiento que siguieron para determinarlo y compártanlo con el grupo.
c) ¿Podemos auxiliarnos del trazo de mediatrices para ubicar la bodega del problema
anterior?
d) Para encontrar un punto que equidiste de los puntos rojos, ¿será necesario trazar las
tres mediatrices o será suficiente con trazar sólo dos de ellas?
2. El dueño de la tienda de ropa finalmente construyó la bodega y ahora desea abrir una nue-
va sucursal. Quiere que ésta se ubique a la misma distancia de la bodega, al igual que las
demás sucursales.
Encuentren en el croquis anterior cinco posibles lugares donde instalarla.
Comparen sus propuestas con las de sus compañeros.
¿Cuáles son todos los posibles lugares en donde pueden situar la nueva sucursal?

S26
195
Consulta en…
En las bibliotecas escolares y de aula busca los libros con las siguientes referencias
para saber más sobre este tema:
José Antonio de la Peña, Geometría y el mundo, México, sep-Santillana, 2002
Carlos Hernández, La geometría en el deporte, México, sep-Santillana, 2002
 Autoevaluación
1. Describe el procedimiento para construir un círculo a partir de tres puntos dados.
2. Si tienes tres puntos, ¿cuántas circunferencias puedes trazar que pasen por ellos?
3. Y si solamente tienes dos puntos, ¿cuántas circunferencias puedes trazar que pasen
por ellos?
3. En su cuaderno marquen tres puntos a diferentes distancias, cuidando de que no sean
colineales (es decir, que no estén en una misma línea recta).
a) Unan los puntos mediante segmentos.
b) Tracen las mediatrices de los segmentos.
c) Encuentren la intersección de las mediatrices y llámenlo O.
d) Tomando como centro el punto O y como radio la distancia de O a cualquiera de los
puntos, tracen una circunferencia. Comprueben que ésta pasa por los puntos marcados.
Comparen con otras parejas los puntos que dibujaron y las circunferencias que trazaron.
4. En grupo, analicen lo siguiente.
Dado que los tres puntos de la actividad anterior no
están en una misma recta, ¿por qué se intersecan
en el mismo punto las mediatrices de los segmen-
tos que los unen?
¿Cuál fue el objetivo de encontrar este punto de in-
tersección?
Dados tres puntos no colineales siempre se puede
trazar una única circunferencia que pase por ellos.
El centro de la misma es el punto de intersección
de las mediatrices.
Cuando los tres puntos son colineales
(es decir, cuando están sobre la misma recta),
no se puede trazar la circunferencia.

196
Secuencia 27
Pi en el círculo
Justificación de la fórmula para calcular la longitud
de la circunferencia y el área del círculo (gráfica
y algebraicamente). Explicación del número π (pi)
como la razón entre la longitud de la circunferencia
y el diámetro.
Sesión 108
En esta sesión medirás el perímetro de una circunferencia.
Observa la siguiente imagen.
Formen parejas y propongan cómo calcular la longitud de la circunferencia (perímetro) y el área
del círculo de la imagen anterior.
¿Qué métodos se les ocurrieron y qué resultados obtienen utilizándolos?
círculo
circunferencia
radio
diámetro

197
1. Usa tu compás para trazar dos círculos distintos en tu cuaderno. Tú determinarás la medida
de los radios. Ahora mide la longitud de las circunferencias. Dos posibles formas de hacer-
lo son:
a) Utiliza un trozo de hilo (lo bastante largo), colócalo sobre la circunferencia y marca el
punto donde se encuentra con el extremo inicial del hilo, y ahora mide la distancia entre
este extremo y la marca que realizaste. Haz lo mismo con la otra circunferencia.
b) Recorta una copia de cada círculo. Colócala sobre el borde más largo de una hoja
de papel (como se muestra en la imagen). Marca en la hoja y en el círculo un punto
inicial. Ahora rueda el círculo sobre el borde hasta que gire completamente (lo sabrás
cuando la marca que hiciste vuelva a estar sobre el borde). Mide lo que abarcó el reco-
rrido de la circunferencia.
2. Para cada uno de los círculos que trazaste en tu cuaderno, mide el diámetro, el perímetro
y calcula
perímetro
diámetro .
3. ¿Qué notas en los resultados de los dos cocientes calculados?
4, Formen equipos, comparen sus resultados y coméntelos.
¿Qué tienen en común los resultados?
Borde de la hoja

B4
198
Sesión 109
En esta sesión aprenderás a calcular el perímetro de una circunferencia.
En la sesión anterior calculaste el cociente perímetro/diámetro en círculos distintos, y notaste
que este cociente es aproximadamente 3.14.
1. Utilizando esta fórmula y un valor aproximado para π de 3.14, calcula el perímetro de
los dos círculos que dibujaste en la sesión anterior.
Anota los resultados en tu cuaderno.
¿Es distinto el resultado al del perímetro que habías medido?
¿A qué se podría deber la diferencia?
2. ¿Cuál es la longitud de una circunferencia cuyo radio mide 10 cm?
3. Lee el siguiente poema.
Soy y seré a todos definible,
mi nombre tengo que daros,
cociente diametral siempre inmedible
soy de los redondos aros.
Manuel Golmayo
Este poema está dedicado al número π, ¿notas alguna relación entre el poema y el valor de π?
Comenta tu respuesta con tu grupo y con ayuda del profesor lleguen a una conclusión.
Para cualquier círculo este cociente da el mismo valor, el cual se denomina pi y se
representa con la letra griega π. El valor de π es aproximadamente 3.1416.
Entonces, dado que para todo círculo tenemos
perímetro
diámetro = π ,
podemos calcular el perímetro del círculo con la fórmula: perímetro = π × diámetro.
Las cifras decimales de π nunca terminan, y además no se puede encontrar un periodo
en ellas. Te presentamos las primeras veinte cifras de π:
3.1415926535897932384…

S27
199
Sesión 110
En esta sesión calcularás el área de círculos.
1. En tu cuaderno traza con color azul un polígono regular (puede ser un triángulo, un cuadra-
do, un pentágono, un hexágono) y encuentra el punto medio de todos sus lados. Luego
traza una circunferencia que pase por tres de estos puntos, y ahora une con color verde los
puntos medios anteriores.
¿Cuál es el área de cada polígono que dibujaste?
¿Qué relación hay entre estas áreas y el área del círculo?
Comenten sus resultados en parejas.
2. En parejas comenten cómo obtener un valor más aproximado para el área del círculo, y con
ayuda de su profesor den una mejor aproximación.
Cuando una circunferencia pasa por todos los vértices de un polígono regular se
dice que ésta circunscribe al polígono, o que el polígono está circunscrito por la
circunferencia. Por ejemplo, el polígono verde que trazaste está circunscrito
por la circunferencia.
En cambio, una circunferencia está inscrita en un polígono regular cuando pasa
por todos los puntos medios de los lados de dicho polígono. Este es el caso
del polígono que trazaste en color azul.

B4
200
Sesión 111
En esta sesión encontrarás una fórmula para calcular el área de un círculo.
1. Observa la imagen.
Mide y calcula el perímetro y el área de los polígonos. Anótalos abajo de cada uno.
¿Qué sucede con los perímetros conforme aumenta el número de lados del polígono?
¿Y con el área?
¿Qué relación hay entre el perímetro de los polígonos y el perímetro de la circunferencia?
¿Qué relación hay entre el área de los polígonos y el área del círculo?
2. En equipos, analicen las construcciones de la sesión anterior.

S27
201
¿Qué sucede con los perímetros de los polígonos azules conforme aumenta el número
de lados del polígono?
¿Y con el área?
¿Qué relación hay entre el perímetro de estos polígonos y el perímetro de la circunferencia?
¿Qué relación hay entre el área de estos polígonos y el área del círculo?
Imagina que cada vez hay más lados en el polígono regular que está inscrito en la circunfe-
rencia. ¿Cómo será el perímetro del polígono respecto al de la circunferencia?
¿Y el área?
Una circunferencia se puede pensar como un polígono regular con una cantidad infinita de lados,
cuyo apotema coincide con el radio (en la imagen se puede notar cómo al aumentar el número de lados
del polígono el apotema es cada vez más cercana a la longitud del radio).
ra
ra
ra
ra
Entonces calculamos el área del círculo utilizando la fórmula del área para polígonos regulares:
Área =
perímetro × apotema
2
Pero sabemos que,
perímetro = π × diámetro
apotema = radio
Así que sustituyéndolos en la fórmula de área se obtiene:
Área =
π × diámetro × apotema
2
Ahora dado que, diámetro = 2 × radio, la fórmula para calcular el área del círculo es:
Área = π × radio × radio, o lo que es lo mismo:
A = π × r2

B4
202
Sesión 112
En esta sesión aplicarás las fórmulas para calcular el perímetro
y el área del círculo.
1. En parejas, completen la siguiente tabla. En ella se encuentran los datos de cinco círculos
distintos. Consideren π = 3.14.
Radio Diámetro Perímetro Área
2 cm
2 cm
3 cm
8 cm
5 cm

Analicen los resultados de la tabla. ¿Qué sucede con el perímetro del círculo cuando se
duplica y se triplica el tamaño de su diámetro?
¿Existe una razón de proporcionalidad? Coméntalo con un compañero.
¿Sucede lo mismo con el área?
Si el diámetro de un círculo aumenta en una unidad, ¿qué sucede con el perímetro?
Resuelvan mentalmente las preguntas siguientes.
a) Si el radio de un círculo mide 6 cm, ¿cuánto será su perímetro?
b) Si el diámetro de otro círculo mide 7 cm, ¿cuánto mide el perímetro?
Comenten sus respuestas para llegar a una conclusión, con la orientación de su profesor.
 Autoevaluación
1. Una aproximación del número π
es:
2. ¿Cuáles son las fórmulas del
perímetro y el área del círculo?
Consulta en…
En las bibliotecas escolares y de aula busca los libros con las
siguientes referencias para saber más sobre este tema:
José Antonio de la Peña, “¿De dónde sale el famoso número Pi?”,
en Geometría y el mundo, México, sep-Santillana, 2002 (Libros
del Rincón).
Carlos Hernández, La geometría en el deporte, México, sep-Santi-
llana, 2002 (Libros del Rincón).
Carlos Hernández, “Perímetro del círculo”, en La geometría
en el deporte, México, sep-Santillana, 2002 (Libros del Rincón).
Luz María Marván, “Números de cuento y de película”,
en Representación numérica, México, sep-Santillana, 2002

203
Secuencia 28
Regla de tres
Análisis de la regla de tres empleando valores
enteros o fraccionarios.
Sesión 113
En esta sesión resolverás problemas para encontrar el valor unitario.
Contesta lo siguiente.
Si se quieren comprar seis latas de rajas, ¿en cuál de las dos tiendas conviene comprar?
$6.74
promoción
2x1
“Abarrotes
Don Domingo”
APROVECHE
3x2
“TIENDITA
DE LA ESQUINA”
$5.90

B4
204
a) Arturo compró 4 kg de azúcar y pagó $48.00, ¿cuánto habría pagado por 2 kg?
¿Y por 13 kg?
¿Cómo obtuviste el precio para 2 kg?
¿Y para 13 kg?
b) Con $71.50 se compraron tres gorras. ¿Cuánto cuesta una gorra?
Completa la tabla.
Núm. de gorras 15 21 55 109 210
Precio
Para saber el precio de cualquier cantidad de gorras, ¿es importante conocer el valor de
una sola gorra? ¿Por qué?
¿Cómo obtuviste el valor de una sola gorra?
La siguiente nota de remisión es del mate-
rial que compró Jesús para la instalación
hidráulica de su baño. El vendedor no lle-
nó la columna de valor unitario.
a) ¿Cuánto cuesta un codo de 90° de
1
2
pulgada?
b) ¿Cuánto se pagará por 3 T de 1
2
?

c) ¿Cuánto cuesta un metro de tubo
de 1
2
?
d) Si se compran 2 llaves de paso y 3 pa-
quetes de soldadura, ¿cuánto se debe
pagar?
Nombre: Jesús
Domicilio: Central #23
Teléfono: 663 0543
Cant. Descripción Precio Unitario Importe
5 Codos de 90°
1
2 pulgada $32.50
2 Tubos de
1
2 pulgada, 6m $688.00
8 T de
1
2 pulgada $88.00
3 Llaves de paso $162.00
4 Paquetes de soldadura $280.00

S28
205
Sesión 114
Dados dos números a y b, al cociente a
b
se le denomina la razón
de a respecto a b.
Dos razones están en proporción si los cocientes respectivos
son equivalentes, esto es:
a
b
= c
d
= constante de proporcionalidad.
Los términos a y d se denominan extremos, y los términos b y c
se denominan medios.
En toda proporción se cumple que el producto de los extremos es
igual al producto de los medios, o lo que es lo mismo, a d = b c.
En esta sesión resolverás problemas con la constante de proporcionalidad.
1. En parejas resuelvan el problema siguiente.
En la tabla se muestra la cantidad de piezas del mismo modelo adquiridas por cada perso-
na y lo que pagaron en total.
Nombre Cantidad de piezas Pago total
Víctor 13 $195.00
Mariana 8 $120.00
Angélica 21 $315.00
Daniel 4 $60.00
a) ¿Cuánto pagaría Víctor por una sola pieza?
b) ¿Cuánto pagaría Mariana por 30 piezas?
c) Si se sabe la cantidad de piezas adquiridas, ¿cómo se puede determinar la cantidad a
pagar?
e) Gabriela pagó $270.00 por todas las piezas adquiridas. ¿Cuántas piezas compró?
f) Si se conoce la cantidad pagada, ¿cómo se puede determinar la cantidad de piezas
adquiridas?

B4
206
2. Resuelve los problemas.
a) Rosalba compró 3 kg de azúcar en $57.00, y su mamá compró 5 kg, ¿cuánto pagó la
mamá de Rosalba por el azúcar que compró?
b) Juan es taquero, y para no equivocarse al hacer las cuentas y determinar la cantidad de
dinero que debe cobrar, decidió elaborar una tabla, sólo que no la concluyó. Escribe los
valores que faltan.
Cantidad
de tacos
1 2 3 5 10
Cantidad a cobrar
(pesos)
60 204
c) Gonzalo y Felipe corrieron a la misma velocidad. Gonzalo corrió 12 km en 48 minutos,
¿en cuánto tiempo corrió Felipe 7 km?
d) Ana, Jesús y Lizbeth tienen el mismo rendimiento de gasolina en sus autos. El auto de
Ana consumió 15 litros de gasolina al recorrer 135 km, Lizbeth recorrió en su auto
99 km, y el auto de Jesús consumió 9 litros de gasolina en su recorrido, ¿cuántos litros
de gasolina consumió el auto de Lizbeth?
La regla de tres es una manera de resolver problemas con valores relacionados en proporción directa,
ésta se denota como a:b : : c:d
también se representa como a
b
= c
d
, que es igual que ad = bc
La regla de tres se aplica cuando se conocen tres valores y necesitamos averiguar un cuarto, y se basa
en el hecho de que en una proporción el producto de los medios es igual al producto de los extremos.
Por ejemplo, en los autos del problema anterior, el gasto de gasolina está en proporción directa con
los kilómetros que se recorren.
Para saber qué distancia recorrió Jesús en su automóvil con 9 litros de gasolina formamos la siguiente
proporción:
Lizbeth Jesús
15 L
135 km
= 9 L
x km
De acuerdo con la propiedad de las proporciones que establece que a d = b c, sustituimos los datos
y tenemos que:
15x = 135(9) Se forma una ecuación
x = 135 (9)
15 Se resuelve la ecuación
x = 81
Jesús recorre 81 km con 9 L de gasolina.

S28
207
Sesión 115
Ensalada de atún
(4 porciones)
2 latas de atún
250 gramos de lechuga
4 zanahorias
4 jitomates
3. Contesten en parejas.
a) Para preparar este platillo para 6 personas, ¿cuántas latas de atún se
necesitan?
b) Para 20 personas, ¿cuántos kilogramos de lechuga se necesitan?
c) En la familia de Reyna prepararon la receta y ocuparon 30 jitomates,
¿para cuántas porciones alcanzará la ensalada?
4. En equipos, comenten cómo encontraron las respuestas a los problemas
de la sesión.
En esta sesión resolverás problemas encontrando el valor faltante en
una proporción.
1. Analiza el procedimiento propuesto y después responde lo que se te pide.
Para transportar a 124 personas se requieren 4 autobuses. Si se emplearon 7 autobuses,
¿cuántas personas se transportaron?
Lo que se tiene es una proporción directa, y para encontrar el valor faltante se multiplican
extremo por extremo y medio por medio.
(124) (7) = (x) (4) Se forma una igualdad (ecuación)
868 = 4 x Se resuelve la ecuación
x = 868
4

x = 217
Entonces, en 7 autobuses se transportaron 217 personas.

B4
208
La información anterior también se puede representar de las siguientes maneras:
a) 124 personas son a 4 autobuses como x perso-
nas son a 7 autobuses
124 : 4 : : x : 7
b) 4 autobuses son a 124 personas como 7 auto-
buses son a x personas
4 : 124 : : 7 : x
¿Se colocaron los valores en cualquier orden ? ¿Por qué?
¿Qué valores son los extremos en el inciso b?
¿Qué valores son los medios en el inciso b?
Para la forma representada en el inciso a), 124 y 7 son los extremos, mientras que x y 4 son
los medios.
Una forma más de expresar lo anterior es:
124 : 4
x : 7
Si aumentan las personas, ¿aumentará la cantidad de autobuses?
Si disminuye la cantidad de personas, ¿qué sucederá con la cantidad
de autobuses?
2. Lee los siguientes problemas y contesta las preguntas.
a) Por 3 árboles frutales del mismo precio Ernesto pagó $270. Laura también compró de
los mismos tipos de árboles. Si terminó pagando $630, ¿cuántos árboles frutales com-
pró Laura?
¿Cómo plantearías la proporción?
¿Cuál es la ecuación que se forma?
Encuentra la solución y escribe un enunciado con tu respuesta.
b) Para recorrer 85 kilómetros se emplearon 17 litros de gasolina. Si en total se emplearon
25 litros de gasolina, ¿cuántos kilómetros se recorrieron?
c) Para construir 5 m2
de pared se emplean 140 tabiques; con 476 tabiques, ¿cuántos
metros cuadrados de barda se pueden construir?
En equipos, comparen sus procedimientos y sus resultados.
En una proporción se tiene a : b : : c : d
(se lee: a es a b como c es a d)

S28
209
Sesión 116
En esta sesión resolverás problemas aplicando lo aprendido en las
sesiones anteriores.
1. Resuelve en tu cuaderno los siguientes problemas.
a) En un edificio todos los departamentos tienen la misma cantidad de puertas. Si para 5
departamentos se colocaron 24 puertas y el edificio tiene 24 departamentos, ¿cuántas
puertas se deben colocar?
b) Por 200 gramos de jamón se pagaron $25, ¿cuánto se deberá pagar por 750 gramos?
c) De un terreno de 8 hectáreas se cosecharon 72.8 toneladas de aguacate, ¿cuántas
toneladas de aguacate se cosecharán en 15.7 hectáreas?
d) Si el rendimiento de un automóvil es de 18 kilómetros por litro de gasolina, ¿cuántos
kilómetros recorrerá ese automóvil con 2 litros de gasolina?
¿Cuál es la expresión algebraica que permite calcular la distancia recorrida para cual-
quier cantidad de litros de gasolina?
¿Cuál es la constante de proporcionalidad que permite encontrar el consumo de gaso-
lina a partir de la distancia que se recorre?
¿Cuál es la expresión algebraica que corresponde a esta situación de proporcionalidad?
Consulta en…
Entra al sitio:
http://recursostic.educacion.es/descartes/web/materiales_didacticos/EDAD_1eso_pro-
porcionalidad/index_1quincena6.htm, ahí podrás conocer más y resolver ejercicios sobre
proporcionalidad.
 Autoevaluación
1. María fue de vacaciones a Acapulco en su camioneta. Desde su casa recorrió 522 kiló-
metros y gastó 63 litros de gasolina. En cambio Pepe, en su automóvil, gastó 21 litros de
gasolina para recorrer los 190 kilómetros que lo separaban de Cuernavaca.
¿El rendimiento de estos vehículos es proporcional? Explica por qué.
2. Si el auto de Javier tiene el mismo rendimiento que la camioneta de María, ¿cuánta
gasolina necesitará para recorrer los 28.8 kilómetros de la avenida Insurgentes, que es la
más extensa de la ciudad de México?

210
Secuencia 29
Proporcionalidad
utilizando escala
Análisis de los efectos del factor inverso en una
relación de proporcionalidad, en particular
en una reproducción a escala.
Sesión 117
En esta sesión trabajarás con problemas de escalas.
Existen varios objetos que se realizan a escala con fines
diversos. Por ejemplo, los mapas cartográficos, las ma-
quetas que utilizan los arquitectos o los autos a escala. En
la imagen de al lado se muestran las principales escalas
usadas en autos, y una medida aproximada.
Si se hiciera un modelo a tamaño real, ¿a qué escala es-
taría?
¿En la imagen, a qué escala está el primer auto con res-
pecto al último?
Si el auto a escala 1:64 mide aproximadamente 7 cm de largo, ¿cuál es la medida aproxi-
mada del auto original?
¿Cuánto medirían los autos de las otras escalas?
Además de estas escalas, también se utiliza la escala 1:87, ¿cuál sería el tamaño del auto
en esta escala?
Comparen sus resultados con los de otras parejas.
1 : 18
24 cm
1 : 24
18 cm
1 : 43
10 cm
1 : 64
7 cm

211
El producto de dos números recíprocos siempre es uno. Por ejemplo,
7 multiplicado por su recíproco 1
7
es igual a 1, y 2
3
multiplicado
por su recíproco 3
2
es igual a 1.
Sesión 118
En esta sesión continuarás trabajando con escalas en distintos contextos.
1. La siguiente imagen muestra el dibujo de un chip, he-
cho a una escala de 10:1 cm.
¿De qué tamaño es el chip real?
¿Cuál es la diferencia entre la escala utilizada en este
dibujo y las que emplearon en los autos de la sesión
anterior?
¿Cómo calculas la razón de proporcionalidad a partir
de la escala?
¿Cuál es la razón de proporcionalidad en este caso?
Si a partir del dibujo anterior se hiciera una réplica que
coincidiera en medidas con el chip real, ¿cuál sería la
escala del segundo dibujo, respecto del primero?
¿Cuál sería la razón de proporcionalidad?
¿La multiplicación de ambas razones de proporcionali-
dad es igual a uno? ¿Por qué?
¿Cuál sería la escala del segundo dibujo respecto del
chip original?
Comenten sus respuestas con sus compañeros.
10 : 1 cm
5 cm
10 cm

B4
212
Sesión 119
En esta sesión aplicarás lo aprendido en las sesiones anteriores.
Se sabe que un rectángulo tiene un área de 24 cm2
y que su base mide 6 cm de longitud.
a) ¿Cuánto mide su altura?
b) Si se conserva el valor del área del rectángulo pero la base midiera 12 cm, ¿cuántos
centímetros medirá su altura?
c) Si ahora la base del rectángulo midiera 8 cm de longitud y conservara la misma área,
¿cuántos centímetros medirá su altura?
d) ¿Habría alguna relación de escala entre estos rectángulos?
Comenta tus respuestas con tus compañeros.
Consulta en…
Entra al sitio http://vela.sep.gob.mx/index.php/primero y selecciona la materia
Matemáticas para ver el video “Proporcionalidad inversa”.
2. Resuelve esta actividad de manera individual.
La siguiente es una imagen de una habitación hecha
a escala 1:12.
a) ¿Cuánto mide la habitación real?
b) ¿Cuál es la razón de proporcionalidad?
c) Si quisieras colocar una réplica tuya en la habita-
ción,¿cuántomediríade estatura?
Si quisieras hacer la habitación con las medidas origi-
nales, ¿a qué escala la harías, tomando como base
la habitación de la imagen?
¿Cuál es la relación entre ambas escalas?
En grupo, analicen las respuestas de esta actividad
y obtengan una conclusión.
160 mm
127 mm
200 mm

S29
213
Sesión 120
En esta sesión aplicarás una proporción para ir de una escala a otra.
1. En equipos, realicen la siguiente actividad.
En su libro de Geografía ubiquen un mapa a escala.
¿A qué escala está el mapa?
Midan la distancia entre dos puntos del mapa, ¿qué distancia encontraron?
¿Cuál es la distancia real entre estos puntos?
Si en el mapa dibujas un cuadrado con lados de 1 cm, ¿cuál sería el área real de la región
que abarca el cuadrado?
Comparen y comenten sus resultados con otros equipos.
2. Responde las siguientes preguntas.
Si hicieras una estatua tuya, ¿de qué tamaño la harías?
¿Qué escala usarías?
Si se hiciera una réplica de tu estatua al doble del tamaño, ¿cuál sería la escala con res-
pecto a la estatua original? ¿Y cuál sería su escala con respecto a ti?
Comenta tus respuestas con un compañero.
 Autoevaluación
Responde lo siguiente, completando la afirmación para que sea verdadera.
1. El producto de dos números recíprocos es:
2. Un busto que mide 84 pulgadas de altura está hecho a una escala 7:1 pulgadas, ¿cuál es
su medida original en centímetros?
3. El muñeco de un superhéroe está hecho a una escala 1:7 pies, ¿cuál es su estatura
original en metros?

214
Secuencia 30
Problemas de conteo
Resolución de problemas de conteo mediante
diversos procedimientos. Búsqueda de recursos
para verificar los resultados.
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
Valle de Bravo Ote 3
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
A
T
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
A
T
Sesión 121
En esta sesión aprenderás a enumerar todos los resultados posibles
de una situación.
 ¿Qué sabes tú?
Adriana vive cerca del centro de Ciudad Nezahualcóyotl,
en la esquina que forman las calles 25 y Valle de Bravo.
Ella va a la tienda que se encuentra en la calle 32 esquina
con Chalco. El mapa muestra el recorrido que ayer hizo
Adriana para ir a la tienda.
Realiza la siguiente actividad.
a) Sobre la imagen anterior marca con rojo otro recorrido
que podría hacer Adriana para ir de su casa a la tienda.
En este recorrido, ¿por qué calles pasa Adriana para
llegar a la tienda?
Marca en la imagen, con color naranja, el recorrido que
hizo alguno de tus compañeros. ¿Por qué calles pasa
este nuevo recorrido?
Casi todas las calles de Ciudad Nezahualcóyotl son
rectas, por lo que es posible representar el recorrido
que hizo Adriana de su casa (A) a la tienda (T), como
muestra el croquis 1.
Croquis 1
Croquis

215
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
A
T
Croquis pareja 2
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
A 3E
3E
1N
1N
1E
1S T
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
A 1E
2E
1N
2E
1N
1N
2E
2S
T
b) Encuentren en el croquis 2 un recorrido en el que
Adriana camine el menor número de cuadras para
llegar a la tienda (T) y represéntenlo.
¿Cuántas cuadras tiene ese recorrido?
¿Cuántos recorridos diferentes hay con este número
de cuadras?
Comparen su solución con las de los otros equipos.
Marquen esos recorridos de distintos colores en el
croquis 2.
Una pareja de alumnos señaló el recorrido que siguió Adriana en color naranja y otra en
color rosa, como sigue:
a) ¿Puede llegar Adriana a la tienda siguiendo el camino 2N, 5E, 2S, 1N?
Utilicen las letras N, S y E para representar en su cuaderno los recorridos que puede
hacer Adriana para ir de su casa a la tienda caminando el menor número de cuadras.
Croquis 2
Croquis pareja 1 Croquis pareja 2

B4
216
b) Jessica (J) es prima de Adriana y vive en la esquina
de la calle 28 y Chimalhuacán. Utilicen el croquis 3
para contestar las preguntas.
¿Cuál es el menor número de cuadras que debe
caminar Jessica para ir de su casa a la tienda (T)?
c) ¿De cuántas formas diferentes puede ir de su casa a
la tienda caminando el menor número de cuadras?
Utiliza el código de las letras N, S y E para repre-
sentar en tu cuaderno los recorridos más cortos
que puede hacer Jessica.
A los recorridos que constan del menor número
de cuadras se les llamará “recorrido óptimo”.
3. Consideren el croquis 4. Si alguien vive en la esquina
de las calles 23 y Valle de Bravo, ¿de cuántas formas
diferentes puede llegar a la tienda (T) caminando el
menor número de cuadras?
Al encontrar cuántas formas diferentes hay de realizar un recorrido se está resolviendo
un problema de conteo. En los problemas de conteo es conveniente utilizar una manera
de distinguir un resultado de otro.
Por ejemplo, en el caso de Adriana se puede diferenciar un camino de otro si cada uno
de ellos se distingue con un símbolo, una letra o un nombre. Una manera de representar
uno de los ocho recorridos óptimos que Adriana puede hacer es: 1E, 1N, 6E.
Esta manera de resolver problemas de conteo se llama “procedimiento de enumeración”.
Croquis 4
Croquis 3
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
J
T
Chalco
19
21
22
Ilhuicamina
Chimalhuacán
Ilhuicamina
VicenteRivaPalacio
22
23
23
25
25
25
26
26
26
27
27
28
28
29
29
29
30
30
30
31
31
31
32
33
33
34
34
?
T

S30
217
Sesión 122
En esta sesión utilizarás tablas de doble entrada como recurso
para ordenar y contar datos.
En la chocolatería La Delicia elaboran chocolates de dife-
rentes tipos, formas y rellenos. Cuando alguien hace un
pedido, el vendedor debe llenar un formato como el si-
guiente:
a) ¿Habrá más de diez chocolates diferentes?
¿Más de veinte? ¿Más de cuarenta?
b) ¿Cuántos chocolates diferentes pueden elaborarse en
La Delicia?
Compara tus respuestas con las del resto del grupo.
2. En parejas, completen las siguientes tablas.
a) ¿Cuántas variedades de chocolates en forma de bolita
hay de chocolate amargo?
b) ¿Cuántas variedades hay de chocolate oscuro con re-
lleno de nuez?
c) Si alguien pide un chocolate con relleno de almendra,
¿entre cuántas variedades de chocolate puede elegir?
d) Observen las tablas. En la primera casilla de cada ta-
bla está identificada la forma del chocolate, de la se-
gunda columna en adelante están los rellenos, y del
segundo renglón hacia abajo, los tipos. Si en vez
de construir las tablas a partir de la forma del choco-
late se construyen a partir de los diferentes tipos,
¿cuántas tablas tendrían que hacerse? .
Elabórenlas en su cuaderno.
e) ¿Cambia el número total de variedades de chocolate?
¿Por qué?
Analicen sus resultados con ayuda del profesor.
La Delicia Chocolatería
Cliente:
Pedido: Precio:
Fecha de entrega:
Marcar la opción deseada
Forma
Barra
Bolitas
Tipo de chocolate
Oscuro
Blanco
Amargo
Relleno
Nuez
Almendras
Cacahuate
Chocolate
en barra
Relleno
nuez
(n)
Relleno
almendras
(a)
Relleno
cacahuate
(c)
Oscuro (O) O-n
Blanco (B) B-a
Amargo (A)
Chocolate
en bolitas
Relleno
nuez
(n)
Relleno
almendras
(a)
Relleno
cacahuate
(c)
Oscuro (O)
Blanco (B)
Amargo (A) A-a

B4
218
Sesión 123
En esta sesión utilizarás como recurso de conteo el diagrama de árbol.
1. En parejas, completen el siguiente diagrama de árbol.
RellenoFormaTipo
Chocolate
Nuez
Bolitas
Obscuro
Blanco
a) ¿Cuántos chocolates diferentes de tipo amargo se pueden elaborar?
b) ¿Cuántos chocolate diferentes se pueden elaborar con relleno cacahuate?
c) ¿Cuántos chocolates diferentes se pueden elaborar en forma de barra?
d) ¿Cuántos chocolates diferentes se pueden elaborar?
e) ¿Obtuvieron el mismo número de chocolates diferentes con las tablas y con el diagrama
de árbol?
f) El diagrama de árbol anterior tiene tres niveles, uno por cada uno de los conjuntos que
definen las características del chocolate, ¿cuál de las tres características del chocolate
se utiliza en el primer nivel del árbol?
g) Supongan que en La Delicia tienen un nuevo relleno: cajeta. ¿Cuántos chocolates dis-
tintos podrían elaborarse ahora? Elaboren en su cuaderno el diagrama de árbol que
represente esta situación.
Un diagrama
de árbol es un
recurso que
permite visualizar
y enumerar todos
los resultados de
un problema de
conteo. Los
diagramas de
árbol están
compuestos por
niveles y ramas.

S30
219
La Delicia puede decorar los chocolates con dos ingredientes: café o azúcar glass.
Ahora los ha incluido en el formato de pedidos.
a) ¿Cuántas opciones distintas de chocolates ofrece ahora La Delicia?
b) ¿Qué recurso les parece más conveniente utilizar para resolver este problema, el diagra-
ma de árbol o las tablas? Empléenlo para resolver este problema en su cuaderno.
3. De los caracteres que los seres vivos heredan hay algunos que son dominantes y otros re-
cesivos. Por ejemplo, en tu familia, ¿cuál color de ojos es un carácter dominante?,
¿cuál color de ojos es un carácter recesivo?
4. Supón que en cierto tipo de maíz, el blanco es un ca-
rácter dominante y el azul es recesivo. Identifica el
blanco con BB (dos letras porque la información de la
herencia biológica se transmite en pares) y el azul con
aa. Si en la primera generación se cruzan una planta
de maíz blanco y otra de maíz azul, tendrás la siguiente
tabla:
En esta generación todo el maíz que se cosecha es
blanco porque B representa al carácter dominante.
Una planta Ba indica que el maíz es blanco, pero lleva
información del maíz azul (aunque no se manifieste).
La única manera de que el maíz sea azul, por ser ca-
rácter recesivo, es cuando ambas letras son aa.
Si se toman dos de los cuatro descendientes y se cru-
zan, ¿de qué color será el maíz? Averígualo completan-
do la tabla:
a) ¿Cuántas plantas dan maíz blanco? (recuerda que
son las que por lo menos tienen una letra B)
b) ¿Cuántas plantas dan maíz azul (aa)?
Las tablas y los diagramas de árbol son dos recursos para encontrar de
manera sistemática todos los resultados posibles en un problema de conteo.
En ambos casos se ha hecho uso de códigos para enumerar los diferentes
resultados. Cuando se realiza un conteo de modo sistemático, el resultado
será siempre el mismo, no importa el recurso que se utilice.
Planta BB
(blanco)
Planta aa (azul)
a a
B Ba Ba
B Ba Ba
Planta
Ba
Planta Ba
B a
B
a

B4
220
Sesión 124
En esta sesión resolverás un problema de conteo utilizando diferentes
recursos para hacer el recuento.
Monterrey
Huatulco
Cancún
Cuidad de
MéxicoGuadalajara
Ciudad de salida Ciudad de llegada
Una aerolínea cubre los siguientes desti-
nos turísticos del país: ciudad de México,
Guadalajara, Monterrey, Huatulco, Can-
cún. La aerolínea ofrece vuelos directos;
por ejemplo, va de Guadalajara a Cancún
sin hacer escalas, ¿cuántos viajes diferen-
tes ofrece la aerolínea?
Compara tus respuestas con las de tus
compañeros.
2. En parejas, realicen lo que se les pide.
a) Completen la tabla.
b) Si una persona sale de Monterrey, via-
jando en esta aerolínea, ¿a cuántos
destinos diferentes puede llegar?

c) Si una persona llega a Huatulco, ¿de
cuántas ciudades diferentes pudo ha-
ber salido?
d) En total, ¿cuántos viajes diferentes
hay?

S30
221
3. La aerolínea ha decidido dar servicio a la ciudad de Los Cabos.
a) ¿Cuántos viajes diferentes ofrece ahora la aerolínea?
Un equipo empezó a resolver el problema mediante el siguiente diagrama de árbol.
b) Complétenlo en su cuaderno.
Avión
Ciudades de salida Ciudades de llegada Resultados viaje
Huatulco
Huatulco-Monterrey
Guadalajara
Monterrey
Cancún
México
a) ¿Cuántos niveles tiene el diagrama de árbol?
b) ¿A qué corresponde cada nivel?
c) ¿Cuántas ramas tiene el primer nivel?
d) ¿A qué corresponde cada rama?
e) ¿Cuántas ramas tiene el segundo nivel?
f) ¿A qué corresponde cada rama?
g) Consideren una ciudad como punto de salida, ¿cuántas opciones
diferentes de viaje hay?
h) Si hay cinco ciudades como punto de salida, ¿cuántas opciones
diferentes de viaje hay?
i) ¿Qué relación encuentran entre el número de ciudades de salida,
el número de ciudades de llegada y el total de viajes que se pue-
den realizar?
Para determinar el número total
de viajes que la aerolínea ofrece se
puede multiplicar el número de
ciudades de salida por el número
de ciudades de llegada. Por ejemplo,
si hay cuatro ciudades de salida y
tres ciudades de llegada el número
total de viajes es 4 × 3 = 12.

B4
222
Sesión 125
En esta sesión resolverás problemas de conteo a partir de reconocer algunas
regularidades y de utilizar distintos recursos y diferentes estrategias.
1. En parejas, contesten las siguientes preguntas, considerando la información de la sesión
anterior.
a) Ahora la aerolínea da servicio a siete ciudades del país. ¿Cuántos viajes diferentes
ofrece la aerolínea?
b) La aerolínea ahora da servicio a diez ciudades. ¿Cuántos viajes diferentes ofrece?
c) Otra aerolínea tiene como destinos las capitales de los 31 estados del país y la ciudad
de México. ¿Cuántos viajes diferentes ofrece esta otra aerolínea?
Los diagramas de árbol y las tablas son recursos que ayudan a encontrar todas y cada
una de las opciones existentes en un problema de conteo. En ocasiones la multiplicación
es la operación que permite encontrar el número total de opciones existentes.
2. Enrique necesita ponerle una clave a su celular para
que nadie pueda ver las fotos que guarda en él. La
clave debe tener dos cifras y ninguna de las dos puede
ser 0 y deben ser diferentes entre sí.
a) ¿Qué números puede utilizar Enrique como primera
cifra?
¿Cuántos son en total?
b) Si la primera cifra fuera 8, ¿qué números podría
utilizar como segunda cifra?
¿Cuántos son en total?
c) Entonces, ¿qué números de dos cifras pueden
ser el número de la clave del celular de Enrique?
¿Cuántos pares de números existen
en total que cumplen con las condiciones del pro-
blema?
Para tener una mayor seguridad Enrique decide que,
en lugar de dos dígitos, su clave tenga tres dígitos,
ahora sí puede utilizar el 0 y repetir dígitos. Supongan
que el primero debe elegirse de los números del 5 al
8, el segundo tiene que ser 1 o 2 y el tercero es menor
que 5.
a) ¿Cuántas claves distintas se pueden formar?
b) Elaboren tablas de doble entrada para representar
los resultados.
c) ¿Cuántas claves para el celular inician con 51?
d) ¿Cuántas claves terminan con 0?
e) ¿Cuántas claves tienen el mismo número en los
tres dígitos?

S30
223
Sesión 126
En esta sesión aprenderás a leer e interpretar un diagrama de árbol.
En parejas, realicen lo que se indica.
1. El siguiente diagrama de árbol muestra algunas de las posibles placas de identificación
vehicular que se pueden formar utilizando únicamente dos dígitos en cada una. Compléten-
lo en su cuaderno.
a) Contesten las siguientes pre-
guntas.
El resultado (2,1) significa que
en la placa se tiene el 2 en el
primer dígito, ¿qué número tie-
ne en el segundo dígito?
¿Qué significa el resultado
(1,2)?
¿Y el resultado (6,6)?
¿Cuántas placas distintas pue-
de haber?
b) De esas placas, ¿en cuántas
se cumplen las siguientes con-
diciones?:
•• Los dígitos se repiten.
•• En el primer dígito hay un
número mayor que en el
segundo.
•• En el primer dígito hay un
número par.
c) Comparen sus respuestas con
las de sus compañeros y con-
testen lo que se les pide.
¿Cuántas placas hay en las
que ambos dígitos son núme-
ros impares?
¿Y cuántas en las que ambos
dígitos son pares?
ALN–8111
ALN–8112
ALN–8113
ALN–8114
ALN–8115
ALN–8116
ALN–8117
ALN–8118
ALN–8119
Posibles placas
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
Combinación dígitosSegundo dígito
1
2
3
4
5
6
7
8
9
Primer dígito
1
2
3
4
5
6
7
8
9
ALN–81 _ _

B4
224
Consulta en…
En las bibliotecas escolares y de aula busca las siguientes referencias para conocer otros
ejemplos de problemas de conteo:
Akiro Nozaki, Trucos con sombreros, México, sep-fce, 2005 (Libros del Rincón).
Mitsumasa Anno, El jarrón mágico. Una aventura matemática, México, sep-Editorial
Juventud, 2005 (Libros del Rincón).
 Autoevaluación
Completa lo que se te pide.
1. Un recurso que permite visualizar y enumerar todos los resultados de un problema de
conteo es:
2. ¿Qué palabras de cuatro letras se pueden crear con las letras de la palabra A M O R?
¿Cuáles de esas palabras tienen un significado?
2. Del diagrama de árbol se ha tomado el siguiente conjunto de resultados:
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (4,7), (4,8), (4,9), (4,0).
¿Qué característica tienen en común estos resultados?
¿Qué característica tienen en común los siguientes conjuntos de resultados?
a) (1,3), (2,3), (3,3), (4,3), (5,3), (6,3)
b) (1,1), (2,2), (3,3), (4,4), (5,5), (6,6)
c) (1,3), (2,2), (3,1)
d) (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
Comenten con el grupo sus resultados.

225
Secuencia 31
Tipos de gráficas
Lectura de información representada en gráficas de barras
y circulares, provenientes de diarios o revistas y de otras
fuentes. Comunicación de información proveniente de estudios
sencillos, eligiendo la representación gráfica más adecuada.
Sesión 127
En esta sesión reconocerás algunos tipos de gráficas.
Una forma de presentar la información para que sea analizada de manera visual es mediante
gráficas. Las más sencillas son la gráfica de barras y la gráfica circular. En ellas se muestra
el comportamiento de los datos de la población que se está estudiando.
Los diferentes medios de comunicación, como los periódicos y las revistas, utilizan las gráficas
de barra y circular para mostrar a los lectores el comportamiento de diferentes noticias o
investigaciones que realizan, ya sea de manera impresa o electrónica. Ejemplo de ello son
las gráficas siguientes.
Fuente: El economista.mx
¿Con qué frecuencia los niñosde
3 a 12 años consumen cereales?
37%
Diario
50%
De 2 a 3
veces por
semana
9%
Cada
semana
3%
Cada mes
1%
Nunca
¿Cuál es la razón principal por la
que compras cereales a los niños?
42% Los niños lo piden (les gusta)
33% Por sus propiedades alimenticias (son nutritivos)
7% Para que desayunen los niños
5% Para darle variedad al desayuno
3% Por costumbre
10% Es práctico (fácil preparación)
REVISTA DEL CONSUMIDOR • MARZO 11 43
Fuente: Revista del Consumidor.

B4
226
1. Observa las gráficas y contesta la pregunta siguiente.
a) ¿Qué tema muestran cada uno de los gráficos?
2. En equipos de cuatro integrantes, realicen la actividad siguiente.
a) Cada uno de los miembros del equipo escojan una de las imágenes anteriores, obsér-
venla, analícenla y, con sus palabras, expliquen al resto del equipo lo que la gráfica
informa.
1. En parejas, observen la gráfica y contesten.
De acuerdo con la Encuesta Nacional sobre Prácticas de Lectura 2006, el promedio de li-
bros leídos por los alumnos de cuarto a sexto de primaria y de secundaria según el servicio
educativo es de 3.6 a nivel nacional.
5
4
3
2
1
0
3.6
4.8
4.1
1.7
2.5 2.4 2.3
Primaria
Multigrado
Primaria
Indígena
Primaria
General
Secundaria
General
Secundaria
Técnica
Telesecundaria
Nacional
Promedio de libros leídos
a) En promedio, ¿qué alumnos leen más libros?
b) ¿Cuál es la diferencia entre el mayor promedio de lectura y el promedio nacional?
c) ¿Qué promedio de libros leídos tiene el servicio educativo que menos lee?
d) Al comparar sólo el nivel de secundaria, ¿en qué lugar se ubica el promedio de lectura
de la telesecundaria?

S31
227
2. La siguiente gráfica muestra información sobre el promedio de libros leídos por los alumnos
de cuarto a sexto de primaria y de secundaria, agrupados por rangos de edad.
Promedio de libros leídos por grupos de edad
1.9
2.9
4.5
De 8 a 11 años
De 12 a 15 años
De 16 años y más
a) ¿En qué grupo de edad se presenta el mayor promedio de libros leídos?
b) ¿Qué grupos de edad presentan un promedio mayor al nacional?
c) ¿Qué promedio de libros leídos presenta el grupo de edad de 8 a 11 años?

B4
228
Sesión 128
En esta sesión resolverás problemas utilizando gráficas de barras.
Un documento del Instituto Mexicano de Cinematografía presenta toda la información per-
tinente sobre el desarrollo anual del cine mexicano. La siguiente tabla muestra la asistencia
al cine por día de la semana.
El miércoles el precio promedio de la entrada fue 18% menor respecto al precio habitual.
21%
26%
14%15%
8%8% 7%
Domingo
Sábado
Viernes
Jueves
Distribución de asistencia
Miércoles
Martes
Lunes
30%
25%
20%
15%
10%
5%
0%
Fuente: IMCINE, con datos de Rentrak / Anuario estadístico 2010.
a) ¿Qué porcentaje de asistencia se presentó el fin de semana en los cines?
b) ¿Qué día se presenta el mayor número de asistentes?
c) El miércoles se presenta un 15% de asistencia. ¿Podrías justificar el motivo?
En grupo, comparen sus respuestas.

S31
229
2. Observa la siguiente gráfica y contesta.
Fuente: IMCINE, con datos de Rentrak / Anuario estadístico 2010.
Otra
película
dehuevosyun
pollo
Una
película
dehuevos
Arráncam
ela
vida
No
erestú,soyyo
Rudo
ycursi
La
mism
a
luna
Ytu
m
am
á
tam
bién
Km
31
Am
oresperros
Elcrim
en
delpadreAm
aro
Películas mexicanas con mayor número de espectadores. 2000–2010
6
5
4
3
2
1
0
Espectadoresenmillones
5.2
4.0 3.5
3.3 3.2 3.1 3.0 2.9
2.5 2.4
a) ¿Cuál es la película con mayor audiencia?
b) ¿Cuál es la diferencia en audiencia entre la película más vista y la menos vista?
En una gráfica de barras, la altura de cada barra es la cantidad que representa. Su principal
finalidad es comparar datos de las distintas categorías de información. Para comparar catego-
rías es recomendable ordenar las frecuencias, ya sea en orden ascendente o descendente.

B4
230
Sesión 129
En esta sesión resolverás problemas utilizando gráficas circulares.
1. La siguiente información se refiere a la distribución porcentual de horas a la semana que los
integrantes del hogar de 12 y más años de edad dedican a actividades de esparcimiento.
Convivencia social
Asistencia a eventos
culturales, deportivos
y de entretenimiento
Deportes y ejercicio físico
Participación en juegos
y aficiones
Utilización de medios
masivos de comunicación
59.0
4.2
2.1
6.7
28.1
Fuente: INEGI, Encuesta Nacional de Uso del Tiempo 2009.
¿A qué actividad le dedican más tiempo?
¿A qué actividad le dedican menos tiempo?
A la gráfica circular se le llama también “de pastel”, o diagrama de sectores, y se
construye empleando la frecuencia relativa (fracción o número decimal) de cada dato.
Al sumar los porcentajes de todos los sectores siempre da como resultado 100%.
Consulta en…
Explora los siguientes sitios para conocer otras interesantes gráficas de estadísticas:
http://eleconomista.com.mx/industrias/2012/01/26/buen-fin-impulsa-ventas-minoristas-mexico
http://revistadelconsumidor.gob.mx/wp-content/uploads/2011/05/estudio-cereales2.pdf
http://revistadelconsumidor.gob.mx/wp-content/uploads/2011/11/bebidas-hidratantes.pdf
http://cuentame.inegi.org.mx/poblacion/default.aspx?tema=P
http://www.imcine.gob.mx/informes-y-estadsticas.html

S31
231
 Autoevaluación
• ¿Es correcto utilizar una gráfica de barras para comparar porcentajes, y una gráfica
circular para comparar frecuencias? Justifica tu respuesta.
2. El gráfico siguiente muestra el tipo de actividad que desempeña el personal de los gobier-
nos estatales de la República Mexicana.
Actividades de gobierno
Servicios educativos
Servicios de salud
y asistencia social
38%
9%
53%
¿En qué actividad se desempeña el mayor número de personas?
¿En qué actividad se desempeña el menor número de personas?

B4
232
Sesión 130
Evaluación
Aplica lo aprendido a lo largo del bloque y selecciona la respuesta a cada problema.
1. ¿Qué distancia hay entre los números –16.01 y 1.08?
a) –15.07
b) –14.93
c) 15.07
d) 14.93
2. Coloca la letra V cuando la afirmación sea verdadera, y la letra F cuando la afirmación sea
falsa.
Para encontrar el centro de un círculo dadas dos paralelas, se traza la mediana a una
de las cuerdas, se identifica el diámetro que está sobre la mediatriz, se obtiene el
punto medio del diámetro, el cual es el centro del círculo.
Dados tres puntos que no son colineales siempre se puede trazar una circunferencia
que pase por ellos. El centro de la circunferencia que pasa por ellos es el punto de
intersección de las mediatrices.
Para encontrar el centro de un círculo dadas dos cuerdas no paralelas, se traza la
mediatriz a cada cuerda y el punto de intersección de las mediatrices trazadas es el
centro de la circunferencia.
3. ¿Cuál es el área de un círculo cuyo diámetro es de 7 cm?
a) 10.9 cm2
b) 21.9 cm2
c) 38.48 cm2
d) 153.93 cm2
4. Si 5 paquetes de arroz cuestan $49.5, ¿cuánto costarán 12 paquetes?
a) $117.6
b) $118.8
c) $119.8
d) $130.8

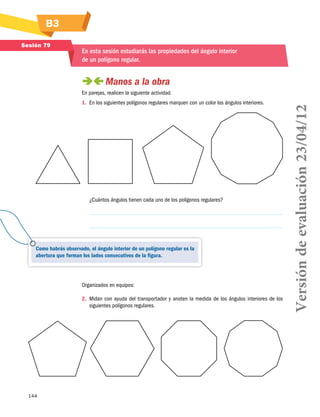
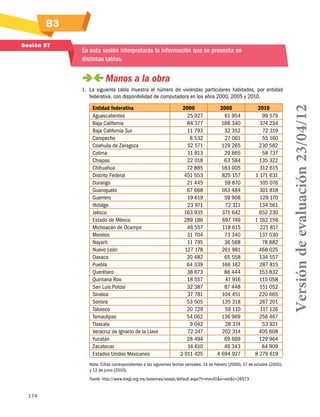
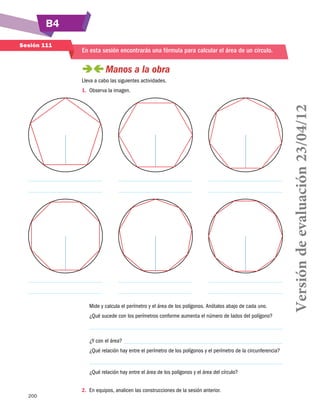
S31
233
5. Si dos albañiles construyen una barda en 3 días, ¿cuánto tardarían en construirla 4 albañiles?
a) Un día y medio
b) Un día
c) Dos días
d) Dos días y medio
6. ¿Cuántas placas como la siguiente es posible obtener si se pueden repetir los dígitos?
a) 72
b) 81
c) 90
d) 100
A – 30 –
7. Con la información de la siguiente tabla construye una gráfica de barras usando la columna
“ambos sexos”.
2012
Nacimientos totales
Ambos sexos Varones Mujeres
Estado de Colima 10 133 5 191 4 942
Armería 365 187 178
Colima 1 842 943 899
Comala 312 160 152
Coquimatlán 246 126 120
Cuauhtémoc 381 195 186
Ixtlahuacán 50 26 24
Manzanillo 2 950 1 511 1 439
Minatitlán 84 44 40
Tecomán 1 800 922 878
Villa de Álvarez 2 103 1 077 1 026
Fuente: SINAIS, Estadística de nacimientos estimados por sexo en el estado de Colima para el año 2012:
http://www.sinais.salud.gob.mx/nacimientos/index.html [Fecha de consulta: 15-12-2011]

Bloque 5

• Resolver problemas aditivos que impliquen el uso de
números enteros, fraccionarios o decimales positivos
y negativos.
• Resolver problemas que impliquen el cálculo de la raíz
cuadrada y potencias de números naturales y decimales.
• Resolver problemas de proporcionalidad directa del tipo
“valor faltante”, en los que la razón interna o externa es
un número fraccionario.

236
Secuencia 32
Sumas y restas con enteros
Resolución de problemas que implican el uso
de sumas y restas de números enteros.
Sesión 131
En esta sesión realizarás operaciones con números enteros.
Recuerda que los enteros son el conjunto de números que incluye
a los naturales, sus negativos y al cero.
En los torneos de futbol, si un equipo gana un partido se le asignan tres puntos, si empata uno,
y si pierde no se le contabiliza nada. Al final del torneo se suman todos los puntos acumulados
y el que tenga más es el ganador. Si dos equipos tuvieran el mismo número de puntos se utili-
za como criterio de desempate la diferencia de goles, es decir, los goles anotados menos los
goles recibidos, de manera que el equipo que tenga un número mayor tendrá mejor posición.
En el mundial de 2010 celebrado en Sudáfrica, la selección mexicana jugó en la primera fase
del torneo contra Sudáfrica, Francia y Uruguay. Los dos primeros lugares del grupo clasificaron
a la segunda ronda. Los resultados de los encuentros de los equipos del grupo se muestran a
continuación.
Sudáfrica 1-1 México
Francia 0-0 Uruguay
Francia 0-2 México
Sudáfrica 0-3 Uruguay
Uruguay 1-0 México
Sudáfrica 2-1 Francia
Fuente: FIFA, World Cup South Africa 2010.
¿Cuántos puntos tuvieron al final de la primera ronda cada uno de los equipos?
¿Qué equipos clasificaron a la siguiente ronda?
¿Por qué?
Comenta con tu grupo tus respuestas.

237
En parejas, realicen las siguientes actividades.
1. A continuación se muestran los tiros penales a favor y en contra marcados a los equipos
participantes en el torneo de apertura 2011-2012 del futbol mexicano. Completen la tabla.
Equipo Penales a favor Penales en contra Diferencia
UNAM 2 2 0
Atlante 6 0
Monterrey 6 2
Querétaro 6 3
Puebla 4 4
San Luis 3 4
Guadalajara 3 2
Morelia 3 3
Pachuca 3 1
Jaguares 2 4 −2
Toluca 2 3
Santos 1 2
América 1 0
Tijuana 1 5
UAG 1 5
Cruz Azul 1 1
Atlas 1 3
UANL 0 2
Fuente: Federación Mexicana de Futbol.
¿Qué equipos tuvieron más penales a favor?
¿Qué equipos tuvieron más penales en contra?
¿Qué equipos tuvieron la misma cantidad de penales a favor y en contra?
¿Qué equipos tuvieron menos penales a favor que en contra?
Comenten sus resultados con el grupo.

B5
238
2. El ingreso y el gasto mensual de cinco familias de cierto poblado se muestran a continuación.
Familia Ingreso Gasto
López $5 000.00 $4 500.00
Hernández $8 500.00 $7 800.00
Pérez $3 500.00 $3 400.00
Rodríguez $6 200.00 $4 950.00
García $7 490.00 $6 325.00
Después de haber realizado sus gastos, ¿qué familia dispone de mayor cantidad de dinero
para hacer frente a alguna eventualidad?
Supóngase que una de estas familias tiene que hacer un desembolso adicional de $900.00
para la atención médica de uno de sus hijos, ¿qué familia podría realizar este pago sin
necesidad de pedir prestado?
Comenten sus respuestas con sus compañeros.
En una adición de dos números enteros, que cuentan con el mismo
signo, el resultado mantendrá el mismo signo.
En una adición de dos números enteros con diferente signo, el resultado
será positivo si el valor absoluto del número positivo es mayor que el
valor absoluto del número negativo; en caso contrario el resultado es
negativo, y es cero si ambos valores absolutos son iguales. Por ejemplo:
9 + (–5) = 4, pues |9| |–5|
–9 + 5 = –4, pues |5| |–9|
–9 + 9 = 0, pues |–9| = |9|

S32
239
Sesión 132
En esta sesión resolverás problemas haciendo sumas de números enteros.
1. En parejas, realicen las siguientes actividades.
a) Un juego de lotería tiene 12 planillas (divididas en 9 casillas) y 52 cartas en las que se
encuentran los personajes. Regularmente, para marcar las casillas se utilizan piedras o
algunas semillas. Si hay 12 personas jugando, ¿cuántas piedras o semillas se necesitan
para llenar todas las planillas?
b) La familia Martínez adquirió una casa a través de un crédito bancario y cada mes va a
pagar al banco $3 500.00, que representan la tercera parte de su ingreso. Por otra
parte, el señor Martínez está preocupado porque uno de sus hijos va a estudiar la pre-
paratoria y mensualmente requiere $1 500.00 para cubrir sus nuevas responsabilida-
des, y además sus gastos habituales por mes ascienden a $4 500.00. ¿Con su ingreso
actual puede cubrir sus gastos?
c) Debido a problemas con el transporte público, Juan casi siempre llega tarde a su traba-
jo. Su jefe y él acordaron que cada vez que llegue tarde deberá quedarse más tiempo al
final de la jornada, o de lo contrario se le descontará un día por cada hora acumulada.
A continuación se muestra el tiempo que Juan llegó tarde en la última semana.
Día Tiempo que llega tarde en minutos
Lunes 68
Martes 43
Miércoles 94
Jueves 16
Viernes 19
¿Cuál fue el total de tiempo que tuvo que reponer Juan en esa semana?
Si no hubiera repuesto el tiempo que llegó tarde, y al día gana $200.00, ¿cuánto dinero
le hubieran descontado?
Comparen sus respuestas con las de sus compañeros y coméntenlas.

B5
240
Sesión 133
En esta sesión realizarás adiciones con enteros.
Para realizar sumas de números enteros tienes que considerar el valor absoluto de las cifras
y sus signos.
1. Resuelve las siguientes sumas de números enteros.
(+427) + (+180) =
(110) + (150) =
(−9470) + (+842) =
(+108) + (−487) =
(−57)+(−84)=
2 ¿Qué número se debe sumar en las siguientes operaciones?
+ (−5792) = 0
+ 4865 = 0
Compara tus resultados con el grupo.
3. En parejas, resuelvan la siguiente actividad.
Durante el ciclo escolar 2006-2007, en Veracruz había en total 1 628 telesecundarias. Si
489 eran consideradas urbanas, ¿cuántas telesecundarias eran rurales?

S32
241
Sesión 134
En esta sesión realizarás sustracciones de números enteros.
Resuelve las actividades siguientes.
1. José va a la feria del pueblo a jugar, lleva $125.00 para gastar. Si gastó $60.00 en juegos
de destreza y $75.00 en juegos mecánicos, ¿cuánto dinero le queda para seguir jugando?
2. Luis va a presentar un informe de la administración de su edificio; los datos de los movi-
mientos del último mes se muestran en la tabla siguiente.
Concepto Entrada Salida
Saldo al cierre del mes anterior $6 530.00
Pago de conserje $1 750.00
Pago de luz $487.00
Pago de agua $230.00
Pago de vigilancia $1 200.00
¿Cuál es el saldo al final del mes?
3. Juan recibe en su tarjeta de débito $1 800.00 por su beca. Durante el mes en curso realiza
tres compras, una de $950.00, otra de $300.00 y una más de $250.00, ¿Cuánto será su
saldo para el siguiente mes?
Siantesdelcorteledepositan $500.00,¿cuántotendráelpróximomes?
4. En equipos, con las siguientes frases construyan un ejemplo para cada una de ellas, com-
pleten la información faltante y comenten sus resultados.
Un número positivo “grande” – un número positivo “pequeño” =
Un número positivo “pequeño” – un número positivo “grande” =
Un número negativo “grande” – un número positivo “pequeño” =
Un número positivo “pequeño” – un número positivo “grande” =
Un número positivo “grande” – un número negativo “pequeño” =
Un número positivo “pequeño” – un número negativo “grande” =
Un número negativo “grande” – un número negativo “pequeño” =
Un número positivo “pequeño” – un número negativo “grande” =

B5
242
Sesión 135
En esta sesión usarás sumas y restas de números enteros
para resolver problemas.
Resuelvan en parejas los siguientes problemas.
1. Un vehículo de transporte público recorre su ruta generalmente en una hora. La ruta se
conforma de cinco paradas; en la siguiente tabla se muestra el número de pasajeros que
utilizaron el vehículo en la ruta de las 9 a las 10 de la mañana del pasado lunes. Completen
la tabla.
Parada
Pasajeros que suben
al vehículo
Pasajeros que
descienden del
vehículo
Pasajeros a bordo al
dejar la parada
Base 60 0 60
La Loma 15 8
El Centro 25 49 43
El Fuerte 13 21
La Plaza 3 29
Base 0 0
¿Cuántos pasajeros descendieron en total del vehículo durante toda la ruta?
Si el vehículo cobra $8.00 por persona, ¿cuánto llevaba recaudado al salir de El Fuerte?
Comenten sus resultados con el grupo.

S32
243
2. En la tabla siguiente se muestran los ingresos y egresos del mes de agosto de una taquería.
Costos $
Ventas de la primera semana 12 000.00
Ventas de la segunda semana 8 000.00
Ventas de la tercera semana 13 500.00
Ventas de la cuarta semana 15 000.00
Renta (mensual) –5 000.00
Agua (bimestral) –200.00
Luz (bimestral) –1 500.00
Pago por seguridad social (mensual) –1 200.00
Salario de tres personas (quincenal) –9 000.00
Materia prima (semanal) –3 500.00
¿Cuál es la ganancia neta del mes de agosto?
Comenten sus respuestas con el resto del grupo.
 Autoevaluación
• ¿Cuáles de las siguientes operaciones resultan en un número negativo? Subráyalas.
–54 + 53
–38 + (–37)
1 – 2
2 – (3)

244
Secuencia 33
Notación exponencial
Uso de la notación científica para realizar
cálculos en los que intervienen cantidades
muy grandes o muy pequeñas.
Sesión 136
En esta secuencia aprenderás a representar dichas cantidades en una forma
abreviada, llamada notación científica, que ayuda a realizar cálculos
con cantidades muy grandes, como la distancia entre la Tierra y el Sol,
que es de 149 597 870 000 m; o con cantidades muy pequeñas,
como la longitud de una bacteria, que puede ser de 0.000005 m.
La imagen muestra las medidas de un abrevadero
que se construirá en un rancho.
1. Completa la tabla con las medidas del abrevadero en las unidades que correspondan.
Metros (m) Centímetros (cm) Milímetros (mm)
Largo 10 10 000
Ancho 100
Altura 70

2. Calcula el área de las caras laterales del abrevadero, según la unidad de medida que se
solicita.
a) ¿Cuántos milímetros cuadrados tienen de área las caras laterales del abrevadero?
b) Comparen sus resultados con el grupo.
10m
1000mm
70cm

245
1. Escribe las siguientes potencias como productos y obtén sus resultados.
26
= 2 × 2 × 2 × 2 × 2 × 2 = 64
53
= = 125
= 10 × 10 =
35
= =
Recuerda que un número que se multiplica varias veces por sí mismo se representa como
una potencia. Por ejemplo: 3 × 3 × 3 × 3 = 34
. En la expresión 34
, 3 es la base y 4 es
el exponente.
2. Calcula las potencias de 10 que se indican en las tablas. Si lo requieres usa números
decimales.
Potencia de 10 Cantidad
10–1
10–2
10–3
10–4
10–5
= 1
105 = (1
10)5
0.00001
10–6
Potencia de 10 Cantidad
105
104
103
102
100
101
100
a) ¿Cuántos ceros hay después del 1 al calcular 103
?
b) ¿Cuántos ceros hay después del 1 al calcular 1012
?
c) ¿Cuántas cifras (ceros y 1) hay después del punto decimal al calcular 10–4
?
d) ¿Cuántas cifras hay después del punto decimal al calcular 10–15
?
3. Analiza tus respuestas y contesta las siguientes preguntas.
a) ¿Qué relación hay entre el exponente positivo de la potencia de 10 con el número de
ceros que van después del 1?
b) ¿Qué relación hay entre el exponente negativo de la potencia de 10 con el número de
cifras que van después del punto decimal?
En grupo, comenten sus respuestas y entre todos establezcan sus conclusiones.

246
B5
Sesión 137
1. Expresa cada cantidad como una potencia de 10.
1 000 = 0.00001 =
10 000 000 = 0.000000001 =
10 = 0.001 =
100 000 = 0.1 =
a) ¿Cómo obtuviste los resultados de la columna izquierda?
b) ¿Cómo obtuviste los resultados de la columna derecha?
2. Analiza los siguientes casos y responde las preguntas. Justifica tus respuestas.
a) Para escribir 10 000 000 como potencia de 10, Ana recorrió el punto decimal hacia la
izquierda hasta llegar a la derecha del 1, luego contó el número de cifras que lo recorrió
y escribió ese número como exponente de la potencia de 10.
10 000 000 = 107
•• ¿Es correcto el procedimiento que siguió Ana?
•• ¿Se puede aplicar este procedimiento en los demás casos de números naturales?
b) Para expresar 0.00001 como potencia de 10, José recorrió el punto decimal hacia la
derecha hasta después del 1, luego contó el número de cifras que lo recorrió y escribió
ese número como exponente de la potencia de 10, pero con signo negativo.
0.00001 = 10−5
•• ¿Es correcto el procedimiento seguido por José?
•• ¿Se puede aplicar este procedimiento en los demás casos de números decimales?
En grupo, comparen sus respuestas. Entre todos redacten en su cuaderno una regla para
escribir la cantidad que le corresponde a una potencia de 10 (consideren que hay exponentes
positivos y negativos).

247
S33
3. Expresa las cantidades como el producto de un número natural por una potencia de 10.
30 000 =
150 000 =
0.12 =
0.04 =
a) José escribió la siguiente respuesta: 30 000 = 34
¿Es correcto el resultado de José? Explica por qué.
b) Ana escribió la siguiente respuesta: 30 000 = 3 × 10 000 = 3 × 104
¿Es correcto el resultado de Ana? Explica por qué.
4. Expresa cada cantidad como el producto de un número por un múltiplo de 10; y luego como
potencia de 10.
a) 200 000 = 2 × 100 000 = 2 × 105
b) 4 000 = × 1 000 = × 103
c) 350 000 000 = 3.5 × =
d) = 1.25 × 1 000 000 =
6. En equipos, comenten lo siguiente.
¿Qué procedimiento se debe realizar para expresar 0.04 en notación científica?
Se le llama notación científica a la forma abreviada
de expresar un número muy grande, con una multipli-
cación donde uno de los factores es una potencia de
10 y el otro es un número menor que 10, por ejemplo:
351 000 000 se puede expresar como 3.51 × 108 Versióndeevaluación23/04/12

248
B5
Sesión 138
En esta sesión transformarás números muy grandes.
a) La distancia media entre la Luna y la Tierra es aproximadamente de 380 000 000 m.
Expresa esta cantidad en notación científica.
Distancia Luna a Tierra = m
b) La vida media de un muón (partícula elemental similar al electrón) es de 0.0000022 s.
Expresa esta cantidad en notación científica.
Vida media del muón = s
2. Escribe cada número en notación científica.
a) 3 640 000 =
b) 0.0000000000000034 =
c) 47 090 000 000 000 000 =
d) 0.000001006 =
e) 21 890 000 000 =
f) 0.00000005402 =
3. En grupo, redacten una regla para escribir números muy grandes o muy pequeños en nota-
ción científica.
En notación científica un número decimal muy
pequeño se expresa con una multiplicación donde uno
de los factores es una potencia de 10 con exponente
negativo, por ejemplo: 0.0000000017 se expresa
como 1.7 × 10–9

249
S33
Sesión 139
En esta sesión utilizarás la notación científica para expresar
la resolución de un problema.
¿Sabías que la luz que nos llega del Sol es historia?, esto se debe a que tarda cerca de 8.3 mi-
nutos en recorrer una distancia aproximada de 149 597 870 km que hay entre el Sol y la Tierra.
Piensa en cuánto tardará en llegar la luz de estrellas que están a miles de millones de kilóme-
tros de nuestro planeta.
a) En números redondos, la distancia media entre la Tierra y el Sol es de 150 000 000 000 m,
y la distancia entre la Tierra y Neptuno es de 4 308 000 000 000 m.
¿Cuál es la distancia aproximada que hay entre el Sol y Neptuno?
b) Expresa las medidas de las distancias de la Tierra al Sol y a Neptuno en notación científica:
Distancia entre la Tierra y el Sol = 150 000 000 000 m = m
Distancia entre la Tierra y Neptuno = 4 308 000 000 000 m = m
Realiza la suma de las dos cantidades expresadas en notación científica.
¿Qué resultado obtuviste?
c) En grupo, comenten los procedimientos que siguieron y sus resultados. ¿Hubo diferen-
tes respuestas? Verifiquen sus resultados escribiéndolos en notación decimal.
2. En parejas, lean los siguientes procedimientos.
Emilio resolvió la suma del problema de la siguiente manera:
•• Primero escribió las cantidades como potencias de 10, de manera que ambas tuviesen
el mismo exponente en la potencia de 10.
Distancia entre la Tierra y el Sol = 150 000 000 000 m = 1.5 × 1011
m
Distancia entre la Tierra y Neptuno = 4 308 000 000 000 m = 43.08 × 1011
m
•• Luego sumó sólo la parte decimal de cada cantidad: 43.08 + 1.5 = 44.58
•• Al resultado de esta suma le escribió el producto por la potencia de 10 de las cantida-
des en notación científica: 44.58 × 1011
•• Al final corrió el punto decimal una cifra hacia la izquierda y cambió el exponente: 4.458 × 1012
a) ¿El resultado que obtuviste es igual al de Emilio?
b) Analiza este procedimiento y determina si es correcto o no. Sigue todos los pasos
y verifica la suma: 39 900 000 + 5 470 100 000 = 5.51 × 109
c) En equipos, comenten lo siguiente: ¿se puede aplicar este procedimiento para la resta
de cantidades escritas en notación científica? Entre todos propongan un ejemplo
y realicen las operaciones necesarias.

250
B5
Sesión 140
En esta sesión trabajarás con notación científica para resolver
problemas con números pequeños.
¿Sabías que en nuestro cuerpo hay más células bacterianas que células humanas? Se calcula
que hay diez veces más, y el mayor número se localiza en el tracto digestivo y en la piel. Las
bacterias son microorganismos unicelulares de formas diversas que alcanzan un tamaño
que va de algunos milímetros hasta milésimas de milímetro o micrómetros (μm).
No todas las bacterias son perjudiciales para el cuerpo humano; de hecho, necesitamos de
ellas para muchas funciones, como la digestión. ¿Qué otros beneficios generan las bacterias?
Se calcula que en un mililitro de agua dulce hay cerca de
un millón de células bacterianas, mientras que en un gra-
mo de tierra hay hasta 40 millones.
¿Cuántas bacterias habrá en 1 3
4
litros de agua dulce?
Comenten el procedimiento que siguieron y sus resulta-
dos. Verifiquen sus respuestas usando la calculadora.
3. Escribe en el paréntesis de cada operación la letra que corresponda al resultado.
( ) 2.3 × 107
+ 608 000 000 =
( ) 971 000 – 77 000 =
( ) 4 806 000 000 + 133 300 000 000 =
( ) 6.501 × 10−11
− 512 × 10−13
=
( ) 3.4 × 10−6
+ 0.00000692 =
( ) 778 000 000 − 1.57 × 108
=
( ) 8.22 × 10–10
+ 4.51 × 10−10
=
(T) 1.381 × 1011
(I) 6.21 × 108
(U) 1.381 × 10–11
(E) 6.31 × 108
(D) 0.00001032
(S) 8.94 × 105
(A) 0.000000001273

251
S33
2. Realiza los siguientes pasos para calcular el producto de 1 000 000 por 1 750:
•• Escribe 1 000 000 en notación científica:
•• Multiplica 1 750 por la parte decimal (sin la potencia de 10) del número escrito en no-
tación científica: 1 750 × =
•• Multiplica el resultado anterior por la potencia de 10 del número en notación científica:
1 750 × =
•• Escribe el resultado en notación científica:
a) ¿El resultado que obtuviste fue 1.75 × 107
? Si no es así, repasa el procedimiento ante-
rior y rectifica.
b) Sigue los pasos anteriores y calcula el producto de 0.000000812 × 1 500.
En grupo, comenten cómo resolvieron los problemas de las actividades 1 y 2. Entre todos
propongan un ejemplo y realicen los pasos anteriores para calcular el producto de un nú-
mero escrito en notación científica por otro escrito en notación decimal.
3. Usa los datos del problema anterior y calcula la cantidad de células bacterianas que hay en
455 g de tierra.
 Autoevaluación
Realiza en tu cuaderno las siguientes operaciones.
• 6.91 × 10–10
× 585 = • 1 071 000 000 − 4.3 × 108
=
• 590 000 000 + 9 060 000 000 = • 4.04 × 10−11
+ 0.000000000839 =
• 5.23 × 105
+ 692 000 − 6.7 × 104
= • 38 000 000 000 × 9 500 =
En general, un número está escrito en notación científica si se expresa de la forma a × 10n
,
donde a es un número decimal mayor o igual que 1 y menor que 10.
Para sumar o restar dos números expresados en notación científica es necesario escribirlos
de manera que sus respectivas potencias de 10 tengan el mismo exponente. Por ejemplo:
(4.6 × 108
) + (5.7 × 106
) = (46 × 107
) + (0.57 × 107
) = 46.57 × 107
= 4.657 × 108
El número 1 seguido de cien ceros, esto es 1 × 10100
, se denomina googol.
Para darnos una idea de lo que representa este número: un googol es
mayor que el número de átomos en el universo conocido.

252
Secuencia 34
Raíz cuadrada
el cálculo de la raíz cuadrada (diferentes métodos)
y la potencia de exponente natural de números
naturales y decimales.
Sesión 141
En esta secuencia estudiarás potencias y la raíz cuadrada.
De manera individual contesta lo que se te pide.
1. Una de las primeras fórmulas que aprendiste en tus cursos de Matemáticas es la que se
utiliza para calcular el área de un cuadrado. Si la medida del lado de un cuadrado es L,
se tiene que su área A se calcula con la fórmula: A = L × L . Esta expresión suele expresarse
como A = L2
. ¿Sabes cómo calcular la medida del lado de un cuadrado si se conoce
la medida de su área?
2. Don Luis va a cercar su terreno para formar parcelas de superficie cuadrada, por lo cual
está calculando las medidas que deben tener los lados y el área de diferentes cuadrados.
Calcula las siguientes medidas.
a) Si el lado de un cuadrado mide 2 m, ¿cuánto mide su área?
b) Si el lado de un cuadrado mide 5 m, ¿cuánto mide su área?
c) Si el lado de un cuadrado mide 3 m, ¿cuánto mide su área?
d) Si un cuadrado tiene un área de 16 m2
, ¿cuánto mide su lado?
e) Si un cuadrado tiene un área de 36 m2
f) Si un cuadrado tiene un área de 32 m2
De manera grupal comparen sus respuestas. Comenten cómo calcularon la medida del
área de un cuadrado cuando se conoce la medida de su lado.

253
1. La imagen representa parte del terreno que va a cercar don Luis. Se trata de un cuadrado
del cual sólo conoce la medida de la diagonal.
Lado
Contesta las siguientes preguntas.
a) Con una regla traza la otra diagonal del cuadrado, así obtendrás cuatro triángulos rec-
tángulos iguales.
¿Cuánto mide el área de cada triángulo?
¿Cuánto mide el área del cuadrado?
¿Cuánto mide el lado del cuadrado?
b) Mide con una regla la longitud del lado del cuadrado.
Aplica la fórmula del área del cuadrado A = L × L y verifica la medida que obtuviste para
el lado del cuadrado.
¿Qué medida del área del cuadrado obtuviste usando la fórmula?
c) Compara los resultados que obtuviste con los procedimientos anteriores y contesta:
De los valores del área que obtuviste con la fórmula, ¿cuál se aproxima más a 32 m2
?
¿Cuál es la mejor aproximación que obtuviste de la medida del lado del cuadrado?

B5
254
Sesión 142
En esta sesión obtendrás valores aproximados de la raíz cuadrada
de números naturales.
Medida del lado (m) Área (m2
)
2
3
16
5
36
5.5
5.6
5.7
5.65
1. Completa la tabla para encontrar valores aproximados de la medi-
da del lado del cuadrado con 32 m2
de área.
a) ¿Cuál es la mejor aproximación que obtuviste para la medida
del lado del cuadrado?
b) ¿Crees que se puede encontrar una mejor aproximación para la
medida del lado? , ¿cuál?
Compartan sus respuestas y entre todos establezcan sus conclu-
siones con respecto a la obtención del lado de un cuadrado cuan-
do se conoce la medida de su área.
2. En parejas, realicen la actividad siguiente.
Un ayudante de don Luis dice que no existe cuadrado alguno que tenga 42 m2
de área;
don Luis asegura que sí.
Medida del lado (m) Área (m2
)
6 36
6.3
6.4
6.5
6.6
7
a) ¿Cuánto medirían los lados del cuadrado?
b) Encuentra algunas aproximaciones a la medida de los lados
que debe tener un cuadrado de 42 m2
de área. Completa la
tabla.
c) ¿Qué valor de la medida del lado genera la mejor aproximación
a 42 m2
?
d) Determina un valor de la medida del lado de un cuadrado, que
se encuentre entre 6.4 m y 6.5 m, cuya área se aproxime más
a 42 m2
.
¿Qué valor del área obtuviste?
e) De acuerdo con tu resultado anterior, ¿entre qué valores se
encuentra ahora la mejor aproximación a la medida del lado del
cuadrado?
¿Qué valor del área obtuviste?
De manera grupal, comparen sus resultados y los procedimientos
que siguieron. Comenten en qué consiste el método que han veni-
do empleando para obtener la medida del lado de un cuadrado,
cuando se conoce la medida del área.

S34
255
Sesión 143
3. Aplica el procedimiento anterior y obtén la mejor aproximación de la medida del lado de
un cuadrado que tiene 53 m2
.
En las actividades anteriores has visto que al multiplicar un número por sí mismo, como en
el cálculo del área de un cuadrado L × L , decimos que se calcula el cuadrado del número
o la segunda potencia. La forma de escribir esto es L 2
.
Por otra parte, al calcular el lado de un cuadrado cuando se conoce la medida de su área,
decimos que se calcula la raíz cuadrada. La raíz cuadrada de a es el número que multipli-
cado por sí mismo da a. La forma de escribir esto es a .
En esta sesión conocerás un procedimiento para calcular
la raíz cuadrada de un número natural.
1. Completa la tabla. Puedes usar calculado-
ra para verificar los resultados.
Número
(x)
Cuadrado del número
(x 2
)
6
49
8
81
10
11
144
169
14
225
16
2. Anota en el paréntesis la letra que relacione correctamente cada
pregunta con su respuesta.
Preguntas Respuestas
( ) ¿Cuánto mide el área de un
terreno cuadrado si sus lados
miden 15 m?
( ) ¿Cuál es la raíz cuadrada de
144 ?
( ) ¿Cuál es el resultado de 289 ?
( ) ¿Cuál es el resultado de 142
?
( ) ¿Cuánto mide el área de un
cuadrado de 10 cm por lado?
( ) ¿Cuál es el resultado de 121 ?
a) 100 cm2
b) 196
c) 11
d) 12
e) 225 m2
f) 17
Comparen sus respuestas y verifiquen sus procedimientos.
A lo largo de la historia se han desarrollado y perfeccionado muchos de los procedimientos
que en la actualidad empleamos. En el caso del cálculo de la raíz de cuadrada, gracias al
Papiro de Ahmes (1650 a.n.e.) se sabe que los antiguos egipcios extraían la raíz cuadrada
al resolver problemas geométricos. Las antiguas culturas india y griega también desarrolla-
ron conocimiento en este tema.

B5
256
Sesión 144
3. Aplica los procedimientos que has practicado a lo largo de la secuencia y obtén una aproxi-
mación de la medida del lado de los siguientes cuadrados:
a) Área = 2 cm2
b) Área = 5 cm2
4. Analiza el siguiente ejemplo:
El cuadrado de 12 está dado por: 122
= 12 × 12 = 144
La raíz cuadrada de 144 está dada por: 144 = 12
¿Qué observas?
Cuando un número natural ( n ) se eleva al cuadrado ( n 2
) y al resultado le aplicas la
raíz cuadrada, el resultado que se obtiene es el número original ( n ). Por ello decimos
que el cuadrado de un número y la raíz cuadrada son operaciones inversas.
En esta sesión conocerás otro procedimiento para calcular
la raíz cuadrada de un número natural.
1. Se va a cercar un terreno de forma cuadrada que tiene de 24 m2
. ¿Cuál es la medida del
lado del terreno?
Para resolver este problema emplearemos un método desarrollado hace varios siglos.
Sigue los pasos que a continuación se describen. En tu cuaderno construye las figuras que se indican.
Paso 1. Elige dos números que multiplicados den 24,
por ejemplo 6 y 4. Estas serán las medidas del primer
rectángulo que construirás.
Con ayuda de regla y escuadra, en tu cuaderno constru-
ye un rectángulo cuyos lados midan 6 cm y 4 cm. Su
área es de 24 cm2
(ilumínalo de amarillo).
Paso 2. Calcula el promedio de las medidas de los la-
dos del rectángulo:
6 + 4 =
2

S34
257
Paso 3. Ahora debes construir otro rectángulo que ten-
ga un lado de 5 cm y área igual a 24 cm2
, por lo tanto
hay que calcular la medida del otro lado del rectángulo.
El área de un rectángulo se obtiene multiplicando la
medida de sus lados. Llamemos x a la medida del lado
desconocida, así obtenemos la ecuación:
5 x = 24
Resuelve la ecuación.
Construye un rectángulo cuyos lados midan 5 cm y 4.8 cm
(ilumínalo de verde).
Repite el paso 2. Calcula el promedio de las medidas
de los lados del último rectángulo:
Repite el paso 3. Debes construir otro rectángulo que
tenga un lado de 4.9 cm y área igual a 24 cm2
, por lo
tanto hay que calcular la medida del otro lado del rec-
tángulo.
Llamemos x a la medida del lado desconocida, así ob-
tenemos la ecuación:
4.9 x = 24
Resuelve la ecuación.
Construye un nuevo rectángulo cuyos lados midan 4.9 cm
y 4.89 cm (ilumínalo de azul).
Continúa con este procedimiento para aproximar cada vez más el valor exacto de la raíz
cuadrada de 24.
Observa que el rectángulo azul es casi un cuadrado. Sus lados miden 4.9 cm y 4.89 cm,
esto significa que la raíz de 24 está entre estos dos números.
El procedimiento que acabas de desarrollar para calcular la raíz cuadrada de 24 es semejan-
te al que empleaban los antiguos babilónicos, por lo que se conoce como método babilónico
para el cálculo de la raíz cuadrada de un número. El método consiste básicamente en
obtener rectángulos cada vez más parecidos a un cuadrado de igual medida del área.
2. Calcula lo siguiente (puedes usar calculadora):
•• 4.92
=
•• 4.892
=
¿Cuál de los dos números es una mejor aproximación
a 24?
3. Los lados del rectángulo verde miden 5 cm y 4.8 cm.
Calcula (pueden usar calculadora):
•• 52
=
•• 4.82
=
Comenta con tus compañeros qué rectángulo da mejo-
res aproximaciones a 24, ¿el verde o el azul?
5 + 4.8 =
2

B5
258
Sesión 145
En esta sesión aplicarás el método babilónico para calcular la raíz cuadrada.
El método babilónico se puede emplear para calcular la raíz cuadrada de cualquier número.
Sigue el procedimiento descrito en la sesión anterior y calcula las raíces cuadradas que se in-
dican en cada caso.
Usa una calculadora para efectuar las operaciones necesarias y tu juego de geometría para
construir los rectángulos.
1. ¿Cuál es la raíz cuadrada de 11.5?
Paso 1. Se eligen dos números que multiplicados den 11.5 (sugerencia: inicia con 1
y 11.5). Construye en tu cuaderno un rectángulo cuyos lados tengan esas medidas.
Recuerda que a partir del siguiente paso el objetivo es encontrar rectángulos cada vez más
parecidos a un cuadrado.
Paso 2. Calcula el promedio de 1 cm y 11.5 cm, ¿cuánto resultó?
Este valor es la medida de uno de los lados del nuevo rectángulo.
Paso 3. Calcula la medida del otro lado del rectángulo.
Para hallar dicha medida resuelve la ecuación: 6.25 x = 11.5
Construye en tu cuaderno un rectángulo cuyas medidas sean las que acabas de obtener.
Se repite el paso 2. Calcula el promedio de 6.25 cm y 1.84 cm, ¿cuánto resultó?
Este valor es la medida de uno de los lados del nuevo rectángulo.
Se repite el paso 3. Calcula la medida del otro lado del nuevo rectángulo.
Para hallar dicha medida resuelve la ecuación: 4.045 x = 11.5
Construye en tu cuaderno un rectángulo cuyas medidas sean las que acabas de obtener.
Continua aplicando los pasos de forma sucesiva hasta que encuentres la mejor aproxi
mación al valor exacto de la raíz cuadrada de 11.5.
¿Cuánto es 11.5?
Comparen las medidas que obtuvieron siguiendo los pasos del método babilónico.
2. Calcula la raíz cuadrada de 20. Realiza el procedimiento y las construcciones en tu cuaderno.

S34
259
Sesión 146
En esta sesión observarás que las potencias y los exponentes ayudan
a obtener modelos matemáticos que representan fenómenos biológicos.
¿Sabías que las células se reproducen por división? La división es parte importante del ciclo
celular, pues en ella sucede que una célula inicial se divide para formar células hijas, luego
éstas se dividen para formar otras, y así sucesivamente.
1. Existe un tipo de división celular que presentan bacterias
y amebas, llamada bipartición, la cual consiste en que una
célula madre se divide en dos células hijas idénticas a
la célula madre.
Llamemos nivel 0 a la etapa en que está solamente la célu-
la madre, sin dividirse.
•• Llamemos nivel 1 a la etapa en que la célula madre se
ha dividido en dos células.
•• Llamemos nivel 2 a la etapa en que las dos células
se dividen cada una en otras dos. Y así sucesivamente.
a) Dibuja las células que se formarán en el nivel 3.
b) ¿Cuántas células hay en el nivel 4?
c) ¿Cuántas células hay en el nivel 6?
d) Si hay 128 células, ¿en qué nivel se encuentra la división
celular?
e) ¿Cuál de las siguientes multiplicaciones permite obtener el número de células en el
nivel 7?
•• 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
•• 2 × 2 × 2 × 2 × 2 × 2 × 2
Comparen sus respuestas y expliquen sus procedimientos.
Comenten cómo calcularían el número de células que habrá en el nivel 20, o en el nivel 50.
2. Expresa las multiplicaciones como potencia:
a) 3 × 3 × 3 × 3 =
b) 5 × 5 × 5 =
c) 2 × 2 × 2 × 2 × 2 × 2 × 2 =
d) 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1 =

B5
260
3. Fernanda decidió poner en práctica una forma de enviar buenos deseos a muchas perso-
nas. Para iniciar, ella enviará buenos deseos a tres amigos. Luego, cada uno de éstos ten-
drá que enviar buenos deseos a tres amigos más, quienes también enviarán buenos deseos
a otros tres, y así sucesivamente. Cada persona tendrá que enviar tres buenos deseos.
a) Completa el diagrama de árbol hasta el nivel 3 de envíos de buenos deseos.
b) Cuántos envíos de buenos deseos hay en el nivel 3?
c) ¿Cuántos buenos deseos hay en el nivel 5?
d) ¿Cuál de las siguientes multiplicaciones permite calcular el número de envíos de buenos
deseos en el nivel 10?
•• 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3
•• 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3
Expresa la multiplicación correcta como una potencia:
e) Si en vez de enviar buenos deseos a tres personas se envían a cinco, ¿cuántos envíos
de buenos deseos hay en el nivel 4?
f) ¿Cuántos envíos de buenos deseos hay en el nivel 7?
g) ¿Cuál de las siguientes multiplicaciones permite encontrar el número de envíos de bue-
nos deseos en el nivel 11?
•• 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5
•• 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 × 5
Expresa la multiplicación correcta como una potencia:
Las potencias permiten expresar multiplicaciones de manera breve. Por ejemplo,
3 × 3 × 3 × 3 × 3 × 3 se abrevia al escribir 36
; y se lee “la sexta potencia de 3”.
Nivel cero (Fernanda inicia el envío)
Nivel 1
Nivel 2
Nivel 3

S34
261
Sesión 147
En esta sesión obtendrás potencias y raíces cuadradas
de números naturales y decimales.
1. Completa la tabla con los números y potencias que
faltan.
a) ¿Qué número multiplicado tres veces por sí mismo
da 2 197?
b) ¿Cuál es la raíz cuadrada de 16?
c) ¿Qué número tiene raíz cuadrada igual a 10?
d) ¿Qué número tiene segunda potencia igual a 25?
f) ¿Qué número tiene cuarta potencia igual a 0.1296?
g) ¿Cuál es la raíz cúbica de 1 000?
h) ¿Cuál es la raíz cuarta de 10 000?
i) La raíz de 1.44 es 1.2.
j) ¿Cuál es la raíz cúbica de 3.375?
k) ¿Cuál es la raíz cuarta de 0.0081?
l) ¿Cuál es la raíz cuadrada de 1?
m) ¿Cuál es la raíz cúbica de 0?
Considera que la raíz cúbica de 27 es 3 y que la
raíz cúbica de 64 es 4. Obtén una aproximación de
la raíz cúbica de 40, con una cifra decimal. Puedes
utilizar tu calculadora.
Número
x
Cuadrado
x 2
Tercera potencia
x 3
Cuarta potencia
x 4
4 256
5 125
100
0.36 0.216
1.2
169 28 561
0.3 0.027
0 0
1
1.5 2.25
16
225 50625
La raíz cúbica de 125 es 5, porque 53
= 125. La raíz
cúbica de 125 se expresa como 3
125 .
De forma general, la raíz cúbica de un número n es
aquel número que tiene tercera potencia igual a n.
La raíz cuarta de 1 296 es 6, porque 64
= 1 296. La
raíz cuarta de 1 296 se expresa como .
De forma general, la raíz cuarta de un número n es
aquel número que tiene cuarta potencia igual a n.
 Autoevaluación
Calcula en tu cuaderno la raíz cuadrada de 53 empleando el método babilónico.
4
1 296

262
Secuencia 35
Sucesiones con progresión
aritmética
Obtención de la regla general (en lenguaje
algebraico) de una sucesión con progresión
aritmética.
Sesión 148
En esta sesión aprenderás a obtener la regla para determinar
los términos de una sucesión dada.
Dibuja los siguientes dos términos que completan la sucesión.
1. Escribe los términos que faltan en la siguiente sucesión numérica.
−5, −2, , 4, 7, 10, , 16, , , 25, 28,
31, , 37, , …
a) Escribe una regla para obtener cada uno de los términos de la sucesión.

b) ¿Cuál es el término que está en el lugar 30?
c) ¿Qué lugar ocupa el número 121 en esta sucesión?
Compara tus respuestas con las de tus compañeros y analicen qué estrategia siguieron
para encontrar la regla de esta sucesión.

263
2. Subraya cuáles de las siguientes sucesiones se pueden obtener utilizando la regla sumar
tres al término anterior.
−15, −11, −7, −3, 1, 5,… 3, 6, 9, 12, 15, 18,…
−4, −1, 2, 5, 8, 11,… −8, −3, 2, 7, 12, 17,…
−7, −4, −1, 2, 5, 8, 11,… −12, −9, −6, −3, 0,3,…
−14, −6, 2, 10, 18, 26,…
3. En parejas, respondan las preguntas.
a) ¿Con la regla suma cinco al término anterior, podemos obtener muchas sucesiones o
una sola sucesión?
b) Propongan un ejemplo de una sucesión que se obtenga con esta regla.

c) Una regla más precisa para obtener la sucesión que propusieron es: sumar cinco al
término anterior y el primer término es
¿Cuál es la diferencia entre dos términos consecutivos de las sucesiones que encontra-
ron en el inciso b)?
d) Obtengan tres sucesiones en las que se cumpla la regla: la diferencia entre dos términos
consecutivos es 7.


B5
264
4. Completen lo que falta en las siguientes expresiones y respondan las preguntas.
a) Una regla para obtener la sucesión 5, 11, 17, 23, 29, 35,… es: sumar seis al término
anterior y el primer término es
¿Cuál es la diferencia entre dos términos consecutivos de la sucesión?
b) Una regla para obtener la sucesión −12, −10, −8, −6, −4, −2,… es sumar
al término anterior, y el primer término es
c) Escriban la sucesión que se obtiene con la regla sumar cinco al término anterior y el
primer término es −14 :
¿Cuál es la diferencia entre dos términos consecutivos de esta sucesión?
Anoten el primer dígito de la sucesión siguiente y completen la regla.
, −9, −3, 3, 9, 15,…
La regla es sumar al término anterior y el primer término es .
a) ¿Cuál es la diferencia entre dos términos consecutivos de la sucesión?
Comparen sus resultados con los de otras parejas.
La regla para obtener este tipo de sucesiones se puede expresar diciendo cuánto hay que
sumar a cada término para obtener el siguiente y cuál es el primer término. Por ejemplo:
en la sucesión −8, −3, 2, 7, 12, 17,… la diferencia entre dos términos consecutivos sería
.
Por lo tanto, la regla sería: sumar 5 al término anterior, y el primer término es −8.
Es importante indicar cuál es el primer término de una sucesión, ya que de lo contrario
se pueden obtener muchas sucesiones usando la misma regla.

S35
265
Sesión 149
En esta sesión estudiarás la relación que hay entre un término en la
sucesión y la posición que ocupa en ella.
En parejas, contesten.
1. Para la siguiente sucesión de números: −11, −8, −5, −2, 1, 4, 7, 10, 13,…
b) ¿Cuál es la regla?
2. Para esta sucesión de números: 2, 6, 10, 14, 18, 22, 26, 30, 34,…
b) ¿Cuál es la regla?
Para las siguientes sucesiones, n indicará el lugar que ocupa un término en ellas.
Obtengan los términos faltantes en la tabla que corresponden a la sucesión establecida
por la expresión algebraica 4n − 2.
Lugar que
ocupa el
término (n)
1 2 3 4 5 6 7 8 9
Expresión
algebraica
4n − 2
4 × 5 − 2 = 18
Término 18
Comparen los términos obtenidos en la tabla con
los de la sucesión anterior, ¿qué observan en ellos?
¿Las sucesiones son distintas?
¿Por qué?
¿Cómo es la regla que establecieron en el inciso b)
respecto a la dada por la expresión algebraica?
Cuando hay varias reglas para obtener la misma
sucesión de números se dice que son reglas
equivalentes. Por ejemplo, las siguientes reglas
son equivalentes:
a) Sumar 5 al término anterior y el primer
término es 12,
b) La regla dada por la expresión algebraica
5n + 7, donde n representa el lugar que ocupa
cada término en la sucesión.

B5
266
Sesión 150
En esta sesión encontrarás expresiones equivalentes
para obtener una sucesión.
1. Responde las preguntas sobre la sucesión que se obtiene con la regla 3n − 7.
a) Una regla equivalente para obtener esta sucesión es sumar al término
anterior y el primer término es .
b) ¿Cuál es el término que está en el lugar 40?
c) ¿Cuál de las dos reglas utilizaste para encontrar ese término?
d) ¿Cuál es el término que está en el lugar 48?
2. En parejas, respondan.
¿Cuál es la diferencia entre dos términos consecutivos de la sucesión 1, 4, 7, 10, 13, 16,…?
Observen las dos sucesiones y respondan.
3, 6, 9, 12, 15, 18,… 1, 4, 7, 10, 13, 16,…
¿Cuál es la expresión algebraica para obtener la primera sucesión?
En las sucesiones en que la diferencia entre dos
términos consecutivos es una constante (k),
podemos obtener la expresión algebraica:
multiplicando el lugar del término (n) por la
diferencia de los términos consecutivos (k) y
sumando o restando, según sea conveniente,
la diferencia (r) entre k y el primer término de la
sucesión, esto es, kn ± r.
Por ejemplo: en la sucesión 2, 7, 12, 17,… para
encontrar la expresión algebraica que la define
obtenemos la diferencia entre dos términos
consecutivos, que es k = 5. Ahora obtenemos la
diferencia entre k = 5 y el primer término de
la sucesión, que es 2, por lo que r = 3. De aquí la
expresión algebraica podría ser 5n + 3 o 5n − 3;
para determinar cuál es la expresión conveniente
calculamos el valor del primer término
empleando las dos expresiones. En este caso
la expresión conveniente es 5n − 3.
Subrayen la operación que debemos hacer para pasar de
un término en la primera sucesión a su correspondiente tér-
mino en la segunda sucesión:
Restar 2 Sumar 2
¿Cuál es la expresión algebraica para obtener la segunda
sucesión?
Comenten qué hicieron para encontrar las expresiones
algebraicas.
3. En parejas, encuentren la regla y la expresión algebraica
para obtener la sucesión −11, −6, −1, 4, 9, 14,…
4. Realicen lo siguiente en parejas. Obtengan la expresión al-
gebraica que defina la sucesión −3, 2, 7, 12, 17, 22,…

S35
267
Sesión 151
En esta sesión completarán sucesiones.
Trabajen en equipos para realizar las siguientes actividades.
1. Encuentren los primeros diez términos de la sucesión que se obtiene con la regla 9n − 3
2. Completen la siguiente sucesión de números:
6, 2, , , −10, , −18, −22, ,
, …
Comenten cómo hicieron para encontrar la diferencia entre dos términos consecutivos.
Comparen con sus compañeros sus respuestas.
3. Dada la regla 7n − 5 obtengan los términos que se encuentran en los lugares 20, 21, 32,
100, 150.
4. Completen la siguiente tabla.
Lugar del
término
4 n + 6 4 n − 2 4 n – 5
35
45
74
324
En grupo, comparen y comenten sus respuestas.

B5
268
Consulta en…
En las bibliotecas escolares y de aula y busca el libro con la siguiente referencia para conocer más sobre este tema:
Concepción Ruiz y Sergio Régules, El piropo matemático, de los números a las estrellas, México, sep-Editorial
Lectorum, 2003 (Libros del Rincón).
Entra a la página del Proyecto Descartes http://descartes.cnice.mec.es/Descartes1/Bach_HCS_2/Sucesiones_
numeros_reales_limites/Progresiones_aritmeticas.htm, y explora las actividades del interactivo “Sucesiones
geométricas con Logo”.
Sesión 152
En esta sesión aplicarás lo aprendido en sesiones anteriores.
En parejas, den una expresión algebraica que determine las siguientes sucesiones.
a) −12, −7, −2, 3, 8, 13,…
b) 5, 10, 15, 20, 25, 30,…
c) 9, 22, 35, 48, 61,…
 Autoevaluación
• Determina una expresión algebraica y encuentra los primeros diez términos de la suce-
sión dada por la regla sumar 15 al término anterior y el primer término es 3.

269
Secuencia 36
Área y perímetro del círculo
Uso de las fórmulas para calcular el perímetro
y el área del círculo en la resolución de problemas.
Sesión 153
En esta sesión resolverás problemas usando la fórmula del perímetro del círculo.
En la siguiente figura marca con rojo el contorno del círculo y su superficie con azul; traza con
verde el radio y con negro el diámetro.
Contesta las siguientes preguntas.
¿A qué se le llama π?
¿Cuál es un valor aproximado de pi?
¿Cómo se calcula el perímetro de un círculo?
¿Qué datos se necesitan para calcular el perímetro del círculo?

270
B5
1. En parejas, calculen el perímetro de los siguientes círculos.
2. Completen la tabla, tomen π = 3.14
Círculo
Radio
R
Diámetro
D
Perímetro
1 5 cm
2 22 cm
3 103.30 cm
4 40.8 cm

¿Cómo obtuvieron el radio del círculo 3?
¿Cómo obtuvieron el radio del círculo 4?
a) Ernesto es herrero y le pidieron que hiciera con perfil redondo dos aros para tableros
de basquetbol. Uno de ellos debe tener 27 cm de radio y el otro 27 cm de diámetro.
¿Qué cantidad de perfil debe cortar para ambos aros?
b) Para reforzar un barril se necesitan tres cinturones de acero inoxidable de 4 cm de an-
cho. Dos de los cinturones tienen 60 cm de diámetro, mientras que el radio del cinturón
que se coloca a la mitad del barril es 4.5 cm más grande que el de los otros dos. ¿Qué
cantidad de lámina se necesita para reforzar medio centenar de barriles?
Comparen sus procedimientos y respuestas, verifiquen que sean correctas. Si hay algún proce-
dimiento diferente verifiquen que sea efectivo.
10 cm 22 cm 32.9 cm 40.8 cm
Para calcular el perímetro de un círculo
podemos usar la fórmula P = 2rπ, donde r
es el radio del círculo, o P = D π, si recorda-
mos que el diámetro es dos veces el radio.

271
S36
Sesión 154
En esta sesión resolverás problemas utilizando la fórmula
del perímetro del círculo.
1. En equipos, resuelvan los siguientes problemas. Tomen π = 3.14
a) ¿Cuál es la longitud de la línea AB?
157.39 m
36.50m
9.76 m 9.76 m
73.00m
92.52m
9.76m9.76m
BA
b) La imagen anterior corresponde a la ciclopista del
deportivo de la comunidad. Edna la recorre diaria-
mente con su bicicleta hasta 9 veces, mientras que
Braulio sólo recorre 5 km.
¿Quién de los dos da más vueltas al circuito?
¿Cómo resolvieron los problemas anteriores?

272
B5
2. En parejas, diseñen una figura empleando círculos del mismo diámetro y planteen un pro-
blema que se resuelva tomando como base su diseño.
¿Cuántos círculos completos tienen en su diseño?
¿Cuánto mide su radio?
¿Cuál es el perímetro?
Intercambien su problema con alguno de sus compañeros y verifiquen que la solución sea
correcta.
Para resolver problemas por medio del cálculo de períme-
tros de figuras compuestas con círculos de un mismo radio,
debemos determinar la cantidad de círculos que forman la
figura para multiplicarla por su perímetro.

273
S36
Sesión 155
En esta sesión resolverás problemas utilizando la fórmula del área del círculo.
1. Calcula el área del siguiente círculo.
¿Cómo se determina el área de un círculo?
Si sólo se conoce el diámetro del círculo, ¿cómo se calcula el área?
2. En equipos, resuelvan los siguientes problemas. Usen 3.14 para π.
a) Una tapa de forma circular de 18 cm de diámetro se empleó para marcar una circun
ferencia sobre un pedazo de tela de forma cuadrada de 20 cm por lado. Después de
recortar el círculo de tela, ¿cuál es el área de la tela que se desperdicia?
b) En el patio de la secundaria el profesor de Educación Física trazó tres círculos para
pintarlos de color amarillo, rojo y azul, como se muestra en la imagen.
Alberto dice que el área de los círculos pequeños es igual a la del círculo azul. ¿Tiene
razón? ¿Por qué?
Para que el área del círculo amarillo, más el área del círculo rojo, sea el área del azul,
¿cuánto tendrá que medir el radio del círculo amarillo?
1 m 1 m80 cm
6 cm

274
B5
c) Reyna decora tablas circulares como las de la imagen para usarlas como portarretratos.
Le han solicitado media docena de cada modelo, ¿cuál es el área total que pintará de
azul?
¿Cómo determinaron el área de la superficie azul?
¿Qué portarretrato tiene la mayor superficie pintada de azul?
Para calcular el área de un círculo se emplea la formula A= π r2
, donde el
radio se multiplica por sí mismo y luego por π. Cuando un círculo está dentro
de otro, sin importar si tienen o no el mismo centro, una forma de calcular
el área limitada entre las dos circunferencias es restar los cuadrados de los
radios y la diferencia multiplicarla por π. Por ejemplo, para calcular el área
limitada entre un círculo cuyo radio mide 4 cm que está dentro de otro cuyo
radio mide 6 cm es: 20π = 62.8 cm2
, dado que 36 – 16 = 20.
3
cm
3
cm
5 cm
5
cm
6
cm
2
cm

275
S36
Sesión 156
En esta sesión resolverás problemas utilizando la fórmula del área del círculo.
1. En parejas, resuelvan el siguiente problema.
¿Cuál es área de cada una de las siguientes figuras?
¿Cómo calcularon el área de la figura naranja?
¿Qué figuras forman la figura verde?
¿Qué figuras forman la figura azul?
¿Cuál de las figuras está formada por más círculos?
2. Resuelvan los problemas.
12 cm
6 cm
40 cm
1.2 m
30 cm
80 cm
1.2 m

276
B5
a) La siguiente figura es el modelo de un aspa que se fabrica en acero, ¿cuál es el área del
aspa?
b) Para una ruleta se cortó un círculo de 60 cm de radio y se decoró como se muestra en
la imagen. ¿Cuál es el área de la superficie en rojo?
c) ¿Cómo determinaron el área solicitada?
d) ¿Cuál es el área de la superficie en negro?
e) Con respecto al problema del aspa y al de la ruleta, ¿cuántos círculos forman las figuras?

¿Cómo resolvieron ambos problemas?
3. Resuelve el problema.
60 cm
60 cm

277
S36
Alexa es pintora y las obras de arte que muestra a continuación están hechas sobre un cuadra-
do de 90 cm por lado. ¿En cuál de ellas utilizó más pintura?
¿Por qué?
 Autoevaluación
Contesta lo siguiente.
• ¿Cómo determinarías el perímetro de la siguiente figura?

• ¿Y el área de la superficie naranja?

278
Secuencia 37
Proporcionalidad múltiple
Resolución de problemas de proporcionalidad
múltiple.
Sesión 157
En esta sesión reconocerás y resolverás problemas que implican el uso
de distintos tipos de proporcionalidad en situaciones de la vida cotidiana.
Para organizar su convivio, los 25 alumnos de 1º A llevaron tostadas y agua de jamaica. Como
la mamá de uno de ellos tiene una fonda les dio la siguiente información:
•• Un paquete de tostadas tiene 20 piezas.
•• 3 1
2
vasos de crema alcanzan para cubrir 40 tostadas.
•• 1 kg de pata de res es suficiente para 10 tostadas.
•• 1
4
kg de queso rallado alcanza para 50 tostadas.
•• 1 kg de pechuga de pollo es suficiente para 25 tostadas.
Si quedaron de acuerdo en que se llevaría lo necesario para que cada quien comiera dos tos-
tadas de pata y dos de pollo, ¿qué cantidad de tostadas se deben comprar?

279
1. En parejas, con la información del problema de las tostadas, completen la tabla.
Ingredientes Cantidad que se requiere
Paquetes de tostadas
Kilogramos de pata
Vasos de crema
Queso rallado
Kilogramos de pechuga de pollo
a) ¿Usaron el mismo procedimiento para encontrar la cantidad de cada ingrediente que se
necesita?
b) Para la kermés de la escuela el grupo decidió preparar todas las tostadas que salieran
con 9 kg de pechuga, ¿qué cantidad de queso rallado se necesitará para las tostadas
que se preparen?
Comparen sus respuestas con las de otras parejas y escriban el procedimiento que siguie-
ron para obtener la respuesta de la última pregunta.
De manera grupal, verifiquen sus procedimientos y reflexionen sobre el uso de distintos
tipos de proporcionalidad para la solución de este problema.
a) En una escuela se va a realizar una excursión. Los organizadores saben que, en prome-
dio, 12 niños consumen 144 litros de agua durante 6 días. ¿Cuántos litros de agua hay
que llevar a una excursión de 3 días, si van a ir 60 niños?
b) Rubén tiene 5 vacas, cada una de ellas produce 6 litros de leche diariamente; con
15 litros de leche obtiene 2.5 litros de crema y vende 2 litros de crema por $75.00. Si
destinó la producción de dos semanas para obtener crema, ¿cuánto dinero recibirá por
la venta de toda la crema producida en el tiempo mencionado?
Compara tus respuestas con las de
otros compañeros. Cuando se usan la proporcionalidad directa y la inversa
en la solución de un mismo problema, se dice que este
problema es de proporcionalidad múltiple.

B5
280
Sesión 158
En esta sesión resolverás problemas de proporcionalidad múltiple en
situaciones como el cálculo de perímetros y áreas.
1. En parejas, realicen la siguiente actividad y contesten las preguntas.
Tracen en hojas blancas tres rectángulos con las siguientes medidas y recórtenlos: Rectán-
gulo 1: 3 cm de base y 4 cm de altura.
Rectángulo 2: 6 cm de base y 8 cm de altura.
Rectángulo 3: 15 cm de base y 20 cm de altura.
Calculen el perímetro y el área y completen la tabla.
Rectángulo 1 Rectángulo 2 Rectángulo 3
Base 3 15
Altura 8 20
Perímetro
Área

¿Cuántas veces es mayor la base del rectángulo 2 con respecto a la base del rectángulo 1?
¿Cuántas veces es mayor el perímetro del rectángulo 2 con respecto al perímetro del rec-
tángulo 1?
¿Cuál es la razón entre el área del rectángulo 1 y el área del rectángulo 2?
¿Cuántas veces es mayor el perímetro del rectángulo 3 con respecto al perímetro del rec-
tángulo 1?
¿Cuál es la razón entre el área del rectángulo 3 y el área del rectángulo 1?
Comparen sus respuestas con las de otras parejas y reflexionen sobre la forma en que au-
mentan el área y el perímetro de un rectángulo cuando aumentan las medidas de sus lados.
Los lados de un rectángulo han aumentado tres veces su tamaño, ¿cuál será la razón
entre los perímetros de los rectángulos?
¿Cuál es la razón entre las áreas de los rectángulos?

S37
281
Sesión 159
a) A un cuadrado de 4.5 cm por lado se le triplicó la longitud de cada uno de sus lados,
¿cuánto mide el perímetro del nuevo cuadrado?
b) Se reproduce un rectángulo con perímetro de 35 cm y 75 cm2
de área hasta obtener
otro rectángulo con un perímetro de 157.5 cm, ¿cuánto mide el área de la figura repro-
ducida?
c) Se tienen dos círculos, uno de 4 cm de radio y otro de 12 cm de radio, ¿cómo es el
perímetro del segundo círculo con respecto al perímetro del primero?
Compara tus respuestas con las de otros compañeros y reflexionen si al duplicar o triplicar
las medidas de los lados en un polígono regular su perímetro y su área también se duplican
o triplican, respectivamente. Escriban sus conclusiones en su cuaderno.
En esta sesión resolverás problemas de proporcionalidad múltiple en
diferentes contextos.
1. En equipos, observen el prisma.
¿Cuántos cubos verdes tiene?
¿Cuántos cubos en total lo forman?
a) Si se aumentan al doble los cubos del ancho, del
largo y de la altura, ¿cuántos cubos formarán
el nuevo prisma?
b) ¿Cuántas veces será mayor el número de cubos
del prisma nuevo con respecto al de la ilustración?
c) ¿Habrá alguna forma directa de conocer el número de cubos sin contarlos uno a uno?
Si al prisma de la ilustración se le triplican los cubos del ancho, del largo y de la altura,
¿cuántos cubos formarán el nuevo prisma?
¿Cuántas veces es mayor el número de cubos de este nuevo prisma con respecto al de
la ilustración?
Largo
Ancho
Alto

B5
282
2. Se sabe que para construir un muro de 3 m de largo y 2 m de altura se necesitan 150 ta-
biques, y que para construir 2 m2
de barda se necesitan 3
4
de un bulto de cemento.
Si el albañil mezcló tres bultos, ¿cuántos tabiques pegará con esa mezcla?
Si en la construcción del baño se ocuparon 600 tabiques, ¿cuántos bultos se emplearon
para levantar las bardas del baño?
Para la cocina se levantaron tres bardas de 12 m2
y una de 9 m2
, ¿qué cantidad de tabiques
y de bultos se emplearon?
3. Damián es un granjero que se dedica a la crianza de guajolotes. Él sabe que 10 guajolotes
consumen aproximadamente 120 kg de alimento durante tres días. También sabe que cada
bulto de alimento contiene aproximadamente 50 kg. ¿Cuántos bultos deberá comprar para
alimentar por tres semanas a las tres docenas de guajolotes que tiene?
Comparen sus resultados con los de otros compañeros, verifiquen que sean correctos
y reflexionen en qué otros contextos se pueden encontrar problemas de proporcionalidad
múltiple.
En esta secuencia observamos que las situaciones de proporcionalidad múltiple se
caracterizan porque dos o más cantidades están relacionadas proporcionalmente.
Una proporción múltiple se denota como:
a : b : : c : d : : e : f , o también se representa como a
b
= c
d
= e
f
, y cumple que
ad = bc = cf = de = af = be
Consulta en…
Entra al sitio: http://www.cidse.itcr.ac.cr/cursoslinea/MATEGENERAL/t5geometria/Geometria/node9.html,
y consulta la información sobre los prismas rectangulares y otras figuras geométricas.
 Autoevaluación
Plantea en tu cuaderno un problema de proporción múltiple.

S37
283
Sesión 160
Evaluación
1. En un congelador se registraron las siguientes variaciones de temperatura: −7°, 12°, −5°,
−10°, 6°; si la temperatura inicial era de −20°, en cuántos grados quedó la temperatura.
a) 40° b) 18° c) −22° d) −24°
2. La distancia media de Urano al Sol es aproximadamente de 525 000 000 km. Señala cuál
de las siguientes expresiones es igual a esta cantidad en notación científica.
a) 525 × 10 6
km b) 5.25 × 10 8
km c) 5.25 × 10 9
km d) 525 × 10 8
km
3. ¿Cuánto mide el lado de un cuadrado que tiene de área 289 cm 2
?
a) 72.25 cm b) 28.9 cm c) 28 cm d) 17 cm
4. Si una persona cuenta una historia a tres personas, y cada una de éstas, a su vez, la cuen-
tan a otras tres, y éstas hacen lo mismo, ¿cuántas personas escucharon la historia?
a) 9 b) 18 c) 27 d) 81
5. ¿Cuál es la regla que forma la sucesión 1, 3, 5, 7, 9,…?
a) 2 x + 1 b) 2 x c) x + 2 d) x − 2
6. ¿Qué operación debe realizarse para obtener el área de un círculo con 15 cm de diámetro?
a) 15 × 3.14 b) 7.5 × 3.14 c) 15 × 15 × 3.14 d) 7.5 × 7.5 × 3.14
7. Si el perímetro de un cuadrado aumenta al doble, su área aumenta:
a) al doble b) al triple c) al cuádruple d) al séxtuple

284
Hoja para las familias
Seguimiento de los avances de los niños
en la escuela
Estimada familia y tutores
Con el propósito de fortalecer su participación en la escuela para impulsar las actividades escola-
res y extraescolares que sus niños y niñas realizan, les presentamos el siguiente cuestionario en el
cual pueden registrar sus avances y tomar decisiones junto con los docentes para mejorar el apro-
vechamiento escolar.
Algunas recomendaciones:
• Si a usted se le dificulta el llenado del cuestionario, solicite ayuda a un familiar o
amigo para responderlo e interpretar el resultado. Recuerde que es muy importante dar
seguimiento a los avances y logros de su niña o niño.
•
asesoría sobre cómo apoyar al niño en su formación académica.
• Si al revisar las tareas y ejercicios del niño no están registradas las calificaciones o algún
dato que le permita responder cuestionario, pida ayuda al maestro para determinar con él
cómo puede dar seguimiento a los resultados del niño.
• Recuerde que este cuestionario no es una evaluación o examen, es un registro que sirve para
reconocer y ayudar a las niñas y los niños a nuestro cargo de una manera oportuna y eficaz.
Para dar seguimiento a los avances de los niños es importante que:
• Revise con atención las tareas, los ejercicios y las actividades del libro de texto y del
cuaderno de trabajo al menos cada dos meses (duración aproximada de un bloque).
• Observe su conducta al realizar las actividades extraescolares y ponga atención en lo que
platica de sus actividades en la escuela.
Cuestionario
Con base en sus observaciones sobre el trabajo del niño, marque la respuesta que corresponde a
cada pregunta.
A. Excelente B. Bueno o bien C. Mal o malo D. No lo he observado
N˚ Reactivos
Bloque
i ii iii iv v
1
Las calificaciones obtenidas en las tareas del libro de texto
reflejan que su trabajo fue
2
Las calificaciones obtenidas en los ejercicios realizados en su
cuaderno reflejan que su trabajo fue
3 Al realizar actividades fuera de la escuela su desempeño fue
Desempeño del niño
Cuando su desempeño no sea óptimo, usted puede acudir a la escuela para recibir

285
N˚ Reactivos
Bloque
i ii iii iv v
4 He observado que trabaja en equipo y lo hace
5 Las actividades de estudio extras las hace
6 Su actitud para sistir a la escuela generalmente es
Mi desempeño
N˚ Reactivos
Bloque
i ii iii iv v
1 Su asistencia a la escuela es
2 Su puntualidad en la escuela es
3 Su aseo personal y de sus útiles para asistir a la escuela es
Recomendaciones para contribuir a mejorar el desempeño de su niño
Si obtuvo de
7 a 10 respuestas
A. Excelente
Se recomienda felicitar
a su niño o niña y
preguntarle sobre el tipo
de apoyo que requiere
para seguir con ese
avance y mantener los
buenos resultados.
Si obtuvo
de 5 a 7 respuestas
B. Bien, aunque necesita
apoyo
Se recomienda poner
atención en aquellas
actividades en las que se
obtuvo esta valoración y
acompañar a los niños
para repasar las tareas
y/o ejercicios en los
cuales no obtuvo un
buen desempeño. Si
tiene dudas al respecto,
es recomendable que se
acerque con el maestro
de grupo.
Si obtuvo en más
de 4 preguntas
C. Mal. Requiere apoyo
urgente
Se recomienda consultar
con el maestro de su hijo
o hija sobre cómo puede
ayudarlo a mejorar el
desempeño educativo.
Si en 2 o más
preguntas respondió
D. No lo he observado
Recuerde que en el buen
desempeño de sus hijos
en la escuela también
influye la familia. Le
recomendamos contribuir
con la escuela estando al
pendiente de sus avances.

Matematicas 1° 2012 2013

Más contenido relacionado

La actualidad más candente

Similar a Matematicas 1° 2012 2013

Más de SEIEM

Último

Matematicas 1° 2012 2013