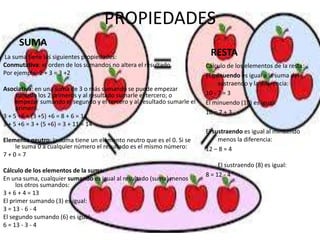
Este documento presenta información sobre los números naturales, sus propiedades y operaciones. Explica que los números naturales incluyen los números cardinales y ordinales, y describe el sistema de numeración decimal. También describe las propiedades de suma y resta, incluidas las propiedades conmutativa, asociativa y neutro. Finalmente, explica los números decimales, incluidos los periódicos puros y mixtos, y cómo realizar operaciones como suma, resta, multiplicación y división con números decimales.

2. NÚMEROS NATURALES
Los números naturales son 0, 1, 2, 3, 4…..
Podemos distinguir entre:
Números cardinales: se utilizan para contar los elementos de un grupo:
1, 2, 3, 4…
Por ejemplo: 3 manzanas, 17 botellas, 4 niños…
Ordinales: se utilizan para determinar la posición que ocupa un elemento
dentro de un conjunto: primero, segundo, tercero, cuarto…
Por ejemplo: La primera camisa, el segundo coche, la cuarta silla…
Utilizamos el sistema de numeración decimal en el que cada 10 unidades
forman una unidad de orden superior:
10 unidades = 1 decena
10 decenas = 1 centena
10 centenas = 1 unidad de millar
10 unidades de millar = 1 decena de millar
….

3. PROPIEDADES
SUMA
La suma tiene las siguientes propiedades:
Conmutativa: el orden de los sumandos no altera el resultado.
Por ejemplo: 2 + 3 = 3 +2
Asociativa: en una suma de 3 o más sumando se puede empezar
sumado los 2 primeros y al resultado sumarle el tercero; o
empezar sumando el segundo y el tercero y al resultado sumarle el
primero.
3 + 5 +6 = (3 +5) +6 = 8 + 6 = 14
3 + 5 +6 = 3 + (5 +6) = 3 + 11 = 14
Elemento neutro: la suma tiene un elemento neutro que es el 0. Si se
le suma 0 a cualquier número el resultado es el mismo número:
7+0=7
Cálculo de los elementos de la suma:
En una suma, cualquier sumando es igual al resultado (suma) menos
los otros sumandos:
3 + 6 + 4 = 13
El primer sumando (3) es igual:
3 = 13 - 6 - 4
El segundo sumando (6) es igual:
6 = 13 - 3 - 4
RESTA
Cálculo de los elementos de la resta:
El minuendo es igual a la suma del
sustraendo y la diferencia:
10 - 7 = 3
El minuendo (10) es igual:
10 = 7 + 3
El sustraendo es igual al minuendo
menos la diferencia:
12 – 8 = 4
El sustraendo (8) es igual:
8 = 12 - 4

4. NUMEROS DECIMALES
Número decimal es aquel que tiene una parte entera y una parte decimal.
3,5
4,765
2,875
La parte decimal, que va a la derecha de la coma (en el primer ejemplo: 0,5), representa una cantidad inferior a la unidad.
Los números decimales tienen un número finito de cifras decimales.
Si el número de decimales es infinito cabe distinguir dos casos particulares:
Números periódicos puros: si la sucesión infinita de decimales se repite siguiendo una secuencia.
Por ejemplo, al dividir 10 : 3 el cociente es 3,333333….
3,33333…
4,75757575…
2.423423423..
Números periódicos mixtos: si la sucesión infinita de decimales no presenta inicialmente ningún patrón y luego comienza
una secuencia.
5,2147777777…
6,91636363636…
7,1332456456456456..
Para comparar números decimales se comienza comparando la parte entera:
23,45 > 12,45
Ya que la parte entera del primer número (23) es mayor que la del segundo (12).
Si las partes enteras fueran iguales, habría que comparar las partes decimales: primero comenzando por las décimas; si son
iguales comparamos las centésimas; y si son iguales comparamos las milésimas…
12,45 > 12,35 Las décimas del primero (0,4) son mayores que las del segundo (0,3)
12,43 > 12,41 Las centésimas del primero (0,03) son mayores que las del segundo (0,01)
12,477 > 12,475 Las milésimas del primero (0,007) son mayores que las del segundo (0,005)

5. operaciones
.Suma con decimales: se realiza como una suma ordinaria. Hay que tener
la precaución de poner las cifras en las columnas correspondientes: las unidades con las unidades,
las décimas con las décimas, las centésimas con las centésimas, etc. Las comas de los decimales deben estar alineadas.
Si en la suma hay alguna cifra sin decimales hay que tener precaución en su colocación (es como si llevara una coma a su derecha).
Resta con decimales: se realiza como una resta ordinaria. Al igual que en la suma hay que tener la precaución de poner las cifras en la columna correspondiente.
Si el minuendo no tuviera tantas cifra decimales como el sustreando, allí donde falten se considera que va el valor " 0 ".
Veamos algunos ejemplos
23,45 + 5,2 + 67,345
33,04 +17 + 0,456
45 – 0,567
Estas operaciones se resuelven:
Multiplicar con decimales: se realiza como una multiplicación ordinaria, pero al resultado hay que ponerle tantos decimales como el total de cifras decimales que tengan
conjuntamente los dos factores.
Veamos un ejemplo:
45,2 x 36,56
Se resuelve:
Como el primer factor tiene un decimal y el segundo dos decimales, en total suman tres cifras decimales, por lo que el producto tendrá tres decimales.
Divisiones con números decimales:
a) Divisor con decimales:
234 : 45,56
Si el divisor tiene decimales hay que eliminarlos multiplicándolo por un 1 seguido de tantos ceros como cifras decimales.
45,56 x 100 = 4556
Para que la división sea equivalente a la inicial, el dividendo hay que multiplicarlo por el mismo número.
234 x 100 = 23400
Luego la división quedaría:
23400 : 4556
Ahora ya operaríamos como en una división normal.
b) Dividendo con decimales:
124,45 : 15
Realizamos la división como si no hubiera decimales:
12445 : 15 = 829 (resto 10)
Pero el cociente llevará tantas cifra decimales como tenga el dividendo.
Cociente 8,29

6. HASTA OTRA Y ESPERO QUE
HALLAIS APRENDIDO MUCHO
SUERTE