Matematica.solucionario uni....

ACADEMIA PITÁGORAS EXAMEN DE ADMISIÓN 2015-I
UNIVERSIDAD NACIONAL DE INGENIERÍA
- 3 -
MATEMÁTICA
01. Sea el número E = 2
2001
+ 3
2001
.
Calcule el residuo de dividir E entre 7.
A) 0 B) 1 C) 2
D) 3 E) 4
02. ¿Cuántos números de la forma
son primos?(4a3)(3b)(4a3)
A) 1 B) 2 C) 3
D) 4 E) 5
03. En la expresión siguiente, b0
0,a - 0,b = 0,4b
Ð
a
Ð
4
Ñ
Entonces la suma de todos los valores
posibles de 0,a que satisfacen lab
Ð
ecuación anterior es:
A) 0,6 B) 1,3 C) 2,11
Ð
3
Ð
6
Ð
D) 3,1 E) 4,11
Ð
6
Ð
04. Se tiene la siguiente igualdad:
(9)(aaa1(9))1/3
 1(a2)
Entonces podemos decir que el
conjunto.
{a  {1, 2, 3, ...., 8} / existe}(aaa1(9))1/2
A) No posee elementos
B) Posee un solo elemento
C) Posee dos elementos
D) Posee tres elementos
E) Posee cuatro elementos
05. Semanalmente, un trabajador ahorra
cierta cantidad en soles, y durante 40
semanas ahorra las siguientes
cantidades:
21 35 29 31 23 22 28 33
28 25 31 26 24 27 27 33
37 29 19 36 23 18 46 12
26 41 30 18 39 15 24 4
25 33 10 28 20 27 17 31
Se construye una tabla de frecuencias
de 7 intervalos de igual longitud fija
A. Si F5 es la frecuencia acumulada
del quinto intervalo (ordenados los
extremos de los mismos de forma
creciente), determine el valor de
(A+F5) - 1.
A) 30 B) 32 C) 37
D) 38 E) 39
06. Indique la alternativa correcta después
de determinar si cada proposición es
verdadera (V) o falsa (F) según el
orden dado:
( ) Sean A  B  C  D, entonces la
probabilidad
P(D) = P(DA) + P(CA) + P(BA) + P(A)
( ) Se lanzan dos dados normales,
entonces la probabilidad que su
suma sea 7 es .
1
2
( ) Se lanzan dos dados normales,
uno cada vez, entonces la
probabilidad de que salga 3 dado
que antes salió 1 es .
1
36
A) VVV B) VFV C) FVV
D) FFV E) FFF
07. Sabiendo que K = = yab(4) cd(5)
a+b+c+d = 11 en el sistema decimal
- 4 -
con a  0, c  0. Determine K en el
sistema decimal.
A) 14 B) 23 C) 32
D) 41 E) 51
08. Se sabe que en una división entera el
divisor en 50 y el residuo es 15.
¿Cuántas unidades como mínimo se
le debe disminuir al dividendo, para
que el cociente disminuya en 13
unidades?
A) 614 B) 615 C) 616
D) 617 E) 618
09. En el primer cuadrante del plano se
forma el conjunto A con los puntos con
coordenadas enteros positivos, esto
es:
A = {(m, n) / m  , n  }
A cada punto (m, n) de A se le asigna
el valor . Calcule la suma de
1
2mn
todos los valores de los puntos (m, n)
de A con coordenadas m  n.
A) B) C) 1
1
3
2
3
D) 2 E) +
10. Si S es el conjunto solución de la
inecuación:
|x1||x2| < 2
se afirma:
I. <1/4; +>  S
II. S  <1/3; +>
III. S  <-; 1/2>  Φ
¿Cuáles son afirmaciones correctas?
A) Sólo I B) Sólo II C) Sólo III
D) I y II E) lI y III
11. Respecto a la función f(x) = |x| - x,
indique la secuencia correcta,
después de determinar si la
proposición es verdadera (V) o falsa
(F).
I. f(x + y)  f(x) + f(y); x, y  
II. Si hacemos g(x) = x
2
- 2x - 3
entonces el conjunto solución de
g(x) = f(x) es  3; 3
III. Si hacemos h(x) = x
2
- 3x + 5
entonces el conjunto solución de
h(x) = f(x) es vacío.
A) VFV B) VFF C) VVV
D) FVV E) FVF
12. Indique el intervalo al cual pertenece
el valor de m, para que la inecuación:
4x4x2
x2
x1
< m
se cumpla para todo x  
A) ; 
13
3
B) <1; ->
C) <2; +>
D) <3; 9>
E) <5; +>
13. Sea una función f:   <0; +> que
cumple f(a + b) = f(a).f(b)  a, b  .
Calcule el valor de f(a).f(-a)
A) -1 B) 0 C) 1
D) 2 E) 3
14. Considere la siguiente función f: 
definida por f(x) = ax
2
+ bx + c, a > 0,
b > 0. Si f(0) = 2 y Rang(f) = [b; +>,
determine el siguiente valor:
M =
8ab 2
ab
A) 1 B) 2 C) 3
D) 4 E) 5
-2- -3-

- 5 -
15. Sea f una función cuya regla de
correspondencia está dada por:
f(x) = loga (x x2
1)
Encuentre su función inversa.
A) a
x
+ a
-x
B) C) a
x
- a
-xa x
a x
2
D) E)
a x
a x
2
a x
2
16. Si A es una matriz invertible, despeje
la matriz X a partir de la expresión.
(AX)1 t
 0,5 B 1
A) X = 0,5 A
-1
B
t
B) X = 0,5 B
t
A
-1
C) X = 2A
-1
B
D) X = 2B
-1
A
t
E) X = 2A
-1
B
t
17. Determine el conjunto solución del
sistema de ecuaciones no lineales:
x2
y 2
2x2y  1  0
x2
2xy1  0
A) {(3, 1), (1, 1), (-1, -1)}
B) {(2, -2), (2, 1), (1, 1)}
C) {(-1, 0), (1, 1), (1, 2)}
D) {(1, 0), (0, 1), (2, 1)}
E) {(1, -1), (1, 0), (2, -1)}
18. Un granjero tiene 480 acres de tierra
en la que puede sembrar maíz o trigo.
Él calcula que tiene 800 horas de
trabajo disponible durante la estación
de verano. En el caso del maíz, el
trabajo demora 2 horas por acre y se
obtiene una utilidad de S/. 40 por acre,
mientras que en el trigo el trabajo es
de 1 hora por acre y la utilidad es de
S/. 30 por acre. ¿Cuántos acres de
maíz y trigo debe plantar,
respectivamente, para maximizar su
utilidad?
A) (160, 320) B) (140, 340)
C) (340, 140) D) (320, 160)
E) (180, 300)
19. Considere la sucesión:
1,
1
22
,
1
32
, ....,
1
n 2
, ...
Determine el menor valor de n  , de
modo que se cumpla:
1
n 2
< 1 × 107
A) 2 081 B) 2 091 C) 2 991
D) 3 001 E) 3 163
20. Halle el menor grado del polinomio
x
n
+ ax + b, a  0, (n > 1) para que
x
2
- 1 sea un divisor.
A) 2 B) 3 C) 4
D) 5 E) 6
21. El punto P se encuentra situado sobre
la altura de un tetraedro regular de
lado a. Si P equidista de cada vértice,
calcule esta distancia.
A) B) C)
a 3
4
a 2
3
a 3
3
D) E)
a 6
4
a 2
2
22. Un vaso de forma de prisma recto
exagonal con diagonal mayor de la
base que mide 6 cm, contiene agua “al
tiempo”. Para enfriarla se coloca un
cubo de hielo y se observa que el nivel
del agua sube 2 cm. Calcule la
longitud de la arista del cubo de hielo
(en cm).
- 6 -
A) 3 B) C)3
6
3 3
4
3
D) E)3
3
3 3 3
23. En un cilindro de revolución de 5 cm
de altura se inscribe un paralelepípedo
rectangular con superficie lateral de
250 cm
2
. Una de sus aristas, ubicada
en la base del cilindro, mide 16 cm.
Calcule la razón (en cm) entre el
volumen y el área lateral del cilindro.
A) B) C)
337
4
337
2
337
4
D) E)
337
2
337
24. En la Panamericana cerca de Casma
se ha formado una duna en forma de
tronco de cono de revolución. Las
longitudes de las circunferencias son
4π m y 2π m. Ver figura. Halle el
volumen de la duna en metros
cúbicos.
A) 3π B) 5π C) 7π
D) 10π E) 11π
25. En un tronco de cono de revolución el
radio de la base mayor es el doble del
radio de la base menor. Si el volumen
del tronco de cono es 336π cm
3
y el
radio de la base menor es 6 cm,
entonces el volumen de una esfera
tangente a las bases del tronco de
cono (en cm
3
) es:
A) π B) π C) π
30
3
31
3
32
3
D) π E) π
33
3
34
3
26. En una pirámide cuadrangular regular
la arista básica mide 8 u y su altura
mide 15 u. ¿A qué distancia (en u) de
la base de la pirámide se debe trazar
un plano paralelo a dicha base, para
que el volumen del prisma recto, que
tiene por base a dicha sección y por
altura la distancia de la sección al
vértice de la pirámide, sea los del
3
8
volumen de la pirámide?
A) 9,5 B) 8,5 C) 7,5
D) 6,5 E) 5,5
27. En el gráfico AB = AD = DC, calcule α
(en grados).
A) 8 B) 9 C) 10
D) 12 E) 13
-4- -5-

- 7 -
28. En la figura las circunferencias tienen
radios r = 3 u y R = 6 u,
respectivamente, C es punto de
tangencia y D es centro. Calcule
producto DA.DB (en u
2
)
A) 18 B) 24 C) 30
D) 36 E) 40
29. En la figura se muestra el triángulo
rectángulo ABC recto en B. Si
AB = 5 cm y AD = 3 cm, entonces la
medida (en cm) del segmento es:EF
A) 2,14 B) 2,16 C) 2,25
D) 2,56 E) 2,82
30. En la siguiente figura, I es el incentro
del triángulo ABC, BI = 6 u, DE = 1 u.
Calcule BE (en u)
A) 8 B) 9 C) 10
D) 11 E) 12
31. En la figura AC = CD, AD = 6 u y área
(∆BCD) = r (área ∆ABD). Halle r.
A) 1 + B) 2 + C) 2 -3 3 3
D) 1 + 2 E) 2 - 13 3
32. ABCD es un cuadrado y desde su
centro O se traza un segmento OE
perpendicular al plano ABC, si
OE = AB entonces la medida del
diedro E - DC - B es:
A) ArcTg
1
2
B) ArcTg(1)
- 8 -
C) ArcTg
3
2
D) ArcTg(2)
E) ArcTg
5
2
33. Si x  entonces determineπ,
3π
2
los valores de y = 4 - 9 Csc
2
x
2π
3
A) <-, -12> B) <-, -11> C) <-, -10>
D) <-, -9> E) <-, -8>
34. Al simplificar la expresión:
k = (1Sen(2x))Cos 2 π
3
x Cos2 π
3
x 
3
2
se obtiene:
A) - Cos
2
(2x)
3
2
B) Sen
2
(2x)
3
2
C) - Sec(2x)
3
2
D) Csc(x)
3
2
E)
3
2
35. Si x  y0,
π
2
= Tg , calcule el
1Sen(x)
1Sen(x)
x
a

π
2a
valor de (a
2
+ 1).
A) 2 B) 3 C) 4
D) 5 E) 6
36. Sea la función f(x) =
x3
ArcTg(x)x
Dadas las siguientes proposiciones:
I. La función f es impar
II. Si x  Dom(f), entonces
-x  Dom(f)
III. La gráfica de f corta a la curva
y = x
2
Son correctas
A) Sólo I B) Sólo II
C) Sólo III D) I y II
E) II y III
37. Si ABCD es un cuadrado de lado 2 u y
T es un punto de tangencia, entonces
el área sombreada (en u
2
) es igual a:
(O centro de la circunferencia que
pasa por A, T y D)
A) 0,57 B) 0,68 C) 0,79
D) 0,81 E) 0,92
38. En todo triángulo ABC la suma de los
cuadrados de sus lados es igual a:
K(bcCosA + acCosB + ab CosC)
donde K vale:
A) B) C) 1
1
4
1
2
D) 2 E) 4
-6- -7-

- 9 -
39. Al resolver la ecuación:
Sen(2x) - 12(Sen(x) - Cos(x)) + 12 = 0
obtenemos como soluciones:
A) kπ , k  Z
B) 2kπ y , k  Zk
1
2
π
C) 2kπ y kπ, k  Z
D) (2k + 1)π y π , k  Z2k
1
2
E) (3k + 1)π y , k  Zk
1
2
π
40. Del gráfico mostrado, el resultado de:
E = Tgθ + Tgβ + TgΦ, es:
A) -4 B) -2 C) 0
D) 2 E) 4
- 10 -
RESOLUCIÓN
01. 2
3
= +12
2001
=(2
3
)
667
=( +1)
667
= +17
o
7
o
7
o
3
3
= -13
2001
=(3
3
)
667
= ( -1)
667
= -17
o
7
o
7
o
E = ( +1)-( -1) =7
o
7
o
7
o
 Resto = 0
Rpta. A
02.
Luego, son primos:
101; 131; 151; 181; 191; 313; 353;
373; 757; 797; 919 y 929
 Hay 12 números NO HAY CLAVE
Observación: Suponiendo que a y b
son enteros, los números primos son:
101; 131 y 191
 Hay 3 números
Rpta. C
03. 0,a - 0,b = 0,4 ; b  0b
Ð
a
Ð
4
Ð
8a - 8b = 40
a - b = 5

6 1
7 2
8 3
9 4
 0,6 + 0,7 + 0,8 + 0,9 = 3,11
Ð
2
Ð
3
Ð
4
Ð
1
Ð
Rpta. D
04.
1/3
= ; a + 2 < 9aaa19 1(a2)9
( +1) = ( +a+2)
3
9
o
9
o
Verificando la igualdad, sólo cumple
para a = 5
 El conjunto posee un elemento
Rpta. B
05. De acuerdo a la tabla:
 A = =6
42
7
-8- -9-

- 11 -
Entonces:
Ahorro
[Li; Ls>
Número de
semanas
fi
4; 10 1
10; 16 3
16; 22 6
22; 28 12
28; 34 12  F5=34
34; 40 4
40; 46 2
 A + F5 - 1 = 39
Rpta. E
06. I. Falso
A  B  C  D
P(DA) = P(D) - P(A)
P(DA) + P(A) = P(D)
P(CA)  0
P(BA)  0
| P(D A) + P(C A) + P(BA) + P(A) P(D)
II. Falso
: se lanzan dos dados
 n() = 6 × 6 = 36
A : La suma es 7
 n(A) = 6
Luego:
P(A) = =
6
36
1
6
III. Falso
Sean los eventos:
A: En el 2do dado salió 3
B: En el 1er dado salió 1
P(A/B) = = =
P(AB)
P(B)
1
36
6
36
1
6
Rpta. E
07. K = (4) = (5)ab cd
a + b + c + d = 11
Se cumple:
Para: K = 14 = 32(4) = 24(5)
Obs: a + b + c + d = 3 + 2 + 2 + 4 = 11
 K = 14
Rpta. A
08. Se tiene:
Se cumple:
D = 50q + 15 ..... (1)
D - x = 50(q-13) + 49 ..... (2)
Restando (1) - (2):
x = 15 + 650 - 49
 x = 616
Rpta. C
- 12 -
09. Como:
(m; n) se le asigna el valor de
1
2mn
al reemplazar se forman las siguientes
series:
S1 =
1
22

1
23

1
24
.... 
1
2
S2 =
1
24

1
25

1
26
 .... 
1
8
S3 =
1
26

1
27

1
28
 .... 
1
32

finalmente:
S = S1 + S2 + S3 + .... =
1
2
1
1
4

2
3
Rpta. B
10. Como:
|x1||x2| < 2
se cumple:
|x+1| - |x-2|  0  2  0  |x+1|-|x-2|<4
I. |x + 1|
2
 |x - 2|
2
x
2
+2x+1x
2
-4x+4  ... (α)x 
1
2
II. 2  0  .... (β)x  
III. |x + 1| - |x - 2| < 4
es equivalente “a”:
|x + 1| - |2 - x | < 4
Se cumple:
|x + 1| - |2 - x|  |x + 1 + 2 - x|
|x + 1| - |2 - x|  3
 |x + 1| - |2 - x| < 4 .... (θ) x  
Finalmente α  β  θ
C.S =
1
2
; 
 S 
1
3
; 
Rpta. B
11. Como f(x) = |x| - x
I. Verdadero
f(x + y)  f(x) + f(y);  x; y  
|x + y| - x - y  |x| - x + |y| - y
 |x + y|  |x| + |y|
II. Verdadero
x
2
- 2x - 3 = |x| - x
|x| = x
2
- x - 3
x = x
2
- x - 3  x = -x
2
+ x + 3
0 = (x  3)(x + 1)  0 = (x + )(x )3 3
x = 3  x = -1  x = -  x =3 3
no cumplen x = -1; x = 3
C.S = {3; - }3
III. Verdadero
x
2
- 3x + 5 = |x| - x
|x| = x
2
- 2x + 5
∆ = (-2)
2
- 4(1)(5)  ∆ < 0
 No hay soluciones reales.
Rpta. C
-10- -11-

- 13 -
12.
4x4x2
x2
x1
< m
Como x
2
- x + 1 > 0, entonces:
4 + x - 4x
2
< mx
2
- mx + m
0 < (m + 4)x
2
- (m + 1)x + m - 4
∆ = [-(m+1)]
2
-4(m+4)(m-4)<0m+4> 0
0 < 3m
2
- 2m - 65
0 < (3m + 13)(m-5)  m > -4
Luego m  <5; +>
 <5; +>
Rpta. E
13. Sea f:   <0; +>
Como:
f(a + b) = f(a)f(b) :  a; b  
hacemos:
a = b = 0
f(0) = f(0).f(0)  f(0) = 0  f(0) = 1
pero f(0) = 0 no cumple:
 f(0) = 1
hacemos b = -a
= f(a)f(-a)f(0)
È
1
 f(a)f(-a) = 1
Rpta. C
14. Se tiene f:   /f(x) = ax
2
+ bx + c
siendo f(0) = 2  Ran(f) = [b; +>
del dato f(0) = 2 resulta que c = 2
Luego la función queda así:
f(x) = ax
2
+ bx + 2
Completando cuadrados:
f(x) = a x
b
2a
2

8ab 2
4a
Además como Ran(f) = [b; +> se
tiene:
b =
8ab 2
4a
 4 =
8ab 2
ab
Rpta. D
15. Tenemos:
y = f(x) Loga(x+ )x2
1
Notamos que f es una función
inversible. Luego, despejando x en
función de y.
x + = a
y
x2
1
 = a
y
- xx2
1

 2xa
y
= a
2y
- 1
 x =
a 2y
1
2a y
 x =
a y
a y
2
 f
-1
(x) =
a x
a y
2
Rpta. D
- 14 -
16. Tenemos A inversible con:
((AX)
-1
)
t
= 0,5B
-1
Como tenemos (AX)
-1
en la igualdad,
podemos concluir que X también es
una matriz inversible. Luego, tomemos
transpuesta a ambos miembros:
(AX)
-1
= 0,5(B
t
)
-1
Multiplicando por AX a la derecha:
I = 0,5(B
t
)
-1
(AX)
Finalmente multiplicando a la derecha
por la matriz 2A
-1
B
t
resulta:
2A
-1
B
t
= X
Rpta. E
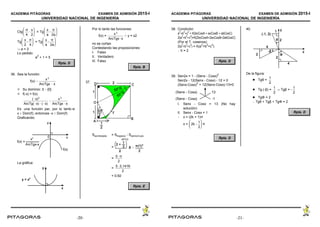
17. Completando cuadrados en las
ecuaciones se tiene:
(x1)2
(y1)2
1 .... Ec. de circunferencia
y(x1)2
..... Ec. de parábola
Graficando:
Aquí los cortes nos representan las
soluciones
| C.S. = {(1; 0); (0; 1); (2; 1)}
Rpta. D
18. Del enunciado tenemos el cuadro:
Horas Terreno
Maíz 2 h 1
Trigo 1 h 1
Total = 800 h Total = 480
Función objetivo:
f(x; y) = 40x + 30y
Las condiciones son:
x, y  0
2x  y  800
x  y  480
El máximo ocurre en (320; 160)
f(320; 160) = 40(320) + 30(160)
= 12 800 + 4 800
= 17 600 soles
Rpta. D
19. Tenemos la sucesión:
{an} = {1; ; ; ...; ; ....}
1
22
1
32
1
n 2
la condición es:
< 1 × 10
-71
n 2
-12- -13-

- 15 -
Se tiene luego de operar:
n > 3 162, 2 ....
 El menor valor de n es 3 163 (n  )
Rpta. E
20. Se tiene el polinomio:
p(x) = x
n
+ ax + b con a  0  n > 1
Por condición x
2
- 1 es un divisor de
p(x), es decir:
x
n
+ ax + b = (x+1)(x-1)q(x)
Si x = 1:
a + b = -1 ............... (I)
Si x = -1:
(-1)
n
+ a(-1)+b = 0
 -a+b = -(-1)
n
...... (II)
Como n > 1, supongamos que n = 2,
entonces se tendría en (II):
-a + b = -1
que al combinar con (I) resulta:
 a = 0  b = -1
ab1
ab1
Pero por dato a  0. Por consiguiente
n  2.
Entonces, si suponemos que n = 3
tenemos en (II):
-a + b = 1
Combinando con (I)
 a = -1  b = 0
ab1
ab1
Conclusión: el menor valor de n es 3.
Rpta. B
21.
En la figura:
“P” es el centro del tetraedro regular,
cuyo circunradio mide R.
Luego: R = ; h =
3h
4
a 6
3
 R =
a 6
4
Rpta. D
22.
En la figura:
2L = 6  L = 3
Luego:
Vsólido = Vlíquido
- 16 -
sumergido desplazado
ÆÉÉÉÈÉÉÉÇ ÆÉÉÉÈÉÉÉÉÇ
Vcubo = Vprisma
x
3
= 6 × 2
3
2
3
4
x
3
= 27 3
 x = 3
6
3
Rpta. B
23.
Se pide:
x 
Vcilindro
SL(cilindro)
x =
π r 2
g
2π rg
x = ..... (I)
r
2
Luego, del dato:
(2r)
2
= 16
2
+ a
2
= 16
2
+ 9
2
r = 337
Reemplazamos en (I):
 x 
337
4
Rpta. A
24.
Del dato:
L1 = 2π = 2πr; r = 1
L2 = 4π = 2πR; R = 2
Por Pitágoras en :
h
2
+ 1
2
=  h = 3( 10)2
-14- -15-

- 17 -
Luego:
V 
π(3)
3
[4 12]
 V = 7π
Rpta. C
25. Dato:
Vtronco = 336π
Por dato:
π(2R)
3
(62
122
6×12)  336π
 VEsfera = π.R
3
=
4
3
32π
3
Rpta. C
26.
Al trazar el plano paralelo a la base de
la pirámide, la pirámide parcial que se
forma será semejante a la pirámide
inicial. Luego en la pirámide parcial:
a = 8k  h = 15k
Por dato:
VPrisma = Vpirámide
3
8
(8k)
2
. 15k =
3
8
.
1
3
.82
.15
k =  h =
1
2
15
2
 x = = 7,5
15
2
Rpta. C
- 18 -
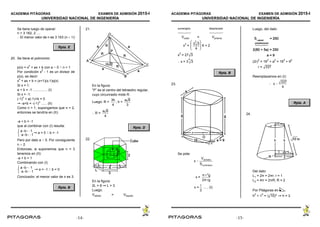
27.
Se traza y se prolonga hastaBD BA
“E”.
En ∆ABD: mABD = mADB = 6α
 mDBC = α
Luego: ∆BDC: Isósc: BD = DC
 ∆ABD: equilátero: 6α = 60
 α = 10
Rpta. C
28. Calcular: DA.DB. Datos:
r = 3 u; R = 6 u
En la circunferencia mayor se traza el
diámetro y se traza . Luego:DE AE
BDC ~ EDA
AD
r

2R
DB
AD . DB = 2Rr
AD . DB = 2(6)(3)
 AD.DB = 36
Rpta. D
29.
En ABD: BD = 4
En ABC: 5
2
= (AC)(3)  AC = 25/3
En ABC: 4
2
= (DC)(3)  DC = 16/3
Luego: ABC ~ DEC:
x
4

16/3
25/3
 x 
64
25
 x = 2,56
Rpta. D
-16- -17-

- 19 -
30.
Del gráfico:
AE = EI = x - 6
(mIAE = mAIE = α + β)
En el triángulo AEB, por propiedad:
(x - 6)
2
= x . 1
x2
13x36  0
x  9
x  4
De donde: x = 9 (x = 4 no es solución)
Rpta. B
31.
Sea P un punto interior al triángulo
DBC, tal que el triángulo PCD sea
congruente con el triángulo BCA.
Luego BC = PC= b, mBCP = 2α 
mBDP = α
Por propiedad en el cuadrilátero
DBCP:
mDBC = 120 - α
En ∆DBC : α = 15
Observe que , del gráficoAB//DC
reemplazamos en el dato:
S(BCD) = rS(ABD)
2k.k
2
r
k( 31).k
2
De donde:
r =
2
31
 r = +13
Rpta. A
- 20 -
32.
Sea: AB = OE = 2a
Se traza:
 y se traza:OM DC EM
| OM = a  EM CD
mOME = x
En OME:
Tgx = 2
 x = ArcTg(2)
Rpta. D
33. x  π,
3π
2
π < x <
3π
2
< x + <
5π
3
2π
3
13π
6
| Csc < -  Csc >2x
2π
3
2
3
x
2π
3
Luego:
Csc
2
>x
2π
3
4
3
-9Csc
2
< -12x
2π
3
4 - 9Csc
2
< -8x
2π
3
 y < -8
y  <-, -8>
Rpta. E
34. k = [Cos
2
(60°+x)Cos
2
(60°x) ](1Sen2x)
3
2
k = [Sen
2
(60°x)Sen
2
(60°+x) ](1Sen2x)
3
2
k = [Sen120° Sen2x  ](1Sen2x)
3
2
k =  (1+Sen2x)(1-Sen2x)
3
2
 k =  Cos
2
2x
3
2
Rpta. A
35. 0 < x <
π
2
= Tg
1Senx
1Senx
x
a

π
2a
= Tg
1Cos
π
2
x
1Cos
π
2
x
x
a

π
2a
-18- -19-

- 21 -
Ctg = Tg
π
4

x
2
x
a

π
2a
Tg = Tg
x
2

π
4
x
a

π
2a
| a = 2
Lo pedido:
a
2
+ 1 = 5
Rpta. D
36. Sea la función:
f(x) 
x3
ArcTgx  x
 Su dominio:  - {0}
 f(-x) = f(x)
(x)3
ArcTg(x)(x)

x3
ArcTgxx
Es una función par, por lo tanto si
x  Dom(f), entonces -x  Dom(f)
Graficando:
La gráfica:
Por lo tanto las funciones:
f(x) =  y = x2
x3
ArcTgxx
no se cortan
Contestando las proposiciones:
I. Falso
II. Verdadero
III. Falso
Rpta. B
37.
Ssombreada = Strapecio - Ssemicírculo
APCD
=
=
5π
2
=
53,1416
2
= 0,92
Rpta. E
- 22 -
38. Condición:
a
2
+b
2
+c
2
= K(bcCosA + acCosB + abCosC)
2(a
2
+b
2
+c
2
)=K(2bcCosA+2acCosB+2abCosC)
(Por el T. cosenos)
2(a
2
+b
2
+c
2
) = K(a
2
+b
2
+c
2
)
 K = 2
Rpta. D
39. Sen2x = 1 - (Senx - Cosx)
2
Sen2x - 12(Senx - Cosx) - 12 = 0
(Senx-Cosx)
2
+ 12(Senx-Cosx)-13=0
I. Senx - Cosx = 13 (No hay
solución)
II. Senx - Cosx = 1
 x = (2k + 1)π
x = 2k
1
2
π
Rpta. D
40.
De la figura:
 Tgθ =
1
2
 Tg (-β) = | Tgβ = -
1
2
1
2
 TgΦ = 2
 Tgθ + Tgβ + TgΦ = 2
Rpta. D
-20- -21-

Matematica.solucionario uni....

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Matematica.solucionario uni....

Último

Matematica.solucionario uni....