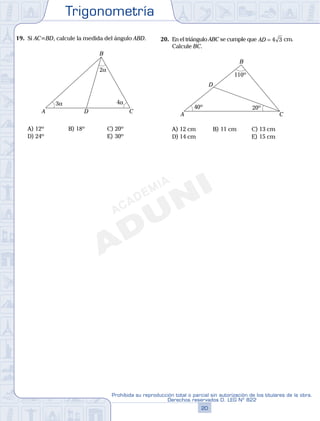
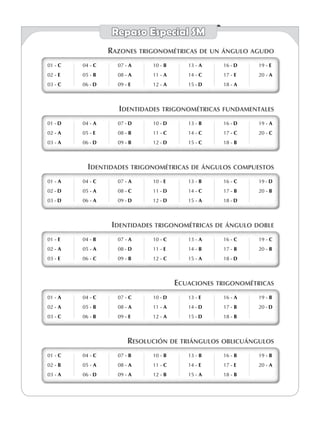
Este documento presenta 20 problemas de trigonometría de diferentes niveles de dificultad. Los problemas incluyen cálculos de funciones trigonométricas, simplificación de expresiones trigonométricas, resolución de identidades trigonométricas y más. Las respuestas a los problemas van desde letras A hasta E.

1. Preguntas propuestasPreguntas propuestas

2. Trigonometría
2
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
3
NIVEL BÁSICO
1. Si a+b=90º y cota=25cotb, calcule
26 3 26sen senα β β+ +( )tan
A) 142 B) 144 C) 146
D) 148 E) 150
2. En el gráfico, BD=2AD y tanα =
4
3
.
Calcule 3cotb.
α
β
A B
C
D
A) 3 B) 4 C) 5
D) 6 E) 8
3. En la figura se tiene el sector circular ABC y
secα =
5
3
. Calcule 9cotq–5.
αθ
A
B C D
E
A) 28 B) 30 C) 32
D) 34 E) 36
4. Del gráfico mostrado, calcule (tanx+tany)coty
si BM=MC y 2(AN)=3(NB).
x
y
MN
A
B
C
A) 3/4 B) 5/4 C) 9/4
D) 3 E) 4
NIVEL INTERMEDIO
5. Del gráfico, calcule tanq si MN=2AB.
θ
θ
A B
M N
A)
1
2
B)
2
2
C) 2
D) 3 E)
3
2
Razones trigonométricas de un ángulo agudo
÷ Ω



2
α

3. Trigonometría
3
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
4
Academia ADUNI Material Didáctico
6. Si ABCD es un cuadrado y secb=3/2, calcule
tana.
α
β
A B
CD
A)
3 5
8
+
B)
3 5
4
−
C)
3 2 5
4
+
D)
3 5
4
+
E)
2 5
4
+
7. Si ABCD es un cuadrado, calcule tanx.
A
B C
D
E
H
x
60º
A)
4 3
3
−
B)
3 1
2
−
C)
2 3
3
+
D)
2 3
6
+
E)
2 3
6
−
8. En un triángulo ABC, recto en A, se tiene que
3(AB+AC)=4(BC). Calcule sena+cosa si a es
la medida del menor ángulo del triángulo.
A) 4/3 B) 5/4 C) 3/2
D) 2/3 E) 5/3
9. Del gráfico se cumple que AM=MC y NB=5AN.
Calcule 6cotq.
120º
θ
A
B
CM
N
A) 2 3 B) 3 C) 10 3
D) 3 3 E) 5 3
10. Del gráfico mostrado, calcule cotx si BM=MQ.
60º
A C
B
H
x
M P
Q
A) 3 1+ B) 3 2+ C) 2 3−
D) 2 3 1+ E) 2 3 1−
11. En el gráfico, calcule la proyección de PQ
sobre BC si AC=3.
α
α
A
P
QB C
A) 3cos3
a
B) 3cos2
acota
C) 3senacosa
D) 3tana
E) 3cota

4. Trigonometría
4
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
5
Repaso Especial San Marcos Trigonometría
12. En el gráfico, AB=AE=m y BE=2(DE).
Calcule BC.
2θ
A
B C
D
E
A) 2msenqsen2q
B) msenqsen2q
C) msenqcsc2q
D) 2msecqcos2q
E) 2mtanqcotq
13. Si el área de la región sombreada es 2 u2
,
calcule tan x −
3
3
. Considere que BC=4 u.
A) 1
A
B
C
D
xx
60º 60º
45º45º
B) 1/2
C) 1/3
D) 2
E) 3
14. En el triángulo ABC se tiene que AB=BD,
AD=4(CD) y cotα =
6
5
. Calcule tanb.
αβ
A
B
CD
A) 1 B) 6/5 C) 5/4
D) 3/2 E) 2
15. Del gráfico, calcule cotatanq
si AB= 6 3 , MN= 4 3 y NC=9.
α
θ
A
B
M
C
N
A) 7/2 B) 3 C) 4
D) 9/2 E) 5
16. Si ABCD es un paralelogramo en el cual AB=2
y BC=3, calcule cosa+senatanq.
α
θ
A
B C
DH
A) 1/2 B) 2/3 C) 2
D) 3/2 E) 3
17. Si ABCD es un cuadrado, AM=4 y MN=10,
calcule sec2
q+tanq.
θ
A
B
C
DM N
A) 1/3 B) 1/2 C) 3/4
D) 5/3 E) 5/2

5. Trigonometría
5
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
6
Academia ADUNI Material Didáctico
NIVEL AVANZADO
18. En la figura, AF=FC y BF=BE.
Calcule
DE
EF
.
α
A
B
D E
F C
A)
sen
sen
α
α
2
2
B)
cos
cos
α
α
2
2
C)
sen
sen
α
α
2
D)
cosα
α
sen
2
E)
senα
α
cos
2
19. En el gráfico
CD=3 y BD=2.
Calcule
cot tan
csc
θ θ
θ
+ 2
2
θ
θ
A B
C
D
A) 2 B) 5/2 C) 3
D) 3/2 E) 7/6
20. Si ABCD es un romboide, tal que AM=MB y
MN=NC, calcule tanxcoty.
A
B C
D
y
M
N
x
A) 1/3 B) 1/2 C) 2/3
D) 2 E) 3

6. Trigonometría
6
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
7
Repaso Especial San Marcos Trigonometría
02
SEMANA
NIVEL BÁSICO
1. Si secx=tany=7, calcule el valor de sec2
y–tan2
x.
A) –2 B) –1 C) 1
D) 2 E) 4
2. Simplifique la siguiente expresión.
tan cot
sec csc tan cot
cos csc
2 2
2 2
2
2
x x
x x x x
x x
+
−
−






A) senx B) cscx C) cotx
D) 1 E) 2
3. Si secxcscx=3, calcule el valor de
sen6
x+cos6
x+sen4
x+cos4
x
A)
13
9
B)
5
3
C)
11
9
D)
15
9
E)
17
9
4. De las condiciones
sen6 6
1
3
x x
n
+ −
=
cos
senx x m− = +cos 1
halle una relación entre m y n.
A) m2
=–4n B) m2
=4n C) n2
=–4m
D) n2
=4m E) m2
=–2n
5. Calcule el valor de la expresión
1 1
1
2
2
2+ +( ) −( )
+
+
sen
sen
θ θ θ
θ
θ
cos cos
cos
A) –1/2 B) –1 C) 1/2
D) 1 E) 2
6. Si seca–tana=1/4, calcule 17(sena+cosa).
A) 20 B) 21 C) 22
D) 23 E) 24
NIVEL INTERMEDIO
7. Reduzca la expresión
csc6
x–3cot2
xcsc2
x–cot6
x
A) 2sen2
x B) senx C) cscx
D) 1 E) cos2
x
8. Simplifique la expresión
csc
csc cot
sec
sec
α
α
α
αa −
+
+1
A) 2sen2
a B) 2csc2
a C) 2cos2
a
D) 2sec2
a E) cos2
a
9. Calcule el valor de
10
15
2
6 6 2 2 2
sen senx x x x+( )− −( )cos cos
A) 2 B) 5/2 C) 5
D) 3 E) 7/2
10. Simplifique la expresión
2 2 1
2 2
4 2
4 2
sen sen
sec
θ θ
θ θ
− +
− +sec
A) sen2
q B) cos2
q C) sen4
q
D) cos4
q E) sec4
q
11. Si sen6 6 2
5
θ θ+ =cos
calcule el valor de
(sec2
q+csc2
q)(cos4
q+sen2
q)
A) 1 B) 2 C) 4
D) 5 E) 6
12. Si senx+cosx=n
halle el equivalente de
sec csc
( cos )
4 4 2 4
1
8
x x n
n x x
−( ) −( )
−sen
A) 1 B) n C) n/2
D) 2 E) 4
Identidades trigonométricas fundamentales

7. Trigonometría
7
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
8
Academia ADUNI Material Didáctico
13. Si x es un ángulo del segundo cuadrante,
simplifique la expresión
senx
x
x
x x
xcsc
cos
csc cot
tan
+
−
+
+
2 2
2
1
1
A) sen2
x B) 2sen2
x C) 1
D) 2 E) cos2
x
14. Si sen2 4 3
4
x x+ =cos , calcule el valor de
cos2
x+sen4
x
A) 1/4 B) 1/2 C) 3/4
D) 1 E) 5/4
15. Calcule el máximo valor de
5 3
2 3
2
sen
sen
x
x x
−
− cos
A) 2 B) 2 C) 5
D) 3 E) 4
NIVEL AVANZADO
16. Calcule el valor de
sec º csc º
sec º csc º sec º csc º
2 2 2
6 6 6 6
20 20
20 20 20 20
+( )
× − −
A) 1/8 B) 1/4 C) 1/2
D) 1/3 E) 1/6
17. Calcule el mínimo valor de la expresión
5+tan2
x(sen2
x+1)+cot2
x(1+cos2
x)
A) 4 B) 6 C) 8
D) 10 E) 12
18. Si la función f definida por
f
x x
x x
x xx( )
tan
cot csc
cot=
+
+



 −
sen
sen2
alcanza su máximo valor, calcule x.
A) p/12 B) p/6 C) p/4
D) 5p/12 E) p/3
19. Si se cumple que
cosx+senxcosx–1=0
calcule el valor de
cot3
x+cot2
x–csc3
x
A) –1 B) –2 C) 1
D) 2 E) 1/2
20. Si sen3
q+senq=1,
calcule el valor
csc cot tan
csc sec
4 2 2
5 2
α α α
α α
+ −
−
A) –1 B) –2 C) 1
D) 2 E) 1/2

8. Trigonometría
8
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
9
Repaso Especial San Marcos Trigonometría
03
SEMANA
NIVEL BÁSICO
1. Si a y b son complementarios que cumplen la
condición
sen senα β
2 3
=
calcule tan(a–b)+tana+tanb.
A) 7/4 B) 7/2 C) 1/4
D) 3/4 E) 2
2. Si tan(a+b)=3 y tan(b–a)=2, calcule el valor
de csc
csc
2
2
α
β
.
A) 1/5 B) –1/5 C) –5
D) 5 E) 2/5
3. A partir de la siguiente identidad
tan tan
sec
tan
π π
4 4 1
2
2
+



 + −



 =
−
x x
k x
x
calcule el valor de k.
A) –2 B) –1 C) 1
D) 2 E) 2 2
4. Calcule el valor de la expresión
sen4 3 1 4 1
3 3 1
ºsec ºsec º tan º
tan º tan º
−
−
A) 1/4 B) 1/2 C) 1
D) –1 E) 4
5. Del gráfico se cumple que BD=10 y tanα =
3
13
.
Calcule
tan ºα +( )30
x
.
30º
α
A B C
D
x
A)
2
9
B)
16
7 3 5−
C)
16
14 3 5−
D)
4
14 3 5−
E)
16
4 3 5−
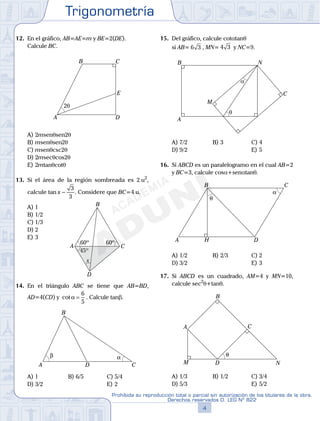
6. De acuerdo con el gráfico, calcule tanx si
2(CD)=3(BC) y tanθ =
1
2
.
θ
A
BCD
x
A) 3/11 B) 3/7 C) 7/3
D) 2/5 E) 11/3
NIVEL INTERMEDIO
7. Si sen(x–y)=ncosxcosy
y sen(x+y)=mcosxcosy
calcule tan(x+y)tan(x–y)[1–tan2
xtan2
y]
A) mn B)
mn
2
C) m2
n2
D)
m
n
E)
n
m
Identidades trigonométricas de ángulos compuestos

9. Trigonometría
9
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
10
Academia ADUNI Material Didáctico
8. Calcule el valor de
tan º tan º cot º
tan º tan º tan ºtan ºtan º
10 70 10
20 50 20 50 70
+ −
+ +
A) –tan20º
B) tan20º
C) –1
D) 1
E) tan40º
9. Si 3 12 12sen º cos º− = k
calcule sen27º–cos27º.
A) −k
2
2
B) −k 2 C) k 2
D) k
2
2
E) 2 2k
10. Si tan20º=b, calcule el valor de tan55º–tan35º.
A) 2/b B) 1/b C) b/2
D) b E) 2b
11. Si tan(60º+a)= 2 3 , calcule el valor de
tan(60º–a).
A)
3
5
B)
2 3
5
C)
4
3
3
D)
3
5
3 E)
2
3
3
12. En el gráfico, AB=5, AE=2 y DE=3
Calcule 19tanx–9.
A
B C
DE
x
A) 13 B) 14 C) 15
D) 16 E) 17
13. Calcule el valor de
cos º cos º
cos º cos º
28 62
43 3 47
+
+
A)
1
2
B)
2
2
C) 2
D) 1 E) 2 2
14. Si (–3; –4) y (4; 3) son puntos pertenecientes a
los lados terminales de los ángulos en posición
normal a y b, respectivamente, calcule
tan tan
tan tan
cot( )
α β
α β
α β
− −
−
A) –5/12 B) 5/12 C) 7/24
D) 24/25 E) 12/5
15. En el gráfico, calcule
cos
cos cos
α θ
α θ
+( )
si 2(BE)=3(EH).
α θ
A
B
C
E
H
M
A) –3/2 B) –1/2 C) 1/2
D) 1 E) 3/2
16. Si se cumple que
tan(x+60º)+tan(x–60º)=8cotx
calcule cos2
x.
A) 2/5 B) 3/5 C) 4/5
D) 1/10 E) 1/15

10. Trigonometría
10
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
11
Repaso Especial San Marcos Trigonometría
17. Calcule el valor de
sec ºsec º tan ºtan º20 25 2 20 25+
A)
2
2
B) 2 C) 1
D) 2 2 E)
2
4
NIVEL AVANZADO
18. Halle el valor de A.
A =
−



 −




cos º cos º
º º
2 2
2 2
31 14
43
2
77
2
sen sen
A) −
6
3
B) −
3
3
C)
3
3
D)
6
3
E)
6
2
19. Si tan40º+tan20º=m y tan40ºtan20º=n
calcule m n mn2 2
3 2 3+ +
A) 1 B) 2 C) 3
D) 3 E) 4
20. Calcule el valor de x
si la expresión
3 2 30cos cos( )x x x+ + −sen
es máxima y 0
2
< <x
π
A)
π
12
B)
π
6
C)
π
4
D)
π
3
E)
5
12
π

11. Trigonometría
11
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
12
Academia ADUNI Material Didáctico
04
SEMANA
NIVEL BÁSICO
1. Calcule el valor de
sen sen
π π π π
12 12
3
6 6
cos cos+
A) −
1
2
B)
1
4
C)
1
2
D)
3
2
E) 1
2. Calcule el valor de
1
15
3
15sen º cos º
−
A) 2 6 2+( )
B) 2 6 2−( )
C) 6 2+
D) 6 2−
E) 2 6 2 2−( )
3. De la siguiente igualdad
sen6
x+cos6
x=1–Msen2
2x
calcule el valor de M.
A) –3/2 B) –3/4 C) 3/2
D) 2 E) 3/4
4. En el gráfico, se cumple que AD=4 y CD=1.
Calcule tan2q.
θ
A
B C
D
A) 7/15 B) 8/15 C) 17/8
D) 15/8 E) 15/7
5. Si se cumple que
sec4
x–tan4
x=4
calcule cos2x.
A) –1/5 B) –1/3 C) 1/3
D) 1/5 E) 3 2/
NIVEL INTERMEDIO
6. De la ecuación
cos cos4
2
1
16
x x− =
calcule cos2x.
A) −
1
2
B) −
2
2
C)
1
2
D)
2
2
E)
3
2
7. En el gráfico se cumple que mSCAM=mS MAB,
además, CM=q y MB=P.
Calcule AB.
A B
C
M
A) P
q P
q P
+
−
B) P
P q
q
+
C) P
P
q P−
D) P
P q
P
+
E) P
P q
q
+
2
8. Si tanx=3/5, calcule el valor de
5sen2x–3cos2x.
A) –3 B) –2 C) 2
D) 3 E) 4
Identidades trigonométricas del ángulo doble

12. Trigonometría
12
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
13
Repaso Especial San Marcos Trigonometría
9. De la condición
csc2a+3=0 y − < <
π
α
π
4 4
calcule tan
π
α
4
+



 .
A) −
2
2
B)
2
2
C) − 2
D) 2 E) 2 2
10. Calcule el valor de
tan ºcos º tan º º
º
70 50 20 40
50
− sen
sen
A) 1/2 B) 1/4 C) 2
D) 1 E) 4
11. Si tan51º–tan39º=m,
calcule 4sec2
12º.
A) m2
B) m2
+1 C) 4m2
+1
D) 1+4m2
E) m2
+4
12. De la condición
cscx–cos10ºtan40º=cos10ºcot40º;
π
π
2
< <x
calcule sen2x.
A) −
1
4
B) −
1
2
C) −
3
2
D)
1
2
E)
3
2
13. Si tanq=2 y π θ
π
< <
3
2
,
calcule el valor de 10 2
3
sen θ
π
+




A) 4 3 3−
B) 3 1−
C) 4 3 3+
D) 3 3 4−
E) 1 3−
14. Si se cumple que cscθ = 5 y
π
θ π
2
< < ,
calcule el valor de
1 4
1 4
2 2
−
+
+
cos
cos
tan
θ
θ
θ
A) –3/4 B) –4/3 C) 3/4
D) 4/3 E) 2/3
15. Halle el equivalente de
4sec2
20ºcos40º+sen2
20º–8tan20ºcot40º
A) sen2
20º B) sen2
40º C) cos2
20º
D) cos2
40º E) tan20º
16. Reduzca la siguiente expresión.
2
10 20
10 10
20 2 102cos ºcos º
cos º º
º º
−



 − −
sen
sen sen
A) 2sen10º B) 2cos10º C) 2sen20º
D) 2cos20º E) tan20º
17. Calcule el valor de
csc º sec º cot º40 3 40 10−( )
A) –4 B) –2 C) 2
D) 4 E) 6
NIVEL AVANZADO
18. Si 2
1
cosθ = +a
a
,
halle el equivalente de 2cos4q.
A) 2(a2
+b2
)
B) a2
+b2
C) 1
2
14
4
a
a
+




D) a
a
4
4
1
+
E) 2
14
4
a
a
+





13. Trigonometría
13
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
14
Academia ADUNI Material Didáctico
19. Si tan tan csc ;
α α
α
2 4
2+ =
π
α π
2
< <
calcule el valor de tan tan
α α
2 4
− .
A)
3
3
B) −
3
3
C)
2 3
3
D) −
4 3
3
E)
4 3
3
20. Si AB=3 y BD=DE=1, calcule EC.
θ
2θ
A
B CD E
A) 5/2
B) 7/2
C) 9/2
D) 11/2
E) 13/2

14. Trigonometría
14
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
15
Repaso Especial San Marcos Trigonometría
05
SEMANA
NIVEL BÁSICO
1. Calcule el menor valor positivo que satisface
la ecuación
3tan2
x=2cos2x
A) p/6 B) p/3 C) p/12
D) p/24 E) 5p/12
2. De la ecuación
3(1+senx)=1+cos2x
calcule la suma de soluciones que pertenecen
al intervalo [0; 2p〉.
A)
9
2
π
B)
7
3
π
C)
13
6
π
D) 3p E)
19
3
π
3. Calcule la suma de soluciones para la ecuación
tan cotx x− − =
2
3
0 si 0≤x≤p.
A)
π
2
B) p
C)
7
6
π
D)
4
3
π
E)
3
2
π
4. Si x pertenece al tercer cuadrante, calcule el
menor valor de x que cumple la ecuación
3cot2
x–16cos2x+3=0
A) 230º B) 260º C) 210º
D) 165º E) 240º
NIVEL INTERMEDIO
5. Calcule la menor solución positiva que satisfa-
ce la ecuación
sen8x+sen4x+2sen2
x–1=0
A)
π
72
B)
π
36
C)
π
20
D)
π
12
E)
π
6
6. Calcule la suma de los tres menores valores
positivos de x que verifican la ecuación
1+4senxsen2x=8cosx
A)
7
3
π
B)
13
3
π
C)
17
3
π
D)
21
3
π
E)
23
3
π
7. Halle la suma de los dos menores valores
positivos que satisfacen
cot4x–tan4x=2
A)
7
32
π
B)
5
32
π
C)
3
16
π
D)
π
8
E)
5
16
π
8. Halle la solución general de la ecuación
4sen2x(sen2x–1)=3
A)
n
n
nπ π
2
1
12
+ −( ) ∈{ }/ 
B)
n
n
nπ π
2
1
6
+ −( ) ∈{ }/ 
C) n n
n
π
π
+ −( ) ∈{ }1
6
/ 
D) n n
n
π
π
+ −( ) ∈{ }1
12
/ 
E) n n
n
π
π
− −( ) ∈{ }1
12
/ 
Ecuaciones trigonométricas

15. Trigonometría
15
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
16
Academia ADUNI Material Didáctico
9. Obtenga el conjunto solución de la ecuación
senx x+ =2 cos
A) 8 1
4
n n+( ) ∈{ }π
/ 
B) 8 3
4
n n+( ) ∈{ }π
/ 
C) 8 3
8
n n+( ) ∈{ }π
/ 
D) 8 1
8
n n−( ) ∈{ }π
/ 
E) 8 1
4
n n−( ) ∈{ }π
/ 
10. Halle el conjunto solución de la ecuación
sen4x+cos4xcot2x=–1
A)
n
n
π π
2 8
+ ∈{ }/ 
B)
n
n
π π
2 4
− ∈{ }/ 
C)
n
n
π π
2 12
+ ∈{ }/ 
D)
n
n
π π
2 8
− ∈{ }/ 
E) n nπ
π
− ∈{ }8
/ 
11. Halle la solución general de la ecuación
2sen3
x–2cos2x–senx=0
A) n nπ
π
± ∈{ }4
/ 
B) n nπ
π
± ∈{ }3
8
/ 
C) 2
6
n nπ
π
± ∈{ }/ 
D) 2
3
n nπ
π
± ∈{ }/ 
E) 2
4
n nπ
π
± ∈{ }/ 
12. Resuelva la ecuación
9senx–12sen3
x=− 3 3cos x
A)
n
n
π π
3 18
− ∈{ }/ 
B)
n
n
π π
3 18
+ ∈{ }/ 
C)
n
n
π π
3 24
+ ∈{ }/ 
D)
n
n
π π
3 12
− ∈{ }/ 
E)
n
n
π π
3 12
+ ∈{ }/ 
13. Calcule la mayor solución negativa de la ecua-
ción sen4x+2sen2xcos2x=2sen2x
A) −
π
3
B) −
5
12
π
C) −
π
2
D) −
π
4
E) −
π
6
14. Halle la solución general de la ecuación
cos6x+secx=0
A)
k
k
π
2
/ ∈{ }
B)
k
k
π
4
/ ∈{ }
C) {2kp/k∈Z}
D) {(2k+1)p/k∈Z}
E) {kp/k∈Z}
15. Halle la suma de las soluciones de la siguiente
ecuación.
cos2xcscx+cscx+cotx=0; x∈〈0; 2p〉
A) 2p B)
8
3
π
C)
10
3
π
D) 4p E)
9
3
π

16. Trigonometría
16
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
17
Repaso Especial San Marcos Trigonometría
16. Halle el número de soluciones de la ecuación
sen5xcscx–2cosx=0, x∈[0; 2p]
A) 8 B) 9 C) 10
D) 11 E) 12
NIVEL AVANZADO
17. Si x∈[0; p], halle el número de soluciones de
la ecuación
tanx+tan2x–tan3x=0
A) 3 B) 4 C) 5
D) 6 E) 7
18. Calcule la menor solución positiva de la ecuación
sen sen5 13 3 5 13x x x x+ = +( )cos cos
A)
π
36
B)
π
27
C)
π
9
D)
π
18
E)
π
6
19. Si x∈[0; 2p〉, halle el número de soluciones de
la ecuación
tan2
xtan2x=tanxtan2x
A) 1 B) 2 C) 3
D) 4 E) 5
20. Si x∈[0; 2p], halle el número de soluciones de
la ecuación
4
2
2 2
2
2 2 1sen sen
x
x
x
xcos cos+ − =
A) 1 B) 2 C) 3
D) 4 E) 5

17. Trigonometría
17
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
18
Academia ADUNI Material Didáctico
06
SEMANA
NIVEL BÁSICO
1. Del gráfico se cumple que BC = 9 6.
Calcule AC.
A
B
C
15º
45º
A) 24 u B) 26 u C) 27 u
D) 28 u E) 30 u
2. En el gráfico, AB=5 u, BD= 2 3 u, DC=3 u y
cosα =
1
3
. Calcule senq.
αθ
A
B
CD
A)
2
5
B)
2 2
5
C)
3 2
5
D)
2
10
E)
3 2
10
3. En la figura, el triángulo BCD es equilátero y
AD=4BC. Calcule sec2
a.
α
A
B
C D
A) 7/3 B) 2 C) 8/3
D) 3 E) 10/3
NIVEL INTERMEDIO
4. Calcule el área de una región triangular cuyos
lados tienen longitudes (en centímetros) ex-
presados por números enteros pares conse-
cutivos y cuyo ángulo menor es la mitad del
ángulo mayor.
A) 5 7 cm2
B) 10 7 cm2
C) 15 7 cm2
D) 15 3 cm2
E) 15 5 cm2
5. El área de una región triangular ABC es 40 u2
. Si
AB=8 u y la suma de los ángulos B y C es 150º,
calcule cotB.
A)
4 5 3
5
−
B)
5 4 3
5
−
C)
4 5 3
3
+
D)
4 5 3
3
−
E)
5 2 3
3
−
Resolución de triángulos oblicuángulos

18. Trigonometría
18
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
19
Repaso Especial San Marcos Trigonometría
6. En el gráfico se cumple que
cos
α β α β
α β
+



−


 = +( )
2 2
1
6
sen sen
y AB=3 u, AC=7 u.
Calcule el perímetro del triángulo ABC.
α
β
A
B
C
A) 20 u B) 21 u C) 22 u
D) 18 u E) 24 u
7. En la figura, AB=AD=BC, mS ABC=90º,
mSBAD=32, mSBCD=q. Calcule cotq.
A) 298/79
A
B
C
D
B) 289/98
C) 289/100
D) 298/89
E) 289/49
8. En un triángulo ABC, halle el equivalente de la
expresión
(b+c)2
(1–cosA)+(b–c)2
(1+cosA)
A
B
C
a
b
c
A) 2a2
B) 2b2
C) 2c2
D) a2
E) b2
9. Si AC=2(AB), calcule 5senθ.
3θ
θ
A
B
C
A)
5
2
B)
5
4
C)
10
2
D)
10
4
E)
5
8
10. Los lados de un triángulo miden 8 cm, 12 cm
y 13 cm. Si q es la medida del mayor ángulo
agudo, calcule 77
2
2
tan .
θ
A) 50 B) 51 C) 52
D) 53 E) 54
11. Si AB=2(AC) y BC=3, calcule AB2
–AC2
.
A) 7
θ
2θ
A
BC
B) 8
C) 9
D) 10
E) 12
12. Si AB=17, AC=21 y BC=10, calcule tan .
α θ−



2
α
θ
A
B
C
A) −
11
31
B) −
22
31
C) −
31
11
D) −
21
31
E) −
31
21

19. Trigonometría
19
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
20
Academia ADUNI Material Didáctico
13. En un triángulo ABC se cumple que
mSBAC=2mSBCA, cosC =
3
4
y AB=4.
Calcule el perímetro del triángulo ABC.
A) 14 B) 15 C) 16
D) 17 E) 18
14. De acuerdo con el gráfico, calcule cos2q si
AB=6 cm y AC=5 cm.
3θ
2θ
A
B
C
A) 1/5 B) 1/3 C) 2/5
D) 1/6 E) 1/8
NIVEL AVANZADO
15. En el triángulo ABC se cumple que
cos cos cosA
a
B
b
C
c
c
ab c
+ + = −
1
2
Calcule la medida del ángulo C.
A
B
C
a
b
c
A) 120º
B) 105º
C) 135º
D) 150º
E) 165º
16. De acuerdo con el gráfico, halle el equivalente
de la expresión
a A c C
A C
cos cos
cos( )
+
−
A
B
C
a
b
c
A) b/2 B) b C) c
D) a E) a/2
17. De acuerdo con el gráfico, calcule
9cosa+7cosq+10cosb.
3 4
6
α β
θ
A B
C
A) 9 B) 10 C) 7
D) 12 E) 13
18. Si BD = 3 y CD=2, calcule x.
A
B
CD
x
2x 60º
A) 8º B) 10º C) 12º
D) 15º E) 18º

20. Trigonometría
20
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
21
Repaso Especial San Marcos Trigonometría
19. Si AC=BD, calcule la medida del ángulo ABD.
3α
2α
4α
A
B
CD
A) 12º B) 18º C) 20º
D) 24º E) 30º
20. En el triángulo ABC se cumple que AD = 4 3 cm.
Calcule BC.
A
B
C
D
110º
40º 20º
A) 12 cm B) 11 cm C) 13 cm
D) 14 cm E) 15 cm

21. 01 - c
02 - e
03 - c
04 - c
05 - b
06 - d
07 - a
08 - A
09 - E
10 - b
11 - a
12 - A
13 - a
14 - c
15 - D
16 - d
17 - E
18 - a
19 - E
20 - a
01 - c
02 - e
03 - c
04 - c
05 - b
06 - d
07 - a
08 - A
09 - E
10 - b
11 - a
12 - A
13 - a
14 - c
15 - D
16 - d
17 - E
18 - a
19 - E
20 - a
Razones trigonométricas de un ángulo agudo
01 - D
02 - a
03 - a
04 - A
05 - E
06 - d
07 - d
08 - b
09 - b
10 - d
11 - c
12 - D
13 - b
14 - c
15 - C
16 - d
17 - c
18 - B
19 - A
20 - c
01 - D
02 - a
03 - a
04 - A
05 - E
06 - d
07 - d
08 - b
09 - b
10 - d
11 - c
12 - D
13 - b
14 - c
15 - C
16 - d
17 - c
18 - B
19 - A
20 - c
Identidades trigonométricas fundamentales
01 - a
02 - d
03 - d
04 - c
05 - a
06 - A
07 - a
08 - c
09 - d
10 - e
11 - d
12 - d
13 - b
14 - c
15 - A
16 - C
17 - B
18 - d
19 - d
20 - B
01 - a
02 - d
03 - d
04 - c
05 - a
06 - A
07 - a
08 - c
09 - d
10 - e
11 - d
12 - d
13 - b
14 - c
15 - A
16 - C
17 - B
18 - d
19 - d
20 - B
Identidades trigonométricas de ángulos compuestos
01 - e
02 - a
03 - e
04 - b
05 - a
06 - c
07 - a
08 - D
09 - B
10 - c
11 - e
12 - c
13 - a
14 - b
15 - a
16 - C
17 - B
18 - d
19 - c
20 - B
01 - e
02 - a
03 - e
04 - b
05 - a
06 - c
07 - a
08 - D
09 - B
10 - c
11 - e
12 - c
13 - a
14 - b
15 - a
16 - C
17 - B
18 - d
19 - c
20 - B
Identidades trigonométricas de ángulo doble
01 - a
02 - A
03 - c
04 - c
05 - B
06 - b
07 - c
08 - a
09 - e
10 - d
11 - A
12 - A
13 - e
14 - d
15 - D
16 - a
17 - b
18 - B
19 - b
20 - d
01 - a
02 - A
03 - c
04 - c
05 - B
06 - b
07 - c
08 - a
09 - e
10 - d
11 - A
12 - A
13 - e
14 - d
15 - D
16 - a
17 - b
18 - B
19 - b
20 - d
Ecuaciones trigonométricas
01 - c
02 - B
03 - A
04 - c
05 - a
06 - d
07 - b
08 - a
09 - a
10 - b
11 - c
12 - b
13 - b
14 - e
15 - a
16 - b
17 - E
18 - b
19 - b
20 - A
01 - c
02 - B
03 - A
04 - c
05 - a
06 - d
07 - b
08 - a
09 - a
10 - b
11 - c
12 - b
13 - b
14 - e
15 - a
16 - b
17 - E
18 - b
19 - b
20 - A
Resolución de triángulos oblicuángulos
Repaso Especial SM