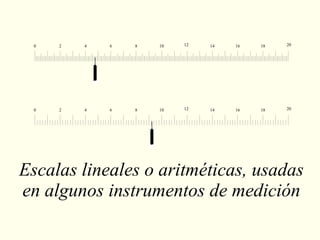
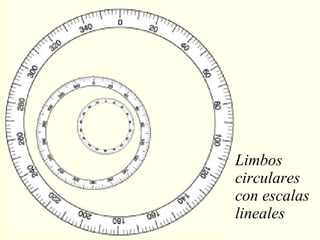
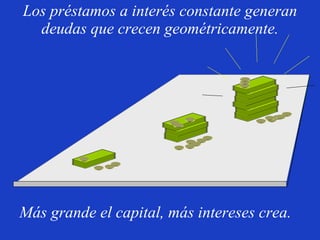
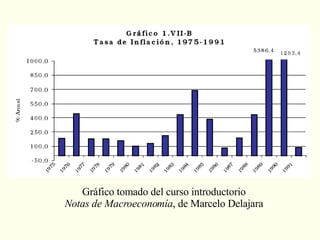
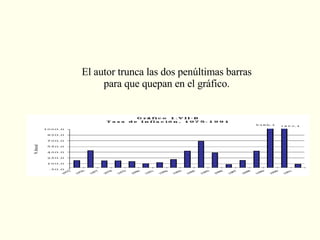
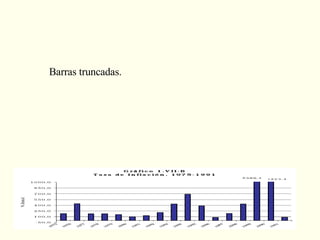
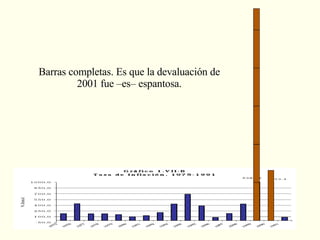
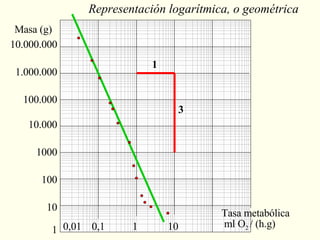
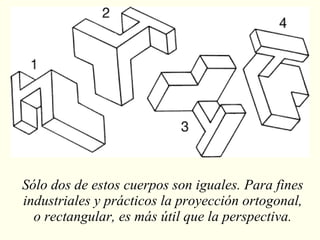
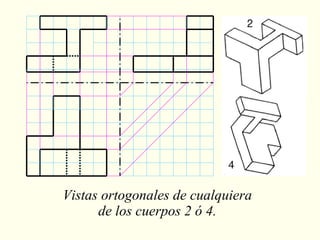
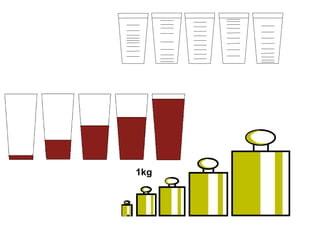
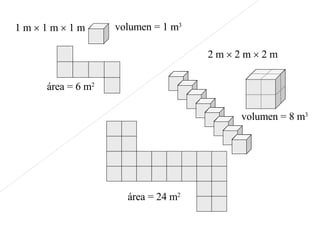
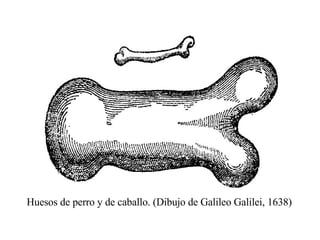
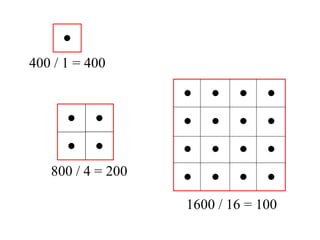
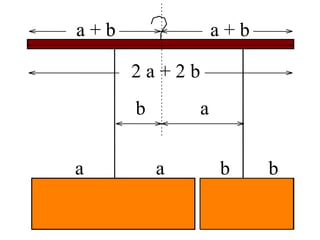
El documento explora la relación entre la matemática y la física con diversas disciplinas, destacando cómo las progresiones aritméticas y geométricas se manifiestan en la naturaleza, el arte y la economía. Se analizan ejemplos de escalas y representaciones que utilizan estas progresiones, así como su aplicación en fenómenos naturales y culturales. Además, se discuten diferentes perspectivas y representaciones visuales que reflejan conceptos matemáticos, subrayando la importancia de la matemática en la comprensión del mundo físico.

1. Matemática y física; algunas conexiones con otras ciencias y artes. Prueba de colores: Agustín Rela º

2. Temas nuevos Temas tradicionales

3. Progresiones geométricas en artes y ciencias Gracias a Beatriz Martinelli

4. Progresión aritmética: Progresión geométrica: 1, 2, 3, 4, 5, 6, ... 1, 10, 100, 1000, 10.000, ... Casos de progresiones

5. Aritmética

6. Geométrica

7. Reglas Pim La regla aritmética, la más común de las escalas lineales 1 10 11 12 13 14 15 8 0 2 3 4 5 6 7 9

8. Escalas lineales o aritméticas, usadas en algunos instrumentos de medición 20 18 16 14 12 10 8 6 4 2 0 20 18 16 14 12 10 8 6 4 2 0

9. Amperímetro de corriente continua, de bobina móvil. Su escala es lineal o aritmética.

10. Limbos circulares con escalas lineales

12. La progresión geométrica aparece frecuentemente en la naturaleza y la sociedad.

13. Los préstamos a interés constante generan deudas que crecen geométricamente. Más grande el capital, más intereses crea.

14. Moneda de mil australes, que en 1991 valía menos de 0,1 dólar. Cinco años antes, si hubiera existido, habría valido mil. La depreciación monetaria argentina es sólo aproximadamente geométrica.

15. Gráfico tomado del curso introductorio Notas de Macroeconomía , de Marcelo Delajara

16. El autor trunca las dos penúltimas barras para que quepan en el gráfico.

17. Barras truncadas.

18. Barras completas. Es que la devaluación de 2001 fue –es– espantosa.

19. El nautilo

20. Radiografía de un nautilo

21. Los septos de un nautilo crecen geométricamente con el tiempo: cuanto más grande es el molusco, con tanta mayor velocidad aumenta de tamaño.

22. Uno de los septos

23. En una escala lineal o aritmética, el crecimiento de los septos del nautilo se representa por una curva. Se puede distorsionar la escala para que la representación esté dada, en cambio, por una recta.

24. La representación en perspectiva cónica, central o fotográfica ofrece al ojo una experiencia mecánica similar a la que brindaría la realidad.

25. La Anunciación, de Guido di Pietro Da Mugello (Fra Angelico, 1400 –1455). Su representación en perspectiva utiliza la progresión geométrica.

26. La perspectiva cónica o fotográfica usa, también, la progresión geométrica

29. Visión de una esquina a través de un vidrio plano transparente Vidrio Observador

30. Vidrio El ojo barre 90 grados cuando pasa de un punto de fuga al otro. Eso ocurre sólo desde cierta distancia del dibujo.

31. Calcado de una fila regular de objetos iguales sobre un vidrio (en azul en la figura). Elijamos O de modo que el dibujo del objeto más cercano duplique en tamaño el del mas lejano. O B C A D

32. Vidrio El dibujo del poste más cercano tiene un tamaño doble del que corresponde al más alejado. (En verde, las diagonales de una supuesta fila de baldosas cuadradas, a 45 grados de la fila de postes.)

33. Trece tubos de la misma medida que los dibujos anteriores suenan como la escala musical dodecafónica del Clave bien temperado , de J. S. Bach. En rojo, la nota do .

34. Tubos Tapones optativos Dividen por dos la frecuencia

35. El antiguo siku, antara o zampoña andina, es conocido universalmente

36. Siku de tubos ajustables para afinar el tono. Los de cañas tapadas abajo se pueden afinar con arena.

37. Longitudes de las cañas en progresión alineal.

40. Sikus, y más sikus.

41. Por su estructura de cavidades resonantes, el oído percibe con sensaciones parecidas dos sonidos cuyas frecuencias sean una el doble de la otra. La forma de la cóclea, o caracol,se parece a la del nautilo

42. Oído externo e interno.

43. Pronunciemos la palabra fatídica...

44. La que produce temor, alarma y espanto...

45. ¡Logaritmo!

46. ¡Aghhh...!

47. El logaritmo, en algunos casos, es sólo la cantidad de ceros: log(1.000.000) = 6 log(100) = 2 log(10) = 1 log(1) = 0 log(0,1) = –1 log(0,001) = –3

48. Escala doble logarítmica, de una década por una década.

49. Otra escala doble logarítmica, de 4 décadas por 5 .

50. Escala semilogarítmica, compuesta por un eje aritmético y otro geométrico (o uno lineal y el otro logarítmico).

51. Otra escala semilogarítmica, de seis décadas horizontales por diez intervalos verticales.

52. Animal g ml O 2 / (h.g) Musaraña 4,8 7,40 Ratón de campo 9.0 2,50 Ratón canguro 5,2 1,80 Ratón 25 1,65 Ardilla terrestre 96 1,03 Rata 290 0,87 Gato 2500 0,68 Perro 11.700 0,33 Cordero 42.700 0,22 Humano 70.000 0,21 Caballo 650.000 0,11 Elefante 3.800.000 0,07 Ballena azul 20.000.000 0,03 Metabolismo de mamíferos

53. Representación lineal o aritmética Masa (g) 0 0,2 0,4 0,6 0,8 1 Tasa metabólica, ml O 2 / (h.g) 10 7 8  10 6 4  10 6 6  10 6 0 2  10 6

54. Representación logarítmica, o geométrica ml O 2 / (h.g) Masa (g) 1 10 100 1000 10.000 0,01 1 3 100.000 1.000.000 10.000.000 0,1 1 10 Tasa metabólica

55. En síntesis, la progresión geométrica se presenta en las artes, las ciencias, la economía y la naturaleza, y eso facilita el estudio.

56. Digresión: ¿Hay representaciones verdaderas y falsas? ¿Son algunas más útiles que otras?

57. Perspectiva engañosa. La parte de arriba parece un pórtico rectangular: la de abajo, tres columnas redondas.

58. Tenedor endiablado (Devil fork)

59. Sólo dos de estos cuerpos son iguales. Para fines industriales y prácticos la proyección ortogonal, o rectangular, es más útil que la perspectiva.

60. Vistas ortogonales de cualquiera de los cuerpos 2 ó 4.

61. La vista en corte de la derecha, en proyección rectangular, es poco fotográfica, pero real.

62. Otra perspectiva falsa. Objeto imposible, diseñado por Mauritis Cornelis Escher (1898 –1972).

63. Figura geométrica fiel, pero engañosa. Las líneas son rectas.

66. Parecen espirales, pero son círculos.

67. Este lugar, visto desde un satélite.

68. Más detalle.

69. El Compumap , menos fiel, pero más útil...

70. ... para llegar.

71. Dibujos en tiza en la calle, por Julian Beever

72. La ilusión que genera la perspectiva es formidable. Pero sólo hay un punto desde el que se la puede apreciar.

73. Aproximación

74. 0 °C 100 °C 20 °C

75. 0 °C 100 °C 20 °C

76. 0 100 T (°C)

77. 0 T (°C) 100

78. Otro ejemplo de aproximación por incrementos finitos: el tiro oblicuo, resuelto sin ecuaciones

82. Alinealidad

84. volumen = 1 m 3 área = 6 m 2 1 m  1 m  1 m volumen = 8 m 3 área = 24 m 2 2 m  2 m  2 m

85. Huesos de perro y de caballo. (Dibujo de Galileo Galilei, 1638)

86. 400 / 1 = 400 800 / 4 = 200 1600 / 16 = 100

87. Palanca

88. La gran utilidad que tiene la matemática para la física es una muestra de qué poco es lo que sabemos del mundo. Bertrand Rusell

89. Nuestras ideas físicas actuales quizá sean muy distantes de la verdad. (Visión artística de Quino)

94. a a b b 2 a + 2 b a + b a + b a + b b a

95. Peso a Peso b Longitud b Longitud a

97. 28.Ago.2007 20:35H Fin

99. Otras ilustraciones

105. París, mayo de 1968

106. Un disco o bola achatada de yeso se impregna en tinta en menos tiempo que una esfera.

107. Y aun más velozmente se impregna un disco adelgazado en el medio.