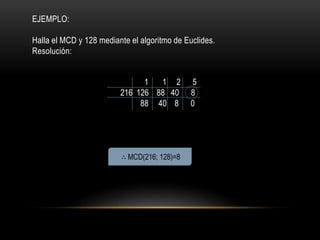
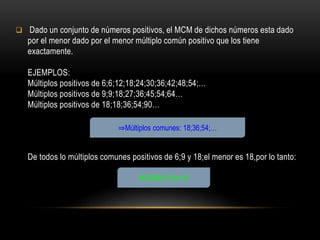
Este documento presenta información sobre el Máximo Común Divisor (MCD) y el Mínimo Común Múltiplo (MCM). Explica que el MCD es el mayor divisor común positivo que comparten dos o más números, y que el MCM es el menor múltiplo común positivo. Proporciona ejemplos y métodos como la descomposición canónica y el algoritmo de Euclides para calcular el MCD y el MCM. También establece propiedades como que el MCD de dos números primos entre sí es 1 y su MCM es

1. I.E.P. JOSÉ GALVÉZ EGÚSQUIZA
ASIGNATURA: MATEMÁTICA
TEMA: M.C.D. – M.C.M.
AÑO: 2DO DE SECUNDARIA
PROFESOR: JULIO BALTAZAR ROMERO
2014

2. MÁXIMO COMÚN DIVISOR
MÍNIMO COMÚN MÚLTIPLO.

5.  Dado un conjunto de números enteros positivos del MCD de dichos
números está dado por el mayor por el mayor de los divisores comunes
positivos que comparten dichos números
EJEMPLO:
Divisores de 24 : 1; 2; 3: 4; 6; 8; 12; 24.
Divisores de 26 : 1; 2; 3; 4; 6; 9; 12; 18; 36.
Divisores de 60 : 1; 2; 3; 4; 5; 6; 12; 15; 20; 30; 60.
Se observa q el mayor de los divisores comunes de 24 ; 36 y 60 es 12,
entonces:
MCD(24; 36; 60) = 12
⇒ Divisores comunes: 1; 2; 3; 4; 6; 12.

6.  POR DESCOMPOSICIÓN CANÓNICA
Dados dos o mas números descompuestos canónicamente, el MCD de dichas
cantidades es numéricamente igual al producto de sus divisores primos
comunes, elevados cada uno a su menor exponente.
⇒ MCD(360; 675)=3² .5=45
EJEMPLO:
360= 2³ .3² .5
675= 3³ .5²

7.  POR DESCOMPOSICIÓN SIMULTANEA
Se extrae de manera simultánea los factores comunes (únicamente) de los
números dados para luego multiplicarlos.
PESÍ
⇒ MCD(60; 72; 48)= 2. 2 .3= 12
EJEMPLO:
60 – 72 – 48 2
30 – 36 – 24 2
15 – 18 – 12 3
5 - 6 - 4

8.  POR ALGORITMO DE EUCLIDES O
DIVISIONES SUCESIVAS
Dados dos números entre positivos, se divide el mayor de los números
entre el menor; luego, el menor de los números iniciales entre el residuo
obtenido, después, el residuo anterior entre el ultimo residuo obtenido y
así sucesivamente hasta que la división resulte exacta; entonces, el ultimo
divisor será el MCD de dichos números. Para remplazar este procedimiento
usamos el siguiente esquema:
División
exacta
Cocientes q₁ q₂ q₃ q₄ q₅
A B r₁ r₂ r₃ r₄
Residuos r₁ r₂ r₃ r₄ 0
Donde A > B; entonces:
MCD(A; B)= r₄

9. EJEMPLO:
Halla el MCD y 128 mediante el algoritmo de Euclides.
Resolución:
1 1 2 5
216 126 88 40 8
88 40 8 0
∴ MCD(216; 128)=8

11.  Dado un conjunto de números positivos, el MCM de dichos números esta dado
por el menor dado por el menor múltiplo común positivo que los tiene
exactamente.
EJEMPLOS:
Múltiplos positivos de 6;6;12;18;24;30;36;42;48;54;…
Múltiplos positivos de 9;9;18;27;36;45;54;64…
Múltiplos positivos de 18;18;36;54;90…
De todos lo múltiplos comunes positivos de 6;9 y 18;el menor es 18,por lo tanto:
⇒Múltiplos comunes: 18;36;54;…
MCM(6;9;18)=18

13.  POR DESCOMPOSICIÓN CANÓNICA
Dados dos o mas números descompuestos canónicamente, el MCM de dichas
cantidades es numéricamente igual al producto de sus divisores primos
comunes y no comunes, elevados cada uno a su mayor exponente.
Ejemplo:
4500= 2² .3² .5²
7425= 3² .5² .11
1470= 2 .3 .5 .7²
⇒MCM(4500;7425;1470)=2².3³.5³.7².11

14.  POR DESCOMPOSICIÓN SIMULTANEA
Se extrae de manera simultanea lo factores comunes y no comunes de los
números dados, para luego multiplicarlos.
Ejemplo:
60 - 90 - 150 2
30 - 45 - 75 2
15 - 45 - 75 3
5 - 15 - 25 3
5 - 5 - 25 5
1 - 1 - 5 5
1 - 1 - 1
MCM(60;90;150)= 2 .2 .3 .3 .5 .5=900

16. 1. Si A y B son PESÍ, entonces:
MCD(A;B)=1
MCM(A;B)=A .B
2. Si A=˚B, entonces:
MCD(A;B)= B
MCM(A;B)= A
3. Si MCD(A;B;C)=d y MCM(A;B;C)=m, entonces:
𝐴
𝑑
= P1
𝐵
𝑑
=P2 Números enteros positivos PESÍ
𝐶
𝑑
= P3
𝑚
𝐴
= k1
𝑚
𝐵
= k2 Números enteros positivos PESÍ
𝑚
𝐶
= k3

17. MCD(Ka;Kb;kC)=kd
MCM(Ka;Kb;kC)=km
MDC( 𝐴
𝑛
; 𝐵
𝑛
; 𝐶
𝑛
)=d/n
MCM( 𝐴
𝑛
; 𝐵
𝑛
; 𝐶
𝑛
)=m/n

18. Edición echa por los alumnos:
- Albert Allende
- Víctor Amanso
- Ken Hamada
-Alessandra Tejada
GRACIAS POR SU ATENCIÓN