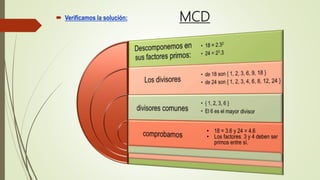
El documento explica los conceptos de máximo común divisor (MCD) y mínimo común múltiplo (MCM) de dos o más números. El MCD es el mayor divisor común entre los números, encontrado descomponiendo los números en factores primos y tomando los factores comunes con el menor exponente. El MCM es el menor múltiplo común entre los números, tomando los factores comunes y no comunes con el mayor exponente. Se proveen ejemplos para ilustrar cómo calcular el MCD y MCM y aplicarlos para resolver problemas práct

1. Tema:
Máximo común divisor y el mínimo común
múltiplo
1º DE SECUNDARIA

2. INTRODUCCIÓN AL TEMA
Antes de iniciar este tema es importante tener en cuenta
Para encontrar el máximo común divisor y el mínimo común
múltiplo debemos tener en claro ciertos conceptos
Como por ejemplo: ¿Qué es el divisor de un número? y
¿Qué es el múltiplo de un número?

3. DIVISOR DE UN NÚMERO
Decimos que un número es divisibles
por otro, cuando la división entre ellos
da un cociente exacto. En este caso el
segundo número se llama divisor del
primero.
Sea el número 60 sus divisores son:
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Múltiplo de un número
Los múltiplos de un numero son todos
aquellos que resultan de multiplicarlo
por otro numero cualquiera.
Como por ejemplo
4 : 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40,
44, 48…

4. Máximo común divisor: MCD
De dos o más
números, es el
mayor de los
divisores
comunes.
Se forma tomando
los factores
comunes a todos
los números con
el menor
exponente que
presenten.
Ejemplo: Hallar el
MCD de los
números 18 y 24
Descomponemos
en sus factores
primos los
números:
18 = 2.32
24 = 23.3
Tomamos los
factores comunes
( 2 y 3 ) con el
menor exponente
de cada uno (1 y 1
respectivamente )
Luego: MCD
(18,24) = 2.3 = 6
El 6 es el mayor
de los divisores
que tienen en
común.

5. MCD Verificamos la solución:
• 18 = 3.6 y 24 = 4.6
• Los factores 3 y 4 deben ser
primos entre sí.

6. MCD
 Ejemplo práctico:
 Dos cuerdas miden 18 y 24 cm. Y deseamos cortarlas en trozos de
igual longitud, siendo ésta la mayor posible.
 Hallamos el mcd de los números 18 y 24
 Como ya hemos visto es 6
 Es el mayor de los divisores comunes.
 Dividimos 18:6 = 3 trozos se obtienen de la cuerda de 18 cm
 Dividimos 24:6 = 4 trozos se obtienen de la cuerda de 24 cm
 En total tendremos 3+4 = 7 trozos de 6 cm cada uno.

7.  Ejemplo práctico:
Tres libros tienen 120, 150 y 180 párrafos cada uno. Deseamos
cortarlos y formar fascículos con la misma cantidad de hojas cada
uno, de forma que esa cantidad sea la mayor posible.
Hallamos el mcd de los
números 120, 150 y 180.
Descomponemos en sus
factores primos
120 = 23.3.5
150 = 2.3.52
180 = 2.32.5
Tomamos factores comunes
con el menor exponente:
MCD = 2.3.5 = 6.5 = 30
Dividimos 120:30 = 4
fascículos de 30 párrafos
cada uno.
Dividimos 150:30 = 5
fascículos de 30 párrafos
cada uno.
Dividimos 180:30 = 6
fascículos de 30 párrafos
cada uno.
En total tendremos:
4+5+6 = 15 fascículos
de 30 párrafos cada uno.

8. Mínimo común múltiplo: MCM
De dos o más números, es el menor de los múltiplos comunes.
Se forma tomando los factores comunes y no comunes a todos los números
con el mayor exponente que presenten.
Ejemplo: Hallar el MCM de los números 18 y 24
Factorizamos los números:
18 = 2.32
24 = 23.3
Tomamos los factores comunes ( 2 y 3 ) con el mayor exponente que presente
cada uno ( 3 y 2 respectivamente ) y todos los factores no comunes ( en este
caso no hay )
Luego: MCM (18,24) = 23.32 = 8.9 = 72
El 72 es el menor de los múltiplos comunes.

9. MCM
 Ejemplo práctico:
 Dos coches de carrera parten a la vez y tardan 18 y 24 min en dar una vuelta a la pista.
¿Cuándo se vuelven a encontrar en la línea de salida?
 Hallamos el mcm de los números 18 y 24
 Como ya hemos visto es 72
 Es el menor de los múltiplos comunes.
 Dividimos 72:18 = 4 vueltas completas da el primer vehículo.
 Dividimos 72:24 = 3 vueltas completas da el segundo vehículo.
 Vuelven a encontrar al cabo de 72 min en la línea de salida, tras dar 3 y 4 vueltas a la
pista cada uno de ellos.

10.  Otro ejemplo práctico:
 Un alumno tarda 25s en leer una página, otro 40s y un tercero tarda 54s en leer una página
similar. En un supuesto maratón, si los tres comienzan a leer a las 9,00 horas, ¿cuándo
volverán a coincidir los tres en volver a comenzar a leer una página?.
• Los siguientes números
• 25 = 52
• 40 = 5.23
• 54 = 2.33
Descomponemos
• De los números 25, 40 y 54
• Tomamos factores comunes y no comunes con el mayor exponente:
• Mcm = 23 . 33 . 52 = 8. 27. 25 = 216. 25 = 5400 s
• Coincidirán nuevamente a los 5400 s = 90 min
Hallamos el mcm
• 5400:25 = 216 párrafos habrá leído el primero.
• 5400:40 = 135 párrafos habrá leído el segundo.
• 5400:54 = 100 párrafos habrá leído el tercero.
Dividimos

11. Relación MCM y MCD
PROPIEDAD:
Sean A y B dos
números naturales
cualesquiera.
Siempre se
cumple: A.B =
MCM.MCD
Veamos con un
ejemplo:
MCM (18 y 24) =
72
MCD (18 y 24) = 6
18.24 = 72.6
432 = 432
Hemos
comprobado que
se cumple la
propiedad
mencionada.