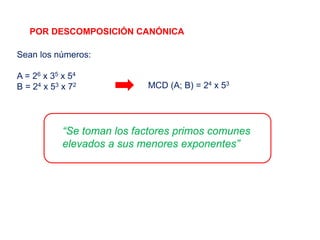
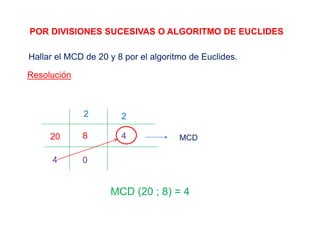
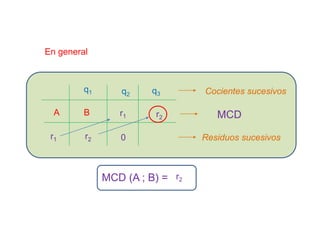
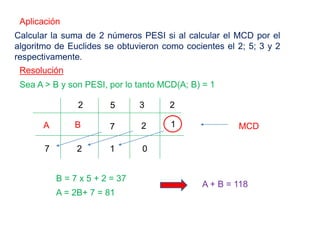
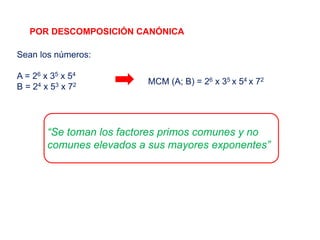
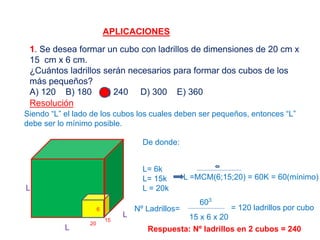
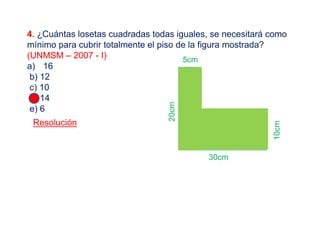
El documento explica los conceptos de máximo común divisor (MCD) y mínimo común múltiplo (MCM) de números. Define el MCD como el mayor divisor común entre números y el MCM como el menor número que es múltiplo común de los números. Presenta métodos como descomposición simultánea y algoritmo de Euclides para calcular el MCD y MCM. Incluye ejemplos y aplicaciones numéricas de estos conceptos.

1. Prof. Jenner Huamán Callirgos

3. MÁXIMO COMÚN DIVISOR
DIVISORES COMUNES. MÁXIMO COMÚN DIVISOR
Ejemplo: Hallar los divisores comunes de los números 72 y 84.
D (72) = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}
D (84) = {1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84}
Los divisores comunes a ambos números son: 1, 2, 3, 4, 6 y 12.
El mayor de estos divisores comunes es 12, por lo tanto se llamará
máximo común divisor (m.c.d.), es decir el m.c.d. (72 , 84) = 12
El mayor de los divisores comunes a
varios números recibe el nombre de
MÁXIMO COMÚN DIVISOR.

4. Ojito
Nº de divisores comunes = Nº de divisores del MCD
Del ejemplo anterior:
Los divisores comunes de 72 y 84 son: 1, 2, 3, 4, 6 y 12.
El mayor divisor común es 12.
Nº de divisores comunes = Nº de divisores de 12
12 = 22 .31 Nº de divisores de 12 = (2+1)(1+1) = 6

5. Debemos tener en cuenta que:
El MCD nunca es mayor que uno de los números.
Ejemplo:
MCD(15; 20; 40) = 5
Si el menor de los números es divisor común de los otros,
entonces el MCD será ese menor.
Ejemplo:
MCD(9; 18; 36; 90) = 9
Menor divisor
común
El MCD de dos números primos entre sí (PESI) es la unidad.
Ejemplo:
MCD(k; k+1) = 1
MCD (31; 17) = 1

6. FORMAS PRÁCTICAS PARA DETERMINAR EL MCD
POR DESCOMPOSICIÓN SIMULTÁNEA
 Se escriben los números en fila, luego se dividen simultáneamente
del menor al mayor factor primo común a dichos números.
 El MCD buscado es el producto de los divisores hallados.
Ejemplo: Hallar el MCD de 2 100; 2 520 y 840
2 100 - 2520 - 840 2
1 050 1 260 420 2
525 630 210 3
175 210 70 5
35 42 14 7
5 6 2
MCD = 22. 3 . 5 . 7
MCD = 420

7. POR DESCOMPOSICIÓN CANÓNICA
Sean los números:
A = 26 x 35 x 54
B = 24 x 53 x 72 MCD (A; B) = 24 x 53
“Se toman los factores primos comunes
elevados a sus menores exponentes”

8. POR DIVISIONES SUCESIVAS O ALGORITMO DE EUCLIDES
Hallar el MCD de 20 y 8 por el algoritmo de Euclides.
Resolución
20 8
2
4
4
2
0
MCD
MCD (20 ; 8) = 4

9. En general
A B
q1 q2 q3
r2r1
r1 r2
0
MCD
Cocientes sucesivos
Residuos sucesivos
MCD (A ; B) = r2

10. Aplicación
Calcular la suma de 2 números PESI si al calcular el MCD por el
algoritmo de Euclides se obtuvieron como cocientes el 2; 5; 3 y 2
respectivamente.
Resolución
Sea A > B y son PESI, por lo tanto MCD(A; B) = 1
A B
352 2
1
1 0
27
27
MCD
B = 7 x 5 + 2 = 37
A = 2B+ 7 = 81
A + B = 118

11. MÍNIMO COMÚN MÚLTIPLO
MÚLTIPLOS COMUNES. MÍNIMO COMÚN MÚLTIPLO
El MCM de varios números naturales es aquel número natural que
cumple dos condiciones:
 Es un múltiplo común de todos
 Es el menor posible.
Ejemplo:
Sean los números 4 y 6.
Números Múltiplos
4 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
6 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
1° Sus múltiplos comunes: 12, 24, 36, 48, ...
2° El menor es 12 => MCM = 12

12. Ojito
Múltiplos comunes de (A,B,C) = Múltiplos del MCM de (A,B,C)
Ejemplo
Hallar cuántos múltiplos comunes tiene 9 y 6 entre 180 y 360
Resolución
MCM (9;6) = 18
Múltiplos comunes = 18k
Dato 180 < 18k < 360
10 < k < 20
K= 11; 12; 13; …..;19
Hay 9 múltiplos comunes

13. Debemos tener en cuenta que:
El MCM nunca es menor que alguno de los números.
Ejemplo:
MCM(6; 9; 27) = 54
Si el menor número es múltiplo de los otros, entonces el
MCM es el menor número.
Ejemplo:
MCM(5; 10; 15; 90) = 90
Mayor múltiplo
común
El MCM de dos números primos entre sí (PESI) es el
producto de dichos números.
Ejemplo:
MCM(k; k+1) = k(k+1)
MCM (31; 17) = 31 x 17

14. FORMAS PRÁCTICAS PARA DETERMINAR EL MCM
POR DESCOMPOSICIÓN SIMULTÁNEA
Se dividen los números dados simultáneamente a todos o algunos de
ellos, del menor al mayor factor primo, hasta que se obtengan
cocientes iguales a la unidad.
Ejemplo:
Hallar el MCM de 2 100; 2 520 y 420
2 100 - 2520 - 420 2
1 050 1 260 210 2
525 630 105 2
525 315 105 3
175 105 35 3
175 35 35 5
35 7 7 5
7 7 7 7
1 1 1
MCM = 23. 32 . 52 . 7
MCD = 12600

15. POR DESCOMPOSICIÓN CANÓNICA
Sean los números:
A = 26 x 35 x 54
B = 24 x 53 x 72
“Se toman los factores primos comunes y no
comunes elevados a sus mayores exponentes”
MCM (A; B) = 26 x 35 x 54 x 72

16. APLICACIONES
1. Se desea formar un cubo con ladrillos de dimensiones de 20 cm x
15 cm x 6 cm.
¿Cuántos ladrillos serán necesarios para formar dos cubos de los
más pequeños?
A) 120 B) 180 C) 240 D) 300 E) 360
Resolución
Siendo “L” el lado de los cubos los cuales deben ser pequeños, entonces “L”
debe ser lo mínimo posible.
L
L
L
15
6
20
De donde:
L= 6k
L= 15k
L = 20k
L =MCM(6;15;20) = 60K = 60(mínimo)
Nº Ladrillos=
603
15 x 6 x 20
= 120 ladrillos por cubo
Respuesta: Nº ladrillos en 2 cubos = 240

17. 2. Hoy José, Carlos y Daniel han salido juntos a caminar por la
mañana. Si en adelante José sale cada 4 días a caminar, Carlos
cada 6 días y Daniel cada 5 días.
¿Dentro de cuántos días volverán a salir juntos?
A) 30 B) 36 C) 45 D) 60 E) 72
Resolución

18. 3. En una pista circular tres atletas corren en una misma dirección. El
primero demora 10 s en dar una vuelta, el segundo 11 s y el tercero
12 s. ¿Cuántos minutos tardan en pasar juntos por la partida por
primera vez? (UNMSM – 2004)
a) 22 b) 12 c) 10 d) 20 e) 11
Resolución

19. 4. ¿Cuántas losetas cuadradas todas iguales, se necesitará como
mínimo para cubrir totalmente el piso de la figura mostrada?
(UNMSM – 2007 - I)
a) 16
b) 12
c) 10
d) 14
e) 6
Resolución
20cm
30cm
10cm
5cm

20. 5. La suma de dos números es 48. Si el producto del máximo común
divisor con el mínimo común múltiplo es 540. Calcular la razón entre
el menor y el mayor.(UNMSM – 2008 - II)
a) 2/5 b) 3/5 c) 1/2 d) 3/4 e) 1/3
Resolución

21. 6. Si E = MCD(6432; 132) – 8, halle el valor de E2 + E + 1.(UNMSM –
2013 - II)
a) 21 b) 157 c) 111 d) 91 e) 43

22. ¿Cuántas cajas cúbicas como máximo se podrán utilizar para
empaquetar 12000 barras de jabón cuyas dimensiones son 8 cm, 15 cm
y 20 cm de modo que todos estén completamente llenas?
A) 30 B) 25 C) 15 D) 16 E) 20
Resolución

23. ¿Cuántos divisores comunes tienen los números:
3050
; 4540
y 6030
?
A) 961 B) 952 C) 852 D) 957 E) 978
Resolución

24. Al calcular el MCD de dos números por el algoritmo de Euclides los
cocientes sucesivos fueron: 3; 1; 3 y 5. Hallar el menor de los números si
la suma es 1200.
A) 252 B) 240 C) 228 D) 276 E) 948
Resolución

25. Resolución
Se trata de depositar el aceite de 3 barriles que tienen 210, 300 y 420
litros de capacidad en envases que sean iguales entre sí. ¿Cuál es la
menor cantidad de envases que se emplearía para que todos estén
llenos y no desperdiciar aceite?
A) 28 envases B) 31 envases C) 36 envases D) 38 envases
E) 40 envases

26. Aquí me quedé