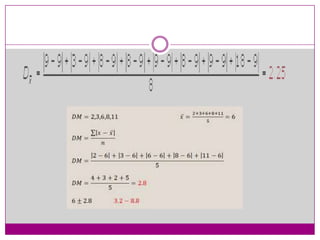
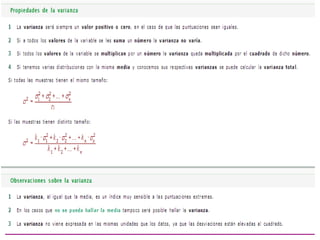
El documento describe diferentes medidas de dispersión como el rango, desviación media, varianza y desviación típica. Explica que las medidas de dispersión nos informan cuánto se alejan los valores de la distribución del centro. Define la desviación típica como la raíz cuadrada de la varianza y la describe como la medida de dispersión más usada.

1. Medidas de
dispersión
•
•
•
•
INTEGRANTES:
BARRERA GONZALEZ LAURA
B.
GARCÍA LÓPEZ B. GABRIELA
GARCÍA VARGAS ANA B.
HORTA GONZALEZ JUAN A.

2. Definición…
Las medidas de dispersión nos informan
sobre cuanto se alejan del centro los
valores de la distribución.

3. Son…
o Rango o recorrido: es la diferencia
entre el mayor y el menor de los
datos de una distribución estadística.

4. Desviación media

6. Ejemplo de desviación media
 Formula:
Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18

8. VARIANZA

12. Desviación típica

13.  Desviación típica
 La desviación típica es la raíz cuadrada de la
varianza.
 Es decir, la raíz cuadrada de la media de los
cuadrados de las puntuaciones de
desviación.
 La desviación típica se representa por σ.

14.  Desviación típica
 La desviación típica es la raíz cuadrada de la
varianza.
 Es decir, la raíz cuadrada de la media de los
cuadrados de las puntuaciones de
desviación.
 La desviación típica se representa por σ.

15. Propiedades
Tiene la misma unidad que los datos y que la media.
Siempre es positiva, será cero si y sólo si todos los datos
son coincidentes.
Es la medida de dispersión más usada.
Es invariante ante cambios de origen .
Si se produce un cambio de escala la nueva
desviación típica es igual a la anterior multiplicada por
el cambio
Si se produce simultáneamente un cambio de origen y
escala en los datos, sólo el cambio de escala afectará
a la desviación típica