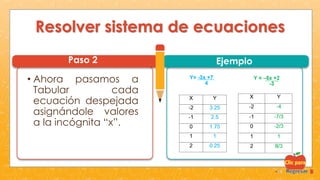
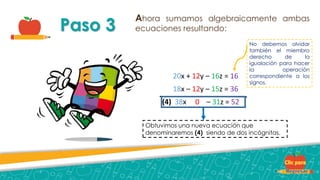
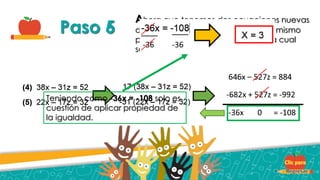
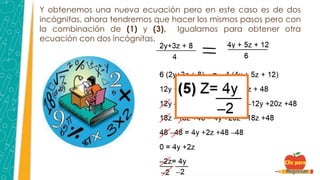
Este documento describe tres métodos para resolver sistemas de ecuaciones: el método gráfico para sistemas 2x2, el método de suma y resta para sistemas 3x3, y el método de igualación para sistemas 3x3. Se proveen ejemplos detallados de cada método con pasos explicados.

1. Reyna Bianey Alonso Cortez
0110220

2. Se cuenta con cuatro métodos para
resolver ecuaciones de primer grado.
Clic aquí para
la Actividad
Clic aquí para
la Actividad
Clic aquí para
la Actividad

3. Este método debemos recordar que solo
funciona para ecuaciones de 2 x 2 debido a que
al momento de graficarlo podremos hacerlo
manualmente por ser una figura plana. Para
resolver por medio de este método ecuaciones
de 3 x 3 debe realizarse con herramientas como
un programa en la computadora o una
calculadora gráficadora por se una figura
tridimensional.
Nota: cuando se habla de
ecuaciones 2 x 2 se refiere a dos
incógnitas de dos ecuaciones. Y
3 x 3 a tres incógnitas con tres
ecuaciones

4. Resolver sistema de ecuaciones
Ejemplo de un Sistema 2 x 2 Paso 1
◦ (1) 3x + 4y = 7
◦ (2) 5x – 3y = 2
Nota:
El (1) significa ecuación 1
Al igual en el (2). Es para identificar
las ecuaciones.
◦ En seguida tenemos que
despejar el coeficiente
literal “y” para poder
resolver el sistema de
ecuaciones por el método
gráfico, así como se muestra
en seguida:

5. Resolver sistema de ecuaciones
Paso 2 Ejemplo
• Ahora pasamos a
Tabular cada
ecuación despejada
asignándole valores
a la incógnita “x”.

6. Paso 3 Graficar
• Ahora con estos datos
obtenidos, graficamos
las dos funciones de la
siguiente manera:
El punto de intersección es el
resultado de las incógnitas “x”
y “y” las coordenadas (1,1)
Corresponde a X= 1 y Y= 1.

7. • Para comprobar solo se sustituye los valores en las
ecuaciones.
(1) 3x + 4y = 7
3(1) + 4(1) = 7
3 + 4 =7
7=7 ✓
(2) 5x – 3y = 2
5(1) – 3(1) = 2
5 – 3 = 2
2=2 ✓
Fin del método

8. En este método usaremos un sistema de
ecuaciones de 3 x 3. De esa forma
abarcaremos el 2 x 2 al mismo tiempo.
Dependiendo de los signos que se
presente en las expresiones algebraicas es
como se usara suma o resta.
Nota: cuando se habla de
ecuaciones 2 x 2 se refiere a dos
incógnitas de dos ecuaciones. Y
3 x 3 a tres incógnitas con tres
ecuaciones

9. Resolver sistema de ecuaciones
Ejemplo de un Sistema 3 x 3 Paso 1
◦ (1) 4x – 2y – 3z= 8
◦ (2) 5x + 3y – 4z = 4
◦ (3) 6x – 4y – 5z = 12
Nota:
El (1) significa ecuación 1
Al igual en el (2) y así sucesivamente. Es para
identificar las ecuaciones.
◦ Escogemos dos
ecuaciones para
eliminar una de sus
literales con el método,
en este caso
escogeremos las
ecuaciones (2) y (3).
Ejemplo
(2) 5x + 3y – 4z = 4
(3) 6x – 4y – 5z = 12

10. Resolver sistema de ecuaciones
Paso 2 Ejemplo
• En seguida multiplicamos los
miembros de la ecuación (2)
por 4 y los de la ecuación (3)
por 3; resultando que los
coeficientes numéricos de “y”
se igualan dando como
resultado un mismo
coeficiente numérico pero
con signo contrario.
4 (5x + 3y – 4z = 4)
3 (6x – 4y – 5z = 12)
Resultado de la
multiplicación
• 20x + 12y – 16z = 16
• 18x – 12y – 15z = 36

11. Paso 3
Ahora sumamos algebraicamente ambas
ecuaciones resultando:
20x + 12y – 16z = 16
18x – 12y – 15z = 36
(4) 38x 0 – 31z = 52
No debemos olvidar
también el miembro
derecho de la
igualación para hacer
la operación
correspondiente a los
signos.
Obtuvimos una nueva ecuación que
denominaremos (4) siendo de dos incógnitas.

12. Entonces proseguimos a realizar lo mismo para la
ecuación (1) utilizando una de las dos ecuaciones que ya
se han usado, en este caso utilizaremos la ecuación (2).
Con estas dos ecuaciones eliminaremos otra vez la literal
“y” para poder conseguir un nueva ecuación.
Obtuvimos una nueva
ecuación que
denominaremos (5) siendo
de dos incógnitas.

13. Paso 5
Ahora que tenemos dos ecuaciones nuevas
de solo dos incógnitas, repetimos el mismo
paso de eliminación de una literal la cual
será en este caso “z”:
Paso 6
Teniendo como -36x = -108 solo es
cuestión de aplicar propiedad de
la igualdad.

14. Consiguiendo la incógnita “x” sustituimos el valor en una de las
dos ecuaciones de 2x2 de ecuación (4) o (5) para encontrar la
incógnita “z” en este caso usaremos la ecuación (4).
38x – 31z = 52
38 (3) – 31z = 52
14 – 31z = 52
Utilizamos la propiedad
de la igualdad
Obteniendo los valores de las incógnitas “x” y “z” solo es sustituir los
valores en las primeras ecuaciones, ya sea en (1), (2) y (3). En este
caso usaremos la (1).
Con eso concluimos el método de
suma y resta, con los resultados de
las incógnitas:
X = 3
Y = -1
Z = 2
Fin del método

15. Este método usaremos un sistema de
ecuaciones de 3 x 3. De esa forma
abarcaremos el 2 x 2 al mismo tiempo. Se
debe recordar muy bien la propiedad de la
igualdad para no fallar en este método, se
recomienda practicar todo sobre una
expresión algebraica.
Nota: cuando se habla de
ecuaciones 2 x 2 se refiere a dos
incógnitas de dos ecuaciones. Y
3 x 3 a tres incógnitas con tres
ecuaciones

16. Resolver sistema de ecuaciones
Ejemplo de un Sistema 3 x 3 Paso 1
◦ (1) x + 2y – z= 2
◦ (2) 2x – y + z = 3
◦ (3) 2x +2y – z = 3
Nota:
El (1) significa ecuación 1
Al igual en el (2) y así sucesivamente. Es para
identificar las ecuaciones.
◦ Considerando las tres
ecuaciones a resolver,
debemos escoger una
ecuación para despejar, de
preferencia la que resulte
fácil realizar el despeje, en
este caso escogeremos la
ecuación (1) para despejar
la incógnita “z”.
Ejemplo

17. Resolver sistema de ecuaciones
Paso 2 Ejemplo
• Teniendo despejada la
incógnita “x” lo
encontrado lo sustituimos
en las otras dos ecuaciones
que quedaron, en esta
ocasión es la ecuación (2)
y (3). Y resolvemos ambas
ecuaciones con el despeje
de “x” de la ecuación (1). Nueva
ecuación
Nueva
ecuación

18. Paso 3 Ahora tenemos dos ecuaciones nuevas
de las cuales ambas contienen dos
incógnitas, enseguida repetimos el
mismo paso, escogemos una de las dos
nuevas ecuaciones (4) y (5) para utilizar
la propiedad de la igualdad y despejar
la incógnita que queramos. En esta
ocasión utilizaremos la ecuación (5)
despejando “z”.
Ya obteniendo el despeje de la
“z” en la ecuación (5). Pasamos a
sustituir la “z” en la otra ecuación
que es la (4). Para encontrar el
valor de la incógnita “y”.

19. Ahora que tenemos el valor de “y” podemos
sustituir ese valor en la ecuación (5) ya que
esta despejada la “z” es más fácil encontrar el
valor.
Ya que tenemos los valores encontrados de “y”
y “z” solo nos falta encontrar el de “x” para eso
tomaremos la ecuación (1) que ya habíamos
despejado la “x”
Fin del método

20. Este método usaremos un sistema de
ecuaciones de 3 x 3. De esa forma
abarcaremos el 2 x 2 al mismo tiempo. Se
debe recordar muy bien la propiedad de la
igualdad para no fallar en este método, se
recomienda practicar todo sobre una
expresión algebraica.
Nota: cuando se habla de
ecuaciones 2 x 2 se refiere a dos
incógnitas de dos ecuaciones. Y
3 x 3 a tres incógnitas con tres
ecuaciones

21. Resolver sistema de ecuaciones
Ejemplo de un Sistema 3 x 3 Paso 1
◦ (1) 4x – 2y – 3z= 8
◦ (2) 5x + 3y – 4z = 4
◦ (3) 6x – 4y – 5z = 12
Nota:
El (1) significa ecuación 1
Al igual en el (2) y así sucesivamente. Es para
identificar las ecuaciones.
◦ El siguiente paso para utilizar el
método de igualación consiste
en despejar una de las
incógnitas de las ecuaciones
anteriores, puede ser “x”, “y” o
“z” pero siempre y cuando sea
la misma incógnita en las tres
ecuaciones, en este caso
despejaremos literal “y” como
se muestra en seguida:
Ejemplo

22. Resolver sistema de ecuaciones
Paso 2 Ejemplo
• A continuación procedemos
a escoger dos ecuaciones
despejadas para igualarlas,
puede ser cualquiera,
puede ser (1) y (2), (1) y (3)
o (2) y (3). En este caso
igualaremos (1) y (2).
Ya igualando las dos
ecuaciones, procedemos
a multiplicar los divisores
por el numerador
contrario:
Paso 3

23. Paso 4 Ahora solo pasamos a multiplicar,
realizar operaciones, agrupar
términos y los reducimos.
Después despejamos una de las dos incógnitas
mediante la propiedad de la igualdad, para obtener
una nueva ecuación, en este caso despejaremos “z”.

24. Y obtenemos una nueva ecuación pero en este caso es de dos
incógnitas, ahora tendremos que hacer los mismos pasos pero con
la combinación de (1) y (3), Igualamos para obtener otra
ecuación con dos incógnitas.

25. Paso 5 Teniendo las dos nuevas ecuaciones y
con despeje de la misma incógnita,
ahora pasamos a igualarlas para
encontrar el valor de “y”.
Ahora se utilizara la propiedad de la igualdad
para poder despejar la única incógnita y
obtener el valor de la misma.

26. Paso 6
• Ahora teniendo el valor de una
incógnita en este caso la “y” la
sustituimos en una de las
ecuaciones donde ya tenemos
solo dos incógnitas en este
caso en las ecuaciones de (4) y
(5). En seguida se mostrara la
sustitución en la ecuación (4).
Y por último sustituimos los
valores encontrados de “y” y “z”
en las ecuaciones despejadas
de (1), (2) y (3), puede ser en
cualquiera para encontrar el
valor de “x”. A continuación se
mostrara el proceso en este
caso con la ecuación
despejada (2).
Fin del método

27. Respuestas
Sino sientes la
seguridad de
contestar, clic aquí
para repasar.
x = −4
y = 6
z = 1
x = −3
y = 7
z = 0
x = −4
y = 5
z = 2

28. Respuestas
Sino sientes la
seguridad de
contestar, clic aquí
para repasar.
x = −8
y = 1
z = 1
x = 0
y = 5
z = 6
x = 1
y = 1
z = 1

29. Respuestas
Sino sientes la
seguridad de
contestar, clic aquí
para repasar.
x = 3
y = -2
z = 4
x = 1
y = 2
z = 3
x = −2
y = 4
z = 2

30. ¡Correcto!

31. ¡Incorrecto!