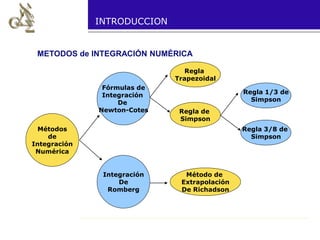
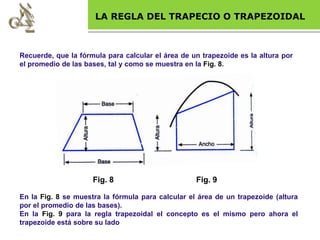
Este documento describe varios métodos de integración numérica, incluida la regla trapezoidal. Explica que la regla trapezoidal aproxima el área bajo una curva como un trapecio y presenta fórmulas para calcular la integral usando este método para un solo intervalo y para múltiples intervalos subdivididos. También describe cómo aplicar la regla trapezoidal para analizar la estabilidad transitoria de sistemas dinámicos.

1. INTRODUCCION
METODOS de INTEGRACIÓN NUMÉRICA
Métodos
de
Integración
Numérica
Fórmulas de
Integración
De
Newton-Cotes
Integración
De
Romberg
Regla
Trapezoidal
Regla de
Simpson
Método de
Extrapolación
De Richadson
Regla 1/3 de
Simpson
Regla 3/8 de
Simpson

2. FORMULAS DE NEWTON-COTES
Las fórmulas de integración de Newton-Cotes son los esquemas de integración
numérica más comunes.
Se basan en la estrategia de reemplazar una función complicada o datos
tabulados con una función aproximada que sea fácil de integrar:
donde fn(x) es igual a un polinomio de la forma:
donde n es el orden del polinomio.
 
b
a
n
b
a
dxxfdxxfI )()( Ec 2
Ec 3

3. FORMULAS DE NEWTON-COTES
Por ejemplo, en la Fig. 2 se usa el polinomio de primer orden (una línea recta)
como una aproximación. Mientras que en la Fig. 3 se emplea una parábola para
el mismo propósito.
Fig 2 Fig 3

4. FORMULAS DE NEWTON-COTES
Por ejemplo, en la Fig. 4 se usan tres segmentos de línea recta para aproximar
la integral. Pueden utilizarse polinomios de orden superior para los mismos
propósitos.
Fig 4

5. Base legalLA REGLA DEL TRAPECIO O TRAPEZOIDAL
La Regla Trapezoidal es la primera de las fórmulas de integración cerrada de
Newton-Cotes. Corresponde al caso donde el polinomio de la Ec 2 es de primer
orden.
Ec 2


 
  2
)()(
)()(
bfaf
abdxxfIdx
b
a
Pero…
QUÉ SIGNIFICA LA REGLA TRAPEZOIDAL?
Geométricamente, la
regla del trapecio es
equivalente a aproximar
el área del trapecio bajo
la línea recta que
conecta a f(a) y f(b)
como se muestra en
Fig. 7.
Fig. 7

6. Base legalLA REGLA DEL TRAPECIO O TRAPEZOIDAL
Entonces, el resultado de la integración es lo que se denomina regla
trapezoidal, resumida en la siguiente ecuación;
Ec 5


 
  2
)()(
)()(
bfaf
abdxxfIdx
b
a
Pero…
QUÉ SIGNIFICA LA REGLA TRAPEZOIDAL?
Geométricamente, la
regla del trapecio es
equivalente a aproximar
el área del trapecio bajo
la línea recta que
conecta a f(a) y f(b)
como se muestra en
Fig. 7.
Fig. 7

7. Base legalLA REGLA DEL TRAPECIO O TRAPEZOIDAL
Recuerde, que la fórmula para calcular el área de un trapezoide es la altura por
el promedio de las bases, tal y como se muestra en la Fig. 8.
En la Fig. 8 se muestra la fórmula para calcular el área de un trapezoide (altura
por el promedio de las bases).
En la Fig. 9 para la regla trapezoidal el concepto es el mismo pero ahora el
trapezoide está sobre su lado
Fig. 8 Fig. 9

8. EJERCICIOS DE APLICACIÓN
Use la Regla del Trapecio para aproximar los valores de las siguientes
integrales:
a) b)

9. Base legal
APLICACIÓN MULTIPLE
DE LA REGLA DEL TRAPECIO
La Regla del Trapecio se puede ampliar si subdividimos el intervalo [a,b] en n
subintervalos, todos de la misma longitud
Sea la partición que se forma al hacer dicha subdivisión.
Usando las propiedades de la integral, tenemos que:
Aplicando la Regla del Trapecio a cada una de las integrales, obtenemos:

10. Base legal
APLICACIÓN MULTIPLE
DE LA REGLA DEL TRAPECIO
Sustituyendo el valor de h y haciendo uso de la notación sigma (sumatoria),
tenemos finalmente:
Esta es la regla del trapecio para n subintervalos.
Obviamente, esperamos que entre más subintervalos usemos, mejor sea la
aproximación a la integral.
Ec. 6
Ahora bien, ya que los subintervalos tienen la misma longitud h, tenemos que:

11. Base legal
APLICACIÓN MULTIPLE
DE LA REGLA DEL TRAPECIO
Ilustración de la Regla Trapezoidal de aplicación múltiple: a) dos segmentos, b)
tres segmentos, c) cuatro segmentos y d) cinco segmentos
Fig. 10 Fig. 11

12. EJERCICIOS DE APLICACIÓN
Use la Regla del Trapecio para aproximar el valor de la siguiente integral:
Si subdividimos en 5 intervalos

13. Base legal
APLICACIÓN A LA ESTABILIDAD
TRANSITORIA
El método de la regla trapezoidal es el más utilizado para la solución de la
ecuación de oscilación ya que es muy sencillo y numéricamente estable.
Aplicando dicho método en la solución de oscilación se tiene:
Lo más importante es escoger un ∆t exitoso en el análisis; el cual debe ser
menor que la constante de tiempo más pequeña del sistema. Cuando no se
consideran los reguladores en el estudio de estabilidad, la experiencia ha
mostrado que ∆t debe estar entre 1 y 2 ciclos. No se debe considerar ∆t iguales
en todo el trayecto del análisis; al acercarse al punto de estabilidad se puede
utilizar ∆t mayores. A continuación se muestra en la Figura 5.4 la descripción de
dicho método considerando ∆t constante.
Descripción de la Regla Trapezoidal

14. Base legal
APLICACIÓN A LA ESTABILIDAD
TRANSITORIA
El área será:
Al sustituir las ecuaciones se tiene lo siguiente:

15. Base legal
APLICACIÓN A LA ESTABILIDAD
TRANSITORIA
Donde:

16. Base legal
APLICACIÓN A LA ESTABILIDAD
TRANSITORIA
Por lo tanto:
De esta manera se puede conocer el comportamiento de la velocidad
Y el ángulo a través del tiempo después de una pequeña perturbación.