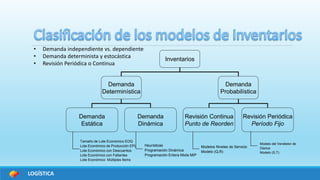
El documento presenta información sobre diferentes modelos de inventario como el tamaño de lote económico (EOQ), el tamaño económico de producción (EPL), revisión continua y periódica, demanda determinista y probabilística, y cómo aplicar estos modelos para resolver problemas de casos reales de empresas. Se explican conceptos como costo de mantener inventario, costo de pedidos, costo de faltantes, y cómo calcular el tamaño de lote óptimo, punto de reorden y costo total anual para minimizar costos.

1. MODELO EOQ CASOS
ING. DONATO TAPIAS
Especialistaen Logística
Magister

2. LOGÍSTICA
Materias primas
Producto en proceso
Producto terminado

3. LOGÍSTICA
Costo de mantener inventario
Costo de hacer pedido
Costo de faltantes

4. LOGÍSTICA
Tamaño de lote económico (EOQ)
Tamaño económico de producción (EPL)
Modelos con descuentos
Modelos multiproductos

5. LOGÍSTICA
Revisión continua: punto de reorden (Q,R)
Revisión periódica: (S,T)

6. LOGÍSTICA
Inventarios
Demanda
Determinística
Demanda
Probabilística
Demanda
Estática
Demanda
Dinámica
Revisión Continua
Punto de Reorden
Revisión Periódica
Período Fijo
Tamaño de Lote Económico EOQ
Lote Económico de Producción EPL
Lote Económico con Descuentos
Lote Económico con Faltantes
Lote Económico Múltiples Items
Heurísticas
Programación Dinámica
Programación Entera Mixta MIP
Modelos Niveles de Servicio
Modelo (Q,R)
Modelo del Vendedor de
Diarios
Modelo (S,T)
• Demanda independiente vs. dependiente
• Demanda determinista y estocástica
• Revisión Periódica o Continua

7. LOGÍSTICA
La empresa Rand esta dedicada a la distribución de varios productos entre estos ,
lámparas , sillas y mesas de madera , estos productos son distribuidos a diferentes
minoristas (50 tiendas pequeñas ) durante 300 días del año, esta empresa esta
ubicada en Kansas y dicha distribución se hace en pequeñas aldeas de este Estado.
• Uno de los productos de mayor rotación corresponde a las lámparas , las cuales
tienen una demanda mensual de 750 unidades según datos históricos. Sin embargo la
gerencia de Rand tiene un problema ; y es que los pedidos se realizan de forma
empírica y por dicha razón en muchas ocasiones o hay una gran cantidad de lámparas
en stock o hay veces que sencillamente no hay disponibles del mismo, por esta razón
se debe determinar cual es el tamaño del pedido optimo y con que frecuencia se
debe realizar dado que se de el menor costo posible .
• De acuerdo a la información anterior se debe tener en cuenta que el costo de
mantener una caja de lámparas es de 120 lo cual corresponde a a conceptos como
impuestos ,seguros , costo de capital etc y por otro lado el costo de realizar un pedido
es de 600. siendo asi el pedido demora 5 días en ser entregado

8. LOGÍSTICA
SOLUCION :
USAREMOS EL MODELO DEL LOTE EOQ (MODELO ECONOMICO A ORDENAR)
• Primero procederemos a calcular la demanda anual : 750 * 12 meses= 9000 lamps
• Sabemos que el costo de mantener un inventario es de 120 ( ch)
• Costo anual de pedido es de 600 (co)
• Días hábiles = 300
• Tiempo de entrega 5 días (m)
SOLUCION

9. LOGÍSTICA
SOLUCION :
Primero se determina el Q optimo a pedir:
• Q =
2∗𝐷∗𝐶𝑂
CH
• Q =
2∗9000∗600
120
• Q= 300 Unidades por pedido
SOLUCION

10. LOGÍSTICA
SOLUCION :
Calculamos el costo de mantenimiento anual del pedido
• CMA =1/2 *Q* CH
• CMA =1/2 *300* 120
• CMA = 18.000
• Calculamos el costo de orden anual
• COA= D/Q*CO
• COA= 9000/300*600
• COA= 18000

11. LOGÍSTICA
SOLUCION :
Calculamos el costo total anual del pedido
COA + CMA = 18000+ 18000
CT = 36000
EL COSTO TOTAL ANUAL CORRESPONDE A 36000 POR CADA PAQUETE DE 300
UNIDADES ( LAMPS)

12. LOGÍSTICA
SOLUCION :
Calculamos el punto de re- orden
R= d* m
R= 9000/300*5
R= 150
Esto indica que se deben pedir un nuevo lote cuando las existencias lleguen a 150
lamparas

13. LOGÍSTICA
SOLUCION :
Calculamos el tiempo de Ciclo
T= (Días hábiles * Q)/D
T= (300*300)/9000
T= 10
Esto indica que cada 10 días se debe colocar un pedido.

14. LOGÍSTICA
SOLUCION :
Que puede concluir usted?

15. LOGÍSTICA
SOLUCION :
Que puede concluir usted?

16. LOGÍSTICA
Sharp es una empresa comercializadora de agujas hipodérmicas indoloras en los
hospitales, desea reducir sus costos de inventario mediante la determinación del
número de agujas hipodérmicas que debe pedir en cada orden. La demanda anual es
de 1000 unidades, el costo de ordenar, es de 10 dólares por orden; y el costo de
manejo por unidad de año es 50 centavos de dólar. Utilizando estos datos calcule el
número optimo (Q*) de unidades por orden (N) en el tiempo transcurrido (T). Y el
costo total anual del inventario, utilice un año laboral de 250 días.
• Determine el Q optimo a pedir
• El tiempo transcurrido
• El costo total anual de inventario

17. LOGÍSTICA
SOLUCION :
Primero se determina el Q optimo a pedir:
• Q =
2∗𝐷∗𝐶𝑂
CH
• Q =
2∗1000∗10
0,50
• Q= 200 Unidades por pedido
SOLUCION

18. LOGÍSTICA
SOLUCION :
Calculamos el costo de mantenimiento anual del pedido
• CMA =1/2 *Q* CH
• CMA =1/2 *200* 0,50
• CMA = 50
• Calculamos el costo de orden anual
• COA= D/Q*CO
• COA= 1000/200*10
• COA= 50

19. LOGÍSTICA
SOLUCION :
Calculamos el costo total anual del pedido
COA + CMA = 50+ 50
CT = 100
EL COSTO TOTAL ANUAL CORRESPONDE A 100 dólares por cada 200 unidades y el
tiempo será:
200/1000= 0,2
0,2* 250= 50 dias

20. LOGÍSTICA
Suponga que R&B Beverage Company dispone de una bebida refrescante que muestra
una tasa anual de demanda constante de 3600 cajas. Una caja de bebida refrescante
cuesta $3. Los costos de ordenar es de $20 por pedido y los costos de retención
ascienden a 25% del valor del inventario. R&B labora 250 días por año y el tiempo de
espera es de 5 días. Identifique los siguientes aspectos de la política de inventario:
a. Cantidad económica del pedido
b. Punto de reorden
c. Tiempo de ciclo
d. Costo anual total

21. LOGÍSTICA
Westside Auto compra un componente utilizado en la fabricación de
generadores automotrices directamente con el proveedor. La operación de
producción de generadores de Westside, la cual funciona a un ritmo
constante, requerirá 1000 componentes por mes durante todo el año (12 000
unidades cada año). Suponga que los costos de ordenar son de $25 por
pedido, el costo unitario es de $2.50 por componente y los costos de
retención anuales son de 20% del valor del inventario. Westside labora 250
días por año y su tiempo de espera es de 5 días. Responda las siguientes
preguntas de política de inventario:
a. ¿Cuál es la EOQ de este componente?
b. ¿Cuál es el punto de reorden?
c. ¿Cuál es el tiempo del ciclo?
d. ¿Cuáles son los costos de retención y pedido anuales totales asociados
con su EOQ recomendada

22. LOGÍSTICA
• En este modelo, el empresario de dedica a la producción de
un bien.
• El lote económico es la cantidad de inventario que debe de
producirse, para satisfacer una demanda futura, de tal
manera que el costo total en que se incurre por: fabricar,
mantener el inventario y por pedidos pendientes sea el
mínimo posible.
• Es un modelo matemático para control de inventarios que
extiende el modelo de Cantidad Económica de Pedido a una
tasa finita de producción.

23. LOGÍSTICA
• Así, en este modelo la recepción de pedidos de inventario y la
producción y venta de productos finales ocurrirán de forma
simultánea, lo que lo diferencia del modelo de cantidad
económica de pedido.
• Su finalidad es encontrar el lote de producción de un único
producto para el cual los costos por emitir la orden de
producción y los costos por mantenerlo en inventario se
igualan
• A diferencia del modelo de cantidad económica de pedido,
este modelo es menos estático que el anterior, adaptándose
más a la realidad.

24. LOGÍSTICA
• Dicho modelo matemático consta de las siguientes formulas:
• Inventario Maximo = (p-d)t
• T = q/p días
• Inventario Maximo = 1/2(1-d/p)q
• Inventario promedio 1/2 (1-d/p ) Q
• Costo anual de retención= (Inventario promedio) (Costo
unitario total) Inventario promedio 1/2 (1-d/p ) QCh
• Costo de preparación anual = (Número de fases de producción
por año) (Costo de preparación por fase) D/Q*Co
• Costo total anual = 1/2 (1-d/p ) QCh + D/Q*Co
• Q =
2∗𝐷∗𝐶𝑂
1−
𝐷
𝑃
∗𝐶𝐻

25. LOGÍSTICA
• Se produce jabón de tocador en una línea de producción cuya
capacidad anual es de 60,000 cajas. La demanda anual se
estima en 26,000 cajas, con la tasa de demanda constante, en
esencia, a lo largo del año. La limpieza, preparación y puesta a
punto de la línea de producción cuesta aproximadamente
$135. El costo de fabricación por caja es de $4.50 y el costo de
retención anual se calculó a una tasa de 24%. Por tanto Ch IC
0.24($4.50) $1.08. ¿Cuál es el tamaño del lote de producción
recomendado?
• se obtiene Q =
2∗𝐷∗𝐶𝑂
1−
𝐷
𝑃
∗𝐶𝐻

26. LOGÍSTICA
• se obtiene Q =
2∗26000∗135
(1 −26,000/60,000)(1.08)
= 3387
• Se obtiene el costo total anual : $2073
• Otros datos pertinentes incluyen un tiempo de espera de
cinco días para programar y preparar una fase de producción
y 250 días hábiles por año. Por tanto, la demanda durante el
tiempo de espera de (26,000/250)(5) 520 cajas es el punto de
reorden. El tiempo de ciclo es el tiempo entre fases de
producción. Al utilizar la ecuación , el tiempo de ciclo es T
250Q*/D [(250)(3387)]/26,000, o 33 días hábiles. Por tanto,
tenemos que planear una fase de producción de 3387
unidades cada 33 días hábiles.