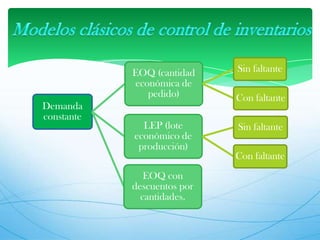
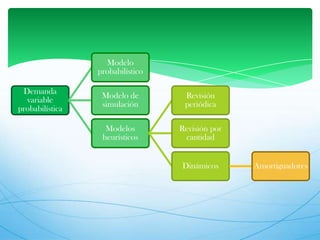
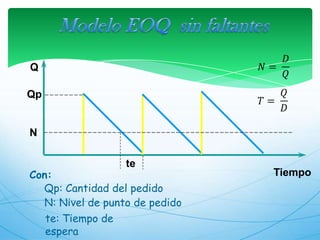
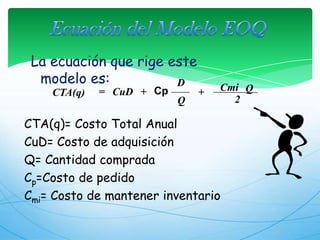
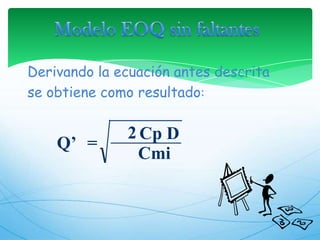
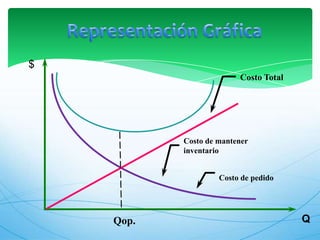
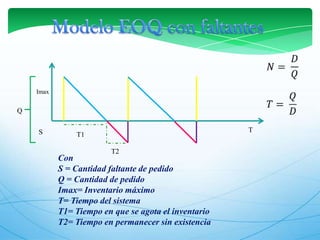
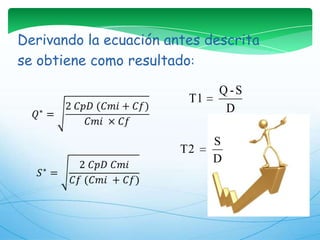
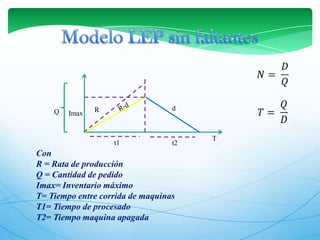
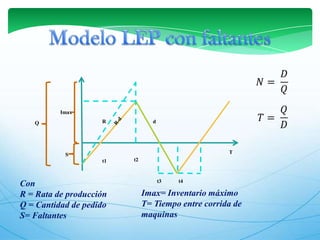
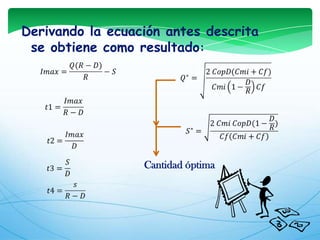
Este documento describe los modelos de gestión de inventarios EOQ y EPQ. El modelo EOQ se usa para determinar la cantidad económica de pedido cuando la demanda es constante. El modelo EPQ se usa cuando la producción es continua en lotes. Ambos modelos buscan minimizar los costos de pedido, mantenimiento e incumplimiento equilibrando esos factores.

1. GESTION DE INVENTARIOSGRACE ACOSTA VILLALOBOS Ingeniería Industrial VII semestre

2. Función de los InventariosAyudar a la independencia de operaciones - Continuidad de las variaciones de demandaDeterminar condiciones económicas de aprovisionamientoDeterminar la óptima secuencia de operacionesUso óptimo de la capacidad productiva

3. OPTICAS DEL INVENTARIO

4. Inventario según la demandaDemanda independiente: es una cantidad determinada por la necesidad de la población, es desconocida y define a la demanda dependiente.Demanda dependiente: es la cantidad de elementos que conforman un producto definido por la población (demanda independiente), en esta demanda se hace necesario emplear el MRP.

5. Modelos clásicos de control de inventarios

7. EOQ cantidad económica de pedido

8. SUPUESTOSDemanda conocida y constante. Tiempo de reposición son instantáneosExistencia de dos costos: Costo de pedir y Costo de mantenimiento del inventario No se admiten faltantesLos costos no varían en el tiempoRelación directa costo - volumen

9. MODELO EOQ SIN FALTANTES

10. QQpNteTiempoCon:Qp: Cantidad del pedidoN: Nivel de punto de pedidote: Tiempo de esperaModelo EOQ sin faltantes𝑁= 𝐷𝑄 𝑇= 𝑄𝐷

11. DCmiQ=CuD++CTA(q)2QEcuación del Modelo EOQLa ecuación que rige este modelo es: CpCTA(q)= Costo Total AnualCuD= Costo de adquisición Q= Cantidad compradaCp=Costo de pedidoCmi= Costo de mantener inventario

12. 2Cp DQ’=CmiModelo EOQ sin faltantesDerivando la ecuación antes descrita se obtiene como resultado:

13. Qop.Representación Gráfica$Costo TotalCosto de mantener inventarioCosto de pedidoQ

14. MODELO EOQ con faltantes

15. Modelo EOQ con faltantes𝑁= 𝐷𝑄 Imax𝑇= 𝑄𝐷 QTST1T2Con S = Cantidad faltante de pedido Q = Cantidad de pedido Imax= Inventario máximo T= Tiempo del sistemaT1= Tiempo en que se agota el inventarioT2= Tiempo en permanecer sin existencia

16. Ecuación del Modelo EOQ con faltantes𝐶𝑇𝐴 𝑞;𝑠=𝐶𝑢𝐷+ 𝐶𝑝 𝐷𝑄+𝐶𝑚𝑖 (𝑄−𝑆)22 𝑄 +𝑆2𝐶𝑓2𝑄 CTA(q; s)= Costo Total AnualCuD= Costo de adquisición Q= Cantidad compradaS= Cantidad faltanteCp=Costo de pedidoCmi= Costo de mantener inventarioCf= Costo de faltante

17. Derivando la ecuación antes descrita se obtiene como resultado:𝑄∗=2 𝐶𝑝𝐷 (𝐶𝑚𝑖+𝐶𝑓)𝐶𝑚𝑖 ×𝐶𝑓 𝑆∗=2 𝐶𝑝𝐷 𝐶𝑚𝑖𝐶𝑓 (𝐶𝑚𝑖 +𝐶𝑓)

18. Lote económico de producción LEP

19. EPQ: (lote económico de producción)Los artículos se producen y se adicionan al inventario gradualmente en lugar de un solo pedido. El modelo EPQ asume entregas graduales continuas al inventario (tasa de reemplazo finita) a lo largo del periodo de producción. Con una tasa de reemplazo finita, el nivel de inventario nunca será del tamaño del lote de producción dado que la producción y el consumo ocurren simultáneamente durante el período de producción.

20. Supuestos del modelo del Lote de producción económicaLa demanda es constante.La tasa producción es mayor que la Demanda.El lote de producción no es recibido instantáneamente (a un valor infinito), la tasa producción es finita. Hay un único producto a considerarEl resto de suposiciones del modelo EOQ permanece iguales.

21. Modelo EPQ sin faltantes

22. Modelo LEP sin faltantes𝑁= 𝐷𝑄 R-d𝑇= 𝑄𝐷 dRQImaxTt1t2Con R = Rata de producción Q = Cantidad de pedido Imax= Inventario máximo T= Tiempo entre corrida de maquinasT1= Tiempo de procesadoT2= Tiempo maquina apagada

23. Ecuación modelo LEP sin faltantes𝐶𝑇𝐴𝑄=CuD+𝐶𝑜𝑝𝐷𝑄+𝐶𝑚𝑖21−𝑑𝑅𝑄 CTA(Q)= Costo Total AnualCuD= Costo de adquisición Q= Cantidad d= Demanda R= Rata de producción Cop=Costo de ordenar Cmi= Costo de mantener inventario

24. Derivando la ecuación antes descrita se obtiene como resultado:𝑄=𝑅×𝑡1 𝑡1=𝑄𝑅 𝐼𝑚𝑎𝑥=1−𝑑𝑅𝑄 𝑄∗=𝐶𝑜𝑝𝐷𝐶𝑚𝑖1−𝑑𝑅 Cantidad óptima

25. Modelo LEP con faltantes

26. Modelo LEP con faltantes𝑁= 𝐷𝑄 𝑇= 𝑄𝐷 ImaxR-dRdQTSt2t1t3t4Con R = Rata de producción Q = Cantidad de pedidoS= Faltantes Imax= Inventario máximo T= Tiempo entre corrida de maquinas

27. Ecuación modelo LEP con faltantes𝐶𝑇𝐴𝑄,𝑆=𝐶𝑢𝐷+𝐶𝑜𝑝𝐷𝑄+𝐶𝑚𝑖𝑄1−𝐷𝑅2−𝐶𝑚𝑖𝑆+𝑆22𝑄1−𝐷𝑅𝐶𝑚𝑖+𝐶𝑓 CTA(Q,S)= Costo Total AnualCuD= Costo de adquisición Q= Cantidad D= Demanda R= Rata de producción S= FaltanteCop=Costo de ordenar un pedidoCmi= Costo de mantener inventarioCf= Costo de faltante

28. Derivando la ecuación antes descrita se obtiene como resultado:𝐼𝑚𝑎𝑥=𝑄(𝑅−𝐷)𝑅−𝑆 𝑄∗=2 𝐶𝑜𝑝𝐷(𝐶𝑚𝑖+𝐶𝑓)𝐶𝑚𝑖1−𝐷𝑅𝐶𝑓 𝑡1=𝐼𝑚𝑎𝑥𝑅−𝐷 𝑆∗=2 𝐶𝑚𝑖 𝐶𝑜𝑝𝐷(1−𝐷𝑅)𝐶𝑓𝐶𝑚𝑖+𝐶𝑓 𝑡2=𝐼𝑚𝑎𝑥𝐷 𝑡3=𝑆𝐷 Cantidad óptima𝑡4=𝑠𝑅−𝐷