El documento habla sobre los tipos de ítems para evaluar el manejo del vocabulario. Explica que el objetivo es medir la competencia del postulante en el uso del léxico. Describe los tres tipos de ítems: semánticos (basados en el significado de las palabras), lógicos (por razonamiento deductivo) y gramaticales (por categorías gramaticales). Proporciona ejemplos de ítems y su clasificación.








































![41
A) 4 B) 16 C) 1024
D) 2 E) 256
15. Halla el número total de palabras “SABIDURÍA”
A) 512 B) 128 C) 256
D) 64 E) 258
16. La figura muestra un triángulo, formado por
circunferencias iguales, contándose 570 puntos de
contacto. Hallar el número total de filas del siguiente
arreglo.
A) 17 B) 18 C) 20
D) 21 E) 25
17. ¿Cuántos triángulos pequeños hay en total?
A) 996 B) 840 C) 1905
D) 3125 E) 1225
12. Determina todos los enteros n tales que
nn
4
625
2
25
4
625
2
25
,
Es entero.
A) 144 B) 1447 C) 1008
D) 30 E) 1232
TERCERA SEMANA
OPERADORES MATEMATICOS
OPERACIÓN MATEMÁTICA
Es un proceso que consiste en la transformación
de una o más cantidades en otra llamada
resultado, bajo ciertas reglas o condiciones en la
cual se define la operación. Toda operación
matemática presenta una regla de definición y
un símbolo que la identifica llamado operador
matemático.
OPERADOR MATEMÁTICO
Es aquel símbolo que representa a una
operación matemática. Nos permite reconocer a
la operación matemática a realizar con su
respectiva regla de definición:
nIntegració
LimLímites
][enteroMáximo
|P|aProductori
Sumatoria
||absolutoValor
Radicación
División
ciónMultiplica
nSustracció
Adición
Matemático
Operador
Matemática
Operación
Las operaciones matemáticas arriba mencionadas
son conocidas universalmente.
En el presente capítulo lo que hacemos es definir
operaciones matemáticas con operadores y reglas
de definición elegidos de forma arbitraria.
El operador matemático puede ser cualquier
símbolo (incluso figuras geométricas).
Ejemplo:
* ; # ; ; ; ; ; ; .......
Las reglas de operación se basan en las
operaciones matemáticas ya definidas, veamos
los siguientes ejemplos:](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-41-320.jpg)
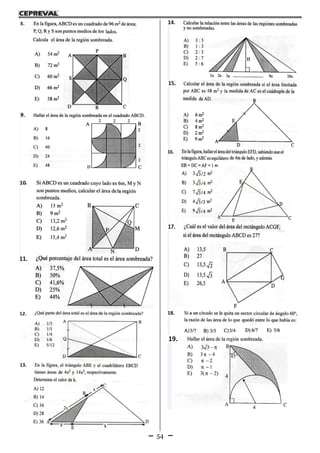
![42
a b = 3a 2b + 5 2
Operador
Matemático
Regla de
definición
REPRESENTACIÓN DE UNA OPERACIÓN
MATEMÁTICA:
Una operación matemática se puede representar
con una regla de definición, mediante una fórmula
o una tabla de doble entrada.
A. MEDIANTE FÓRMULA:
En este caso, la regla de definición está
representada por una fórmula, en la cual
solamente hay que reconocer los elementos y
reemplazarlos en la regla de definición para
obtener el resultado buscado.
El reemplazo del valor numérico de los
elementos en la regla de definición puede ser un
reemplazo directo (como en el ejemplo 1), o
puede ser un problema que primero hay que
darle forma al valor numérico que nos piden
para luego recién reconocer los elementos y
reemplazar en la regla de definición.
Operaciones matemáticas con regla de
definición Implícita.
Son aquellas operaciones en los cuales la regla
de definición no ha sido definida de manera
explícita, por lo que hay que darle una forma de
definición a lo que nos pide; para
posteriormente reemplazar y operar los datos.
PROBLEMAS
1. Si: P # Q = 3P2 + P, Calcular:
4 # [5 # (4 # (5 # .........)]
A) 52 B) 48 C) 50
D) 46 E) 13
2. Si: 1x = x2
– 1
Calcular: A = 2 - 1
A) 0 B) –1 C) 1
D) 2 E) 3
3. Se define:
x =
2x
4x
además: a =
7
11
Hallar: 3a - 5
A) 5/3 B) 5/2 C) 7/2
D) 1 E) 4/3
4. Si: ab
ba
= 2
b
2
b
ba
Calcular: 81 64
A) 25 B) 5 C) 6
D) 36 E) 7
5. Se define:
m n =
nm0
nm
nm
nm
22
;
;
Si: 5 x = 2 [1 (-2 3)], donde:
x 5. ¿Cuál es el valor de “x”?
A) 0 B) 1 C) –3
D) 3 E) 2
6. Se define: a * b = a2
+ 2a + b0
, hallar:
20072005975E *.....***
A) 5 B) 35 C) 6
D) 7 E) 8
7. Si:
A* = A2
+ A; A0
= A2
+ A +1;
además:
A
156
A *
Determinar uno de los valores de “A”
A) 1 B) 2 C) 3
D) 4 E) 5
8.Si: (a + 3) * (b – 2) = 3a2
+ b
Hallar: 5 * 12](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-42-320.jpg)


![45
x = (30*42)/((2*6)*(12*20)) es:
A)10 B) 12 C) 7
D) 13 E)11
31.Se define:
x =
2x
4x
además:
a =
7
11
Hallar: 3 a - 5
A) 5/3 B) 5/2 C) 7/2
D) 1 E) 4/3
32. Si: ab
ba
= 2
b
2
b
ba
Calcular: 81 64
A) 25 B) 5 C) 6
D) 36 E) 7
33. Se define:
m n =
nm0
nm
nm
nm
22
;
;
Si: 5 x = 2 [1 (-2 3)], donde:
x 5. ¿Cuál es el valor de “x”?
A) 0 B) 1 C) –3
D) 3 E) 2
34. Se define: a * b = a2
+ 2a + b0
, halla:
20072005975E *.....***
A) 5 B) 35 C) 6
D) 7 E) 8
35. Si:
x = 2x2
- 3x – 13
P = 1 + 2 - 0
3 + -1
Hallar: P
A) 14 B) –14 C) 13
D) –13 E) –8
OPERADOR BINARIO
Operaciones matemáticas que no tienen regla de
definición Explícita ni Implícita.
En este caso se tiene que hacer uso de mucha
creatividad e ingenio, pues el resultado se puede
obtener de muchas maneras (realizando ciertas
operaciones).
OPERADOR BINARIO
Es aquella operación matemática que relaciona
dos elementos de un conjunto para obtener un
nuevo elemento.
Una operación binaria es "CERRADA" cuando el
resultado obtenido es un elemento del conjunto en
el cual se definió la operación, en caso contrario
se llamará "ABIERTA".
Operación Binaria
Clausura
Conmutativa Distributiva
Asociativa Elemento
neutro
Elemento
inverso
Operaciones en Tablas de Doble Entrada
Sea el siguiente conjunto no vacío
A = {a, b, c}, en el cual se define la operación
iguiente
tabla.
Fila de entrada
Columna
de entrada
cba
caba
cbab
bcac
Operador
Diagonal
Para operar se recomienda realizar la siguiente
operación:](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-45-320.jpg)


![48
A)
a
b
B)
c
b
c)
a
c
D)
b
c
E) No se puede
10. De acuerdo a la tabla adjunta: qué número
falta en el recuadro, si se cumple que:
( 4 6 ) www = 2
2 4 6
2 4 2 6
4 2 4 4
6 6 6 2
A) 2 B) 4 C) 6
D) 4 ó 6 E) cualquiera
11. De acuerdo a la tabla adjunta, qué número
falta en el recuadro, si se cumple que:
( 4 666 ) 4 = 2
1 2 4 8
1 4 8 2 2
2 8 1 8 4
4 2 8 4 1
8 2 4 1 2
A) 8 B) 4 C) 2
D) 1 E) ninguno
16. De acuerdo a las tablas adjuntas, determinar
qué número falta en el recuadro:
1 2 3 3 2 1
1 3 3 2 3 1 1 2
2 2 1 1 2 1 2 3
3 3 2 1 1 2 3 3
[ ( 3 2 ) 111 ] [ 1 ( 2 2 ) ] = 2
A) 1 B) 2 C) 3
D) 4 E) 5
19. Se define la operación * en el conjunto
M={a;b;c;d} mediante la siguiente tabla de
doble entrada:
* a b c d
a c b a b
b d a b c
c a B c d
d b C d a
Hallar el valor de “x” en la siguiente igualdad
a * b = x * c
A) a B) b C) c
D) d E) Otro valor
20. Con los elementos del conjunto
A{-2;-1;0;1;2} se define la operación:
a * b = ab + a + b, entonces el valor de “x” e
“y” en el cuadro de la figura adjunta es:
* -2 -1 0 1 2
-2 Y
-1 x
0
1
2
A) x = +1 ; y = -2 B) x = -2 ; y = -1
C) x = -1 ; y = -3 D) x = 1 ; y = 3
E) Otros valores
21.Si
Calcula: (4 * 40) + (3 * 13)
A)-14 B)-17 C)-13
D)-12 E)-15
22. Sea las operaciones por
Si: x = b # c, determine el valor de (c # x) @
(b # a)
A)a B)b C)c
D)d E)-1
13. Se define en A={1,5,8,10}
La operación matemática mediante
@ 8 10 1 5
8 5 8 10 1
10 8 10 1 5
1 10 1 5 8
5 1 5 8 10](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-48-320.jpg)














![65
FONOLOGÍA Y FONÉTICA
La fonética y la fonología son dos disciplinas de
las lingüísticas encargadas de estudiar los
sonidos del lenguaje.
1. FONOLOGÍA
Estudia a los sonidos del lenguaje a nivel de la
lengua. Su unidad mínima de estudio es el
fonema.
2. FONÉTICA
Es una disciplina auxiliar de la lingüística que
estudia los sonidos desde el punto de vista
articulatorio; es decir, en función del habla.
Analiza las propiedades acústicas (físicas) de
los sonidos y los procedimientos fisiológicos de
la formación de los sonidos: es decir la
articulación. Su mínima unidad de estudio es el
fono (sonido pronunciado).
EL APARATO FONADOR HUMANO
Se da este nombre al conjunto de órganos que
intervienen en la producción de la voz, al usar las
lenguas para comunicarnos en los distintos actos
del habla.
El aparato fonador se divide en tres zonas:
1. Zona infraglótica, inferior, espiración
Pulmones
Bronquios
Tráquea
2. Zona glótica, media, fonación
___________________
Cuerdas vocales
Glotis (no es un órgano sino el espacio
dejado por las cuerdas vocales)
3. Zona supraglótica, superior, articulación
Faringe
Cavidad bucal
Cavidad nasal
EL SISTEMA FONOLÓGICO DEL ESPAÑOL
A. LOS FONEMAS
Son unidades psíquicas, abstractas: están
en la mente del hablante. Se materializan
(se hacen concretos), cuando uno habla,
mediante los fonos; también, cuando uno
escribe, a través de los grafemas.
Son indivisibles.
Carecen de significado: un fonema solo no
significa nada.
Tiene valor distintivo: sirven para
diferenciar significados.
B. EL FONO
Es la materialización del fonema a través del
aparato fonador. El fono se representa entre [ ]
que significa que hablamos de un sonido
concreto (que se puede escuchar), material y
no de un fonema. Los fonos son ilimitados.
CUADRO COMPARATIVO
FONOLOGÍA FONÉTICA
Estudia el sonido
abstracto, ideal,
mental a nivel de la
lengua.
Su unidad de
estudio es el
fonema.
Le interesa el
fenómeno psíquico.
Su transcripción
siempre se hace
con barritas
oblicuas / /.
Son de número
limitado.
Estudia el sonido
concreto, real, y físico
a nivel del habla.
Su unidad de estudio
es el fono.
Le interesa lo
fisiológico y físico.
Su transcripción
siempre se hace con
los corchetes [ ].
Son de número
ilimitado.
Órganos de articulación
Órganos activos Órganos inactivos
Lengua:
………………
……………………
…………
………………
____________
____________
.
Los incisivos
___________
___________
___________](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-65-320.jpg)




















![87
los mensajes escritos. La puntuación organiza el
discurso y sus diferentes elementos y permite
evitar la ambigüedad en textos que, sin su
empleo, podrían tener interpretaciones diferentes.
El español cuenta con los siguientes signos de
puntuación:
1. El punto ( . )
2. Puntos suspensivos (...)
3. Corchetes [ ]
4. La coma ( , )
5. Signos de interrogación ¿?
6. Raya –
7. Punto y coma ( ;)
8. Dos puntos :
9. Signos de exclamación ¡!
10. Paréntesis ( )
11. Comillas " ", ´ `, « »
12. Cursivas y negritas
En esta oportunidad solo analizaremos la COMA y
el PUNTO Y COMA.
LA COMA
La coma presenta varios matices. Así pues, la
denominación que se le asigna será en función
al significado que encierra la unidad de
pensamiento.
A continuación los tipos de coma:
ENUMERATIVA
Existe enumeración cuando se mencionan, uno
a continuación del otro, los distintos
miembros integrantes de un conjunto.
EJEMPLOS
Una luz clara, limpia, diáfana, llenó la
habitación.
ELÍPTICA
Expresiones elípticas son aquellas en las que
se ha omitido una palabra o conjunto de
palabras cuyo sentido se sobrentiende. Esta
omisión se efectúa con el fin de evitar la
reiteración de algo que ya se ha dicho.
EJEMPLOS
Tú, a trabajar, y él, a descansar.
VOCATIVO
El vocativo es la palabra o frase que se refiere
a la persona o al ser personificado a quien
nos dirigimos.
EJEMPLOS
Acuérdate, Lucerito, acuérdate de
mí.
INCIDENTAL
Las expresiones incidentales vienen a ser
una palabra o un conjunto de palabras que
amplían, concretan o explican lo que se
dice. No son indispensables.
Las expresiones incidentales van entre
comas.
EJEMPLOS
Juan, que no se calla nada, me lo
contó.
IPERBÁTICA
Se da cuando alteramos el orden regular de
una oración e iniciamos esta con una
circunstancial, entonces este debe ir
seguido de una coma.
EJEMPLOS
Por la barba del viejo, cruzó un
estremecimiento.
CONJUNTIVA
Se utilizará la comas en algunas
conjunciones y frases conjuntivas:
Algunas conjunciones (claro, cierto,
seguramente, pues, etc.) y frases
conjuntivas (sin embargo, no obstante, es
verdad, es decir, vale decir, o sea, por
Funciones:
Sirve para dotar de significado a
un escrito.
Señala pausas respiratorias para
la lectura adecuada del texto.
Separa palabras.
Proporciona la entonación
adecuada tanto en la prosa
como en la poesía.
Separa expresiones con sentido incompleto,
pero lógicamente relacionadas entre sí.](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-87-320.jpg)














![104
SEMANA Nº 2 – (2)
PRODUCTOS NOTABLES
1. Binomio al cuadrado
2 2 2
(a b) a 2ab b
2 2 2
(a b) a 2ab b
2. Identidades de Legendre
2 2 2 2
2 2
(a b) (a b) 2(a b )
(a b) (a b) 4ab
3. Diferencia de cuadrados
2 2
(a b)(a b) a b
4. Binomio al cubo
3 3 2 2 3
3 3 3
(a b) a 3a b 3ab b
(a b) a b 3ab(a b)
5. Identidades de Steven
2
(x a)(x b) x (a b)x ab
6. Suma y diferencia de cubos
2 2 3 3
2 2 3 3
(a b)(a ab b ) a b
(a b)(a ab b ) a b
7. Trinomio al cuadrado
2 2 2 2
(a b c) a b c 2(ab ac bc)
8. Trinomio al cubo
3 3 3 3
(a b c) a b c
3(a b)(a c)(b c)
IDENTIDADES ADICIONALES
1. Identidad de Argan'd
2n n m 2m 2n n m 2m 4n
2n 2m 4m
(a a b b )(a a b b ) a
a b b
* Caso particular:
2 2 4 2
(x x 1)(x x 1) x x 1
2. Identidades de Lagrange
2 2 2 2 2 2
(a b )(x y ) (ax by) (ay bx)
2 2 2 2 2 2 2
2 2 2
(a b c )(x y z ) (ax by cz)
(ay bx) (az cx) (bz cy)
3. Identidad de Gauss
3 3 3 2 2 2
a b c 3abc (a b c)(a b c
ab ac bc)
De donde :
3 3 3 2
2 2
1
a b c 3abc (a b c)[(a b)
2
(b c) (c a) ]
4. Otras identidades:
4 4 2 2
2 2 2 2 2 2 2
(a b c)(ab ac bc) (a b).(a c).
(b c) abc
(a b) (a b) 8ab(a b )
(ab ac bc) a b a c b c
2abc(a b c)
ALGUNAS RELACIONES CONDICIONADAS
I. Si: a + b + c = 0
1. 2 2 2
a b c 2(ab ac bc)
2.
3 3 3
a b c 3abc
3.
4 4 4 2 2 2 21
a b c (a b c )
2
4. 5 5 5
a b c 5abc(ab ac bc)
II. Si: x; y; z є R
2 2 2
/ x y z xy yz zx
Entonces: x = y = z.
III. Si: x; y; z, є R, m; n;
p 2m 2m 2p
Z / x y z 0
Entonces: x = 0; y = 0; z = 0.](https://image.slidesharecdn.com/modulo1-140716200002-phpapp01/85/Modulo-1-cursos-generales-104-320.jpg)



















