El documento presenta los conceptos básicos de límites de funciones. Introduce los límites en un punto de manera intuitiva a través de ejemplos y tablas de valores. Luego define formalmente el límite en un punto estableciendo una relación entre ε y δ que garantice que la función f se aproxime al valor L cuando la variable x se aproxime a un punto x0. Finalmente, demuestra formalmente algunos límites aplicando esta definición rigurosa.


















![Moisés Villena Muñoz Cap. 1 Límites de Funciones
19
Ejercicios Propuestos 1.2
1. Demostrar formalmente utilizando la definición de límites laterales:
a. 0
lím
0
=
→
x
x
b. ( ) 3
lím
2
−
=
→
x
f
x
; si ( )
⎩
⎨
⎧
−
≥
−
=
2
,
4
5
2
,
7
2
x
x
x
x
x
f
c. ( ) 3
lím
2
=
→
x
f
x
; si ( )
⎩
⎨
⎧
+
≥
−
=
2
,
1
2
,
1
2
x
x
x
x
x
f
d. a b
( )
2
lím 2 3
x
x x
−
→
− =
e. a b
( )
3
lím 3 6
x
x x
+
→
− =
2. Demostrar formalmente que ( )
x
f
x 1
lím
→
no existe, si ( )
⎩
⎨
⎧
+
≥
−
=
1
,
2
1
,
1
3
x
x
x
x
x
f
3. Trace la gráfica y determine, por inspección, el límite indicado si existe, si no existe justifique.
a. ( )
⎪
⎩
⎪
⎨
⎧
=
−
=
1
,
3
1
,
1
1
,
2
x
x
x
x
f ; ( )
x
f
x 1
lím
→
b. ( )
2
2
x
f x
x
+
=
+
; ( )
2
lím
x
f x
→−
; ( )
2
lím
x
f x
→
c. ( )
⎩
⎨
⎧
−
≥
−
=
2
,
4
5
2
,
7
2
x
x
x
x
x
f ; ( )
x
f
x 2
lím
→
d. ( ) a b
f x x x
= − ; ( )
x
f
x −
→0
lím , ( )
0
lím
x
f x
+
→
e. ( )
a b
( )
( )
, 1
3 , 1 4
, 4
x x x
f x Sgn x x
x x
μ
⎧ + ≤ −
⎪
= − − ≤
⎨
⎪
⎩
; ( )
1
lím
x
f x
→−
( )
5
2
, lím
x
f x
→−
4. Bosqueje la gráfica de una función que cumpla las condiciones siguientes:
• R
f
Dom =
• f es decreciente en ( ) ( )
2
,
0
3
, ∪
−
−∞
• f es creciente en ( ) ( )
+∞
∪
− ,
2
0
,
3
• [ ]
ε
δ
δ
ε
−
⇒
−
−
∀
∃
∀ 2
)
(
3
0
,
0
0 x
f
x
x
• [ ]
ε
δ
δ
ε
⇒
+
∀
∃
∀ )
(
3
0
,
0
0 x
f
x
x
• [ ]
ε
δ
δ
ε
+
⇒
−
∀
∃
∀ 1
)
(
2
0
,
0
0 x
f
x
x
• ( ) ( ) 0
2
3 =
=
− f
f y 5
)
0
( =
f
5. Bosqueje el gráfico de una función que cumpla las condiciones siguientes:
• R
f
Dom =
• f es creciente en ( ) ( )
,0 0,3
−∞ ∪
• f decreciente en ( )
∞
,
3
• [ ]
ε
δ
δ
ε
−
⇒
−
∀
∃
∀ 3
)
(
0
,
0
0 x
f
x
x
• [ ]
ε
δ
δ
ε
⇒
∀
∃
∀ )
(
0
,
0
0 x
f
x
x
• [ ]
ε
δ
δ
ε
−
⇒
−
∀
∃
∀ 5
)
(
3
0
,
0
0 x
f
x
x
• ( ) ( ) 0
)
6
(
3
3 =
=
=
− f
f
f y 2
)
0
( =
f](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-19-320.jpg)
![Moisés Villena Muñoz Cap. 1 Límites de Funciones
20
1.3 TEOREMAS SOBRE LÍMITES
1.3.1 TEOREMA PRINCIPAL SOBRE LÍMITE
Sean f y g funciones con límite en 0
x ;
es decir, suponga que
0
lím ( )
x x
f x L
→
= y
0
lím ( )
x x
g x M
→
= . Entonces:
1.
0
lím
x x
k k
→
= , k R
∀ ∈
2.
0
0
lím
x x
x x
→
=
3.
0 0
lím ( ) lím ( )
x x x x
kf x k f x kL
→ →
= = , k R
∀ ∈
4. [ ]
0 0 0
lím ( ) ( ) lím ( ) lím ( )
x x x x x x
f x g x f x g x L M
→ → →
+ = + = +
5. [ ]
0 0 0
lím ( ) ( ) lím ( ) lím ( )
x x x x x x
f x g x f x g x L M
→ → →
− = − = −
6. [ ]
0 0 0
lím ( ) ( ) lím ( ) lím ( )
x x x x x x
f x g x f x g x LM
→ → →
= =
7. 0
0
0
lím ( )
( )
lím
( ) lím ( )
x x
x x
x x
f x
f x L
g x g x M
→
→
→
⎡ ⎤
= =
⎢ ⎥
⎣ ⎦
;siempre que
0
lím ( ) 0
x x
g x
→
≠
8. [ ]
0 0
lím ( ) lím ( )
n
n n
x x x x
f x f x L
→ →
⎡ ⎤
= =
⎢ ⎥
⎣ ⎦
, n N
∀ ∈
9.
0 0
lím ( ) lím ( ) n
n
n
x x x x
f x f x L
→ →
= =
siempre que
0
lím ( ) 0
x x
f x
→
≥ cuando n es par.
Demostraciones
1. ( )
0
0
lím 0, 0/ 0
x x
k k x x k k
ε ε
→
= ≡ ∀ ∃∂ − ∂ ⇒ −
El consecuente de la implicación es verdadero porque ε
0 . Por tanto, la proposición es siempre
verdadera.
2. ( )
0
0 0 0
lím 0, 0/ 0
x x
x x x x x x
ε ε
→
= ≡ ∀ ∃∂ − ∂ ⇒ −
Si ε
=
∂ la proposición es verdadera siempre.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-20-320.jpg)
![Moisés Villena Muñoz Cap. 1 Límites de Funciones
21
3. ( )
0
0
lím ( ) 0, 0/ 0 ( )
x x
kf x kL x x kf x kL
ε ε
→
= ≡ ∀ ∃∂ − ∂ ⇒ −
Observe el consecuente, la expresión ε
− kL
x
kf )
( es equivalente a
( ) ε
− L
x
f
k )
( .
Por hipótesis, en la cercanía de 0
x , f se aproxima a L , por tanto kf se aproximará a kL .
4. Debemos demostrar que si
L
x
f
x
x
=
→
)
(
lím
0
M
x
g
x
x
=
→
)
(
lím
0
entonces [ ] M
L
x
g
x
f
x
x
+
=
+
→
)
(
)
(
lím
0
Asegurar que L
x
f
x
x
=
→
)
(
lím
0
significa que:
1
1
0
1
1 )
(
0
0
,
0 ε
ε
−
⇒
∂
−
∃∂
∀ L
x
f
x
x
que
tal
Y asegurar que M
x
g
x
x
=
→
)
(
lím
0
significa que:
2
2
0
2
2 )
(
0
0
,
0 ε
ε
−
⇒
∂
−
∃∂
∀ M
x
g
x
x
que
tal
Lo cual quiere decir si tomamos
2
2
1
ε
ε
ε =
= y { }
2
1,∂
∂
=
∂ min tenemos:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
−
⇒
∂
−
∃∂
∀
2
)
(
2
)
(
0
/
0
,
0 0
ε
ε
ε
M
x
g
L
x
f
x
x
Sumando término a término la desigualdad resulta:
2
2
)
(
)
(
ε
ε
+
−
+
− M
x
g
L
x
f
Y por la desigualdad triangular ( ) ( ) M
x
g
L
x
f
M
x
g
L
x
f −
+
−
≤
−
+
− )
(
)
(
)
(
)
(
Por lo tanto ( ) ( ) ε
+
−
+ M
L
x
g
x
f )
(
)
(
Finalmente, se observar que:
( ) ( ) ε
ε
+
−
+
⇒
∂
−
∃∂
∀ M
L
x
g
x
f
x
x )
(
)
(
0
/
0
,
0 0
lo que nos asegura que [ ] M
L
x
g
x
f
x
x
+
=
+
→
)
(
)
(
lím
0
El resto de las demostraciones se deja como ejercicio para el lector.
Observe que el recíproco del teorema anterior es falso.
Ejemplo
Suponga que se tiene
⎩
⎨
⎧
≤
=
0
;
0
0
;
1
)
(
x
x
x
f y
⎩
⎨
⎧
≥
=
0
;
1
0
;
0
)
(
x
x
x
g
entonces ( )
⎩
⎨
⎧
=
≠
=
+
0
;
0
0
;
1
)
(
x
x
x
g
f
Observe que:
0
lím ( )
x
f x
→
no existe y que
0
lím ( )
x
g x
→
tampoco existe, sin embargo ( )
0
lím ( ) 1
x
f g x
→
+ =
(existe). Es decir, “ Si ( )
g
f + es una función con límite en un punto, entonces no podemos
asegurar que f y g también tienen límite en ese punto”](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-21-320.jpg)
































![Moisés Villena Muñoz Cap. 1 Límites de Funciones
54
4.
2
2
7
1
lim
49
x
x
x
−
→−
+
−
5.
2
4
16
lim
4
x
x
x
+
→
−
−
9. lim 1 2
x
x
→−∞
−
10.
5
1
lim
x
x
x
→∞
+
4. Bosqueje la gráfica de una función que cumpla con lo siguiente:
• ( ) [ ] ( )
+∞
∪
−
∪
−
−∞
= ,
2
1
,
1
2
,
f
Dom
• 1
1
0
)
( −
=
∨
=
⇔
= x
x
x
f
• [ ]
N
x
f
x
N
⇒
∂
−
−
∃∂
∀ )
(
2
0
0
,
0
• [ ]
N
x
f
x
N
⇒
∂
−
∃∂
∀ )
(
2
0
0
,
0
• [ ]
ε
ε
−
⇒
∃
∀ 1
)
(
0
,
0 x
f
M
x
M
• [ ]
ε
ε
−
⇒
−
∃
∀ 1
)
(
0
,
0 x
f
M
x
M
• 1
)
0
( =
f
5. Bosqueje el gráfico de una función que satisfaga las condiciones siguientes:
• [ ]
ε
ε
−
⇒
∂
∀
∃∂
∀ 1
)
(
0
,
0
0 x
f
x
x
• [ ]
ε
ε
+
⇒
∂
−
∀
∃∂
∀ 1
)
(
0
,
0
0 x
f
x
x
• [ ]
ε
ε
⇒
∀
∃
∀ )
(
,
0
0 x
f
N
x
x
N
• [ ]
M
x
f
x
x
M
⇒
∂
+
∀
∃∂
∀ )
(
1
0
,
0
0
• 0
)
0
( =
f
Misceláneos
1. Califique cada una de las proposiciones siguientes como verdadera o falsa. Justifique formalmente.
1. Si 3
2
5
)
(
lím
2
=
−
−
+
→
x
x
f
x
, entonces 0
)
(
lím
2
=
+
→
x
f
x
2. Si f y g son funciones tales que 1
)
(
lím
0
=
+
→
x
f
x
y ∞
=
+
→
)
(
lím
0
x
g
x
, entonces
1
)
(
lím )
(
0
=
+
→
x
g
x
x
f
3. Sea f una función de variable real tal que )
(
lím x
f
a
x +
→
existe y 1
)
(
lím =
−
+
→
x
f
a
x
a
x
. Entonces
0
)
(
lím =
+
→
x
f
a
x
.
4. Sean f y g funciones tales que ∞
=
+
→
)
(
lím x
f
a
x
y ∞
=
+
→
)
(
lím x
g
a
x
. Entonces el
)
(
)
(
lím
x
g
x
f
a
x +
→
no existe.
5. Sean f y g funciones tales que e
x
g
a
x
=
+
→
)
(
lím y ( )
)
(
ln
)
( x
g
x
f = . Entonces
( ) 1
)
(
lím =
+
→
x
g
f
a
x
D
6. Si 1
)
(
lím
0
=
+
→
x
x
f
x
entonces 0
)
(
lím
0
=
+
→
x
f
x
7. Si [ ]
)
(
)
(
lím x
g
x
f
a
x
+
→
existe, entonces existen )
(
lím x
f
a
x→
y ( )
x
g
a
x→
lím
8. Si ( )
x
g
x
f ≠
)
( para toda x , entonces ( )
x
g
x
f a
x
a
x →
→
≠ lím
)
(
lím
9. Si ⎥
⎦
⎤
⎢
⎣
⎡
→
)
(
)
(
lím
x
g
x
f
a
x
existe y 0
)
(
lím =
→
x
f
a
x
entonces 0
)
(
lím =
→
x
g
a
x
10. Si f y g son funciones definidas en IR entonces:
( )
( )
)
(
lím
))
(
(
lím x
g
f
x
g
f
IR
a a
x
a
x →
→
=
∈
∀](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-54-320.jpg)
![Moisés Villena Muñoz Cap. 1 Límites de Funciones
55
11. Si
a
x
a
a
x
x
a
x
−
−
−
−
+
→
2
2
lím existe entonces 0
=
a .
12. Si [ ]
)
(
)
(
lím x
g
x
f
a
x→
existe y )
(
lím x
f
a
x→
existe entonces )
(
lím x
g
a
x→
existe.
13. Si +∞
=
→
)
(
lím x
f
a
x
entonces −∞
=
−
→
)
(
lím x
f
a
x
14. ( )
( ) ( )
1
lím 3 1 2 0, 0, 0 1 3 1 2
x
x x x x
ε ε
→
⎡ ⎤
− = ⇔ ∀ ∃∂ ∀ − ∂ ⇒ − −
⎣ ⎦
15. Si 0
)
(
lím
0
=
+
→
x
f
x
y ∞
=
+
→
)
(
lím
0
x
g
x
entonces 0
)
(
)
(
lím
0
=
+
→
x
g
x
f
x
.
16. Existen dos funciones de variable real f y g tales que 0
)
(
lím
)
(
lím
0
0
=
=
+
→
+
→
x
g
x
f
x
x
y
e
x
g
x
f
x
=
+
→ )
(
)
(
lím
0
17. Si lím ( ) 0
x
f x
→∞
= y
( )
lím 2
( )
x
f x
g x
→∞
⎛ ⎞
=
⎜ ⎟
⎝ ⎠
entonces lím ( ) 0
x
g x
→∞
=
18. No existen dos funciones f y g tales que
0
lím ( ) 0
x
f x
→
= ,
0
lím ( ) 0
x
g x
→
= y
0
( )
lím 5
( )
x
f x
g x
→
=
19. Si 3
)
(
lím =
→
x
f
a
x
, 2
)
(
lím −
=
→
x
g
a
x
, entonces
1
)
(
)
(
1
)
(
)
(
lím
3 −
+
−
+
→ x
g
x
f
x
g
x
f
a
x
=1
2. Empleando la definición de límite, demuestre que:
1.
2
1
2 1
lím 3
1
x
x x
x
+
→
− −
=
−
2. 2
1
lím
5
=
−
+
→
x
x
3. 0
3
lím
3
=
−
+
→
x
x
4. 2
2
4
lím
4
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
→
x
x
5. 4
2
4
lím
2
2
−
=
+
−
+
−
→
x
x
x
3. Determine
1.
2
3
lím 2
x
x x
+
→
+
c f
d g
e h
2.
x
x
e x
x
4
sen
2
cos
lím
3
0
−
+
→
3. 2
0
3
cos
cos
lím
x
x
x
x
−
+
→
4.
x
x x
x
3
5
2
3
2
lím ⎥
⎦
⎤
⎢
⎣
⎡
−
+
+∞
→
5.
1
lím
2
1 −
−
+
→ x
e
xex
x
6.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
− π
+
π
→ 2
2
cos
lím
x
x
x
7.
tan
4
2
3
lím 4
2
x
x
x
π
+
→
⎛ ⎞
−
⎜ ⎟
⎝ ⎠
8. 3
2arctan
lím
1
x
x
x
e
π
→∞
⎡ ⎤
−
⎢ ⎥
⎢ ⎥
−
⎣ ⎦
9. ( )
2
tan 2
4
lím sen 2
x
x
x
π +
→
20. ⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
+
∞
→
x
x
x
x
sen
1
sen
lím
21.
( )
2
1
arctan arctan1
lím
1
x
x
x
+
→
−
−
22.
1
2
1
lím
2
1
−
−
−
→
x
x
x
x
23.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
→ 2
1
2
1
2
1
arcsen
arcsen
lím
x
x
x
24.
0
sen
lím
x
x
x
+
→
25. a b
( )
0
lím Sgn( ) 1 ( 1)
x
x x x
μ
+
→
⎡ ⎤
+ + −
⎣ ⎦
26.
( )
x
x
x
sen
sen
lím
0+
→
27. a b a b
( )
0
lím
x
x x
→
+ −
28. ( ) ( )
2
lím tan x
x
x
π
π
→
−
29.
2
2
2 5
2
2
3
lím
1
x x
x x
x x
+ +
− −
→
⎛ ⎞
⎜ ⎟
+
⎝ ⎠](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-55-320.jpg)
![Moisés Villena Muñoz Cap. 1 Límites de Funciones
56
10.
x
x
e x
x
5
sen
3
cos
lím
2
0
−
→
11. ( ) ( )
lím ln 2 1 ln 2
x
x x
→+∞
⎡ + − + ⎤
⎣ ⎦
12.
2
lím arctan
1
x
x
x
→−∞
⎡ ⎤
⎛ ⎞
⎢ ⎥
⎜ ⎟
+
⎢ ⎥
⎝ ⎠
⎣ ⎦
13.
( )
x
e
lím
x
x
+
+∞
→
1
ln
14.
1
1
1
lím 2
2
1
−
−
−
−
+
→
x
x
x
x
15. ( )
sec
2
lím 1 cot
x
x
x
π +
→
+
16.
0
lím ( )
x
f x
→
donde
2
1 cos3
; 0
( ) 5 ; 0
sen10 tan
; 0
sen 2
x
x
x
f x x
x x
x
x
−
⎧
⎪
⎪
= =
⎨
⎪ −
⎪
⎩
17.
2 7
0
lím
sen 2 tan9
x x
x
e e
x x
+
→
−
+
18.
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
+
→ 1
1
1
1
lím
1 x
x
x
19. ⎟
⎠
⎞
⎜
⎝
⎛
−
+
→ x
x
x
x 2
cos
1
3
sen
lím
0
30. ( )
3
2 3 3
lím 1 1
x
x x x
→+∞
⎡ ⎤
+ − −
⎢ ⎥
⎣ ⎦
31.
( )
6
6
3
2
sen
lím
cos
x
x
x
π
π
→
⎛ ⎞
−
⎜ ⎟
⎜ ⎟
−
⎝ ⎠
32.
2
2 2
0
1 cos
lím
sen
x
x
x x
→
−
33. ( )
1
2ln
lím 1 2 x
x
x
→+∞
+
34. 3
64
8
lím
4
x
x
x
→
⎛ ⎞
−
⎜ ⎟
⎜ ⎟
−
⎝ ⎠
35.
1
2
0
1 5
lím
1 3
x
x
x
x
→
+
⎛ ⎞
⎜ ⎟
−
⎝ ⎠
36. ( )
0
lím 1 cos cot
x
x x
→
−
37.
5
2
0
cos2 1
lím
x
x
xe x x
x
−
→
⎛ ⎞
− − +
⎜ ⎟
⎝ ⎠
38.
3
0
cos2
lím
sen5
x
x
e x
x x
→
⎛ ⎞
−
⎜ ⎟
−
⎝ ⎠
39.
0
lím
1 1
x
x
x x
→
⎛ ⎞
⎜ ⎟
− − +
⎝ ⎠
40. ( )
3 3
lím 1
x
x x
→∞
+ −
41. lím
x
x
x a
x a
→∞
+
⎛ ⎞
⎜ ⎟
−
⎝ ⎠
4. Calcular )
(
lím
0
x
f
x +
→
si 1
)
(
x
x
f
para 0
≠
x
5. Bosqueje la gráfica de una función que cumpla con lo siguiente:
• ε
ε
−
⇒
∂
∃∂
∀ 3
)
(
0
:
0
,
0 x
f
x
• N
x
f
x
N
⇒
∂
+
∃∂
∀ )
(
3
0
:
0
,
0
• 0, 0 : 0 3 ( )
N x f x N
∀ ∃∂ − − ∂ ⇒ −
• ε
ε
−
⇒
∃
∀ 1
)
(
:
0
,
0 x
f
M
x
M
• 0, 0: ( )
M x M f x
ε ε
∀ ∃ − ⇒
6. Bosqueje la gráfica de una función que cumpla con lo siguiente:
• ( ) ( ) ( )
Dom , 1 1,1 1,
f = −∞ − ∪ − ∪ +∞
• [ ]
ε
ε
⇒
∂
∃∂
∀ )
(
0
0
,
0 x
f
x
• [ ]
M
x
f
x
M −
⇒
∂
−
∃∂
∀ )
(
1
0
0
,
0
• [ ]
M
x
f
x
M
⇒
∂
−
∃∂
∀ )
(
1
0
0
,
0
• [ ]
M
x
f
x
M
⇒
∂
+
∃∂
∀ )
(
1
0
0
,
0
• [ ]
ε
ε
+
⇒
∃
∀ 1
)
(
0
,
0 x
f
N
x
N
• [ ]
ε
ε
⇒
−
∃
∀ )
(
0
,
0 x
f
N
x
N](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-56-320.jpg)





![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
46
Demostración.
Demostremos lo siguiente:
Si f y g son funciones continuas en el punto 0
x entonces
g
f + también es continua en 0
x
Las hipótesis serían :
1
H )
(
)
( 0
0
x
f
x
f
lim
x
x
=
→
y
:
2
H )
(
)
( 0
0
x
g
x
g
lim
x
x
=
→
Como [ ] )
(
)
(
)
(
)
(
0
0
0
x
g
lim
x
f
lim
x
g
x
f
lim
x
x
x
x
x
x →
→
→
+
=
+ entonces [ ] )
(
)
(
)
(
)
( 0
0
0
x
g
x
f
x
g
x
f
lim
x
x
+
=
+
→
Es decir ( )
[ ] ( ) )
(
)
( 0
0
x
g
f
x
g
f
lim
x
x
+
=
+
→
Lo cual indica que la función g
f + también es continua en 0
x
Las demostraciones del resto del teorema se la dejamos como
ejercicio al lector.
2.3.2 Teorema del Límite de la composición.
Si f y g son funciones tales que
L
x
g
x
x
=
→
)
(
lím
0
y f es continua en L,
entonces )
(
))
(
(
lím
0
L
f
x
g
f
x
x
=
→
. En particular, si
g es continua en 0
x y f continua en
)
( 0
x
g entonces g
f D es continua en 0
x
En límites nos interesaba indicar si la función se aproximaba a un
punto, en cambio en continuidad estamos interesados, además, en
determinar si la función toma el valor correspondiente en ese punto. Esto
puede ocurrir en ambas direcciones de acercamiento, como lo acabamos
de definir, o en una sola dirección, como lo vamos a definir a continuación.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-62-320.jpg)


![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
49
2.4.2 CONTINUIDAD EN [ ]
b
a,
Una función f es continua en un intervalo
cerrado [ ]
b
a, si es continua en ( )
b
a, y
además continua a la derecha de a
( )
(
)
(
lím a
f
x
f
a
x
=
+
→
) y a la izquierda de b
( )
(
)
(
lím b
f
x
f
b
x
=
−
→
).
Ejemplo
Una función continua en [ ]
b
a,
2.4.3 CONTINUIDAD EN [ )
b
a,
Una función f es continua en un intervalo
semiabierto [ )
b
a, , si es continua en ( )
b
a, y
además continua a la derecha de a .
Ejemplo 1
Una función continua en [ )
b
a,](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-65-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
50
Ejemplo 2
Otra función continua en [ )
b
a,
2.4.4 CONTINUIDAD EN ( ]
b
a,
Una función f es continua en un intervalo
semiabierto ( ]
b
a, , si es continua en ( )
b
a, y
además continua a la izquierda de b.
Ejemplo 1
Ejemplo 2](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-66-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
51
Ahora analicemos los siguientes ejercicios resueltos.
Ejercicio resuelto 1
Hallar los valores de a y b para que
⎪
⎩
⎪
⎨
⎧
−
≤
≤
−
+
−
−
=
3
;
5
3
3
;
3
;
2
)
(
x
x
b
x
b
ax
x
a
x
x
f
sea continua en todo R .
SOLUCIÓN:
Note que las reglas de correspondencia que definen a f son lineales y por tanto f será continua en
los respectivos intervalos. Entonces debemos procurar que f sea continua en los puntos donde
cambia de regla de correspondencia, es decir en 3
−
=
x y en 3
=
x , lo que significa dos cosas:
1.
6
2
3
)
3
(
2
)
(
lím
)
2
(
lím
3
3
=
−
+
=
−
+
=
− +
−
−
→
−
→
b
a
b
a
a
b
ax
a
x
x
x
2.
5
15
3
)
3
(
5
)
3
(
)
5
(
lím
)
(
lím
3
3
−
=
−
=
−
/
=
/
+
−
=
+ +
−
→
→
a
a
b
b
a
x
b
b
ax
x
x
reemplazando el valor de a en la primera ecuación obtenida, resulta:
16
6
)
5
(
2
−
=
=
−
−
b
b
Es decir, que la función
⎪
⎩
⎪
⎨
⎧
−
−
≤
≤
−
−
−
−
+
=
3
;
5
16
3
3
;
16
5
3
;
5
2
)
(
x
x
x
x
x
x
x
f será continua en todo R .
Ejercicio resuelto 2
Analizar la continuidad de la función
6
9
)
(
−
−
=
x
x
x
f
SOLUCIÓN:
El asunto aquí es sinónimo de establecer el dominio natural. Entonces debemos resolver 0
6
9
≥
−
−
x
x
Por tanto, f tendrá gráfica sólo en el intervalo( ]
9
,
6 que será también su intervalo de continuidad.
Ejercicio resuelto 3
Bosqueje el gráfico de una función f que satisfaga las siguientes condiciones:
1. f es continua en ( ) ( ] ( )
+∞
∪
−
∪
−
−∞ ,
1
1
,
2
2
,
2. [ ]
ε
ε
−
⇒
−
∀
∃
∀ 2
)
(
,
0
,
0 x
f
N
x
x
N
3. [ ]
M
x
f
x
x
M −
⇒
∂
+
∀
∃∂
∀ )
(
2
0
,
0
,
0
4. [ ]
M
x
f
x
x
M
⇒
∂
−
∀
∃∂
∀ )
(
1
0
,
0
,
0
5. [ ]
M
x
f
N
x
x
N
M −
⇒
∀
∃
∀ )
(
,
0
,
0
6. [ ]
ε
ε
+
⇒
+
∂
−
∀
∃∂
∀ 2
)
(
0
2
,
0
,
0 x
f
x
x
7. [ ]
ε
ε
−
⇒
∂
−
∀
∃∂
∀ 2
)
(
1
0
,
0
,
0 x
f
x
x
8. 1
)
2
(
,
0
)
3
(
,
0
)
1
(
,
1
)
0
(
,
1
)
2
( =
=
=
−
=
=
− f
f
f
f
f](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-67-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
52
SOLUCIÓN:
Las condiciones dadas significan:
1. Intervalos de continuidad ( ) ( ] ( )
+∞
∪
−
∪
−
−∞ ,
1
1
,
2
2
,
2. 2
)
(
lím =
−∞
→
x
f
x
asíntota horizontal 2
=
y para x negativos.
3. −∞
=
+
−
→
)
(
lím
2
x
f
x
asíntota vertical 2
−
=
x por derecha
4. ∞
=
+
→
)
(
lím
1
x
f
x
asíntota vertical 1
=
x por derecha
5. −∞
=
∞
→
)
(
lím x
f
x
6. 2
)
(
lím
2
−
=
−
−
→
x
f
x
límite por izquierda de 2
−
=
x
7. 2
)
(
lím
1
=
−
→
x
f
x
límite por izquierda de 1
=
x
8. Puntos que pertenecen a f
Por tanto la grafica sería:
Ejercicios Propuestos 2.1
1. Grafique las funciones dadas y determine los puntos de discontinuidad e indique los intervalos de continuidad
1.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≤
≤
−
=
1
;
1
0
;
0
;
)
(
2
x
x
x
x
x
x
x
f
2.
4
16
)
(
2
−
−
=
x
x
x
f
3. )
2
(
)
2
(
)
( +
+
−
= x
Sgn
x
x
f μ
4. ⎥
⎦
⎤
⎢
⎣
⎡
+
=
2
1
)
( x
x
f
5. [ ] x
x
x
f −
=
)
(
6. [ ] ( )
π
π 2
,
2
;
)
( −
∈
= x
senx
x
f](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-68-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
53
2. Analice la continuidad de las siguientes funciones:
1.
x
sen
x
x
f
2
1
)
(
−
=
2.
3
2
1
)
(
2
+
+
=
x
x
x
h
3.
12
5
6
8
2
)
(
2
3
2
−
+
+
−
+
=
x
x
x
x
x
x
f
4.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
=
1
1
)
( 2
2
x
x
sen
x
f
3. Calcular el valor de A , si existe, para que
⎪
⎩
⎪
⎨
⎧
=
≠
=
0
;
0
;
)
(
x
A
x
x
senx
x
f sea continua en todo R .
4. Hallar los valores de a y b para que f sea continua en R .
1.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥
−
+
≤
=
4
;
6
2
4
1
;
1
;
)
(
2
x
x
x
b
ax
x
x
x
f
2.
⎪
⎩
⎪
⎨
⎧
≥
−
+
≤
=
4
;
2
4
1
;
1
;
)
(
x
x
x
b
ax
x
x
x
f
3.
⎪
⎩
⎪
⎨
⎧
≥
≤
+
+
=
2
;
3
2
1
;
1
;
1
)
(
x
x
x
b
ax
x
x
x
f
4. [ ]
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥
−
+
−
≤
−
=
2
;
2
2
;
cos
2
;
2
)
(
π
π
π
π
x
senx
x
bx
x
a
x
senx
x
f
5. Sean las funciones:
⎪
⎩
⎪
⎨
⎧
−
=
=
0
;
1
0
;
0
0
;
1
)
(
x
x
x
x
f y 2
1
)
( x
x
g +
=
Para que valores de x , es continua: a) ( )( )
x
g
f D b) ( )( )
x
f
g D
6. Determine el máximo valor de k para que la función:
⎥
⎦
⎤
⎢
⎣
⎡ −
= 2
)
( 2
x
x
f sea continua en el intervalo
[ )
k
+
3
,
3
7. Bosqueje el gráfico de una función f que satisfaga las siguientes condiciones:
ƒ ( ) [ )
+∞
∪
−
∞
−
= ,
0
1
,
Domf
ƒ [ ) ( ]
+∞
∪
= ,
,
1 e
e
rgf
ƒ 1
)
0
( =
f
ƒ [ ]
ε
ε
−
⇒
∀
∃
∀ e
x
f
N
x
x
N )
(
,
0
,
0
ƒ [ ]
M
x
f
x
x
M
⇒
+
−∂
∀
∃∂
∀ )
(
0
1
,
0
,
0
8. Bosqueje el gráfico de una función f que satisfaga las siguientes condiciones:
ƒ Dom f=IR,
ƒ 0
)
(
x
f para ( ] ( )
1
,
0
1
, ∪
−
−∞
∈
x
ƒ 1
)
(
0
)
1
(
)
0
(
1
)
1
(
0
=
∧
=
=
∧
=
− +
→
x
f
lím
f
f
f
x
ƒ [ ]
ε
ε
−
⇒
−
∀
∃
∀ 1
)
(
,
0
,
0 x
f
N
x
x
N
ƒ [ ]
ε
ε
+
⇒
∀
∃
∀ 1
)
(
,
0
,
0 x
f
N
x
x
N
ƒ [ ]
M
x
f
x
x
M
⇒
∂
−
∀
∃∂
∀ )
(
1
0
,
0
,
0
ƒ [ ]
M
x
f
x
x
M
⇒
∂
+
∀
∃∂
∀ )
(
1
0
,
0
,
0
ƒ [ ]
ε
ε
−
⇒
∂
−
∀
∃∂
∀ )
0
(
)
(
0
,
0
,
0 f
x
f
x
x
ƒ [ ]
ε
ε
⇒
∂
−
∀
∃∂
∀ )
(
1
0
,
0
,
0 x
f
x
x](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-69-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
54
9. Bosqueje el gráfico de una función f que satisfaga las siguientes condiciones:
ƒ f es continua en ( ) ( ]
10
,
2
2
,
5 ∪
−
ƒ 0
)
10
(
)
3
( =
= f
f
ƒ [ ]
ε
ε
−
⇒
∂
+
∀
∃∂
∀ 3
)
(
5
0
,
0
,
0 x
f
x
x
ƒ [ ]
M
x
f
x
x
M
⇒
∂
−
∀
∃∂
∀ )
(
2
0
,
0
,
0
ƒ [ ]
M
x
f
x
x
M −
⇒
∂
−
∀
∃∂
∀ )
(
2
0
,
0
,
0
10. Bosqueje el gráfico de una función f que satisfaga las siguientes condiciones:
ƒ f es continua en ( ] ( ) ( )
∞
∪
∪
−∞ ,
3
3
,
0
0
,
ƒ [ ]
ε
ε
⇒
−
∀
∃
∀ )
(
,
0
,
0 x
f
N
x
x
N
ƒ [ ]
ε
ε
−
⇒
∂
−
∀
∃∂
∀ 2
)
(
0
,
0
,
0 x
f
x
x
ƒ [ ]
M
x
f
x
x
M −
⇒
∂
∀
∃∂
∀ )
(
0
,
0
,
0
ƒ [ ]
M
x
f
x
x
M
⇒
∂
−
∀
∃∂
∀ )
(
3
0
,
0
,
0
ƒ [ ]
ε
ε
⇒
∂
−
∀
∃∂
∀ )
(
3
0
,
0
,
0 x
f
x
x
ƒ [ ]
ε
ε
+
⇒
∀
∃
∀ 1
)
(
,
0
,
0 x
f
N
x
x
N
ƒ 0
)
7
(
,
2
)
5
(
)
3
( =
=
= f
f
f
2.5 TEOREMA DEL VALOR INTERMEDIO PARA FUNCIONES
CONTINUAS
Sea f definida en el intervalo cerrado
[ ]
b
a, y sea w un número entre )
(a
f y
)
(b
f . Si f es continua en [ ]
b
a, entonces
existe al menos un número 0
x entre a y b
tal que w
x
f =
)
( 0 .](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-70-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
55
Ejemplo
Demuestre que la ecuación 0
2
3
3
=
−
+ x
x tiene una solución real entre 0 y 1.
SOLUCIÓN:
Definamos la función 2
3
)
( 3
−
+
= x
x
x
f .
Observamos que: 2
)
0
( −
=
f y 2
)
1
( =
f
y como f es continua en [ ]
1
,
0 , por ser polinómica; aplicando el Teorema del Valor Intermedio,
tenemos que si 0
=
w existirá un x elemento de [ ]
1
,
0 que lo satisfaga. Es decir: [ ]
1
,
0
∈
∃x tal que
0
2
3
)
( 3
=
−
+
= x
x
x
f
Ejercicios Propuestos 2.2
1. Enuncie y demuestre el teorema de Bolzano.
2. Enuncie y demuestre el teorema de Weierstrass.
3. Diga si son VERDADERAS o FALSAS las siguientes proposiciones. En caso de ser verdaderas demuéstrelas y
en caso de ser falsa, dé un contraejemplo.
a) Si f es continua y no tiene ceros en [ ]
b
a, , entonces 0
)
(
x
f para toda x en [ ]
b
a, o
0
)
(
x
f , ∈
∀x [ ]
b
a,
b) Si f es continua en 0
x y 0
)
( 0
x
f , hay un intervalo ( )
∂
+
∂
− 0
0 , x
x tal que 0
)
(
x
f en ese
intervalo.
c) El producto de dos funciones f y g es continua en 0
x ,si f es continua en 0
x pero g no.
d) Si f es continua en 0
x y g es discontinua en 0
x , entonces g
f + es discontinua en 0
x .
e) Toda función continua en ( )
b
a, es acotada.
f) Toda función acotada en [ ]
b
a, es continua en [ ]
b
a,
g) Si f es continua e inyectiva en [ ]
b
a, entonces su función inversa
1
−
f es continua en [ ]
b
a,
4. Demuestre que la ecuación: 0
1
3
4 3
5
=
+
−
− x
x
x tiene una solución en el intervalo [2,3].
5. Si el peso de un niño al nacer es de 8 libras y después de un año el mismo niño tiene un peso de 16 libras,
demuestre, empleando el teorema del valor intermedio para funciones continuas, que en algún instante de
tiempo el niño alcanzó un peso de 11 libras.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-71-320.jpg)
![Moisés Villena Muñoz Cap. 2 Continuidad de funciones
56
Misceláneos
1. Diga si son VERDADERAS o FALSAS las siguientes proposiciones. En caso de ser verdaderas demuéstrelas y
en caso de ser falsa, dé un contraejemplo.
a) )
(
lím
)
(
lím x
f
x
f
a
x
a
x −
+
→
→
= entonces f es continua en a
x = .
b) Si f y g son funciones continuas en a
x = entonces la función fg también es continua en a
x = .
c) La función de variable real con regla de correspondencia
⎪
⎩
⎪
⎨
⎧
≤
−
−
+
−
=
2
;
2
2
;
4
2
2
)
( 2
x
x
x
x
x
x
f es
continua en 2
=
x .
d) Si f es una función tal que IR
f
dom = y IR
a ∈
∀ )
(
lím x
f
a
x +
→
existe, entonces f es continua
en todo su dominio.
e) Si f es una función continua en [ ]
b
a, tal que 0
)
(
a
f y 0
)
(
b
f entonces existe al menos un
( )
b
a
c ,
∈ tal que 0
)
( =
c
f .
f) Si f es una función de IR en IR tal que [ ]
x
x
f sen
)
( = entonces f es continua en π
=
x .
g) Sea f una función continua en [ ]
b
a, tal que 0
)
(
)
(
• b
f
a
f entonces no existe un valor [ ]
b
a
c ,
∈
tal que 0
)
( =
c
f .
h) Si f y g son funciones que no son continuas en a
x = entonces la función g
f + no es continua en
a
x = .
i) La función
⎪
⎩
⎪
⎨
⎧
≥
−
−
=
2
;
2
2
;
1
)
( 2
x
x
x
x
x
x
f es continua en todo su domino.
j) Sea f una función de variable real con regla de correspondencia
⎪
⎩
⎪
⎨
⎧
=
≠
−
=
0
;
0
0
;
cos
1
)
( 2
x
x
x
x
x
f ,
entonces f es continua en todo su dominio.
2. Determine el valor de a para que
⎪
⎩
⎪
⎨
⎧
≥
−
π
−
=
π
π
2
2
;
1
;
cos
2
cot
)
(
x
ax
x
x
x
x
x
f sea continua en
2
π
=
x
3. Sea f una función de variable real tal que
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≥
−
−
−
−
+
−
≤
−
=
1
;
1
1
;
1
1
;
1
)
(
2
2
4
5
2
x
x
x
x
B
Ax
Bx
Ax
x
x
x
f
Determine los valores de A y B para que f sea continua en todos los reales.
4. Realice el bosquejo de la gráfica de una función f que satisfaga cada una de las siguientes proposiciones:
• f es continua en los intervalos ( )
0
,
−∞ ; [ ]
1
,
0 ; ( )
+∞
,
1 .
• 0
)
5
(
)
3
(
)
0
( =
=
= f
f
f 1
)
2
(
)
1
( =
= f
f
• 1
)
(
0
−
=
−
→
x
f
lim
x
−∞
=
−∞
→
)
(x
f
lim
x
• [ ]
N
x
f
x
N
⇒
δ
−
δ
∃
∀ )
(
1
0
0
0
• [ ]
ε
ε
−
⇒
∃
∀ 1
)
(
0
0 x
f
M
x
M
• ( )[ ]
0
)
(
5
,
3
∈
∀ x
f
x](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-72-320.jpg)


![Moisés Villena Muñoz Cap. 3 La derivada
85
La pendiente de la recta secante entre los puntos ( )
0 0
, ( )
x f x y
( )
0 0
, ( )
x h f x h
+ + sería
0 0
sec
( ) ( )
f x h f x
m
h
+ −
=
La pendiente de la recta tangente se obtendría haciendo que h se haga cada
vez más pequeña, porque en este caso la recta secante toma la posición de la
recta tangente, y resolveríamos nuestro problema; es decir:
0 0
tg
0
( ) ( )
lím
h
f x h f x
m
h
→
+ −
=
3.2 VELOCIDAD INSTANTÁNEA
Suponga que se tengan la ecuación del espacio e recorrido por un móvil, y
que sea función del tiempo; es decir ( )
e f t
= . Suponga ahora que se quiere
determinar la velocidad media m
v en un intervalo de tiempo [ ]
0 0
,
t t h
+ , esta
estaría dada por:
( ) ( )
0 0
0 0
m
f t h f t
e
v
t t h t
+ −
Δ
= =
Δ + −
La velocidad instantánea v sería la velocidad media calculada en intervalos de
tiempo t
Δ cada vez más pequeño; es decir:
x
y
0
x h
+
( )
0
f x
( )
y f x
=
0
x
( )
0
f x h
+
h
( ) ( )
0 0
f x h f x
+ −
N
N
Fig. 3.2](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-75-320.jpg)


![Moisés Villena Muñoz Cap. 3 La derivada
88
Ejemplo 1
Empleando la definición, hallar la derivada ( ) 2 1
f x x
= +
SOLUCIÓN:
( ) [ ]
0
0
0
0
0
( ) ( )
´( ) lím
2 1 2 1
lím
2 2 1 2 1
lím
2
lím
lím2
´( ) 2
h
h
h
h
h
f x h f x
f x
h
x h x
h
x h x
h
h
h
f x
→
→
→
→
→
+ −
=
+ + − +
⎡ ⎤
⎣ ⎦
=
+ + − −
=
=
=
=
Empleando la forma alternativa:
( ) ( )
( )
( )
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
( ) ( )
´( ) lím
2 1 2 1
lím
2 1 2 1
lím
2 2
lím
2
lím
lím 2
´( ) 2
x x
x x
x x
x x
x x
x x
f x f x
f x
x x
x x
x x
x x
x x
x x
x x
x x
x x
f x
→
→
→
→
→
→
−
=
−
+ − +
=
−
+ − −
=
−
−
=
−
−
=
−
=
=
Ejemplo. 2
Empleando la definición, hallar la derivada 2
( )
f x x
=
SOLUCIÓN:
( )
( )
( )
x
x
f
h
x
h
h
x
h
h
x
h
xh
x
h
x
h
x
h
x
f
h
x
f
x
f
h
h
h
h
h
2
)
´(
2
lím
2
lím
2
lím
lím
)
(
)
(
lím
)
´(
0
0
2
2
2
0
2
2
0
0
=
+
=
+
=
−
+
+
=
−
+
=
−
+
=
→
→
→
→
→](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-78-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
90
3.5 DIFERENCIABILIDAD
Se tratará ahora de especificar las condiciones para que la derivada de una
función de una variable real exista, lo cual dará paso a decir que la función será
derivable o diferenciable en un punto. La diferenciabilidad es equivalente a
derivabilidad para funciones de una variable real.
3.5.1 TEOREMA DE DERIVABILIDAD.
Si f es diferenciable en 0
x , es decir
)
´( 0
x
f existe, entonces f es continua en
0
x
Demostración.
Expresemos lo siguiente:
)
(
)
(
)
(
)
( 0
0 x
f
x
f
x
f
x
f +
−
=
Agrupando los dos primeros términos, dividiéndolo y multiplicándolo por ( )
0
x
x − , suponga 0
x x
≠ ,
tenemos:
( ) )
(
)
(
)
(
)
( 0
0
0
0
x
f
x
x
x
x
x
f
x
f
x
f +
−
−
−
=
Ahora, tomando límite a todos los miembros de la ecuación, resulta:
( ) )
(
)
(
)
(
)
( 0
0
0
0
0
0
0
0
x
f
lím
x
x
lím
x
x
x
f
x
f
lím
x
f
lím
x
x
x
x
x
x
x
x →
→
→
→
+
−
−
−
=
La expresión
0
0 )
(
)
(
0 x
x
x
f
x
f
lím
x
x −
−
→
es igual )
´( 0
x
f , debido a que de hipótesis se dice que f es
derivable en 0
x . Entonces:
( )
[ ]
)
(
)
(
)
(
0
)
(
0
)
´(
)
(
)
(
)
(
)
(
0
0
0
0
)
(
tan
0
0
0
)
´(
0
0
0
0
0
0
0
0
0
x
f
x
f
lím
x
f
x
f
x
f
x
f
lím
x
x
lím
x
x
x
f
x
f
lím
x
f
lím
x
x
x
f
te
cons
x
x
x
x
x
f
x
x
x
x
=
+
=
+
=
+
−
−
−
=
→
→
→
→
→
Por tanto, la última expresión indica que f es continua en 0
x . L.Q.Q.D.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-80-320.jpg)





![Moisés Villena Muñoz Cap. 3 La derivada
96
2. Sea ( )
f x x
= entonces:
( )
0 0
( ) lím lím 1
x
h h
x h x h
D x
h h
→ →
+ −
= = =
3. Sea ( ) n
f x x
= entonces:
( )
0
( ) lím
n n
n
x
h
x h x
D x
h
→
+ −
= . Consideraremos n∈` . Desarrollando el
binomio y simplificando:
( )
( )
( )
( )
( )
N
1
1 2 2 1
2
0 0
1
1 2 2 1
2
0
1
1 2 2 1
2
0
1
1 2 2
2
0
0 0
0
...
( ) lím lím
...
lím
...
lím
lím ...
n n
n n n n n n
n n
n
x
h h
n n
n n n n
h
n n
n n n n
h
n n
n n n
h
x nx h x h nxh h x
x h x
D x
h h
nx h x h nxh h
h
h nx x h nxh h
h
nx x h nxh
−
− − −
→ →
−
− − −
→
−
− − − −
→
−
− − −
→
⎡ ⎤
+ + + + + −
+ − ⎣ ⎦
= =
+ + + +
=
⎡ ⎤
/ + + + +
⎣ ⎦
=
/
= + + +
N
( )
1
0
1
( )
n
n n
x
h
D x n x
−
−
⎡ ⎤
⎢ ⎥
+
⎢ ⎥
⎣ ⎦
=
4. Sea ( ) x
f x e
= entonces:
( ) ( )
0 0 0 0
1
1 1
( ) lím lím lím lím
x h h
x h x x h x
x x x
x
h h h h
e e e
e e e e e
D e e e
h h h h
+
→ → → →
− −
− −
= = = = =
6. Sea ( ) ln
f x x
= entonces:
( )
x
x
D
e
x
h
x
h
h
x
h
h
x
h
x
h
x
h
x
x
D
x
x
h
h
h
h
h
h
x
x
x
h
1
)
(ln
ln
1
lím
ln
1
ln
lím
1
ln
lím
ln
lím
ln
ln
lím
)
(ln
1
1
0
1
0
0
0
0
1
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⎟
⎠
⎞
⎜
⎝
⎛ +
=
−
+
=
→
→
→
→
→
8. Sea ( )
f x sen x
= entonces:
[ ]
( ) ( )
x
x
D
x
x
h
x
h
x
h
x
h
x
h
x
x
h
x
x
x
h
x
h
x
x
D
x
h
h
h
h
h
h
h
x
cos
)
(sen
)
1
(
cos
)
0
(
sen
senh
lím
cos
)
1
(cosh
lím
sen
cos
senh
lím
)
1
(cosh
sen
lím
cos
senh
)
1
(cosh
sen
lím
sen
cos
senh
cosh
sen
lím
sen
)
sen(
lím
)
(sen
0
0
0
0
0
0
0
=
+
=
+
−
=
+
−
=
+
−
=
−
+
=
−
+
=
→
→
→
→
→
→
→
La demostración del resto de estas fórmulas se la dejamos para el lector.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-86-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
98
3.6.2 REGLAS DE DERIVACIÓN
Sean f y g funciones diferenciables y k una
constante, entonces:
1. ( ( )) ´( )
d
kf x kf x
dx
= (Múltiplo constante)
2. ( ( ) ( )) ´( ) ´( )
d
f x g x f x g x
dx
+ = + (Suma)
3. ( ( ) ( )) ´( ) ´( )
d
f x g x f x g x
dx
− = − (Resta)
4. ( ( ) ( )) ´( ) ( ) ( ) ´( )
d
f x g x f x g x f x g x
dx
= + (Producto)
5.
[ ]
2
( ) ´( ) ( ) ( ) ´( )
( ) ( )
d f x f x g x f x g x
dx g x g x
⎛ ⎞ −
=
⎜ ⎟
⎝ ⎠
(Cociente)
Demostración
La justificación de las dos primeras de estas reglas sería:
1.
[ ]
0
0
0
( ) ( )
( ( )) lím
( ) ( )
lím
( ) ( )
lím
´( )
h
h
h
d kf x h kf x
kf x
dx h
k f x h f x
h
f x h f x
k
h
kf x
→
→
→
+ −
=
+ −
=
+ −
=
=
2.
[ ] [ ]
[ ] [ ]
[ ] [ ]
0
0
0 0
( ) ( ) ( ) ( )
( ( ) ( )) lím
( ) ( ) ( ) ( )
lím
( ) ( ) ( ) ( )
lím lím
´( ) ´( )
h
h
h h
f x h g x h f x g x
d
f x g x
dx h
f x h f x g x h g x
h
f x h f x g x h g x
h h
f x g x
→
→
→ →
+ + + − +
+ =
+ − + + −
=
+ − + −
= +
= +
3.
[ ] [ ]
0
( ) ( ) ( ) ( )
( ( ) ( )) lím
h
f x h g x h f x g x
d
f x g x
dx h
→
+ + −
=
Al numerador le sumamos y restamos ( ) ( )
f x g x h
+
( ) ( ) ( ) ( )
0
( ) ( ) ( ) ( )
lím
h
f x h g x h f x g x f x g x h f x g x h
h
→
+ + − − + + +
Agrupando y aplicando propiedades de los límites:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-88-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
100
Para el caso del producto de tres funciones, la regla sería:
[ ]
( ) ( ) ( ) ´( ) ( ) ( ) ( ) ´( ) ( ) ( ) ( ) ´( )
d
f x g x h x f x g x h x f x g x h x f x g x h x
dx
= + +
¡Generalícela!
Ejemplo 5 (Derivada del producto)
Si ( ) ln
x
f x e senx x
= entonces
( )
´ ln ln ln
1
ln cos ln
x x x
x x x
d d d
f x e senx x e senx x e senx x
dx dx dx
e senx x e x x e senx
x
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
= + +
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
⎛ ⎞
= + + ⎜ ⎟
⎝ ⎠
Ejemplo 6 (Derivada de cociente)
Si ( )
2
3
2
1
x
f x
x
+
=
+
entonces
( )
( ) ( ) ( ) ( )
( )
( )( ) ( )( )
( )
( ) ( )
2 3 2 3
3 2 2
2 2
3 3
4 4 2 4 2
2 2
3 3
2 1 2 1 2 1 2 3
´
1 1
2 2 3 6 6 2
1 1
d d
x x x x x x x x
dx dx
f x
x x
x x x x x x x
x x
⎡ ⎤ ⎡ ⎤
+ + − + +
⎢ ⎥ ⎢ ⎥ + − +
⎣ ⎦ ⎣ ⎦
= =
+ +
+ − − − − +
= =
+ +
Con lo anterior, podemos resolver otros tipos problemas.
Ejemplo 7
Determine ( ),
0
f ′ si ( ) ( )( ) ( )
1 2 ... 100
f x x x x x
= + + + .
SOLUCIÓN:
La derivada de f sería
( ) ( )( )( ) ( ) ( )( ) ( ) ( )( ) ( )
´ 1 1 2 100 1 2 100 1 1 ... 100
f x x x x x x x x x x
= ⎡ + + + ⎤ + ⎡ + + ⎤ + ⎡ + + ⎤ +
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
Ahor
a evaluamos la derivada en cero:
( ) ( )( )( ) ( ) ( )( ) ( ) ( )( ) ( )
( ) ( )( ) ( )
0 0
´ 0 1 0 1 0 2 0 100 0 1 0 2 0 100 0 0 1 1 ... 0 100
´ 0 1 2 100 100!
f
f
= ⎡ + + + ⎤ + ⎡ + + ⎤ + ⎡ + + ⎤ +
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
= =](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-90-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
102
Estos valores los reemplazamos en
2
0 0 0
4
y x x
= + , y obtenemos los respectivos 0
y :
( ) ( )
2
0 3 4 3 9 12 3
y = − + − = − = −
( ) ( )
2
0 1 4 1 1 4 3
y = − + − = − = −
Por tanto, los puntos de tangencia son ( )
3, 3
− − y ( )
1, 3
− − .
Las respectivas pendientes serían:
( )
( )
2 3 4 2
2 1 4 2
tg
tg
m
m
= − + = −
= − + = +
Finalmente las ecuaciones de las rectas tangentes serían:
( ) ( )
( )
( )
3 2 3
3 2 3
2 9
y x
y x
y x
− − = − − −
+ = − +
= − −
y
( ) ( )
( )
( )
3 2 1
3 2 1
2 1
y x
y x
y x
− − = − −
+ = +
= −
Ejemplo 9
Si f , g y h son funciones tales que
( ) ( )
( )
2 ( ) 3 ( )
f x g x
h x
f x g x
=
+
, (1) 3
f = , (1) 3
g = − ,
´(1) 2
f = − , ´(1) 1
g = . Determine ´(1)
h .
Solución:
La derivada de h sería:
[ ][ ] [ ]
[ ]
[ ][ ] [ ]
[ ]
2
2
( ) ( )
´( )
2 ( ) 3 ( )
( ) ( ) 2 ( ) 3 ( ) ( ) ( ) 2 ( ) 3 ( )
2 ( ) 3 ( )
´( ) ( ) ( ) ´( ) 2 ( ) 3 ( ) ( ) ( ) 2 ´( ) 3 ´( )
2 ( ) 3 ( )
x
x x
f x g x
h x D
f x g x
D f x g x f x g x f x g x D f x g x
f x g x
f x g x f x g x f x g x f x g x f x g x
f x g x
⎡ ⎤
= ⎢ ⎥
+
⎣ ⎦
+ − +
=
+
+ + − +
=
+
Ahora evaluando en 1:
[ ][ ] [ ]
[ ]
[ ][ ] [ ]
[ ]
[ ][ ] [ ]
[ ]
[ ][ ] [ ]
[ ]
2
2
2
2
´(1) (1) (1) ´(1) 2 (1) 3 (1) (1) (1) 2 ´(1) 3 ´(1)
´(1)
2 (1) 3 (1)
( 2)( 3) (3)(1) 2(3) 3( 3) (3)( 3) 2( 2) 3(1)
2(3) 3( 3)
6 3 6 9 9 4 3
6 9
9 3 9 1
3
36
9
´(1) 4
f g f g f g f g f g
h
f g
h
+ + − +
=
+
− − + + − − − − +
=
+ −
+ − + − +
=
−
− + −
=
−
−
=
= −](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-92-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
104
4. Encuentre las ecuaciones de las rectas que contienen al punto ( )
2,5 y que son tangentes a la curva definida
por la ecuación
2
4
y x x
= − .
5. Determine las ecuaciones de las rectas tangentes a la función f definida por
3 2
( ) 2 3 24
f x x x x
= + − y
que son paralelas a la recta cuya ecuación es 0
7
12 =
+
− y
x .
6. Una partícula se desplaza de izquierda a derecha siguiendo una trayectoria definida por la ecuación
2
y x
= .
Determine el punto de la trayectoria para que la partícula se desplace ahora por la tangente de la trayectoria en
ese punto y logre alcanzar el punto (4,15).
7. Una partícula se desplaza de izquierda a derecha siguiendo una trayectoria definida por la ecuación
2
7 x
y −
= . Un observador se encuentra el punto (4,0). Encuentre la distancia cuando la persona observa la
partícula por primera vez.
8. Determine ( ),
0
f ′ si ( ) ( )( ) ( )
50
...
2
1 −
−
−
= x
x
x
x
x
f
9. Si f , g y h son funciones tales que
)
(
4
)
(
3
)
(
)
(
)
(
x
g
x
f
x
g
x
f
x
h
−
= , 2
)
3
( =
f , 2
)
3
( −
=
g , 1
)
3
´( −
=
f ,
2
)
3
´( =
g . Determine )
3
´(
h .
Para funciones compuestas disponemos de la regla de la cadena.
3.6.2.1 Regla de la Cadena
Sea ( )
y f u
= y ( )
u g x
= . Si g es
diferenciable en 0
x y f diferenciable
en ( )
0
g x entonces la función
compuesta ( )( ) ( )
( )
f g x f g x
=
D es
diferenciable en 0
x y
( ) [ ]
0
0 0
( )
( ( ) ´( ) ´( )
x x
g x
d
f g x f g x
dx =
=
O lo que es lo mismo
( )
u g x
dy dy du
dx du dx =
=
Ejemplo 1
Si ( )20
2
2
+
= x
y entonces haciendo 2
)
( 2
+
=
= x
x
g
u tenemos ( ) 20
u
u
f
y =
= de donde
19
20u
du
dy
= y x
dx
du
2
= .](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-94-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
105
Por tanto ( )( )
x
u
dx
du
du
dy
dx
dy
2
20 19
=
= que al reemplazar u resulta
( )
( )( ) ( )19
2
19
2
2
40
2
2
20 +
=
+
= x
x
x
x
dx
dy
El ejemplo anterior fue resuelto con un enfoque de cambio de variable para
observar la regla de cadena. Pero en la práctica esto no es necesario, la regla de
la cadena puede ser aplicada de manera rápida.
Ejemplo 2
Si ( )
u
x
x
sen
y 3
3
−
= entonces ( ) ( ) ( )
[ ][ ]
3
3
3
cos
3
´ 2
3
3
−
−
=
−
= x
x
x
x
x
D
senu
D
y x
u
Ejemplo 3
Si
30
2
2
3
1
3
u
x
x
x
x
y
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
+
= entonces
( )( ) ( )( )
( )
29
3 2 3 2
2 2
29 2 2 3 2
3 2
2 2
2
3 3
´ 30
1 1
3 6 1 1 3 2
3
30
1 1
x
x x x x x x
y D
x x
x x x x x x x
x x x
x x
⎡ ⎤ ⎡ ⎤
+ + + +
= ⎢ ⎥ ⎢ ⎥
− −
⎣ ⎦ ⎣ ⎦
⎡ ⎤
+ + − − + +
⎡ ⎤
+ + ⎢ ⎥
= ⎢ ⎥ ⎢ ⎥
−
⎣ ⎦ −
⎣ ⎦
Para el caso de funciones de la forma ( )
( ( )
y f g h x
= haciendo que
( )
v h x
= tenemos ( )
( )
y f g v
= y ahora haciendo que ( )
u g v
= tenemos
( )
y f u
= ; entonces
dy dy du dv
dx du dv dx
= .
O más simplemente ( ) [ ][ ]
´ ´ ( ( )) ´( ( )) ´( )
y f g h x g h x h x
= ⎡ ⎤
⎣ ⎦
Ejemplo 4
Si ( ) ( )
N
4
2
2
4
3
cos
3
cos
u
v
x
x
y
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
= entonces:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-95-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
106
( )
[ ] ( )
[ ]
( )
[ ] ( )
[ ] ( )
( )
[ ] ( )
[ ][ ]
x
x
x
x
D
x
x
x
D
x
y
x
x
6
3
sen
3
cos
4
3
3
sen
3
cos
4
3
cos
3
cos
4
´
2
3
2
2
2
3
2
2
3
2
−
=
−
=
=
Ahora analicemos los siguientes ejercicios resueltos:
Ejercicio Resuelto 1
Si ( ) 4
2 =
f , ( ) 6
4
´ =
f , ( ) 2
2
´ −
=
f hallar:
a) [ ]3
)
(x
f
dx
d
en 2
=
x b) ( ) )
2
´(
f
f D
SOLUCIÓN:
a) [ ] [ ] )
´(
)
(
3
)
( 2
3
x
f
x
f
x
f
dx
d
= que en 2
=
x sería:
[ ] ( ) ( ) 96
2
4
3
)
2
´(
)
2
(
3 2
2
−
=
−
=
f
f
b) ( ) [ ] [ ] [ ][ ] 12
)
2
)(
6
(
)
2
´(
)
4
´(
)
2
´(
))
2
(
(
´
´
)
2
(
(
)
2
´(
4
−
=
−
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
= f
f
f
f
f
f
f
f
f
D
Ejercicio Resuelto 2
Si
h
g
f
H
D
= y además: ( ) ( ) ( ) ( ) ( ) ( ) 3
2
;
5
3
;
2
2
;
2
3
;
3
2
;
1
2 −
=
′
=
′
−
=
′
=
=
−
= g
f
h
f
g
h ; determine
( )
2
H ′ .
SOLUCIÓN:
Como
h
g
f
x
H
D
=
)
( entonces:
[ ]
[ ]
[ ]
[ ]2
2
)
(
)
´(
))
(
(
)
(
)
´(
))
(
´(
)
(
)
´(
))
(
(
)
(
))
(
(
)
(
))
(
(
)
´(
x
h
x
h
x
g
f
x
h
x
g
x
g
f
x
h
x
h
x
g
f
x
h
x
g
f
D
x
h
x
g
f
D
x
H x
x
−
=
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
que en 2
=
x sería:
[ ]
[ ] [ ]
19
)
2
´(
1
)
2
)(
2
(
)
1
)(
3
)(
5
(
)
1
(
)
2
(
)
3
(
)
1
)(
3
(
)
3
´(
)
2
(
)
2
´(
))
2
(
(
)
2
(
)
2
´(
))
2
(
(
´
)
2
´(
2
2
3
=
−
−
−
−
=
−
−
−
−
−
=
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
H
f
f
h
h
g
f
h
g
g
f
H](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-96-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
107
Ejercicio Resuelto 3
Demuestre que la derivada de una función par es una función impar
SOLUCIÓN:
Sea f una función par, entonces se cumple que )
(
)
( x
f
x
f =
− . Ahora tomando derivada a ambos
miembros de la igualdad tenemos:
[ ] [ ]
[ ]( )
)
´(
)
´(
)
´(
)
´(
)
´(
1
)
´(
)
(
)
(
x
f
x
f
x
f
x
f
x
f
x
f
x
f
D
x
f
D x
x
−
=
−
=
−
−
=
−
−
=
−
La última igualdad nos indica que ´
f es una función impar. L.Q.Q.D
Finalmente las fórmulas de derivadas para funciones compuestas quedarían:
Sea )
(x
u
u = , entonces:
1. ( ) ´
)
( 1
u
u
n
u
D n
n
x
−
=
2. ´
)
( u
e
e
D u
u
x
=
3. ( ) ´
ln
)
( u
a
a
a
D u
u
x =
4. ´
1
)
(ln u
u
u
Dx =
5. ´
ln
1
)
(log u
a
u
u
D a
x =
6. ( ) ´
cos
)
(sen u
u
u
Dx =
7. ( ) ´
sen
)
(cos u
u
u
Dx −
=
8. ( )
2
(tan ) sec ´
x
D u u u
=
9. ( )
2
(cot ) csc ´
x
D u u u
= −
10. ( )
(sec ) sec tan ´
x
D u u u u
=
11. ( )
(csc ) csc cot ´
x
D u u u u
= −](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-97-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
108
Ejercicios Propuestos 3.4
1. Calcular las derivadas de las funciones cuyas reglas de correspondencia son:
a) ( ) 2
2 2
f x x x
= − +
b) ( )
1
2 3
f x
x
=
−
c) ( )
x x
x x
e e
f x
e e
−
−
−
=
+
d) ( )
2
2
1
1
x
f x
x
−
=
+
e) ( )
3
cos2
senx
f x
x
⎛ ⎞
= ⎜ ⎟
⎝ ⎠
f) ( ) ( )
2
ln ln 1
f x x
⎡ ⎤
= +
⎣ ⎦
g) ( )
2
2 2
1 1
ln
4 4 4
x
f x
x x
⎛ ⎞
= −
⎜ ⎟
− −
⎝ ⎠
2. Si { }
I
ervalo
un
en
derivable
función
una
es
f
f
V int
/
= . Demuestre que:
[ ]
)
(
'
)
(
'
)
(
)
( x
f
x
f
x
f
x
f
V
f =
−
⇒
−
=
−
∈
∀ (La derivada de una función impar es una función par)
3. Hallar ( ) ( )
x
g
f ′
D , si ( )
2
u
e
u
f = y ( ) ( )
4 2
2
cos
1 x
x
g
u +
=
=
4. Sean f, g y h funciones diferenciales para todo IR
x ∈ , tales que:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2
,
,
5
3
,
3
3
,
1
2
,
3
2
,
2
,
2 −
=
′
=
−
=
′
=
−
=
′
=
−
=
′
= a
f
a
a
f
f
f
h
h
a
g
a
g .
4
)
´(
,
)
( =
= a
h
a
a
h
En a
x = determine el valor de:
a) ( )´
f
g D b) ( )´
h
g D c) ( )´
g
h D
d) ( )´
g
h
f D
D e)
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ −
f
g
g
h
g
h
f
D
D
D
D
5. Sea 0
)
0
( =
f y 2
)
0
(
' =
f , encuentre la derivada de ))))
(
(
(
( x
f
f
f
f en 0
=
x .
6. Suponga que f es derivable y que existen 2 puntos 1
x y 2
x tales que 2
1)
( x
x
f = y 1
2)
( x
x
f = . Sea
( ) ( )
( )
( )
( )
x
f
f
f
f
x
g = pruebe que )
(
'
)
(
' 2
1 x
g
x
g =
7. Pruebe que si un polinomio )
(x
p es divisible entre ( )2
b
ax + entonces )
(
' x
p es divisible entre ( )
b
ax + .
Sugerencia: Escriba el polinomio de la forma ( ) ( ) ( )
2
p x c x ax b
= +
⎡ ⎤
⎣ ⎦ y derívelo.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-98-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
110
Ejemplo 2
Hallar
1
1 3
n
x
D
x
⎛ ⎞
⎜ ⎟
+
⎝ ⎠
SOLUCIÓN:
Aquí tenemos: ( )
1
1
1 3
1 3
y x
x
−
= = +
+
.
Obteniendo derivadas:
( ) ( )
( ) ( )
( )( ) ( )
( )
2
3 2
4 3
5 4
´ 1 3 3
´´ 2 1 3 3
´´´ 2 3 1 3 3
(2 3 4) 1 3 (3 )
IV
y x
y x
y x
y x
−
−
−
−
= − +
= + +
= − × +
= + × × +
Directamente la quinta derivada sería ( )( ) ( )
6 5
5! 1 3 3
V
y x
−
= − +
Por tanto la n-ésima derivada sería: ( ) ( )( ) ( )
( )
1
1 ! 1 3 3
n n
n n
y n x
− +
= − +
Ejemplo 3
Demuestre que ( ) !
n
x
D n
n
x = ; n∈ `
SOLUCIÓN:
Como n
x
y = entonces:
( )
( )( )
( )( )( ) ( )
( )
( )( )( ) ( )
1
2
3
´
´´ 1
´´´ 1 2
1 2 3 1
1 2 3 1
!
n
n
n
n n n
y nx
y n n x
y n n n x
y n n n n n n x
n n n n
n
−
−
−
−
=
= −
= − −
= − − − − −
= − − −
=
Ejercicio Propuesto 3.5
1. Calcular las derivadas de orden superior indicadas.
a. ( )
[ ]
2
4
4
cos x
dx
d
b.
( )
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+ x
x
sen
x
dx
d
1
2
2
2
π
c. [ ]
x
n
n
xe
dx
d
d. ⎟
⎠
⎞
⎜
⎝
⎛
− x
D n
x
4
5
e. ⎥
⎦
⎤
⎢
⎣
⎡
−
+
x
x
Dx
1
1
30
f. [ ]
xsenx
dx
d
35
35](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-100-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
111
2. Determine
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+ x
dx
d
x
dx
d
1
1
2
2
3. Usando el símbolo factorial, encuentre una fórmula para:
( )
0
1
1
1 ... a
x
a
x
a
x
a
D n
n
n
n
n
x +
+
+
+ −
− , n∈`
4. Determine un polinomio P de grado 3 tal que 1
)
1
( =
P , 3
)
1
´( =
P , 6
)
1
´´( =
P , 12
)
1
´´´( =
P .
Hasta aquí hemos tratado con funciones cuyas reglas de correspondencia
estaban dadas por una ecuación de la forma ( )
y f x
= , esta forma la llamaremos
en adelante EXPLÍCITA; suponga ahora que la ecuación de una función esté dada
en la forma ( , ) 0
F x y = , forma que le llamaremos IMPLÍCITA, y suponga que se
desea obtener la derivada ´
y de esta ecuación sin necesidad de despejar y ; de
ahí la necesidad de mencionar mecanismo de derivación para este tipo de
problema.
3.6.4 DERIVACIÓN IMPLÍCITA
Para obtener ´
y en una función implícita ( , ) 0
F x y = sin necesidad de
despejar y ; es más, suponga que no se pueda despejar y , hay que considerarla
como 0
))
(
,
( =
x
f
x
F y derivando cada miembro de la ecuación tomando en cuenta
las reglas mencionadas lograríamos lo deseado.
Ejemplo
Sea
4 5
0
x y
− = la ecuación de una función (asegúrese que en verdad representa una función) la derivada la
podemos obtener por una de las siguientes formas:
1. Despejando y (forma explícita:
4
5
y x
= ) entonces:
1
5
4
´
5
y x
−
=
2. Sin despejar y (forma implícita:
4 5
0
x y
− = ).
La consideraremos como ( )
5
4
0
x f x
− =
⎡ ⎤
⎣ ⎦ . Ahora derivamos cada miembro de la ecuación:
( ) [ ]
( ) ( )
5
4
4
3
0
4 5 ´ 0
x x
D x f x D
x f x f x
⎡ ⎤
− =
⎡ ⎤
⎣ ⎦
⎣ ⎦
− =
⎡ ⎤
⎣ ⎦
Ahora despejamos ( )
´
f x :
( )
( )
3
4
4
´
5
x
f x
f x
=
⎡ ⎤
⎣ ⎦
Por ahora podemos comprobar que los resultados son los mismos, simplemente habría que reemplazar
( )
4
5
f x x
= :](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-101-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
112
( )
( )
3 3 3
1
5
4 4 16
4 5
5
4 4 4 4
´
5
5 5
5
x x x
f x x
f x x
x
−
= = = =
⎡ ⎤ ⎡ ⎤
⎣ ⎦
⎢ ⎥
⎣ ⎦
Ejemplo 2
Sea 1
2
2
=
+ y
x con 0
y ≥ (semicircunferencia), hallar ´
y
SOLUCIÓN:
PRIMER MÉTODO.
Como es posible despejar y , tenemos
2
1
y x
= + −
Entonces:
( ) ( )
1
2
2
1
2
2
´ 1 2
1
y x x
x x
y
x
−
= − −
= − = −
−
SEGUNDO MÉTODO.
Implícitamente consiste en observar la ecuación dada como [ ] 1
)
( 2
2
=
+ x
f
x y tomar derivada a ambos
miembros de la igualdad:
[ ]
( ) ( )
0
)
´(
)
(
2
2
1
)
( 2
2
=
+
=
+
x
f
x
f
x
D
x
f
x
D x
x
que es lo mismo que: 0
´
2
2 =
+ yy
x
despajando ´
y resulta:
2
´
1
x x
y
y x
= − = −
−
Una dificultad puede ser que la ecuación dada no represente lugar geométrico.
Ejemplo
Suponga que la ecuación fuese 1
2
2
−
=
+ y
x
Esta ecuación no representa lugar geométrico, sin embargo obtener ´
y sería de la misma forma que el ejemplo
anterior.
En los ejemplos anteriores se demuestra que la derivación implícita es válida,
la comprobación no siempre va a ser posible. Pero lo que se requiere es obtener
la derivada y es lo que hemos dejado explicado.
Observe además que las ecuaciones implícitas podrían representar no sólo
funciones sino una relación cualquiera, entonces estaríamos en capacidad de
obtener la derivada en cualquier punto de esa relación.
Ahora analicemos los siguientes ejercicios resueltos.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-102-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
113
Ejercicio Resuelto 1
Hallar ´
y para
3
2
3
2
7
4 y
xy
x =
+
SOLUCIÓN:
Obteniendo derivada a ambos miembros y resolviendo tenemos:
( ) ( )
( )
´
6
´
14
7
12
´
6
´
2
7
7
12
2
7
4
2
2
2
2
2
2
3
2
3
y
y
xyy
y
x
y
y
yy
x
y
x
y
D
xy
x
D x
x
=
+
+
=
+
+
=
+
Despejando ´
y resulta:
xy
y
y
x
y
14
6
7
12
´ 2
2
2
−
+
=
Ejercicio Resuelto 2
Hallar ´
y para ( ) 1
2
3
ln 2
2
2
−
=
+
+ x
y
y
x
x
SOLUCIÓN:
Obteniendo derivada a ambos miembros, tenemos:
( )
( ) ( )
[ ]
x
yy
y
y
x
x
yy
y
x
xy
y
x
x
D
y
y
x
x
D x
x
4
´
6
´
2
1
4
´
6
´
2
1
1
1
2
3
ln
2
2
2
2
2
=
+
+
+
=
+
+
+
−
=
+
+
Despejando ´
y resulta:
y
x
y
x
y 1
2
6
1
4
´
+
−
−
=
Ejercicio Resuelto 3
Hallar ´
y para ( ) y
x
x
y
xy +
+
= 2
2
cos
SOLUCIÓN:
Obteniendo derivada a ambos miembros, tenemos:
( )
( ) ( )
( )[ ] ( ) ( )
[ ]
( ) ( ) y
x
xy
y
x
x
y
x
yy
xy
xyy
xy
y
y
y
x
x
y
x
yy
yy
x
y
xy
y
x
x
y
D
xy
D x
x
+
+
+
+
+
+
=
−
−
+
+
+
+
+
=
+
−
+
+
=
−
2
´
2
´
2
´sen
2
sen
´
1
1
´
2
´
2
1
sen
cos
2
2
2
2
1
2
2
2
2
2
1
Despejando ´
y resulta:
( )
( )
2
2
2
sen
2
2
2
2
sen
´
xy
xy
y
x
x
y
y
x
x
y
x
xy
y
y
+
+
+
+
−
+
−
−
=](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-103-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
114
Ejercicio Resuelto 4
Determinar la ecuación de la recta normal a la curva cuya ecuación es ( )
y
x
sen
y
cos
x +
= en
P(0,0).
SOLUCIÓN:
La recta normal es la perpendicular a la recta tangente, por tanto
tg
1
m
mnormal −
=
Ahora ( )
0
,
0
tg ´
y
m = . Obteniendo ´
y resulta:
( ) ( )
( )
( ) [ ]
´
1
)
cos(
´
sen
cos
1
sen
cos
y
y
x
yy
x
y
y
x
D
y
x
D x
x
+
+
=
−
+
+
=
En la última expresión se puede reemplazar las coordenadas del punto, es decir: 0
=
x y 0
=
y y luego
despejar ´
y :
( ) [ ]
0
´
´
1
0
1
´
1
)
0
0
cos(
´
0
sen
0
0
cos
=
+
=
+
+
+
=
−
+
y
y
y
y
.
Esto quiere decir que la recta tangente es horizontal y por tanto la recta normal será vertical con pendiente
1
0
normal
m = − = −∞
Y su ecuación será:
( )
0
0
0
1
0
=
−
−
=
−
x
x
y
(el eje y ).
Ejercicio Resuelto 5
Sea 2
2 3
2
=
− y
y
x . Encuentre '
'
y en (2,1).
SOLUCIÓN:
Primero se encuentra '
y :
( ) ( )
0
´
6
´
2
2
2
2
2
3
2
=
−
+
=
−
y
y
y
x
xy
D
y
y
x
D x
x
En )
1
,
2
( sería:
2
´
0
´
)
1
(
6
´
)
2
(
)
1
)(
2
(
2 2
2
=
=
−
+
y
y
y
Ahora encontramos '
'
y volviendo a derivar implícitamente:
( ) ( )
( ) 0
´´
6
´
´
12
´´
´
2
´
2
2
0
´
6
´
2
2
2
2
2
=
+
−
+
+
+
=
−
+
y
y
y
yy
y
x
xy
xy
y
D
y
y
y
x
xy
D x
x
En )
1
,
2
( sería:
15
´´
0
´´
6
48
´´
4
8
8
2
0
´´
)
1
(
6
)
2
)(
2
)(
1
(
12
´´
)
2
(
)
2
)(
2
(
2
)
2
)(
2
(
2
)
1
(
2 2
2
=
=
−
−
+
+
+
=
−
−
+
+
+
y
y
y
y
y](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-104-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
115
Ejercicios Propuestos 3.6
1. Encontrar
dx
dy
para:
a. 1
3
2
3
2
=
+ y
x
b. ( )
ln 1
xy y
+ =
c. ln 0
xy
e y
+ =
d. sec tan
y y xy
+ =
e. ( )
ln 5
xy y
+ =
2. Demuestre que la rectas tangente a las curvas definidas por las ecuaciones
3
2
4x
y = y 14
3
2 2
2
=
+ y
x
en el punto ( )
2
,
1 son perpendiculares entre sí.
3. Hallar la ecuación de la recta tangente a la curva definida por la ecuación 5
3 3
3
=
+
+ y
xy
x en el punto
( )
1
,
1
4. Encuentre la ecuación de la recta tangente a la grafica de ( ) 2
2
3
2
2
8 y
x
y
x =
+ en el punto ( )
1
,
1 −
5. Determine la ecuación de la recta tangente a la curva definida por la ecuación ( )
[ ] 2
1
2
=
+
+
− y
x
sen
xy π
en el punto )
1
,
1
(
6. Determine la ecuación de la recta tangente a la curva definida por la ecuación 2
2
3
2
3
=
+ y
x que es paralela a
la recta 0
6 =
+
+ y
x
7. Determine las ecuaciones de la recta normal a la curva que tiene por ecuación ( ) ( )2
2
2
2
4
1 y
y
y
x −
+
= en
el punto ( )
2
,
0 − .
8. Determine la ecuación de la recta normal a la curva definida por la ecuación ( ) ( )
y
x
y
x +
= sen
3
2
cos en el
punto ( )
0
,
0 .
9. Determine todos los puntos de la función f que define la ecuación xy
y
x 2
3
2
=
+ donde la recta tangente
a f sea horizontal.
10. Encuentre '
'
y si 0
3
4 2
3
=
+
− y
x
11. Calcula:
2
2
dx
y
d
para 1
3
2
3
2
=
+ y
x
12. Para la función )
(x
f
y = dada en forma implícita por la ecuación
2
tg 4 =
+
−
π
−
y
e
y
x determine
2
2
dx
y
d
en el punto ( )
4
,
2 π .
3.6.5 DERIVACIÓN PARAMÉTRICA
Las ecuaciones de ciertas trayectorias son dadas en la forma:
⎩
⎨
⎧
=
=
)
(
)
(
:
t
y
y
t
x
x
C
Tanto x como y están expresadas en términos del parámetro t , el objetivo
será hallar directamente
dx
dy
.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-105-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
116
3.6.5.1 Teorema de la derivada de funciones definidas por ecuaciones
paramétricas.
Suponga que )
(t
x
x = y )
(t
y
y = son
funciones continuamente diferenciables,
y que 0
)
´( ≠
t
x para cualquier t de cierto
intervalo. Entonces las ecuaciones
paramétricas definen a y como una
función diferenciable de x y su
derivada es:
dt
dx
dt
dy
dx
dt
dt
dy
dx
dy
=
=
Ejemplo 1
Sea la circunferencia con ecuación cartesiana 1
2
2
=
+ y
x , la derivada también puede ser hallada partiendo
de su ecuación paramétrica
⎩
⎨
⎧
=
=
t
y
t
x
C
sen
cos
: , es decir:
y
x
t
t
dt
dx
dt
dy
dx
dy
−
=
−
=
=
sen
cos
Esta manera representaría un tercer método para hallar la derivada, tal como se puede observar.
Ejemplo 2
Sea
⎪
⎩
⎪
⎨
⎧
=
=
sent
e
y
t
e
x
t
t
cos
hallar
dy
dx
SOLUCIÓN:
sent
t
t
sent
sent
e
t
e
t
e
sent
e
dt
dx
dt
dy
dx
dy
t
t
t
t
−
+
=
−
+
=
=
cos
cos
cos
cos
Para hallar derivadas de orden superior, observe que la primera derivada es
función de t , es decir que )
´(t
y
dx
dy
= ; por tanto:
Segunda derivada: [ ] [ ]
[ ]
)
´´(
)
´(
)
´(
)
´(
2
2
t
y
dt
dx
dt
t
y
d
dx
dt
dt
t
y
d
t
y
dx
d
dx
y
d
=
=
=
=](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-106-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
117
Tercera Derivada: [ ] [ ]
[ ]
)
´´´(
)
´´(
)
´´(
)
´´(
3
3
t
y
dt
dx
dt
t
y
d
dx
dt
dt
t
y
d
t
y
dx
d
dx
y
d
=
=
=
=
Y así sucesivamente.
Ejemplo 1
Sea
⎩
⎨
⎧
=
=
t
y
t
x
C
sen
cos
: hallar
3
3
d y
dx
.
SOLUCIÓN:
Ya encontramos la primera derivada: ( )
cos
cot
sen
dy
dy t
dt t
dx
dx t
dt
= = = −
−
La segunda derivada sería:
( ) ( ) ( )
2
2
3
2
´ cot csc
csc
d d
y t t
d y dt dt t
dx dx
dx sent
dt dt
− − −
= = = = −
−
La tercera derivada sería:
( ) ( ) ( )
3
2
3
4
3
d d
y´´ csc t 3csc t csctcotgt
d y dt dt 3csc tcotgt
dx dx
dx sent
dt dt
− − −
= = = = −
−
Ejemplo 2
Sea
⎪
⎩
⎪
⎨
⎧
=
=
sent
e
y
t
e
x
t
t
cos
hallar
2
2
d y
dx
SOLUCIÓN:
La primera derivada ya la encontramos:
sent
t
t
sent
sent
e
t
e
t
e
sent
e
dt
dx
dt
dy
dx
dy
t
t
t
t
−
+
=
−
+
=
=
cos
cos
cos
cos
La segunda derivada sería:
( )
( )( ) ( )( )
( )
( ) ( )
( )
2
2
2
2 2
2
2 2 2 2
cos
´
cos
cos cos cos cos
cos
cos
cos cos
cos
cos
cos 2cos 2cos cos
t t
t t
d sent t
d
y
d y dt t sent
dt
dx dx
dx
dt dt
t sent t sent sent t sent t
t sent
e t e sent
t sent sent t
t sent
e t e sent
t tsent sen t sen t tsent t
+
⎛ ⎞
⎜ ⎟
−
⎝ ⎠
= =
− − − + − −
−
=
−
− + +
−
= =
−
− + + + +
=
( )
( )
3
2
3
2
cos
2
cos
t
t
e t sent
d y
dx e t sent
−
=
−](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-107-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
118
Ejemplo 3
Calcular
n
n
dx
y
d
para:
⎪
⎩
⎪
⎨
⎧
∈
=
=
R
m
t
y
t
x
m
;
ln
SOLUCIÓN:
Hallando las primeras derivadas, suficientes hasta poder generalizar, tenemos:
Primera derivada: m
m
m
mt
t
t
mt
t
mt
dt
dx
dt
dy
dx
dy
=
=
=
=
−
−
−
1
1
1
1
Segunda derivada:
[ ]
m
m
t
m
t
t
m
dt
dx
dt
t
y
d
dx
y
d 2
1
1
2
2
2
)
´(
=
=
= −
−
Tercera derivada:
[ ]
m
m
t
m
t
t
m
dt
dx
dt
t
y
d
dx
y
d 3
1
1
3
3
3
)
´´(
=
=
= −
−
Directamente, la cuarta derivada sería:
m
t
m
dx
y
d 4
4
4
=
Por tanto:
m
n
n
n
t
m
dx
y
d
=
Ejercicios Propuestos 3.7
1. Hallar
dx
dy
para:
a.
( )
( )
⎩
⎨
⎧
−
=
+
=
t
t
sent
a
y
tsent
t
a
x
cos
cos
b.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
−
=
+
=
1
1
1
2
2
t
t
y
t
x
2. Encuentre la ecuación de la recta tangente a la curva
( )
( )
⎩
⎨
⎧
−
=
−
=
t
a
y
t
t
a
x
cos
1
sen
en
2
π
=
t
3. Hallar la ecuación de la recta tangente a la curva
⎪
⎩
⎪
⎨
⎧
−
=
−
=
3
2
3
2
t
t
y
t
t
x
en el punto (1,2)
4. Encuentre la ecuación de la recta tangente a la curva
⎩
⎨
⎧
+
=
−
=
t
t
y
t
t
x
2
cos
4
sen
3
3
cos
3
2
sen
4
en 0
=
t
5. Sea C la curva con ecuaciones paramétricas
⎪
⎩
⎪
⎨
⎧
−
+
=
=
1
4
2 3
2
t
t
y
t
x
; IR
t ∈ . Encontrar las ecuaciones de las
rectas tangentes a C y que pasen por el origen.
6. Sea C la curva con ecuaciones paramétricas
( )
cos
ln cos
y t
x t
=
⎧
⎪
⎨
=
⎪
⎩
. Calcule a)
2
2
dx
y
d
y b)
3
3
dx
y
d](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-108-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
120
( )
( )
0
0
0
0
0
0
0
0
0
0
0
0
0
0
)
(
cos
)
´(
cos
)
(
)
´(
cos
0
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
sen
f
f
f
sen
f
d
dx
d
dy
dx
dy
m
sen
f
y
f
x
−
+
=
=
=
=
=
=
Ejemplo
Encuentre la ecuación de la recta tangente a θ
=
θ
= 3
sen
4
)
(
f
r en 4
0
π
=
θ
SOLUCIÓN:
Observa la gráfica:
En este caso [ ]
2
4
cos
3
sen
4
)
cos(
)
(
)
cos(
)
(
0
2
2
2
2
4
4
4
4
0
0
0
=
=
=
=
θ
θ
=
π
π
π
π
x
f
f
x
y [ ]
2
4
sen
3
sen
4
)
sen(
)
(
)
sen(
)
(
0
2
2
2
2
4
4
4
4
0
0
0
=
=
=
=
θ
θ
=
π
π
π
π
y
f
f
y
Para la pendiente, tenemos: θ
=
θ 3
cos
12
)
´(
f
Entonces:
[ ] [ ]
[ ] [ ]
2
1
2
6
2
6
4
12
4
12
3
4
cos
3
cos
12
cos
3
4
3
cos
12
)
(
cos
)
´(
cos
)
(
)
´(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
4
4
4
0
0
0
0
0
0
0
0
=
−
−
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
⎥
⎦
⎤
⎢
⎣
⎡
−
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
+
=
−
+
=
m
sen
sen
sen
sen
sen
f
f
f
sen
f
m
π
π
π
π
π
π
π
π
θ
θ
θ
θ
θ
θ
θ
θ
Por lo tanto, la ecuación de la recta tangente estaría dada por:
)
2
(
2
)
(
2
1
0
0
−
=
−
−
=
−
x
y
x
x
m
y
y
Fig. 3.14](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-110-320.jpg)


![Moisés Villena Muñoz Cap. 3 La derivada
123
Ejemplo 2
Obtenga la derivada para la función inversa de
x
e
x
f =
)
( empleando el teorema de la
derivada de la función inversa.
SOLUCIÓN:
De acuerdo al Teorema de la Derivada de la Función Inversa ( )
( )
y
f
x
f
dx
d
´
1
1
=
⎥
⎦
⎤
⎢
⎣
⎡ −
Como
x
e
y
x
f =
=
)
( tenemos que
x
e
x
f =
)
´( y
y
e
y
f =
)
´( y además al cambiar la variable resulta
y
e
x = , lo cual nos permite decir que: x
y
f =
)
´(
Bien, reemplazando
( ) x
y
f
x
f
dx
d 1
´
1
)
(
1
=
=
⎥
⎦
⎤
⎢
⎣
⎡ −
(No olvide la inversa de la función exponencial es la logarítmica, es decir:
1
( ) ln
f x x
−
= , cuya derivada la
determinamos con su definición)
3.6.7.3 Derivadas de las Funciones Trigonométricas
Inversas
( ) 1
1
;
1
1
arcsen
2
−
−
= x
x
x
Dx
( ) 1
1
;
1
1
arccos
2
−
−
−
= x
x
x
Dx
( ) 2
1
1
arctg
x
x
Dx
+
=
( ) 2
1
arc tg
1
x
D co x
x
= −
+
( ) 1
;
1
1
sec
2
−
= x
x
x
x
arc
Dx
Demostración:
Demostraremos la primera.
Planteemos el problema de la siguiente manera:
Sea x
y
x
f sen
)
( =
= hallar [ ] [ ]
x
D
x
f
D x
x arcsen
)
(
1
=
−
SOLUCIÓN:
Aplicando el teorema de la Derivada de la función inversa tenemos:
[ ] [ ]
)
´(
1
)
(
1
y
f
arcsenx
D
x
f
D x
x =
=
−
Entonces, y
y
f cos
)
´( = . Ahora habrá que encontrar y
cos , sabiendo que seny
x = (cambiando la
variable en la función dada).
Por trigonometría, decir que
1
x
seny = significa que 2
1
cos x
y −
= (observe la figura 3.16)](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-113-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
124
Por lo tanto, [ ]
2
1
1
cos
1
x
y
arcsenx
Dx
−
=
= L.Q.Q.D.
Las fórmulas anteriores pueden ser generalizadas para una función
)
(x
u
u =
( ) 1
1
;
´
1
1
arcsen
2
−
−
= u
u
u
u
Dx
( ) 1
1
;
´
1
1
arccos
2
−
−
−
= u
u
u
u
Dx
( ) ´
1
1
arctg 2
u
u
u
Dx
+
=
( ) 1
;
´
1
1
sec
2
−
= u
u
u
u
u
arc
Dx
Ejemplo
Hallar ´
y para 2
2
ln
tg y
x
x
y
arc +
=
⎟
⎠
⎞
⎜
⎝
⎛
SOLUCIÓN:
Derivando implícitamente, tenemos:
( )
[ ]
( )
( )[ ]
( )
( )
( )
( )
y
x
y
x
y
y
x
yy
xy
yy
x
y
xy
y
x
yy
x
y
x
x
y
xy
x
y
x
yy
x
x
y
xy
x
y
x
yy
x
y
x
x
y
x
y
y
x
D
y
x
x
y
D
y
x
D
x
y
tg
arc
D
x
y
x
x
x
y
x
x
−
+
=
+
=
−
+
=
−
+
+
=
+
−
+
/
+
/
=
⎥
⎦
⎤
⎢
⎣
⎡ −
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡ −
+
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
´
´
´
´
´
´
´
2
´
2
´
1
´
2
2
2
1
)
1
(
´
1
1
1
2
1
1
1
ln
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
2
Fig. 3.16](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-114-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
126
( ) ( )
[ ]
[ ]
1
ln
´
1
ln
´
1
ln
)
1
(
´
1
ln
ln
+
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
=
x
x
y
x
y
y
x
x
x
y
y
x
x
D
y
D
x
x
x
Ejemplo 2
Hallar
dx
dy
para [ ] x
x
y arctg
2
sen
=
SOLUCIÓN:
Primero, aplicando logaritmo, tenemos:
[ ]
( )
( )
x
x
y
x
y x
2
sen
ln
arctg
ln
2
sen
ln
ln arctg
=
=
Ahora derivando implícitamente, resulta:
( )
[ ]
( ) ( )( )
( )
[ ] ( )
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
=
x
x
x
x
x
x
y
x
x
x
x
x
y
y
x
x
x
x
x
y
y
x
x
D
y
D
x
x
x
2
sen
2
cos
arctg
2
1
2
sen
ln
2
sen
´
2
sen
2
cos
arctg
2
1
2
sen
ln
´
2
2
cos
2
sen
1
arctg
2
sen
ln
1
1
´
1
2
sen
ln
arctg
ln
2
arctg
2
2
Ejemplo 3
Hallar
dx
dy
para
x
x
x
y =
SOLUCIÓN:
Ahora, hay que aplicar dos veces logaritmo.
Primero, aplicando logaritmo tenemos:
( )
x
x
y
x
y
x
xx
ln
ln
ln
ln
=
=
Luego, volvemos a aplicar logaritmo:
( ) ( )
)
ln(ln
ln
)
ln(ln
)
ln(ln
ln
)
ln(ln
ln
ln
ln
ln
x
x
x
y
x
x
y
x
x
y
x
x
+
=
+
=
=
Y ahora sí, derivamos implícitamente:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-116-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
127
[ ] [ ]
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
+
+
=
+
=
x
x
x
x
x
x
y
x
x
x
x
x
y
x
x
x
y
y
y
x
x
x
x
x
y
y
y
x
x
x
D
y
D
x
x
x
x
x
x
x
x
x
ln
1
1
ln
ln
´
ln
1
1
ln
ln
´
ln
1
1
ln
ln
´
1
ln
1
1
ln
)
1
(
´
1
ln
1
)
ln(ln
ln
)
ln(ln
Existen situaciones en que es recomendable emplear la derivación logarítmica
Ejemplo
Hallar
dx
dy
para
4
3
2
1
arctg
1
2
x
e
x
x
y
+
+
+
=
SOLUCIÓN:
Primero, aplicando logaritmo, tenemos:
[ ]
( ) ( ) ( )
x
x
e
x
x
y
e
x
x
y
+
−
+
+
+
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+
+
=
1
ln
arctg
1
ln
2
ln
ln
1
arctg
1
2
ln
ln
4
1
3
1
2
2
1
4
3
2
Ahora derivando implícitamente, resulta:
( ) ( ) ( ) ( )
( )
( ) ( )
( ) ( )⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+
+
=
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+
+
=
+
−
+
+
+
=
x
x
x
x
x
x
x
e
e
x
arctgx
x
x
y
y
e
e
x
arctgx
x
x
y
y
e
arctgx
x
D
y
D
1
1
4
1
1
1
1
1
3
1
2
2
1
2
1
´
1
1
4
1
1
1
1
1
3
1
2
2
1
2
1
´
1
1
ln
1
ln
2
ln
ln
2
2
2
2
4
1
3
1
2
2
1
Finalmente, reemplazando resulta:
( ) ( )⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+
+
+
+
+
= x
x
x
e
e
x
arctgx
x
x
e
arctgx
x
y
1
1
4
1
1
1
1
1
3
1
2
2
1
2
1
1
1
2
´
2
2
4
3
2
Ejercicios Propuestos 3.10
1. Calcular
dx
dy
, para :
a.
4
csc
1
sec
3
3
5
−
+
=
x
tgx
x
y
b.
( )5
3
3 2
4 3
4
1
4
cos
x
x
x
x
x
y
−
−
=
e.
x
n
n
x
y =
f.
( )
( )
x
arctg
x
x
sen
arcsen
y
2
2
2
cos
arccos ⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-117-320.jpg)


![Moisés Villena Muñoz Cap. 3 La derivada
130
3.7.4 DERIVADAS DE FUNCIONES HIPERBÓLICAS
( ) x
x
Dx cosh
senh =
( ) x
x
Dx senh
cosh =
( ) x
h
x
Dx
2
sec
tgh =
( ) x
h
x
c
Dx
2
csc
tgh −
=
( ) x
hx
hx
Dx tgh
sec
sec −
=
( ) x
hxc
hx
Dx tgh
csc
csc −
=
¡Demuéstrelas!
Misceláneos
1. Determine si las siguientes proposiciones son verdaderas o falsas. Justifique formalmente su respuesta.
a) Si 2
)
2
(
)
2
´(
)
2
´( =
=
= g
g
f entonces
( ) 4
)
2
( =
⎟
⎠
⎞
⎜
⎝
⎛
dx
g
f
d D
b) La función x
x
f sen
)
( = no es derivable en 0
=
x
c) Si f y g son derivables en c
x = y 0
)
(
)
´( =
= c
g
c
f y )
(
)
(
)
( x
g
x
f
x
h = entonces
0
)
´( =
c
h .
d) La ecuación de la recta tangente a la curva
3
x
y = en el punto ( )
1
,
1 es ( )
1
3
1 −
=
− x
y .
e) La expresión
2
1
sen
2
π
→ −
−
π
x
x
lim
x
es la derivada de x
x
f sen
)
( = cuando
2
π
=
x .
f) La función 3
5
6
)
( 3
−
+
= x
x
x
f no tiene rectas tangentes con pendiente 4.
g) Si
x
x
x
x
y =
)
( entonces ⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
x
x
x
x
x
x
y x
xx 1
ln
ln
)
´( 2
h) Si ( )
)
(
)
( x
f
e
f
x
g = tal que 2
ln
)
0
( =
f , 2
)
0
´( −
=
f y 3
)
2
´( =
f entonces 12
)
0
´( −
=
g
i) Si f es una función continua en el intervalo cerrado [ ]
b
a, y )
(
)
( b
f
a
f = entonces en algún punto
del intervalo abierto ( )
b
a, , la función f tiene una recta tangente que es paralela al eje x .
j) Si f es una función invertible entonces
)
´(
1
)
(
1
x
f
x
f
dx
d
=
⎟
⎠
⎞
⎜
⎝
⎛ −
.
k) Si f , g y h son funciones tales que ( ) 4
)
2
´( =
h
g
f D
D , 1
)
1
´(
)
1
( −
=
= g
g y
1
)
2
´(
)
2
( =
= h
h entonces 0
)
1
´( =
−
f
l) Si f es una función inversible y derivable tal que 4
)
1
´( =
f y 2
)
1
( −
=
f entonces
1
)
2
(
1
=
−
⎟
⎠
⎞
⎜
⎝
⎛ −
f
dx
d
.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-120-320.jpg)

![Moisés Villena Muñoz Cap. 3 La derivada
132
3. Hallar [ ]
[ ]
1
)
( 2 +
x
f
dx
d
4. Determine los valores para a , b y c de modo que la función
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
≤
≤
+
⎟
⎠
⎞
⎜
⎝
⎛
=
1
;
1
0
;
0
;
sen
)
(
2
1
4
4
x
d
cx
x
b
ax
x
x
x
f
x
Sea continua en 0
=
x y derivable en 1
=
x . Además determine, de ser posible,
[ ] ( )
[ ] ( )
1
´
.
)
2
´( 2
1 +
−
− π
f
f
f
5. Encuentre la ecuación de la recta tangente a la curva definida por las ecuaciones paramétricas
⎩
⎨
⎧
=
=
tant
y
t
x
2
sec
2
en
6
π
−
=
t
6. Si
2
3
)
´( x
e
x
x
f = , 0
)
1
( =
f y ( ) 3
1
)
( 2
+
+
= x
x
g determine el valor de ( ) )
1
´(
f
g D .
7. Determine las ecuaciones de las rectas tangentes a la curva definida por las ecuaciones paramétricas
⎩
⎨
⎧
=
=
t
t
y
t
x
cos
sen
cos
en el punto )
0
,
0
( .
8. Determine la ecuación de la recta tangente a la función f en 1
=
x donde f , g y h son funciones
diferenciables en todo IR . f tiene como regla de correspondencia a ( )
)
(
)
( 2
x
g
x
h
x
f = y se conoce que
2
)
1
( =
g , 2
)
1
´( −
=
g , 3
)
2
´( −
=
h y 1
)
2
( −
=
h
9. Determine los puntos del intervalo [ ]
2
,
1
− donde la función [ ] 1
)
( −
+
= x
x
x
f sea derivable.
10. Determine los valores reales que puede tomar k para que
k
k
f
dx
d
5
1
)
1
( 2
1
+
=
⎟
⎠
⎞
⎜
⎝
⎛ −
. Considere que
1
)
4
( =
f y x
x
x
f 10
)
´( 2
+
−
= .
11. Para la función )
(x
f
y = cuyas ecuaciones paramétricas son
⎩
⎨
⎧
−
=
=
t
t
y
t
x
arcsen
arccos
, ( )
1
,
1
−
∈
t determine
3
3
dx
y
d
.
12. Para la función )
(x
f
y = cuyas ecuaciones paramétricas son
⎪
⎩
⎪
⎨
⎧
=
+
=
t
t
y
t
x
ln
1 2
, 0
t determine
3
3
dx
y
d
en el
punto )
0
,
2
(
13. Determine a, b y c conociendo que las curvas b
ax
x
y +
+
= 2 y 2
x
cx
y −
= tienen una recta tangente
común en el punto )
0
,
1
( .
14. Determine la ecuación de la recta tangente a la curva cuya ecuación es ( ) xy
x
y
y
x =
−
− tg
ln 2 en el punto
)
0
,
1
( .
15. Encuentre la ecuación de la recta normal a la curva C en el punto )
2
,
1
( . Donde C está definida por las
ecuaciones paramétricas
⎪
⎩
⎪
⎨
⎧
=
=
−
+
t
t
t
t
y
x
3
1
2 2
, { }
0
,
1
−
−
∈ IR
t](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-122-320.jpg)
![Moisés Villena Muñoz Cap. 3 La derivada
133
16. Hallar
2
2
dx
y
d
para
⎪
⎩
⎪
⎨
⎧
=
=
t
e
y
t
e
x
t
t
sen
cos
, IR
t ∈
17. Hallar
dx
dy
en el punto ( )
π
,
0 donde x e y satisfacen la ecuación ( ) 0
sen
2
=
−
+
+ x
y
x
xy .
18. Sea )
(x
f
y = función tal que
1
−
= f
h . Sea 0
≥
y si
2
2
1
)
(
+
−
+
=
y
y
y
y
h calcular )
1
´(
f
19. Determine la ecuación de la recta tangente y normal a la curva definida por las ecuaciones paramétricas
⎪
⎩
⎪
⎨
⎧
=
=
t
a
y
t
a
x
3
3
sen
cos
; [ ]
π
∈ 2
,
0
t ; 0
a en el punto
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
3
2
2
3
2
2
,a
a .
20. Determine los valores de a, b, c para que las funciones f y ´
f sean continuas en todo su dominio; donde f
es una función tal que
⎪
⎩
⎪
⎨
⎧
+
≥
+
=
0
;
0
;
sen
)
(
x
c
be
x
a
x
x
f x
.
21. Determine la ecuación de la recta tangente a la curva definida por las ecuaciones paramétricas
( )
( )
⎩
⎨
⎧
+
=
+
=
t
t
y
t
t
x
sen
cos
1
cos
cos
1
en
2
π
=
t .
22. Hallar la ecuación de la recta tangente a la curva definida por la ecuación ( ) 4
3
cos 2
2
=
+
+ x
xy
y ; en el
punto )
0
,
1
( .
23. Hallar le ecuación de la recta tangente a la curva definida por la ecuación 1
ln =
+ y
xy ; en el punto )
1
,
1
( .
24. Determine la ecuación de la recta tangente a la curva definida por las ecuaciones paramétricas
⎪
⎩
⎪
⎨
⎧
−
=
−
=
3
2
3
2
t
t
y
t
t
x
en el punto ( )
2
,
1 .
25. Demuestre que la derivada de [ ]
)
(cos
sen
)
( x
f
x
x
F = es una función Par.
26. Determine el valor de k de manera que la recta definida por 0
3 =
+
− k
y
x sea tangente a la parábola
definida por 1
5
2 2
+
−
= x
x
y .
27. Hallar ⎥
⎦
⎤
⎢
⎣
⎡
+
−
x
x
dx
d
1
1
50
50
28. Determine la ecuación de la recta tangente a la curva definida por las ecuaciones paramétricas
⎪
⎩
⎪
⎨
⎧
+
=
−
=
−
2
1
2
2
t
t
e
y
e
x
cuando 0
=
t
29. Determine la ecuación de la recta tangente a la función f cuya regla de correspondencia es
6
6
)
( 2
+
−
= x
x
x
f , y además dicha recta es paralela a la recta que contiene al origen y al vértice de la
parábola.
30. Si f es una función de en inversible y con regla de correspondencia 10
3
)
( 3
−
+
= x
x
x
f
entonces determine ( )
4
1
⎥
⎦
⎤
⎢
⎣
⎡ −
f
dx
d](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-123-320.jpg)





































![Moisés Villena Muñoz Cáp.4 Aplicacionesde la Derivada
118
4.11.2 TEOREMA DE ROLLE
Si f es una función continua en
b
a, y
derivable en
b
a, y si )
(
)
( b
f
a
f entonces,
existe al menos un número “ 0
x ” en
b
a, tal
que 0
)
´( 0
x
f
Ejercicios Propuestos 4.12
1. Sea .
2
)
( 2
4
x
x
x
f
Hallar todos los valores de 0
x en el intervalo [-2,2] tales que 0
)
(
' 0
x
f
2. La función x
x
f
)
( satisface la hipótesis del teorema del valor medio en el intervalo [0,2]. Diga si esto es
verdadero o falso, justificando apropiadamente su respuesta.
El teorema del valor medio para dos funciones sería:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-161-320.jpg)









![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
110
4.1 MONOTONÍA
La derivada nos permite determinar los intervalos de crecimiento y de
decrecimiento de una función.
4.1.2 Teorema de Monotonía
Sea ƒ una función continua en un
intervalo [ ]
b
a, y diferenciable en todo
punto interior de [ ]
b
a, . Entonces:
1. Si [ ]
b
a
x
x
f ,
,
0
)
´( ∈
∀
entonces ƒ es
creciente en [ ]
b
a,
2.Si [ ]
b
a
x
x
f ,
,
0
)
´( ∈
∀
entonces ƒ es
decreciente en [ ]
b
a, .
DEMOSTRACIÓN.
Se demostrará el primer inciso del teorema.
Suponga que 0
)
´(
x
f entonces 0
)
(
)
(
0
0
0
−
−
→ x
x
x
f
x
f
lím
x
x
; es decir 0
)
(
)
(
0
0
−
−
x
x
x
f
x
f
.
Suponga ahora que x
x
0 , entonces )
(
)
( 0 x
f
x
f , lo cual indica que f es creciente.
Si 0
x x
entonces 0
( ) ( )
f x f x
lo cual también indica que f es creciente
Para el caso 0
)
´(
x
f , la demostración es análoga.
Ejemplo 1
Analice la monotonía de
2
( ) 2 4 5
f x x x
= − +
SOLUCIÓN:
De acuerdo al teorema anterior para determinar los intervalos de crecimiento y los intervalos de decrecimiento
analizamos la primera derivada de f . Es decir, a 4
4
)
´( −
= x
x
f
El asunto es determinar en que intervalo para x esta derivada tiene valores positivos y en qué intervalo tiene
valores negativos, para lo cual factorizamos )
1
(
4
)
´( −
= x
x
f ; se observa que:
x )
´(x
f f
1
x Negativa (-) decrece
1
x Positiva(+) crece](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-171-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
112
Ahora debemos dar las condiciones para garantizar la existencia de los valores
extremos.
4.2.2 TEOREMA. Condición suficiente para la existencia de
Máximos y Mínimos
Si f es una función continua definida en
un intervalo [ ]
b
a, entonces f alcanza un
valor máximo y un valor mínimo en [ ]
b
a, .
Lo anterior quiere decir que siempre encontraremos extremos cada vez que
trabajemos con funciones continuas en un intervalo cerrado. Pero sigue habiendo
una interrogante ¿cómo obtenerlos?
Podemos suponer que deben existir puntos candidatos a ser extremos. Es
decir, dedicarnos a analizar sólo cierta clase de puntos. Estos serán los
denominados Puntos críticos.
4.2.3 DEFINICIÓN. Puntos Críticos.
Sea f una función definida en un
intervalo [ ]
b
a, que contiene a “ 0
x ”.
Entonces “ 0
x ” es llamado Punto Crítico si
es:
• Un punto extremo del intervalo, es
decir a
x =
0
, b
x =
0
. Estos serán
denominados Puntos Críticos de
Frontera.
O bien,
• Un punto donde la derivada es igual a
cero; es decir 0
)
´( 0
=
x
f . Estos serán
denominados Puntos Críticos](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-173-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
113
Estacionarios. (En estos puntos la recta
tangente es horizontal).
O bien,
• Un punto donde la derivada no existe;
es decir )
´( 0
x
f no está definida. Estos
serán denominados Puntos Críticos
Singulares. (En estos puntos la gráfica de f
tiene unos picos. Por ejemplo ( )
f x x
= , tiene un punto
crítico singular (pico) en 0
x = )
4.2.4 TEOREMA
Sea f una función definida en un
intervalo [ ]
b
a, que contiene a “ 0
x ”. Si
)
( 0
x
f es un valor extremo entonces “ 0
x ”
es un Punto Crítico.
Para el caso de puntos críticos de frontera, no se requiere demostración,
debido a que obviamente estos serán candidatos a que allí se produzcan los
extremos de la función. La demostración se la realizará para los casos de puntos
críticos estacionarios y puntos críticos singulares.
DEMOSTRACIÓN.
Sea )
( 0
x
f un valor máximo; es decir ( ) )
(
0 x
f
x
f ≥ , entonces: 0
)
(
)
( 0 ≤
− x
f
x
f
Si 0
x x
, dividiendo por 0
x
x − tenemos 0
)
(
)
(
0
0
≤
−
−
x
x
x
f
x
f
Ahora obteniendo límite 0
)
(
)
(
0
0 0
0
+
+
→
→
≤
−
−
x
x
x
x
lím
x
x
x
f
x
f
lím resulta 0
)
´( 0 ≤
+
x
f .
Para 0
x
x , tenemos, obteniendo límite 0
)
(
)
(
0
0 0
0
−
−
→
→
≥
−
−
x
x
x
x
lím
x
x
x
f
x
f
lím resulta 0
)
´( 0 ≥
−
x
f
Suponga que f es derivable en 0
x , entonces 0
)
´( 0 =
x
f ; es decir 0
x es un punto crítico estacionario.
Suponga que f no es derivable en 0
x , entonces )
´( 0
x
f no existe; es decir 0
x es un punto crítico singular.
La demostración sería análoga para el caso de que )
( 0
x
f sea un valor mínimo.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-174-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
115
Ejemplo 1
Determinar los extremos para 5
4
2
)
( 2
+
−
= x
x
x
f en [ ]
3
,
0
SOLUCIÓN:
De acuerdo a lo enunciado, debemos analizar solamente los puntos críticos.
1.Puntos críticos de Frontera: 0
0 =
x y 3
0 =
x
2.Puntos críticos Estacionarios: valores de x para los cuales la derivada es igual a cero. Para obtenerlos
analizamos la derivada 4
4
)
´( −
= x
x
f
Ahora
0
)
1
(
4
0
)
´(
=
−
=
x
x
f
, entonces sería: 1
0 =
x .
3.Puntos críticos Singulares: valores de x para los cuales la derivada no existe. Al observar la derivada
notamos que se define para toda x ; por tanto, no existe puntos críticos singulares. Es lo que se espera
debido a que las funciones polinomiales son continuas y derivables en todo .
Bien, ahora nos corresponde clasificar a los puntos críticos, para lo cual, evaluamos la función en los puntos
críticos (Esto es suficiente debido a que se trata de una función polinómica, más adelante aprenderemos
criterios más fuertes, para otros casos):
( ) ( ) ( )
( ) ( ) ( )
3
)
1
(
11
5
3
4
3
2
3
5
5
0
4
0
2
0
2
2
=
=
+
−
=
=
+
−
=
f
f
f
Por inspección, se determina que:
En 3
0 =
x se encuentra el Valor Máximo f .
Y en 1
0 =
x se encuentra el Valor Mínimo de f .
Ejemplo 2
Determinar los extremos para 3 2
( ) 3 3
f x x x
= − + en [ ]
2,3
−
SOLUCIÓN:
Primero determinamos los puntos críticos.
1.Puntos críticos de Frontera: ´0 2
x = − y 0 3
x =
2.Puntos críticos Estacionarios: Analizando la derivada
2
´( ) 3 6
f x x x
= − , tenemos:
2
´( ) 0
3 6 0
3 ( 2) 0
f x
x x
x x
=
− =
− =
Entonces serían: 0
0 =
x y 0 2
x = .
3.Puntos críticos Singulares: No hay.
Bien, ahora evaluando en la función:
( ) ( ) ( )
( )
3 2
3 2
3 2
2 2 3 2 3 8 12 3 17
3 (3) 3(3) 3 27 27 3 3
(0) 3
(2) (2) 3(2) 3 1
f
f
f
f
− = − − − + = − − + = −
= − + = − + =
=
= − + = −](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-176-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
116
De acuerdo a estos resultados se puede concluir que el valor máximo de la función es 3, que se produce tanto
en 0 3
x = como en 0 0
x = ; y, el valor mínimo de la función es -17 que se produce en 0 2
x = − .
Ejercicios Propuestos 4.2
1. Determine el valor máximo y el valor mínimo :
1. 17
12
4
3
)
( 2
3
4
+
−
−
= x
x
x
x
f en [ ]
2,3
−
2.
5
3
4
( )
5 3
x
f x x
= − en [ ]
3,3
−
3. 3
1
( ) 4 2
3
f x x x
= − + en [ ]
5,3
−
4. 5
12
3
3
)
( 2
3
−
+
−
= x
x
x
x
f en [ ]
1,1
−
5. ( ) ( )4
2
1
−
= x
x
f en [ ]
2,2
−
6. ( )4
3
1
)
( −
= x
x
f en [ ]
1,2
−
Hasta el momento nos habíamos preocupado de determinar el mayor de todos
los valores de la función y el menor de todos en todo su dominio o en un intervalo
de su dominio, pero esto nos deja insatisfechos con respecto a puntos críticos que
bien pudieron ser extremos, u otros puntos que los pudiéramos considerar
máximos o mínimos cuando no lo son.
4.2.5 Máximos y Mínimos Locales O Relativos
Sea f una función de variable real. Sea
“ 0
x ” un punto del dominio de f . Entonces:
1. )
( 0
x
f es un valor máximo local de f , si
existe un intervalo ( )
b
a, en el dominio
de f que contiene a “ 0
x ” tal que )
( 0
x
f
es el valor máximo de f en ( )
b
a, .
2. )
( 0
x
f es un valor mínimo local de f , si
existe un intervalo ( )
b
a, en el dominio
de f que contiene a “ 0
x ” tal que )
( 0
x
f
es el valor mínimo de f en ( )
b
a, .
3. )
( 0
x
f es un valor extremo local de f ,
si es un máximo o un mínimo local.
Al mayor valor y al menor valor de todos, se les llamará extremos absolutos.
Observe el siguiente gráfico:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-177-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
118
Ejemplo
Para 3 2
( ) 3 3
f x x x
= − +
Analizando la primera derivada ( )
´( ) 3 2
f x x x
= − se observó que:
x )
´(x
f f
0
x Positiva (+) crece
0 2
x
Negativa (-) decrece
2
x Positiva (+) crece
Entonces:
1. Como antes de 0
x = la derivada es positiva y después es negativa se concluye que (0) 3
f = es un
máximo local.
2. Como antes de 2
x = la derivada es negativa y después es positiva se concluye que (2) 1
f = − es un
mínimo local.
Ejercicios Propuestos 4.3
Emplee el criterio de la primera derivada para clasificar los extremos locales:
1. 17
12
4
3
)
( 2
3
4
+
−
−
= x
x
x
x
f
2.
5
3
4
( )
5 3
x
f x x
= −
3. 3
1
( ) 4 2
3
f x x x
= − +
4. 5
12
3
3
)
( 2
3
−
+
−
= x
x
x
x
f
5. ( ) ( )4
2
1
−
= x
x
f
6. ( )4
3
1
)
( −
= x
x
f
Si nuestro objetivo ahora fuese trazar la gráfica de las funciones analizadas, no
tendríamos inconveniente, debido a que la información que hemos obtenido nos
permite hacerlo.
Ejemplo 1
Trazar la gráfica de 5
4
2
)
( 2
+
−
= x
x
x
f en [ ]
3
,
0 .
SOLUCIÓN:
Se ha obtenido 1
0 =
x como Punto Critico Estacionario y también se ha determinado que antes de este
punto la gráfica de la función es decreciente y después es creciente, por tanto su gráfica sería:
•
•
•
5
4
2
)
( 2
+
−
= x
x
x
f
( )
3
,
1
( )
5
,
0
( )
11
,
3](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-179-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
119
Note que para obtener la gráfica de la función anterior no es necesario el
análisis que se realizó, hubiera bastado con los criterios conocidos acerca de
funciones cuadráticas. Sin embargo se decidió realizarlo para que el lector
compruebe la concordancia de los resultados, aplicando uno u otro criterio, y
además para que se vaya familiarizando con los criterios nuevos, expuestos en
esta sección.
Para otros casos se hace imprescindible los nuevos criterios.
Ejemplo 2
Graficar 3 2
( ) 3 3
f x x x
= − + en [ ]
2,3
−
SOLUCIÓN:
Ya se obtuvieron los Puntos Críticos Estacionarios 0
0 =
x y 0 2
x = , también se determinó que antes de
0
0 =
x la gráfica de la función es creciente y después es decreciente hasta el otro punto 0 2
x = ; y después
de este punto crítico es otra vez creciente; por tanto, su gráfica es:
Ejercicios Propuestos 4.4
Elabore la gráfica de:
1. 17
12
4
3
)
( 2
3
4
+
−
−
= x
x
x
x
f
2.
5 3
3 20
y x x
= −
3.
3
1
3
9 2
y x x
= − +
4. 5
12
3
3
)
( 2
3
−
+
−
= x
x
x
x
f
5. ( ) ( )4
2
1
−
= x
x
f
6. ( )4
3
1
)
( −
= x
x
f
Para los casos de funciones polinomiales, los criterios estudiados podrían ser
suficientes para obtener una buena aproximación de su gráfica, debido a que son
funciones continuas y derivables en todo su dominio y se puede concluir sobre su
.
máx
y
mín
y
3 2
( ) 3 3
f x x x
= − +](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-180-320.jpg)









![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
129
2
2 2
2 2 2
1 1
1 1 1
1 0
x
x
x x
lím
x
x
x
x x x
→∞
= = = = ∞
+ + +
Por tanto, no hay asíntota horizontal.
ASÍNTOTA OBLICUA:
En ciertas funciones se cumple que: ( )
lím ( ) 0
x
f x mx b
→∞
− + =
⎡ ⎤
⎣ ⎦
donde
x
x
f
m
x
)
(
lím
∞
→
= y [ ]
mx
x
f
b
x
−
=
∞
→
)
(
lím
Si los límites existen, se dice que la gráfica de f tiene una asíntota oblicua
b
mx
y +
=
Entonces, para esta función sería:
2
2
2 2
2 2
2 2
1 1
1 1
1 1
1
x x x x
x
x
x
x x
m lím lím lím lím
x x x x x
x
x x
→∞ →∞ →∞ →∞
+
= = = = = =
+ +
+
2 2 2
1
1 2 2
x x x
x x x x x
b lím x lím lím
x x x
→∞ →∞ →∞
⎡ ⎤ ⎡ ⎤
− − −
⎡ ⎤
= − = = = −
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
+ − −
⎣ ⎦
⎣ ⎦ ⎣ ⎦
Por tanto, hay una asíntota oblicua 1
y x
= −
Paso 4. PUNTOS CRÍTICOS:
• P.C.F : no hay
• P.C.E:
( )( ) ( )
( )
( ) ( )
( )
( )
2
2
2
2 2 2
2 2
2
2 1 1
´( )
1 1
2 2 2
1 1
2
´( )
1
x
x x x
x
f x D
x x
x x x x x
x x
x x
f x
x
+ −
⎡ ⎤
= =
⎢ ⎥
+ +
⎣ ⎦
+ − +
= =
+ +
+
=
+
por lo tanto, tenemos P.C.E: 0
=
x y 2
x = −
• P.C.S: no hay
Paso 5. MONOTONÍA: Analizando el signo de ´
f
Paso 6: EXTREMOS: por el criterio de la primera derivada observamos que:
1. En 2
x = − la primera derivada cambia de signo, de positivo a negativo, por tanto aquí existe un Máximo
local.
2. En 0
x = la primera derivada cambia de signo, de negativo a positivo, por tanto aquí existe un Mínimo
local.
Paso 7. CONCAVIDAD: Debemos analizar la segunda derivada
2
−
+
+
+
+
+
+ −
−
−
−
−
−
´
f
f
+
+
+
+
+
+
crece crece
decrece
0](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-190-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
131
Cuando no se dispone de la regla de correspondencia, se deberá tener
condiciones que nos permitan concluir sobre la gráfica de una función.
Ejemplo
Bosqueje una función f de variable real que cumpla las siguientes condiciones:
1. Dom f =
2. f continua en ( ) ( )
∞
∪
−∞ ,
0
0
,
3. 0
)
1
( =
−
f , 0
)
4
(
)
(2
3 =
= f
f , 2
)
0
(
)
3
( =
=
− f
f , 4
)
2
( =
−
f , 2
)
3
( −
=
f , 1
)
1
( =
f
4. ε
−
⇒
−
∀
∃
ε
∀ 1
)
(
:
;
0
,
0 x
f
N
x
x
N
5. ε
−
⇒
∂
∀
∃∂
ε
∀ 3
)
(
0
:
;
0
,
0 x
f
x
x
6. −∞
=
−
→
)
(
lím
0
x
f
x
7. [ ] 0
)
3
(
)
(
lím =
−
−
+∞
→
x
x
f
x
8. 0
)
2
(
' =
−
f ,
9. 0
)
(
'
x
f para 3
2
∨
−
x
x ,
10. 0
)
(
'
x
f ,para 3
0
0
2
∨
− x
x
11. 0
)
1
(
'
' =
f
12. 0
)
(
'
'
x
f para 3
1
3
∨
−
x
x
13. 0
)
(
'
'
x
f para 3
1
0
0
3
∨
∨
− x
x
x
SOLUCIÓN:
Interpretemos las condiciones, tenemos:
1. Dominio de la función.
2. Intervalos de continuidad. Como es abierto tanto a la izquierda como a la derecha de cero, entonces se puede
esperar que exista una asíntota vertical o un punto de no definición.
3. Puntos de la gráfica de la función. Hay que ubicarlos en el plano cartesiano.
4. 1
)
(
lím =
−∞
→
x
f
x
. Asíntota horizontal 1
=
y , para x negativos.
5. 3
)
(
lím
0
=
+
→
x
f
x
. La función se aproxima a 3, por la derecha de 0.
6. −∞
=
−
→
)
(
lím
0
x
f
x
. Asíntota vertical, el eje y por la izquierda de 0
7. [ ] 3
)
(
lím −
=
+∞
→
x
x
f
x
Asíntota oblicua 3
−
= x
y para x posoitivos.
8. Punto crítico estacionario en 2
−
=
x
9. f crece en los intervalos ( )
2
,−
−∞ o en ( )
∞
,
3
10. f decrece en los intervalos ( )
0
,
2
− o en ( )
3
,
0
11. Punto de inflexión: ( )
1
,
1
12. f es cóncava hacia arriba en ( )
3
,−
−∞ o en ( )
3
,
1
13. f es cóncava hacia abajo en ( )
0
,
3
− o en ( )
1
,
0 o en ( )
∞
,
3
Entonces la grafica sería:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-192-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
133
2. Bosqueje una función f de variable real que cumpla las siguientes condiciones:
ƒ )
(
)
( x
f
x
f −
=
ƒ 2
)
(
lím −
=
−∞
→
x
f
x
ƒ +∞
=
+
→
)
(
1
x
f
lím
x
ƒ ∞
=
+
−
→
)
(
lím
1
x
f
x
ƒ 0
)
2
/
3
(
'
)
0
(
'
)
3
(
' =
=
=
− f
f
f
ƒ ( ) 0
3 =
−
f , ( ) 1
2
3 −
=
f ,
2
1
)
2
( −
=
f , 0
)
0
( =
f
ƒ 0
)
(
'
x
f en ( )
1
,
0 y ⎟
⎠
⎞
⎜
⎝
⎛
3
,
2
3
ƒ 0
)
2
(
'
' =
f
3. Bosqueje el gráfico de una función f tal que:
ƒ Dominio f =IR
ƒ Contínua en ( ) ( )
∞
∪
−∞ ,
2
2
,
ƒ f(-1)=4, f(0)=6, f(2)=-3, f(3)=0
ƒ ε
ε
+
⇒
∂
−
∀
∃∂
∀ 1
)
(
2
0
:
;
0
,
0 x
f
x
x
ƒ M
x
f
x
x
M −
⇒
∂
−
∀
∃∂
∀ )
(
2
0
:
;
0
,
0
ƒ ε
−
⇒
−
∀
∃
ε
∀ 2
)
(
:
;
0
,
0 x
f
N
x
x
N
ƒ [ ] 0
)
(
lím =
−
+∞
→
x
x
f
x
ƒ ( ) ( ) ( )
2
,
0
,
0
)
(
'
;
,
2
0
,
,
0
)
(
' ∈
∞
∪
−∞
∈
x
para
x
f
x
para
x
f
ƒ ( ) ( ) ( )
∞
∪
−
∈
−
−∞
∈
,
2
2
,
1
,
0
)
(
'
'
;
1
,
,
0
)
(
'
' x
para
x
f
x
para
x
f
4. Suponga que ( )
2
'( ) ( 3)( 1) 2
f x x x x
= − − + y (1) 0
f = , ( )
2 5
f − = , (3) 5
f = − ,
esboce una gráfica para f .
5. Bosqueje el gráfico de una función f continua en IR tal que ( 4) (5) 0
f f
− = = , (0) 8
f = ,
(1) 6
f = , ( )
1 7
f − = − , ( )
2 3
f = − y además la gráfica de su derivada es:
6. Bosqueje el gráfico de una función f continua en IR tal que ( 2) 4
f − = , (1) 0
f = , (2) 1
f = ,
(3) 3
f = y además la gráfica de su derivada es:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-194-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
135
4.5 TEOREMA DEL VALOR MEDIO PARA DERIVADAS
(TEOREMA DE LAGRANGE)
Si f es una función continua en [ ]
b
a, y
derivable en ( )
b
a, entonces, existe al
menos un número “ 0
x ” en ( )
b
a, tal que
a
b
a
f
b
f
x
f
−
−
=
)
(
)
(
)
´( 0
Lo que nos indica este teorema es que si la función es continua en un intervalo
cerrado y suave en su interior entonces existirá un punto en ese intervalo para el
cual la recta tangente y la recta secante en los extremos del intervalo tienen igual
pendiente.
Demostración:
Sea )
(
)
(
)
( x
g
x
f
x
S −
= donde g es la recta entre los puntos ( )
)
(
, a
f
a y ( )
)
(
, b
f
b ,
entonces podemos obtener su ecuación:
( )
( )
a
x
a
b
a
f
b
f
a
f
y
x
x
m
y
y
−
−
−
=
−
−
=
−
)
(
)
(
)
(
0
0
, es decir
( )
a
x
a
b
a
f
b
f
a
f
x
g
y −
−
−
+
=
=
)
(
)
(
)
(
)
(
b- a
f
(
b
)
-
f
(
a
)
a b
)
(a
f
)
(b
f
0
x
)
(x
f
y =
Recta Tangente
Recta Secante](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-196-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
136
Reemplazando, resulta: ( )⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
+
−
= a
x
a
b
a
f
b
f
a
f
x
f
x
S
)
(
)
(
)
(
)
(
)
(
Obtengamos ( ) 0
)
(
)
(
)
(
)
(
)
( =
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
+
−
= a
a
a
b
a
f
b
f
a
f
a
f
a
S y
( ) 0
)
(
)
(
)
(
)
(
)
( =
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
+
−
= a
b
a
b
a
f
b
f
a
f
b
f
b
S
Por tanto, ( )
b
a
x ,
0 ∈
∃ tal que 0
)
´( 0 =
x
S
Para lo cual ⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
=
a
b
a
f
b
f
x
f
x
S
)
(
)
(
)
´(
)
´( y 0
)
(
)
(
)
´(
)
´( 0
0 =
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
=
a
b
a
f
b
f
x
f
x
S
Por lo último
a
b
a
f
b
f
x
f
−
−
=
)
(
)
(
)
´( 0 L.Q.Q.D.
Ejemplo 1
Encuentre el número “ 0
x ” garantizado por el teorema del valor medio para derivadas si
2
( )
f x x
= en [ ]
1,2
− .
SOLUCIÓN:
Observe que f es continua en [ ]
1,2
− y como ´( ) 2
f x x
= por tanto es diferenciable en ( )
1,2
− se
cumplen las hipótesis del teorema del valor medio, por tanto la existencia de 0
x en ( )
1,2
− tal que
( )
0
(2) ( 1)
´( )
2 1
f f
f x
− −
=
− −
está garantizada y lo podemos encontrar.
Para lo cual 0 0
´( ) 2
f x x
= y
( )
(2) ( 1) 4 1 3
1
2 1 3 3
f f
− − −
= = =
− −
Igualando y despejando, resulta:
0
0
2 1
1
2
x
x
=
=
.
Geométricamente.
Recta Tangente
Recta Secante
2
( )
f x x
=
[ ]
0.5](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-197-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
137
Ejemplo 2
Use el teorema del valor medio para demostrar que: b
a
a
sen
b
sen −
≤
−
SOLUCIÓN:
Usemos ( )
f x senx
= . Note que es una función continua en [ ]
,
a b y derivable en ( )
,
a b por tanto de
acuerdo al teorema de Lagrange , existe un ( )
0 ,
x a b
∈ tal que 0
( ) ( )
´( )
f b f a
f x
b a
−
=
−
.
Reemplazando y simplificando
0
cos
senb sena
x
b a
−
=
−
Por otro lado
0
0 cos 1
x
≤ ≤
Entonces 0 1
senb sena
b a
−
≤ ≤
−
Aplicando propiedades del valor absoluto y despejando.
1
senb sena
b a
senb sena b a
−
≤
−
− ≤ −
Que es lo que se quería demostrar.
Ejemplo 3
Dos carros de la policía de transito equipadas con radar están situadas a 7 kilómetros de
distancia en una autopista, cuando un camión pasa junto al primero de ellos, se le mide una
velocidad de 90 km por hora; 4 minutos después al pasar junto al otro coche, éste le mide 70
km por hora. Aunque el camión bajó la velocidad, pruebe que en algún momento en esos 4
minutos ha superado el límite de velocidad permitida que es de 100 km por hora.
SOLUCIÓN:
Sea ( )
e f t
= , el espacio recorrido por el camión, una función del tiempo, continua y diferenciable en el
cualquier intervalo de tiempo mientras dure el movimiento.
Primeramente calculemos la velocidad media del camión en esos 4 minutos:
7
105
4
60
m
e km km
v
h
t horas
Δ
= = =
Δ
Sea 1
t el momento en que se le mide al camión una velocidad de 1 90km
v
h
= y sea 2
t el momento en que
se mide una velocidad de 2 70km
v
h
= . De acuerdo al teorema de Lagrange existe un ( )
0 1 2
,
t t t
∈ en el cual
( )
0
´
de
f t
dt
= , la velocidad instantánea del camión, fue igual a la velocidad media (105km
h
), lo cual
demuestra que ha superado el límite de velocidad (100km
h
).
Como particularidad del teorema de Lagrange tenemos el teorema de Rolle.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-198-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
138
4.6 TEOREMA DE ROLLE
Si f es una función continua en [ ]
b
a, y
derivable en ( )
b
a, y si )
(
)
( b
f
a
f = entonces,
existe al menos un número “ 0
x ” en ( )
b
a, tal
que 0
)
´( 0 =
x
f
El teorema del valor medio para dos funciones sería:
Ejercicios Propuestos 4.7
1. La función x
x
f =
)
( satisface la hipótesis del teorema del valor medio en el intervalo [0,2]. Diga si esto es
verdadero o falso, justificando apropiadamente su respuesta.
2. Sea .
2
)
( 2
4
x
x
x
f −
= Hallar todos los valores de 0
x en el intervalo [-2,2] que satisfacen el teorema de
Rolle.
3. La altura que alcanza una bola t segundos después de ser lanzada, está dada por la siguiente función:
32
48
16
)
( 2
+
+
−
= t
t
t
f .
a) Comprobar que f (1) = f (2).
b) Según el teorema de Rolle, ¿qué velocidad ha llevado en algún momento del intervalo [1,2]?
4. Sea .
,
,
;
)
( 2
IR
x
x
x
f ∈
∂
+
+
= δ
β
α
β
α Encontrar el valor de 0
x que satisfaga el teorema del
valor medio para derivadas en [a,b].
5. Dos carros patrullas equipadas con radar están situadas a 5 millas de distancia en una autopista, cuando un
camión pasa junto al primero de ellos, se le mide una velocidad de 55 millas por hora; 4 minutos después al
pasar junto a otro coche, éste le mide 50 millas por hora. Probar que en algún momento en esos 4 minutos ha
superado el límite de velocidad de 70 millas por hora.
6. Use el teorema del valor medio para demostrar que: cos cos
b a b a
− ≤ −](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-199-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
139
7. Considere
4
5
( )
f x x
= en el intervalo [ ]
1,2
− . Demuestre que no se cumple la conclusión del Teorema de
Lagrange. Justifique.
8. Considere ( ) 3
f x x
= en el intervalo [ ]
1,8
− . Verifique que no se cumple una de las hipótesis del Teorema
de Lagrange, sin embargo la conclusión sí se cumple. Justifique.
4.7 TEOREMA DE CAUCHY
Sean f y g funciones continuas en [ ]
b
a, y diferenciables en
( )
b
a, entonces, existe al menos un número “ 0
x ” en ( )
b
a, tal
que
)
(
)
(
)
(
)
(
)
´(
)
´(
0
0
a
g
b
g
a
f
b
f
x
g
x
f
−
−
=
No olvide demostrarlo.
Con los resultados del teorema anterior, se pueden calcular indeterminaciones.
4.8 TEOREMA DE L’HOPITAL
Suponga que 0
)
(
lím
)
(
lím =
=
→
→
x
g
x
f
u
x
u
x
o también
∞
=
=
→
→
)
(
lím
)
(
lím x
g
x
f
u
x
u
x
. Si
)
´(
)
´(
lím
x
g
x
f
u
x→
existe en sentido finito
o infinito; entonces:
)
´(
)
´(
lím
)
(
)
(
lím
x
g
x
f
x
g
x
f
u
x
u
x →
→
=
Donde −∞
+∞
= −
+
,
,
,
, a
a
a
u
No olvide demostrarlo.
Ejemplo 1
Calcular
x
x
x
sen
lím
0
→
SOLUCIÓN:
Aplicando el teorema de L´hopital, tenemos:
1
0
cos
1
cos
lím
sen
lím
0
0
=
=
=
→
→
x
x
x
x
x](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-200-320.jpg)
![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
140
Ejemplo 2
Calcular ( ) x
x
x
1
0
1
lím +
→
SOLUCIÓN:
Transformando la expresión primero, resulta:
( ) ( )
( ) ( )
x
x
x
x
x
x
x
x
x
x
x
e
e
e
x
+
+
→
+
→
→
→
=
=
=
+
1
ln
lím
1
ln
0
1
ln
0
1
0
0
1
lím
lím
1
lím
Aplicando el teorema de L´hopital al exponente, tenemos:
1
1
1
1
lím
)
1
ln(
lím
0
0
=
+
=
+
→
→
x
x
x
x
x
Por tanto, ( ) e
e
x x
x
=
=
+
→
1
1
0
1
lím
Ejemplo 3
Calcular
3
0
sen
lím
x
x
x
x
−
→
SOLUCIÓN:
Aplicando el teorema de L´hopital, tenemos:
2
0
3
0 3
1
cos
lím
sen
lím
x
x
x
x
x
x
x
−
=
−
→
→
Como se mantiene la indeterminación, volvemos a aplicar la regla de L´Hopital, y así tantas veces como sea
necesario:
6
1
6
sen
lím
3
1
cos
lím
0
2
0
−
=
−
=
−
→
→ x
x
x
x
x
x
Ejemplo 4
Calcular
3
2
4
1
5
3
lím 2
2
−
+
+
−
∞
→ x
x
x
x
x
SOLUCIÓN:
Note que aquí tenemos:
∞
∞
Aplicando el teorema de L´hopital, tenemos:
2
8
5
6
lím
+
−
∞
→ x
x
x
Volviendo a aplicar L´Hopital resulta:
4
3
8
6
lím =
∞
→
x
Ejemplo 5
Calcular ( ) x
x
x 2
tg
1
2
lím
π
→
−
SOLUCIÓN:
Observe que aquí tenemos ∞
1 . Entonces la regla de L´hopital no es aplicable directamente.
Transformando la expresión primero, resulta:
( ) ( ) ( ) ( )
[ ]
( )
x
g
x
x
x
x
x
x
x
x
x
x
e
e
e
x 2
cot
1
2
2
tg
2
ln
lím
2
ln
tg
1
2
ln
1
2
tg
1
lím
lím
2
lím
π
→
π
π
−
−
→
−
→
π
→
=
=
=
−](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-201-320.jpg)

![MOISES VILLENA MUÑOZ Cáp. 4 Temas Adicionales de la derivada
142
Misceláneos
1. Bosqueje el grafico de f analizando dominio, simetría , asíntotas, intervalos de monotonía y
concavidad, extremos locales y puntos de inflexión
a)
1
2
)
(
−
−
=
x
x
x
f h) 5
5
)
( 2
3
−
−
+
= x
x
x
x
f
b)
1
2
)
(
2
−
−
=
x
x
x
f i) 3
5
)
( x
x
x
f −
=
c)
1
)
(
2
−
=
x
x
x
f j) ( )
8
)
( 2
3
2
−
= x
x
x
f
d)
1
2
)
(
2
−
=
x
x
f k)
3
4
4
)
(
2
2
+
−
−
=
x
x
x
x
x
f
e) ( )
x
x
x
f −
= 8
)
( 3
f) 1
)
( 3
2
+
=
x
xe
x
f
g)
x
x
x
f
1
)
(
2
−
=
2. Bosqueje una gráfica posible de una función f que tenga todas las siguientes características:
• f es continua en toda su extensión
• 3
)
4
( −
=
−
f , 0
)
0
( =
f , 2
)
3
( =
f
• 0
)
4
´( =
−
f , 0
)
3
´( =
f , 0
)
´(
x
f para 4
−
x , 0
)
´(
x
f para 3
4
− x ,
0
)
´(
x
f para 3
x .
• 0
)
4
´´( =
−
f , 0
)
0
´´( =
f , 0
)
´´(
x
f para 4
−
x
• 0
)
´´(
x
f para 0
4
− x , 0
)
´´(
x
f para 0
x
3. Bosqueje una gráfica posible de una función f que tenga todas las siguientes características:
• +∞
=
→
)
(
lím x
f
a
x
0
)
(
lím =
−∞
→
x
f
x
−∞
=
+∞
→
)
(
lím x
f
x
e
d
b
a
0
• 0
)
(
)
( =
= e
f
c
f , 5
)
( =
b
f , 3
)
0
( =
f , 1
)
(
)
( =
= d
f
a
f
• 0
)
´´( =
b
f , )
´´(c
f no existe, 0
)
´( =
d
f , 0
)
´´(
d
f ,
• ( ) ( )[ ]
0
)
´(
,
,
∪
−∞
∈
∀ x
f
d
c
a
x , ( ) ( )[ ]
0
)
´(
,
,
+∞
∪
∈
∀ x
f
d
c
a
x
• ( ) ( )[ ]
0
)
´´(
,
,
∪
−∞
∈
∀ x
f
b
a
a
x , ( ) ( )[ ]
0
)
´´(
,
,
+∞
∪
∈
∀ x
f
c
c
b
x
4. Grafique f tal que la gráfica de su derivada ´
f es:
Suponga que 1
)
1
( −
=
−
f
x
y
1
−
2
3
−](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-203-320.jpg)















![MOISES VILLENA MUÑOZ Cap. 5 Aplicaciones de la derivada
5.3.3 ESTIMACION DE ERRORES
Sea la variación en
)
(x
f
y = y cuando varía se la se la calcula
empleando la formula
x
x
x
f
y ∆
≈
∆ )
´(
Ejemplo
El lado de un cubo se midió en 11.4 cm. con un posible error de ± 0.05 cm. Calcule el volumen
del cubo y proporcione una estimación para el posible error de este valor.
SOLUCIÓN:
El volumen del cubo se lo obtiene con la formula .
3
l
V =
Como entonces
cm
l 4
.
11
= ( ) 3
3
5
.
1481
4
.
11 cm
V =
= .
Pero como hay un margen de error (variabilidad) en la medición del lado: , se propaga
un error en el valor del volumen calculado.
cm
l 05
.
0
±
=
∆
Este margen de error en el volumen se lo calcula de la siguiente manera: l
dl
dV
V ∆
≈
∆ Es decir:
3
2
2
5
.
19
)
05
.
0
(
)
4
.
11
(
3
3
cm
V
V
l
l
V
±
≈
∆
±
≈
∆
∆
≈
∆
Esto quiere decir que ( ) 3
5
.
19
5
.
1481 cm
V ±
=
Ejercicios Propuestos 5.3
1. En los siguientes ejercicios use diferenciales para calcular valores aproximados de los números dados.
Compare con los valores reales:
a) 402 b) 3 91
.
26 c) 9
.
35 d) 6 05
.
64
2. El diámetro exterior de un delgado casquete esférico es de 12 pies. Si el casquete tiene 0.3 pulgadas de
espesor, use diferenciales para calcular el volumen aproximado de la región interior del mismo.
3. Un rodillo cilíndrico mide exactamente 12 pulgadas de longitud y se ha estimado su diámetro en 6 ± 0.005
pulgadas. Calcule su volumen con una estimación del error.
4. Se mide el radio de una esfera con un instrumento cuya precisión es de 0.05 cm.. Si la medición registra un
radio de 15 cm. Determine el error que tendrá el volumen de la esfera
5.4 POLINOMIO DE TAYLOR
La ecuación de la recta tangente en el punto es
es decir
( )
)
(
, 0
0 x
f
x
[ 0
0
0 )
´(
)
( x
x
x
f
x
f
y −
=
− ] [ ]
0
0
0 )
´(
)
( x
x
x
f
x
f
y −
+
= .
En la vecindad de ,
0
x )
(x
f
y ≈ ; por tanto una buena aproximación
para una función diferenciable en un punto sería la recta tangente en ese
punto; es decir:
[ ]
0
0
0 )
´(
)
(
)
( x
x
x
f
x
f
x
f −
+
≈ .
141](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-219-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 5 Aplicaciones de la derivada
Lo anterior corresponde a la aproximación de una función mediante
un polinomio lineal.
Para mayor orden tenemos:
[ ] [ ] [ ] [ ]n
n
x
x
n
x
f
x
x
x
f
x
x
x
f
x
x
x
f
x
f
x
f 0
0
3
0
0
2
0
0
0
0
0
!
)
(
...
!
3
)
´´´(
!
2
)
´´(
)
´(
)
(
)
( −
+
+
−
+
−
+
−
+
≈
El Polinomio de Taylor de orden “n” para una función.
NO OLVIDE DEMOSTRARLO.
Si 0 se llama Polinomio de Mclaurin. En tal caso sería:
0 =
x
[ ] [ ] [ ] ...
!
3
)
0
´´´(
!
2
)
0
´´(
)
0
´(
)
0
(
)
(
3
2
+
+
+
+
≈ x
f
x
f
x
f
f
x
f
Ejemplo
Hallar el polinomio de Taylor de orden 4 para y empleelo para calcular .
x
e
x
f =
)
( 1
.
0
e
SOLUCIÓN:
[ ] [ ] [ ] [ ]4
0
0
3
0
0
2
0
0
0
0
0
!
4
)
(
!
3
)
´´´(
!
2
)
´´(
)
´(
)
(
)
( x
x
x
f
x
x
x
f
x
x
x
f
x
x
x
f
x
f
x
f
IV
−
+
−
+
−
+
−
+
≈
[ ] [ ] [ ] [ ]
24
6
2
1
0
!
4
0
!
3
0
!
2
0
4
3
2
4
0
3
0
2
0
0
0
x
x
x
x
e
x
e
x
e
x
e
x
e
e
e
x
x
+
+
+
+
≈
−
+
−
+
−
+
−
+
≈
bien, ahora reemplazando 1
.
0
=
x resulta:
000004166
.
0
000166666
.
0
005
.
0
1
.
0
1
)
1
.
0
( +
+
+
+
≈
f
105170833
.
1
)
1
.
0
( ≈
f
Ejercicios Propuestos 5.4
1. Hallar el polinomio de Maclaurin de orden “n” para:
a) ; n=4 c)
( ) x
e
x
f 3
= x
x
f π
= sen
)
( ; n=3
b) ; n=4 d)
x
e
x
x
f −
= 2
)
(
1
1
)
(
2
+
=
x
x
f ; n=4
d)
2
cosh
)
(
x
x
e
e
x
x
f
−
+
=
= ; n=10
2. Hallar el polinomio de Taylor de grado n, alrededor de .
0
x
a)
x
x
f
1
)
( = ; n=4; 1
0 =
x c) ; n=4;
x
x
f ln
)
( = 1
0 =
x
b) x
x
f =
)
( ; n=4; 4
0 =
x
142](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-220-320.jpg)





![MOISES VILLENA MUÑOZ La integral Indefinida
Las primeras 11 fórmulas se las puede entender fácilmente de
acuerdo a las formulas que se proporcionaron para derivadas.
Ejemplo 1
Calcular ∫ dx
x2
SOLUCIÓN:
Sería cuestión de emplear la formula 2.
C
x
C
x
dx
x +
=
+
+
=
+
∫ 3
1
2
3
1
2
2
Ejemplo 2
Calcular
∫ dx
x
1
SOLUCIÓN:
Sería cuestión de emplear la formula 2.
C
x
dx
x
dx
x
+
=
=
+
−
+
−
−
∫
∫ 1
1
2
1
2
1
2
1
1
Ejemplo 3
Calcular
∫ +
dx
x2
4
1
SOLUCIÓN:
Sería cuestión de emplear la formula 17.
( ) C
dx
x
x
+
=
+
∫ 2
2
2
arctan
2
1
2
1
Para suma, resta de funciones y multiplicación por escalares
hacemos uso de las siguientes propiedades.
1.2.2 PROPIEDADES.
La Integral Indefinida cumple con propiedades de linealidad, es
decir:
1. [ ]
∫
∫ ∫ ±
=
± dx
x
g
dx
x
f
dx
x
g
x
f )
(
)
(
)
(
)
(
2.
∫
∫ ∈
= R
k
dx
x
f
k
dx
x
kf ;
)
(
)
(
4](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-226-320.jpg)







![MOISES VILLENA MUÑOZ La integral Indefinida
Entonces, aquí sería también x
u ln
= y dx
dv = . Entonces dx
x
du
1
= y
x
dx
v =
=
∫
Por tanto:
C
x
x
x
dx
x
x
x
x
xdx
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
∫
∫ ln
1
ln
ln
Ejemplo 6
Calcular
∫ dx
x
x arctg
SOLUCIÓN:
Tomamos x
u y
arctg
= xdx
dv = , entonces: dx
x
du
2
1
1
+
= y
2
2
x
v =
Por tanto:
( )
dx
x
x
x
x
dx
x
x
x
x
xdx
x
∫
∫
∫
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
1
arctg
1
1
2
2
arctg
arctg
2
2
2
1
2
2
1
2
2
2
Para la última integral dividimos el numerador entre el denominador, resulta:
1
1
1
1 2
2
2
+
−
=
+ x
x
x
Reemplazando
∫ ∫
∫
∫ −
=
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
+
x
x
dx
x
dx
dx
x
dx
x
x
arctg
1
1
1
1
1
1 2
2
2
2
FINALMENTE: [ ] C
x
x
x
x
xdx
x +
−
−
=
∫ arctg
arctg
arctg 2
1
2
2
1
Ejercicios Propuestos 1.3
Encuentre las antiderivadas de:
1.
∫ dx
e
x x
3
2. ( )
∫ + dx
e
x x
2
1
3. ( )
∫ − xdx
x 3
sen
1
2
4. ( )
∫ − dx
x
x 1
3
sen
5.
∫ −
dx
e
x x
2
2
6. ( )
∫ +
− dx
e
x
x x
2
2
2
3
7. ( )
∫ − xdx
x ln
1
2
11. ( )
∫ dx
x
x 2
arctg
12.
∫ dx
e x
13.
∫ ⎟
⎠
⎞
⎜
⎝
⎛
+
+ dx
x
x 2
1
ln
14.
∫ dx
x
arcsin
15.
∫ xdx
arctg
16. ( )
∫ dx
x
tan
arc
17. ( )
∫ dx
x
ln
cos
12](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-234-320.jpg)



![MOISES VILLENA MUÑOZ La integral Indefinida
TIPO III. Integrales de la forma: nxdx
x
m cos
sen
∫ , ,
nxdx
x
m sen
sen
∫
nxdx
x
m cos
cos
∫
En este caso se recomienda usar, las siguientes identidades como
sea conveniente:
( ) ( )
[ ]
( ) ( )
[ ]
( ) ( )
[ ]
x
n
m
x
n
m
nx
mx
x
n
m
x
n
m
nx
mx
x
n
m
x
n
m
nx
mx
−
+
+
=
−
−
+
−
=
−
+
+
=
cos
cos
2
1
cos
cos
cos
cos
2
1
sen
sen
sen
sen
2
1
cos
sen
Ejemplo 1
Calcular: dx
x
x
∫ 3
cos
2
sen
SOLUCIÓN:
Empleando la identidad trigonométrica respectiva y simplificando, resulta:
( ) ( )
[ ]
( )
C
x
x
dx
x
xdx
dx
x
x
dx
x
x
+
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
=
−
+
+
=
∫ ∫
∫
∫
cos
5
5
cos
2
1
sen
5
sen
2
1
3
2
sen
3
2
sen
2
1
3
cos
2
sen
Ejemplo 2
Calcular xdx
x
x 3
sen
2
sen
sen
∫
SOLUCIÓN:
Agrupando y aplicando identidades, tenemos:
( )
( ) ( )
[ ]
( )
[ ]
[ ] [ ]
C
x
x
x
xdx
xdx
xdx
dx
x
x
x
x
xdx
x
xdx
x
dx
x
x
x
x
xdx
x
x
xdx
x
x
xdx
x
x
+
⎥
⎦
⎤
⎢
⎣
⎡
+
+
−
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
+
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
=
−
−
−
=
−
−
+
−
=
=
∫ ∫ ∫
∫ ∫
∫
∫
∫
∫
∫
∫
2
2
cos
4
4
cos
6
6
cos
4
1
2
sen
4
sen
6
sen
4
1
2
sen
4
sen
2
1
0
sen
6
sen
2
1
2
1
cos
3
sen
3
cos
3
sen
2
1
3
sen
cos
3
sen
3
cos
2
1
3
sen
2
1
cos
2
1
cos
2
1
3
sen
2
sen
sen
3
sen
2
sen
sen
16](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-238-320.jpg)





![MOISES VILLENA MUÑOZ La integral Indefinida
Ejemplo 2
Calcular
( )
∫ + 2
3
2
3
9
x
dx
x
SOLUCIÓN:
En este caso hacemos t
x tg
3
= entonces dt
t
dx 2
sec
3
=
Reemplazando y resolviendo, resulta:
( )
( )
( )
( )
( )
( )
[ ] C
t
t
tdt
tdt
t
dt
t
t
dt
t
t
t
dt
t
t
t
dt
t
t
t
dt
t
t
dt
t
t
t
dt
t
t
t
dt
t
t
t
tdt
t
t
x
dx
x
+
+
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
−
=
=
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
=
+
∫ ∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
cos
sec
3
sen
tg
sec
3
sec
tg
sec
sec
tg
3
sec
1
sec
tg
3
sec
tg
tg
3
sec
tg
3
sec
27
sec
tg
81
sec
3
sec
tg
81
9
tg
9
sec
3
tg
27
sec
3
9
tg
3
tg
3
9
2
2
2
3
3
2
3
3
2
3
3
2
2
3
2
2
3
2
3
2
3
2
3
Ahora por trigonometría, del cambio de variable
3
tg
x
t = tenemos el siguiente triángulo:
9
2
+
x
t
Por tanto
3
9
sec
2
+
=
x
t y
9
3
cos
2
+
=
x
t
FINALMENTE,
( )
C
x
x
x
dx
x
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+
+
=
+
∫ 9
3
3
9
3
9
2
2
2
3
2
3
x
3
22](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-244-320.jpg)


![MOISES VILLENA MUÑOZ La integral Indefinida
Entonces
3
arcsen
u
t = y
3
9
cos
2
u
t
−
=
Por tanto,
[ ]
C
u
u
u
C
t
t
t
du
u
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡ −
+
⎟
⎠
⎞
⎜
⎝
⎛
=
+
+
=
−
∫
3
9
3
3
arcsen
2
9
cos
sen
2
9
9
2
2
Finalmente, como 2
+
= x
u , reemplazando resulta:
( ) ( )
C
x
x
x
C
u
u
u
du
u
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡ +
−
+
+
⎟
⎠
⎞
⎜
⎝
⎛ +
=
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡ −
+
⎟
⎠
⎞
⎜
⎝
⎛
=
−
∫
9
2
9
2
3
2
arcsen
2
9
9
9
3
arcsen
2
9
9
2
2
2
Ejercicio Propuestos 1.5
Encuentre las antiderivadas de:
1.
∫ − dx
x
x 2
2
9
2.
( )
∫ − 2
3
2
1 x
dx
3.
( )
∫ −
dx
x
x
2
3
2
2
1
4.
∫ −
dx
x
x
2
2
9
5.
∫ + 9
2
x
x
dx
6.
∫ − 9
2
3
x
x
dx
7.
∫ −1
2
4
x
x
dx
8.
∫ −
dx
x
x
2
2
2
9.
∫ − 2
2
4 x
x
dx
x
10.
( )
∫ +
+
3
2
13
4x
x
dx
11.
∫ + x
e
dx
2
1
12.
∫ +
+ 1
tg
4
tg
sec
2
2
x
x
xdx
13.
∫ + x
xdx
x
4
sen
9
cos
sen
14.
∫ + 2
1
arctg
x
xdx
x
15.
( )
∫ +
dx
x
e
x tanx
arc
2
3
2
1
16.
∫ dx
x
arc
x cos
2
17.
∫ −
− x
x
x
dx
x
2
ln
ln
4
1
ln
18.
( )
∫ −
+ 4
2
1
1 x
x
xdx
19.
∫ +
− 2
2
4
3
x
x
dx
x
20.
∫ +
+ 2
3 4
8
11
x
x
dx
x
25](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-247-320.jpg)



x
C
x
B
x
x
A
x +
−
+
+
−
=
+ 4
2
5
4
2
5 2
2
Evaluando para 0
=
x ,
( ) ( ) ( )
( ) ( )
( )
[ ]( )
5
2
5
2
0
4
0
2
5
0
4
0
2
0
5 2
2
=
=
+
−
+
+
−
=
+
A
A
C
B
A
Para 2
=
x , porque anulamos el término que contiene a B y como ya se conoce el valor de A
( ) ( ) ( )
( ) ( )
( )
[ ]( )
( )
5
54
2
1
22
2
4
2
2
5
2
4
2
2
2
5
5
2
2
2
=
+
=
+
−
+
+
−
=
+
C
C
C
B
A
Evaluando para 1
=
x y empleando lo valores de A y C, tenemos:
( ) ( ) ( )
( ) ( )
( )
[ ]( )
( ) ( )
[ ]
10
23
2
2
7
1
4
1
2
5
1
4
1
2
1
5
5
54
5
2
5
54
2
5
2
2
=
+
−
+
=
+
−
+
+
−
=
+
B
B
B
Ahora, integrando resulta
( )
( )
( ) C
x
x
x
x
dx
x
x
x
x
dx
x
x
dx
x
x
x
dx
x
dx
x
x
x
x
dx
x
x
x
x
+
−
+
+
−
+
=
+
−
+
+
−
+
=
+
−
+
+
−
−
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
+
−
+
=
+
−
+
∫
∫
∫
∫
∫
∫
2
arctg
5
54
5
4
ln
10
23
ln
5
2
1
2
1
5
54
5
4
ln
10
23
ln
5
2
5
4
1
5
54
5
4
4
2
10
23
1
5
2
5
4
4
2
5
4
2
5
2
2
2
2
2
2
5
54
10
23
5
2
2
3
2
Ejemplo 2
Calcular
∫ +
−
dx
x
x
x
3
3
1
SOLUCIÓN:
Note que en esta integral la fracción no es propia, el grado del numerador es 3 y el del
denominador también; por tanto dividiendo primero, se obtiene:
x
x
x
x
x
x
+
+
−
=
+
−
3
3
3
1
1
1
La integral sería ahora:
28](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-250-320.jpg)

x
C
x
B
x
A
x +
+
+
=
+ 2
1
1 2
Evaluando para 0
=
x , resulta:
( ) ( )
[ ]( )
1
)
1
(
1
0
)
0
(
2
1
0
1
0 2
=
=
+
+
+
=
+
A
A
C
B
A
Evaluando para 1
=
x y utilizando el valor obtenido para A, resulta
( ) ( )
[ ]( )
0
2
2
2
2
1
)
1
(
2
1
1
1
1
1 2
=
+
+
+
=
+
+
+
=
+
C
B
C
B
C
B
Evaluando para 1
−
=
x y utilizando el valor obtenido para A, resulta
( )
( ) ( )
( )
[ ]( )
2
2
2
2
0
1
1
2
1
1
1
1
1 2
−
=
−
−
+
=
−
+
−
+
+
−
=
+
−
C
B
C
B
C
B
Tomando simultáneamente, ambos resultados, encontramos los valores de B y C
⎩
⎨
⎧
−
=
−
=
+
2
2
0
2
C
B
C
B
Bastaría con sumar miembro a miembro las ecuaciones y obtendríamos B:
2
1
2
4
−
=
−
=
B
B
Entonces
1
2
1
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
−
=
C
C
B
C
OTRO MÉTODO para obtener A, B y C, que en ocasiones es más ventajoso, es el que sigue:
En la expresión ( ) ( )
[ ]( )
x
C
x
B
x
A
x +
+
+
=
+ 2
1
1 2
simplificamos hasta obtener un polinomio
reducido en ambos lados de la ecuación, es decir:
( ) A
Cx
x
B
A
x
Cx
Bx
A
Ax
x
+
+
+
=
+
+
+
+
=
+
2
2
2
2
1
2
1
De la última expresión, rápidamente se puede decir que:
⎪
⎩
⎪
⎨
⎧
=
=
+
=
A
C
B
A
1
1
2
0
Por tanto
⎪
⎩
⎪
⎨
⎧
=
−
=
=
1
2
1
1
C
B
A
En fin, ahora integrando tenemos:
29](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-251-320.jpg)



















![MOISES VILLENA Cap. 6 Series
6. 2. SERIES DE TÉRMINOS POSITIVOS
TEOREMA
Una serie ∑ de términos no negativos converge si y
n
a
sólo si, sus sumas parciales están acotadas por arriba.
6.2.1 CRITERIOS PARA ESTABLECER LA CONVERGENCIA DE
SERIES DE TERMINOS POSITIVOS.
6.2.1.1 CRITERIO DE LA INTEGRAL
Sea f una función continua positiva, no creciente,
definida en el intervalo [ )
∞
,
1 y suponga que ( )
n
f
an
=
para todo entero positivo . Entonces la seria ∑
n
∞
=1
n
n
a
converge si y sólo si la integral impropia
∫
∞
1
)
( dx
x
f
converge.
Ejemplo 1
Determine si la SERIE ARMÓNICA
∑
∞
=1
1
n
n
converge o diverge
SOLUCIÓN:
Aplicando el criterio de la integral, debido a que es una serie de términos positivos
decrecientes.
[ ] ∞
=
=
=
=
∞
→
∞
→
∞
→
∞
∫
∫ N
lím
x
lím
x
lím
x n
N
n
N
n
ln
ln
1
1
1
1
1
Por tanto la serie diverge.
111](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-271-320.jpg)
![MOISES VILLENA Cap. 6 Series
Ejemplo 2.
Sea la serie “p”
∑
∞
=1
1
n
P
n
, determine para qué valores de “ ” converge y para que
p
valores diverge.
SOLUCIÓN:
Analizando la integral
∫
∫ ∞
→
∞
=
N
P
n
P
x
lím
x 1
1
1
1
Si 1
=
P , tenemos la serie armónica, que es divergente
Si , la integración es diferente
1
≠
p
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
−
+
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
=
−
∞
→
+
−
+
−
∞
→
+
−
∞
→
∞
→ ∫
1
1
1
1
1
1
1
1
1
1
1
1
1
1
P
P
N
lím
p
p
N
lím
p
x
lím
x
lím
P
n
P
P
n
N
P
n
N
P
n
Ahora, si 1
P ,
1
1
1
1
1
0
1
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+
−
∞ −
p
P
P
P
3
2
1
, la integral converge
Si 1
P , ∞
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+
−
∞
∞
−
1
1
1
1
P
P
P
3
2
1
la integral diverge
En conclusión, la serie
⎪
⎩
⎪
⎨
⎧
≤
−
=
∑
∞
= diverge
P
Si
p
a
converge
P
Si
n
n
P
1
1
1
1
1
1
Ejemplo 3
Determine si la serie
∑
∞
=2
ln
1
n
n
n
converge o diverge.
SOLUCIÖN:
Aplicando el criterio de la integral
( ) ( )
[ ] ∞
=
−
=
∫
∞
∞
→
2
ln
ln
ln
ln
ln
1
2
N
lím
x
x x
Por tanto diverge
Ejercicios propuestos 6.2
Usando el criterio de la Integral, determine la convergencia o divergencia de la siguiente serie
numérica
1)
( )
∑
+∞
=2
2
ln
1
n
n
n
2)
∑ 3)
+∞
=
−
1
n
n
ne
( ) ( )
∑
+∞
=
+
+
1
1
ln
1
1
n
n
n
112](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-272-320.jpg)







![MOISES VILLENA Cap. 6 Series
Ejemplo 1
Analice la serie ( )
∑
∞
=
+
−
1
2
1
2
3
1
n
n
n
n
n
.
SOLUCIÓN:
Debido a la forma de la serie, se aplica el criterio de la raíz.
0
3
3
3
2
1
2
2
1
2
2
1
2
=
=
=
=
+
∞
→
+
∞
→
+
∞
→
∞
→ n
lím
n
lím
n
lím
a
lím
n
n
n
n
n
n
n
n
n
n
n
n
n
n
Como el resultado es un número menor que 1 por tanto la serie es absolutamente
convergente.
Ejemplo 2
Analice la serie
( )
[ ]
∑
∞
=
+
1
1
ln
1
n
n
n
.
Debido a la forma de la serie, se aplica el criterio de la raíz.
( )
[ ] ( )
[ ] ( )
[ ]
0
1
1
ln
1
1
ln
1
1
ln
1
=
∞
=
+
=
+
=
+
=
∞
→
∞
→
∞
→
∞
→ n
lím
n
lím
n
lím
a
lím
n
n
n
n
n
n
n
n
n
n
Como el resultado es un número menor que 1 por tanto la serie es absolutamente
convergente.
Ejercicios Propuestos 6.4
Determine la convergencia absoluta, convergencia condicional o divergencia de las siguientes
series numérica:
a. ( )
( )
∑
+∞
=
−
+
−
1
1
4
3
1
1
1
n
n
n
b. ( )
∑
+∞
=
−
1
!
1
n
n
n
n
c. ( )
( )
∑
+∞
=
+
+
−
1
1
2
!
1
2
5
1
n
n
n
n
d. ( )
∑
+∞
=
−
−
1
3
1 2
1
n
n
n
n
n
e. ( )
∑
+∞
=
−
1
1
ln
1
n
n
n
f. L
+
•
+
•
+
•
+
• 8
7
1
6
5
1
4
3
1
2
1
1
120](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-280-320.jpg)




![MOISES VILLENA Cap. 6 Series
Ahora, en 0
=
x , tenemos una serie no convergente.
( )
∑
∞
=
−
0
1
0
n
n
n
En 2
=
x , , una serie no convergente.
( ) ( )
∑
∑
∞
=
∞
=
=
−
0
0
1
1
2
n
n
n
n
n
n
Por tanto la serie converge para ( )
2
,
0
∈
x
Ejercicios propuestos 6.5
Determine el intervalo de convergencia para:
a) ( )
( )
∑
+∞
=
−
−
−
1
1
2
1
!
1
2
1
n
n
n
n
x
b)
( )
∑
+∞
=
−
1
!
1
n
n
n
x
c)
∑
+∞
=1
!
n
n
n
n
x
n
d)
( )
∑
+∞
=2
ln
n
n
n
x
e)
( )
( )
∑
∞
+
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
−
n
n
n
n
x
ln
3
2
6.4.3 SERIE DE TAYLOR
Una serie de potencia particular es la serie de Taylor.
Suponga que:
( ) ( ) ( ) ( ) L
+
−
+
−
+
−
+
=
−
= ∑
∞
=
3
0
3
2
0
2
0
1
0
0
0
)
( x
x
a
x
x
a
x
x
a
a
x
x
a
x
f
n
n
n
Los coeficientes pueden ser determinados en términos de la función f
Evaluando en 0
x
x =
[ ] [ ] [ ] [ n
n x
x
a
x
x
a
x
x
a
x
x
a
a
x
f 0
0
3
0
0
3
2
0
0
2
0
0
1
0
0 )
( −
+
+
−
+
−
+
−
+
= L ]
Obtenemos: )
( 0
0 x
f
a =
Para encontrar el segundo coeficiente, derivamos y evaluamos en 0
x
x =
[ ] [ ] [ ]
[ ] [ ] [ ] 1
0
0
2
0
0
3
0
0
2
1
0
1
0
2
0
3
0
2
1
3
2
)
´(
3
2
)
´(
−
−
−
+
+
−
+
−
+
=
−
+
+
−
+
−
+
=
n
n
n
n
x
x
na
x
x
a
x
x
a
a
x
f
x
x
na
x
x
a
x
x
a
a
x
f
L
L
Entonces: )
´( 0
1 x
f
a =
Obteniendo la segunda derivada y evaluando en 0
x
x =
125](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-285-320.jpg)
![MOISES VILLENA Cap. 6 Series
( )( ) [ ] ( )( ) [ ]
( )( ) [ ] ( )( ) [ ]
2
0
2
0
0
0
0
3
2
0
2
0
0
3
2
2
)
´´(
1
2
3
2
)
´´(
1
2
3
2
)
´´(
a
x
f
x
x
a
n
n
x
x
a
a
x
f
x
x
a
n
n
x
x
a
a
x
f
n
n
n
n
=
−
−
+
+
−
+
=
−
−
+
+
−
+
=
−
−
L
L
De la última expresión, se tiene
2
)
´´( 0
2
x
f
a =
Ahora, obteniendo la tercera derivada y evaluando en 0
x
x =
( )( ) ( )( )( ) [ ]
( )( ) ( )( )( ) [ ]
( )( ) 3
0
3
0
0
3
0
3
0
3
2
3
)
´´´(
2
1
2
3
)
´´´(
2
1
2
3
)
´´´(
a
x
f
x
x
a
n
n
n
a
x
f
x
x
a
n
n
n
a
x
f
n
n
n
n
=
−
−
−
+
+
=
−
−
−
+
+
=
−
−
L
L
De la última expresión, se tiene
!
3
)
´´´( 0
3
x
f
a =
Por lo tanto:
[ ] [ ] [ ]
[ ]
∑
∞
=
−
=
+
−
+
−
+
−
′
+
=
0
0
0
3
0
0
´´´
2
0
0
´´
0
0
0
!
)
(
)
(
!
3
)
(
!
2
)
(
)
(
)
(
)
(
n
n
n
x
x
n
x
f
x
f
x
x
x
f
x
x
x
f
x
x
x
f
x
f
x
f L
Si 0
0 =
x se llama Serie de Maclaurin, es decir:
[ ] L
+
′
′
′
+
′
′
+
′
+
=
= ∑
∞
=
3
2
0
6
)
0
(
2
)
0
(
)
0
(
)
0
(
!
)
0
(
)
( x
f
x
f
x
f
f
x
n
f
x
f
n
n
n
Ejemplo 1
Hallar la serie de Taylor para x
e
x
f =
)
( , alrededor de 0
0 =
x
SOLUCIÓN:
Obtenemos primero
x
x
x
x
e
x
f
e
x
f
e
x
f
e
x
f
=
′
′
′
=
′
′
=
′
=
)
(
)
(
)
(
)
(
⇒
1
)
0
(
1
)
0
(
1
)
0
(
1
)
0
(
=
′
′
′
=
′
′
=
′
=
f
f
f
f
Luego, reemplazando en: L
+
′
′
′
+
′
′
+
′
+
= 3
2
6
)
0
(
2
)
0
(
)
0
(
)
0
(
)
( x
f
x
f
x
f
f
x
f
Resulta
∑
∞
=
=
+
+
+
+
+
=
0
4
3
2
!
!
4
1
!
3
1
2
1
1
n
n
x
n
x
x
x
x
x
e L
126](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-286-320.jpg)



![MOISES VILLENA Cap. 6 Series
Ejemplo 2.
a) Encuentre una serie de potencia para
x
x
f
+
=
1
1
)
(
La expresión anterior puede ser observada como la suma de un serie geométrica infinita
con primer término igual a 1y razón x
r −
= entonces:
( ) ( )
∑
∑
∞
=
∞
=
−
=
−
=
+
=
0
0
1
1
1
)
(
n
n
n
n
n
x
x
x
x
f
b) Emplee la serie anterior para obtener la serie de ( )
1
ln
)
( +
= x
x
f
Integrando ( ) ( ) ( )
∑
∫ ∑
∫
∞
=
+
∞
=
+
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
+
=
+
=
0
1
0
1
1
1
1
1
1
ln
)
(
n
n
n
n
n
n
n
x
x
dx
x
x
x
f
c) Determine su intervalo de convergencia.
Aplicando el criterio
1
1
1
1
2
1
lim
1
1
2
lim 1
2
−
+
+
+
+
∞
→
+
+
∞
→
x
x
n
n
x
x
n
n
x
n
n
n
n
Si 1
−
=
x , tenemos ( ) ( ) ( ) L
−
−
−
−
−
=
+
−
=
+
−
−
∑
∑
∞
=
+
∞
=
+
4
1
3
1
2
1
1
1
1
1
1
1
0
1
2
0
1
n
n
n
n
n
n
n
una serie
divergente. ¿por qué?
Si 1
=
x tenemos ( ) ( ) ( )
∑
∑
∞
=
∞
=
+
+
−
=
+
−
0
0
1
1
1
1
1
1
1
n
n
n
n
n
n
n
una serie alternante convergente.
Por tanto su intervalo de convergencia es ( ]
1
,
1
−
∈
x
Ejercicios Propuestos. 6.6
1. a) Encuentre los tres primeros términos diferentes de cero de la serie de Taylor para
)
tan(
)
( x
x
f = alrededor de 0
0 =
x .
b) Emplee el resultado obtenido en a) y la diferenciación término a término con la finalidad de
encontrar los primeros tres términos diferentes de cero de la serie de Taylor para .
)
(
sec
)
( 2
x
x
g =
c) Utilice el resultado obtenido en a) y la integración término a término para encontrar los primeros
tres términos que no sean cero de la serie de Taylor para ))
ln(cos(
)
( x
x
h = .
2. a) Encuentre los tres primeros términos diferentes de cero de la serie de Taylor para x
x
f ln
)
( =
alrededor de 1
0 =
x .
b) Determine su intervalo de convergencia.
3. Encuentre el desarrollo en series de potencias de x y analice su convergencia:
130](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-290-320.jpg)



![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Observe que si tomamos 1
1 x
x = , 2
2 x
x = , 3
3 x
x = , …, i
i x
x = , se
tienen rectángulos circunscritos; en cambio si se toma 0
1 x
x = , 1
2 x
x = ,
2
3 x
x = , …, 1
−
= i
i x
x se tendrían rectángulos inscritos.
La suma de las áreas de los rectángulos sería:
n
( ) ( ) ( ) ( ) n
n x
x
f
x
x
f
x
x
f
x
x
f ∆
+
+
∆
+
∆
+
∆ K
3
3
2
2
1
1
Que de manera abreviada tenemos:
( )
∑
=
∆
n
i
i
i x
x
f
1
Bien, lo que se quiere es el área de la región, por tanto se debería
considerar una suma de una cantidad muy, pero muy grande de
rectángulos, es decir una suma infinita. Por tanto, el área de la región
estaría dada por:
( ) ⎥
⎦
⎤
⎢
⎣
⎡
∆
= ∑
=
∞
→
n
i
i
i
n
x
x
f
lím
A
1
De aquí surge la definición de Integral Definida.
Sea f una función que está definida en el intervalo [ ].
b
a,
Al ( ) ⎥
⎦
⎤
⎢
⎣
⎡ ∆
∑
=
∞
→
n
i
i
i
n
x
x
f
1
lím se le denomina la integral definida (o
integral de Riemann) de f de a b y se denota de la
a
siguiente manera: .
∫
b
a
dx
x
f )
(
Además, si existe este límite decimos que f es integrable
en [ ].
b
a,
Ahora, con el siguiente teorema dejamos sentado el hecho de cuando
una función es integrable.
45](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-294-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
3.2 TEOREMA DE INTEGRABILIDAD
Si f es acotada en [ ]
b
a, y si f es continua a excepción de
un número finito de puntos, entonces f es integrable [ ]
b
a, .
En particular si f es continua en todo [ ]
b
a, entonces es
integrable en [ ]
b
a,
Ejemplo
Hallar el área bajo la curva
2
)
( x
x
f = en [ ]
3
,
1
SOLUCIÓN:
Aplicando la definición (Suma de Riemann) se tiene:
]
)
(
)
(
)
(
)
(
[
lím
)
(
lím 3
3
2
2
1
1
1 n
n
n
i
n
i
i
n
x
x
f
x
x
f
x
x
f
x
x
f
x
x
f
A ∆
+
+
∆
+
∆
+
∆
=
∆
= ∑
=
∞
→
∞
→
K
PRIMER MÉTODO. RECTANGULOS CIRCUNSCRITOS.
Escogemos 1
1 x
x = , 2
2 x
x = , 3
3 x
x = , …, i
i x
x =
Representando la región, tenemos:
0
x 1
x 2
x n
x
{
x
∆
{
x
∆
{
x
∆
2
x
y =
Ahora bien, observe que si tomamos a todas las particiones de igual dimensión, tendríamos
n
n
n
a
b
x
2
1
3
=
−
=
−
=
∆
y
46](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-295-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
1
0 =
= a
x
n
x
x
x
2
1
0
1 +
=
∆
+
=
n
n
x
x
x
x
x
4
1
2
2
1
2
0
1
2 +
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
∆
+
=
∆
+
= ,
n
n
x
x
x
x
x
6
1
2
3
1
3
0
2
3 +
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
∆
+
=
∆
+
=
M
⎟
⎠
⎞
⎜
⎝
⎛
+
=
∆
+
=
∆
+
=
n
i
x
i
x
i
x
xi
2
1
1
0
Entonces:
( ) ( ) ( ) ( )
[ ]
3
26
3
4
3
8
8
6
3
2
2
3
4
2
3
2
3
2
6
4
2
3
2
3
)
1
2
)(
1
(
2
)
1
(
2
2
6
)
1
2
)(
1
(
4
2
)
1
(
4
2
4
4
1
2
4
4
1
2
2
2
1
)
(
2
2
2
1
2
2
1
1
1
2
2
1
2
1
3
2
1
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
+
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡ +
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡ +
+
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡ +
+
+
+
+
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
∆
=
∆
+
∆
+
∆
+
∆
=
∞
→
∞
→
∞
→
∞
→
∞
→
=
=
=
∞
→
=
∞
→
=
∞
→
=
∞
→
∞
→
∑
∑
∑
∑
∑
∑
A
n
n
lím
n
n
n
n
lím
n
n
n
n
n
lím
n
n
n
n
n
n
lím
n
n
n
n
n
n
n
n
n
lím
i
n
i
n
n
lím
n
i
n
i
n
lím
n
n
i
lím
x
x
f
lím
x
x
f
x
x
f
x
x
f
x
x
f
lím
A
n
n
n
n
n
n
i
n
i
n
i
n
n
i
n
n
i
n
n
i
i
n
n
n
L
SEGUNDO MÉTODO. RECTANGULOS INSCRITOS.
Escogemos 0
1 x
x = , 1
2 x
x = , 2
3 x
x = , …, 1
−
= i
i x
x
Representando la región, tenemos:
47](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-296-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Ahora, igual que el método anterior:
0
x 1
x 2
x n
x
{
x
∆
{
x
∆
{
x
∆
2
x
y =
1
−
n
x
n
x
2
=
∆ y ⎟
⎠
⎞
⎜
⎝
⎛
+
=
n
i
xi
2
1
Entonces:
( ) ( ) ( ) ( )
[ ]
( ) ( ) ( ) ( )
[ ]
3
26
3
4
3
8
10
6
3
2
2
3
4
3
3
2
3
2
6
4
3
3
2
3
)
1
2
)(
1
(
2
)
1
(
2
1
2
6
1
1
2
)
(
1
4
2
)
(
1
4
1
2
4
4
1
2
4
4
1
2
2
2
1
)
(
2
2
2
1
2
2
1
1
0
1
0
2
2
1
0
2
1
0
1
2
1
0
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡ +
−
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡ −
−
+
−
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡ +
−
−
+
−
+
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
∆
=
∆
+
∆
+
∆
+
∆
=
∞
→
∞
→
∞
→
∞
→
∞
→
=
=
−
=
∞
→
−
=
∞
→
−
=
∞
→
−
=
∞
→
−
∞
→
∑
∑
∑
∑
∑
∑
A
n
n
lím
n
n
n
n
lím
n
n
n
n
n
lím
n
n
n
n
n
n
lím
n
n
n
n
n
n
n
n
n
lím
i
n
i
n
n
lím
n
i
n
i
n
lím
n
n
i
lím
x
x
f
lím
x
x
f
x
x
f
x
x
f
x
x
f
lím
A
n
n
n
n
n
n
i
n
i
n
i
n
n
i
n
n
i
n
n
i
i
n
n
n
L
48](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-297-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Note que el asunto no es tan sencillo. Se podría volver aún más
engorroso si la función f tuviese regla de correspondencia compleja.
El teorema siguiente nos permitirá evaluar integrales definidas de
una manera muy rápida y sencilla, liberándonos de la ideas de calcular
integrales definidas empleando su definición.
3.3 TEOREMA FUNDAMENTAL DEL CÁLCULO
Sea f continua en [ ]
b
a, y sea cualquier
F
antiderivada de f en [ ]
b
a, entonces:
)
(
)
(
)
( a
F
b
F
dx
x
f
b
a
−
=
∫
Demostración:
En la expresión , haciendo
)
(
)
( a
F
b
F − n
x
b = y 0
x
a = tenemos:
)
(
)
(
)
(
)
( 0
x
F
x
F
a
F
b
F n −
=
−
Restando y sumando términos, resulta:
[ ] [ ] [
[ ]
∑
=
−
−
−
−
−
−
=
−
+
−
−
+
−
+
−
=
−
=
−
n
i
i
i
n
n
n
n
n
n
x
F
x
F
x
F
x
F
x
F
x
F
x
F
x
F
x
F
x
F
x
F
x
F
a
F
b
F
1
1
0
1
1
2
2
1
1
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
K ]
Aplicando el teorema del valor medio para derivadas a en el intervalo
F [ ]
i
i x
x ,
1
−
Como es continua y diferenciable en
F [ ]
i
i x
x ,
1
− entonces i
x
∃ tal que
( )
1
1
)
(
)
´(
−
−
−
−
=
i
i
i
i
i
x
x
x
F
x
F
x
F
Como )
(
)
´( i
i x
f
x
F = y i
i
i x
x
x ∆
=
− −1 entonces:
( )
i
i
i
i
x
x
F
x
F
x
f
∆
−
= −1
)
(
)
(
Despejando resulta: ( ) i
i
i
i x
x
f
x
F
x
F ∆
=
− − )
(
)
( 1 .
49](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-298-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Reemplazando en tenemos:
[ ]
∑
=
−
−
=
−
n
i
i
i x
F
x
F
a
F
b
F
1
1)
(
)
(
)
(
)
(
∑
=
∆
=
−
n
i
i
i x
x
f
a
F
b
F
1
)
(
)
(
)
(
Tomando límite queda:
[ ]
∫
∑
∑
=
∆
=
−
∆
=
−
=
∞
→
=
∞
→
∞
→
b
a
n
i
i
i
n
n
i
i
i
n
n
dx
x
f
x
x
f
a
F
b
F
x
x
f
a
F
b
F
)
(
)
(
lím
)
(
)
(
)
(
lím
)
(
)
(
lím
1
1
La parte derecha de la última igualdad, por definición es la integral definida de en [ ].
f b
a,
Por tanto L.Q.Q.D.
∫
=
−
b
a
dx
x
f
a
F
b
F )
(
)
(
)
(
Ejemplo
Hallar el área bajo la curva en
2
x
y = [ ]
3
,
1
SOLUCIÓN:
El área bajo la curva estará dada por , aplicando el teorema fundamental del calculo
dx
x
A
∫
=
3
1
2
3
26
3
1
3
27
3
1
3
3
3
3
3
3
1
3
3
1
2
=
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
=
∫ C
C
C
x
dx
x
A
Hemos dado solución a una gran problemática.
Observe que 0
)
( =
∫
a
a
dx
x
f y
∫
∫ −
=
a
b
b
a
dx
x
f
dx
x
f )
(
)
( ¿Porqué?
50](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-299-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
3.4 PROPIEDADES DE LA INTEGRAL DEFINIDA
3.4.1 PROPIEDAD DE LINEALIDAD
Suponga que f y g son integrables en el intervalo
[ b
a, ] y sea R
k ∈ , entonces:
1. [ ] [ ] [
∫
∫
∫ ±
=
±
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f )
(
)
(
)
(
)
( ]
2. ∫
∫ =
b
a
b
a
dx
x
f
k
dx
x
kf )
(
)
(
3.4.2 PROPIEDAD DE ADITIVIDAD
Si f es integrable en un intervalo que contiene a los
puntos a, b y c (no importar su orden), entonces:
∫
∫
∫ +
=
b
c
c
a
b
a
dx
x
f
dx
x
f
dx
x
f )
(
)
(
)
(
Demostración:
Por el teorema fundamental del cálculo:
∫
∫
∫ =
−
=
−
+
−
=
+
b
a
b
c
c
a
dx
x
f
a
F
b
F
c
F
b
F
a
F
c
F
dx
x
f
dx
x
f )
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
PREGUNTA: ¿Verdadero o falso?
∫
∫
∫ +
=
3
5
2
5
1
2
3
1
2
dx
x
dx
x
dx
x
51](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-300-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Ejemplo 1
Calcular
∫ donde
5
1
)
( dx
x
f
⎩
⎨
⎧
+
−
≥
−
=
3
;
1
3
3
;
1
2
)
( 2
x
x
x
x
x
x
f
SOLUCIÓN:
Como tiene dos reglas de correspondencia, es decir:
f
Entonces aplicando la propiedad de aditividad, tenemos:
( ) ( )
( ) (
[ ]
)
3
38
3
9
5
25
1
2
3
3
1
3
2
27
9
2
2
2
3
3
1
2
1
3
)
(
5
3
2
3
1
2
3
5
3
3
1
2
5
1
=
−
−
−
+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
−
+
+
−
=
∫
∫
∫
x
x
x
x
x
dx
x
dx
x
x
dx
x
f
Ejemplo 2
Calcular ∫
−
−
−
4
2
2
1 dx
x
SOLUCIÓN:
Para obtener las reglas de correspondencia que definen a , obtenemos la gráfica de
f
2
1 −
−
= x
y
Entonces:
52](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-301-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
( ) ( ) ( ) ( )
( ) ( )
5
9
2
9
12
8
3
2
1
9
2
9
1
2
1
1
2
1
2
2
1
2
1
3
2
3
2
2
2
3
3
1
1
2
1
4
3
2
3
1
2
1
1
2
1
2
2
4
3
3
1
1
1
1
2
4
2
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
+
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
−
+
+
−
+
+
+
−
−
=
−
−
−
−
−
−
−
−
−
∫
∫
∫
∫
∫
x
x
x
x
x
x
x
x
dx
x
dx
x
dx
x
dx
x
dx
x
3.4.3 PROPIEDAD DE COMPARACIÓN
Si f y g son integrables en [ ]
b
a, y si )
(
)
( x
g
x
f ≤ ,
[ b
a
x ,
∈
∀ ]; entonces: dx
x
g
dx
x
f
b
a
b
a
∫
∫ ≤ )
(
)
(
3.4.4 PROPIEDAD DE ACOTAMIENTO
Si f es integrable en [ ]
b
a, y si
M
x
f
m ≤
≤ )
( , [ ]
b
a
x ,
∈
∀ ; entonces:
( ) )
(
)
( a
b
M
dx
x
f
a
b
m
b
a
−
≤
≤
− ∫
3.4.5 PROPIEDAD DE SUSTITUCIÓN
Supóngase que g tiene una derivada continua en [ ]
b
a,
y sea f continua en el rango de g . Entonces:
donde
∫
∫
=
=
=
=
=
)
(
)
(
)
(
)
´(
))
(
(
b
g
t
a
g
t
b
x
a
x
dt
t
f
dx
x
g
x
g
f )
(x
g
t =
Ejemplo
Calcular
∫
π
π
4
9
2
2
cos
dx
x
x
SOLUCIÓN:
53](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-302-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Tomando el cambio de variable x
t = entonces tenemos dt
x
dx 2
= , y para los límites de
integración
⎪
⎩
⎪
⎨
⎧
=
⇒
=
=
⇒
=
π
π
π
π
3
9
2
4
2
2
t
x
t
x
por tanto la integral en términos de t sería:
( ) 3
2
2
3
2
1
2
sen
2
sen
2
sen
2
cos
2
2
cos
3
2
2
3
2
3
2
3
−
=
−
=
−
=
=
= π
π
π
π
π
π
π
π
∫
∫ t
tdt
dt
x
x
t
Note que para resolver la integral anterior no es necesario aplicar la
propiedad de sustitución; la integral puede ser resulta como en el caso de
las integrales indefinidas y luego ser evaluada para x. ¿cómo sería?.
3.4.6 PROPIEDAD DE SIMETRÍA
1. Si es una función PAR entonces:
f
dx
x
f
dx
x
f
a
a
a
)
(
2
)
(
0
∫
∫ =
−
2. Si es una función IMPAR entonces:
f
0
)
( =
∫
−
dx
x
f
a
a
Demostraremos sólo la primera parte, la segunda es de forma
análoga y se recomienda al lector que la realice.
DEMOSTRACIÓN
Aplicando la propiedad de aditividad dx
x
f
dx
x
f
dx
x
f
a
a
a
a
)
(
)
(
)
(
0
0
∫
∫
∫ +
=
−
−
Para la primera integral aplicando la propiedad de sustitución:
Si tomamos el cambio de variable x
t −
= entonces dx
dt −
= y para los límites de integración
. Sustituyendo resulta
⎩
⎨
⎧
=
⇒
−
=
=
⇒
=
a
t
a
x
t
x 0
0
[ ]
∫
∫ −
−
=
−
−
0
0
)
(
)
(
a
a
dt
t
f
dt
t
f
54](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-303-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Por hipótesis es una función par, por tanto se cumple que y además si
invertimos los límites de integración, tenemos:
f )
(
)
( t
f
t
f =
−
∫
∫ =
−
−
a
a
dt
t
f
dt
t
f
0
0
)
(
)
(
la última integral si x
t = queda [ ]
∫
∫ =
−
−
a
a
dx
x
f
dt
t
f
0
0
)
(
)
(
Finalmente L.Q.Q.D.
dx
x
f
dx
x
f
dx
x
f
dx
x
f
a
a
a
a
a
)
(
2
)
(
)
(
)
(
0
0
0
∫
∫
∫
∫ =
+
=
−
Ejemplo
Calcular dx
x
x
∫
−
+
5
5
2
5
4
SOLUCIÓN:
Obtengamos primero )
( x
f − para
4
)
( 2
5
+
=
x
x
x
f .
4
4
)
(
)
(
)
( 2
5
2
5
+
−
=
+
−
−
=
−
x
x
x
x
x
f
Observe )
(
)
( x
f
x
f −
=
− , por tanto es una función impar y por la propiedad de simetría,
rápidamente concluimos que:
f
0
4
5
5
2
5
=
+
∫
−
dx
x
x
3.4.7 PROPIEDAD DE PERIODICIDAD
Si f es periódica con período T , entonces:
∫
∫ =
+
+
b
a
T
b
T
a
dx
x
f
dx
x
f )
(
)
(
DEMOSTRACIÓN
En la integral , haciendo cambio de variable
∫
+
+
T
b
T
a
dx
x
f )
( T
x
t −
= .
55](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-304-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Del cambio de variable se obtiene T
t
x +
= , dt
dx = y los límites para la nueva variable son:
⎩
⎨
⎧
=
⇒
+
=
=
⇒
+
=
a
t
T
a
x
b
t
T
b
x
Reemplazando, resulta: y como, por hipótesis, es una función
periódica se cumple que
∫
∫ +
=
+
+
b
a
T
b
T
a
dt
T
t
f
dx
x
f )
(
)
( f
)
(
)
( t
f
T
t
f =
+ , entonces
∫
∫ =
+
b
a
b
a
dt
t
f
dt
T
t
f )
(
)
(
Que finalmente, si x
t = quedaría L.Q.Q.D.
∫
∫ =
+
+
b
a
T
b
T
a
dx
x
f
dx
x
f )
(
)
(
3.4.8 PROPIEDAD DE LA DERIVADA DE UNA INTEGRAL
Algunos autores le llaman Segundo Teorema fundamental del
Cálculo.
Sea f continua en [ ]
b
a, y sea x un punto variable
de . Entonces:
)
,
( b
a
)
(
)
( x
f
dt
t
f
dx
d x
a
=
⎥
⎦
⎤
⎢
⎣
⎡
∫
Ejemplo 1
Calcular
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
∫
x
x dt
t
t
D
2
2
2
3
17
SOLUCIÓN:
Aplicando la propiedad anterior, rápidamente concluimos que:
17
17 2
2
3
2
2
2
3
+
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
∫ x
x
dt
t
t
D
x
x
56](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-305-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Ejemplo 2
Calcular
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
∫
2
2
2
3
17
x
x dt
t
t
D
SOLUCIÓN:
Invirtiendo los límites de integración y aplicando la propiedad, concluimos que:
17
17 2
2
3
2
2
2
3
+
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
−
∫ x
x
dt
t
t
D
x
x
La propiedad anterior puede ser generalizada de la siguiente manera:
[ ]
dx
du
u
f
dt
t
f
dx
d
x
u
a
)
(
)
(
)
(
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∫
Ejemplo 3
Calcular
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
∫
3
2
2
2
3
17
x
x dt
t
t
D
SOLUCIÓN:
Aplicando la propiedad, concluimos que:
( )
( )
( )
17
3
3
17
17 6
2
13
2
2
3
2
3
3
2
2
2
3
3
+
=
+
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
∫ x
x
x
x
x
dt
t
t
D
x
x
Ejemplo 4
Calcular
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
∫
3
2
17
2
2
3
x
x
x dt
t
t
D
SOLUCIÓN:
Aplicando la propiedad de aditividad, tenemos que:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+ ∫ ∫
∫
0
0
2
2
3
2
2
3
2
2
3
2
3
3
2
17
17
17
x
x
x
x
x
x dt
t
t
dt
t
t
D
dt
t
t
D
Derivando cada término y aplicando la propiedad, resulta:
57](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-306-320.jpg)

![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Ejemplo 6
Calcular
x
dt
t
x
x
∫ −
→
0
2
0
1
lím
SOLUCIÓN:
La expresión presenta una indeterminación de la forma:
0
0
Aplicando la regla de L´Hopital, tenemos:
[ ]
1
1
0
1
1
1
lím
1
lím
2
2
0
0
2
0
=
−
=
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
→
→
∫ x
x
D
dt
t
D
x
x
x
x
x
Ejercicios Propuestos 3.1
1. Calcular
a. si
( ) ,
3
2
∫
−
dx
x
f
( )
⎪
⎩
⎪
⎨
⎧
≤
−
≤
≤
−
=
3
1
,
2
1
1
2
,
2 2
x
x
x
x
x
f
b.
∫ −
4
0
1 dx
x
c.
∫
−
−
4
2
1
3 dx
x
d. ( )dx
x
x
∫
−
−
+
−
4
2
2
1
3
e. dx
x
∫
−
−
−
5
2
2
1
f.
∫
10
0
dx
x
g. [ ]
( )
∫ −
4
0
dx
x
x
h.
∫
4
9
2
2
cos
π
π
dx
x
x
i.
( )
∫ +
+
+
1
0
2
2
1
4
2
dx
x
x
x
j. ( )
[ ]
∫ −
+
1
0
3
3
cos
3 dx
x
x
k. ( )
∫ π
2
1
0
2
sen dx
x
l. dx
x
∫ −
5
0
2
9
m. ( ) ( )
∫ +
−
e
dx
x
x
x
1
2
ln
3
2
n.
( )
∫
−
+
1
1
4
2
3
1
dx
x
x
o. ( )
∫
−
−
100
100
3
97
2
3 dx
x
x
sen
x
2. Determine el valor de verdad de las siguientes proposiciones: Si es verdadera demuéstrela y en caso de ser
falsa de un contraejemplo.
a. Si ( ) ( )
x
g
x
f ≤ en [ ] ( ) ( )
∫
∫ ≤
b
a
b
a
dx
x
g
dx
x
f
b
a ,
,
b. ( ) ∫
∫ =
+
+
−
99
0
2
99
99
2
3
2 dx
bx
dx
cx
bx
ax
59](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-308-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
c. Si f es periódica con período T, entonces: ( ) ( )
∫
∫ =
+
+
b
a
T
b
T
a
dx
x
f
dx
x
f
d. ,
f
∀ ( ) ( )
∫
∫
−
−
=
−
a
b
b
a
dx
x
f
dx
x
f
e. Si es una función par
f [ ]
a
a
x ,
−
∈
∀ , entonces ( )
∫
∫ =
−
a
a
a
dx
x
f
dx
x
f
0
)
(
2
f. Si ( ) ( )
x
g
x
f ≤ en [ ]
b
a, , entonces ( ) ( )
∫
∫ ≤
b
a
b
a
dx
x
g
dx
x
f
g. Si ( ) ( ) [ ] ( ) ( ) ( ) ( )
a
G
b
G
a
F
b
F
b
a
x
x
G
x
F −
=
−
∈
∀
′
=
′ ,
,
h. Sea g una función derivable y supóngase que es una antiderivada de . Entonces
F f
( )
( ) ( ) ( )
( )
∫ +
=
′ C
x
g
F
dx
x
g
x
g
f
3. Encuentre si toma las siguientes reglas de correspondencia:
f ′ f
a. dt
t
x
x
∫ −
ln
sen
0
1
1
b. dt
t
x
x
tanx
x
∫ −
sec
2
ln
3 5
3
1
c. dt
t
x
x
e
x
x
e
∫ −
3
sec
ln
2
1
d.
∫
+
−
x
x
x
dt
t
t
sen
4 5
3
2
1
2
e.
( )
( )
∫+
−
−
tanx
x
x
dt
t
t
t
sen
1
ln
3
3
2
sen
cos
1
f.
∫ −
+
2
3
2
log
6
cos
1
sen
1
x
x
dt
t
t
4. Determine:
a.
( )
3
0
2
0
lim
x
dt
t
sen
x
x
∫
→
b.
1
lim 1
1 −
∫
+
→ x
dt
sent
x
x
c.
x
dt
e
x
t
x
∫ −
∞
→
+
1
1
lim
d.
2
0
2
2
5
1 ⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
∫
x
t
dt
dx
d
60](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-309-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
Misceláneos
1. A cada una de las proposiciones siguientes, califíquelas como Verdadera o Falsa. En cada caso justifique su
respuesta.
a) Si es una función continua en el intervalo
´
f [ ]
b
a , entonces
[ ] [ ]
∫ −
=
b
a
a
f
b
f
dx
x
f
x
f 2
2
)
(
)
(
)
´(
)
(
2
b) Si entonces
0
)
( =
∫
b
a
dx
x
f 0
)
( =
x
f para [ ]
b
a
x ,
∈
∀
c) Si es una función continua en
f IR , entonces:
( ) ( )
2
2
1
)
(
2
x
f
x
arctgx
f
dx
x
f
dx
d
arctgx
x
−
+
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
∫
d) [ ] ( ) IN
n
n
n
dx
x
n
∈
+
=
∫
+
;
2
1
1
0
e) Si y
f g son funciones impares y continuas en IR , entonces
( )( ) 0
5
5
=
∫
−
dx
x
g
f o
f) 4
4
4
1
2
1
2
x
x
dt
t
D
x
x +
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
∫
g)
∫
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
2
2
4
3
4
64
1
5
2
dx
x
x
xe
x x
h) Si y
f g son funciones continuas en el intervalo [ ]
1
,
0 entonces
( ) ( ) ( ) ( )
∫
∫ −
=
−
1
0
1
0
1
1 dx
x
g
x
f
dx
x
g
x
f
i) Si entonces para
0
)
( ≥
∫
b
a
dx
x
f 0
)
( ≥
x
f [ ]
b
a
x ,
∈
∀
j)
∫ ∫
=
π
π
2
2
2
0
4 senxdx
dx
senx
k) Si y entonces
3
)
(
3
0
=
∫ dx
x
f 7
)
(
4
0
=
∫ dx
x
f 4
)
(
3
4
−
=
∫ dx
x
f
l)
∫
∫ +
≥
1
0
2
1
0
1 dx
x
xdx
61](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-310-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
m) Si es una función continua en
f IR tal que para cualquier número real x ,
entonces es una función impar.
0
)
(
)
(
1
2
1
2
=
=
∫
∫
−
x
x
x
x
dt
t
f
dt
t
f f
n) Si es una antiderivada de la dunción , entonces
F f
∫ +
=
+ dx
x
f
x
F )
1
2
(
)
1
2
(
o) Si es una función continua en el intervalo
f [ ]
5
,
2 y entonces
7
)
(
5
2
=
∫ dx
x
f
7
)
(
5
2
−
=
∫
−
−
dx
x
f
p) Si es una función tal que
f 0
cos
3
)
(
2
2
0
=
+
∫ dt
t
x
f
x
entonces x
x
x
f cos
3
)
´( −
=
q) Si y
f g son funciones tales que y para todo
x
xe
x
f =
)
( )
(
)
( x
g
x
f ≥
[ ]
1
,
0
∈
x entonces .
( )
∫ ≤
1
0
1
dx
x
g
r) Si [ ] 1
)
(
0
,
2
,
0 ≤
≤
∈
∀ x
f
x entonces 1
)
(
0
2
0
≤
≤
∫ dx
x
f
s) Si es una función continua en el intervalo
f [ ]
10
,
0 y
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
=
∫
2
3
0
2
1
)
(
x
t
x dt
t
e
D
x
f para
[ ]
10
,
0
∈
x entonces 3
5
3
)
1
´( e
f = .
t)
∫
∫ =
π
π 2
2
2
2
cos dx
x
dx
senx
u) π
π
π
=
⎟
⎠
⎞
⎜
⎝
⎛
∑
=
+∞
→ n
i
n
n
i
n
cos
lim
1
v)
2
cos
lim 2
1
0
π
=
∑
=
→
i
n
i
p
x donde { }
i
x
max
p ∆
= . p es una partición del intervalo [ ]
π
,
0 .
w) Si , entonces
( ) 1
)
(
2
2
1
2
=
+
∫
−
dx
x
x
f 1
)
(
2
1
−
=
∫
−
dx
x
f
62](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-311-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
x)
( )
3
1
lim
2
3
0
2
0
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
∫
+
→
x
tg
dt
t
sen
x
x
y) 1
2
lim 2
1
2
1
−
=
∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
∞
→
e
n
e
n
i
n
i
n
z)
∫
∫
+
+
=
∈
∀
π
π 2
2
cos
,
,
b
b
a
a
xdx
dx
senx
R
b
a
2. Calcular
a.
( )
3
0
0
cos
1
lim
x
dt
t
x
x
∫ −
→
b.
( )
∫ −
2
1
2
3
2
6
1
dx
x
c.
∫
2
0
3
2
cos
π
xdx
xsen
d.
∫ +
+
2
1
2
2
2
3
dx
x
x
e.
( )
6
0
2
0
2
lim
x
dt
t
sen
x
x
∫
→
f. [ ]
( )
∫ −
3
0
2 dx
x
x
g. ( )
∫
−
−
−
+
3
2
2
1 dx
x
x
x
h.
∫ −
+
5
1
1
2
1
dx
x
i.
∫ −
−
4
2
3
4
dx
x
x
x
j.
∫ +
5
ln
2
ln
2
16
12
dt
e t
k. ( )
∫
−
−
−
21
2
3
1
2 dx
x
l.
∫
−
+
3
2
3
2 dx
x
m.
∫
+
π
π
2
2
2
cos
1
dx
x
n.
( )
3
0
2
0
2
1
lim
x
dt
t
t
sen
x
x
∫ +
→
o.
∫
−
−
−
4
3
3
2
dx
e
x
p.
( ) dx
e
x
x
sen x
∫
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
2
2
2
3
1
63](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-312-320.jpg)
![MOISES VILLENA MUÑOZ Cap 3 La Integral Definida
3. Si es una función tal que . Determine los intervalos donde el
gráfico de es cóncava hacia arriba.
f ( )
∫ ∈
+
−
= −
3
3
2
,
56
48
9
)
(
x
t
IR
x
dt
e
t
t
x
f
f
4. Si y
f g son funciones tales que , y , entonces calcule
el valor de
3
)
(
4
1
=
∫ dx
x
f 2
)
(
7
4
−
=
∫ dx
x
f 6
)
(
3
7
1
=
∫ dx
x
g
[ ]
∫ +
1
7
)
(
)
(
5 dx
x
g
x
f
64](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-313-320.jpg)

![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
4.1 AREAS DE REGIONES PLANAS
4.1.1 ÁREA BAJO UNA CURVA
En el capítulo anterior se mencionó que para calcular el valor del
área bajo una curva, se particiona la región plana y luego se hace una
suma infinita de las áreas de las particiones, lo cual equivale a una
integral definida.
Ahora podemos hacerlo de una manera abreviada. Considerando
sólo una partición representativa, un rectángulo diferencial que
represente a cualquier partición de la región plana
El área del elemento diferencial será: dx
x
f
hdx
dA )
(
=
=
Por tanto, el área de la región plana es:
∫
=
b
a
dx
x
f
A )
(
4.1.2 ÁREA ENTRE CURVAS
Si la región plana tuviera la siguiente forma:
El área del elemento diferencial será: [ ]dx
x
g
x
f
hdx
dA )
(
)
( −
=
=
66](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-315-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
Entonces el área de la región plana esta dada por: [ ]
∫ −
=
b
a
dx
x
g
x
f
A )
(
)
(
CONCLUSIÓN:
Para hallar el área de una región plana, siga los
siguientes pasos:
1. Dibuje las curvas dadas.
2. Identifique la región plana. Aquí se definen los
límites de integración.
3. Defina el rectángulo diferencial, el elemento
representativo.
4. Defina la integral o las integrales para él área.
5. Evalúe la integral definida.
Ejemplo 1
Calcular el valor del área de la región limitada por
⎪
⎩
⎪
⎨
⎧
−
=
+
=
2
4
2
x
y
x
y
SOLUCIÓN:
PASO 1: Graficamos en un mismo plano 4
+
= x
y y 2
2
−
= x
y
PASO 2: Identificamos la región plana, sombreándola y hallando las intercepciones de las curvas.
PASO 3: Definimos el elemento diferencial.
PASO 4: La integral definida para el área sería:
( ) ( )
[ ]
∫
−
−
−
+
=
3
2
2
2
4 dx
x
x
A
PASO 5: Evaluando la integral definida, tenemos:
( )
2
3
0
)
2
(
3
0
6
2
4
2
2
−
=
∨
=
=
+
−
=
−
−
−
=
+
x
x
x
x
x
x
x
x
67](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-316-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( ) ( )
[ ] [ ]
( ) ( ) ( )
6
5
12
2
3
8
18
2
9
9
2
6
2
2
3
2
)
3
(
6
2
3
3
3
6
2
3
6
2
4
2
3
2
3
3
2
2
3
3
2
2
3
2
2
=
−
+
−
+
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−
+
−
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−
=
+
+
−
=
−
−
+
=
−
−
−
∫
∫
A
x
x
x
dx
x
x
dx
x
x
A
Ejemplo 2
Calcular el valor del área de la región limitada por
⎪
⎩
⎪
⎨
⎧
=
−
−
=
0
6
2
3
y
x
x
x
y
SOLUCIÓN:
PASO 1: Dibujamos x
x
x
y 6
2
3
−
−
=
PASO 2: Identificamos la región plana, sombreándola y hallando las intercepciones de la curva con
el eje x.
PASO 3: Definimos el elemento diferencial.
PASO 4: La integral definida para el área sería:
( )
[ ] [ dx
x
x
x
dx
x
x
x
A
∫
∫ −
−
−
+
−
−
−
=
−
3
0
2
3
0
2
2
3
6
(
)
0
(
)
0
(
6 ]
PASO 5: Evaluando la integral definida, tenemos:
0
( )
( )
2
3
0
)
2
(
3
0
6
0
6
2
2
3
−
=
∨
=
∨
=
=
+
−
=
−
−
=
−
−
x
x
x
x
x
x
x
x
x
x
x
x
68](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-317-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( )
[ ] [ ]
[ ] [ ]
( ) ( ) ( )
12
253
27
9
4
81
12
3
8
4
)
0
(
2
3
6
3
3
4
3
2
2
6
3
2
4
2
0
2
6
3
4
2
6
3
4
6
6
6
(
)
0
(
)
0
(
6
2
3
4
2
3
4
3
0
2
3
4
0
2
2
3
4
3
0
2
3
0
2
2
3
3
0
2
3
0
2
2
3
=
+
+
−
+
−
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ −
−
−
−
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
+
+
−
+
−
−
=
−
−
−
+
−
−
−
=
−
−
−
∫
∫
∫
∫
A
x
x
x
x
x
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
A
4.1.3 ÁREA DE REGIONES SIMPLE- y
Si la región plana tuviese la siguiente forma:
Es más conveniente tomar el elemento diferencial representativo
en disposición horizontal
El área del elemento diferencial será: dy
y
f
xdy
hdy
dA )
(
=
=
=
Entonces el área de la región plana es:
∫
=
d
c
dy
y
f
A )
(
Y para el caso de regiones simple-y más generales, tenemos:
69](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-318-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
El área del elemento diferencial será: [ ]dy
y
g
y
f
hdy
dA )
(
)
( −
=
=
Entonces el área de la región plana esta dada por:
[ ]
∫ −
=
d
c
dy
y
g
y
f
A )
(
)
(
Ejemplo 3
Calcular el área de la región limitada por
⎪
⎩
⎪
⎨
⎧
=
+
−
=
=
0
6
y
x
y
x
y
SOLUCIÓN:
PASO 1: Se dibuja en un mismo plano x
y = y 6
+
−
= x
y
PASO 2: Identificamos la región plana, sombreándola y hallamos las intercepciones de las curvas.
PASO 3, 4 y 5: En este caso observamos que el elemento diferencial puede ser de las dos formas.
PRIMER MÉTODO.
Escogemos el elemento diferencial vertical
( ) ( )
( )( )
4
9
0
4
9
0
36
13
36
12
6
6
2
2
2
2
=
∨
=
=
−
−
=
+
−
+
−
=
+
−
=
+
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
El área está dado por:
70](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-319-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( )
( )
( ) ( ) ( )
3
22
24
8
36
18
3
16
4
6
2
4
6
6
2
6
0
4
6
2
6
2
2
2
3
3
2
6
4
2
4
0
2
3
3
2
6
4
4
0
=
−
+
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
+
=
+
−
+
=
∫
∫
A
x
x
x
dx
x
dx
x
A
SEGUNDO MÉTODO.
Escogiendo el elemento diferencial horizontal:
El área está dada por:
( )
[ ]
( ) ( )
3
22
3
8
2
12
0
3
2
2
2
2
6
3
2
6
6
3
2
2
0
3
2
2
0
2
=
−
−
=
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
−
−
=
∫
A
y
y
y
dy
y
y
A
Ejemplo 4
Calcular el área de la región limitada por
⎪
⎩
⎪
⎨
⎧
−
=
−
=
2
3
1
y
x
x
y
SOLUCIÓN:
PASO 1, PASO 2 y PASO 3: El elemento diferencial sería mejor horizontal en este caso
71](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-320-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( )( )
1
2
0
1
2
0
2
3
1
2
2
=
∨
−
=
=
−
+
=
−
+
−
=
+
y
y
y
y
y
y
y
y
Paso 4 y 5: El área de la región sería:
( ) ( )
[ ]
[ ]
( ) ( ) ( ) ( )
2
9
4
2
3
8
2
2
1
3
1
2
2
2
2
3
2
1
2
2
1
3
1
2
2
3
2
1
3
2
3
2
3
1
2
2
3
1
2
2
1
2
2
=
+
+
−
+
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−
−
−
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
=
+
−
−
=
+
−
−
=
−
−
−
∫
∫
A
y
y
y
dy
y
y
dy
y
y
A
Ejercicios propuestos 4.1
Hallar el área de la región limitada por las curvas:
1. ,
,
2 2
x
y
x
y =
−
=
2. entre
,
0
,
4 2
=
−
= y
x
x
y 1
=
x y 3
=
x .
3. 8
,
0
,
4 =
=
−
= x
y
x
y .
4. .
0
1
,
3
4
2
=
−
−
+
−
= y
x
x
x
y
5. 0
,
4
2
,
2 =
−
=
= x
x
y
x
y .
6. .
0
12
4
,
0
2 2
2
=
−
+
=
− x
y
x
y
7. 4
2
2
−
=
+
= x
y
,
x
y
8. x
x
y
x
y 4
, 2
2
+
−
=
=
9. ,
,
6 3
x
y
x
y =
+
=
4
2x
y −
= .
10. 3
,
1 2
−
=
−
= x
y
x
y
11. ,
,
3 2
3
x
y
x
x
y =
+
=
12. x
x
y
x
x
x
y 4
,
8
6 2
2
3
−
=
+
−
=
72](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-321-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
4.1.4 AREAS EN COORDENADAS POLARES.
Ahora trataremos regiones simple-θ , regiones que están limitadas
por curvas cuyas ecuaciones están dadas en forma polar.
En este caso, el elemento diferencial tiene la forma de un sector
circular, entonces su área está dada por:
θ
= d
r
dA 2
2
1
Por tanto el área de la región está dada por:
[ ]
∫
θ
θ
θ
θ
=
2
1
2
)
(
2
1
d
f
A
Ejemplo 1
Hallar el área de la región encerrada por a
r =
SOLUCIÓN:
Graficando la circunferencia a
r = e identificando la región, tenemos:
73](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-322-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
El área estaría dada por:
[ ]
[ ]
2
2
0
2
2
0
2
2
0
2
2
2
1
2
1
2
1
)
(
2
1
2
1
a
A
a
d
a
d
a
d
f
A
π
=
θ
=
θ
=
θ
=
θ
θ
=
π
π
π
θ
θ
∫
∫
∫
Ejemplo 2
Hallar el área de la región encerrada por θ
+
= cos
1
r
SOLUCIÓN:
Graficando la cardioide θ
+
= cos
1
r e identificando la región, tenemos:
El área estaría dada por:
[ ]
[ ]
[ ]
π
=
θ
+
+
θ
+
θ
=
θ
⎟
⎠
⎞
⎜
⎝
⎛ θ
+
+
θ
θ
+
θ
=
θ
θ
+
θ
θ
+
θ
=
θ
θ
+
θ
+
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
θ
θ
+
=
θ
θ
=
π
π
π
π
π
π
π
π
π
θ
θ
∫
∫
∫
∫
∫
∫
∫
∫
∫
A
A
d
d
d
d
d
d
d
d
d
f
A
0
2
1
0
0
0
0
2
0
0
0
2
0
2
2
4
2
sen
sen
2
2
2
cos
2
1
cos
2
cos
cos
2
cos
cos
2
1
cos
1
2
1
2
)
(
2
1
2
1
74](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-323-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
Ejemplo 3
Hallar el área de la región encerrada por θ
= 3
sen
4
r
SOLUCIÓN:
Graficando la rosa θ
= 3
sen
4
r e identificando la región, tenemos:
El área estaría dada por:
[ ]
[ ]
[ ]
π
π
π
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
π
π
π
π
π
θ
θ
4
6
24
6
0
0
6
6
6
24
6
6
24
2
6
cos
1
48
3
16
3
3
4
2
1
6
)
(
2
1
6
6
0
6
0
6
0
2
6
0
2
2
2
1
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡ −
=
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
=
∫
∫
∫
∫
A
A
sen
sen
A
sen
d
d
sen
d
sen
d
f
A
Ejemplo 4
Hallar el área de la región encerrada por el rizo de θ
−
= cos
4
2
r
SOLUCIÓN:
Graficando el caracol θ
−
= cos
4
2
r e identificando la región, tenemos:
75](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-324-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
El área estaría dada por:
[ ]
( )
[ ]
[ ] [ ] [ ]
[ ]
( )
3
7
4
2
3
2
2
3
16
4
0
sen
2
0
sen
16
)
0
(
12
3
2
sen
2
3
sen
16
3
12
2
2
sen
4
8
sen
16
4
2
2
cos
1
16
cos
16
4
cos
16
cos
16
4
cos
16
cos
16
4
cos
4
2
2
1
2
)
(
2
1
3
0
3
0
3
0
3
0
3
0
2
3
0
3
0
3
0
2
3
0
2
2
2
1
−
π
=
+
−
π
=
+
−
−
⎟
⎠
⎞
⎜
⎝
⎛ π
+
π
−
π
=
θ
+
θ
+
θ
−
θ
=
θ
⎥
⎦
⎤
⎢
⎣
⎡ θ
+
+
θ
θ
−
θ
=
θ
θ
+
θ
θ
−
θ
=
θ
θ
+
θ
−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
θ
θ
−
=
θ
θ
=
π
π
π
π
π
π
π
π
π
θ
θ
∫
∫
∫
∫
∫
∫
∫
∫
∫
A
A
A
A
d
d
d
d
d
d
d
d
d
f
A
Ejemplo 5
Hallar el área de la región interior a ambas curvas
⎩
⎨
⎧
θ
+
=
θ
=
cos
1
sen
3
r
r
SOLUCIÓN:
Graficando las figuras e identificando la región, tenemos:
76](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-325-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
El ángulo de intersección se la obtiene igualando las ecuaciones de las curvas y luego
resolviendo la ecuación trigonométrica que se forma, es decir:
( ) ( )
( )
( )( )
3
2
1
cos
1
cos
0
1
cos
2
1
cos
0
1
cos
cos
2
0
2
cos
2
cos
4
cos
cos
2
1
cos
1
3
cos
cos
2
1
sen
3
cos
1
sen
3
cos
1
sen
3
2
2
2
2
2
2
2
2
π
=
θ
∨
π
=
θ
=
θ
∨
−
=
θ
=
−
θ
+
θ
=
−
θ
+
θ
=
−
θ
+
θ
θ
+
θ
+
=
θ
−
θ
+
θ
+
=
θ
θ
+
=
θ
θ
+
=
θ
El área estaría dada por:
[ ] [ ]
3
4
3
4
3
3
16
9
4
4
3
3
16
3
4
8
3
3
2
2
3
2
1
8
3
6
2
3
4
2
sen
2
1
sen
2
2
1
4
2
sen
2
1
2
3
cos
1
2
1
sen
3
2
1
3
3
0
3
2
3
0
2
−
π
=
−
π
−
π
+
−
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
π
−
⎟
⎠
⎞
⎜
⎝
⎛
π
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
π
=
⎥
⎦
⎤
⎢
⎣
⎡ θ
+
θ
+
θ
+
θ
+
⎟
⎠
⎞
⎜
⎝
⎛ θ
−
θ
=
θ
θ
+
+
θ
θ
=
π
π
π
π
π
π
∫
∫
A
A
A
A
d
d
A
Ejercicios propuestos 4.2
1. Hallar el área limitada por la curva θ
3
cos
a
r = .
2. Determinar el área de la región exterior a θ
+
= sen
2
r , e interior a θ
= sen
5
r
3. Determine el área de la región interior de la cardioide θ
cos
3
3+
=
r y exterior a la cardioide
θ
sen
r 3
3+
= en el primer cuadrante
4. Determine el área de la región dentro de la circunferencia θ
sen
r 3
= y fuera de θ
sen
r −
= 2 .
77](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-326-320.jpg)

![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
Observe que lo anterior también se lo puede ver como que se
rebana el sólido y se determina el volumen de una partición. En este
caso el sólido diferencial tiene la forma un DISCO, por tanto su
volumen está dado por:
[ ] dx
x
f
dx
r
dV
2
2
)
(
π
=
π
=
Segundo: El volumen de todo el sólido es una suma infinita de los
volúmenes de las particiones, es decir:
[ ] dx
x
f
V
b
a
2
)
(
∫
π
=
CASO II. Suponga ahora que la región plana fuese como la que
se sombrea en la figura. Al girar la región alrededor del eje x se genera
un sólido de revolución de la siguiente forma:
Primero: El sólido diferencial que se genera al rotar el elemento
diferencial alrededor del eje x, para cada partición tiene la forma de
un ANILLO
79](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-328-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
El volumen del sólido diferencial estaría dado por:
[ ]dx
r
r
dV
2
1
2
2 −
π
=
pero observe que: y
)
(
2 x
f
r = )
(
1 x
g
r = entonces:
( ) ( )
[ ]dx
x
g
x
f
dV
2
2
)
(
)
( −
π
= .
Segundo: EL volumen total del sólido que se genera al girar la
región plana alrededor del eje x, estaría dado por:
( ) ( )
[ ]
∫ −
π
=
b
a
dx
x
g
x
f
V
2
2
)
(
)
(
CASO III. Ahora en cambio suponga que si tuviésemos que girar
la región anterior en torno al eje y:
El sólido diferencial tendría la forma de una CORTEZA:
80](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-329-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
Para determinar el volumen de este elemento diferencial, lo
cortamos y lo abrimos, se obtiene un prisma rectangular:
dx
h
r
π
2
Su volumen sería:
rhdx
dV π
= 2
Pero observe que: )
(
)
( x
g
x
f
h
x
r
−
=
=
Por tanto el volumen total del sólido sería:
[ ]dx
x
g
x
f
x
V
b
a
)
(
)
(
2 −
π
=
∫ .
Para regiones simples-y, los procedimientos son análogos.
Ejemplo 1
Hallar el volumen del sólido que se genera al girar la región plana
⎪
⎩
⎪
⎨
⎧
=
=
x
y
x
y
R
8
:
2
alrededor del eje x.
SOLUCIÓN:
PASO 1: trazamos las gráficas de las curvas dadas.
PASO 2: Identificamos la región.
PASO 3: El elemento diferencial, lo escogemos vertical
81
( )
2
0
0
8
8
8
3
4
2
=
∨
=
=
−
=
=
x
x
x
x
x
x
x
x](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-330-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
Al hacer girar el elemento diferencial en torno al eje indicado se forma un anillo, cuyo volumen está
dado por: [ ]dx
r
r
dV 2
1
2
2 −
π
= y en este caso x
r 8
2 = y
2
1 x
r =
PASO 4: Por tanto
( ) ( )
[ ]
3
2
0
5
2
2
0
4
2
0
2
2
2
5
48
5
32
16
5
2
8
8
8
u
V
x
x
dx
x
x
dx
x
x
V
π
=
⎟
⎠
⎞
⎜
⎝
⎛
−
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
π
=
−
π
=
⎥
⎦
⎤
⎢
⎣
⎡ −
π
=
∫
∫
NOTA: resuelva el ejemplo tomando el elemento diferencial horizontal.
Ejemplo 2
Hallar el volumen del sólido que se genera al girar la región plana
⎪
⎩
⎪
⎨
⎧
=
=
x
y
x
y
R
8
:
2
alrededor del eje y.
SOLUCIÓN:
PASO 1 Y PASO 2: La región plana es la misma que la del ejercicio anterior
PASO 3: El elemento diferencial girado en torno al eje y da lugar a una Corteza
Cuyo volumen está dado por rhdx
dV π
= 2 y en este caso x
r = y
2
8 x
x
h −
=
PASO 4: Por tanto:
82](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-331-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( )
[ ]
3
4
2
5
2
0
4
2
5
2
0
3
2
3
2
0
2
5
24
4
5
32
2
)
0
(
4
2
2
5
8
2
2
4
5
8
2
2
8
2
8
2
u
V
x
x
dx
x
x
dx
x
x
x
V
π
π
π
π
π
π
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
−
=
∫
∫
Ejemplo 3
Hallar el volumen del sólido que se genera al girar la región plana
⎪
⎩
⎪
⎨
⎧
=
=
x
y
x
y
R
8
:
2
alrededor del eje 4
=
y
SOLUCIÓN:
PASO 1 Y PASO 2: La región plana es la misma que la de los ejercicios anteriores
PASO 3: El elemento diferencial girado en torno al eje 4
=
y da lugar a una Anillo
El volumen de este diferencial está dado por [ ]dx
r
r
dV 2
1
2
2 −
π
= y en este caso 2
2 4 x
r −
=
y x
r 8
4
1 −
=
PASO 4: Por tanto, calculando el volumen tenemos:
83](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-332-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( ) ( )
( ) ( )
[ ]
3
2
3
2
3
5
2
0
2
3
2
3
5
2
0
2
1
2
4
2
0
4
2
2
0
2
2
2
15
206
3
128
16
3
64
5
32
)
0
(
2
3
2
32
2
2
8
3
2
8
5
2
3
2
32
2
8
3
8
5
8
8
8
8
8
8
8
16
8
16
8
4
4
u
V
x
x
x
x
dx
x
x
x
x
dx
x
x
x
x
dx
x
x
V
π
π
π
π
π
π
π
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
=
+
−
−
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
=
∫
∫
∫
Ejemplo 4
Hallar el volumen del sólido que se genera al girar la región plana
⎪
⎩
⎪
⎨
⎧
=
=
x
y
x
y
R
8
:
2
alrededor del eje 1
−
=
y
SOLUCIÓN:
PASO 1 Y PASO 2: La región plana es la misma que la de los ejercicios anteriores
PASO 3: El elemento diferencial girado en torno al eje 1
−
=
y da lugar a una Anillo
El volumen de este diferencial está dado por [ ]dx
r
r
dV 2
1
2
2 −
π
= y en este caso
2
1 1 x
r +
= y x
r 8
1
2 +
=
PASO 4: Por tanto:
84](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-333-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( ) ( )
( ) ( )
[ ]
( )
( )
3
5
3
2
2
3
2
0
5
3
2
2
3
2
0
4
2
2
1
2
0
4
2
2
0
2
2
2
15
174
5
32
3
16
16
3
32
)
0
(
5
2
3
2
2
2
4
2
3
2
8
5
3
2
2
8
2
3
8
2
2
8
8
2
2
1
8
8
2
1
1
8
1
u
V
x
x
x
x
dx
x
x
x
x
dx
x
x
x
x
dx
x
x
V
π
π
π
π
π
π
π
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
+
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
+
+
−
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=
∫
∫
∫
Ejemplo 5
Hallar el volumen del sólido que se genera al girar la región plana
⎪
⎩
⎪
⎨
⎧
=
=
x
y
x
y
R
8
:
2
alrededor del eje 2
=
x
SOLUCIÓN:
PASO 1 Y PASO 2: La región plana es la misma que la de los ejercicios anteriores
PASO 3: El elemento diferencial girado en torno al eje 2
=
x da lugar a una corteza
El volumen de este diferencial está dado por rhdx
dV π
= 2 y en este caso x
r −
= 2 y
2
8 x
x
h −
=
PASO 4: Por tanto:
85](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-334-320.jpg)






![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
4.3.1 LONGITUD DE ARCO EN COORDENADAS
POLARES.
La longitud de arco esta dada por:
θ
⎟
⎠
⎞
⎜
⎝
⎛
θ
+
⎟
⎠
⎞
⎜
⎝
⎛
θ
=
∫
θ
θ
d
d
dy
d
dx
s
2
1
2
2
Reemplazando, tenemos:
( )
( ) ( )
( )
[ ] [ ]
[ ] [ ]
[ ] ( ) [ ] ( ) θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
d
sen
f
sen
f
s
d
f
sen
f
f
sen
f
sen
f
sen
f
f
f
s
d
f
sen
f
sen
f
f
s
∫
∫
∫
+
+
+
=
+
+
+
+
+
−
=
+
+
−
=
2
1
2
1
2
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
cos
)
(
cos
)
´(
cos
)
(
cos
)
(
)
´(
2
)
´(
)
(
cos
)
(
)
´(
2
cos
)
´(
cos
)
(
´
)
(
cos
´
Resultando finamente:
( ) ( ) θ
θ
+
θ
=
∫
θ
θ
d
f
f
s
2
1
2
2
)
´(
)
(
Ejemplo 1
Hallar la longitud de la circunferencia a
r =
SOLUCIÓN:
Aplicando la formula y resolviendo, resulta:
( ) ( )
a
s
a
s
d
a
s
d
o
a
s
d
f
f
s
π
=
θ
=
θ
=
θ
+
=
θ
θ
+
θ
=
π
π
π
θ
θ
∫
∫
∫
2
)
´(
)
(
2
0
2
0
2
0
2
2
2
2
2
1
Ejemplo 2
Hallar la longitud de la cardioide θ
+
= cos
1
r
SOLUCIÓN:
Aplicando la formula y resolviendo, resulta:
92](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-341-320.jpg)

![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( ) ( ) ( ) ( )
2
3
3
4
4
3
3
sen
4
3
cos
2
cos
3
sen
3
sen
cos
1
cos
3
sen
3
2
1
3
2
3
0
3
2
3
0
2
2
3
2
2
3
0
2
2
+
π
=
−
+
π
=
+
θ
=
θ
+
θ
θ
+
θ
=
θ
−
+
θ
+
+
θ
θ
+
θ
=
π
π
θ
π
π
π
θ
π
π
π
π
∫
∫
∫
∫
Per
Per
Per
d
d
Per
d
Per
Ejercicios propuestos 4.5
1. Determine el área y el perímetro de la región interior a las curvas θ
= cos
3
r y .
θ
+
= cos
1
r
2. Determinar:
a) El valor de para el cual el área de la región limitada por la cardioide
a ( )
θ
cos
1−
= a
r sea igual
a π
9 unidades cuadradas.
b) La longitud de la cardioide definida en el literal a).
4.4 VALOR MEDIO DE UNA FUNCIÓN DE UNA VARIABLE
Sea f una función continua en el intervalo [ ]
b
a, . El VALOR
MEDIO O VALOR PROMEDIO de , denotado como
f f , está dado
por:
∫
−
=
b
a
dx
x
f
a
b
f )
(
1
Ejemplo
Las estadísticas indican que t meses después del principio de año, el precio de la carne
de res era dólares por libra. ¿Cuál fue el precio medio de la
carne durante los 3 primeros meses?.
6
.
1
2
.
0
09
.
0
)
( 2
+
−
= t
t
t
p
SOLUCIÓN:
El promedio del precio durante los 3 primeros meses es:
94](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-343-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 4 Aplicaciones de la Integral
( )
[ ]
57
.
1
$
8
.
4
9
.
0
81
.
0
3
1
6
.
1
2
2
.
0
3
09
.
0
3
1
6
.
1
2
.
0
09
.
0
0
3
1
)
(
1
3
0
2
3
3
0
2
=
+
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
=
+
−
−
=
−
=
∫
∫
p
t
t
t
dt
t
t
dt
t
p
a
b
p
b
a
Misceláneos
1. Sea R la región definida por : ( )
{ }
e
x
y
x
IR
y
x
R ≤
≤
∧
≤
≤
∈
= 1
1
ln
/
, 2
. Calcule:
a) El área de la región R.
b) El volumen del sólido que se genera al rotar la región R alrededor del eje y
2. Sea la región
( ) [ ] [ ]
{ }
0
4
2
0
4
2
/
, 2
2
≥
∧
−
≤
≤
+
∨
≤
∧
−
≤
≤
+
∈
= x
x
y
x
x
x
y
x
IR
y
x
R
Calcule:
a) El área de la región R.
b) El volumen del sólido que se genera al rotar la región R alrededor de la recta 4
=
y
c) El volumen del sólido que se genera al rotar la región R alrededor de la recta 1
=
x
3. Calcule el volumen del sólido de revolución que se genera al rotar la región
( )
{ }
x
y
x
IR
y
x
R ≤
≤
−
∈
= 14
/
, 2
2
alrededor de la recta 4
=
x .
4. Calcular el área de la región interior a la rosa θ
2
cos
2
=
r y exterior a la circunferencia 1
=
r .
5. Sea la región R limitada por la recta 0
=
x y la curva . Determine el valor de de tal
modo que la recta
x
y −
= 4
2
a
a
x = divida a la región R en dos regiones de igual área.
6. Sea la región ( )
{ }
2
4
0
/
, x
y
y
x
R −
≤
≤
= . Determine el valor de de tal modo que la recta
a a
y =
divida a la región R en dos regiones de igual área.
7. Calcule el área de la región ( )
{ }
x
y
x
x
y
x
y
y
x
R 2
12
2
2
/
, 2
−
≤
∧
+
≤
∧
≥
=
8. Calcular el área de la región interior al rizo grande y exterior al rizo pequeño de θ
cos
2 −
=
r .
9. Sea ( )
{ }
1
0
1
2
/
, 2
≤
≤
∧
+
≤
≤
= x
x
y
x
y
x
R . Calcule el volumen del sólido que se genera al rotar la
región R alrededor de la recta 1
=
x
10. Calcular el área de la región interior al rizo grande y exterior al rizo pequeño de θ
cos
4
2 +
=
r .
11. Determine la longitud de la curva definida por las ecuaciones paramétricas
[ ]
π
2
,
0
,
2
2
2
cos
cos
2
∈
⎩
⎨
⎧
−
=
−
=
t
t
sen
sent
y
t
t
x
12. Sea R la región limitada por
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
−
=
=
=
x
x
y
x
y
y
4
0
2
2
Calcule:
a) El área de la región R.
b) El volumen del sólido que se genera al rotar la región R alrededor de la recta 1
−
=
x
13. Calcular el área de la región interior a θ
cos
2
1+
=
r y exterior a la 1
=
r .
14. Sea ( ) ( )
{ }
2
2
2
3
0
/
, y
x
y
x
y
y
x
R ≤
∧
−
≥
∧
≥
= . Calcule el volumen del sólido que se genera al rotar
la región R alrededor del eje 1
=
y .
95](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-344-320.jpg)



![MOISES VILLENA MUÑOZ Cap. 5 Integrales Impropias
El área de la región estaría dada por
∫
∞
−
=
0
dx
e
A x
, la cual es una integral impropia, que
escribiéndola con propiedad tenemos:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
=
∫
∫ −
∞
→
∞
−
N
x
N
x
dx
e
dx
e
A
0
0
lím
Al calcular la integral definida y luego tomando límite resulta:
[ ] [ ] 1
1
1
lím
lím
lím 0
0
=
−
=
−
=
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∞
−
−
∞
→
−
∞
→
−
∞
→ ∫ e
e
e
dx
e N
N
N
x
N
N
x
N
En este caso se dice que el área converge a 1 ( )
2
1u
A =
Ejemplo 2
Hallar el área de la región
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥
≥
≤
0
1
1
:
y
x
x
y
R
SOLUCIÓN:
El área de la región estaría dada por
∫
∞
=
1
1
dx
x
A , la cual es una integral impropia, que
escribiéndola con propiedad tenemos:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
=
∫
∫ ∞
→
∞ N
N
dx
x
dx
x
A
1
1
1
lím
1
Al calcular la integral definida y luego tomando límite resulta:
[ ] [ ] ∞
=
−
∞
=
−
=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∞
→
∞
→
∞
→ ∫ 1
ln
ln
1
ln
ln
lím
ln
lím
1
lím 1
1
N
x
dx
x N
N
N
N
N
En este caso se dice que la integral DIVERGE ( ∞
=
A ) es decir que haciendo la integral entre 1
y un número muy grande, el resultado es una cantidad muy grande.
99](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-348-320.jpg)

![MOISES VILLENA MUÑOZ Cap. 5 Integrales Impropias
[ ]
[ ]
π
=
=
−
∞
=
=
+
=
+
=
π
∞
→
∞
→
∞
→
∫
∫
k
A
k
k
x
k
dx
x
k
dx
x
k
A
N
N
N
N
N
N
2
0
0
2
0
2
2
0
arctg
arctg
2
arctg
lím
2
1
1
lím
2
1
lím
2
Si la condición es que
2
1u
A = entonces 1
=
π
k por tanto
π
=
1
k
Ejemplo 4
Determine para que valores de p la integral impropia
∫
∞
1
1
dx
x p
converge y para
que valores diverge.
SOLUCIÓN:
Escribiendo con propiedad la integral impropia tenemos:
∫
∞
→
N
p
N
dx
x
1
1
lím
Se observa que hay que considerar 2 casos: si 1
=
p y si 1
≠
p
Primero si 1
=
p tenemos:
[ ] [ ] ∞
=
−
=
=
∞
→
∞
→
∞
→ ∫ 1
ln
lím
ln
lím
1
lím 1
1
LnN
x
dx
x N
N
N
N
N
(Diverge)
Segundo si 1
≠
p tenemos:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
=
−
−
∞
→
+
−
∞
→
−
∞
→ ∫ p
p
N
p
x
dx
x
p
p
N
N
p
N
N
p
N 1
1
1
lím
1
lím
lím
1
1
1
1
1
de lo último hay que considerar dos casos:
Si 1
p entonces ∞
=
−
−
∞
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
−
−
∞
→ p
p
p
N p
p
N 1
1
1
1
1
lím
1
1
(diverge)
Si 1
p entonces
p
p
p
p
N p
p
N −
−
=
−
−
∞
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
−
−
∞
→ 1
1
0
1
1
1
1
1
1
lím
1
1
(converge)
Por lo tanto:
⎪
⎩
⎪
⎨
⎧
−
≤
∞
=
∫
∞
1
;
1
1
1
;
1
1
p
p
p
dx
x p
101](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-350-320.jpg)
![MOISES VILLENA MUÑOZ Cap. 5 Integrales Impropias
5.2 INTEGRANDOS INFINITOS
Ahora trataremos regiones que están limitadas por curvas no
acotadas, las graficas de las curvas tienen asíntotas verticales
Ejemplo 1
Hallar el área de la región
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≤
≥
≤
0
0
1
:
y
x
x
y
R .
SOLUCIÓN:
La región referida sería:
La integral para el área es:
∫
=
1
0
1
dx
x
A note que la función
x
x
f
1
)
( = no está definida en
por tanto es una integral impropia, que escribiéndola con propiedad y resolviendo resulta:
0
=
x
[ ] [ ] ∞
=
−
=
−
=
=
=
= +
→
→
→ +
+
+
∫
∫ 0
ln
0
ln
1
ln
lím
ln
lím
1
lím
1
0
1
0
1
0
1
0
t
x
dx
x
dx
x
A
t
t
t
t
t
(diverge)
Ejemplo 2
Calcular
∫
−
2
1
2
1
dx
x
SOLUCIÓN:
102](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-351-320.jpg)















![Moisés Villena Muñoz Coordenadas Polares
90
Entonces:
( ) ( )
( )
[ ]
( )
( )
( )
[ ]
( )
φ
−
θ
+
=
=
φ
−
θ
+
=
φ
−
θ
+
φ
−
θ
−
=
φ
−
θ
−
=
=
cos
1
cos
1
cos
cos
cos
,
,
e
ed
r
ed
e
r
ed
er
r
er
ed
r
r
d
e
r
l
P
d
e
F
P
d
Casos especiales son:
1. Si D
0
=
φ tenemos
θ
+
=
cos
1 e
ed
r
2. Si π
=
φ tenemos
θ
−
=
cos
1 e
ed
r
3. Si
2
π
=
φ tenemos
θ
+
=
sen
1 e
ed
r
4. Si
2
3
π
=
φ tenemos
θ
−
=
sen
1 e
ed
r
Ejemplo 1
Graficar
θ
+
=
cos
1
6
r
SOLUCIÓN:
En este caso 1
=
e (el coeficiente del coseno) por tanto tenemos una parábola con
foco el polo (el origen) y directriz con ecuación cartesiana 6
=
x (a la derecha y
paralela al eje
2
π
). Parábola cóncava a la izquierda.](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-367-320.jpg)






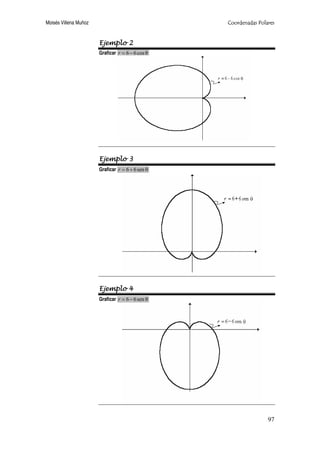





















![Moisés Villena Muñoz Cónicas
63
( ) ( )
( ) cx
a
y
c
x
a
y
c
xc
x
y
c
x
a
a
y
c
xc
x
y
c
x
y
c
x
a
a
y
c
x
y
c
x
a
y
c
x
4
4
4
2
)
(
4
4
2
)
(
)
(
4
4
)
(
)
(
2
)
(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
+
=
+
+
+
+
−
+
+
+
−
=
+
+
−
+
−
+
+
+
−
=
+
−
+
+
−
=
+
−
Dividiendo para 4, elevando al cuadrado y reduciendo términos
semejantes:
( ) ( )
[ ]
[ ] 2
2
2
4
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
)
(
)
(
x
c
cx
a
a
y
c
cx
x
a
x
c
c
a
a
y
c
x
a
cx
a
y
c
x
a
+
+
=
+
+
+
+
+
=
+
+
+
=
+
+
( ) ( )
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
c
a
a
y
a
x
c
a
c
a
a
y
a
x
c
x
a
x
c
cx
a
a
y
a
c
a
cx
a
x
a
−
=
+
−
−
=
+
−
+
+
=
+
+
+
Dividiendo para ( )
2
2
2
c
a
a −
2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2
( ) ( )
( ) ( ) ( )
x a c a y a a c
a a c a a c a a c
− −
+ =
− − −
1
2
2
2
2
2
=
−
+
c
a
y
a
x
Finamente, llamando 2
2
2
c
a
b −
= tenemos:
1
2
2
2
2
=
+
b
y
a
x
Ecuación canónica de la elipse con centro ( )
0
,
0
O y
eje focal horizontal
“b” representa la longitud del semieje menor, Observe la gráfica
anterior.
Aquí el lado recto tiene dimensión
a
b2
2
. ¡Demuéstrelo!
Para los casos generales tenemos:
Suponga que el vértice es el punto )
,
( k
h
V , y que el eje focal sea
horizontal entonces su ecuación sería:
( ) ( ) 1
2
2
2
2
=
−
+
−
b
k
y
a
h
x
Y su gráfica sería:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-396-320.jpg)





![Moisés Villena Muñoz Cónicas
69
Despejando un radical, elevando al cuadrado y reduciendo términos
semejantes:
( ) ( )
( ) 2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
4
4
2
)
(
4
4
2
)
(
)
(
4
4
)
(
)
(
2
)
(
y
c
x
a
a
cx
y
c
xc
x
y
c
x
a
a
y
c
xc
x
y
c
x
y
c
x
a
a
y
c
x
y
c
x
a
y
c
x
+
−
=
−
+
+
−
+
+
−
+
=
+
+
+
+
−
+
+
−
+
=
+
+
+
−
+
=
+
+
Dividiendo para 4, elevando al cuadrado y reduciendo términos
semejantes:
( ) ( )
[ ]
[ ]
2
2
2
2
4
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
)
(
2
)
(
y
c
cx
x
a
a
cx
a
x
c
y
c
x
a
a
cx
a
x
c
y
c
x
a
a
cx
+
+
−
=
+
−
+
−
=
+
−
+
−
=
−
( ) ( )
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
a
c
a
y
a
x
a
c
a
c
a
y
a
x
a
x
c
y
a
c
a
cx
a
x
a
a
cx
a
x
c
−
=
−
−
−
=
−
−
+
+
−
=
+
−
Dividiendo para ( )
2
2
2
a
c
a −
)
(
)
(
)
(
)
(
)
(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
a
c
a
a
c
a
a
c
y
a
a
c
a
a
c
x
−
−
=
−
−
−
−
1
2
2
2
2
2
=
−
−
a
c
y
a
x
Finamente, llamando
2
2
2
a
c
b −
= tenemos:
1
2
2
2
2
=
−
b
y
a
x
Ecuación canónica de la hipérbola con centro ( )
0
,
0
O
y eje focal horizontal
Aquí “b” representa la longitud del segmento (Observe la gráfica
anterior) llamado semieje conjugado.
Para los casos generales tenemos:
Suponga que el vértice es el punto )
,
( k
h
V , y que el eje focal sea
horizontal entonces su ecuación sería:
( ) ( ) 1
2
2
2
2
=
−
−
−
b
k
y
a
h
x
Y su gráfica sería:](https://image.slidesharecdn.com/moisesvillenamunoz-1-230227174034-6916eeed/85/Moises_Villena_Munoz-1-pdf-402-320.jpg)








