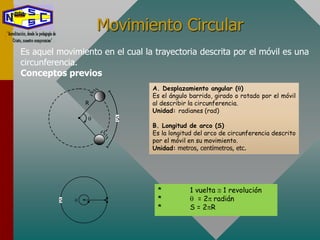
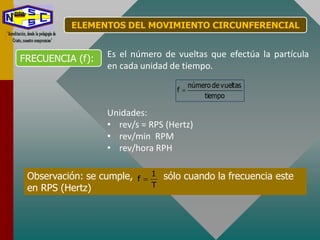
Este documento describe el movimiento circular y sus elementos clave como la velocidad angular, velocidad tangencial, periodo, frecuencia y aceleración centrípeta. También presenta ejemplos de cálculos relacionados con estos conceptos para sistemas de transmisión de movimiento circular como discos y licuadoras.

1. MOVIMIENTO CIRCULAR
SISTEMAS DE TRANSMISIÓN DE
MOVIMIENTO
Área de Ciencia, Tecnología y Ambiente
Prof. Zayda Alegre Ibarra
INSTITUCIÓN EDUCATIVA PARROQUIAL
“NUESTRA SEÑORA DEL SAGRADO
CORAZÓN DE JESÚS”

2. Movimiento Circular
Es aquel movimiento en el cual la trayectoria descrita por el móvil es una
circunferencia.
Conceptos previos
A. Desplazamiento angular (q)
Es el ángulo barrido, girado o rotado por el móvil
al describir la circunferencia.
Unidad: radianes (rad)
B. Longitud de arco (S)
Es la longitud del arco de circunferencia descrito
por el móvil en su movimiento.
Unidad: metros, centímetros, etc.
* 1 vuelta @ 1 revolución
* q = 2p radián
* S = 2pR

3. Movimiento Circular Uniforme MCU
Velocidad Tangencial
Es aquel movimiento de la partícula a lo largo de una
circunferencia cuyas características son:
* Barre ángulos centrales iguales en tiempos iguales.
* Recorre longitudes de arcos iguales en tiempos
iguales
.


Velocidad Angular

4. Relación entre velocidad tangencial y
velocidad angular
 


5. ELEMENTOS DEL MOVIMIENTO CIRCUNFERENCIAL
El período de la Tierra será.................. El período de la Tierra será
cuando gira alrededor del sol. ................ cuando gira sobre su eje.
Es el tiempo que demora una partícula en dar una
vuelta o revolución. Unidad: s, min, hora, día, etc.
PERÍODO (T):

6. ELEMENTOS DEL MOVIMIENTO CIRCUNFERENCIAL
Es el número de vueltas que efectúa la partícula
en cada unidad de tiempo.
Unidades:
• rev/s = RPS (Hertz)
• rev/min RPM
• rev/hora RPH
FRECUENCIA (f):
Observación: se cumple, sólo cuando la frecuencia este
en RPS (Hertz) T
1
f 

7. ¿Existe aceleración en el MCU?
En la imagen observamos que el módulo de la velocidad (rapidez) no varía pero la
dirección del vector velocidad sí varía, por lo tanto sí existe aceleración y se llama
aceleración centrípeta.
Aceleración centrípeta (ac ): Es la aceleración que mide los cambios de
velocidad en dirección.
Dirección: Radial dirigida hacia el centro de la trayectoria circular.
Módulo:
V = velocidad tangencial
w = velocidad angular
R = Radio de la circunferencia.
R.2

R
2
V
ca 

8. SISTEMAS DE TRANSMISIÓN DE
MOVIMIENTO

9. Un disco gira a razón de 7 rad/s (constante) durante 10 s.
Hallar el número de vueltas que genera en ese tiempo.
Ejemplo 1:

10. Ejemplo 2:
Las cuchillas de una licuadora giran a razón de 90 RPM.
Hallar la velocidad tangencial de los puntos que se
encuentran a 5 cm del eje de rotación en cm/s.

11. Ejemplo 3:
Un disco gira a razón de 45 RPM. Calcular la aceleración
de aquellos puntos ubicados a 0,12 m del centro del
disco (m/s2).

12. Ejemplo 4:
Un disco que tiene agujero a 50 cm de su centro
geométrico, gira con velocidad angular constante en
un plano horizontal. Respecto a un eje vertical, desde una altura H
= 1,25 m se abandona una bolita en el instante en que el agujero
y la bolita están en la misma vertical. Hallar la mínima velocidad
del disco, tal que la bolita pueda pasar por el agujero. (g=10 m/s2)

13. Ejemplo 5:
Si la velocidad angular
del disco "A" es 9 rad/s,
hallar la velocidad
angular del disco "B".
Ejemplo 6:
Si la velocidad tangencial del disco
"A" es 4 m/s, hallar la velocidad
tangencial del disco "B".

14. Ejemplo 7:
Si la velocidad angular
de "C" es 7 rad/s, hallar
la velocidad tangencial
de "B".
Ejemplo 8:
Si la velocidad angular de "A" es 9
rad/s, hallar la velocidad angular
de "B".

15. Ejemplo 9:
Si la velocidad angular
de "B" es 3 rad/s, hallar
la velocidad tangencial
de "C".
Ejemplo 10:
Si la velocidad tangencial de "B" es
10 m/s, hallar la velocidad
tangencial de "C".