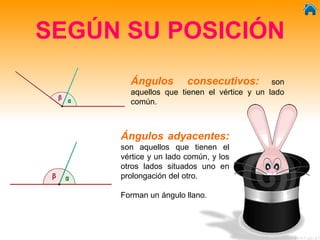
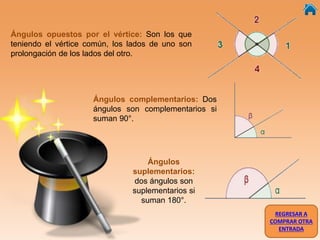
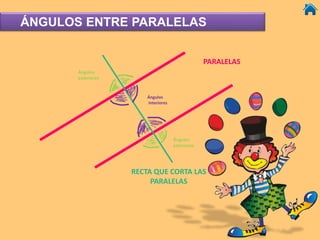
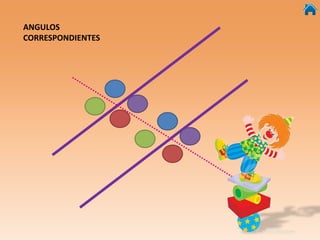
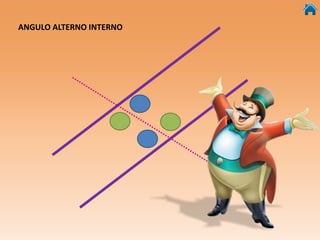
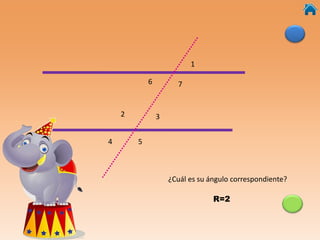
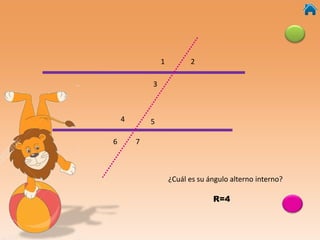
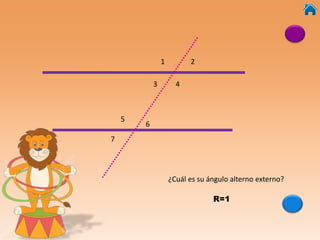
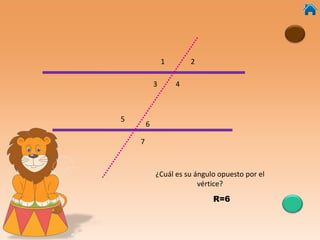
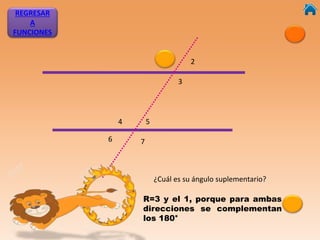
Este documento presenta información sobre ángulos, incluyendo definiciones de ángulo, paralela, y tipos de ángulos según su medida y posición. También explica conceptos como ángulos entre paralelas, ángulos correspondientes, ángulos alternos internos y externos. Incluye ejercicios interactivos para evaluar conocimientos sobre estos temas.