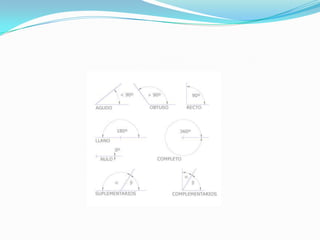
Este documento resume conceptos básicos de geometría incluyendo: 1) Puntos, rectas, segmentos y sus características. 2) Ángulos, su medida y clasificación. 3) Relaciones entre ángulos como ángulos complementarios, suplementarios y determinados por una recta secante. 4) Operaciones con ángulos como suma, resta, multiplicación y división.

1. 1. Puntos y rectas
1. Posiciones respectivas de las rectas.
2. Segmentos y semirrectas
3. Mediatriz de un segmento
2. Ángulos
1. Medida de Ángulos
3. Clasificación y relaciones entre ángulos
1. Clasificación
2. Ángulos complementarios y suplementarios
3. Ángulos determinados por una recta secante
4. Bisectriz de un ángulo.
4. Operaciones con Ángulos

2. 1. PUNTOS Y RECTAS
 Una recta es una línea sin principio ni final formada
por infinitos puntos.
 Para referirnos a los puntos utilizaremos letras
mayúsculas: A, B, C …, sin embargo, pera referirnos a
las rectas utilizamos letras minúsculas: r, s, t…

3. 1.1 Posiciones relativas de las
rectas.
 Dadas dos rectas r y s en el mismo
plano, entonces r y s pueden ser:
 Paralelas (no tienen puntos en común).
 Secantes (tienen un punto en común).
 Llamaremos rectas perpendiculares a las
rectas secantes que forman cuatro ángulos
rectos iguales.
 Coincidentes (todos sus puntos son
comunes)

4. 1.2 Segmentos y semirrectas.
 Una semirrecta es una recta que tiene principio pero
no final.
 Un segmento es la parte de una recta delimitada por
dos puntos. El segmento tiene principio y final. A estos
puntos se les llama EXTREMOS del segmento.
Extremo inicial, y extremo final.
A B A
Segmento Semirrecta

5. 1.3 Mediatriz de un segmento
 La mediatriz de un segmento es la recta perpendicular
a él que pasa por el punto medio.
Mediatriz de un segmento
FIN.

6. 2. ÁNGULOS
 Llamaremos ángulo a la región del plano delimitada
por dos semirrectas con el mismo origen denominado
vértice.

7. 2.1. Medida de los ángulos
 Al igual que las horas, los grados es otro sistema
sexagesimal, es decir 60 unidades es una unidad de
orden superior.
 Para medir los ángulos se utiliza el grado como unidad
de medida, un grado son 60 minutos y un minuto, 60
segundos.
 10 = 60 ´
 1´= 60 ”

8. 3. Clasificación y relaciones entre
ángulos
 3.1 Clasificación y 3.2 Ángulos complementarios y
suplementarios:
 Hay dos tipos de ángulos que nos sirven para comparar
el ángulo recto (90 º) y el ángulo llano 180º.
 Comparado con 90 º, un ángulo podrá ser agudo (< 90º),
recto (=90º) y obtuso (>90º).
 Un ángulo nulo es el que tiene 0º, y un ángulo completo
el que tiene los 360º

10. 3.1 Clasificación
 Si comparamos los ángulos con un ángulo llano,
obtendremos que un ángulo puede ser:
 Convexo: si mide menos de 180 º
 Cóncavo : si mide más de 180º
 Posición relativa de dos ángulos:
 Ángulos opuestos por el vértice: Son ángulos que tienen en
común un vértice y sus lados están sobre las mismas
rectas.
 Ángulos consecutivos: Tienen en común el vértice y el
lado.
 Ángulos Adyacentes: dos ángulos consecutivos que formen
180º
 Ángulos complementarios: Dos ángulos que, al sumarlos
dan uno recto.
 Ángulos suplementarios: Dos ángulos que, al sumarlos
dan 180º.
 OJO: Los ángulos adyacentes son suplementarios, pero los
suplementarios sólo serán adyacentes si tienen un lado en
común.

11. 3.3. Ángulos determinados por una
recta secante a dos paralelas
 Al cortase dos rectas por una transversal quedan determinados
varios ángulos: ocho en total. Los ángulos que están ubicados
en la región comprendida entre las dos paralelas se denominan
internos y los de afuera se denominan externos.
Los pares de ángulos no adyacentes que están en el mismo
semiplano respecto de la secante, siendo uno interno y el otro
externo, se llaman ángulos correspondientes. En la figura,
los ángulos 2 y 6 y 1 y 5 son correspondientes.
Los ángulos alternos internos son aquellos pares de ángulos
no adyacentes que están en distintos semiplanos respecto de la
transversal. En la figura son alternos internos los ángulos 3 y 5
y 4 y 6.
Los ángulos alternos externos son aquellos ángulos no
adyacentes que están en distintos planos respecto de la
transversal. En la figura son alternos externos los ángulos 2 y 8
y 1 y 7.
Los ángulos que están en el mismo semiplano respecto de la
transversal se llaman ángulos conjugados internos (como el
3 y el 4 y el 6 y el 5) o externos (el 2 y el 1 y el 7 y el 8).

12. 3.4. Bisectriz de un ángulo
 La bisectriz de un ángulo es la semirrecta que divide
en dos ángulos iguales.
¿Cómo dibujar bisectriz con regla y compás?

13. 4. Operaciones con ángulos
 Resta:
 Multiplicación:
 Multiplicar y sumar
 División de ángulos entre escalar