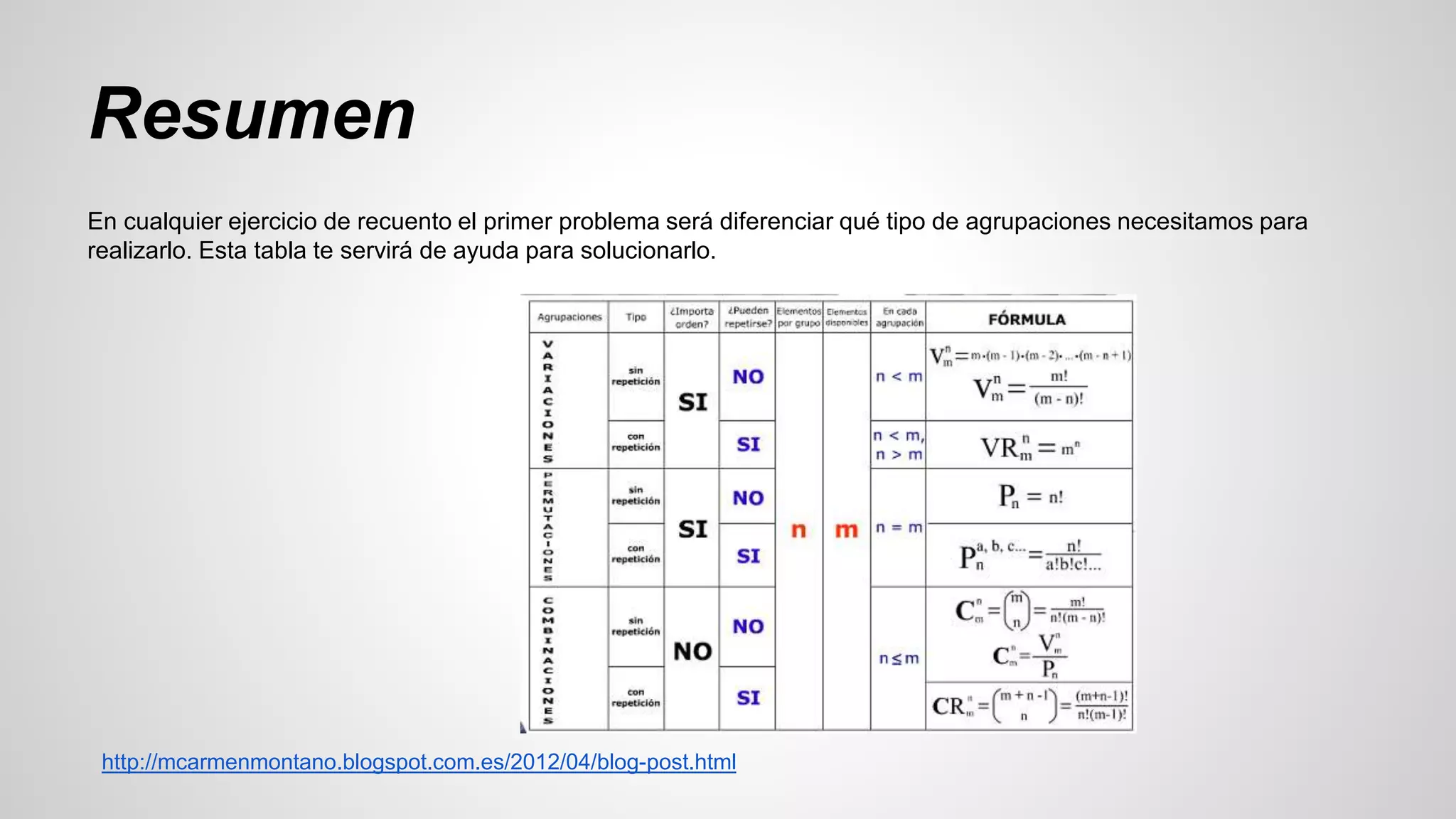
El documento aborda conceptos fundamentales de la combinatoria, como las variaciones, permutaciones y combinaciones, tanto con como sin repetición. Se introducen principios de adición y multiplicación para el recuento de elementos y se explican los factoriales y números combinatorios. Además, se proporcionan fórmulas y ejemplos para calcular cada tipo de agrupación en problemas prácticos.

1. UNIDAD DIDÁCTICA.
COMBINATORIA
Matías Jiménez Albaladejo

2. Combinatoria
● Combinatoria
● Factorial. Nº combinatorio
● Propiedades de los números combinatorios.
● Principios de adición y multiplicación.
● Variaciones sin repetición.
● Variaciones con repetición.

3. Combinatoria
● Permutaciones sin repetición.
● Permutaciones con repetición.
● Combinaciones sin repetición.
● Combinaciones con repetición.
● Resumen.
● Examen.

4. Combinatoria
La Combinatoria es la parte de las Matemáticas que se dedica a buscar procedimientos y estrategias para el recuento
de los elementos de un conjunto o la forma de agrupar los elementos de un conjunto.
Es decir, dentro de la Combinatoria es dónde tienen sentido preguntas del tipo:
1. ¿Cuántas quinielas distintas pueden hacerse?.
2. ¿Cuántas posibles combinaciones pueden darse en la lotería primitiva?.
3. ¿Qué posibilidades hay de que me toquen los cuatro ases en una mano de tute?
4. ¿De cuántas formas se pueden sentar 5 personas en 5 asientos de un cine?.
Trataremos de dar respuesta a estas cuestiones y algunas más.
http://www.unlu.edu.ar/~dcb/matemat/combina1.htm

5. Factorial. Nº combinatorio
Se llama factorial de un número natural "n" y se representa por n!, al producto de los n primeros números naturales
(excluido el 0).
n! = n · (n-1) · (n-2) · . . . · 1
Para el número 0 esta definición no tiene sentido. Se define el factorial de 0 por 1: 0! = 1
Se llama número combinatorio m sobre n a la expresión:
Hoy en día, con la utilización de la calculadora, es fácil calcular cualquier
número combinatorio, sin embargo resulta bastante interesante el cálculo
de números combinatorios con el siguiente triángulo, conocido entre otros
nombres como Triángulo de Pascal, en la que cada número combinatorio
se obtiene sumando los dos que tiene encima.
http://www.sangakoo.com/es/temas/factorial-y-numeros-combinatorios

6. Propiedades de los números
combinatorios
http://www.sangakoo.com/es/temas/factorial-y-numeros-combinatorios

7. Principios de adición y
multiplicación
Cardinal de un conjunto. Se llama cardinal de un conjunto A y se representa por card(A)
o por |A| al número de elementos que tiene el conjunto.
Principio de adición. Para contar los elementos de dos o más conjuntos que no tengan
elementos comunes, basta con sumar el número de elementos de cada uno de los
conjuntos:
En caso de que los conjuntos tengan elementos comunes, para contar el número total de
elementos habrá que sumar los elementos de ambos conjuntos y restar el número de
elementos repetidos.
Principio de multiplicación. Para contar los elementos de un conjunto de forma que
sus elementos están formados por pares de elementos, en los que el primer elemento
pertenece al primer conjunto y el segundo elemento al segundo conjunto (producto
cartesiano), se multiplica el número de elementos de cada conjunto.
http://www.sangakoo.com/es/temas/factorial-y-numeros-combinatorios

8. Variaciones sin repetición
Las variaciones sin repetición de n elementos tomados de p en p se definen como las distintas agrupaciones formadas con
p elementos distintos, eligiéndolos de entre los n elementos de que disponemos, considerando una variación distinta a otra
tanto si difieren en algún elemento como si están situados en distinto orden. El número de variaciones que se pueden
construir se puede calcular mediante la fórmula:
http://www.ematematicas.net/combinavordinarias.php

9. Variaciones con repetición
Las variaciones con repetición de n elementos tomados de p en p se definen como las distintas agrupaciones
formadas con p elementos que pueden repetirse, eligiéndolos de entre los n elementos de que disponemos,
considerando una variación distinta a otra tanto si difieren en algún elemento como si están situados en distinto orden.
El número de variaciones que se pueden construir se puede calcular mediante la fórmula:
http://www.ematematicas.net/combinavrepeticion.php

10. Permutaciones sin repetición
Las permutaciones sin repetición de n elementos se definen como las distintas formas de ordenar todos esos
elementos distintos, por lo que la única diferencia entre ellas es el orden de colocación de sus elementos. El número
de estas permutaciones será:
http://www.ematematicas.net/combinapermutaciones.php

11. Permutaciones con repetición
Llamamos a las permutaciones con repetición de n elementos tomados de a en a, de b en b, de c en c, etc,
cuando en los n elementos existen elementos repetidos (un elemento aparece a veces, otro b veces, otro c veces, etc)
verificándose que a+b+c+...=n. El número de estas permutaciones será:
http://www.ematematicas.net/combinaprepeticion.php

12. Combinaciones sin repetición
Las combinaciones sin repetición de n elementos tomados de p en p se definen como las distintas agrupaciones
formadas con p elementos distintos, eligiéndolos de entre los n elementos de que disponemos, considerando una
variación distinta a otra sólo si difieren en algún elemento, (No influye el orden de colocación de sus elementos). El
número de combinaciones que se pueden construir se puede calcular mediante la fórmula:
http://www.ematematicas.net/combinacombinaciones.php

13. Combinaciones con repetición
Las combinaciones con repetición de n elementos tomados de p en p se definen como las distintas agrupaciones
formadas con p elementos que pueden repetirse, eligiéndolos de entre los n elementos de que disponemos,
considerando una variación distinta a otra sólo si difieren en algún elemento, (No influye el orden de colocación de sus
elementos). El número de combinaciones que se pueden construir se puede calcular mediante la fórmula:
http://www.ematematicas.net/combinacrepeticion.php

14. Resumen
En cualquier ejercicio de recuento el primer problema será diferenciar qué tipo de agrupaciones necesitamos para
realizarlo. Esta tabla te servirá de ayuda para solucionarlo.
http://mcarmenmontano.blogspot.com.es/2012/04/blog-post.html