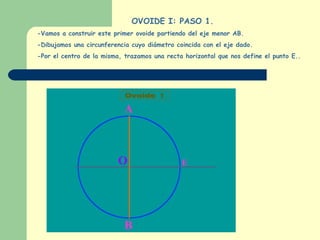
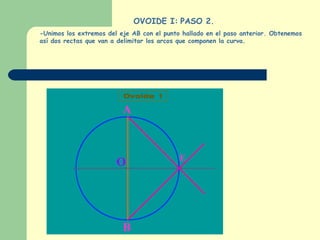
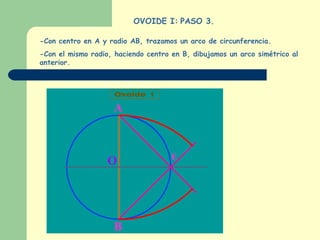
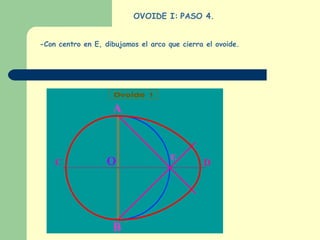
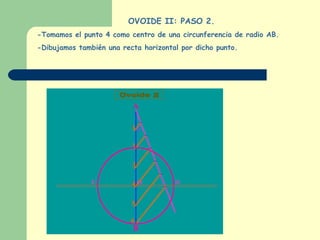
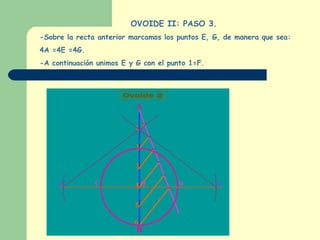
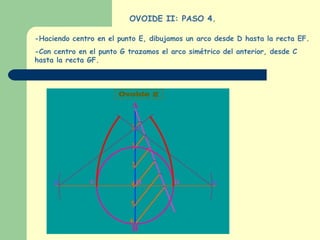
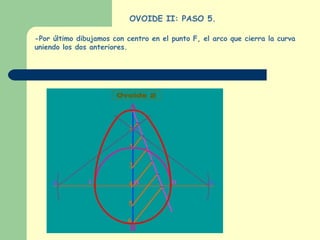
Este documento explica cómo construir dos tipos de ovoides mediante pasos geométricos. Un ovoide es una curva cerrada simétrica formada por cuatro arcos de circunferencia, dos iguales y dos desiguales. El primer ovoide se construye a partir del eje menor, mientras que el segundo lo hace a partir del eje mayor. El documento incluye instrucciones detalladas sobre cómo trazar los arcos necesarios para cada figura, así como ejemplos del uso de los ovoides en el arte y la tarea de buscar más ejemplos para

1. GEOMETRIA 4º E.S.O. Construcciones de Ovoides (II).

2. Un ovoide es una curva plana y cerrada, simétrica sólo respecto a su eje mayor, y formada por cuatro arcos de circunferencia, de los que dos son iguales y los otros dos son desiguales. Visita recomendada: Agradezco y reconozco el trabajo de Javier de Prada Pareja de quien he tomado las imágenes. www.javierdeprada.com

3. -Los ovoides son curvas cerradas de la misma naturaleza que los óvalos. Por lo tanto tienen también sus mismas propiedades. -Pero hay una diferencia importante:

4. OVOIDE I: PASO 1. -Vamos a construir este primer ovoide partiendo del eje menor AB. -Dibujamos una circunferencia cuyo diámetro coincida con el eje dado. -Por el centro de la misma, trazamos una recta horizontal que nos define el punto E..

5. OVOIDE I: PASO 2. -Unimos los extremos del eje AB con el punto hallado en el paso anterior. Obtenemos así dos rectas que van a delimitar los arcos que componen la curva.

6. OVOIDE I: PASO 3. -Con centro en A y radio AB, trazamos un arco de circunferencia. -Con el mismo radio, haciendo centro en B, dibujamos un arco simétrico al anterior.

7. OVOIDE I: PASO 4. -Con centro en E, dibujamos el arco que cierra el ovoide.

8. OVOIDE II: PASO 1. -En esta ocasión el dato de partida es el eje mayor AB. -Comenzamos dividiendo dicho eje en seis partes iguales. (Utilizamos el procedimiento ya visto en el apartado de trazados básicos).

9. OVOIDE II: PASO 2. -Tomamos el punto 4 como centro de una circunferencia de radio AB. -Dibujamos también una recta horizontal por dicho punto.

10. OVOIDE II: PASO 3. -Sobre la recta anterior marcamos los puntos E, G, de manera que sea: 4A =4E =4G. -A continuación unimos E y G con el punto 1=F.

11. OVOIDE II: PASO 4. -Haciendo centro en el punto E, dibujamos un arco desde D hasta la recta EF. -Con centro en el punto G trazamos el arco simétrico del anterior, desde C hasta la recta GF.

12. OVOIDE II: PASO 5. -Por último dibujamos con centro en el punto F, el arco que cierra la curva uniendo los dos anteriores.

13. Realiza los dos ejercicios anteriores, cada uno en una lámina. Pasarlos a limpio. Escanearlos y guardarlos en formato pdf. Enviarlos al profesor adjuntándolos a un correo electrónico. Y después deberás…

14. Algunos ejemplos de aplicación de los ovoides en el arte.

15. Busca mas ejemplos del uso de los ovoides en el arte, el diseño, la industria, etc. e inclúyelos en el Blog de clase poniendo en el titulo de la entrada tu nombre.