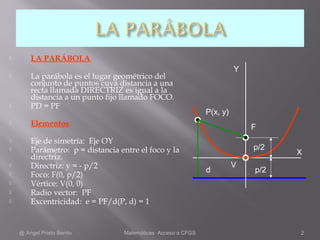
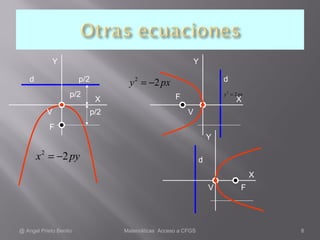
1. La parábola es el lugar geométrico de puntos cuya distancia a una recta directriz es igual a la distancia a un punto fijo llamado foco. Se describen los elementos de la parábola y se presentan ejemplos de hallar su ecuación a partir de los datos del foco, directriz y vértice. 2. Se presenta la ecuación general de la parábola cuando el vértice no está en el origen, y más ejemplos de hallar la ecuación cuando se conocen los datos del foco, directriz y vértice.

1. 1
Conceptos ecuaciones y ejercicios

2.  LA PARÁBOLA
 La parábola es el lugar geométrico del
conjunto de puntos cuya distancia a una
recta llamada DIRECTRIZ es igual a la
distancia a un punto fijo llamado FOCO.
 PD = PF
 Elementos
 Eje de simetría: Eje OY
 Parámetro: p = distancia entre el foco y la
directriz.
 Directriz: y = - p/2
 Foco: F(0, p/2)
 Vértice: V(0, 0)
 Radio vector: PF
 Excentricidad: e = PF/d(P, d) = 1
X
Y
F
p/2
V
P(x, y)
d p/2
@ Angel Prieto Benito Matemáticas Acceso a CFGS 2

3.  ECUACIÓN REDUCIDA
 Aplicando la definición:
 d(P, F) = d(P, d)
x + y - p = y + p
2 ( )2 | |
2 2
X
Y
F
p/2
V
P(x, y)
d p/2
• Elevando todo al cuadrado:
2 2
x 2 + y 2 - p = y 2
+ p + py
4 4
• Y simplificando, queda:
x2 = 2 py
• Que es la ECUACIÓN REDUCIDA
@ Angel Prieto Benito Matemáticas Acceso a CFGS 3

4.  Hallar la ecuación de la parábola cuyos datos conocidos son:
 1º.- Foco: F(0, 4) ,, Directriz d: y = - 4
 Vértice: V(0, (4-4)/2) ,, V(0,0)
 Parámetro: p = 4-(-4)=8
 Ecuación: x2 = 2py ,, x2 = 16y ,, y = x2 /16 Cóncava
 2º.- Foco: F(0, 0,25) ,, Directriz d: y = - 0,25
 Vértice: V(0, (0,25-0,25)/2) ,, V(0,0)
 Parámetro: p = 0,25-(-0,25)= 0,5
 Ecuación: x2 = 2py ,, x2 = y ,, y = x2 Cóncava
 3º.- Foco: F(0, -3) ,, Directriz d: y = 3
 Vértice: V(0, (3-3)/2) ,, V(0,0)
 Parámetro: p = 3-(-3)=6
 Ecuación: x2 = - 2py ,, x2 = - 12y ,, y = - x2 /12 Convexa
@ Angel Prieto Benito Matemáticas Acceso a CFGS 4

5.  ECUACIÓN GENERAL
 Lo general es que el vértice de la parábola
no sea el V(0, 0) sino un punto cualquiera
V(k, h)
• La fórmula quedaría:
x2 = 2 py
2
x k p y h
x kx k py ph
x kx py k ph
- = -
- + = -
- - + + =
( ) 2 ( )
2 2
2 2 2 )
2 2 ( 2 ) 0
2 2
X
Y
F
p/2
P(x, y)
V(k, h)
d p/2
• Que es la llamada
• ECUACIÓN GENERAL DESARROLLADA O
@ Angel Prieto Benito Matemáticas Acceso a CFGS 5

6.  Hallar la ecuación de la parábola cuyos datos conocidos son:
 4º.- Foco: F(-1, 3) ,, Directriz d: y = - 1
 Vértice: V(k, h) ,, V(-1, (3+1)/2) ,, V(-1, 2)
 Parámetro: p = 3 -(-1)= 4
 Ecuación: (x – k)2 = 2p(y – h) ,, (x + 1)2 = 8(y – 2)
 x2 + 2x + 1 = 8y – 16 ,, x2 + 2x – 8y + 17 = 0
 5º.- Foco: F(3, 5) ,, Directriz d: y = 2
 Vértice: V(k, h) ,, V(3, (5-2)/2) ,, V(3, 1,5)
 Parámetro: p = 5 – 2 = 3
 Ecuación: (x – k)2 = 2p(y – h) ,, (x – 3)2 = 6(y – 1,5)
 x2 – 6x + 9 = 6y – 9 ,, x2 – 6x – 6y + 18 = 0

 6º.- Foco: F(0, -3) ,, Directriz d: y = 5
 Vértice: V(k, h) ,, V(0, (5 – 3)/2) ,, V(0, 1)
 Parámetro: p = 5-(-3)=8
 Ecuación: (x – k)2 = – 2p(y – h) ,, x2 = – 16.(y – 1)
 x2 = – 16y + 16 ,, x2 + 16 y – 16 = 0 Convexa
@ Angel Prieto Benito Matemáticas Acceso a CFGS 6

7.  Hallar el foco, vértice y directriz de las parábolas siguientes:
 Ecuación general cóncava: x2 – 2kx – 2py + k2 + 2ph = 0
 7º.- P: x2 – x – 3y + 7 = 0
 Identificando términos, tenemos:
 2k=1  k=1/2 ,, 2p = 3  p = 3/2 = 1,5
 k2 + 2ph = 7  0,25 + 3 h = 7 ,, h = (7 – 0,25)/ 3 = 6,75/3 = 2,25
 V(0’5, 2’25) ,, p = 1’5 ,, d: y = h – p/2 = 2,25 – 0,75 = 1,5 ,, F(0’25, 3)
 8º.- P: x2 – 4x + 4y = 0
 Identificando términos, tenemos:
 2k=4  k=2 ,, 2p = – 4  p = – 2  p = 2, pero es convexa
 El parámetro p es una distancia. Si da negativo, la parábola es convexa.
 k2 + 2ph = 0  4 + 4h = 0 ,, h = – 1  V(2 , – 1)
 d: y = h + p/2 = – 1 + 1 = 0 ,, d: y = 0
 F(2, h – p/2)  F(2, – 1 – 1 ),, F(2 , –2)
@ Angel Prieto Benito Matemáticas Acceso a CFGS 7

8. Y
d p/2
p/2
V p/2
F
x2 = -2 py
d
y2 = 2 px
X
y2 = -2 px
X
Y
F
V
X
Y
d
V F
@ Angel Prieto Benito Matemáticas Acceso a CFGS 8