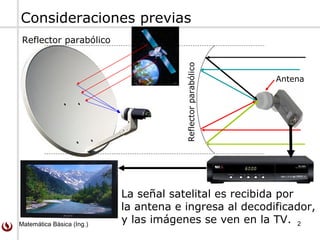
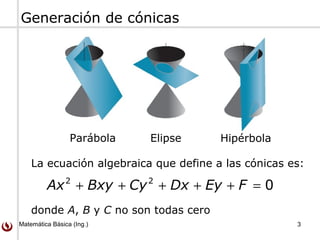
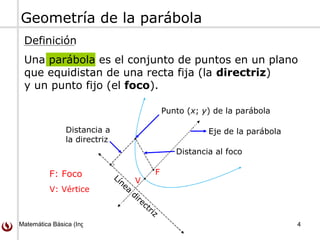
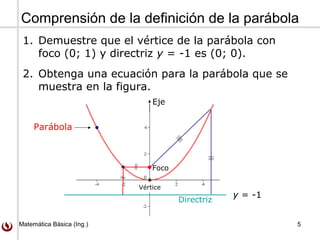
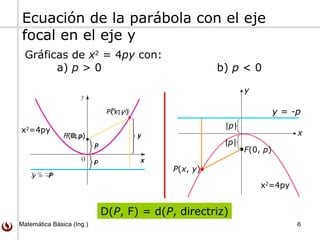
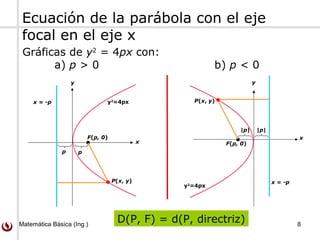
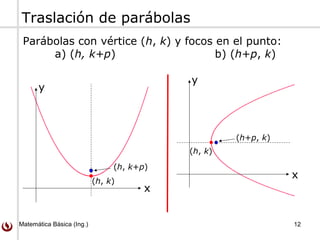
Este documento trata sobre parábolas y su geometría. Explica que una parábola es el conjunto de puntos equidistantes de una línea fija llamada directriz y un punto fijo llamado foco. Presenta las ecuaciones de parábolas estándares y cómo se pueden trasladar. También incluye ejemplos y ejercicios sobre parábolas.

1. Matemática Básica (Ing.) 1
Cónicas: Parábola
Alumna: Rocio Daga Sabelino

2. Matemática Básica (Ing.) 2
Consideraciones previas
Antena
Reflector parabólico
La señal satelital es recibida por
la antena e ingresa al decodificador,
y las imágenes se ven en la TV.
Reflectorparabólico

3. Matemática Básica (Ing.) 3
Generación de cónicas
Parábola Elipse Hipérbola
La ecuación algebraica que define a las cónicas es:
022
=+++++ FEyDxCyBxyAx
donde A, B y C no son todas cero

4. Matemática Básica (Ing.) 4
Geometría de la parábola
Definición
Una parábola es el conjunto de puntos en un plano
que equidistan de una recta fija (la directriz)
y un punto fijo (el foco).
Línea
directriz
F: Foco
Distancia a
la directriz
Punto (x; y) de la parábola
V: Vértice
Distancia al foco
F
V
Eje de la parábola

5. Matemática Básica (Ing.) 5
Comprensión de la definición de la parábola
1. Demuestre que el vértice de la parábola con
foco (0; 1) y directriz y = -1 es (0; 0).
2. Obtenga una ecuación para la parábola que se
muestra en la figura.
y = -1
Parábola
Foco
Vértice
Eje
Directriz

6. Matemática Básica (Ing.) 6
Ecuación de la parábola con el eje
focal en el eje y
D(P, F) = d(P, directriz)
Gráficas de x2
= 4py con:
a) p > 0 b) p < 0
x
y
F(0, p)
y = -p
P(x, y)
|p|
|p|
x2
=4py
x2
=4py
);( yxP
);0( pF
P
P
Py −=
y
x
x2
=4py

7. Matemática Básica (Ing.) 7
Ejercicios
1. Determine el foco, la directriz y el ancho focal de
la parábola:
a) .
b)
21
4
= −y x
2
6=x y

8. Matemática Básica (Ing.) 8
y
x
F(p, 0)
x = -p
P(x, y)
p p
y2
=4px
y
x
F(p, 0)
x = -p
P(x, y)
|p||p|
y2
=4px
D(P, F) = d(P, directriz)
Gráficas de y2
= 4px con:
a) p > 0 b) p < 0
Ecuación de la parábola con el eje
focal en el eje x

9. Matemática Básica (Ing.) 9
Ejercicios
2. Determine el foco, la directriz y el ancho focal de
la parábola:
y2
= –8x

10. Matemática Básica (Ing.) 10
Parábolas con vértice en (0; 0)
Ecuación
estándar
Abre
Foco
Directriz
Eje
Longitud focal
Ancho focal
x2
= 4py
Hacia arriba
o hacia abajo
(0; p)
y = -p
eje y
|p|
|4p|
y2
= 4px
Hacia la der.
o hacia la izq.
(p; 0)
x = -p
eje x
|p|
|4p|

11. Matemática Básica (Ing.) 11
Ejercicios
3. Determine la ecuación estándar de una parábola
cuya directriz es la línea x = 2 y cuyo foco es el
punto (-2; 0)
4. Determine la ecuación estándar de una parábola
que satisface las condiciones dadas:
a) Foco (-4; 0), directriz x = 4.
b) Vértice (0; 0), se abre a la derecha, anchura
focal = 8.

12. Matemática Básica (Ing.) 12
Traslación de parábolas
(h, k)
(h, k+p)
x
y
Parábolas con vértice (h, k) y focos en el punto:
a) (h, k+p) b) (h+p, k)
x
y
(h, k)
(h+p, k)

13. Matemática Básica (Ing.) 13
Parábolas con vértice (h, k)
Ecuación
estándar
Abre
Foco
Directriz
Eje
Longitud focal
Ancho focal
(x–h)2
= 4p(y–k)
Hacia arriba
o hacia abajo
(h, k+p)
y = k – p
x = h
|p|
|4p|
(y–k)2
= 4p(x–h)
Hacia la derecha
o hacia la izq.
(h+p, k)
x = h – p
y = k
|p|
|4p|

14. Matemática Básica (Ing.) 14
Ejercicios
5. Obtenga la forma estándar de la ecuación de la
parábola con vértice (3; 4) y foco (5; 4).
6. Determine la ecuación estándar de una parábola
que satisface la condición dada: Foco (3; 4),
directriz y = 1.
7. Pruebe que la gráfica de la ecuación es una
parábola y obtenga su vértice, foco y directriz
y2
– 2y + 4x - 12 = 0

15. Matemática Básica (Ing.) 15
Modelación
En las líneas laterales de cada juego de fútbol
transmitido por TV, la cadena CMD (Cable Mágico
Deportes) utiliza un reflector parabólico con un
micrófono en el foco del reflector para captar las
conversaciones entre los jugadores en el campo.
Si el reflector parabólico es de 3 pies de ancho
y un pie de profundidad, ¿dónde se debería
colocar el micrófono?
V(0, 0)
(1,5; 1)
x
y
(-1,5; 1)
F(0, p)

16. Matemática Básica (Ing.) 16
Los alumnos deben revisar los ejercicios del libro
texto guía.
Ejercicios: 6, 18, 20, 22, 30,
34 y 36 de la página 641.
Importante