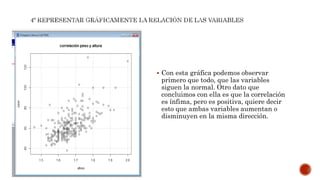
El documento describe los pasos para realizar una correlación entre las variables de peso y altura. Explica que ambas variables deben ser cuantitativas y seguir una distribución normal, lo cual se comprueba con la prueba de Shapiro. Luego, como siguen una distribución normal, se utiliza la prueba de correlación de Pearson, la cual arroja un valor p muy pequeño, indicando que la relación entre peso y altura es casi nula.

1. Estadística
Ana Belén García Martín

2.  Para hacer una correlación es necesario que ambas variables sean cuantitativas,
en este caso hemos elegido el peso y la altura. Le aplicamos por separado el test de
shapiro para comprobar que siguen o no una distribución normal.
 Con los resultados obtenidos de p valor
podemos decir que ambas siguen una distribucion normal

3.  Como hemos comprobado con el test de shapiro, ambas variables siguen una
distribución normal por ello utilizaremos el test de correlación de Pearson, si una
siguiera la normal y la otra no, utilizaríamos rho sperman
 cuando ya tenemos los resultados del test aplicado, nos volvemos a centrar en el p
valor, que debe oscilar entre -1 y 1, sabiendo que si es 0, no hay ninguna
correlación entre ambas. En este caso es muy pequeña y por eso decimos que la
relación es casi nula, porque además no está dentro del intervalo de confianza que
nosotros mismos hemos establecido para acertar en un 95% de los casos

4.  Con esta gráfica podemos observar
primero que todo, que las variables
siguen la normal. Otro dato que
concluimos con ella es que la correlación
es ínfima, pero es positiva, quiere decir
esto que ambas variables aumentan o
disminuyen en la misma dirección.