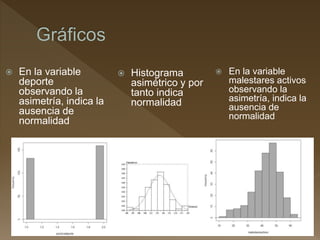
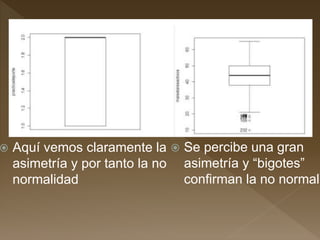
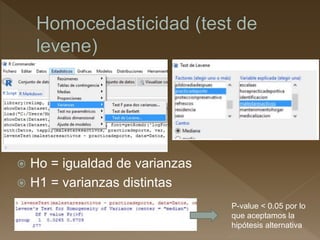
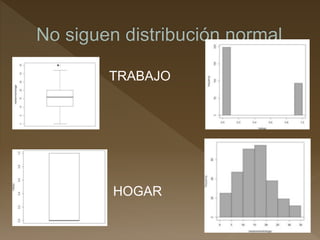
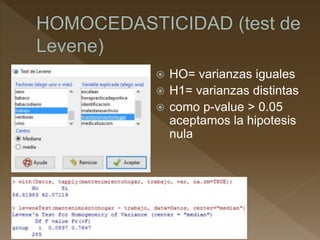
Este documento resume los pasos para determinar si existe una relación entre una variable cuantitativa y cualitativa. Revisa la normalidad y homocedasticidad de las variables a través de pruebas como Shapiro-Wilk y Levene. Luego aplica pruebas no paramétricas como Wilcoxon para determinar si existe relación entre las variables analizadas.

2.  Determina si existe relación entre una
variable cuantitativa y una variable
cualitativa

3.  Homocedasticidad o igualdad de varianzas (
test de levene)
 Normalidad
 N muestral > 30

4.  Variable: practica
deporte
 Ho= normalidad
 H1= no normal
 Con un p-value < 0.05
se rechaza la hipotesis
nula. No sigue una
distribucion normal
 Variable: malestares
activos
 Ho= normalidad
 H1= no normal
 Con un p-value < 0.05 se
rechaza la hipótesis nula
y no sigue una
distribución normal

6.  En la variable
deporte
observando la
asimetría, indica la
ausencia de
normalidad
 Histograma
asimétrico y por
tanto indica
normalidad
 En la variable
malestares activos
observando la
asimetría, indica la
ausencia de
normalidad

8.  Aquí vemos claramente la
asimetría y por tanto la no
normalidad
 Se percibe una gran
asimetría y “bigotes”
confirman la no normali

9.  Ho = igualdad de varianzas
 H1 = varianzas distintas
P-value < 0.05 por lo
que aceptamos la
hipótesis alternativa

10.  Estadisticos test no parametrico
 test de wilconxon para dos muestras
y elegimos nuestras dos variables : nuestra
p-value > 0.05 aceptamos la hipótesis nula

12.  Test de Shapiro-Wilk
 Variable: trabajo
 Ho= normalidad
 H1= no normal
 Con un p-value < 0.05 se
rechaza la hipótesis nula.
No sigue una distribución
normal
 Variable: mantenimiento
del hogar
 Ho= normalidad
 H1= no normal
 Con un p-value < 0.05 se
rechaza la hipótesis nula.
No sigue una distribución
normal

13.  TRABAJO
 HOGAR

14.  HO= varianzas iguales
 H1= varianzas distintas
 como p-value > 0.05
aceptamos la hipotesis
nula

15.  Como p-value > 0.05 aceptamos la hipótesis
nula y afirmamos que no existe relación entre
las variables luego el trabajo no influye en el
mantenimiento del hogar