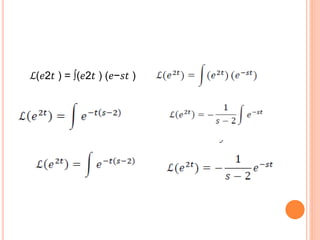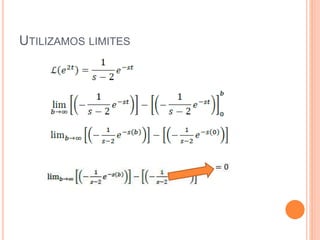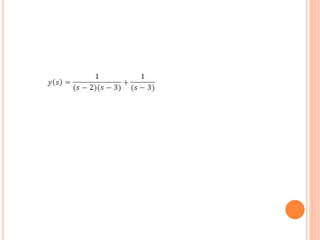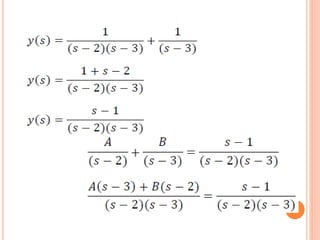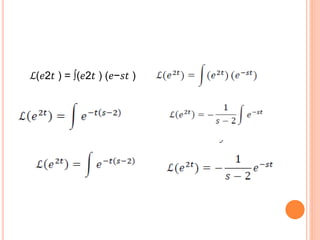
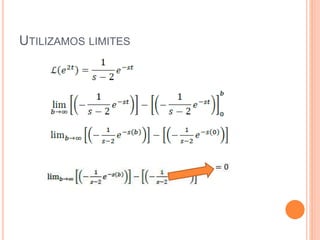
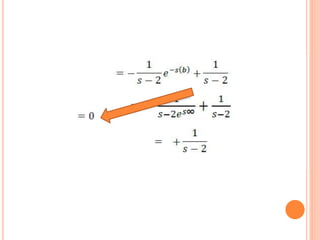
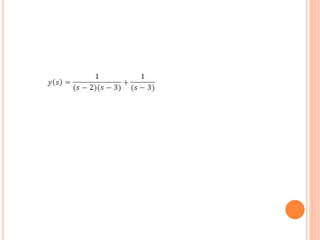
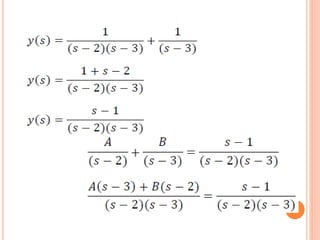
Este documento describe cómo resolver una ecuación diferencial utilizando el método de la transformada de Laplace. Se aplica la transformada de Laplace a ambos lados de la ecuación diferencial y(t) - 3y = e^2t con la condición inicial y'(0) = 1. Esto resulta en una solución algebraica para y en términos de s. Luego, se asignan valores convenientes para los parámetros y se aplica la antitransformada de Laplace para obtener la solución cuando t = 0.

2.  En la siguiente presentación resolveremos A
ecuación diferencial utilizando el método de la
transformada de Laplace para la solucion
emplearemos las fracciones parciales asi como la
anti transformada de Laplace.

3. A continuacion la ecuacion diferencial a resolver
𝑦′ − 3𝑦 = 𝑒2𝑡
Por lo tanto comenzaremos con la condición de
𝑦′ (0) = 1 y y’ (0)= 1

4. Entonces aplicamos la transformada en ambos
términos de la ecuacion que tenemos
ℒ(𝑒2𝑡 ) = ∫(𝑒2𝑡 ) (𝑒−𝑠𝑡 )

5. ℒ(𝑒2𝑡 ) = ∫(𝑒2𝑡 ) (𝑒−𝑠𝑡 )

6. NOS QUEDA DETERMINADA COMO
Y DESPUES LA RESOLVEMOS POR PARTES

7. UTILIZAMOS LIMITES

9. SOLUCION ALGEBRAICA
2
1
)(3)0()(


s
syyssy
Se sutituye con l a
condicion inicial y esta
es la solucion
algebraica para y

12. SE ASIGNAN LOS VALORES QUE MAS NOS PUEDAN
AYUDAR LOS CONVENIENTES
AL OBTENER LOS VALORES DE A Y B COMO VALORES
CONVENIENTES APLICAMOS LA ANTITRANSFORMADA

13. APLICANDO LA ANTITRANSFORMADA
LA SOLUCION CUANDO ES 𝑦(0) = 1

14. PARA LA ANTITRANSFORMADA SE USA LAS
TABLAS DE LA TRANSFORMADA Y
ANTITRANSFORMADA SEGÚN SEA EL CASO