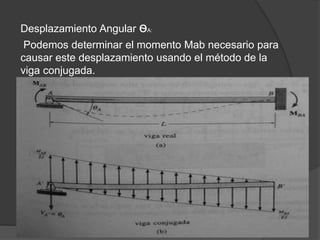
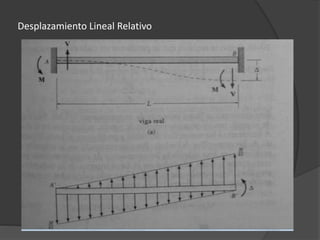
El documento resume el método de pendiente-deflexión para el análisis estructural. 1) El método fue desarrollado originalmente por Manderla y Mohr en 1915 y perfeccionado por George A. Maney para analizar vigas y marcos indeterminados. 2) Calcula los momentos flexionantes restringiendo las deformaciones y corrigiendo desequilibrios mediante rotaciones y desplazamientos en los nudos. 3) Deriva ecuaciones que relacionan los momentos en los extremos de los miembros con los desplazamientos en los extremos y las c

1. ANÁLISIS ESTRUCTURAL III
Paola Sánchez
José R. Valdés
Gredhell Ledezma
Danilo Espinosa
Sibelis Santamaría

2. INTRODUCCION
Acontinuacion se detallara el método pendiente
deflexión el cual requiere primero satisfacer las
ecuaciones de equilibrio de la estructura.
También se deducirán las ecuaciones del método
pendiente-deflexión utilizando el análisis de vigas
conjugadas y teorema de superposición.

3. OBJETIVOS
1. Estudiar brevemente las ideas básicas del análisis de estructuras
mediante el método de los Desplazamientos.
2. Entender el Concepto «Grado de Libertad» y su importancia en el
Análisis de las estructuras utilizando este método.
3. Desarrollar las Ecuaciones Generales del Método Pendiente –
Desviación ó Pendiente – Deflexión.

4. RESEÑA HISTORICA
El método Pendiente – Desviación fue desarrollado por
Heinrich Manderla y Otto Mohr con el fin de estudiar los
esfuerzos Secundarios en Armaduras.
Mas tarde en 1915, George A. Maney desarrollo una
versión perfeccionada del método y la aplico al análisis de
vigas y marcos indeterminados.

5.  El método de pendiente deflexión fue desarrollado por George A. Maney en
la Universidad de Minnesota en 1915. Su trabajo fue una continuación e
interpretación de las investigaciones realizadas por Manderla y Mohr con el
fin de estudiar los esfuerzos secundarios en armaduras.
 Este método es útil por varias razones:
1. Su estudio sirve de base para entender el método de Cross.
2. Para algunas estructuras no muy complejas resulta de fácil aplicación.
3. Es un caso especial del enfoque general del método de las rigideces que
proporciona una buena introducción a la formulación matricial.
4. Hay una buena interpretación de las deformadas de las estructuras al
determinar las pendientes y deflexiones.

6. ENFOQUE DEL METODO
 El método pendiente deflexión se basa
en calcular los momentos flexionantes
de una estructura en la que se
restringen las deformaciones y en
corregir los desequilibrios resultantes
imponiendo rotaciones y
desplazamientos lineales en los nudos
de la estructura.

7. Grados De Libertad
Cuando se carga una estructura, puntos
específicos de ella, llamados Nodos, sufrirán
desplazamientos. A esos desplazamientos se
les llama grados de libertad de la estructura;
en el método los grados de libertad son
importantes especificar esos grados de
libertad, ya que con ellos se conocen las
incógnitas cuando se aplica el método.

8. Grados de Libertad

9. DEDUCCION DE LAS
ECUACIONES
 Para desarrollar la ecuación de pendiente-
deflexion que relaciona los momentos en los
extremos de los miembros con los
desplazamientos en sus extremos y las
cargas aplicadas. Se analiza el claro AB de
la figura siguiente:

10. Desplazamiento Angular ѳA:
Podemos determinar el momento Mab necesario para
causar este desplazamiento usando el método de la
viga conjugada.

11. Aplicando una sumatoria de Momentos en
B´y en A´ se llega obtener de la viga
conjugada los Momentos: Mab y Mba

12. Desplazamiento Angular ѳB
 Se hace de la misma manera que se hizo para el
desplazamiento angular en a, con la diferencia que ahora el
extremo empotrado será el nodo «A».

13. Desplazamiento Lineal Relativo

14. Al igual que antes el momento M puede
relacionarse con el desplazamiento Δ,
usando el método de la viga conjugada, en
este caso la VC se encuentra libre en ambos
puntos. Si se hace una sumatoria de
momentos en el punto B´ se obtiene que:

15. Ecuaciones de Pendiente - Deflexión
Si se suman los momentos de extremo
debidos a cada desplazamiento y a la
carga los momentos finales pueden
escribirse como:

16.  Como estas dos ecuaciones son similares
pueden escribirse como una sola Ecuación:
Mn = Momento interno en el extremo cercano del claro
E, K = Modulo de Elasticidad del material y rigidez del claro en
donde k = I/L
Ѳn, Ѳf = Pendientes de los extremos cercano y alejado en los
soportes.
Ѱ = Rotacion de la cuerda del claro debido a un
desplazamiento lienal ѱ= Δ/L
FEMn = Momento de empotramiento en el soporte Cercano.

17.  Claro con Extremo Articulado

18. Si el desplazamiento angular en B es cero,
en este soporte no tiene que ser
determinado por lo tanto podemos modificar
la ecuación de modo que tenga que usarse
una vez.
Aquí el FEMb=0, multiplicamos la 1era
ecuación por 2 y le restamos la segunda.

19.  GRACIAS POR SU ATENCION