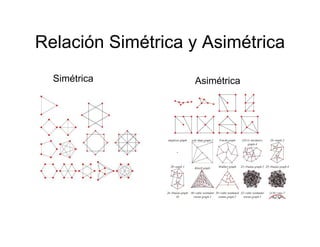
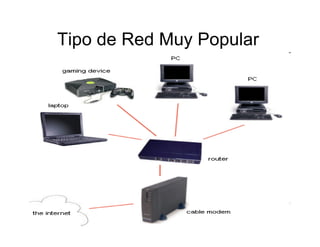
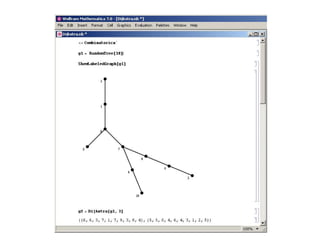
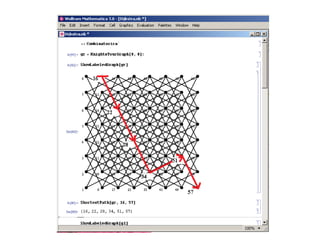
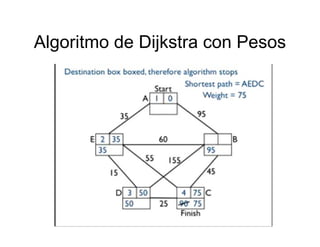
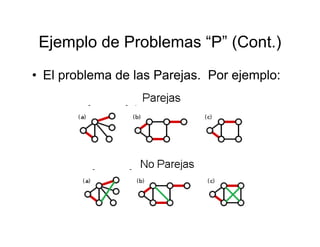
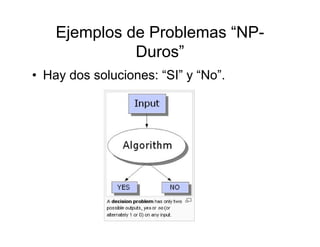
La teoría de redes se deriva de la ciencia de computadoras, ciencia de redes y teoría de grafos. Estudia grafos que representan relaciones simétricas y asimétricas entre objetos discretos. Algunos ejemplos populares de redes son la World Wide Web, redes regulatorias de genes y redes sociales. Algoritmos como el de Dijkstra se usan para encontrar el camino más corto en un grafo y ayudan a resolver problemas de optimización. Los problemas que se pueden resolver en tiempo polinómico (P) incluyen encontrar

1. Teoría De Redes
Por: José L. Rodríguez Rivera
Clase de Maestría: Investigación
De Operaciones

2. ¿Que Es La Teoría De Redes?
• Derivada de la Ciencia de Computadoras,
Ciencia de Redes y Teoría de Grafos.
• Se enfatiza en el estudio de grafos
representando su forma simétrica y su
forma asimétrica entre objetos discretos.

3. Relación Simétrica y Asimétrica
Simétrica Asimétrica

4. Tipo de Red Muy Popular

5. Algunos Ejemplos de Redes
• World Wide Web
• Redes Regulatoria de Genes
• Redes Metabólicas
• Redes Sociales
• Redes Epistemología

6. Algoritmo de Dijkstra
• Fue inventado por Edward F. Moore en
1957.
• Se utiliza para encontrar el camino más
corto aplicable a un grafo y a un árbol.
• Generalmente se utiliza como problema
de optimización como: llegar de un lugar
a otro en el menor tiempo posible con un
costo eficiente.

9. Algoritmo de Dijkstra con Pesos

10. Problemas Solubles en Tiempo
Polinómico (P)
• Son problemas matemáticos, algoritmos que
pueden ser resueltos en un tiempo módico,
razonable y costo eficiente.
• Ejemplos de estos problemas (P), el tiempo que
toma un cartero en recorrer n casas, también
relacionado con el camino mas corto y el
algoritmo de Dijkstra.
• Dentro de los tiempos polinómicos, podemos
distinguir los logarítmicos (log(n)), los lineales
(n), los cuadráticos (n^2), cúbicos (n^3), etc.
• Funciones con 2^n, no están en tiempo
polinómico, porque son números gigantescos.

11. Ejemplo de Problemas “P”
• La versión de decisiones en programación
linear, por ejemplo el uso de matrices en
programación en paralelo.
• También en calcular el divisor común mas
grande; por ejemplo: el 48 tiene múltiplos de 2 x
2 x 2 x 2 x 3 y el 180 tiene múltiplos de 2 x 2 x 3
x 3 x 5, según el diagrama de Ven el 48 y el 180
tienen en común el 2 x 2 x 3 que es igual 12
como el divisor común mas grande.

12. Ejemplo de Problemas “P” (Cont.)
• El problema de las Parejas. Por ejemplo:

13. Problemas “NP-Completos”
• Tarda mas tiempo que los problemas “P”, o no
tienen solución.
• Si se tiene una solución para un problema de
tipo “NP-Completos” debería tener solución
entonces todos los problemas “NP-Completos”
en un tiempo módico.
• Stephen Cook en 1971 demostró que el
Problema de satisfacibilidad booleana era del
tipo “NP-Completos”.

14. Ejemplos de Problemas “NP-
Completos”
• En Teoría de Grafos es difícil demostrar que
en existe un ciclo en los ciclos Hamiltonianos.
• En el Viaje del Vendedor es difícil demostrar el
lugar mas corto por donde viajar dependiendo
de sus pesos y sus ciclos hamiltonianos.
• El camino mas corto del árbol: también es
difícil demostrar la forma mas eficiente de
completar los vértices dependiendo de sus
pesos.

15. Problemas “NP-Duros”
• Son los problemas mas difícil de resolver,
se necesitarían cálculos extremos para
resolverlos.
• Pueden ser resueltos efectivamente solo
por supercomputadoras.
• Entre estos están los problemas de
decisión, de búsqueda y optimización

16. Ejemplos de Problemas “NP-
Duros”
• Hay dos soluciones: “SI” y “No”.

17. Ejemplos de Problemas “NP-
Duros” (Cont).
• Problemas de búsquedas:
1)Buscan exhaustivamente datos hasta que lo
encuentran.
2)Actualmente siguen renovando nuevos
algoritmos para una mejor búsqueda.
3)El algoritmo de búsqueda Breadth-first es un
algoritmo eficiente dependiendo del tipo de
búsqueda. Breadth-first tiene su parecido al
algoritmo de Dijkstra en buscar la forma más
rápida en resolver un problema o algoritmo.

18. Relación entre P,NP-Completo y
NP-Duros
• Problemas P son problemas que tienen solución
en tiempo módico, los Problemas NP-Completo
son problemas que son difícil de resolver pero
pueden ser resueltos como los P. Los
problemas NP-Duros son también NP pero
mucho mas complicado de resolver. Si P=NP,
entonces todos los algoritmos tienen solución.
Si P no es igual NP, entonces caemos en el
problema que existe en la actualidad, no todo
algoritmo es programable.

19. Bibliografías
• http://en.wikipedia.org/wiki/Main_Page
• http://es.wikipedia.org/wiki/Wikipedia:Porta
da
• http://au.youtube.com/results?search=relat
ed&search_query=%20computer%20scien
ce%20graphs&v=8Ls1RqHCOPw
• http://www.math.ohiou.edu/~just/bioinfo05/
supplements/Lect_NP.ppt.
• http://users.iems.northwestern.edu/~giden/